兵棋推演技术在各个作战领域都有非常广泛的应用场景. 通过兵棋推演系统, 可以推测在一些应用场景下, 采取不同的行动而产生的后续作战结果, 根据结果的好坏, 对所作决策进行适当调整[1]. 这种调整过程异常繁琐, 当场景环境复杂多变时, 所考虑的决策数量巨大, 导致推演需要消耗大量的人力物力, 最终决策结果一定程度上也无法满足作战要求.
深度强化学习算法作为一种常见的智能探索算法, 已经开始应用于仿真推演领域. 深度强化学习算法应用于仿真推演智能化具有两大优势.
(1)利用深度学习算法(DL)对战场感知数据进行充分的分析处理, 可以帮助作战人员快速判断当前战况.
(2)在强化学习算法(RL)的帮助下, 作战人员能够更有效的进行决策, 对战争结果产生重要的影响.
利用深度强化学习算法探究作战最优策略逐渐成为兵棋推演智能化的一个重要研究热点.
邓克波等[2]在强化学习的基础上提出了面向作战方案分析的计算机兵棋推演系统. 殷宇维等[3]改进了DDPG算法并将其应用到空战决策中, 使决策过程更加平稳可控. 王兴众等[4]提出一种基于SAC算法的仿真推演决策技术, 提高了决策结果的获胜率.
现有基于DRL算法的众多决策模型, 其训练时间过长, 算力开销过大, 无法满足作战任务的实时性需求.
在深度强化学习中, 神经网络的复杂性是影响训练速度的重要因素之一, 网络中众多的参数会增加模型的训练负担, 耗费大量的训练时间. 针对此问题, Li等[5]提出了将BNN应用在DQN算法中, 并取得了较好的加速效果, 虽然BNN减少模型训练的计算量, 但是对特征的提取能力降低, 导致在一些训练中, 模型的最终效果不理想. 在off-policy强化学习算法中, 经验回访缓冲池用来保存经验样本数据, 然后随机采样历史数据更新深度神经网络的参数, 采用合适的采样策略对缓冲池内的数据集进行采样, 可以加速训练的过程, Schaul等[6]提出了优先级经验回放的思想, 将经验数据的TD-error作为采样的优先级对数据进行优先级采样, 加快了DQN模型的收敛速度. Hou等[7]又将这种思想从离散领域的DQN算法扩展到了连续领域的DDPG算法, 并认为这种方法能够明显缩短模型的训练时间, 增强模型训练时的可靠性. 张建行等[8]提出了一种基于情节的双缓冲池结构, 提高经验采样的有效性.
尽管这些研究在一定程度上提高了模型训练效率, 但是训练过程中的操作会使训练中间信息丢失, 导致最终模型精度下降, 训练结果无法满足实际作战需求. 针对此问题, 本文提出一种基于轻量级深度确定性策略梯度(BN-DDPG)算法的智能推演方法, 使用混合BNN网络作为DDPG的actor网络作为训练加速的方法, 在减少计算量的基础上保证网络的特征提取能力; 同时采用基于环境相似度的优先提取方法, 对缓冲池中的历史经验数据进行采样, 加快训练时的收敛速度. 最后, 使用自主研制的仿真推演平台进行实例验证, 以轰炸机轰炸目标机场为任务想定, 验证提出算法的有效性.
1 相关技术 1.1 DDPG经验回放缓冲机制DDPG算法[9]是DQN算法的扩展版本, 在连续控制领域有很好的表现[10], 采用目标网络和经验回放的技巧, 基于actor-critic体系结构, actor网络和critic网络相互独立.
经验回放缓冲池[9]是DDPG中的信息库可以将模型探索环境得到的经验数据储存起来, 然后通过采样这些数据对网络模型进行训练, 最终过去的experience和目前experience混合, 从而减少了信息相关性.
DDPG算法作为一个off-policy离线学习法, 能同时对当前和过去的经验数据进行学习, 在学习过程中可以随机增加之前的经验数据, 这会使神经网络更加高效. 经验池的出现, 成功解决了相关性及非静态分布问题, 每个time step下agent与环境交互得到的转移经验数据(st, at, rt, st+1), 然后保存到回放的记忆网络上, 可以按照一定的方式提取这些数据用于训练, 打乱数据之间的相关关系[11].
1.2 二值神经网络二值神经网络(BNN)[12]把权值W和隐藏层激活值二值化为1或者−1. 通过这种操作, 使模型的参数占用更小的存储空间, 存储器能耗在理论方面上减少为原来的1/32, 从float32到1 bit; 同时利用位操作来取代了乘加运算, 从而大大降低了计算成本.
关于怎么把浮点型的神经网络进行二值化, 一般给出两种方法.
(1)基于符号变量sign的定义方法, 大于0就为+1, 小于0则为−1, 如式(1):
| xb=sign(x)={+1,x⩾0−1,x<0 | (1) |
(2)第2种是随机二值化方法:
| xb={+1,with probability ρ=σ(x)−1,with probability1−ρ | (2) |
BNN计算梯度的方式, 是通过使用二值化的权值和激活值, 这里的梯度必须是高精度的实际值, SGD在计算梯度的时候, 量级一般比较小, 再加之计算的中间过程会有服从正态分布的噪声, 所以如果算子没有较高的精度会影响模型最后的实际效果. 另外, 为帮助避免过拟合现象的发生[13], 可以在计算梯度的时候, 给二值化后的权值和激活值添加噪声.
2 BN-DDPG模型BN-DDPG模型将DDPG算法作为主体框架, 将get-actor当前网络设计为混合BNN网络, 缓冲池结构设计为基于环境相似度的双缓冲池结构.
2.1 BNN模块传统的DRL算法中, 不管是在单智能体系统或是多智能体系统, 都是在强化学习算法的基础上, 通过神经网络拟合Q函数, 利用深度学习网络的特征提取能力, 将Q值函数尽可能优化, 大部分使用的是DNN、CNN或者LSTM等网络, 虽然这些网络虽然具有强大的学习能力, 但也要更根据研究目的或应用场景合理设计网络结构, 例如卷积核大小和网络深度等, 才能发挥出更有效的作用. 对于CNN[14]来讲, 单个卷积层的时间复杂度为:
| Time:O(M2×K2×Cin×Cout) |
其中, M表示卷积核输出的特征图的边长, K则表示各个卷积核的边长, Cin表示各个卷积核的通道数. Cout表示在当前卷积层卷积核的总个数.
卷积神经网络整体的时间复杂度为:
| Time:O(D∑l=1M2l×K2l×Cl−1×Cl) |
其中, D表示在神经网络中的卷积层数, 也就是网络的深度. CNN网络的整体复杂度为各个卷积层的复杂度的累加之和. 如此的复杂度通常是不适用于嵌入式电子设备等小型设备, 这限制了深度强化学习在一些急迫任务中应用真实世界.
直观来讲, 减少复杂度最容易想到的方式是减少的网络的深度和宽度. 不过这种操作会带来一个很大的缺点: 容易出现欠拟合. 当我们直接对网络的基础参数进行消减后, 网络的性能一定会在不同程度上受到影响, 从导致网络不能很好拟合函数的情况发生. Li等[5]将BNN使用到了DDPG中并完成了对星际争霸游戏的训练加速, 其使用的神经网络层全部是二值神经网络层如图1所示, 这在提取特征时虽然会大幅度减少计算量, 但特征提取能力下降的过快, 我们重新设计使用轻量级的神经网络BNN来拟合DDPG中的actor网络, 卷积层使用二值网络和全精度网络交替提取特征, 在尽可能保留了神经网络强大的特征提取能力的同时, 将其复杂度极大简化.
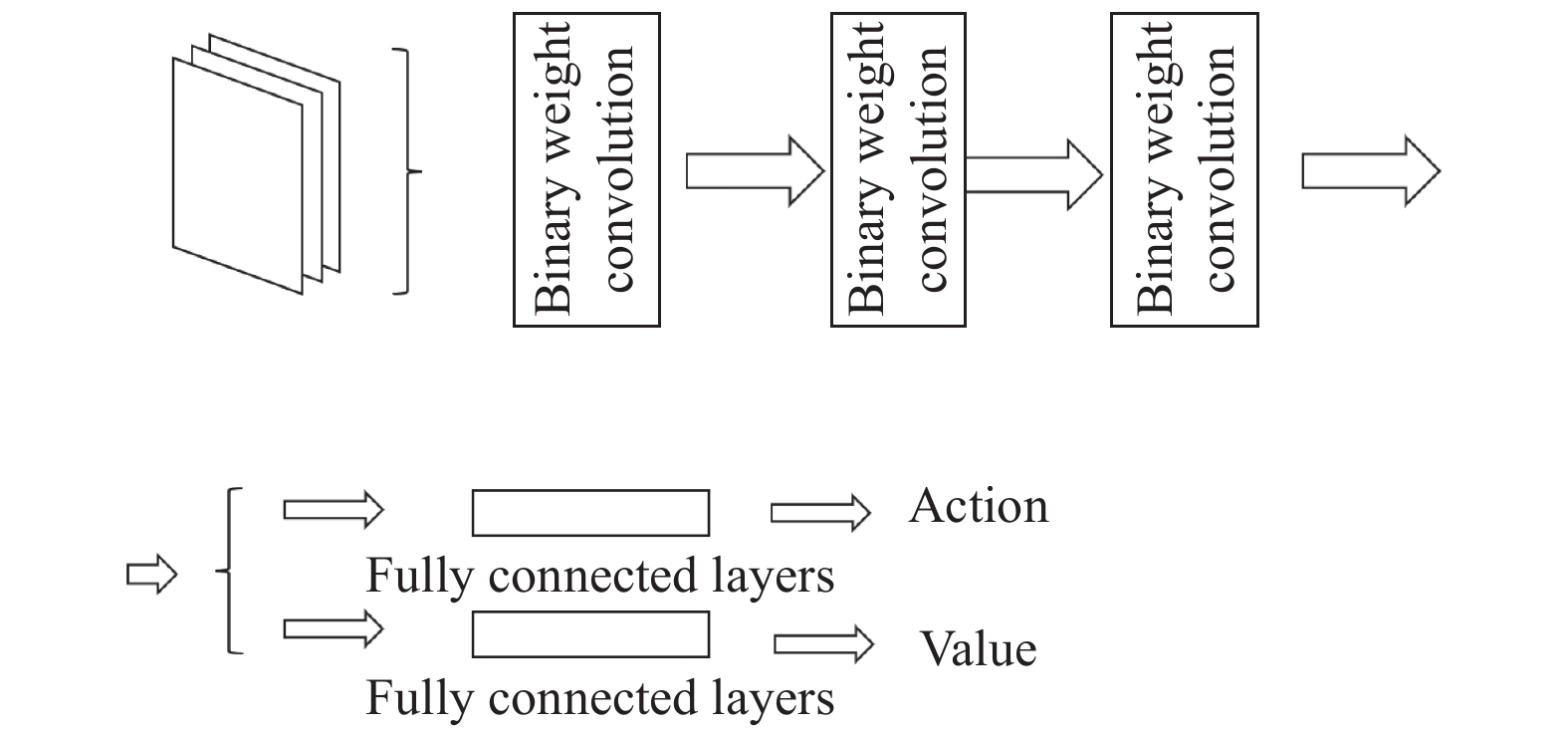
|
图 1 卷积层全部二值化的BNN网络 |
对于混合BNN网络的设计, 采用3层神经隐藏层的结构, 为了保证网络的特征提取质量, 第1层使用全精度网络层, 第2、3层采用二值网络层, 降低计算量以及复杂度, 混合BNN具体网络结构见图2.

|
图 2 卷积层二值化和全精度的混合BNN网络 |
2.2 双缓冲池模块设计
传统DDPG算法[9]中, 经验回放采用单缓冲池结构, 模型会将采集得到的数据不加以区分全部放入单个缓冲池当中, 这样做操作简单, 但是忽略了不同的历史数据对模型的训练所起到的效果并不相同, 针对这一问题, Schaul等[6]提出了缓冲池优先级经验回放机制, 并应用在DQN中, 这种方法可以使重要的经验被回放的概率变大, 从而使学习更有效率, 并在一些实验中取得了较好的结果. 具体的该机制使用TD-error来表示优先级的大小, 当前Q值与目标Q值两者之间差值的大小, 计算方式如式(3), TD-error的值越高, 就反映了预测效果不好, 还需要进一步提升, 此样本数据就越值得被学习, 也就是该样本数据的优先级p越高.
| δ=Rt+γtmaxQ(St,a)−Q(St−1+At−1) | (3) |
其中, Rt是前t步所获得的累计回报, γ是折扣率. 当reward有噪声时, TD-error来估计优先级不稳定, Schaul等[6]又补充了greedy TD-error prioritization算法, 在经验池中存储了每轮交互最后的TD-error, 用这种方式, 将会以TD-error的绝对值最大的进行回放. 如果当一个新的transition到来时, 不知道它的TD-error, 那么就把这个transition的TD-error值设置为最大, 这样可以保证所有的经验都会被至少回放一次.
为了提高经验回放机制在DDPG中的效率, 张建行等[8]提出一种基于情节经验回放的深度确定性策略梯度方法(EEP-DDPG), 将样本数据以情节为单元进行保存, 再按照情节回报的情况通过两个缓冲池分类存放. 最后, 网络训练阶段着重选择累积回报较大的数据进行采样, 以提高训练效率.
以上对缓冲池的改进主要思路都集中在使用较多的回报值较大的经验数据来提升经验回放的效率. 本文从每条经验数据的环境状态出发, 设计优先提取机制的双缓冲池结构.
在挑选经验数据时, 与当前训练的环境状态相似的经验数据有更大的可选取性和参考价值, 根据环境状态的相似程度, 将不同的经验数据存放在不同的数据缓冲池中. 具体的, 新增超参数distance, 作为经验数据状态相似程度的区分, 在开始收集数据时, 如果两条经验数据状态差的绝对值小于distance, 则认为两条经验数据环境相似, 放入相同的经验池中, 否则放入不同的经验池中. 两个经验池分别维护一个变量xi, 记录第i个经验池内存放数据状态的平均值, 计算方式如式(4):
| xi=si1+si2+si3+⋯+sinn | (4) |
其中, i表示第i个经验回放池, n为该经验池目前保存的经验数据的个数. 在经验回放阶段, 使用此时的环境状态与每个经验池的平均状态作比较, 在差值更小的经验池内, 取出所需数据总数的70%, 在另一个经验池内取出所需数据总数的30%, 并把这一步所获得的经验数据加入到差值更小的经验池内, 并更新该回放池的x, 更新方式如式(5):
| xt+1i=n×x+st+1n+1 | (5) |
其中, x是第i个经验回放缓冲池未更新前, 经验回放缓冲池环境状态的平均值, s(t+1)为t+1时刻智能体的环境状态. 利用相似环境下数据的高参考性, 提升经验回放的效率. 具体操作如图3.
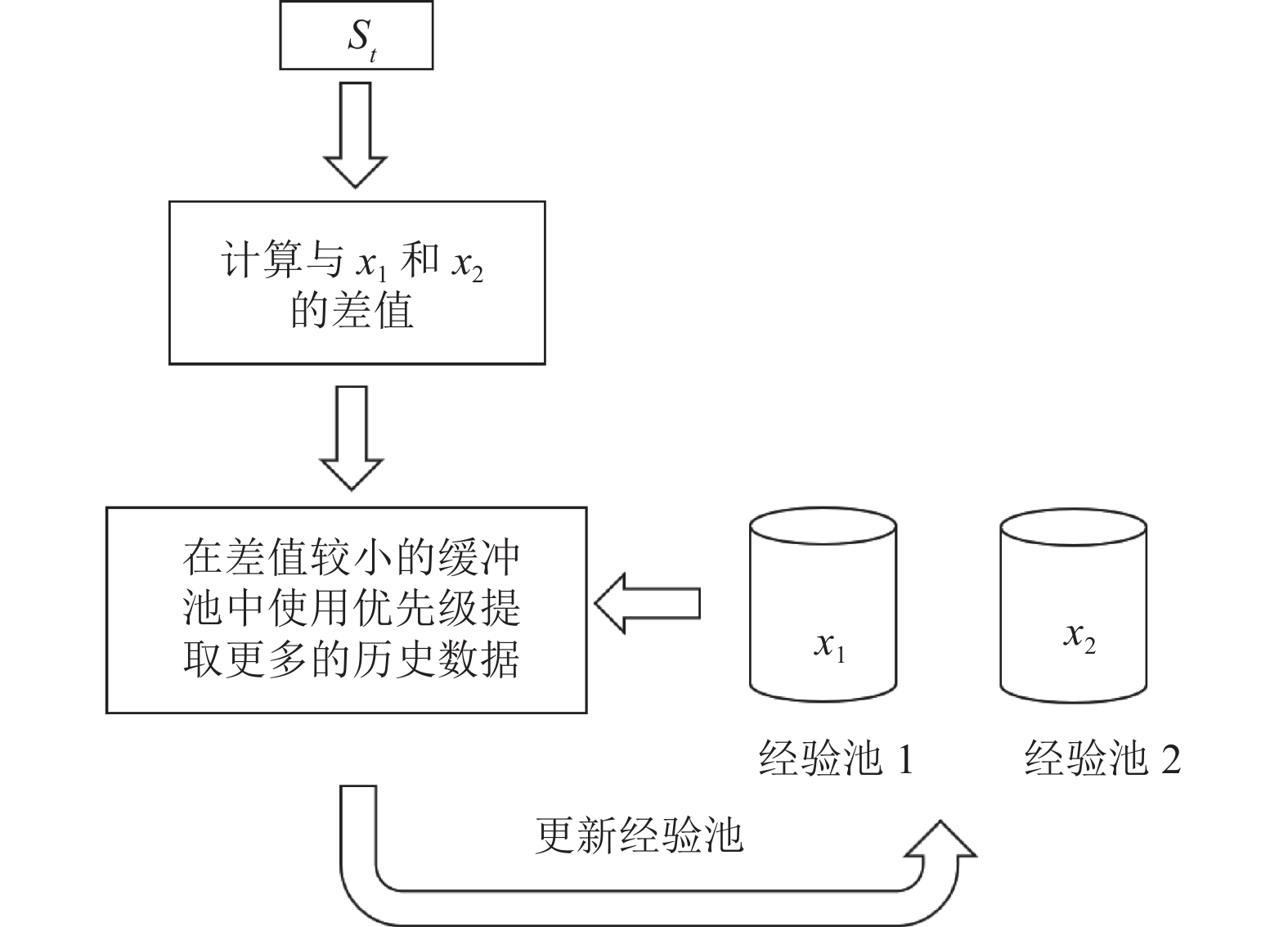
|
图 3 基于环境状态的双经验池结构 |
2.3 BN-DDPG算法
BN-DDPG算法整体基于DDPG算法, 因此两者流程类似. 算法输入为: actor当前网络, actor-target网络, critic当前网络, critic-target网络, 参数分别为θ,θ', ω, ω', 折扣因子γ, 软更新系数τ, 批量梯度下降的样本数m, target-Q网络参数的更新频率C, 训练的最大迭代次数T, 环境状态差异值distance; 算法的输出为: 训练后的actor网络参数θ和critic网络参数ω.
算法的具体流程见算法1.
算法1. BN-DDPG算法
1) 随机初始化
2) for i from 1 to T, 进行迭代;
a) 初始化
b) 在actor当前网络基于状态
c) 执行步骤b)中得到的动作A, 在与环境交互后获得新状态
d) 如果D1、D2均没有数据, 那么将四元组{
e)
f) 根据相似原则, 从相似度高的缓冲池使用优先级策略选取N1个数据集, 从另一个缓冲池选取N2个数据集, N1>N2;
g) 计算当前目标Q值;
h) 更新critic当前网络的所有参数
i)更新actor当前网络的所有参数
j) 更新critic-target和actor-target参数;
k) 对S'进行判断, 如果S'满足中止条件, 本轮迭代完毕, 如果S'不满足终止条件, 则跳转到步骤b);
3 仿真推演实例分析 3.1 推演任务想定设计搭载空对地导弹轰炸机对目标进行战略轰炸推演想定的场景如下: 蓝方部队在某地有威胁红方的军用机场, 蓝方在机场周围部署有拦截导弹车对空中威胁进行打击, 并有侦察机监视一定区域内的敌方威胁, 一旦侦察机发现威胁, 导弹车会发射导弹对目标进行拦截. 红方派遣轰炸机前往搜寻蓝方的机场, 并对其进行轰炸. 红方轰炸机要做的就是尽可能避开蓝方侦察机的侦察, 并以最快的速度完成轰炸任务. 红蓝双方的设定的兵力编成如表1和表2所示.
| 表 1 红方军队兵力编成 |
| 表 2 蓝方军队兵力编成 |
3.2 红方轰炸机建模
在第3.1节的想定任务下, 对红方轰炸机进行强化学习训练, 通过与环境的不断交互, 不断优化轰炸机的决策策略, 最终完成想定任务. MDP过程以四元组(s , a, s', r)的形式表示, 这里s为红方轰炸机状态空间, a为红方轰炸机的动作决策空间, s'为采取动作之后轰炸机转移到的状态空间,r是此次状态转移所获得的回报.
1)状态空间设置
红方轰炸机返回的态势数据维度较多, 其中执行任务时的最关键因素有5个, 分别是经纬度、海拔、航向以及存货状态, 所以状态空间确定为S=[经度, 纬度, 海拔, 航向, 存活状态]. 如图4所示, 经纬度和海拔可以锁定当前轰炸机的所在位置, 航向α表示红方轰炸机与蓝方目标机场的偏差角度, 存活状态status表示目前飞机是否被击落.
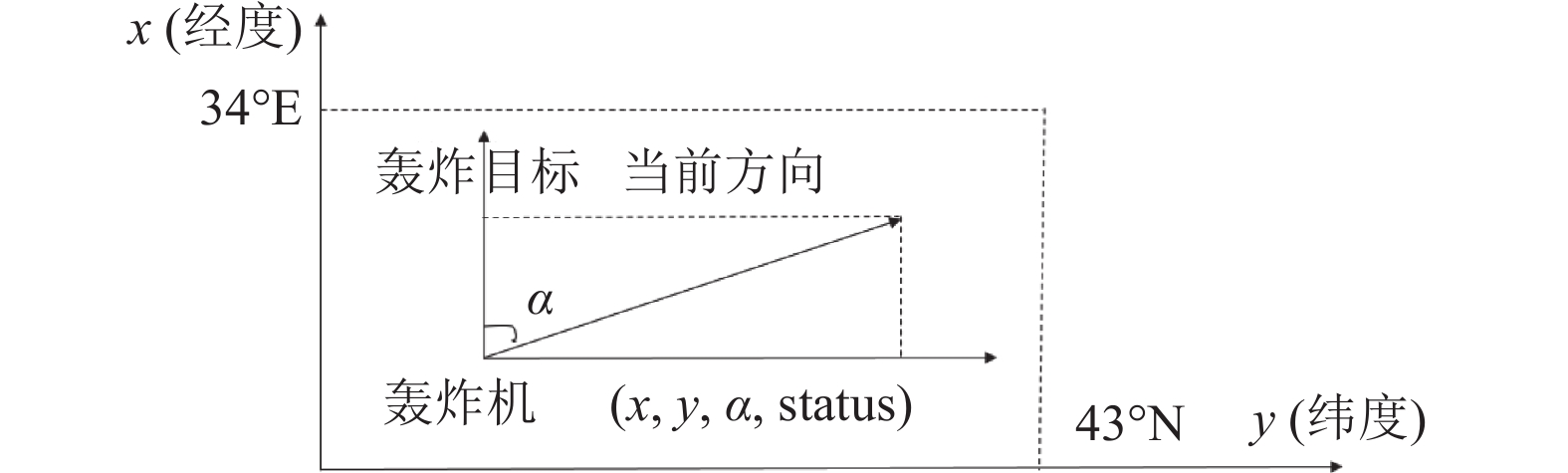
|
图 4 红方轰炸机状态分析 |
2)动作空间设置
红方轰炸机可执行的动作也相对较多, 动作空间选择最能影响任务成败的动作. 在该任务中, 轰炸机的方向即航向角, 决定了轰炸机是否能顺利绕过侦察机, 抵达机场附近执行轰炸任务, 因此选择轰炸机航向角作为动作空间, 即A=[航向].
3)奖励函数设置
回报函数的设置如下: 红方轰炸机朝向目标机场移动, 此次移动如果使得轰炸机更接近机场, 获得正回报, 反之获得负回报. 若轰炸机与机场方向的偏向角在0到180°之间, 获得正回报, 若轰炸机与机场夹角在180° (包含180°)到360°之间, 获得负回报. 若机场进入轰炸机攻击范围, 获得一个较大的正回报. 若轰炸机成功摧毁机场, 获得一个更大的正回报. 若飞机被摧毁(status状态为0), 轰炸机获得一个负回报.
将网络模型推算的动作列表作为推演系统的输入, 并在推演系统中完成执行该动作后各单位状态的改变, 以获得的新状态, 判断红方轰炸机在此动作下所应该获得的回报, 具体计算公式如式(6)所示:
| Rt={+100,轰炸机摧毁机场−80,轰炸机被击落−50,轰炸机飞出指定区域ρ(α,dis,t),其他 | (6) |
其中, dis表示轰炸机与机场在推演开始的原始距离, dist表示t时刻机场距离轰炸机的位置, dist–1表示在t–1时刻, 机场距离轰炸机的位置,
函数
| ρ(α,dis,t)=[(20×sinα)+(dist+dist−1)]dis |
在第3.1节介绍的仿真任务下, 在实验环境中开展仿真推演, 实验的第1部分通过与连续DQN算法进行对比实验BN-DDPG算法的优越性; 实验的第2部分通过消融实验, 验证改进部分对于模型整体的贡献.
4.1 推演结果分析本文的实验环境基于团队开发的智能推演系统. 在轰炸机执行任务的开始阶段, 需要不断试错寻找机场位置并避开侦察机的侦察, 因此开始阶段回报相对较低. 经过不断的迭代, 回报值最终可以趋于平稳. 在不断地学习下, 轰炸机能够不断减少发现机场所用的时间, 最终成功执行任务. BN-DDPG训练时的超参数设置如表3所示.
| 表 3 超参数设置 |
将BN-DDPG算法与连续DQN进行实验对比, 对比结果如图5所示.
训练初期, BN-DDPG和连续DQN的平均回报均上升的较快, 利用连续DQN算法训练智能体, 在经过1 000轮训练后开始收敛, 平均回报值也趋于稳定; 而使用BN-DDPG算法收敛的速度相对更快, 从实验结果中可以看出, BN-DDPG算法在迭代850轮左右就已经趋于稳定, 且BN-DDPG的收敛后的平均回报略大于连续DQN算法. 两种算法模型训练完毕后, 分别对其进行100次的仿真推演实验, 两种算法的获胜概率的比较分析结果如表4所示, 采用连续DQN算法, 红方轰炸机的平均获胜概率是50.5%; 采用BN-DDPG算法, 红方轰炸机获胜概率为58.4%, 提高了8个百分点左右. 图6为DQN算法与BN-DDPG算法收敛轮数对比的箱线图.

|
图 5 BN-DDPG算法与连续DQN算法平均回报对比 |
| 表 4 红方轰炸机获胜概率对比(%) |

|
图 6 BN-DDPG与连续DQN收敛轮数对比 |
4.2 消融实验
为检验BN-DDPG中提出的改进方法的有效性, 同时为分别研究算法中的混合二进制网络和基于环境状态相似度的双缓冲池结构这些改进机制对算法实验效果的影响, 在BN-DDPG算法的基础上分别减去这些机制进行消融对比试验. 消融实验的设置如表5所示, 消融实验结果如图7. 红方轰炸机获胜概率对比如表6, 平均收敛轮数对比如图8所示.
| 表 5 消融对比实验设置 |

|
图 7 消融实验平均回报对比 |
| 表 6 红方轰炸机获胜概率对比(%) |
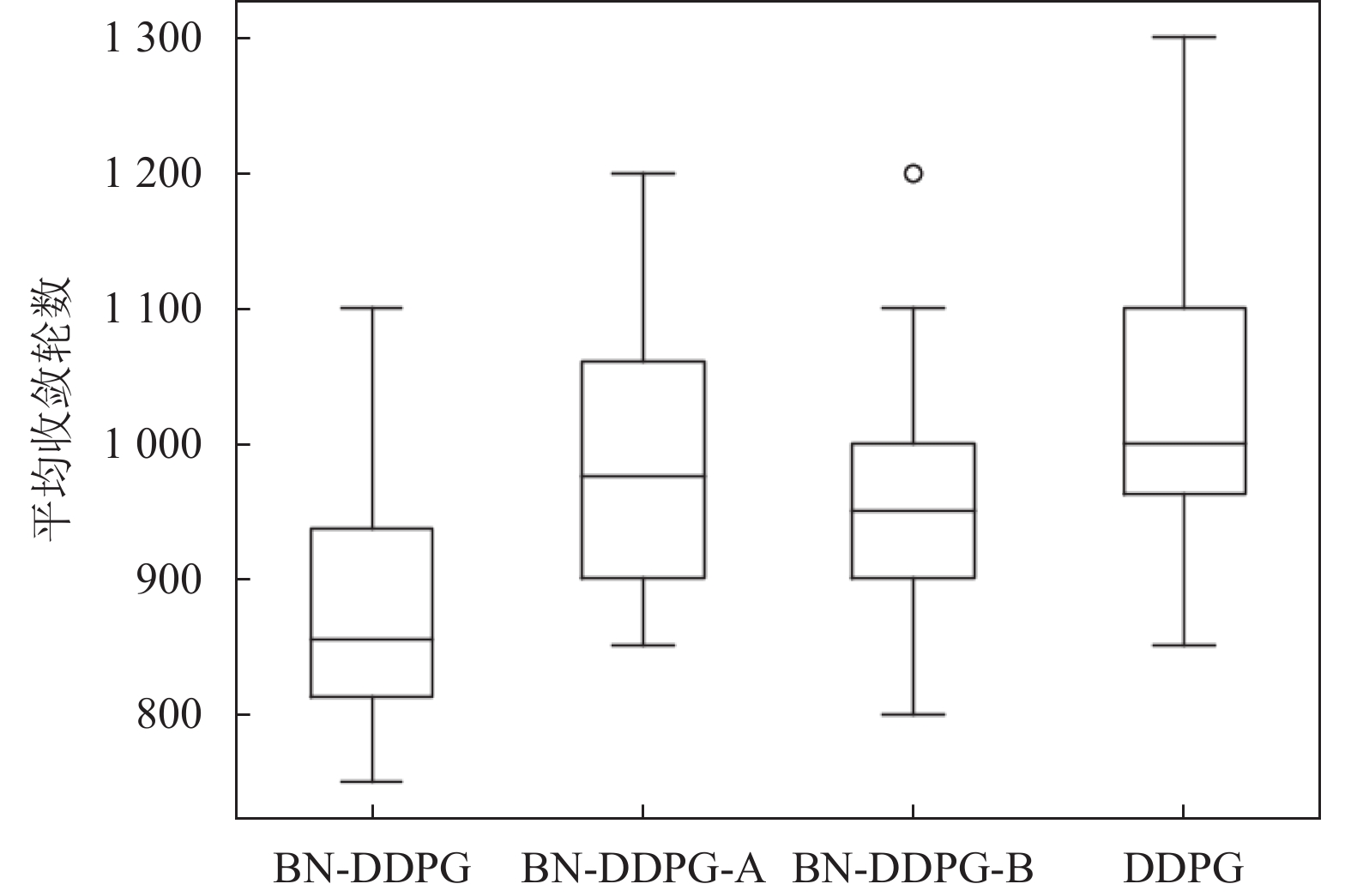
|
图 8 消融实验平均收敛轮数对比 |
实验结果表明, 传统的DDPG算法在该任务中, 训练1 000轮之后基本可以收敛; 分别采用混合二进制神经网络和基于环境状态的双缓冲池结构对DDPG进行优化, 可以在800轮左右稳定收敛; 采用BN-DDPG算法训练该任务时, 在训练到700轮左右, 即可稳定收敛, 并且收敛后的平均回报值明显大于传统DDPG算法, 这也说明了我们所提供的优化方案, 相比于常规DDPG算法不管从有效性还是收敛效率方面, 都有了一定的提高.
5 总结与展望本文在DDPG算法的基础上, 使用混合二进制神经网络和基于环境状体的双缓冲池结构对算法进行优化, 并将其应用在自定义的推演作战任务中. 从实验结果可以看出, 新提出的模型在收敛速度和平均回报上均优于原始模型, 通过消融实验证了模型优化部分的有效性. 在作战任务中, 大部分情况下是作战单元的协同作战, 下一步工作将着重探索将该优化方式应用于多智能体算法, 对推演的协同作战任务策略制定进行优化.
| [1] |
戴勇, 黄杏花. 人工智能在计算机兵棋推演领域的应用. 集成电路应用, 2020, 37(5): 67-69. |
| [2] |
邓克波, 朱晶, 韩素颖, 等. 面向作战方案分析的计算机兵棋推演系统. 指挥信息系统与技术, 2016, 7(5): 73-77. |
| [3] |
殷宇维, 王凡, 吴奎, 等. 基于改进DDPG的空战行为决策方法. 指挥控制与仿真, 2022, 44(1): 97-102. DOI:10.3969/j.issn.1673-3819.2022.01.014 |
| [4] |
王兴众, 王敏, 罗威. 基于SAC算法的作战仿真推演智能决策技术. 中国舰船研究, 2021, 16(6): 99-108. |
| [5] |
Li YF, Fang YC, Akhtar Z. Accelerating deep reinforcement learning model for game strategy. Neurocomputing, 2020, 408: 157-168. DOI:10.1016/j.neucom.2019.06.110 |
| [6] |
Schaul T, Quan J, Antonoglou I, et al. Prioritized experience replay. arXiv:1511.05952, 2015.
|
| [7] |
Hou YN, Liu LF, Wei Q, et al. A novel DDPG method with prioritized experience replay. Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics. Banff: IEEE, 2017. 316–321.
|
| [8] |
张建行, 刘全. 基于情节经验回放的深度确定性策略梯度方法. 计算机科学, 2021, 48(10): 37-43. DOI:10.11896/jsjkx.200900208 |
| [9] |
Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms. Proceedings of the 31st International Conference on Machine Learning. Beijing: ACM, 2014. I–387–I–395.
|
| [10] |
Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. arXiv:1509.02971, 2015.
|
| [11] |
Adam S, Busoniu L, Babuska R. Experience replay for real-time reinforcement learning control. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2012, 42(2): 201-212. |
| [12] |
Courbariaux M, Bengio Y, David JP. BinaryConnect: Training deep neural networks with binary weights during propagations. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: ACM, 2015. 3123–3131.
|
| [13] |
Li ZF, Ni BB, Zhang WJ, et al. Performance guaranteed network acceleration via high-order residual quantization. Proceedings of the IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 2603–2611.
|
| [14] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
 2023, Vol. 32
2023, Vol. 32



