2. 国网信息通信产业集团有限公司, 北京 102200;
3. 上海电力大学 电气工程学院, 上海 201306
2. State Grid Information and Telecommunication Group Co. Ltd., Beijing 102200, China;
3. College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 201306, China
伴随5G通信技术的发展, 移动游戏、图像视频处理和流媒体等服务变得越来越广泛[1]. 用来提供服务的应用程序需要大量的计算资源, 而移动设备有限的计算能力降低了应用程序的使用性能. MEC促进应用程序的使用更节能、低时延和高灵敏[2]. 在MEC中, 大量MEC服务器部署在多个基站上, 形成移动边缘网络(mobile edge network, MEN)[3]. 移动用户可以通过MEN卸载密集型任务, 需要大量计算资源的任务卸载至MEN中的一个或多个MEC服务器上进行处理. 与传统云计算相比, MEC服务器比远程云端服务器更接近移动用户, 所以计算和传输的能耗与延迟更少[4].
目前, MEC的研究工作主要集中在卸载决策问题, 考虑不同的环境因素与用户需求, 如计算速度、能耗优化和资源成本等, 来获取最优的卸载解决方案[5]. 传统的卸载决策适用于用户位置是静态的, 但是移动用户设备一般具有很高的流动性, 所以传统卸载决策不适用于现实应用场景. 当考虑用户移动时, 每个移动用户在通信范围内会有多个MEC服务器, 将任务直接分配给一个MEC服务器并将所有任务卸载至此服务器不一定是最佳卸载决策, 移动用户还可以将任务上传至一个MEC服务器, 然后通过传输到另一个MEC服务器来获取结果, 但这一过程还需要考虑MEC服务器之间通信和传输成本的影响.
为了有效解决用户移动性对任务执行与卸载决策的影响, 本文通过随机路径点模型表示移动用户轨迹, 将问题建模为满足时延约束的最小能耗MEC服务器优化模型, 同时提出一种求解满足时延约束的卸载决策的最优解算法. 仿真结果表明, 所提出的算法可以找到最小能耗MEC服务器协同卸载并显著降低MEN中任务卸载的能耗与时延.
1 国内外研究现状计算卸载是MEC中的关键技术之一, 可以有效降低任务能耗与时延. Lin等人[6]研究在用户移动性下将任务卸载至位于用户轨迹的MEC服务器的最佳任务卸载MEC服务器, 没有考虑任务属性与约束条件. 协同边缘计算(collaborative edge computing, CEC)允许多个服务器协同卸载不同类型的任务, Wang等人[7]研究在CEC环境下的高效节能任务卸载, 提出基于匈牙利算法的任务卸载方案, 减少了时延与能耗. Kai等人[8]研究了D2D通信技术在MEN中满足时延约束并找到可卸载任务, 然后提出低任务复杂度切换算法进行系统最小化能耗. Wang等人[9]使用基于粒子群优化算法(particle swarm optimization, PSO)和博弈论的MEC分配策略来最小化时延. 在大部分MEC计算卸载方案中, 没有考虑移动用户的移动性, 讨论均假设用户是静态的且用户与MEC服务器之间的通信是一直存在的. 但在现实应用场景中并不具备实用性, 移动用户普遍具有移动性, 一旦超出规定边缘服务器的传输范围, 被卸载的任务就会传输失败, 从而延长应用程序的响应时间, 导致边缘计算资源的浪费. 因此, 考虑边缘移动用户设备的移动性是非常必要的. Wu等人[10]讨论了基于移动感知的任务卸载, 实时寻找每个任务最适合的云或边缘服务器, 通过基于深度学习(deep learning, DL)的算法来预测用户轨迹. Liu等人[11]研究在MEC环境下通过最优卸载来减少任务的传输, 并提出一种次遗传算法(secondary genetic algorithm, SGA), SGA将任务卸载到位于用户轨迹上的MEC服务器, 从而降低任务时延与能耗. 本文针对用户移动性和延迟约束, 利用沿用户轨迹的基站之间的协作, 提出满足约束最小时延与能耗卸载方案.
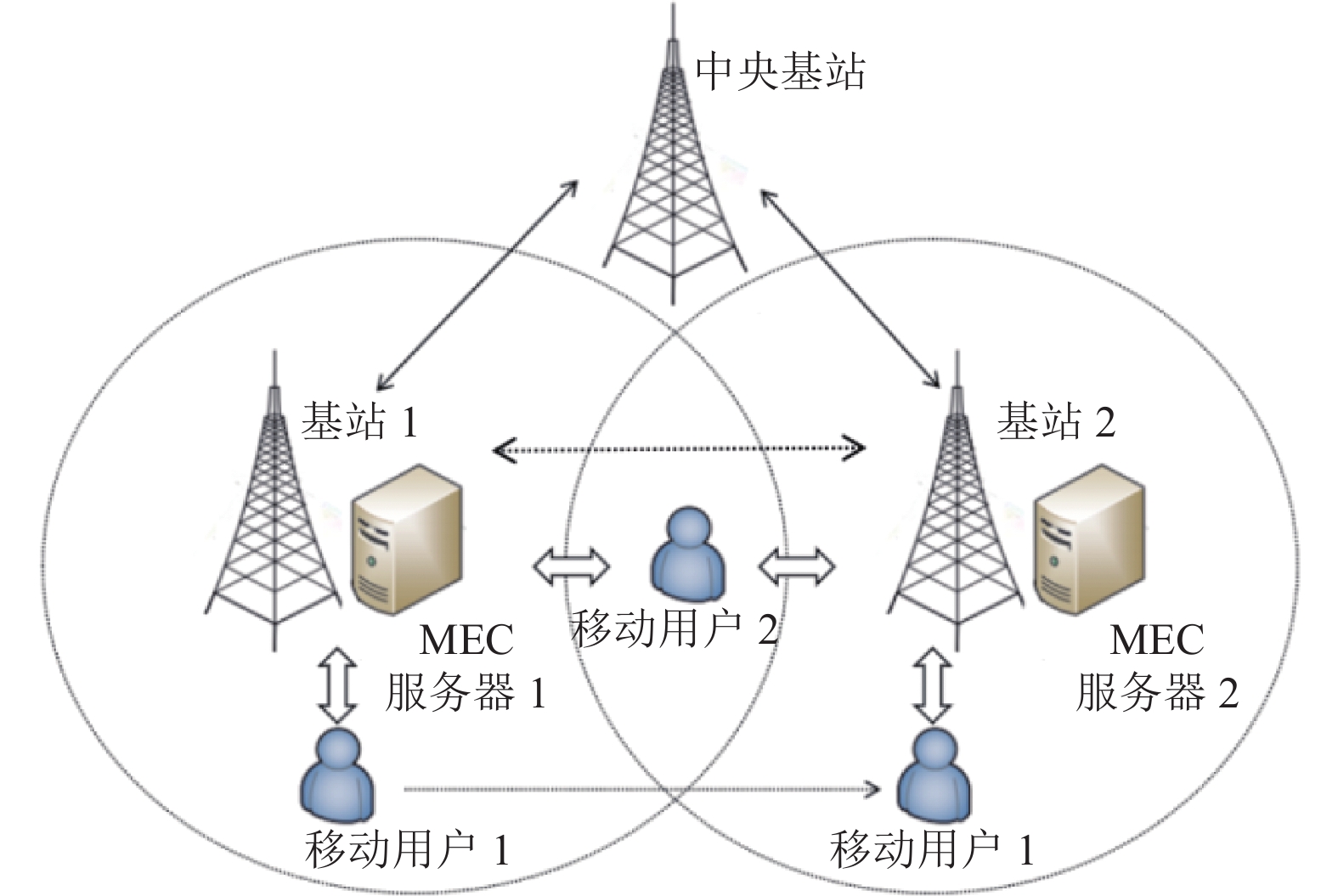
2 系统模型如图1所示, MEN由多个基站组成, 每个基站部署一台MEC服务器, MEC服务器用于接收、执行和传输基站信号范围内用户卸载的计算任务[12], 基站之间通过中央基站进行通信, 移动用户可以随时离开基站的信号范围, 在用户轨迹中的所有边缘服务器都可以执行被卸载的任务. 在图1中, 移动用户1卸载任务后离开基站1的范围并前往基站2. 在这种情况下, 基站1的MEC服务器1可以将卸载的任务发送给用户当前所在的基站2的MEC服务器2中.
|
图 1 系统模型 |
2.1 终端任务模型
假设移动用户表示为
移动用户首先进行卸载任务, 假设用户
| vij=Blog2(1+pid−αijN0B) | (1) |
其中,
任务上传时间取决于任务大小与通信速率, 则可以表示为:
| tij=rivij | (2) |
任务上传能耗取决于上传时间与用户传输速率, 则可以表示为:
| eij=tij⋅pi | (3) |
MEC网络中, 任务可以通过基站之间相互通信, 服务器
| vj1j2=Blog2(1+pj1d−αj1j2N0B) | (4) |
其中,
传输时间与能耗分别为:
| tj1j2=riνj1j2 | (5) |
| ej1j2=tj1j2⋅pj1 | (6) |
服务器
| tcij=cicj | (7) |
计算能耗为:
| ecij=tcij⋅pj | (8) |
其中,
由于执行处理后任务数据非常小, 并且能耗与时延可忽略不计, 所以不考虑下载传输延迟和能耗[13-15].
3 基于移动边缘计算的任务卸载方案 3.1 问题建立假设每个用户
| {min∑i∈N∑j∈SixijEijC1:tij⩽ | (9) |
其中, 约束1 (C1)表示总时延小于最大时延, 约束2 (C2)和约束3 (C3)表示任务
总能耗
| E_{i j}=e_{i j_1}+\sum_{t=t_1}^{t_2} e_{j \in S_i^t j \in S_i^{t+1}}+e_{i j}^c | (10) |
| T_{i j}=t_{i j_1}+\sum_{t=t_1}^{t_2} t_{j \in S_i^t j \in S_i^{t+1}}+t_{i j}^c | (11) |
其中,
本节目标为中央基站将每个任务分配给满足最大时延且产生最小能耗的MEC服务器, 对于每个用户
对每个可用服务器
将t−1之前的传输能耗与t+1时任务从服务器卸载至用户所需的能耗相加, 即可得在时间t传输所产生的能耗.
最后输出
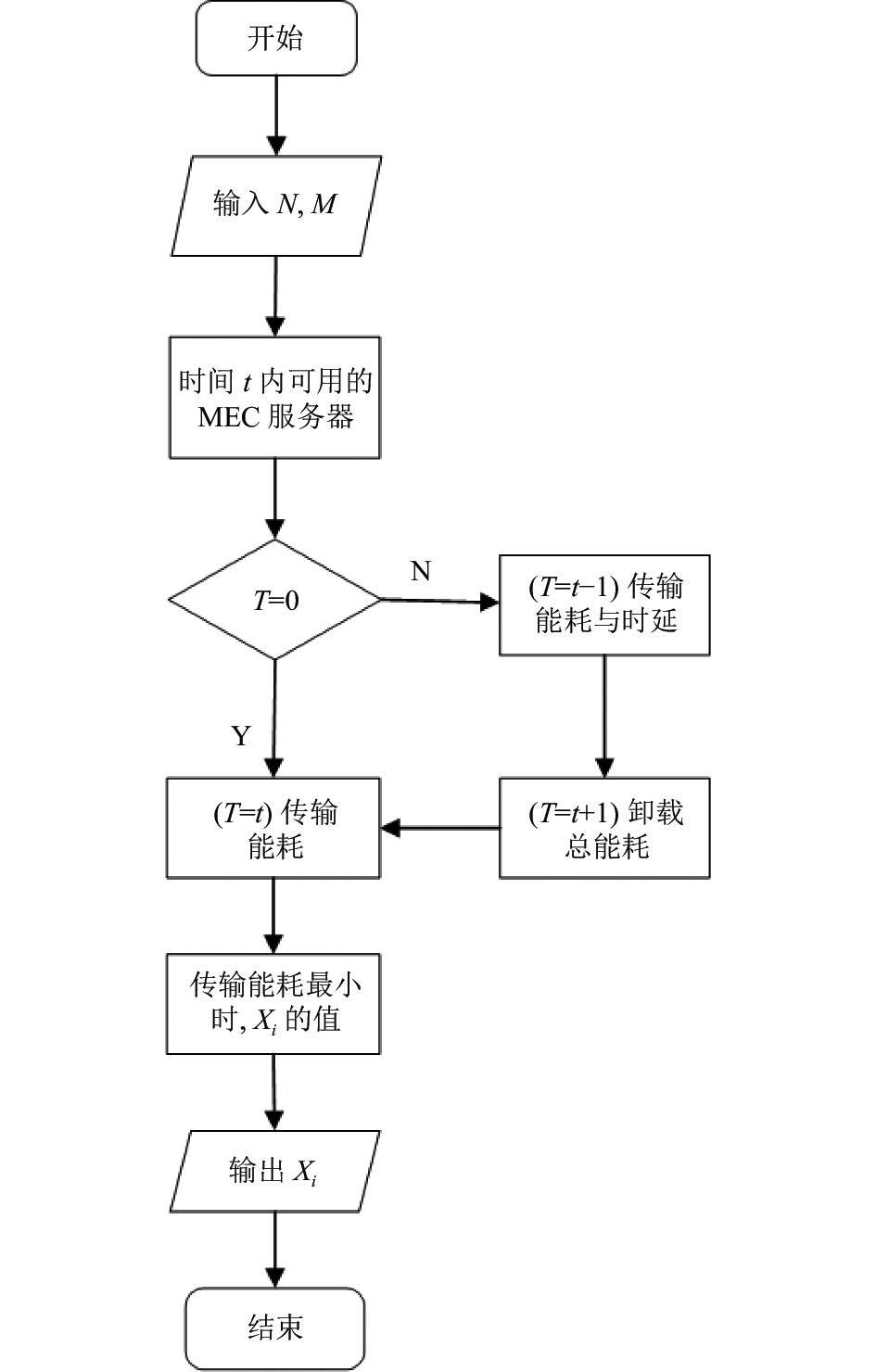
本文算法简要流程图如图2所示.
|
图 2 简要流程图 |
本文算法流程如算法1所示.
| 算法1. 延迟约束最小能耗卸载算法 |
| 输入: 移动用户
|
| 1) for each
|
| 18) end if19) end if20) end for22) for each
|
本节中, 通过Python编程语言评估所提出算法在考虑用户移动性和延迟约束下通过将任务卸载至最佳MEC服务器实现最小能耗的任务卸载性能. 引入文献[16]中的参数设置, 设置区域范围内共有126个基站, 在基站覆盖区域内的移动用户遵循随机路径点模型[17]. 随机路径点模型是移动用户移动的随机模型, 包含各移动用户的位置、速度和加速度随时间的变化情况. 基站的覆盖半径大小取[70, 100] m, MEC服务器的CPU容量取[7, 20] GHz, 计算能力取[3, 5] cycles/s, 传输功率取[0.1, 1] W, 通信信道带宽为1 MHz, 用户取[1, 3] km/h的速度移动, 时延约束在[0.1, 1] s. 移动用户的CPU容量取[1, 10] GHz, 传输功率取[7, 15] W, 计算功率取[7, 10] W. 本文提出的算法与本地执行(local execution, LE)算法、随机分配(random assignment, RA)算法[18]和贪婪分配(greedy assignment, GA)算法[19]进行比较.
LE: 任务在本地服务器进行存储和处理.
RA: 将一个任务划分为多个子任务, 随机分配给多个相邻的MEC服务器进行处理. 这是目前工业上最常见、应用最广泛的任务卸载算法.
GA: 将在本地服务器未卸载的任务分配至相邻CPU容量最大的MEC服务器进行卸载.
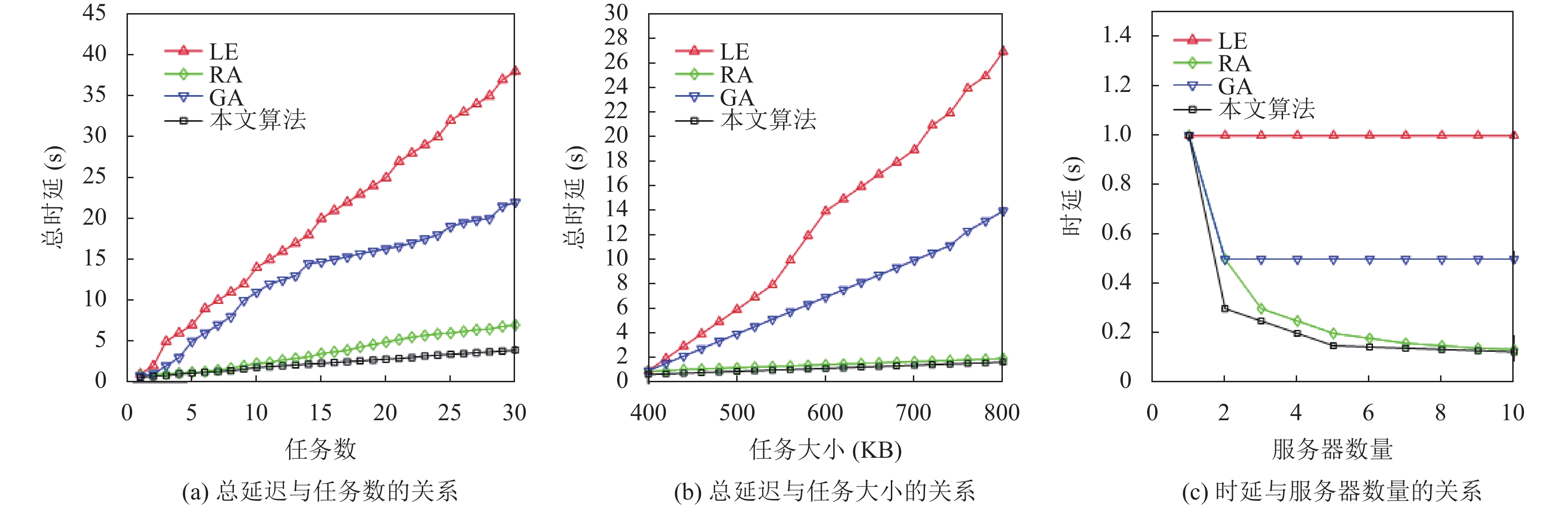
图3(a)表示总延迟与移动用户任务数的关系. 总延迟随任务数的增加而增加. 当任务数达到最大时, 本文算法较LE算法、GA算法和RA算法时延分别降低约89.37%、79.81%和41.26%. 分析可得, 一方面, 本文算法将任务划分为多个子任务, 提高了任务卸载效率. 另一方面, 将子任务分配给附近产生最低能耗的MEC服务器进行分布式处理, 所以产生的时延少于其他算法. 因此, 本文提出的算法更适用于大规模任务分配卸载场景. 图3(b)表示总延迟与输入任务数据大小的关系. 总延迟随任务大小的增加而增加. 当任务大小数据增加至800 KB时, 本文算法较LE算法、GA算法和RA算法时延分别降低约93.70%、84.03%和13.25%. 因此, 本文提出的算法更适用于大数据任务分配卸载场景. 从图3(a)和图3(b)可知, LE算法与GA算法产生时延远高于RA算法与本文算法, 证明将任务分成各个子任务并分配给其他MEC服务器可以有效降低时延, 提高任务处理效率. 图3(c)表示时延与MEN系统中MEC服务器的数量的关系. 当只有一台MEC服务器时, 只有本地服务器进行任务处理, 因此4种算法时延相同. 在任务输入大小且服务器CPU计算能力相同情况下, 随着周围服务器数量的增加, 任务划分后的子任务数量增加, 子任务数据量减少, 相应处理时间减少. 所以, MEN中MEC服务器数量越多, 本文所提算法产生的时延就越少.
|
图 3 总延迟与任务数和任务大小的关系, 时延与服务器数量的关系 |
|
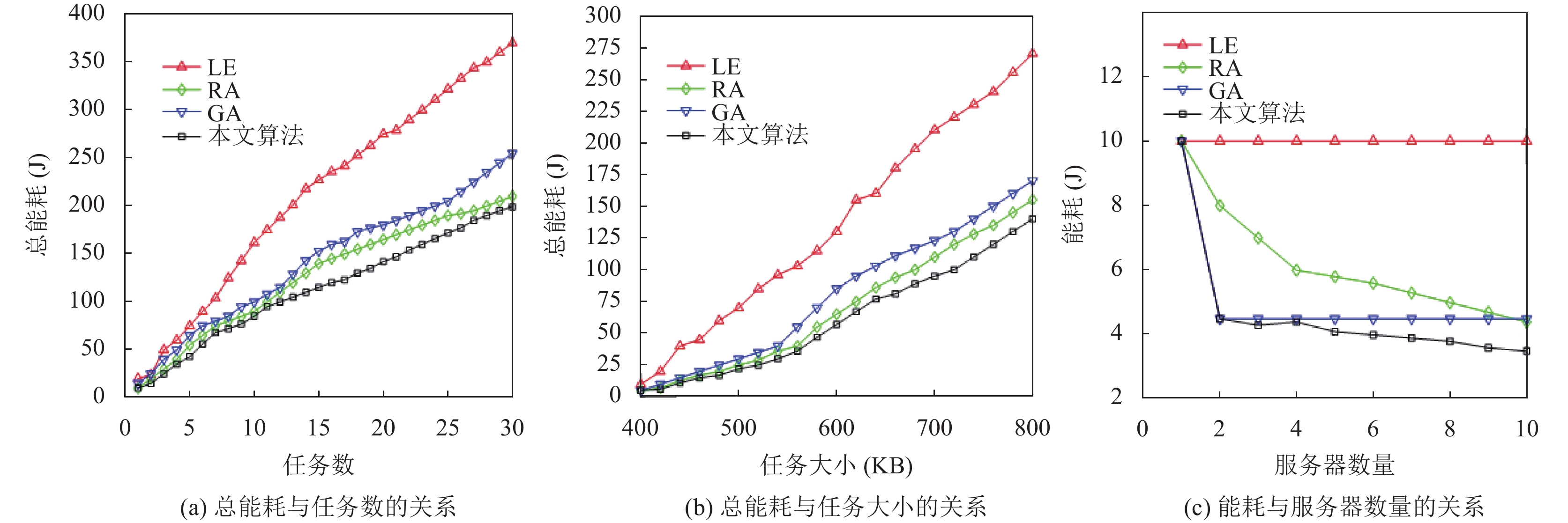
图 4 总能耗与任务数和任务大小的关系, 能耗与服务器数量的关系 |
图4(a)表示总能耗与任务数的关系. 当任务数达到最大时, 本文算法较LE算法、GA算法和RA算法能耗分别降低约51.35%、29.41%和14.29%. 表明本文算法可以有效降低能耗, 并且分布式任务分配的方式比集中式任务分配方式所产生的总能耗更小. 图4(b)表示总能耗与任务数据大小的关系. 在服务器数量一定的条件下, 随着任务数据大小增加至800 KB时, 本文算法较于LE算法、GA算法和RA算法所产生的能耗降低约48.15%、17.54%和9.68%, 表明该算法更适合处理大数据任务分配场景. 图4(c)表示能耗与服务器数量大小的关系. 在任务输入大小且服务器CPU计算能力相同情况下, 本文算法较LE算法、GA算法和RA算法产生的能耗最小. 由图可知, 随着服务器数量增加, RA算法产生的能耗高于GA与本文算法, 所以RA算法在降低能耗方面具有局限性.
结合以上对比, 本文算法相较于现有算法, 更适用于大规模和大数据量的任务卸载的物联网体系应用环境.
5 总结与展望面向MEC中任务属性、移动用户移动性和时延约束的情况, 本文提出了一种基于边缘计算下的任务卸载优化算法. 该算法将任务与MEN中产生最小能耗的MEC服务器协同卸载, 根据用户移动性优化任务的时延与能耗. 通过对该算法的大量仿真并与LE算法、GA算法和RA算法进行比较, 结果表明, 本文所提算法在优化时延和能耗方面都优于其他算法且更适用于5G大规模和大数据的物联网体系. 今后的研究将考虑系统成本模型改进与新变量的插入, 应用于新的智慧物联场景中.
| [1] |
齐彦丽, 周一青, 刘玲, 等. 融合移动边缘计算的未来5G移动通信网络. 计算机研究与发展, 2018, 55(3): 478-486. DOI:10.7544/issn1000-1239.2018.20170801 |
| [2] |
施巍松, 张星洲, 王一帆, 等. 边缘计算: 现状与展望. 计算机研究与发展, 2019, 56(1): 69-89. DOI:10.7544/issn1000-1239.2019.20180760 |
| [3] |
Ma X, Lin C, Zhang H, et al. Energy-aware computation offloading of IoT sensors in cloudlet-based mobile edge computing. Sensors, 2018, 18(6): 1945. DOI:10.3390/s18061945 |
| [4] |
Elgendy IA, Zhang WZ, Zeng YM, et al. Efficient and secure multi-user multi-task computation offloading for mobile-edge computing in mobile IoT networks. IEEE Transactions on Network and Service Management, 2020, 17(4): 2410-2422. DOI:10.1109/TNSM.2020.3020249 |
| [5] |
Wang Z, Zhao ZW, Min GY, et al. User mobility aware task assignment for mobile edge computing. Future Generation Computer Systems, 2018, 85: 1-8. DOI:10.1016/j.future.2018.02.014 |
| [6] |
Lin H, Zeadally S, Chen ZH, et al. A survey on computation offloading modeling for edge computing. Journal of Network and Computer Applications, 2020, 169: 102781. DOI:10.1016/j.jnca.2020.102781 |
| [7] |
Wang J, Wu WB, Liao ZF, et al. An energy-efficient off-loading scheme for low latency in collaborative edge computing. IEEE Access, 2019, 7: 149182-149190. DOI:10.1109/ACCESS.2019.2946683 |
| [8] |
Kai Y, Wang JY, Zhu HL. Energy minimization for D2D-assisted mobile edge computing networks. Proceedings of the 2019 IEEE International Conference on Communications. Shanghai: IEEE, 2019. 1–6.
|
| [9] |
Wang YT, Sheng M, Wang XJ, et al. Mobile-edge computing: Partial computation offloading using dynamic voltage scaling. IEEE Transactions on Communications, 2016, 64(10): 4268-4282. |
| [10] |
Wu CR, Peng QL, Xia YN, et al. Mobility-aware tasks offloading in mobile edge computing environment. Proceedings of the 2019 7th International Symposium on Computing and Networking. Nagasaki: IEEE, 2019. 204–210.
|
| [11] |
Liu ZL, Wang XX, Wang DY, et al. Mobility-aware task offloading and migration schemes in SCNs with mobile edge computing. Proceedings of the 2019 IEEE Wireless Communications and Networking Conference. Marrakesh: IEEE, 2019. 1–6.
|
| [12] |
Tran TX, Pompili D. Joint task offloading and resource allocation for multi-server mobile-edge computing networks. IEEE Transactions on Vehicular Technology, 2019, 68(1): 856-868. DOI:10.1109/TVT.2018.2881191 |
| [13] |
张海波, 李虎, 陈善学, 等. 超密集网络中基于移动边缘计算的任务卸载和资源优化. 电子与信息学报, 2019, 41(5): 1194-1201. DOI:10.11999/JEIT180592 |
| [14] |
Deng XH, Yin J, Guan PY, et al. Intelligent delay-aware partial computing task offloading for multi-user industrial Internet of things through edge computing. IEEE Internet of Things Journal, 2021, 8(16): 12559–12568.
|
| [15] |
Choi J, Ahn S. Scalable service placement in the fog computing environment for the IoT-based smart city. Journal of Information Processing Systems, 2019, 15(2): 440-448. |
| [16] |
Peng QL, Xia YN, Feng Z, et al. Mobility-aware and migration-enabled online edge user allocation in mobile edge computing. Proceedings of 2019 IEEE International Conference on Web Services. Milan: IEEE, 2019. 91–98.
|
| [17] |
Lai P, He Q, Abdelrazek M, et al. Optimal edge user allocation in edge computing with variable sized vector bin packing. Proceedings of the 16th International Conference on Service-oriented Computing. Hangzhou: Springer, 2018. 230–245.
|
| [18] |
Xing H, Liu L, Xu J, et al. Joint task assignment and resource allocation for D2D-enabled mobile-edge computing. IEEE Transactions on Communications, 2019, 67(6): 4193-4207. DOI:10.1109/TCOMM.2019.2903088 |
| [19] |
Wei F, Chen SX, Zou WX. A greedy algorithm for task offloading in mobile edge computing system. China Communications, 2018, 15(11): 149-157. DOI:10.1109/CC.2018.8543056 |
 2023, Vol. 32
2023, Vol. 32



