2. 南京航空航天大学 民航学院, 南京 211106
2. College of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China
在地形复杂、环境恶劣等条件下, 人们往往无法顺利到达某些区域完成特定任务. 无人机技术作为新兴手段在应急救援、物流运输等方面的作用日益凸显, 而无人机航路规划作为执行任务的基础更加关键[1]. 无人机自主飞行航路规划, 是在任务所处地形环境下, 寻找一条从起飞点出发到目标区域, 高效实现无人机任务, 如拍摄影像图、检测生命信号、运送物资等的最优路径的航路设计过程.
无人机航路规划算法主要分为传统经典算法和现代智能算法两大类[2]. 前者主要包含有Dijkstra算法[3]、模拟退火算法[4]以及人工势场法[5]. 传统算法在求解多维问题时往往计算量大, 过程复杂等问题, 而智能优化算法通过规则可在一定时间内得到较好的结果[6]. 其中遗传算法稳定性强, 但收敛速度不快, 容易早熟. 稀疏A*算法能够减少搜索空间, 但求解时间随着规划空间的增大越来越长[7]. 而粒子群算法作为一种最典型的人工智能算法, 由于其基于种群特性、易于实现和快速收敛等优势, 近几年也被广泛用于求解路径规划问题[8-12]. 本文提出一种改进PSO算法, 在优化调整自适应参数的基础上综合引入全局极值变异与加速度项, 以平衡全局和局部搜索效率, 避免种群陷入“早熟”. 通过对多个基准测试函数对改进算子的有效性进行测试验证, 结果表明, 本文所提改进PSO算法收敛速度更快, 精度更高.
基于以上研究, 以满足约束下的无人机最短飞行时间为目标, 构建无人机航路规划模型, 采用所提改进PSO算法进行求解, 经实例验证所提算法在航路规划中具有高效及实用性.
1 改进粒子群优化算法 1.1 粒子群算法概述PSO算法初始化为一群随机粒子
| {Vi+1=ωVi+c1r1(pbesti−Xi)+c2r2(gbest−Xi)Xi+1=Xi+Vi+1 | (1) |
其中,
粒子群算法的优点是具有较强的鲁棒性, 对种群大小敏感性不高, 参数少, 前期收敛速度快, 然而, 常规PSO算法具有如下两个缺陷: ① 不能很好地平衡粒子的全局和局部搜索能力; ② 极易过早陷入迭代停滞. 因此, 在使用PSO算法求解航迹规划问题时, 为了提高算法搜索航迹的优越性, 克服PSO算法的这两个缺陷显得尤为重要.
1.2 自适应参数优化在进化初期, 通常要求粒子的自我学习能力较强而社会学习能力较弱; 后期, 则要求粒子的自我学习能力较弱而社会学习能力较强. 因而对于学习因子进行线性变化, 如式(2)所示.
| {c1=(c1MIN−c1MAX)kkMAX+c1MAXc2=(c2MAX−c2MIN)kkMAX+c2MIN | (2) |
对粒子群算法的优化研究中, 对于惯性权重因子
| ω=ωend+(ωsta−ωend)exp[(−λ(kkMAX)γ)] | (3) |
经试验发现, 通过对于惯性权重、学习因子的动态调整, PSO算法的全局搜索能力和局部搜索能力有所改善, 但其容易陷入局部极值的问题还是存在.
1.3 针对陷入局部极值的优化研究粒子陷入局部极值的产生机理, 其中文献[12]通过严格数学推导, 得到粒子收敛情况, 如式(4)所示:
| limt→+∞x(t)=p∗=c1c1+c2⋅pbest + c2c1+c2⋅gbest | (4) |
由式(4)可知, 由于随着迭代次数,
| gbest=[1+α×U(0,1)]gbest | (5) |
其中,
极值变异是为了帮助粒子群跳出局部阻滞, 而为了避免陷入局部极值, 参考文献[12], 并进行参数改进, 即在速度更新公式中加上加速度项, 如式(6):
| a(t+1)=B×(f(xi(t))−f(gbest(t)))/(fm(X(t))−f(gbest(t))) | (6) |
其中, B为加速度量程系数, 根据多次试验取该维度上粒子运动范围大小的1/50, 例如当xi属于[−500, 500]时,B=20.
M表示粒子的维数, N表示粒子的个数. 使用粒子群算法求解最优航迹时, 每个粒子
Step 1. 初始化. 初始化粒子群, 包括种群大小、迭代次数、初代粒子位置和速度以及其他各参数等.
Step 2. 适应度计算. 确定目标函数, 根据目标函数得出粒子在搜索区域内适应度值, 并保存和更新个体最优及群体最优.
Step 3. 自适应参数计算. 计算自适应惯性权重、学习因子、加速度等.
Step 4. 极值变异. 比较本次迭代适应度值与前k次迭代的适应度值, 如果连续k+1次群体最优适应度相同或相差在设定范围内, 则可判断粒子陷入局部最优, 对全局最优值进行变异.
Step 5. 种群更新. 用更新后的参数和极值继续对群体中粒子的速度和位置进行更新; 如果粒子的速度和位置超出最大值和边界值, 则按最值计算.
Step 6. 循环条件检查. 根据目标函数值或最大迭代次数判断是否符合循环终止要求, 符合条件时结束算法循环, 否则转到Step 2继续执行.
PSO 算法可用伪代码表示如算法1.
算法1. PSO算法
初始化粒子群及参数;
DO
For 各个粒子
计算其适应度值;
按式(2), 式(3), 式(6)更新自适应惯性权重、学习因子加速度等参数;
If (粒子个体适应度优于个体历史最优值)
用
End
选取当前粒子群中最优的粒子位置作为全局最优;
If (当前最优粒子优于全局历史最优粒子)
用当前全局最佳粒子更新
If (若连续k+1次群体最优适应度相同或相差在设定范围内)
按式(5)对全局最优值进行变异;
For 各个粒子
按式(1) 更新粒子速度各位置;
End
Until 满足终止条件.
1.5 改进算子有效性仿真验证在内存16 GB, Intel(R) Core(TM) i7-1165G7 @ 2.20 GHz CPU的计算机上进行仿真, 选用Win 10, Matlab R2016a编程实现各测试试验. 通过设计对比试验, 对改进粒子群算法提出的参数改进和阻滞优化进行验证. 设置种群大小为100, 最大迭代次数为1 000. 速度限制设为该维度粒子运动范围阈值大小. 依次使用常规PSO算法和添加不同优化方式的PSO算法, 分别称为PSO1–PSO6, 对6个标准测试函数分别进行试验, 验证算法在二维和高维、单模态和多局部极值等不同情况下的性能. 为了降低数据的随机性, 对于算法PSO1–PSO6, 对应6种测试函数的组合都分别独立进行20次运算.
对比算法对应的参数选择和改进设计如下.
(1)算法PSO1: 常规PSO算法,
(2)算法PSO2:
| {ω=ωend+(ωsta−ωend)exp[(−3(kkMAX)3)]c1=c2=1.49445 | (7) |
(3)算法PSO3:
(4)算法PSO4: 基于PSO3, 增加加速度项.
(5)算法PSO5: 基于PSO3, 增加极值变异算子.
(6)算法PSO6: 本文提出的综合改进PSO算法.
| {c1=(c1MIN−c1MAX)⋅kkMAX+c1MAX,c1MIN=0.5,c1MAX=2c2=(c2MAX−c2MIN)⋅kkMAX+c2MIN,c2MIN=0.5,c2MAX=2ω=ωend+(ωsta−ωend)exp[(−3(kkMAX)3)],ωend=0.4,ωsta=0.9 | (8) |
选择的测试函数如表1所示.
| 表 1 测试函数及参数设置 |
对20次计算结果取平均值, 得到对比试验显示的目标函数收敛结果如图1(a)–图1(f)所示. 由图可知, 常规PSO算法前期得到的适应度值普遍较大, 而且很快在20代左右就陷入到局部极值直到迭代结束. 在常规PSO算法中引入自适应惯性权重后在前期寻优中发生明显改善, 延后了陷入局部最优的时间, 寻到的极值也相对较好, 而叠加动态变化的学习因子后, 这种效果得到了加强, 然而算法仍然难以逃脱局部极值. 在此基础上, 加速度和极值变异均能很好地达到摆脱局部最优的效果. 数据显示, 极值变异的效果明显更好. 但单独使用并不能保证达到全局收敛到最优的效果, 如Sphere、Rastrigin中单独使用都没有在预设迭代次数中找到全局最优, 而综合使用则在70代左右就成功快速找到极值. 在Schwefel函数测试中, 虽然各种算法都未能找到最优解, 但综合使用算子较好平衡了全局和局部寻优, 找到的解质量最高. 从Schatter测试中可以发现, 改进算法对于高维的效果更好, 而在二维环境下仍然是综合使用算子效果更好. 因此, 对比试验充分验证了改进算法的高效性与实用性.
2 路径规划问题建模无人机根据任务要求, 如何规划穿过危险区域, 避免禁飞区, 躲过飞行威胁或障碍物等, 顺利从起始点安全飞行到各目标点完成任务是需要考虑的重中之重. 因此, 需要根据已知静态环境规划满足各项约束且综合评价高的可飞路径. 为了直观表述路径的预计总飞行成本并便于计算, 针对飞行过程中的各类威胁和约束, 具体包括恶劣天气威胁、地形障碍威胁、地形高度限制、飞行距离限制、转弯角约束、俯仰角约束等, 采用罚函数的方式, 将不利因素转化为罚函数.
2.1 场景建模 2.1.1 山体建模本文主要考虑山区飞行, 无人机不能通过山脉飞行. 本文采用如式(9)所示的数学模型模拟山体:
| zm=fm(x,y)=hi⋅exp[−(x−xoixsi)2−(y−yoiysi)2],i∈(0,N] | (9) |
其中, (x, y)表示地形投影在水平面上的点坐标,

|
图 1 测试函数收敛曲线 |
2.1.2 地形建模
在无人机飞行场景中, 还要考虑地形的起伏. 同样采用函数模拟的方法进行地形建模. 模拟山区地形起伏的函数表示为式(10), 其中,
| ft(x,y)=a⋅[sin(y+b)+csinx+cos(d⋅√x2+y2)+esiny+fsin(g⋅√x2+y2)+hcosy] | (10) |
| z(x,y)=zm+zt=fm(x,y)+ft(x,y) | (11) |
除此以外, 常见的还有恶劣天气及各种因素造成的禁飞区, 无人机飞行过程中需要避开这些危险区域. 根据常见障碍区域廓形, 本文将障碍区域建模为长方体和圆柱体. 因此, 无人机飞行场景建模如图2所示.

|
图 2 应急无人机飞行场景模型 |
2.2 约束建模 2.2.1 避障约束
无人机可飞路径是不能从障碍物中穿过的, 所以必须避免与山峰丘陵等地形障碍的碰撞以及飞入威胁天气或者禁飞区范围.
为了保证这种避障行为, 本文采用罚函数, 对存在至少一个航路点落在障碍物内的解进行惩罚. 假设函数
| J1=∑Mi=1μi,μi={1, ifzi<f(xi,yi)orγ<10, otherwise | (12) |
由于无人机的性能限制, 同时一些受地面站控制的无人机需要与地面站联系, 所以一般需要考虑无人机的最大飞行高度限制, 而飞行高度过低又会增大与建筑物、山峰等的碰撞风险, 同时过高或过低的飞行高度也将消耗更多的燃料. 因此在建模中, 相对于地形的最小和最大飞行高度被设置为约束条件. 通过累计计算无人机各航路点的飞行高度(相对于该处地形高度), 再除以规划轨迹中的总航路点数得到平均高度. 使无人机在满足性能要求的情况下倾向于搜索低高度的航线. 因此对应的罚函数如式(13):
| J2={∑Mi=1(zi−f(xi,yi)−Hmin)M, ifzi>f(xi,yi)+Hmin∑Mi=1(f(xi,yi)+Hmin−zi)M, otherwise | (13) |
其中,
首先, 水平方向上无人机在任意航路点的转弯角度
| J3=1M∑Mi=1δi,δi={1,ifΩi>Ωmax0,otherwise | (14) |
其次, 无人机只能在特定角度范围内进行俯仰动作, 要求无人机在某一航迹点i的俯仰角
| J4={∑Mi=1(θi−w)w,ifθi > w∑Mi=1(σ−θi)σ,ifθi < σ0,otherwise | (15) |
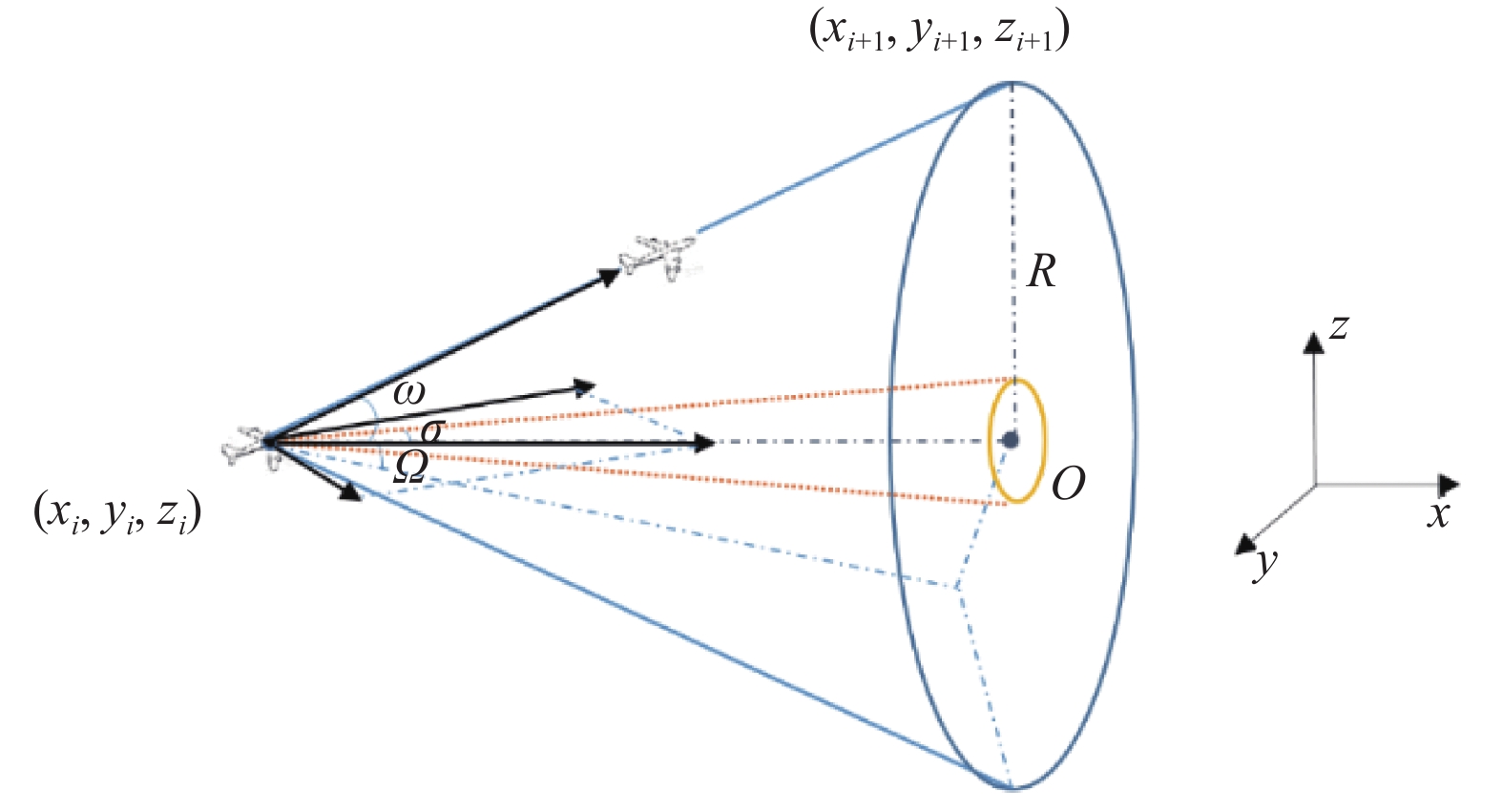
|
图 3 无人机俯仰角和爬升角示意图 |
2.3 目标函数
无人机应急飞行任务对时效性要求高, 越快到达目标地点越好. 假设无人机在飞行过程中匀速飞行, 因此对于任意一架无人机来说, 在相同的条件下, 路径越短, 飞行时间就越少, 在复杂环境中面临未知风险威胁的概率也会减少. 同时无人机因为自身性能, 飞行受到最大飞行长度的限制. 因此, 优化目标为满足约束条件下的最小化路径长度, 如式(16)所示:
| minf=L + ∑4k=1Jk | (16) |
然而由于路径长度
| J5 = {Lw−LmaxLmax | (17) |
其中,
因此式(16)中的目标函数可转化为式(18):
| minf=∑5k=1Jk | (18) |
建立仿真环境, 假设无人机的飞行区域在XOY平面内为70 km×70 km的矩形, 出发点坐标为(0, 0, 0), 目的地坐标为(68, 55, 0). 地形模型的参数分别为 a=0.01, b=c=6, d=1.1, e=1.5, f=2, g= 5, h=6. 山峰模型的参数分别为
分析试验数据, 如表2所示, 可以看到, 本文所提算法找到的航路适应值最小, 质量最高, 算法运算时间等性能相对较高. 因此, 基于本文所提改进粒子群算法的无人机航路规划方法具有可行性与有效性.
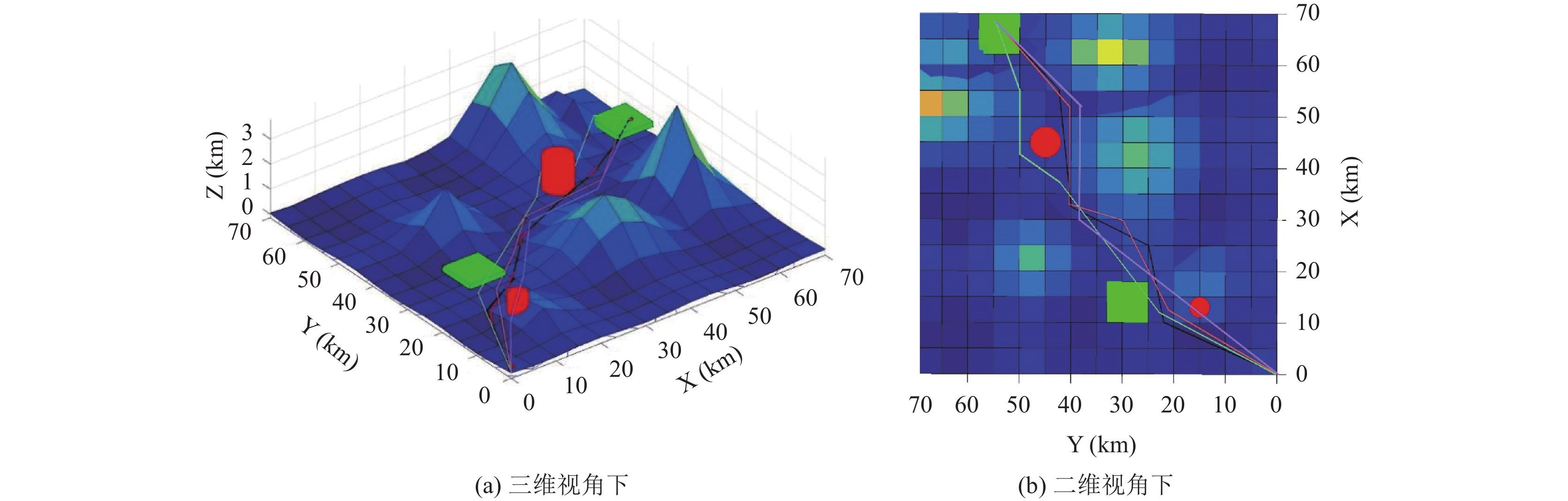
|
图 4 对比算法飞行路径规划结果效果图 |
| 表 2 实例验证结果数据 |
4 结束语
针对无人机在执行任务时路径规划的特殊性, 分析飞行环境特征并结合无人机性能限制进行综合建模. 结合粒子群算法参数少、搜索快但极易陷入局部最优的特性, 提出了一种综合参数自适应、加速度和全局极值变异的无人机路径规划方法. 仿真实验结果表明, 通过引入非线性自适应惯性权重和线性变化学习因子, 动态地调节了算法在全局搜索能力与局部搜索能力之间的平衡. 增加条件触发下的全局极值变异算子, 帮助粒子群尽量避免陷入局部最优, 并提高了粒子群摆脱局部极值的能力. 改进的算法具有较好的搜索能力, 也能保持较好的求解稳定性.
由于在执行特殊任务时, 路径规划时间对于执行任务尤为重要, 即算法的计算时间对寻优的质量具有较大影响, 因此, 后续将继续研究算法效能提升方法. 此外, 近几年极端天气情况出现频繁, 后期需要进一步研究天气对于航路规划的影响.
| [1] |
邹蒲, 邓吉秋, 刘立, 等. 地质灾害应急中无人机运输与飞行路径规划. 测绘与空间地理信息, 2017, 40(10): 15-17, 20. DOI:10.3969/j.issn.1672-5867.2017.10.005 |
| [2] |
王琼, 刘美万, 任伟建, 等. 无人机航迹规划常用算法综述. 吉林大学学报(信息科学版), 2019, 37(1): 58-67. DOI:10.19292/j.cnki.jdxxp.2019.01.008 |
| [3] |
Li M, Zhang F, Fang JY. Optimal path solution based on Dijkstra algorithm. Frontiers in Economics and Management, 2021, 2(6): 170-176. |
| [4] |
Xiao SC, Tan XJ, Wang JP. A simulated annealing algorithm and grid map-based UAV coverage path planning method for 3D reconstruction. Electronics, 2021, 10(7): 853. DOI:10.3390/electronics10070853 |
| [5] |
Wang X, Yong EM, He KF, et al. Research on artificial potential field route planning method based on threat level assessment. Proceedings of the 33rd Chinese Control and Decision Conference. Kunming: IEEE, 2021. 510–516.
|
| [6] |
康玉祥, 姜春英, 秦运海, 等. 基于改进PSO算法的机器人路径规划及实验. 机器人, 2020, 42(1): 71-78. DOI:10.13973/j.cnki.robot.190035 |
| [7] |
李鹏, 李兵舰, 亓亮, 等. 一种改进的粒子群优化算法及其在无人机航路规划中的应用. 舰船电子对抗, 2019, 42(5): 59-64. DOI:10.16426/j.cnki.jcdzdk.2019.05.015 |
| [8] |
Liu Y, Zhang XJ, Zhang Y, et al. Collision free 4D path planning for multiple UAVs based on spatial refined voting mechanism and PSO approach. Chinese Journal of Aeronautics, 2019, 32(6): 1504-1519. DOI:10.1016/j.cja.2019.03.026 |
| [9] |
付兴武, 胡洋. 基于改进粒子群算法的三维路径规划. 电光与控制, 2021, 28(3): 86-89. DOI:10.3969/j.issn.1671-637X.2021.03.017 |
| [10] |
杨超杰, 裴以建, 刘朋. 改进粒子群算法的三维空间路径规划研究. 计算机工程与应用, 2019, 55(11): 117-122. DOI:10.3778/j.issn.1002-8331.1808-0245 |
| [11] |
Clerc M, Kennedy J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation, 2002, 6(1): 58-73. DOI:10.1109/4235.985692 |
| [12] |
谢勇宏, 孔月萍. 基于改进粒子群算法的三维路径规划. 计算机测量与控制, 2022, 30(3): 179-182, 191. |
 2023, Vol. 32
2023, Vol. 32



