运路径规划是AGV (automated guided vehicle)技术发展的关键技术之一. AGV的路径规划技术是指某一参数的指数(如工作一代的最小值, 选择最短的路径, 最短的操作时间等)[1], AGV在仓库的众多可以行驶的路线中选择一个最优的路径, 该路径可以连接起始点和目标点, 并且同时躲避道路上的障碍物[2]. 它的本质就是AGV在进行路径规划的时候会受到很多个外界条件的干扰, 在此干扰的条件下寻找到最优路径或者可行解. AGV经过全局路径规划得到的路径的好坏会直接影响AGV完成货物分拣任务的进度[3].
常用的全局路径规划的方法有蚁群算法[4, 5]、人工鱼群算法[6-8]、概率路图法[9]、粒子群算法[10-13]及 A*算法[12-14]等. 也有一些应用于局部路径规划的算法, 包括人工势场法[15-17]和动态窗口法[18-21]等. A*算法作为典型节点搜索式算法, 在不同场合具有很强实用性.
目前, A*算法是一种常见的AGV路径规划方法, 文献[22]提出采用自适应系数对评价系数进行加权, 在搜索前期, 希望能快速找到方向, 该方法虽然提高了搜索速度, 但是生成的路径不是最优路径; 文献[23]提出将传统的A*算法的8邻域搜索进行扩展至32邻域, 该方法虽然扩大了搜索范围, 但是存在AGV在运作的过程中存在穿墙的可能性; 文献[24]提出将人工势场法与蚁群算法结合, 机器人能够很好地局部避障, 但路径轨迹平滑度不高.
针对以上的不足之处, 考虑通过使用动态加权, 改变搜索邻域的方法对传统的A*算法提出改进, 最后使用高阶贝塞尔曲线对A*算法规划出来的路径进行平滑处理.
1 传统的A*算法A*算法经典的启发式算法之一, 与传统的快速扩展随机树算法不同的是, A*算法为了使路径规划在搜索时搜索的方向更加清晰, 它在自己的搜索领域里面加入了启发函数[25]. A*算法的核心是, 确定起始点与目标点后, 按照起始点周围上下左右, 左上, 右上, 左下, 右下这8个方向进行搜索和评估, 并计算这8个点的估价函数值最小的点, 并把这个点放入open列表中, 再从这个点的周围上下左右, 左上, 右上, 左下, 右下8个方向进行搜索和评价, 重复上述过程, 直到搜索到目标节点. 经过多次的搜索与评估最终找到一条从起始点到目标点的最短路径.
A*算法的代价函数定义如下:
| $ f(n) = g(n) + h(n) $ | (1) |
其中, g(n)代表AGV在路径规划的途中从当前移动到的节点到起始节点所消耗的实际代价, h(n)代表AGV在路径规划的途中从当前运动到的节点到目标节点所消耗的估计代价, 也就是A*算法的启发函数. g(n)是已知的, 所以A*算法的优势主要体现在它的启发函数上, h(n)代表了A*算法搜索的启发信息. 换句话说,g(n)体现了A*算法的广度优先趋势. 如果h(n)=0, 那么只有g(n)实际上是有用的, 这时A*算法退化成迪杰斯特拉算法, 它能保证一定可以找到一条最优路径, 但是它浪费了时间去探索那些没有前途的方向.
A*算法的优劣就体现启发函数的选取上, 目前常用的启发函数有欧几里得距离, 曼哈顿距离和对角线距离. 为了提高AGV的搜索效率, 也就是让AGV的实际成本大于估计成本, 本文使用欧几里得距离作为启发函数进行评估.
h(n)的欧氏距离计算公式如下:
| $ h(n) = \sqrt {\mathop {(\mathop x\nolimits_n - \mathop x\nolimits_{{\rm{goal}}} )}\nolimits^2 + \mathop {(\mathop y\nolimits_n - \mathop y\nolimits_{{\rm{goal}}} )}\nolimits^2 } $ | (2) |
其中, (xn, yn)为检查点坐标, (xgoal, ygoal)为终点坐标. A*算法原理是通过建立两个列表: Open_set列表和Close_set列表来进行相关节点信息的存储, Open_set列表用来存放接下来有能被搜索但是还没有被搜索到的节点信息, 然后计算这些搜索到的节点的评价函数值, 并按照函数评价值的大小进行排序. Close_set列表用来存放不再被访问到的节点信息. 连接AGV访问到的Open_set列表中评价值最小的点, 即为A*算法规划出来的最优路径. 从起始点开始评估, 搜索起始节点附近8个搜索方向的节点, 对这8个节点的评估函数进行比较, 选取评价函数值最小的点, 最后如果Open_set列表为空, 则表示A*的所有路径规划过程结束, 或者最后经过搜索找到目标点, 过程也结束.
针对传统A*算法规划出来的路径较长、转折角度较大、路径不够平滑等问题, 本文将考虑从增加权重系数, 改变搜索策略, 路径平滑处理等方面对A*算法进行优化.
2 改进的A*算法 2.1 动态加权主要是对估价函数即式(1)进行改进, 改进的原理是改变AGV在路径规划的途中从当前移动到的节点到起始节点所消耗的实际代价与AGV在路径规划的途中从当前运动到的节点到目标节点所消耗的估计代价在估价函数中所占的权重比例.
改进后的估价函数的公式如下:
| $ f(n) = g(n) + w(n)\times h(n) $ | (3) |
即在h(n)前增加一个权重系数w(n), 即weight(n), g(n)与h(n)原本是1:1的权重分配, 假如w(n)=2, 权重分配变为1:2, 这样对规划效果带来的影响是相比实际代价g(n)会更偏向用估计代价h(n).
结果显示在保留规划出较优路径的前提下, 搜索节点减少、搜索速度大大提升. 当权重系数w较大的时候, 此时A*算法会尽快向终点扩展, 搜索速度虽然很快但会错过最优路径; 当w较小的时候, 此时的A*算法会倾向于搜索最优路径而减慢搜索速度.
在路径规划的过程中不可能只考虑搜索速度而不考虑规划的路径, 也就是不可能一直让w=2, 此时就考虑使用动态加权的方式, 即在路径规划的途中改变w的值, 不让它一直固定的等于某个常数值, 在AGV刚开始路径规划并且距离目标点较远的时候增加w的权重系数, 在AGV的路径规划快到达目标点的时候减小w的权重系数.
动态加权: 在放弃搜索最优路径的情况下, 使用动态加权来缩短A*搜索的时间. 其原则为, 在搜索开始时, 快速到达目的地所在区域更重要; 在搜索结束时, 得到到达目标的最佳路径更重要.
当h(n)较大时, 权重系数w也应该较大, 此时A*算法会尽快向终点扩展, 搜索速度很快但会错过最优路径; 当h(n)较小时, w也应该较小, 此时A*算法会倾向于搜索最优路径而减慢搜索速度.
以原本的启发函数h(n)为判断依据, 把它声明为d, 在路径规划的途中根据具体的搜索情况, 计算w的取值.
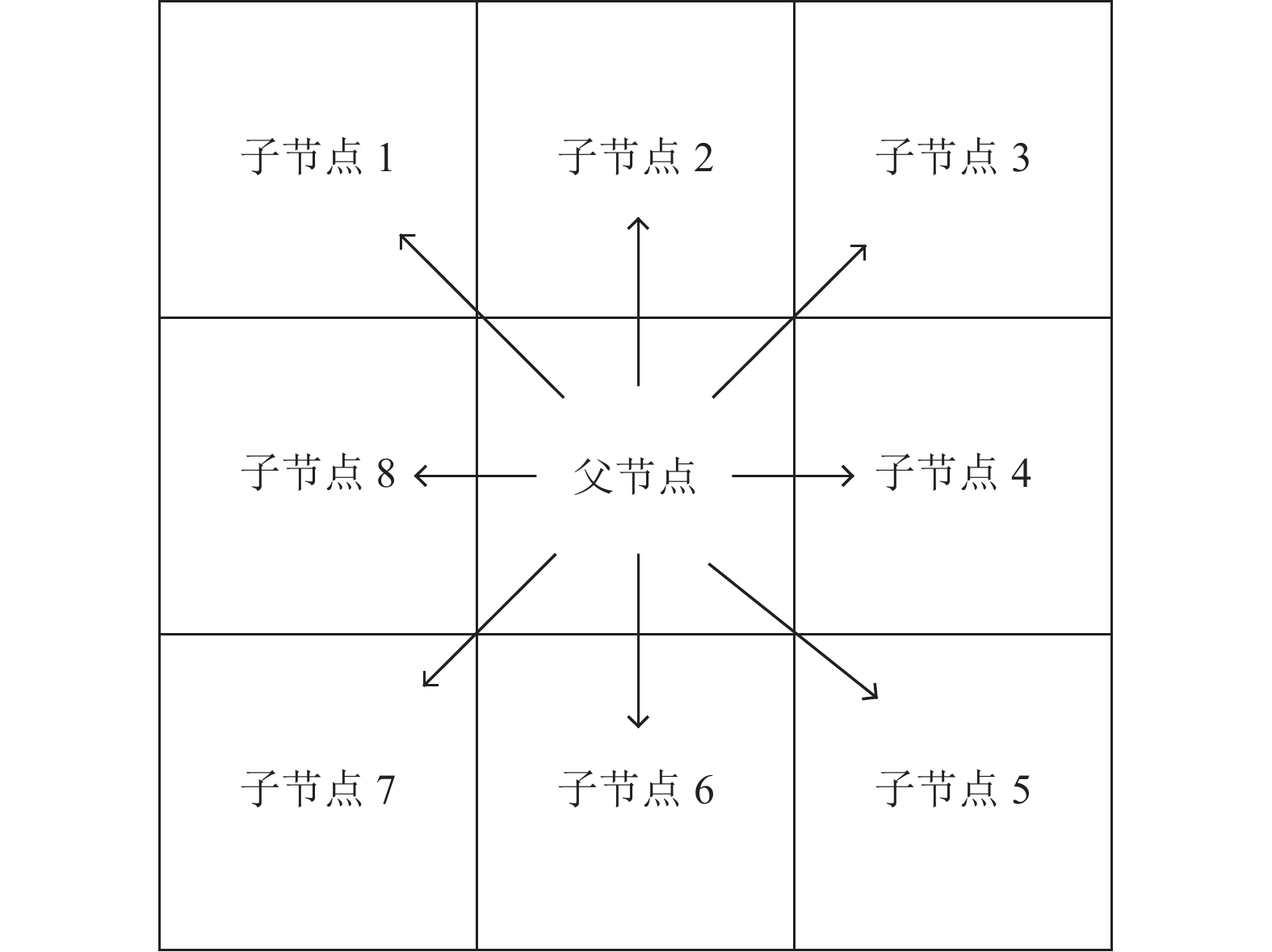
2.2 改进搜索邻域传统的A*算法是在当前节点(即父节点)的周围的8个方向进行搜索, 图1为A*算法的8搜索邻域, 即AGV会沿着当前节点的上下左右, 以及左上, 右上, 左下, 右下这8个方向进行运动, 极大程度地限制了AGV的搜索范围, 使全局路径规划的搜索节点更多.
针对传统A*算法的8邻域搜索的搜索节点过多的问题, 本文提出5邻域搜索对A*算法进行改进. 主要的原理是, 根据实际仓库的地图, 舍弃3个方向的搜索, 具体的判断依据是起始点与目标点的连线与正北方向的夹角, 舍弃的规则 如表1所示.
|
图 1 A*算法的8搜索邻域 |
| 表 1 舍弃规则 |
2.3 轨迹曲线优化处理 2.3.1 贝塞尔曲线的原理
在平面内随机选取3个点, 记作点A, 点B, 点C, 依次连接点A, 点B, 点C, 得到线段AB和线段BC. 在第1条线段AB上任意选取一点记作点D, 计算该点到线段起点A的距离(AD)与该线段总长AB的比例. 根据上一步得到的比例, 在线段BC上找到对应的点E, 使得AD:AB=BE:BC, 连接点D与点E, 得到线段DE. 从新的线段DE上再次找到相同比例的点F, 使得DF:DE=AD:AB=BE:BC. 到这里就找到贝塞尔曲线上的一点F, 利用极限的知识, 让选取的点D在第1条线段上从起点A移动到终点B, 在移动的过程中, 会有许多个新的点F产生, 找到所有的贝塞尔曲线上的F点, 所有的F点被找到以后, 也就得到了这条贝塞尔曲线.
2.3.2 贝塞尔曲线的公式B(t)为t时间下的坐标点,
(1) 一阶贝塞尔曲线
一阶贝塞尔曲线只有起点和终点, 并没有控制点, 所以绘制出来的图形仅是一条直线, 在时间t为1 s的情况下, 其公式为:
| $ B(t) = (1 - t){p_0} + t{p_1}, t \in [0, 1] $ | (4) |
一阶贝塞尔曲线是由
(2)二阶贝塞尔曲线
二阶贝塞尔曲线只存在一个控制点, 此时从起点到终点的线段发生变化, 具体的变化是由控制点的位置而改变的, 其公式为:
| $ B(t) = {(1 - t)^2}{p_0} + 2t(1 - t){p_1} + {t^2}{p_2},\; t \in [0, 1] $ | (5) |
原理: 由
(3)高阶贝塞尔曲线
从三阶开始贝塞尔曲线就开始显得复杂了, 高阶的通用公式如下:
| $ p_i^k = (1 - t)p_i^{k - 1} + tp_{i + 1}^{k - 1},\; t \in [0, 1] $ | (6) |
其中, k=1, 2, …, n, i=0, 1, …, n–k.
2.3.3 贝塞尔曲线与A*算法的结合针对A*算法规划后的路线存在拐角过多的问题, 使用高阶贝塞尔曲线进行平滑处理的关键在于修改贝塞尔曲线的控制点, 将A*算法最终运行得到的pathx, pathy两个列表中的值作为控制点, 作为points.
根据控制点的选取不同, 采用的贝塞尔曲线的公式也会有所不同. 鉴于本文的起始点与目标点距离过远, 使用改进后的A*算法规划出来的最终的路径长度仍然不短. 如果只使用一条高阶贝塞尔曲线进行平滑处理, 平滑处理后的路径并不理想, 一些控制点会在障碍物附近, 致使平滑处理后的路径有穿越障碍物的可能性. 因此本文会根据规划出的实际路径来选取控制点, 即会把规划出来的路径分成几段, 分别使用高阶贝塞尔曲线进行平滑处理.
3 仿真实验改进A*算法在路径搜索中的效果需要通过试验进行验证. 本文的路径规划在Python 3.7.0的环境中进行验证.
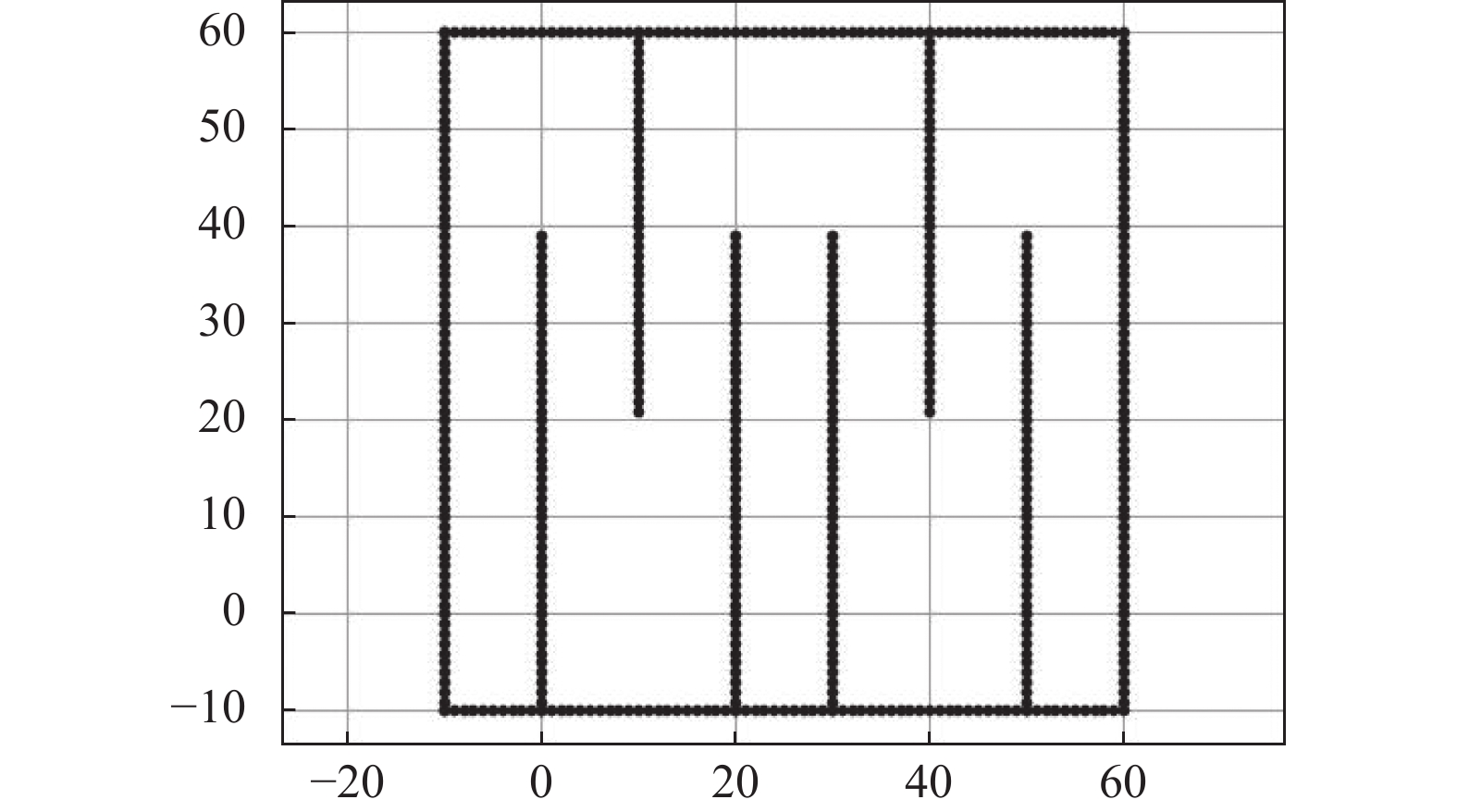
根据AGV工作的具体环境以及障碍物的所处位置, 在Python中进行地图绘制, 图2为仓库具体地图.
用黑色的点代表障碍物, 即AGV运行仓库中的货品摆放的架子, 用绿色的点代表起始点, 坐标为(−5, −5), 用蓝色的叉代表目标点, 坐标为(50, 50), 用黄色的点代表A*算法的搜索节点, 便于进行对比实验.
|
图 2 仓库地图 |
3.1 基于动态加权A*算法的仿真实验
文献[22]采用自适应系数对评价系数进行加权, 在搜索前期, 希望能快速找到方向, 让 h(n)的权重系数占比增大, 并设置权重系数初始值
|
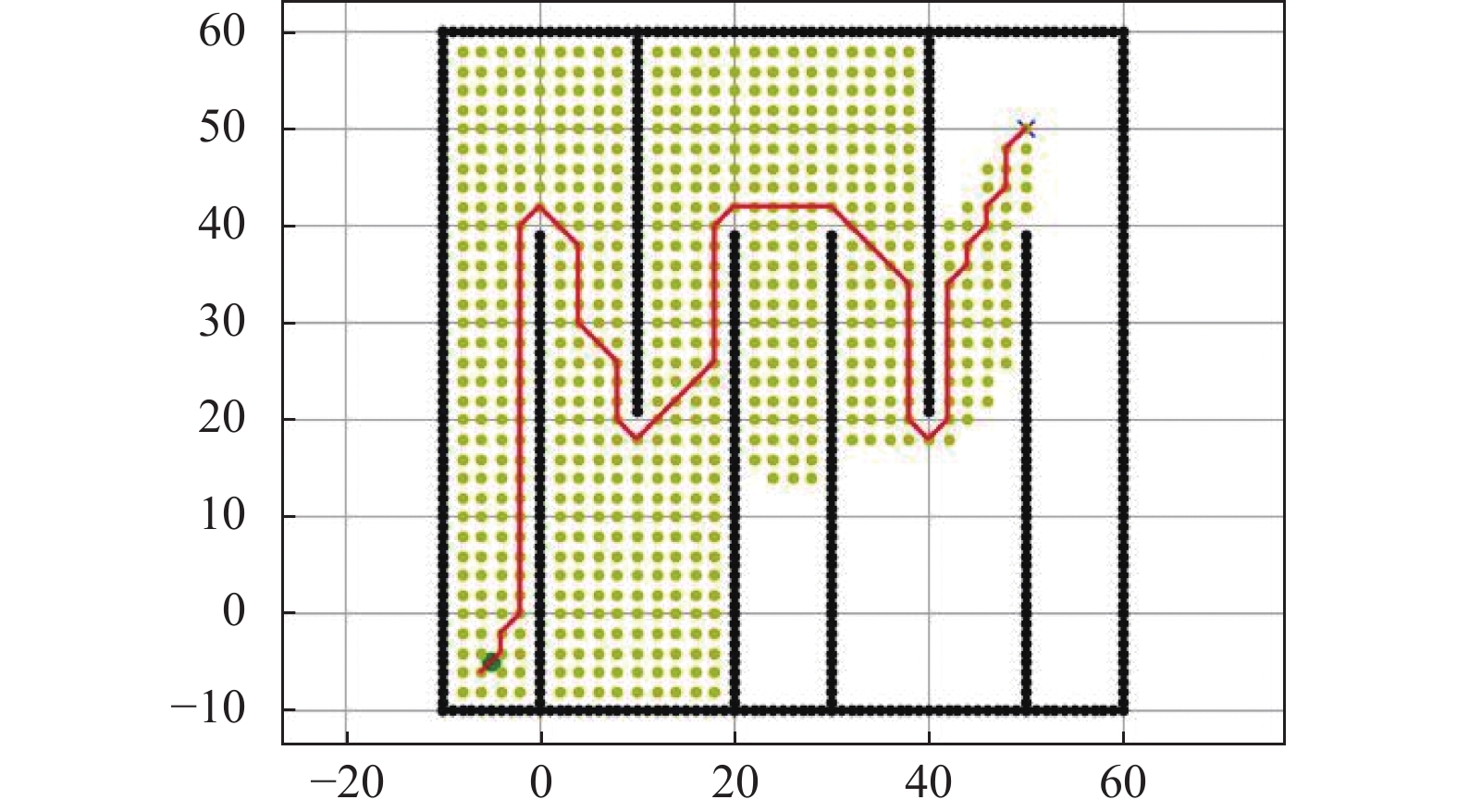
图 3 传统A*算法 |

|
图 4 加权A*算法 |
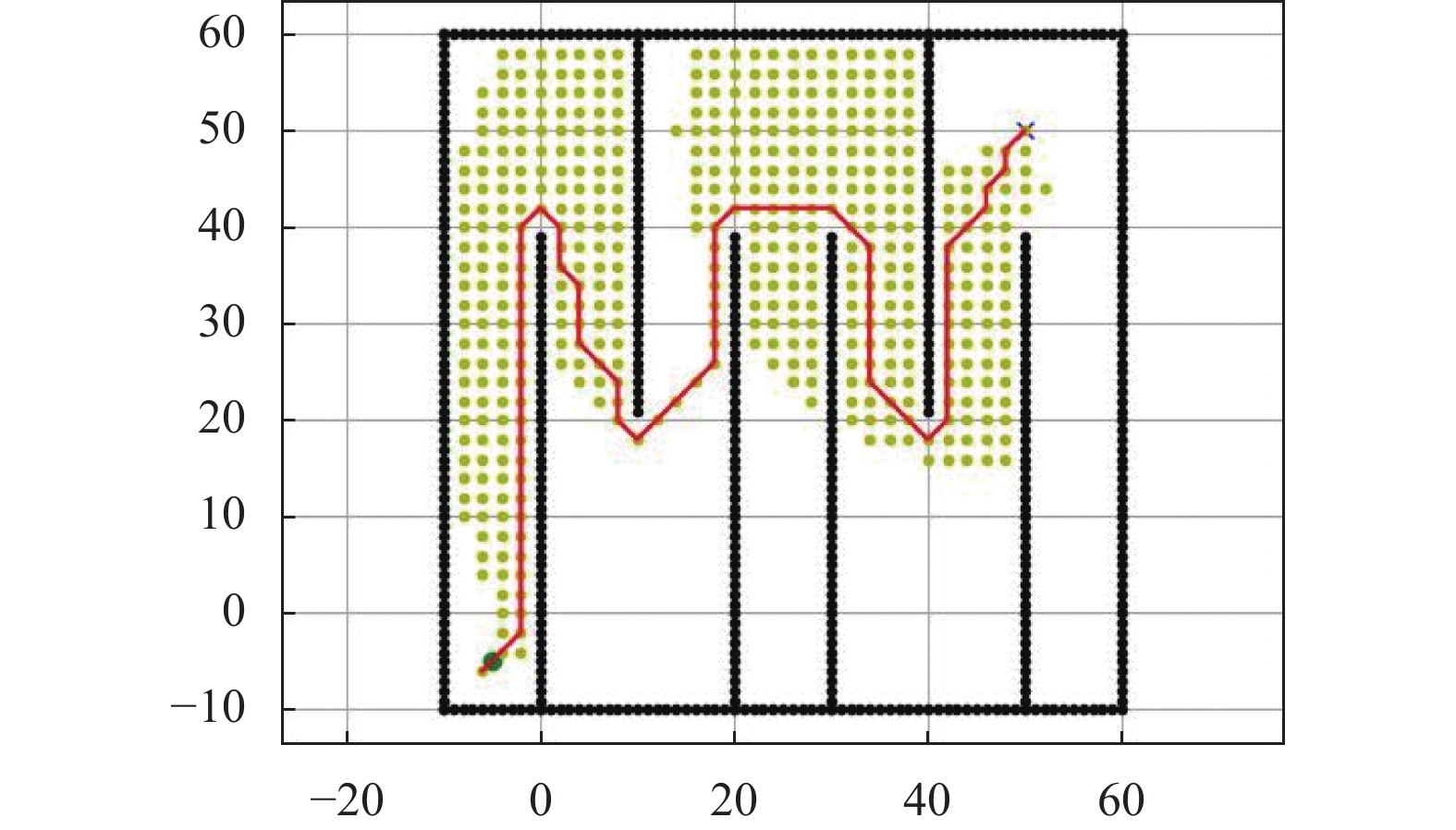
实验结果显示, 搜索速度虽然有所提升, 但是搜索的路径并不是最优的. 本文采用动态加权的方法对A*进行优化, 即在搜索开始时, 快速到达目的地所在区域更重要; 在搜索结束时, 得到到达目标的最佳路径更重要. 图5为它的实验结果.
|
图 5 动态加权的A*算法 |
以原本的启发函数h(n)为判断依据, 把它声明为d, 在路径规划的途中根据具体的搜索情况, 计算w的取值. 其中
| $ w = \left\{ \begin{gathered} {w_0} + g/{{maxgen\times}}({w_0}\times0.618) \\ {w_0} - g/{{maxgen}}\times({w_0}\times0.618) \\ \end{gathered} \right. $ | (7) |
其中, g为当前迭代次数, maxgen为最大迭代数. 在多次的仿真实验过程中发现, 当d>18时, 随着迭代次数的增加,w的权值从2线性递增至3.236, 此时算法搜索速度更快; 当d<18时, 随着迭代次数的增加,w的权值从2线性递减至0.746, 此时的路径规划优先考虑探索最优路径.
经过对比实验发现, 本文提出的动态加权的优化方法, 搜索的节点更少, 规划出的路径更优.
3.2 改进搜索邻域的A*算法的仿真实验传统的A*算法只能向节点的8邻域范围内进行搜索, 这种范围的搜索使AGV只能向8个方向前进, 限制了AGV的搜索范围, 使全局路径规划的搜索节点更多. 文献[23]将8搜索邻域扩展为32扩展邻域, 使机器人能够沿32个方向进行移动, 缩小了每个方向之间的夹角. 图6为32搜索邻域的A*算法实验结果.
实验结果显示, 虽然搜索节点减少了, 但是因为它扩大了搜索范围, 会使当前节点在进行下一步搜索时搜到的最优节点可能会是障碍物身后的节点, 这样AGV就会有穿越障碍物的现象出现.
针对此问题, 本文把8邻域搜索改为5邻域搜索, 根据实际地图舍弃3个方向的搜索, 图7为5搜索邻域的A*算法的实验结果.

|
图 6 32搜索邻域的A*算法 |

|
图 7 5搜索邻域的A*算法 |
通过对比实验发现, 本文提出的改进可以在减少搜索节点的基础上解决文献[23]提出的将搜索邻域改为32搜索邻域出现AGV穿越障碍物的问题, 改进的算法更优.
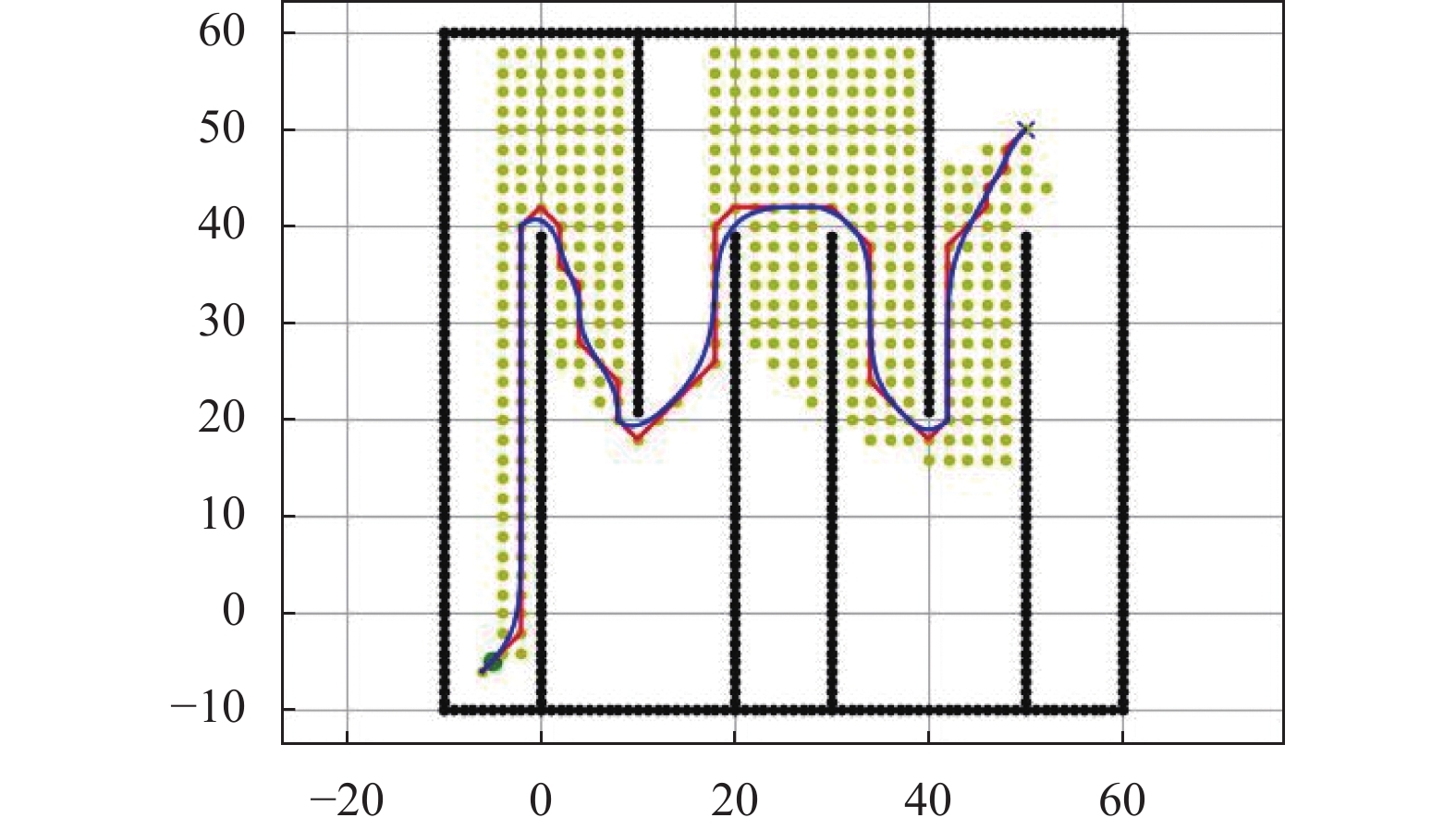
3.3 路径平滑处理后的A*算法的仿真实验观察以上两个改进的实验结果, 发现最终规划出的路径拐点过多, 路径不够平滑, 导致AGV在实际运作的过程中会出现震荡的问题. 针对此问题, 本文把规划出的路径分成8段, 分别使用高阶贝塞尔曲线进行平滑处理, 图8为贝塞尔曲线平滑后的A*算法的实验结果.
|
图 8 贝塞尔曲线平滑后的A*算法 |
图8中红色的直线代表经过前两个改进后的A*算法规划出的最终的路径, 蓝色的曲线代表使用高阶贝塞尔曲线平滑后的最终路径, 结果显示优化后的路径更短加平滑, 改进后的算法能有效地减少A*算法在路径规划后产生的拐点.
4 结论与展望本文针对传统A*算法搜索速度慢, 搜索时间长的缺点, 使用动态加权对A*算法进行改进; 针对传统A*算法搜索节点过多的缺点, 使用改变搜索邻域的方法对传统的A*算法进行改进; 最后针对改进后的A*算法规划出来的路径存在拐点过多的问题, 使用高阶贝塞尔曲线进行路径平滑处理. 通过3组仿真实验的对比得出本文提出的改进算法更优, 因此, 本文算法具有研究意义和实用价值. 但是在路径规划的途中会存在动态的障碍物, 下一步的研究把A*算法与其他路径规划的算法结合, 进行动态避障处理.
| [1] |
Wang C, Mao J. Summary of AGV path planning. Proceedings of the 2019 3rd International Conference on Electronic Information Technology and Computer Engineering (EITCE). Xiamen: IEEE, 2019. 332–335.
|
| [2] |
赵连强, 柳国良, 李鹏远. 一种自动规划路径AGV机器人的设计. 科技风, 2021(32): 7-9. DOI:10.19392/j.cnki.1671-7341.202132003 |
| [3] |
于佳乔. AGV系统路径规划与任务调度研究[硕士学位论文]. 长春: 长春工业大学, 2021.
|
| [4] |
刘加奇, 王泰华, 董征. 基于改进蚁群算法的移动机器人路径规划. 传感器与微系统, 2022, 41(5): 140-143. |
| [5] |
孙宇翔, 陈浩鹏, 任传荣. 基于精英策略的蚁群算法在AGV路径优化中的应用. 物流工程与管理, 2022, 44(3): 30-32. |
| [6] |
陈靖. 基于人工鱼群和动态窗口法的农用机器人路径规划研究[硕士学位论文]. 合肥: 安徽农业大学, 2020.
|
| [7] |
Chen TB, Zhang P, Gao S, et al. Research on the dynamic target distribution path planning in logistics system based on improved artificial potential field method-fish swarm algorithm. Proceedings of 2018 Chinese Control and Decision Conference (CCDC). Shenyang: IEEE, 2018. 4388–4391.
|
| [8] |
张宁, 陈茜茜, 李微, 等. 改进人工鱼群法的机器人路径规划方法. 计算机技术与发展, 2022, 32(4): 210-214. |
| [9] |
陈洋, 赵新刚, 韩建达. 移动机器人3维路径规划方法综述. 机器人, 2010, 32(4): 568-576. |
| [10] |
王翼虎, 王思明. 基于改进粒子群算法的无人机路径规划. 计算机工程与科学, 2020, 42(9): 1690-1696. DOI:10.3969/j.issn.1007-130X.2020.09.020 |
| [11] |
Coello CAC, Pulido GT, Lechuga MS. Handling multiple objectives with particle swarm optimization. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279. DOI:10.1109/TEVC.2004.826067 |
| [12] |
Wang CB, Wang L, Qin J, et al. Path planning of automated guided vehicles based on improved A-Star algorithm. Proceedings of 2015 IEEE International Conference on Information and Automation. Lijiang: IEEE, 2015. 2071–2076.
|
| [13] |
Saian PON. Optimized A-Star algorithm in hexagon-based environment using parallel bidirectional search. Proceedings of the 2016 8th International Conference on Information Technology and Electrical Engineering. Yogyakarta: IEEE, 2016. 1–5.
|
| [14] |
袁薪凯, 晏林冲, 方明辉, 等. 基于A*算法的自动寻路避障小车送餐系统. 科技创新与应用, 2022, 12(14): 35-38. |
| [15] |
陈田田. 基于改进人工势场法的室内移动机器人路径规划研究[硕士学位论文]. 郑州: 郑州大学, 2019.
|
| [16] |
Sang HQ, You YS, Sun XJ, et al. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean Engineering, 2021, 223: 108709. DOI:10.1016/j.oceaneng.2021.108709 |
| [17] |
Chang ZY, Zhang ZW, Deng Q, et al. Route planning of intelligent bridge cranes based on an improved artificial potential field method. Journal of Intelligent & Fuzzy Systems, 2021, 41(3): 4369-4376. |
| [18] |
张棹轻. 动态障碍物环境下无人艇避碰方法研究[硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [19] |
Ogren P, Leonard NE. A convergent dynamic window approach to obstacle avoidance. IEEE Transactions on Robotics, 2005, 21(2): 188-195. DOI:10.1109/TRO.2004.838008 |
| [20] |
杨周, 刘海滨. 基于改进蚁群与动态窗口法的AGV动态路径规划. 计算机工程与应用, 2022, 58(6): 287-295. DOI:10.3778/j.issn.1002-8331.2108-0501 |
| [21] |
林泽南. 基于全局改进势场与局部动态避障的移动机器人路径规划方法研究[硕士学位论文]. 大连: 大连理工大学, 2021.
|
| [22] |
牟德君, 初鹏祥. 基于改进A*算法的仓储环境AGV路径规划. 自动化与仪表, 2022, 37(4): 40-45. |
| [23] |
杨芳清, 刘吉成. 融合改进A*算法与动态窗口法的移动机器人路径规划. 工业控制计算机, 2021, 34(5): 106-108, 112. DOI:10.3969/j.issn.1001-182X.2021.05.044 |
| [24] |
李印宏. 基于改进蚁群算法的移动机器人路径规划研究[硕士学位论文]. 曲阜: 曲阜师范大学, 2021.
|
| [25] |
付道阔, 范平清. 改进A*算法的三维无人机路径规划. 智能计算机与应用, 2020, 10(12): 155-159. DOI:10.3969/j.issn.2095-2163.2020.12.034 |
 2023, Vol. 32
2023, Vol. 32


