在人工智能领域, 深度学习已经越来越受到关注[1], 电机在运行过程中一般都会有温升, 而产生的温度过高会直接导致电机的损坏, 所以在电机的运行过程中温度是否过高是对电机是否能正常运行是很重要的因素.
对于电机的故障识别研究, 电机信号采集方法主要有温度采集法[2]、声音采集法[3]、电流采集法[4]、振动采集法; 常用的电机智能故障诊断方法主要有基于SVM (support vector machines)的诊断方法[5]、基于神经网络的诊断方法[6]、基于深度学习的诊断方法[7]以及基于迁移学习的诊断方法[8]; 随着计算机和深度学习技术的不断发展, 神经网络中的卷积神经网络是被广泛应用的模型之一; 传统的机器学习需要人工来进行分析和提取特征, 导致提取出的特征具有较大的主观性和误差性, 所以这种传统的方法的准确率不高以及会消耗很大的人力等缺点[9]; 针对传统机器学习的不足, 将卷积神经网络(convolutional neural network, CNN)应用于电机的故障识别, 对于深度学习中的CNN是通过使用权值共享、局部连接等方式来自动学习数据的特征[10], 相对于传统的方法来说, CNN具有强大的特征学习能力. 并且卷积神经网络在电机故障识别方面的研究越来越多. 文献[11]将小波分析与卷积神经网络相结合, 对电机故障进行了有效的诊断. 文献[12]基于定子电流特征与振动特征永磁电机, 利用残差连接的卷积神经网络较好的对电机故障进行诊断. 文献[13]结合不同变换与深度学习卷积神经网络的方法, 对电机系统的故障诊断提供了新的途径. CNN作为一种机器学习在机械故障识别领域得到了广泛的应用.
因此, 本文提出了在电机运行温度发生变化时, 通过随机失活、NLWTCE与卷积神经网络相结合, 可以对电机故障进行准确且快速的识别. 提出的模型只需要输入处理好的数据, 不需要人工提取特征向量, 这样可以减少在提取特征时的损失, 还大大减少了人力, 用NLWT对图像进行增强, 从而提高模型的识别准确率. 在构建基于CNN的电机故障诊断模型, 提出了一种随机失活、非线性小波变换图像增强的改进卷积神经网络模型的识别诊断方法, 不仅能有效地减少过拟合的产生, 还能提高识别的准确率, 对采集到的信号进行特征提取, 实验结果显示该模型取得更好地识别效果.
1 理论基础 1.1 小波变换的图像增强数据图像可以看成是一个二维信号, 可以通过二维小波变换对图像进行分解和重构. 在模型程序中, 小波变换的图像增强可以很好地实现, 首先输入原图像, 对原图像的数据进行小波分解, 得到低频和高频部分; 对分解后的高频系数进行非线性增强, 这样可以实现图像增强的目的, 将处理好的小波系数进行重构, 从而得到增强后的数据图像. 其函数表达式为:
| Cout(i,j)={G⋅Cin(i,j),Cin(i,j)>TK⋅Cin(i,j),Cin(i,j)⩽ | (1) |
其中, G是小波系数增强倍数, K(K<1)是小波系数弱化倍数,T是小波系数阈值,
CNN是深度学习算法和人工神经网络的结合, 如图1所示, 为网络模型的结构图. 卷积神经网络中, 输入层是还未经过处理的原始图像, 输出层是特征分类的结果, 隐含层是具有复杂多层非线性结构的神经元层, 包括卷积层和池化层, 在隐含层中这两层可以交替使用, 为了能更好地提取出图像特征.
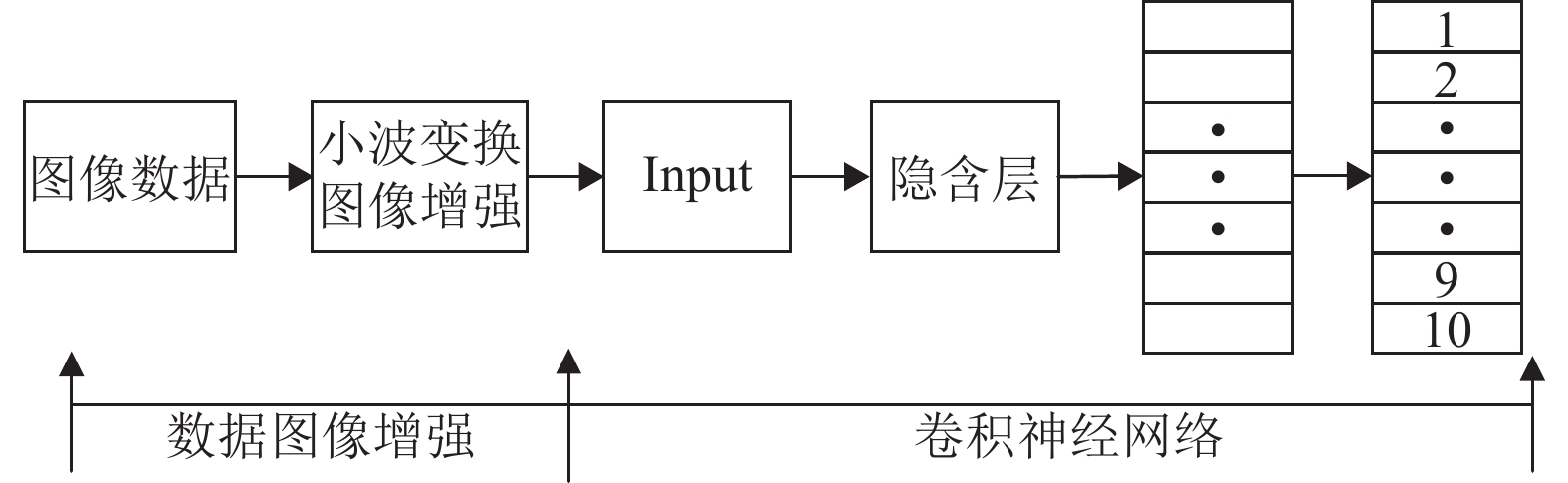
|
图 1 网络模型的结构 |
1.2.1 卷积层
卷积层的主要作用是利用卷积核对图像特征进行初步提取, 增强原始图像的特征信息, 在卷积中使用20个
| x = f\left({\sum {x * \omega } _{ij}} + b\right) | (2) |
其中, *为卷积运算符, b为偏差,
池化层是CNN中的隐含层, 输入图像进行卷积后得到20个
| x = f(\beta down(x) + b) | (3) |
其中,
在本文中, 选用了tanh激活函数, 它的取值范围在−1~1, 输出均值是0, tanh函数表示为:
| {{\rm{tanh}}} (x) = {\kern 1pt} {{({{\rm{e}}^x} - {{\rm{e}}^{ - x}})} \mathord{\left/ {\vphantom {{({{\rm{e}}^x} - {{\rm{e}}^{ - x}})} {({{\rm{e}}^x} + {{\rm{e}}^{ - x}})}}} \right. } {({{\rm{e}}^x} + {{\rm{e}}^{ - x}})}} | (4) |
全连接层的特征是每一个神经元都与上一层的所有神经元相连. 将隐含层输出的20个
| F(x) = f(\omega x + b) | (5) |
其中,
为了进一步降低过拟合现象的产生, 在全连接层加入随机失活(Dropout)层, 在运行时以一定的概率让一些神经元随机的停止工作, 从而达到防止过拟合产生.
| Dropout(x) = x | (6) |
其中,
输出层一般是分类器层(Softmax层), 其主要目的是对识别目标进行分类; Softmax层的输入是上一层全连接层的数据, 输出的数据的每个值范围在0–1, 输出值表示的是样本属于这一类别的概率.
在本实验中, 所构建的CNN模型的结构参数如表1所示.
| 表 1 电机故障识别模型结构参数 |
电机故障识别的过程分为以下几个步骤.
(1) 采集电机信号图.
(2) 将采集到的电机信号图进行预处理(裁剪、转换模式等).
(3) 将预处理后的图像通过NLWT进行图像增强.
(4) 建立卷积神经网络模型并初始化网络的参数(根据实验需求, 确定合适的学习率、迭代次数等网络参数).
(5) 卷积神经网络模型训练(将处理好的图像输入到模型中, 通过运行得到网络的输出误差, 判断网络模型是否收敛, 不收敛, 执行步骤(6); 若收敛, 则执行步骤(7).
(6) 进行权值修改和更新(通过反向传播将得到的误差反向传播到各个神经网络, 以此来更新权值, 重复执行步骤(4)和步骤(5), 直到网络模型达到收敛).
(7) 测试样本数据精度、损失函数等是否满足要求(若满足要求直接输出结果; 否则回到步骤(3)修改网络模型参数, 直至满足要求).
(8) 网络模型输出, 判断电机运行的状态.
2 电机故障识别方法 2.1 CNN故障识别模型图像故障识别结果可以基于以下指标进行评价.
(1)损失函数[14]
是用于评估模型预测值与真实值之间的不一致程度. 损失函数越小, 代表模型的鲁棒性越好.
其函数形式为:
| {{Loss}} = - \sum\limits_x {p(x)\log (q(x))} | (7) |
其中, 变量
(2)结构相似指标函数(SSIM)[15]
是用于评估电机识别图片的失真程度, 也可以评估两张图片的相似程度.
| {\textit{SSIM}} = \frac{{(2{\mu _x}{\mu _y} + {C_1})(2{\sigma _{xy}} + {C_2})}}{{(\mu _x^2 + \mu _y^2 + {C_1})(\sigma _x^2 + \sigma _y^2 + {C_2})}} | (8) |
其中,
本文的方法描述: 总体上主要是由数据采集、构建模型、电机故障识别组成; 首先采集电机数据作为数据集, 将采集到的数据集预处理之后划分为训练集和测试集, 使用Dropout函数、NLWTCE与卷积神经网络相结合构建改进的网络模型, 并设置好合适的参数, 用训练集对网络模型进行训练, 将训练好的模型对测试集进行识别诊断, 实现电机的运行状态识别.
2.2 数据采集及预处理该实验所使用的数据集是实验室电机运行正常图像和异常电机图像, 本文需要判断电机图片是否发生异常为研究对象; 所用数据由实验室实际测试所得, 首先需要通过热像仪设备来采集图像数据, 所采集的图像格式为BMP. 异常电机图像的主要特征是温度过高, 使得图像在模型中数据偏大.
为了使电机图像有更好的识别效果, 有利于卷积神经网络模型对图像特征进行学习, 把电机原图像删掉空白和坐标部分之后变换为灰度图, 为了使卷积神经网络更方便的计算和训练, 将图片压缩为28×28的尺寸大小, 如图2所示, 然后将处理后的图像制作成数据集并用于实验中. 由于在实验数据台上模拟出来的电机状态有限, 本文只研究了这3种状态, 在相同的环境下, 每个不同状态下采集了800个数据, 随机选取不同电机状态样本的20%作为测试数据, 剩余的作为训练数据.

|
图 2 部分图像的预处理 |
实验中, 如图2所示, 为了能更好地从多方位了解电机运行时的工作特点, 比较不同方向采集的电机数据图像发现, 热像仪对电机运行时所采集的图像, 由于在采集时温度差的不同导致图像轮廓清晰度不同, 但在最后识别之后得到的都是相同的结果.
3 实验结果与分析 3.1 实验对比分析本文以Matlab为基础搭建神经网络模型, 实验中所使用的数据集是根据实验室平台而构建的, 首先搭建卷积神经网络模型, 使用Matlab搭建卷积神经网络模型, 运用了梯度下降法对模型进行优化, 用评价指标来对网络的识别性能进行评价. 在对电机运行状态进行识别时, 将随机失活函数、NLWTCE与卷积神经网络模型结合, 来实现对电机运行状态进行识别. 使用Dropout函数来减少网络模型过拟合的产生, NLWT提高模型的准确率, 从而完成电机故障的诊断. 该实验平台主要由电力电子技术及电机控制实验装置、电机、热像仪和计算机组成. 在电机运行状态下, 将电机分为3种不同的电机状态, 即停止状态、正常运行和异常状态.
将预处理后的图像输入到所改进的卷积神经网络模型, 实验结果显示如图3所示, 将非线性小波变换图像增强和没有加图像增强的情况下进行了对比, 可以发现, 再加入NLWT图像增强之后的识别效果更好, 经过多次迭代后其损失值和准确率都能达到很好地识别效果, 验证了我们改进的CNN方法能够快速有效地识别, 完成电机的运行状态识别.
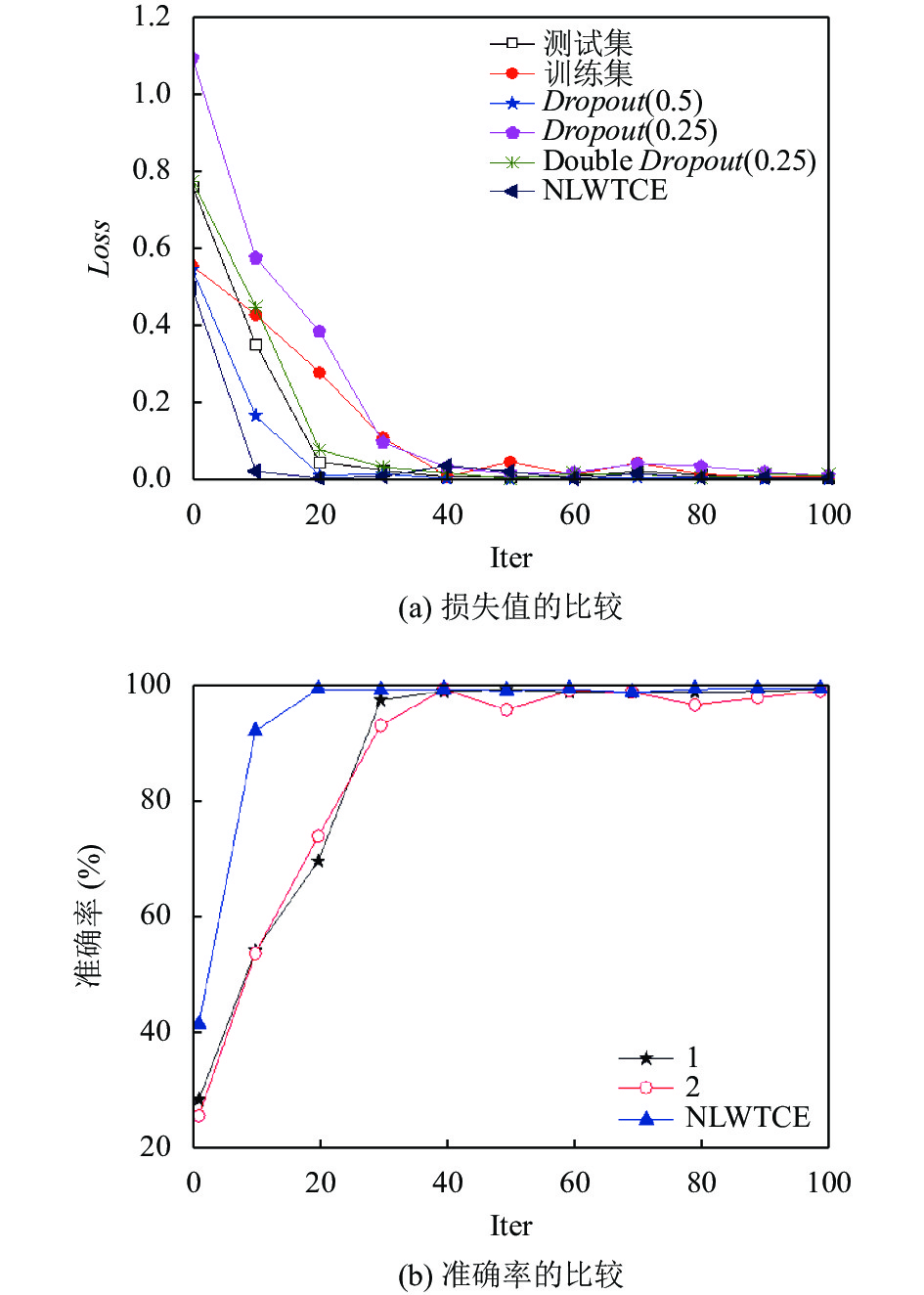
|
图 3 数据图像在不同迭代次数时的对比 |
由图3显示, 随着迭代次数的不断增加, 模型在运行时其损失函数的值不断减小最后趋向于零, 且准确率不断增大最后逐渐趋向于1, 准确率是指在测试过程中网络模型的识别成功率. 将本文所提出的NLWT系数增强的随机失活CNN在不同Dropout概率值下进行到100次迭代次数电机故障识别的实验对比; 将图像数据直接输入到网络模型中, 如表2和图3所示, 电机故障识别的准确率与损失值的在不同Dropout下对比情况. 本文所改进的方法中, 在迭代次数较小的情况下, 故障识别的损失值和准确率都比较差, 相对来说, 在加入NLWT图像增强的Dropout概率值为0.5时的损失值和准确率均比Dropout(0)、Dropout(0.25)和double Dropout(0.25)时的情况还要好. 在使用NLWT对数据进行图像增强后, 识别精度和损失函数值相对地都有所提高并能更快的趋于稳定. 通过实验结果分析可知, 本文所提出的基于NLWT系数增强的随机失活CNN故障识别准确率和损失值上表现的更有优势. 在卷积神经网络中, 对该模型进行100次迭代实验, 由实验结果可知, 在迭代次数达到40时, 测试集在网络模型中的损失值为1.5%, 准确率为99.5%, 在迭代40次之后, 随着迭代次数的增加, 其损失值和准确率趋于稳定或不变, 网络模型在运行时所需要耗费的时间随着迭代次数的增大而增加, 为了确保网络模型的损失值小且准确率高的情况下, 也要保准运行时间要尽可能的少, 所以本文的迭代次数选取40次. 分析实验的方法是NLWT系数增强的随机失活CNN电机运行状态识别.
| 表 2 不同迭代次数在不同Dropout值下准确率的比较(%) |
3.2 WTCE与NLWTCE实验结果对比分析
为了验证本方法的优越性, 将本文方法NLWTCE与小波变换数据增强(WTCE)的实验结果进行了比较, 图4为WTCE与NLWTCE在不同学习率下损失值的趋势.
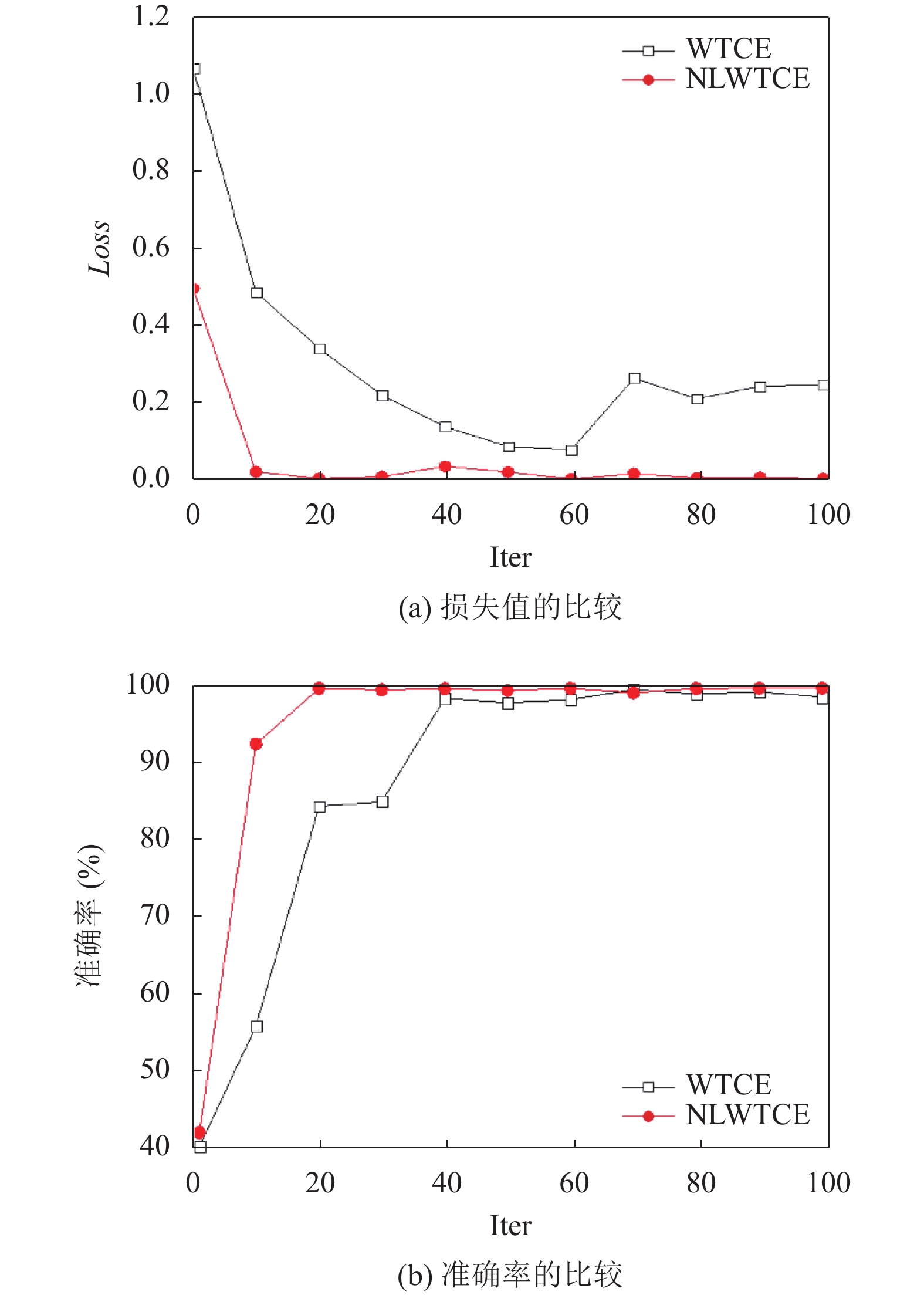
图5为WTCE与NLWTCE在不同迭代次数时准确率的趋势.
从图4、图5的比较结果表明, 学习率过小、过大都会导致损失值过大且准确率降低, 但在学习率适中时, NLWTCE的损失值相对更小以及准确率更高且稳定; WTCE和NLWTCE的损失值都会随着迭代次数的增加而逐渐降低, 识别准确率随着迭代次数的增加逐渐升高最后趋于稳定, 但NLWT的实验结果效果更好; 可以看出NLWTCE的实验结果有较好的性能, 该方法在保证识别准确率的前提下, 其迭代次数比较少, 所需要的训练样本越少, 可以节省实验时间, 则该方法能更好地对数据图像进行识别. 相比基于WTCE的学习算法, 在相同的训练样本集下, 本文提出的NLWTCE的随机失活CNN的电机运行状态识别准确率最好, 具有更高的可行性和操作性.
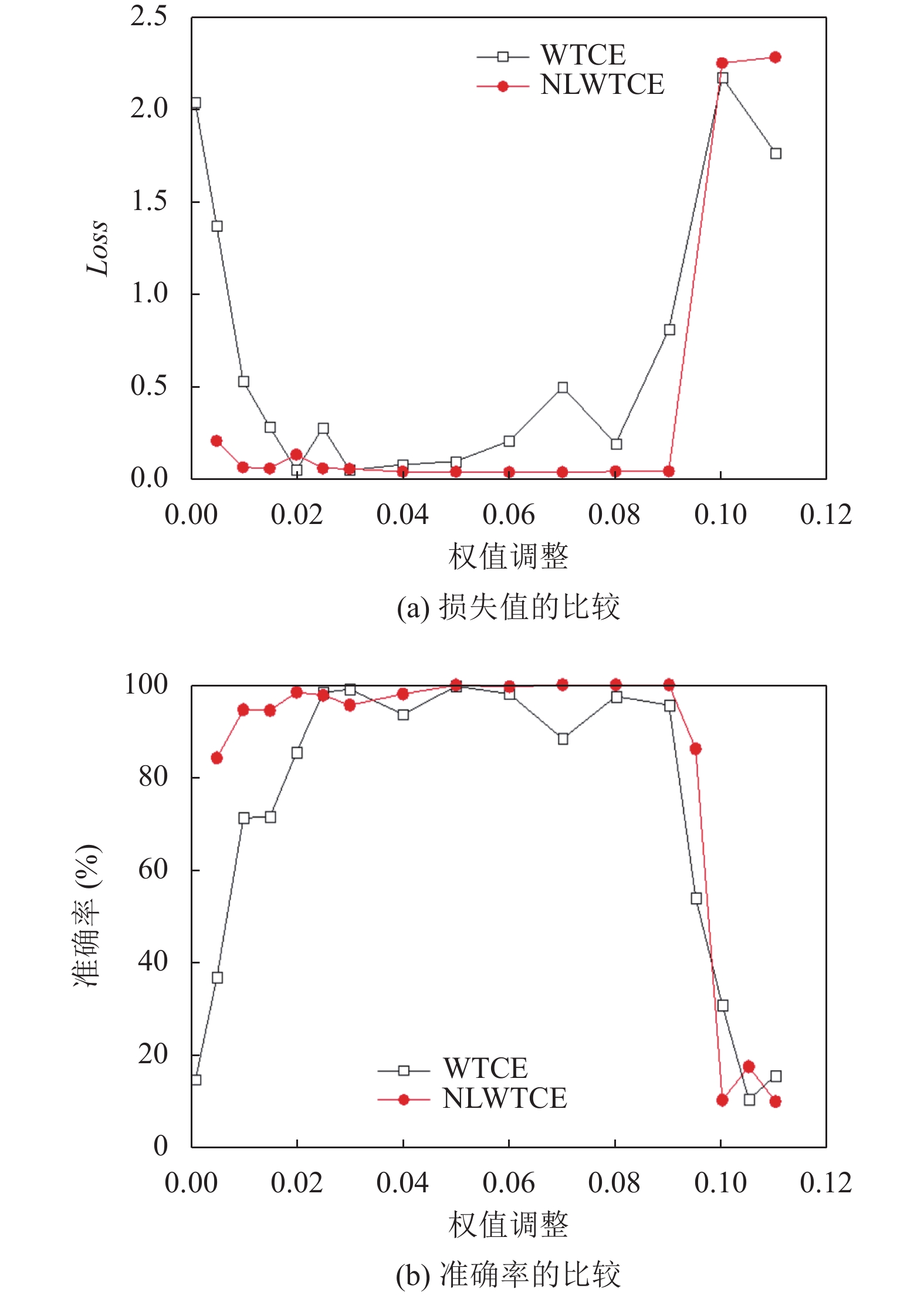
|
图 4 WTCE与NLWTCE在不同学习率时 |
3.3 实验结果
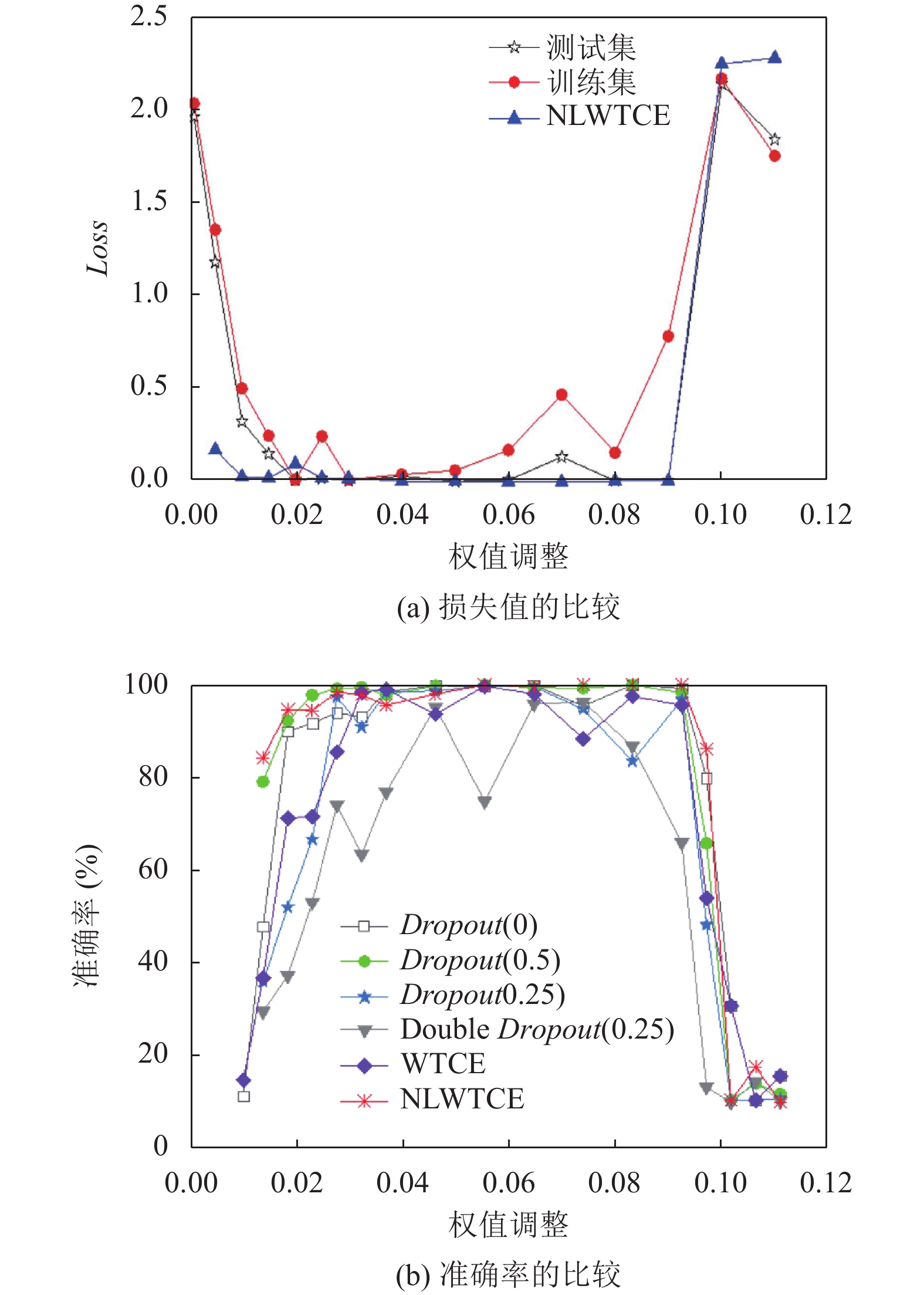
将预处理后的数据集输入到本文改进的CNN模型, 运用NLWT对图像进行增强、Dropout函数对模型进行优化, 其中权值调整是影响误差收敛、评价指标的一个重要参数. 在网络模型训练中, 为了提高模型运行的效率, 选择一个合适的权值调整步进是相当重要的, 在实验中, 我们在保持其余参数相同时, 采用不同的权值调整来训练卷积神经网络模型, 实验结果如图6所示. 从图6可以看出, 权值调整步进过大或者过小网络模型的识别准确率都会减小, 训练和测试时的损失函数都会增大; 图6(b)可以看出, Dropout概率值为0.5时, 其识别准确率相比效果是最好的. 在模型中, 选择一个合适的权值调整参数, 能够使网络模型更快的收敛, 减少其损失值, 还能提高模型的准确率. 在保证损失值小且准确率高的情况下, 本文实验选取的权值调整参数为0.03.
|
图 5 WTCE与NLWTCE在不同迭代次数时 |
在使用NLWT对数据图像进行增强之后, 电机识别准确率和损失函数相对来说效果更好. 随机失活函数在模型运行时能避免产生过拟合, 而NLWT图像增强保证了识别的准确率; 在模型运行时随机失活函数和NLWTCE既能防止过拟合的产生又能保证识别准确率.
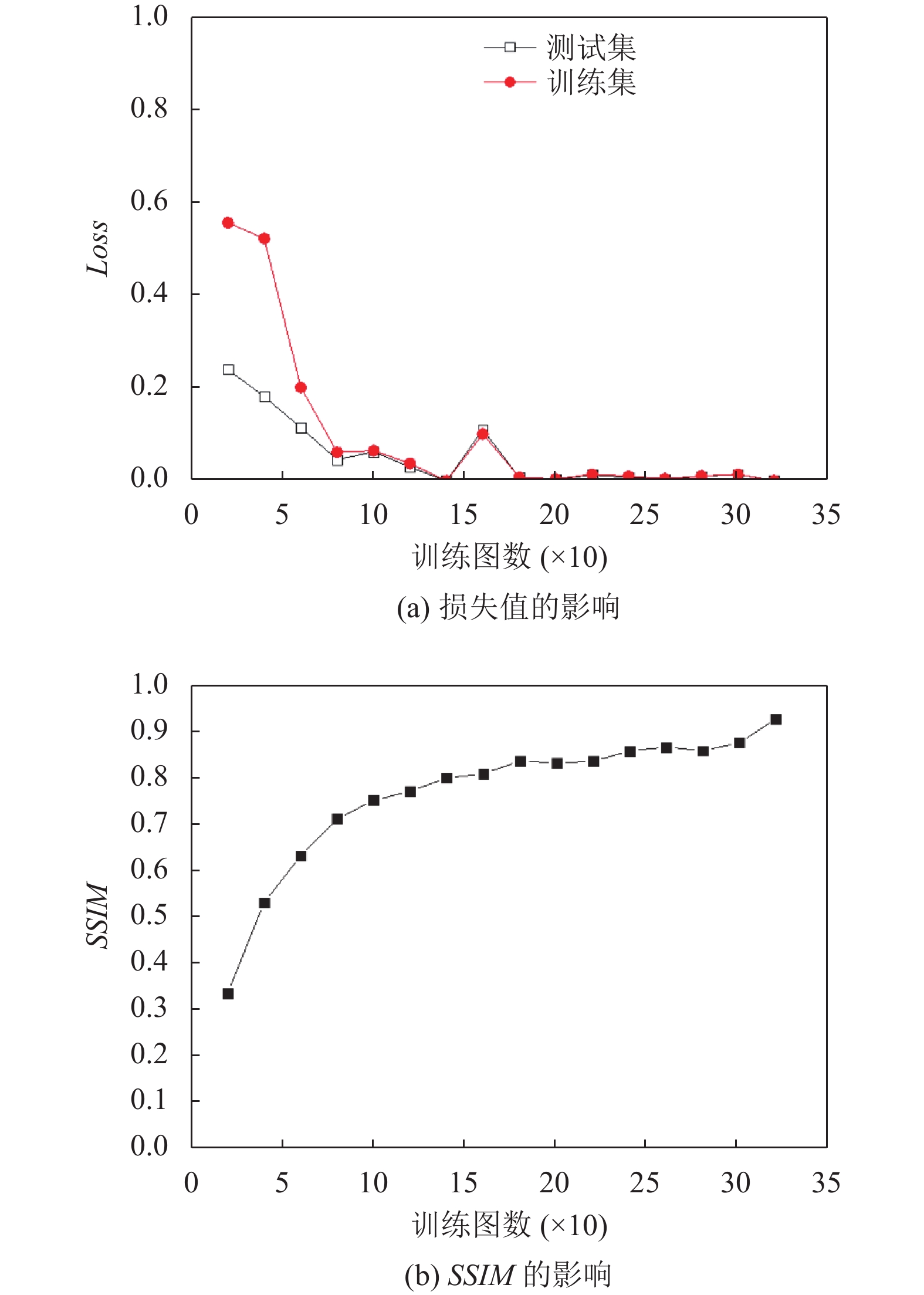
在网络模型中, 由于样本数大、电脑配置等条件限制, 无法一次将全部样本用于网络训练, 在保持其他参数不变的情况下, 本实验在对训练图的数量进行改变, 其实验结果如图7所示, 在训练图数量在不断地增加的同时, 其训练集和测试集的损失值不断减少, 且SSIM在不断增加, 但网络模型训练所花费的时间也在不断增加. 从实验结果可以看出, 当训练图很少时, 网络模型训练和测试的损失值相对来说比较大, 且SSIM相对较低. 当训练样本越来越大时, 模型训练和测试的损失值越来越低, SSIM越来越高, 但网络模型运行一次所需要的时间却越来越多. 在实验中, 所采用的训练数为20, 在保证了损失值、准确率和SSIM的同时, 还相对降低了训练的时间.
|
图 6 数据图像在不同学习率下的比较 |
4 结语
本文利用NLWT图像增强、改进的卷积神经网络实现了电机运行状态的识别. 在CNN中, 选择合适的参数是相当重要的, 实验结果显示, 改进的卷积神经网络在迭代次数和训练样本小以及权值调整过大或过小的情况下, 对电机的运行状态识别都有一定的影响, 识别的损失函数值相对来说都比较大且识别的准确率也会过低, 但在选择合适的迭代次数、权值调整和训练样本数时, 电机故障识别的准确率均达到97%以上, 随机失活函数可以很好地避免过拟合的产生, 而NLWT图像增强能很好地保证电机故障识别的精度, 通过两者结合能更有效地对电机的运行状态进行识别. 通过实验结果对比可知, 本文所提出的方法在电机运行状态识别的准确率和损失值上均表现出了明显的优势, 效果更好.
|
图 7 数据图像在不同训练图数的影响 |
| [1] |
李亚召, 云利军, 叶志霞, 等. 基于卷积神经网络的霉变烟叶图像识别方法研究. 计算机工程与科学, 2021, 43(3): 473-479. DOI:10.3969/j.issn.1007-130X.2021.03.012 |
| [2] |
刘欢, 陈力, 田建涛, 等. 红外诊断技术在电机故障诊断中的应用. 装备制造技术, 2014(9): 255-256, 262. DOI:10.3969/j.issn.1672-545X.2014.09.096 |
| [3] |
王新杰, 董志学, 潘颖辉. 机车牵引电机声音检测与故障诊断系统应用研究. 计算机应用与软件, 2016, 33(10): 103-107, 171. DOI:10.3969/j.issn.1000-386x.2016.10.023 |
| [4] |
张明杰, 曾祥东. HXN3型机车牵引电机故障诊断技术研究. 中国新技术新产品, 2016(2): 44-45. DOI:10.13612/j.cnki.cntp.2016.02.034 |
| [5] |
郑小霞, 周国旺, 任浩翰, 等. 基于变分模态分解和排列熵的滚动轴承故障诊断. 振动与冲击, 2017, 36(22): 22-28. DOI:10.13465/j.cnki.jvs.2017.22.004 |
| [6] |
胡耀斌, 谢静, 胡良斌. 基于神经网络与小波变换的滚动轴承故障诊断. 机械设计与研究, 2013, 29(6): 33-35. DOI:10.13952/j.cnki.jofmdr.2013.06.011 |
| [7] |
Wang F, Jiang HK, Shao HD, et al. An adaptive deep convolutional neural network for rolling bearing fault diagnosis. Measurement Science and Technology, 2017, 28(9): 095005. DOI:10.1088/1361-6501/aa6e22 |
| [8] |
符羽. 基于卷积神经网络的三相异步电机故障诊断方法研究[硕士学位论文]. 南昌: 华东交通大学, 2021.
|
| [9] |
李志军, 陈伟根, 周湶, 等. 基于改进深度学习混合网络与小波分析的电机故障诊断方法. 三峡大学学报(自然科学版), 2021, 43(6): 94-99. DOI:10.13393/j.cnki.issn.1672-948x.2021.06.015 |
| [10] |
Sun TC, Wang YL, Yang J, et al. Convolution neural networks with two pathways for image style recognition. IEEE Transactions on Image Processing, 2017, 26(9): 4102-4113. DOI:10.1109/TIP.2017.2710631 |
| [11] |
王红君, 刘冬生, 岳有军. 基于小波分析和神经网络的电机故障诊断方法研究. 电气传动, 2010, 40(3): 69-73. DOI:10.3969/j.issn.1001-2095.2010.03.017 |
| [12] |
杨柏. 基于改进卷积神经网络永磁电机故障诊断方法研究[硕士学位论文]. 沈阳: 沈阳工程学院, 2020.
|
| [13] |
毛向向, 王红军, 韩凤霞, 等. 基于深度卷积神经网络的机电系统故障分类识别方法. 电子测量与仪器学报, 2021, 35(2): 87-93. DOI:10.13382/j.jemi.B2003659 |
| [14] |
Zhou YC, Gao ZX. Intelligent recognition of medical motion image combining convolutional neural network with Internet of Things. IEEE Access, 2019, 7: 145462-145476. DOI:10.1109/ACCESS.2019.2945313 |
| [15] |
Wang Z, Bovik AC, Sheikh HR, et al. Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
 2023, Vol. 32
2023, Vol. 32



