随着经济社会的发展, 自行车从传统代步工具逐步演变为集交通旅游、健身竞技为一体的重要工具. 由于自行车骑行运动既方便, 也不受年龄性别限制的特点, 自行车骑行逐渐成为一项全民运动. 然而, 人在长时间骑行过程中, 不规范的自行车骑行姿势不仅会使运动效果大打折扣, 而且容易造成肌肉骨骼系统慢性疾病, 严重者出现关节损伤等状况. 同时, 对于规范骑行运动的研究多数未考虑个体及骑行场景的不同, 不具有广泛的参考价值. 因此, 通过计算机仿真技术, 实现规范骑行动作的参数化模拟, 有助于帮助骑行者纠正骑行姿势, 指导骑行者规范骑行、改善骑行体验.

近年来, 计算机与网络技术不断发展^[1], 广大国内外研究学者将计算机仿真技术应用于骑行运动过程中, 分析整个骑行过程, 推动了骑行运动仿真的发展, 并取得了一些成果. 高飞等^[2]以公路自行车为例, 通过Anybody软件创建人-车系统模型并进行一系列仿真, 分析了自行车速度、车座与人体肌肉受力间的关系. 孟杰等^[3]以山地自行车为例, 在LifeMOD软件中利用数字仿真模型数据包, 建立人-车耦合系统, 分析骑行动作与骑行周期, 研究了人体下肢肌肉的工作情况. 谢宏宇等^[4]研究骑行过程中人体下肢运动学和动力学, 运用矢量方程解析法和牛顿-欧拉法完成动力学方程推导, 并对各个关节角度求解, 在ADAMS环境下进行仿真验证. 严旎伟等^[5]在CATIA中建立自行车模型, 并利用ADAMS软件进行骑行仿真, 从而分析自行车稳态转向的原因.

李晓娜等^[6]利用生物力学软件ADAMS和Life-MOD软件建立人-车系统模型并进行仿真与分析, 研究了人在骑自行车过程中下肢主要肌肉和关节的反应, 并通过调节车座的高度进行对比, 简单分析了2种不同骑行状态对人骑行舒适度的影响, 进而发现疲劳产生的可能原因, 为自行车的舒适性设计提供参考. Wang^[7]使用SolidWorks软件实现基于人体工程学的骑马机三维建模, 通过机构的运动学分析建立鞍座、踏板和扶手的位置方程, 并确定了每个组件的最佳长度.

Thejasree等^[8]讨论了在Matlab/Simulink环境中开发的电动自行车数学模型, 研究了与自行车相关的动力学方程. Han等^[9]实现一种用于传统自行车的新型驱动系统的可行性研究, 将腿部-自行车系统建模为与原始五连杆物理模型等效的四连杆机. Machida等^[10]对竞赛人自行车系统进行仿真, 分析出骑行者站立于踏板时, 膝关节扭矩和曲柄扭矩在动力阶段增加, 而曲柄扭矩在恢复阶段减少. 目前骑行运动仿真研究成果主要集中在骑行过程中的动力学和运动学分析以及骑行过程的仿真, 对规范骑行参数化过程的相关研究较少, 难以对规范骑行提供参数方面的指导作用.

考虑到不同身高的骑行者在长时间骑行过程中, 不仅骑行姿态各异, 而且骑行姿势普遍存在错误的问题, 本文提出一种用于规范骑行的参数化建模方法, 指导骑行者使用正确的骑行姿势. 首先, 创建人体模型和自行车模型并进行语义参数定义, 通过语义参数控制模型的形态变化; 其次, 分析骑行过程中人-车系统受力情况, 构建动力学模型; 最后, 结合人机工程学、机器人运动学建立骑行过程中人车参数间约束关系, 实现人体与自行车模型的动态合一.

1 论文框架

为指导骑行者使用规范的姿势骑行, 本文提出了一种用于规范骑行的参数化建模方法, 具体流程如图1所示.

实现步骤如下.

Step 1. 自行车的模型构建及参数化定义. 根据自行车几何数据, 构建自行车模型, 定义自行车模型部件的语义参数.

Step 2. 人体的模型构建及参数化定义. 根据人体结构特征, 通过骨骼绑定与权重绘制重建人体三维模型, 对参与骑行运动的人体关节进行语义参数定义, 设置关节层级关系.

Step 3. 骑行规范参数化. 对骑行过程中的自行车进行动力学分析, 建立动力学模型, 使虚拟骑行符合自然规律. 通过骑行姿态的变化, 分析关节运动, 根据人体下肢和上肢为骑行过程中主要活动部位, 构建自行车参数与人体上下肢参数之间的约束关系, 实现人-车协调规范运动.

2 自行车模型构建及参数化定义

本文在实体模型几何和图像数据的基础上, 创建自行车模型, 并进行语义参数定义, 通过语义参数控制模型的形态变化.

2.1 自行车模型的构建

通过几何和图像相结合的建模技术, 构建自行车三维模型. 具体步骤如下.

Step 1. 采集模型数据. 通过拆卸得到竹子自行车零部件, 采集自行车的三维数据, 利用相机拍摄其正视图、侧视图和俯视图信息.

Step 2. 构建基础模型. 根据模型数据, 使用3ds Max中的基础建模, 建立自行车的三维模型, 并利用可编辑多边形修改器, 精准配准模型顶点、边、面, 得到基础模型.

Step 3. 添加材质和贴图. 参照实际物体的颜色和光照, 选取模型材质, 利用材质编辑器修改材质属性并进行光照处理, 使模型在外观上更加贴近真实模型.

Step 4. 模型优化. 考虑到成品模型的顶点、边和面数量较多, 利用基于二次误差矩阵(quadric error metrics, QEM)的边折叠简化算法^{[11, 12]}, 减少模型的边、面和顶点数, 降低模型几何数据冗余度, 模型制作后效果如图2所示.

2.2 自行车语义参数定义

由于在骑行过程中, 自行车部分部件相对车架存在几何偏移, 如车轮的旋转、曲柄的旋转等, 因此本文将自行车部件划分为静态部件和动态部件两类. 将静态部件外的曲柄、前轮、后轮、脚踏、坐垫等动态部件进行语义参数定义. 以特征点、模型动态部件参数、描述自行车形状特征的语义参数分别作为自行车的底层参数、中间层参数及高层参数.

自行车模型特征 $ {F_C} $ 可表示为:

$ \left\{ \begin{aligned} &{F_C} = \{ C, R\} \\ & C = \{ {C_1}, {C_2}\} , {C_1} = \{ {C_{W1}}, {C_F}, {C_{HM}},\cdots\} \\ & {C_2} = \{ {C_{W1A}}, {C_{W1B}}, {C_{STH}},{C_{STL}},\cdots\} \\ &R = \{ {R_{\text{l}}}, {R_m}, {R_h}\} \\ \end{aligned} \right. $

(1)

其中, $ {F_C} $ 包括特征点 $ C $ 和语义参数 $ R $ ; 特征点 $ C $ 包括自行车部件中心特征点集合 $ {C_1} $ , 边缘特征点集合 $ {C_2} $ , 中心特征点和边缘特征点共同控制自行车部件长度、高度、半径和旋转角参数; 语义参数 $ R $ 包括底层参数 $ {R_1} $ 、中间层参数 $ {R_m} $ 、高层参数 $ {R_h} $ .

图3(a)表示自行车侧视图中特征点与语义参数定义. $ {C_{W1}} $ 、 $ {C_{W2}} $ 、 $ {C_F} $ 、 $ {C_{HM}} $ 、 $ {C_{HM}} $ 、 $ {C_{CR}} $ 、 $ {C_C} $ 、 $ {C_{S2}} $ 、 $ {C_{ST}} $ 为前车轮、后车轮、前叉、把横、曲柄、车架、坐垫、座管部件的几何中心位置. $ {C_{S1}} $ 、 $ {C_{STH}} $ 、 $ {C_{STL}} $ 、 $ {C_{SA}} $ 、 $ {C_{W2A}} $ 、 $ {C_{W1A}} $ 、 $ {C_{W1B}} $ 、 $ {C_{W2B}} $ 、 $ {C_{PR1}} $ 、 $ {C_{PR2}} $ 、 $ {C_{HM}} $ 为边缘特征点, 其中线段 $ {C_{HM}} $ $ {C_{SA}} $ 和 $ {C_{SA}} $ $ {C_F} $ 形成的夹角控制把立旋转角度 $ {\alpha _{SA}} $ ; 线段 $ {C_{W1B}} $ $ {C_{W2B}} $ 和 $ xy $ 水平面形成的夹角控制自行车仰角参数 $ {\alpha _E} $ ; 线段 $ {C_{CR1}} $ $ {C_{CR}} $ 和线段 $ {C_{CR}} $ $ {C_{CR2}} $ 形成的夹角控制曲柄旋转角度 $ {\alpha _{CR}} $ ; 线段 $ {C_{PR1}} $ $ {C_{PR2}} $ 和水平面形成的夹角控制右踏板旋转角度参数 $ {\alpha _{PL}} $ ; $ {C_G} $ 和 $ {C_{STH}} $ 控制坐垫前后移动距离 $ {L_{S1}} $ ; $ {C_{STH}} $ 和 $ {C_{STL}} $ 控制坐垫上下移动距离 $ {L_{S2}} $ ; $ {C_{W1B}} $ 控制前车轮半径参数 $ {R_{W1}} $ ; $ {C_{W2B}} $ 控制后车轮半径参数 $ {R_{W2}} $ ; $ {C_{CR}} $ 和 $ {C_{CR2}} $ 控制曲柄臂长度 $ {L_{CR}} $ ; $ {C_S} $ 和 $ {C_{W2B}} $ 控制自行车高度参数 $ {H_C} $ ; $ {C_{W1A}} $ 和 $ {C_{W2A}} $ 控制自行车长度参数 $ {L_C} $ ; 线段 $ {C_{W1B}} $ $ {C_{W2B}} $ 和水平面形成的夹角控制自行车仰角参数 $ {\alpha _E} $ .

图3(b)表示自行车俯视图中特征点与语义参数定义. 其中 $ {C_{PR}} $ 、 $ {C_{PL}} $ 为右踏板、左踏板部件几何中心位置. 边缘中心点 $ {C_{HR}} $ 、 $ {C_{HL}} $ 表示左右车把部件表面中心位置. $ {C_{HR}} $ 、 $ {C_{HL}} $ 、 $ {C_{PR}} $ 、 $ {C_{PL}} $ 分别控制人体右手掌、左手掌、右脚掌、左脚掌接触点位置; $ {C_{HM}} $ 、 $ {C_{HL}} $ 控制把横旋转角度 $ {\alpha _{HM}} $ ; 线段 $ {C_{HM}} $ $ {C_{SA}} $ 和线段 $ {C_{W2A}} $ $ {C_F} $ 形成的夹角控制前叉转角参数 $ {\alpha _F} $ ; $ {C_{W2'}} $ 控制后车轮旋转角参数 $ {\alpha _{W1}} $ ; $ {C_{W1'}} $ 控制前车轮旋转角 $ {\alpha _{W2}} $ ; 线段 $ {C_F} $ $ {C_{W2A}} $ 和 $ xy $ 平面形成的夹角控制自行车水平转角参数 $ {\alpha _B} $ .

结合式(1), 自行车模型特征 $ {F_C} $ 表示如下:

$ \begin{gathered} {F_C} = \left\{ \begin{aligned} &{C_1} = \{ {C_{W1}}, {C_{W2}}, {C_F}, {C_{HM}}, {C_{CR}}, {C_C}, {C_{S2}}, {C_{ST}},\\ & \qquad\; {C_{PR}}, {C_{PL}}\} \\ & {C_2} = \{ {C_S}, {C_{S1}}, {C_{SA}}, {C_{STH}}, {C_{STL}}, {C_{W2A}}, {C_{W1A}},\\ &\qquad\; {C_{W1B}}, {C_{W2A, }}{C_{W2B}}, {C_{PR1}}, {C_{PR2}}, {C_{HR}}, {C_{HL}}\} \\ & {R_l} = \{ ({x_1}, {y_1}, {{\textit{z}}_1}), ({x_2}, {y_2}, {{\textit{z}}_2}), ({x_3}, {y_3}, {{\textit{z}}_3}), \cdots ,\\ &\qquad\; ({x_{22}}, {y_{22}}, {{\textit{z}}_{22}}) \} \\ &{R_m} = \{ {R_{W1}}, {R_{W2}}, {L_{CR}}, {L_{S1}}, {L_{S2}}, {\alpha _{SA}}, {\alpha _{CR}}, {\alpha _{PL}},\\ & \qquad\; {\alpha _{W1}}, {\alpha _{W2}}, {\alpha _F}, {\alpha _{HM}}\} \\ &{R_{{h}}} = \{ {H_C}, {L_C}, {\alpha _B}, {\alpha _E}\} \end{aligned} \right. \end{gathered} $

(2)

3 人体模型构建及参数化定义

在骑行时, 骑行者在不断运动, 为使人体模型可在骑行过程中实现人体姿态动态调整, 本文根据人体结构, 对人体模型建模, 并对重建后的模型进行参数化定义及人体关节层级关系设置, 实现语义参数控制模型变化.

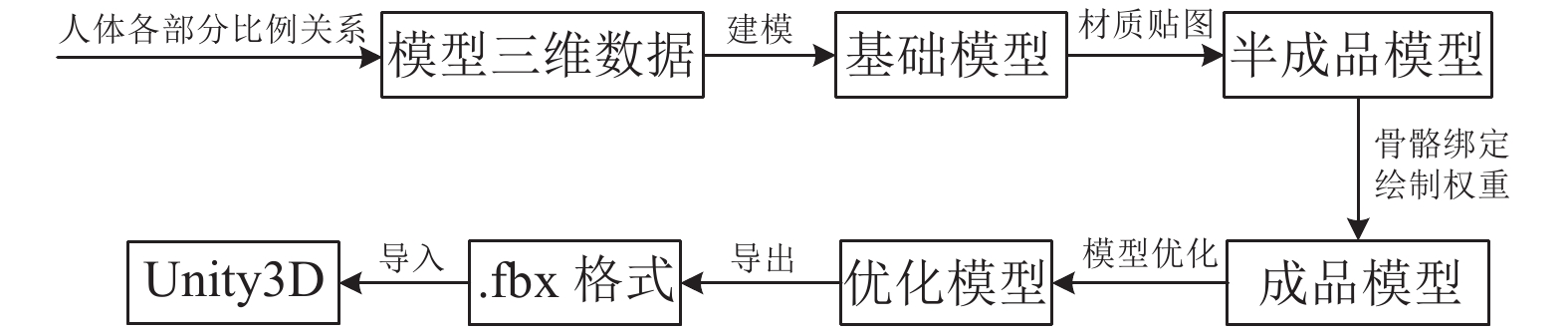
3.1 人体模型的构建

人体模型构建流程与自行车模型构建流程类似, 如图4(a)所示. 但存在两点不同: 其一, 人体模型数据来源于人体结构各部分比例关系^[13]. 其二, 得到半成品模型后需进行骨骼绑定和权重绘制. 骨骼绑定的作用是使创建的模型受控制器控制移动, 人体关节能和真实关节一样做关节运动. 权重是指骨骼对模型上点的控制权, 一根骨骼可控制多个顶点, 同时一个顶点也可被多个骨骼控制, 通过绘制权重使得关节运动与模型变形更加合理. 为方便骑行者了解骑行姿势, 本文在保留人体整体特征的前提下, 对人体结构进行精简.

3.2 人体语义参数定义

为了在骑行过程中能够根据自行车参数, 实时调整人体参数, 本文建立3层语义参数, 分别为人体模型内部特征点参数、人体模型结构参数、人体模型形状特征参数, 实现人体模型参数化.

人体模型特征 $ {F_H} $ 可表示为:

$ \left\{ \begin{aligned} &{F_H} = \{ P, R\} \\ &P = \{ {P_1}, {P_2}\} \\&{P_1} = \{ {P_{WR}}, {P_{ER}}, {P_L}, {P_{KL}},\cdots\} \\ &{P_2} = \{ {P_T}, {P_{FR}}, {P_M}, {P_{BR}}, {P_{BL}}, {P_{FL}}\} \\ &R = \{ {R_{\text{l}}}, {R_m}, {R_h}\} \\ \end{aligned} \right. $

(3)

$ {F_H} $ 包括特征点 $ P $ 和语义参数 $ R $ ; 特征点 $ P $ 包括人体关节中心特征点集合 $ {P_1} $ 和边缘特征点集合 $ {P_2} $ , 用于控制人体结构各部位的长度参数与关节角参数; 语义参数 $ R $ 包括底层参数 $ {R_1} $ , 中间层参数 $ {R_m} $ , 高层参数 $ {R_h} $ .

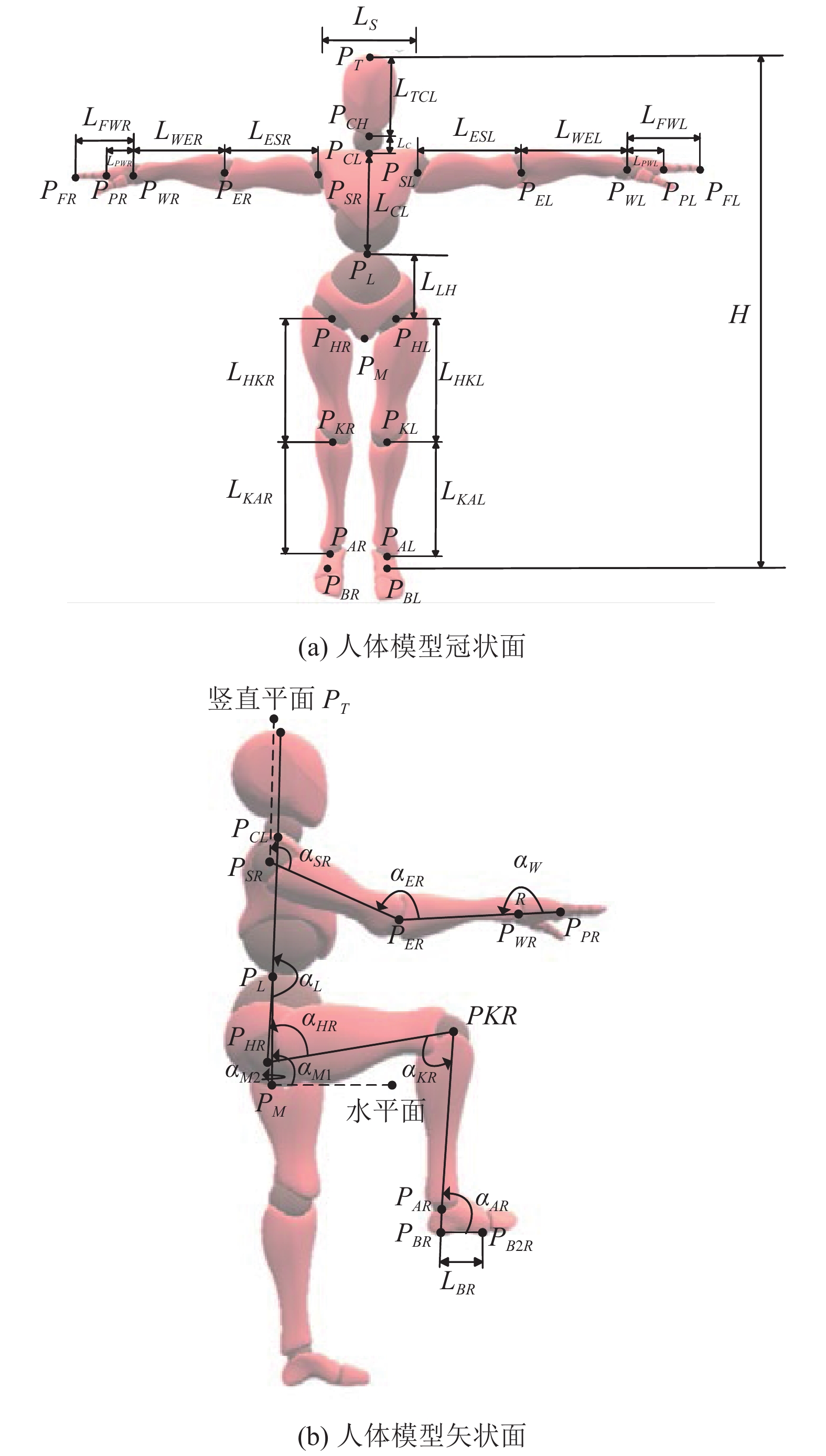
人体三维模型在冠状面特征点与语义参数定义如图5(a)所示, 其中 $ {P_{CH}} $ 、 $ {P_{CL}} $ 、 $ {P_{SR}} $ 、 $ {P_{ER}} $ 、 $ {P_{WR}} $ 、 $ {P_{PR}} $ 、 $ {P_{SL}} $ 、 $ {P_{EL}} $ 、 $ {P_{WL}} $ 、 $ {P_{PL}} $ 、 $ {P_L} $ 、 $ {P_{HR}} $ 、 $ {P_{KR}} $ 、 $ {P_{AR}} $ 、 $ {P_{HL}} $ 、 $ {P_{KL}} $ 、 $ {P_{AL}} $ 为人体关节中心位置特征点. $ {P_T} $ 、 $ {P_{FR}} $ 、 $ {P_{FL}} $ 、 $ {P_M} $ 、 $ {P_{BR}} $ 、 $ {P_{BL}} $ 分别表示头部最顶端、右臂最右端、左臂最左端、裆部最下端、右脚最下端和左脚最下端. $ {P_T} $ 、 $ {P_{CH}} $ 控制头部长度 $ {L_{TCL}} $ ; $ {P_{CH}} $ 、 $ {P_{CL}} $ 控制颈部长度 $ {L_C} $ ; $ {P_{SR}} $ 、 $ {P_{SL}} $ 控制肩部长度 $ {L_S} $ ; $ {P_{SR}} $ 、 $ {P_{ER}} $ 控制右上臂长度 $ {L_{ESR}} $ ; $ {P_{ER}} $ 、 $ {P_{WR}} $ 控制右前臂长度 $ {L_{WER}} $ ; $ {P_{PR}} $ 、 $ {P_{WR}} $ 控制右手掌长度 $ {L_{PWR}} $ ; $ {P_{ER}} $ 、 $ {P_{WR}} $ 控制右手长度 $ {L_{FWR}} $ ; $ {P_{SL}} $ 、 $ {P_{EL}} $ 控制左上臂长度 $ {L_{ESL}} $ ; $ {P_{EL}} $ 、 $ {P_{WL}} $ 控制左前臂长度 $ {L_{WEL}} $ ; $ {P_{WL}} $ 、 $ {P_{PL}} $ 控制左手掌长度 $ {L_{PWL}} $ ; $ {P_{WL}} $ 、 $ {P_{FL}} $ 控制左手长度参 $ {L_{FWL}} $ ; $ {P_{CL}} $ 、 $ {P_L} $ 控制躯干上段长度 $ {L_{CL}} $ ; $ {P_L} $ 、 $ {P_M} $ 控制躯干下段长度 $ {L_{LH}} $ ; $ {P_{HR}} $ 、 $ {P_{KR}} $ 控制右大腿长度 $ {L_{HKR}} $ ; $ {P_{KR}} $ 、 $ {P_{AR}} $ 控制右小腿长度 $ {L_{KAR}} $ ; $ {P_{HL}} $ 、 $ {P_{KL}} $ 控制左大腿长度 $ {L_{HKL}} $ ; $ {P_{KL}} $ 、 $ {P_{AL}} $ 控制右小腿长度 $ {L_{KAL}} $ ; $ H $ 为人体身高参数.

人体三维模型在矢状面特征点与语义参数定义如图5(b)表示, 其中 $ {P_{B2R}} $ 为边缘特征点, 定义在右前脚掌底部. $ {P_{BR}} $ 、 $ {P_{B2R}} $ 控制右脚掌有效长度; 线段 $ {P_{SR}} $ $ {P_{ER}} $ 与竖直平面形成的夹角控制右上肢肩关节角度 $ {\alpha _{SR}} $ ; 线段 $ {P_{SR}} $ $ {P_{ER}} $ 和线段 $ {P_{ER}} $ $ {P_{WR}} $ 形成的夹角控制右上肢肘关节角度 $ {\alpha _{ER}} $ ; 线段 $ {P_{ER}} $ $ {P_{WR}} $ 和线段 $ {P_{WR}} $ $ {P_{PR}} $ 形成的夹角控制右上肢腕关节角度 $ {\alpha _{WR}} $ ; 线段 $ {P_{CL}} $ $ {P_L} $ 和线段 $ {P_L} $ $ {P_M} $ 形成的控制腰椎关节角度 $ {\alpha _L} $ ; 线段 $ {P_{HR}} $ $ {P_{KR}} $ 与竖直平面形成的夹角控制右下肢髋关节角度 $ {\alpha _{HR}} $ ; 线段 $ {P_{HR}} $ $ {P_{KR}} $ 和线段 $ {P_{KR}} $ $ {P_{AR}} $ 形成的夹角控制右下肢膝关节角度 $ {\alpha _{KR}} $ ; 线段 $ {P_{KR}} $ $ {P_{AR}} $ 和线段 $ {P_{AR}} $ $ {P_{BR}} $ 形成的夹角控制右下肢踝关节角度 $ {\alpha _{AR}} $ ; 同理左下肢关节角定义同右下肢关节角定义, 线段 $ {P_L} $ $ {P_M} $ 与水平面形成的夹角控制人体仰角 $ {\alpha _M} $ .

结合式(3), 人体三维模型特征 $ {F_H} $ 表示如下:

$ {F_H} = \left\{ \begin{aligned} &{P_{\text{1}}} = \{ {P_{CH}}, {P_{CL}}, {P_{SR}}, {P_{ER}}, {P_{WR}}, {P_{PR}}, {P_{SL}}, {P_{EL}}, {P_{WL}},\\ &\qquad {P_{PL}}, {P_L}, {P_{HR}}, {P_{KR}}, {P_{AR}}, {P_{HL}}, {P_{KL}}, {P_{AL}}\} \\ &{P_2} = \{ {P_T}, {P_{FR}}, {P_M}, {P_{BR}}, {P_{B2R}}, {P_{BL}}, {P_{FL}}\} \\ & {R_1} = \{ ({x_1}, {y_1}, {{\textit{z}}_1}), ({x_2}, {y_2}, {{\textit{z}}_2}), ({x_3}, {y_3}, {{\textit{z}}_3}), \cdots,\\ &\qquad ({x_{2{\text{3}}}}, {y_{2{\text{3}}}}, {{\textit{z}}_{2{\text{3}}}})\} \\ & {R_m} = \{ {L_S}, {L_{TCL}}, {L_C}, {L_{ESR}}, {L_{WER}}, {L_{PWR}}, {L_{FWR}}, {L_{ESL}}, \\ &\qquad {L_{WEL}}, {L_{PWL}}, {L_{FWL}}, {L_{CL}}, {L_{LH}}, {L_{HKR}}, {L_{KAR}}, \\ &\qquad {L_{HKL}}, {L_{KAL}}, {\alpha _{SR}}, {\alpha _{ER}}, {\alpha _{WR}}, {\alpha _L}, {\alpha _{HR}}, {\alpha _{KR}}, {\alpha _{AR}}\} \\ & {R_{{h}}} = \{ H, {\alpha _{M1}}, {\alpha _{M2}}\} \\ \end{aligned} \right. $

(4)

4 骑行规范参数化

骑行者在三维虚拟场景中骑行时, 要求骑行过程符合自然运动规律要求. 因此, 本文通过对骑行过程中人-车系统进行受力分析, 建立动力学方程, 实现虚拟环境骑行与真实环境负荷相一致; 并分析骑行过程中上下肢关节运动, 建立自行车参数与人体参数间约束关系, 实现人车合一.

4.1 人体语义参数定义

从骑行过程中人-车系统的受力出发, 进行动力学分析, 建立数学模型, 为后续骑行运动模拟提供理论支撑. 骑行过程中人-车系统受力示意图如图6所示.

在骑行过程中, 人-车系统整体主要受到重力 $ {F_g} $ 、地面支持力 $ {F_s} $ 、人-车系统迎风阻力 $ {F_d} $ , 车轮旋转时产生的空气阻力 ${F_{{w}}}$ , 轮胎与地面产生的摩擦力 $ {F_f} $ ^[14]. 在非水平路上骑行过程中, 重力 $ {F_g} $ 可分解成与运动方向同在一条直线上的分力 ${F_g{'}}$ , 以及与地面垂直的正压力 ${F_g{''}}$ . 上坡骑行过程中, ${F_g{'}}$ 方向与骑行方向相反; 下坡骑行过程中, ${F_g{'}}$ 方向与骑行方向相同. 在水平路上骑行, 重力将只提供等同重力大小的正压力作用. 运动方向的分力和正压力表达式为:

$ \left\{ \begin{gathered} {F_g{'}} = {F_g}\sin \theta = M{{g}}\sin \theta \\ {F_g{''}} = {F_g}\cos \theta = M{{g\cos}}\theta \\ \end{gathered} \right. $

(5)

其中, $ M $ 为人-车系统整体质量, $ \theta $ 为路面与水平面形成的夹角, 在上坡过程中 $ \theta $ 为正值, 下坡过程中 $ \theta $ 为负值, 平路骑行过程中 $ \theta $ 为0.

骑行者踩动踏板, 由链条带动后车轮转动, 地面产生与运动方向相同的摩擦力. 后车轮的运动推动前车轮运动, 地面产生阻碍自行车向前的摩擦力. 地面产生的摩擦力为:

$ {F_f} = {C_r}Mg\cos \theta $

(6)

其中, $ {C_r} $ 为轮胎与地面的滚动摩擦系数, 摩擦系数由路面状况和轮胎的材质决定.

骑行过程中, 向前运动时, 前方空气被压缩产生压力, 两侧表面与空气存在相对运动, 产生与运动方向相反的摩擦力, 共同形成阻碍骑行的空气阻力, 空气阻力表达式为:

$ {F_w} = \frac{1}{2}{C_d}A\rho {V^2} $

(7)

其中, $ C_{d} $ 为空气阻力系数, $ A $ 为迎风面最大横截面面积, $\; \rho $ 为当前所处海拔下空气的密度, $ V $ 为骑行过程中自行车与空气的相对速度.

在骑行过程中, 车轮旋转因非对称流体的动力效应, 产生旋转阻力. Greenwell等研究表明^[15], 旋转阻力大小由车轮半径以及轮毂的外形决定. 由于人体和自行车竖管的存在, 后车轮受到的空气阻力会减少25%, 同时考虑到自行车前后车轮半径相同, 因此前后车轮在转动过程中受到的空气阻力大小表达式为:

$ \begin{split} {F_d}& = {F_{fd}} + {F_{bd}} \\ &= \frac{1}{2}{C_w}\rho {V^2}\pi {r^2} + \frac{3}{4} \times \frac{1}{2}{C_w}\rho {V^2}\pi {r^2} \\ &=\frac{7}{8}{C_w}\rho {V^2}\pi {r^2} \end{split} $

(8)

其中, ${C_w}$ 为车轮空气阻力系数, $ \rho $ 为当前所处海拔下空气密度, $ V $ 为骑行过程中自行车与空气的相对速度, $ r $ 为车轮半径.

根据牛顿第二定律建立动力学方程, 如式(9):

$ F - {F_g{'}} - {F_f} - {F_w} - {F_d} = Ma $

(9)

其中, $ F $ 为骑行者蹬踏过程中施加给踏板的力, 由于在周期性蹬踏过程中, 施加的力大小和方向都不固定, 因此本文采用即时功率与速度的比值表示 $ F $ . 考虑到链条带动后轮转动过程中能量损耗问题, 自行车在链条转化效率约为98.5%, 因此式(9)可转化为:

$ \begin{split} &\frac{{P \times 0.985}}{V} - Mg\sin \theta - \frac{1}{2}{C_d}A\rho {V^2} - {C_r}Mg\cos \theta - \\ &\frac{7}{8}{C_w}\rho {V^2}\pi {r^2} = \left(M + \frac{{{I_f}}}{{{r^2}}} + \frac{{{I_b}}}{{{r^2}}}\right){V^{'}}(t) \end{split} $

(10)

其中, $ P $ 表示骑行者蹬踏提供的平均功率, $ I_{f} $ 和 $ I_{b} $ 分别表示前后车轮的转动惯量.

4.2 基于参数约束的上下肢关节运动

人体下肢和上肢为骑行过程中主要活动部位, 需对其进行关节运动分析及相应约束关系建立. 因此, 本文通过构建自行车参数与人体参数间的约束关系, 实现骑行过程中人体模型与自行车模型的动态合一.

(1)人体下肢运动学分析及约束关系建立

人体下肢是骑行过程中姿态变化的主要结构之一, 由关节和骨骼构成. 关节主要包括髋关节、膝关节和踝关节等; 骨骼主要包括大腿、小腿和脚掌等. 从力学性能来看, 人体骨骼与普通刚性材料在承受拉压应力和弯曲应力方面特性相似, 可将人体骨骼等效为刚性连杆^[16]. 在骑行过程中, 髋关节固定于坐垫上, 大腿绕其进行摆动, 故可将髋关节视为固定铰链座; 膝关节只有一个伸屈自由度, 可等效为活动铰链; 踝关节具有3个自由度, 但踝关节主要在矢状面内作定轴转动, 因此可将踝关节等效为活动铰链. 考虑到骑行过程中人体下肢主要在矢状面内运动, 在水平面和冠状面运动幅度较小, 故本文不在这两个平面进行分析.

以骑行过程中右下肢运动为例, 将其简化为人-车连杆模型如图7(a)所示. 其中 $ {P_{HR}} $ 为髋关节, $ {P_{KR}} $ 为膝关节, $ {P_{AR}} $ 为踝关节, $ {P_{BR}} $ 为前脚掌中心点, 已知参数为右大腿长度 $ {L_{HKR}} $ 、右小腿长度 $ {L_{KAR}} $ 、右脚掌长度 $ {L_{BR}} $ 、中轴 $ {L_{CR}} $ 坐标、曲柄长度 $ {L_{CR}} $ 、坐垫 $ {C_S} $ 坐标和曲柄旋转角 $ {\alpha _{CR}} $ . 下肢运动区域参数约束关系建立包含以下两方面: 一方面是建立脚掌掌心与踏板、髋关节与坐垫之间的参数约束关系; 另一方面是建立脚掌掌心、髋关节等与踝关节、膝关节之间的参数约束关系. 根据骑行中髋关节固定于坐垫上, 前脚掌掌心固定在踏板处, 可建立约束关系: $ {P_{BR}} = {C_{CR}} $ , $ {P_{HR}} = {C_S} $ . 通过人机工程学及几何知识计算人体下肢其他相关参数, 建立相应约束关系.

中间参数的具体表达式如式(11)所示:

$ \left\{ \begin{gathered} {\alpha _3} = {\rm{arc}}\tan \frac{{{x_{{P_{AR}}}} - {x_{{P_{HR}}}}}}{{{x_{{P_{HR}}}} - {x_{{P_{AR}}}}}} \\ {L_0} = ||\overrightarrow {{P_{AR}}{P_{HR}}} || \\ {\alpha _1} = {\rm{arc}}\cos \frac{{{L_{KAR}}^2 - {L_{HKR}}^2 - {L_0}^2}}{{ - 2 \times {L_{HKR}} \times {L_0}}} \\ \end{gathered} \right. $

(11)

人体下肢部位关节角及坐标值如表1、表2所示.

随着曲柄在骑行运动过程中周期性转动, 左右下肢的运动状况存在 $ {\text{18}}{{\text{0}}^{{\circ }}} $ 的相位差, 因此将右下肢的角位移代入相位差, 即可得到左下肢的关节参数.

(2)人体上肢运动学分析及约束关系建立

人体上肢在骑行过程中负责控制前行方向, 姿态相对固定, 由关节和骨骼构成. 关节包括肩关节、肘关节和腕关节; 肢体包括上臂、前臂和手掌. 其中肩关节具有3个自由度, 可做屈伸、收展、内外旋运动; 肘关节可做屈伸和旋前旋后运动; 腕关节可做屈伸、收展和环转运动; 考虑到规范骑行过程中人体上肢结构主要在矢状面内运动, 其他两个基本面, 运动幅度较小, 故不在这两个平面进行分析.

相关文献^[17]表明, 骑行过程中, 人体手臂应向前、肘部微微弯曲、背部需从臀部前倾且笔直, 本文以此为依据在矢状面内建立上肢人-车连杆模型, 如图7(b)所示. 其中 $ {P_M} $ 为臀部, $ {P_L} $ 为腰椎关节, $ {P_{SR}} $ 为肩关节, $ {P_{ER}} $ 为肘关节, $ {P_{WR}} $ 为腕关节、 $ {P_{PR}} $ 为手掌掌心. 在骑行过程中已知的参数为坐垫 $ {C_S} $ 的坐标, 自行车车把 $ {C_{HR}} $ 的坐标. 根据骑行中臀部固定在坐垫上, 手掌掌心固定在车把处, 建立自行车参数与人体上肢参数间约束关系, 即 $ {P_M} = {C_S} $ , $ {P_{PR}} = {C_{HR}} $ . 再通过人机工程学与几何知识计算人体上肢区域其他相关参数, 建立相应约束关系.

中间参数具体表达式如式(12)所示:

$ \left\{ \begin{array}{l} {L_{MWR}} = \left\| \overrightarrow {{P_M}{P_{WR}}} \right\|\\ {L_{SWR}} = \sqrt {L_{ESR}^2 + L_{WER}^2 - 2{L_{ESR}}{L_{WER}}{\alpha _{ER}}} \\ {L_{EPR}} = \left\| \overrightarrow {{P_{ER}}{P_{PR}}} \right\|\\ {\alpha _1} = {\rm{arc}}\tan\dfrac{{{x_{{P_{WR}}}} - {x_{{P_M}}}}}{{{y_{{P_{WR}}}} - {y_{{P_M}}}}}\\ {\alpha _2} = {\rm{arc}}\cos \dfrac{{L_{SWR}^2 - L_{MWR}^2 - L_{SM}^2}}{{ - 2\times {L_{MWR}}\times {L_{SM}}}}\\ {\alpha _3} = {\rm{arc}}\cos \dfrac{{L_{WER}^2 - L_{SWR}^2 - L_{ESR}^2}}{{ - 2\times L_{SWR}^{}\times L_{ESR}^{}}}\\ {\alpha _5} = {90^ \circ } - {\alpha _1} - {\alpha _2}\\ {\alpha _4} = {\rm{arc}}\cos \dfrac{{L_{MWR}^2 - L_{SWR}^2 - L_{SM}^2}}{{ - 2\times L_{SWR}^{}\times {L_{SM}}}} \end{array} \right. $

(12)

人体上肢部位关节角及坐标值如表3、表4所示.

通过Unity3D物理引擎对自行车施加合理的驱动力, 驱动自行车前行, 随着自行车在骑行过程中参数的不断变化, 根据上述建立的约束关系, 计算人体参数, 实现人体骑行姿态动态调整.

5 仿真实例

为验证本文方法的合理性和可行性, 将本文所提出的方法在Unity3D、VS2017平台上进行实例测试, 分别进行骑行场景仿真和骑行规范运动仿真, 以三维可视化的方式呈现骑行姿势, 指导骑行者正确骑行.

5.1 骑行场景仿真

为使骑行效果更符合实际场景, 本文对常见的直行、转向和上下坡场景进行骑行运动模拟设计与实现, 证明本文方法的普适性.

首先, 针对骑行者的身高、身体比例存在差异造成初始自行车座椅适合高度不同的问题, 在骑行前, 根据人体模型实时调整并规范初始骑行姿态. 设置人体身高参数, 对人体模型进行尺寸变化, 如图8(a)和图8(b)所示. 并根据用户设置的自行车部件参数, 实时调整自行车模型. 计算人体模型裆部与坐垫间位移, 将人体模型平移到车体上, 根据定义的特征点计算人体模型上下肢部位参数, 由已知的左、右踏板坐标、坐垫坐标、左、右车把坐标和曲柄旋转角度等自行车参数, 结合上下肢的约束关系计算规范骑行姿势下髋关节等人体参数, 重新调整人体关节, 改变人体姿态, 初始骑行姿势如图8(c)所示.

(1) 直行骑行模拟

直行骑行模拟具体实现步骤如下.

Step 1. 驱动骑行运动. 获取参数设置界面中人体提供的平均功率, 根据动力学模型计算当前功率下的驱动力, 对人-车系统施加合理驱动力, 驱动人车前行.

Step 2. 踏板旋转变换. Unity3D更新频率默认0.02 s执行一次, 即每次施加力的作用效果为0.02 s. 根据车轮外圈行驶距离与自行车行驶距离相等, 建立等式如式(13)所示, 其中, $ R $ 为车轮半径, $ \theta $ 为车轮及曲柄旋转角度, $ V $ 为自行车速度, 根据其求得车轮和曲柄旋转角度. 由于踏板为曲柄的子物体, 本文先对踏板逆向旋转 $ \theta $ , 使其恢复到初始水平状态, 然后根据曲柄角度计算并设置踏板旋转角度, 踏板旋转效果如图9所示.

$ {\text{2}}\pi R\times \frac{\theta }{{360}} = V\times 0.02 $

(13)

Step 3. 计算并设置腿部关节参数. 考虑到直行过程中只有下肢参与运动, 上肢及其他关节保持相对不变, 因此仅需对腿部关节进行操作. 根据踏板旋转变换后位置、坐垫位置和下肢关节运动约束关系, 重新计算并设置腿部关节值, 得到当前时刻的骑行姿势.

Step 4. 重复执行Step 1到Step 3, 实现直行道路场景下规范骑行运动模拟.

(2)转向骑行模拟

转弯过程可近似为绕某个定点 $ O $ 作圆周运动, 图10(a)为自行车转弯过程中简化俯视图. 其中, $ A $ 、 $ B $ 分别为前、后车轮与地面接触的点, $ \theta $ 为前叉转向角, $ L $ 为 $ AB $ 间距离, $ {r_1} $ 、 $ {r_2} $ 分别为前后车轮转弯半径, 虚线为车轮运动轨迹. 转向骑行姿势效果如图10所示.

自行车转向场景具体实现步骤如下.

Step 1. 上肢自适应调整. 在转弯前将前车轮、把立等导航系统部件的父物体设为前叉部件, 便于进行旋转操作. 根据转向角 $ \theta $ 对前叉部件进行旋转, 得到左、右车把新位置, 利用上肢约束关系计算人体肩、肘和腕关节角度, 将计算出的新值赋给人体模型对应关节, 实现上肢姿势自适应调整.

Step 2. 由 $ \theta $ 、 $ L $ 和 $ B $ 点坐标, 根据式(14), 计算后车轮旋转半径 $ {r_2} $ 和后车轮旋转点 $ O $ 坐标值:

$ \left\{ \begin{gathered} {r_2} = L \times \cot \theta \\ {x_o} = {x_b} \\ {y_o} = {y_b} \\ {{\textit{z}}_o} = {{\textit{z}}_b} - {r_2} \\ \end{gathered} \right. $

(14)

Step 3. 计算 $ B $ 点在时间间隔 $0.02\;{\rm{s}}$ 内以速度 $ V $ 绕 $ O $ 点旋转角度 $ \theta $ , 计算公式如式(15)所示, 接着对人体与自行车以 $ \theta $ 进行旋转操作:

$ 0.02 \times V = {r_2} \times \theta $

(15)

Step 4. 根据直行骑行中踏板、前后车轮、曲柄计算公式, 计算并设置其旋转角度, 通过下肢约束关系计算并设置腿部髋关节、膝关节、踝关节角度参数.

Step 5. 重复执行Step 3和Step 4, 直到人-车系统旋转角度与场景转角度的误差在一定阈值内为止.

(3)上下坡骑行模拟

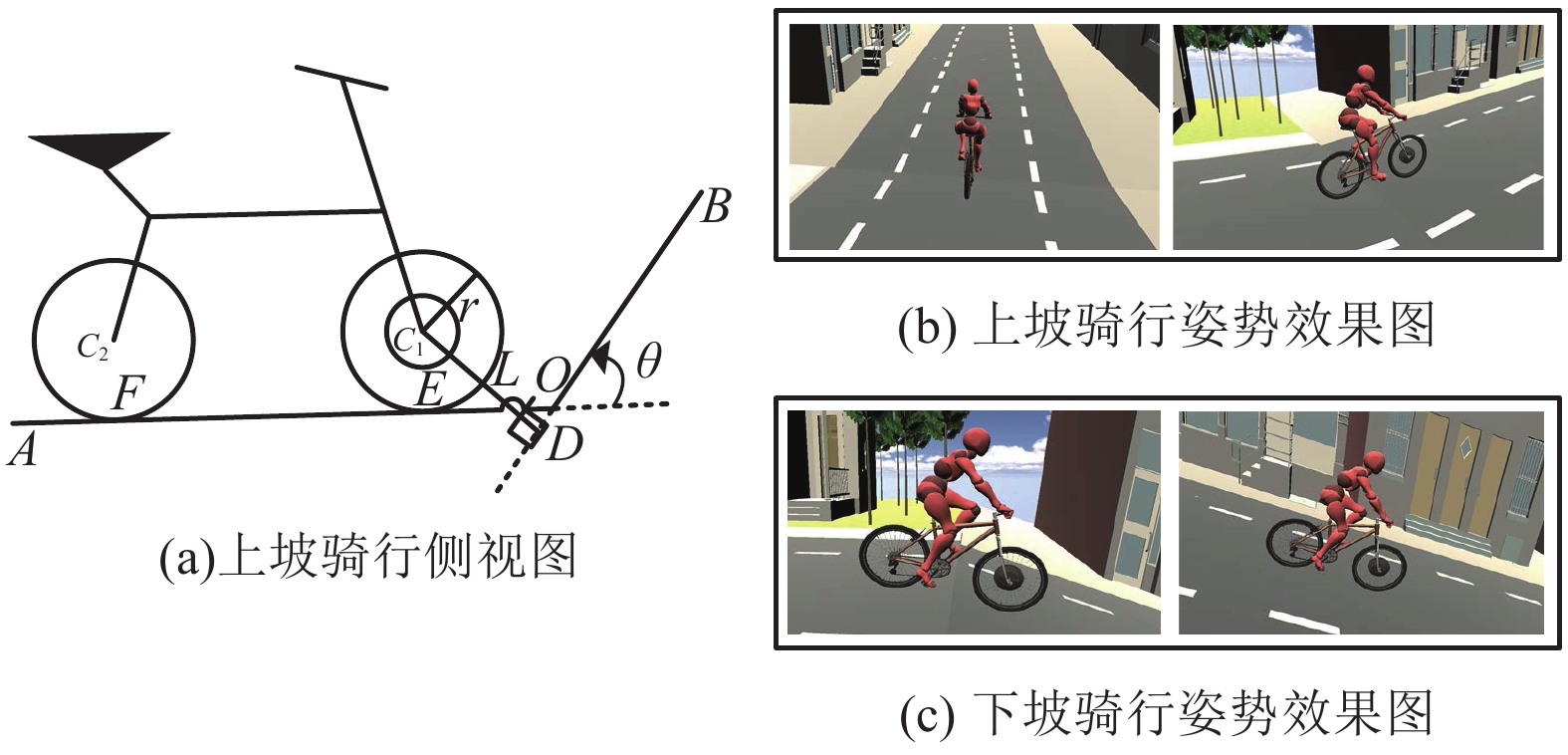
以上坡为例, 上坡骑行简化侧视图如图11(a)所示, 其中线段 $ OA $ 、 $ OB $ 为水平地面和斜坡面, $ {C_1} $ 点为前车轮中心, $ {C_2} $ 为后车轮中心, $ E $ 、 $ F $ 点为前后车轮与地面的接触点, $ r $ 为车轮半径, $ \theta $ 为上坡坡度值.

上坡场景骑行实现步骤如下: 首先, 根据用户输入上坡场景参数值, 自定义场景, 判断前轮中心 $ c $ 点到线段 $ OB $ 的距离 $ L $ 是否小于车轮半径 $ r $ , 若条件成立, 则表明已经骑行到转角处, 自行车需进行旋转上行操作. 其次, 简化上坡骑行过程中复杂运动计算过程. 在后车轮位于地面 $ OA $ 且前车轮处于坡面 $ OB $ 时, 对自行车施加力的方向始终为 $ \overrightarrow {FE} $ , 接着对自行车绕 ${{F}}$ 点进行旋转, 直到前车轮刚好落在坡面 $ OB $ 上, 即前车轮与坡面 $ OB $ 相切. 然后, 根据上下肢参数约束关系, 重新计算并设置人体上下肢关节、踏板、前后车轮、曲柄等旋转参数. 当后车轮与坡面 $ OB $ 相切时, 更改自行车速度的方向为 $ \overrightarrow {OB} $ , 同时计算并更改力的方向为 $ \overrightarrow {OB} $ , 最终实现上坡场景中的模拟骑行过程. 上下坡骑行姿势效果如图11(b)和图11(c)所示.

5.2 骑行规范运动仿真

骑行过程中人-车系统受力模型计算由环境指标、人体指标和自行车指标构成. 常温标准大气压下空气密度为 $0.5\;{{\rm{m}}^2}$ . 人体指标方面, 骑行者身高为 $180\;{\rm{cm}}$ , 体重 $72\;{\rm{kg}}$ , 在规范骑行姿势下, 该身高的人体最大迎风面积约为 $0.5\;{{\rm{m}}^2}$ , 风阻系数为 $ 0.5 $ , 平均输出功率为 $300\;{\rm{W}}$ . 自行车车轮半径为 $0.36\;{\rm{m}}$ , 空气阻力系数约为 $0.039\;8$ , 车轮的转动惯量为 $0.08\;{\rm{kg}}\cdot{{\rm{m}}}^{2}$ , 宽度 $20\;{\rm{mm}}$ , 胎压 $120\;{\rm{P}}$ 轮胎在沥青柏油路上的滚动摩擦系数为 $ 0.004 $ . 本文以直行场景为例, 进行规范仿真.

首先, 在参数设置模块, 选择直行场景, 道路宽度设置为 $6\;{\text{ m}}$ , 长度设置为 ${\text{2 000 m}}$ , 系统根据用户输入的参数对场景及人体模型进行实时调整, 人体模型身高自适应调整效果如图12(b)所示.

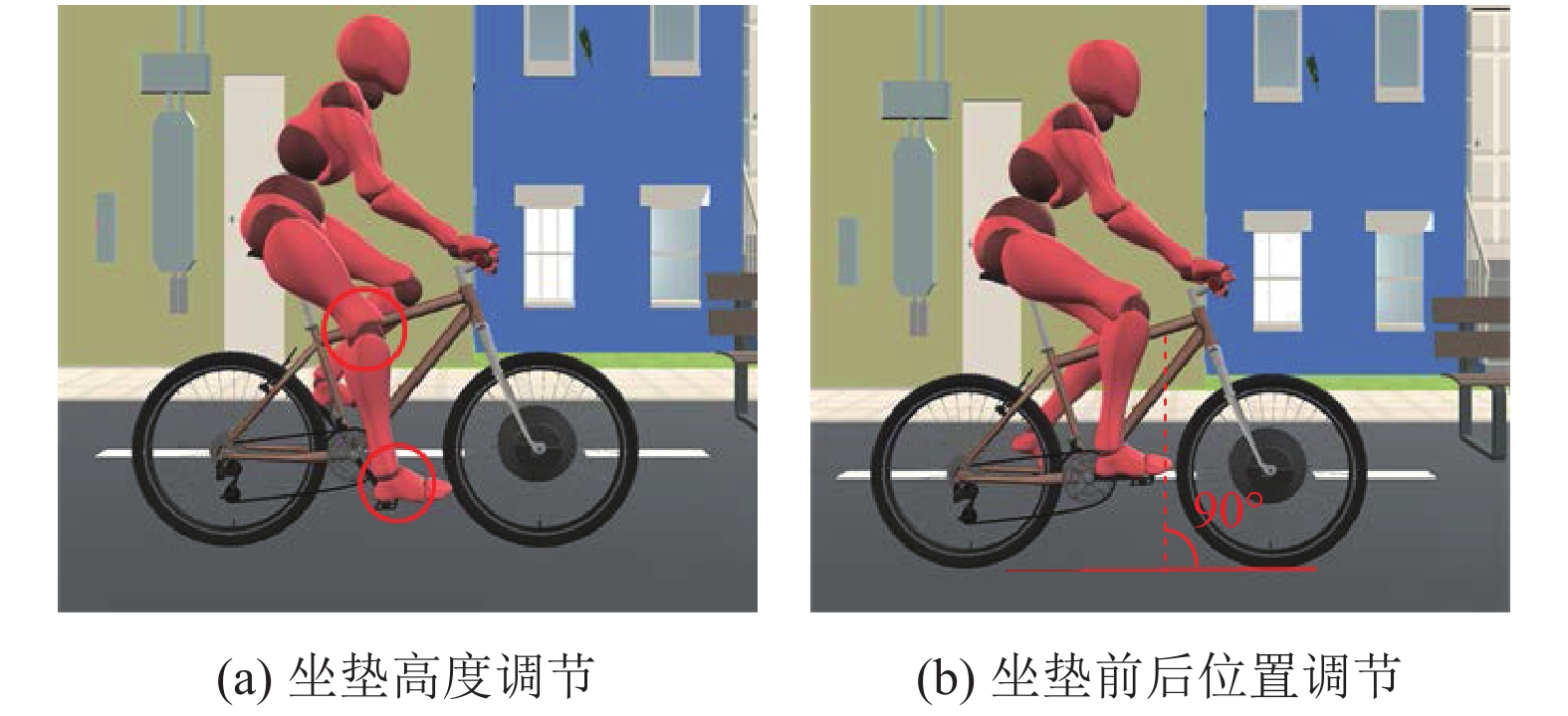
接着, 由用户交互完成对自行车的局部调整, 主要为坐垫的手动调整和自动调整. 手动调整需用户自主调节坐垫前后距离和坐垫高度参数, 自动调整由系统自动计算并设置坐垫参数, 使腿部能处于最佳发力状态, 避免因坐垫调整不当导致骑行舒适度不佳, 坐垫调整效果如图13所示. 最后, 进行直行场景骑行运动的仿真, 系统将根据建立的人体参数与自行车参数间约束关系, 对人体姿态进行动态调整, 实现人车合一效果. 图14(a)为直行场景中规范骑行姿势过程.

由上述对直行骑行过程模拟可得右下肢关节的变化曲线图, 如图14(b)所示. 骑行过程中下肢关节做周期性运动, 在一个周期内, 膝关节运动幅度最大, 其活动范围约为60°–150°; 髋关节活动范围约为105°–150°; 踝关节活动范围约为67°–110°. 在曲柄角度处于–30°~150°时, 膝关节处于伸展状态, 为骑行过程中右脚发力阶段; 当曲柄角度位于150°–330°时, 膝关节处于屈曲状态, 做提拉踏板运动, 此时右脚基本不发力, 左脚处于发力阶段. 因此, 通过下肢关节角变化图能够在骑行过程中指导骑行者正确、省力骑行.

6 结论

针对骑行者在骑行过程中姿势不规范的问题, 本文提出了一种用于规范骑行的参数化建模方法, 通过建立骑行过程中自行车参数与人体参数间约束关系, 对骑行过程进行运动仿真, 为骑行者提供正确的姿势指导. 本文方法的主要特色有: 1)利用构建的自行车模型和人体模型, 对其进行特征点、特征部件和三维模型间的层次约束, 通过语义参数控制模型的形态变化. 2)通过对骑行过程中人-车系统进行受力分析并建立动力学方程, 使得虚拟场景与实地一致, 提高仿真的真实性. 3)建立人-车参数间约束关系, 通过获取骑行运动过程中的自行车参数, 计算人体参数, 实现人体关节协调运动, 为骑行者提供直观的骑行姿势指导. 但本文侧重于参数化规范骑行过程, 缺乏骑行者在实际骑行中的实时指导, 未来还需结合传感器等设备采集骑行者骑行姿势数据, 并利用5G通信技术提高设备与系统间的传输效率, 从而为骑行者提供针对性的骑行姿势指导.