机制砂是粒径小于2.36 mm的颗粒碎块. 经过开采天然岩石, 对天然岩石进行除土, 对其进行机械的破碎, 之后用2.36 mm的筛子进行筛分得到机制砂. 在工业应用中, 混凝土的用处非常广泛, 例如: 各种建筑桥梁的建设过程中, 混凝土就有非常重要的用途, 而机制砂是构成混凝土非常重要的原材料. 机制砂的质量严重影响着混凝土的性能, 特别是机制砂在进行开采岩石, 除土, 破碎的过程中容易引入一些非机制砂的物质, 这些物质的含量无论高低都会对机制砂的性能产生影响. 机制砂的杂质含量可以用细粉含量^[1]来表示. 目前对于机制砂的细粉含量的测量是用传统的规范《公路工程集料试验规程》提及的细集料砂当量试验, 但该方法程序繁琐且时间久, 由于人为的观察、环境及其他因素, 导致该检测方法的准确性和高效性难以保证.

目前, 关于机制砂, 大多数人研究的是机制砂对混凝土的影响或者改进细集料砂当量试验的方法, 而对于机制砂细粉含量的数据预测还是比较少的. 胡胜荣^[2]研究了路面性能和细集料的关系, 路面主要研究的是沥青混合料的路面. 陆宇等^[3]研究了机制砂砂当量对沥青混合路面性能的影响, 该研究对于机制砂的工业应用具有非常深远的意义. 马兴等^[4]研究了砂当量试验仪的内容, 主要研究了该试验仪的试验原理和功能, 建立了研究所用的模型. 朱立无等^[5]制定了《砂当量试验仪校准规范》, 该规范中规定的校准的方法非常合理和科学, 可以为之后研究机制砂砂当量的测量提供一个较为标准的对比参考.

用预测网络预测机制砂细粉含量的现阶段研究较少, 但是如今对于数据预测相关内容却越来越常见. 如: 2019年, 为解决原砂含泥量检测的不精确和步骤繁琐的问题, 郭景宝等^[6]设计了一种原砂含泥量检测装置, 但是其并未解决全部问题, 虽然提高了检测精度, 但是并未放慢了检测过程. 2019年, 刘泽宇^[7]研究了浊度和含泥量的对应关系, 一般情况下, 含泥量越高, 配置成的溶液越浑浊, 所以浑浊度和含泥量是具有对应关系的, 刘泽宇具体化了这种关系. 2019年郭景宝^[8]主要研究原砂的相关内容, 之前进行原砂含泥量的检测都较为复杂, 为了缩短检测时间, 其研究出一种新型检测含泥量的装置. 2020年, 马旭梁等^[9]提出了一种可以进行速度较快的检测原砂含泥量的方法, 解决了之前研究所出现的检测精度不高的问题. 2021年, 王风雅^[10]提出一种利用计算机图像分析技术定量测定原砂含泥量的方法. 首先将泥砂分离, 采用较为传统的方法: 涡洗法, 之后以数字图像分析技术为基础, 根据不同的含泥量其洗砂液颜色会发生变化, 采用数字图像采集技术对涡洗之后的原砂浊液进行图像采集, 再结合数字图像处理分析技术, 对原砂含泥量进行预测.

传统的细粉含量的测量用到《公路工程集料试验规程》中的细集料砂当量试验(国外的某些地方也会用到亚甲蓝试验), 需要经过试验制备(需各种化学试剂: 氯化钙、甘油、甲醛)、测含水率、配置冲洗液、多次震荡等步骤, 程序非常繁琐. 综上所述, 若将预测网络运用到机制砂细粉含量预测, 将可以很好地解决机制砂细粉含量预测繁杂、效率低、耗时间等问题. 故本文针对机制砂溶液图片的亮度、色度、色调等特征提出一种XGBoost预测网络来解决机制砂细粉含量预测难题. 针对本文的预测方法, 具体实现思路是对机制砂细粉所制得的溶液拍照, 提取其RGB颜色特征, 转换颜色空间至LCH, 将L,C,H这3个分量取均值, 输入L,C,H值和细粉含量值进入XGBoost网络进行训练, 得到预测值.

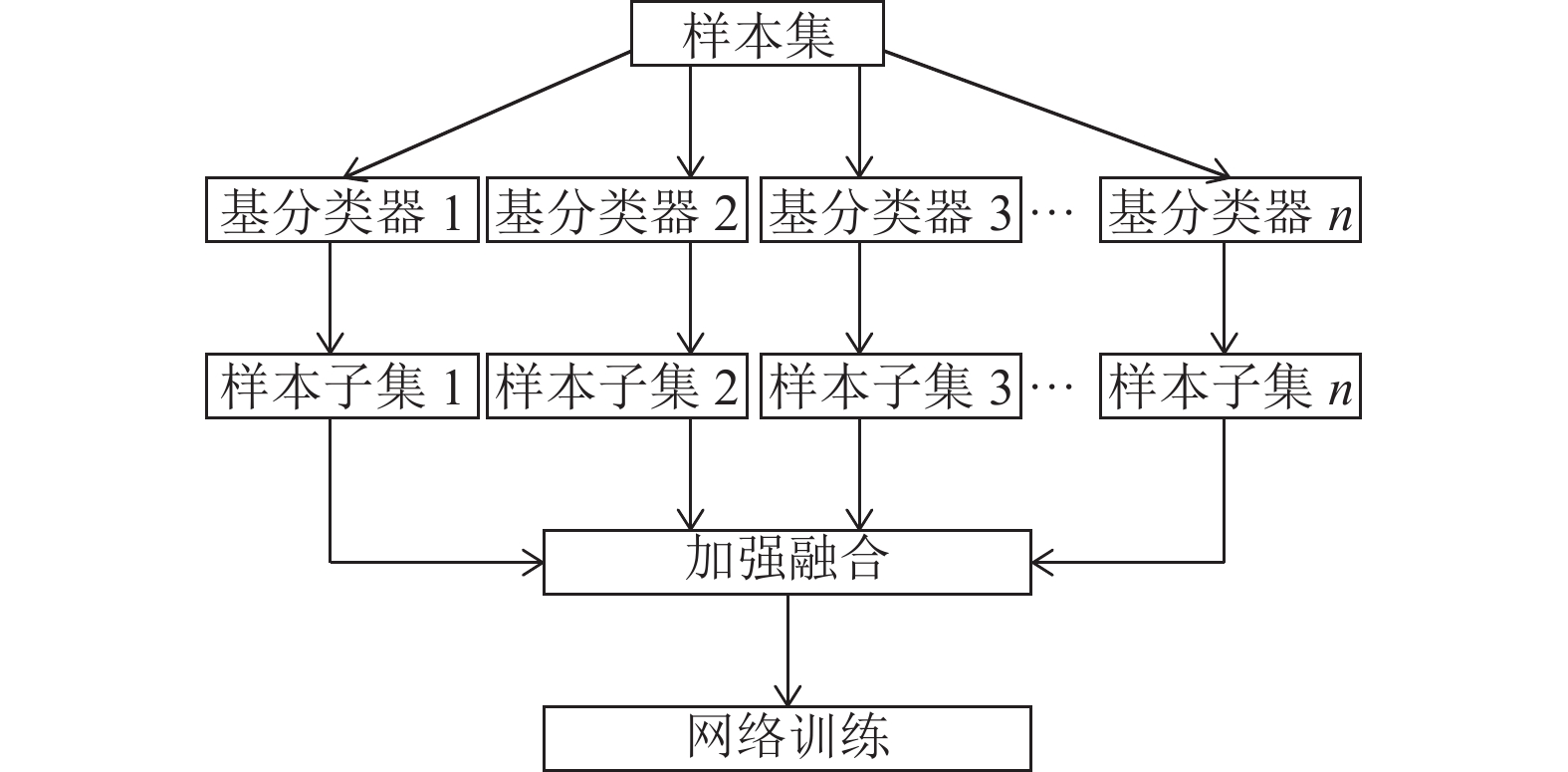
1 算法和预处理 1.1 Boosting算法

在一般的监督式学习中, 会有固定的偏差, Boosting算法可以减小这种偏差, 提高精确度. Boosting算法示意图如图1所示.

1)弱学习

在做预测工作时, 训练的网络的精确度不是很高, 可以说明该预测或识别网络属于弱学习器. 该学习效率不是很高, 需要再进行模型优化来达到学习的效果.

2)强学习

强学习是相对于弱学习而言的, 在做识别和预测工作时, 训练的网络的精度很高, 可以说明该预测或识别网络属于强学习器.

3) Boosting算法

在进行模型训练时, 需要确定样本集, 样本集是进行网络训练的基础. 进行预处理之后需要进行加强融合, 加强融合可以结合不同分类器的优点, 对于模型训练有很大的帮助作用.

1.2 XGBoost网络

1)目标函数

损失函数和惩罚函数共同组成XGBoost模型的目标函数^[11-13], 提高预测精度通过最小化损失函数来达到. 目标函数的化简方法较为简单, 一般情况下, 对目标函数进行泰勒展开, 泰勒展开式可以使目标函数更加直观, 可以使模型较快运行, 较快得出预测结论. 图2为机制砂细粉含量预测流程.

2)基于决策树^[14,15]的目标函数

决策树是一种运用概率分析进行决策的方法, 决策树的决策运用到很多概率论的内容, 是根据概率论的内容来进行决策. 图3为决策树在预测中的流程.

决策树的复杂度是由叶子节点的多少决定, 目标函数正则项可以用式(1)表示:

$ {\Omega }_{({f}_{t})}=\gamma T+\frac{1}{2}\gamma {\displaystyle \sum _{j=1}^{T}{w}_{j}{}^{2}} $

(1)

也就是说, 决策树的模型复杂度由两个变量决定: 一个是叶子节点数量, 表示生成的决策树的叶子节点数量之和; 另外一个是目标函数正则项, 该正则项将所有节点的权重进行计算, 可以很好地作为模型复杂度的构成因子.

1.3 改进型XGBoost网络-贝叶斯优化

XGBoost算法精确度还有待提升, 运用贝叶斯优化可以进行模型参数的选择. 本文用贝叶斯优化的方法进行模型改进^[16-20], 将模型的r2_score由XGBoost的0.95提升至改进型XGBoost的0.96左右.

1)贝叶斯定理

贝叶斯定理的公式如下:

$ p(f|{D_i}) = \frac{{p({D_i}|f)p(f)}}{{p({D_i})}} $

(2)

其中, f表示目标函数, 但是其在初始迭代阶段是未知的, D_i表示已知的集合, 用类似位置坐标表示, 即(x₁, y₁), (x₂, y₂),…, 其中x_i表示用来进行决策的向量.

2)贝叶斯优化步骤

贝叶斯定理是贝叶斯优化参数优化的基础, 同时, 下一个采样的超参数组合也是参数优化的基础. 贝叶斯优化可以较为充分的利用某一个采样点的位置信息, 它的方式是通过学习目标函数形状, 不断迭代, 当结果向全局最大提升时, 迭代的参数就是本文所要确定的结果. 贝叶斯优化流程如图4所示.

假设一组超参数组合是X=x₁,_{x2,…, xn, 超参数和函数的关系如下:}

$ {x^*} = \arg \min f(x) ^{ } $

(3)

其中, x表示超参数, 在XGBoost中, 超参数就是学习率、树的最大深度等这些参数.

凸优化可以很好地解决二阶导数大于零出现的各种问题, 例如每次计算超参数的时候, 会进行人工操作来计算结果, 耗费许多人力资源. 为了解决这一问题, 本文假设高斯分布为搜索的模型空间, 利用高斯过程, 每次计算得到的结果都比上次计算得到的结果更优, 得到该结果是利用迭代的方法贝叶斯优化的步骤.

① 输入: f (每次输入一组超参数得出的一个值)、X (超参数的定义域)、S (可以进行参数选择的算法)、M(对初始化数据进行拟合得到的模型).

② 初始化: 初始化获取数据集D=(x₁, y₁), …, (x_n, y_n), 其中y_i=f(x_i).

③ 循环迭代参数: 若是按照手动选参的方法, 每次选中参数, 需要计算它的f(x), 这样需耗费较多的人力. 为了使选参过程更加快速, 本文固定选参次数, 具体步骤如下: 利用高斯过程, 设模型M服从高斯分布, 且已知了数据集D, 通过计算得出具体的模型具体函数表示.

高斯过程是多元高斯分布向无穷维的扩展, 高斯过程函数的分布可以由均值函数和协方差函数组成:

$ f(x)\sim GP(m(x), k({x_{{i}}}, {x_{{j}}})) $

(4)

其中, GP表示高斯过程, $ m(x) $ 是均值函数, $k({x_{{i}}}, {x_{{j}}})$ 表示协方差函数.

在式(4)中, $k({x_{{i}}}, {x_{{j}}})$ 表示的协方差函数即是高斯过程的核函数, 核函数是高斯过程的核心, 其起衡量任意两个点之间的距离的作用:

$ k({x_i}, {x_j}) = {\sigma ^2}\exp \left( - \frac{{||{x_i} - {x_j}||_2^2}}{{2{l^2}}}\right) $

(5)

其中, $ {x_i}, {x_j} $ 表示本文中模型运行时不同时间点, $ ||{x_i} - {x_j}||_{}^2 $ 表示一个二范式, 表示 $ {x_i}, {x_j} $ 之间的距离.

将模型建立成如下的形式:

$ y = f(x) + N(0, \sigma _{}^2) $

(6)

其中, $ f(x) $ 表示高斯过程函数的分布, $ N(0, \sigma _{}^2) $ 表示模型建立过程中的噪音, $ \sigma _{}^2 $ 表示高斯过程的方差.

建模之后, 本文尝试抽样进行样本计算, 该优化方法在局部最优解上不断采样.

④ 确定最优参数: 通过多次迭代找到最优参数, 达到模型优化.

1.4 图像预处理

图片预处理流程如图5所示.

1)图片裁剪

图6为原始溶液图像, 图7为不同细粉含量的原始图片裁剪之后的图片.

2) 图片裁剪区域的确定

图8–图10分别为不同区域L, C, H值与细粉含量的关系.

图像大小为1628×1236, 现有溶液的位置为[400, 1236; 0, 628], 选取x的位置为[0, 1628], 将y位置分为两个区域[400, 800]和[800, 1236].

当y的取值范围为[800, 1236]时, 特征值L、C、H值在不同细粉含量之间存在较大的波动, 且各特征值与细粉含量的线性关系较差; 当y的取值范围为[400, 800]时, 特征值L、C、H值在不同细粉含量之间波动较小, 且各特征值与细粉含量的线性关系较好. 所以选取特征区域时, 选择x的取值范围为[0, 1628], y的取值范围为[400, 800].

2)读取特征区域的RGB值

一张图片是由许多个像素组成的, 彩色图片的每个像素有3个通道, 分别为RGB通道, 其分别对应R、G、B值, 图像的R、G、B值可以表征图像内容.

3)将图片的RGB值全部转换成LCH值

LCH颜色空间首次将亮度和色度分开表示, 且该颜色空间是国际上通用颜色体系之一. 将RGB转换到LCH, 需要用中间颜色空间Lab来转换, 转换公式如下:

$ \left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.412453}&{0.357580}&{0.180423} \\ {0.212671}&{0.715160}&{0.072169} \\ {0.019334}&{0.119193}&{0.950227} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} R \\ G \\ B \end{array}} \right] $

(7)

$ \left\{ {\begin{array}{*{20}{l}} {{L^*} = 116f\left(\dfrac{{{Y^*}}}{{100}}\right) - 16} \\ {{a^*} = 500\left[f\left(\dfrac{{{X^*}}}{{95.047}}\right) - f\left(\dfrac{{{Y^*}}}{{100}}\right)\right]} \\ {{b^*} = 200\left[f\left(\dfrac{{{Y^*}}}{{100}}\right) - f\left(\dfrac{{{Z^*}}}{{108.883}}\right)\right]} \end{array}} \right. $

(8)

其中, f函数为:

$ f(t) = \left\{ {\begin{array}{*{20}{l}} {{t^{\tfrac{1}{3}}}},&{t > {{\left(\dfrac{6}{{29}}\right)}^3}} \\ {\dfrac{1}{3}{{\left(\dfrac{{29}}{6}\right)}^2}t + \dfrac{4}{{29}}},&{{\rm{otherwise}}} \end{array}} \right. $

(9)

$ \left\{ {\begin{array}{*{20}{l}} {{X^*} = \dfrac{X}{{255 \times 0.950456}}} \\ {{Y^*} = \dfrac{Y}{{255}}} \\ {{Z^*} = \dfrac{Z}{{255 \times 1.088754}}} \end{array}} \right. $

(10)

$ \left\{ {\begin{array}{*{20}{l}} {{h^*} = {\rm{arctan}}\dfrac{{{b^*}}}{{{a^*}}}} \\ {{c^*} = \sqrt {{a^*}^2 + {b^*}^2} } \end{array}} \right. $

(11)

4)对转换得到的LCH值取均值

LCH颜色空间中, L表示亮度, C表示饱和度, H表示色相, 对该3项取均值做预测网络的输入值.

2 实验仪器和流程 2.1 实验仪器

本文实验所用的叶轮搅拌机, 玻璃杯, 相机如图11–图13所示.

2.2 试验流程

1)模型训练试验流程

用烘箱开300 ℃烘干机制砂, 时间可用机制砂烘干情况来定; 之后用0.075 mm的筛子筛出石粉和泥, 取出一定量的石粉和泥放入烧杯中, 在烧杯中加入600 mL水, 并放到叶轮搅拌机上, 设置搅拌时间为5 min, 转速为600 r/min, 开始搅拌; 搅拌之后倒入玻璃杯中, 用60 mL的水对玻璃杯进行清洗, 将清洗的溶液倒入玻璃杯中, 开始计时, 静置3 min拍照, 拍照时采取曝光时间为30000 μs, 采取上侧光源和右侧光源(图14中的玻璃杯上侧和右侧都有光源且都可以固定)同时开启, 之后拍照, 将拍照之后的图片进行预处理得到预测网络的输入数据. 机制砂实验流程如图15所示.

静置时间过短 , 细粉还没有完全沉在玻璃杯的底部; 静置时间过长, 部分细粉会沉到玻璃杯底部导致检测不准确. 选取在搅拌300 s后静置的第2.5 min开始每隔30 s采集一张图像, 到第10 min, 特征值与静置时间的变化规律如图16所示.

从图16可以发现在提取区域不变的情况下特征值L, C, H与不同的细粉含量会出现如下变化规律. 在静置3 min时, 从图16可以发现特征值L、特征值C和特征值H在不同的含泥量之间的差异明显无重合现象; 在静置7−10 min时间时, 细粉含量为0.5和0.6的L几乎相近, 明显有重合现象; 在4−7 min时, 细粉含量为0.5和0.6的C值相近, 所以不可作为静置时间; 在2.5 min时, 细粉含量为0.8和0.7的H值有明显的重合现象. 综上所述, 选取3 min为静置时间.

2)实际应用中得到输入数据的试验流程

机制砂超声波清洗: 通过筛子筛足够长的时间之后, 再用超声波清洗机进行清洗, 发现仍有质量差. 此结果表明, 机制砂通过筛子筛出细粉无法完全筛出干净, 因为有些细粉是附着在机制砂上的. 所以, 在实际操作中, 直接筛出机制砂中的石粉, 进行称重来计算细粉含量是不现实的. 大量实验表明, 超声波清洗9 min可以将机制砂上附着的细粉完全震至水中. 所以采用该方法来实现细粉含量检测的数据输入. 经实验表明, 将石粉通过超声波震入水中, 和通过叶轮搅拌机将石粉放入水中的效果相同, 因为测的细粉含量和机制砂无关, 只和细粉有关. 我们在进行模型训练时, 可以采用通过使用叶轮搅拌机的方法(约15 min左右)来进行数据采集训练模型, 该方法较超声波清洗较为省时, 超声波清洗之后过滤得到的溶液图像进行预测. 超声波清洗的步骤如下.

a) 取机制砂样品200 g烘干2小时.

b) 将烘干的样本一半左右(100 g左右)放入超声波清洗机, 倒入300 mL纯净水, 开始超声波清洗, 边清洗边搅拌, 设置时间为9 min.

c) 清洗之后将机制砂溶液全部倒入烧杯中.

d) 将另一半样本放入超声波清洗机, 加入300 mL水, 重复步骤b)和步骤c).

e) 用60 mL水清洗超声波清机, 将清洗之后的溶液倒入烧杯中.

f) 将烧杯中的溶液通过0.075 mm的筛子, 将机制砂筛出, 溶液倒入玻璃杯中.

g) 将玻璃杯中的溶液静置3 min, 拍照.

3) 确定超声波清洗时间

确定超声波清洗时间过程如图17所示.

首先随机确定一个时间7 min, 进行超声波清洗步骤a)–f), 对筛出的机制砂烘干, 测量质量, 当设置超声波清洗时间为8 min时, 若烘干质量小于设置为7 min的烘干质量时, 继续增加分钟数, 继续试验, 直到找到使机制砂质量稳定的最小分钟数; 若设置8 min的烘干质量等于7 min的烘干质量时, 应逐渐减少清洗分钟数, 直到找到数量增加的分钟数, 来确定机制砂质量稳定的最小分钟数, 通过多次试验, 得机制砂超声波清洗能将机制砂上附着得细粉全部震下来的时间为9 min. 表1为清洗时间和剩余质量的关系.

3 实验结果与分析 3.1 模型预测

图片大小为1628×1236, 采集之后首先进行预处理, 预处理之后的数据需要划分为训练集和测试集.

在本实验中共进行了41组数据的实验, 其中32组为训练集, 9组为测试集.

3.2 实验结果

1)模型预测结果

表2中实测值和预测值都为归一化之后的结果, 表中实测值是指直接称重的测量值归一化之后的结果, 预测值为模型训练验证集的结果.

表3为本文算法与多元线性回归模型的比较. MAE(平均绝对误差), MSE(均方误差), r2_score(决定系数)这3个评价指标计算方式如下:

$ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {| {{\hat y_i}} - {y_i}|} $

(12)

$ {\textit{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{( {{\hat y_i}} - {y_i})}^2}} $

(13)

$ r2\_score = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{\hat y_i}} )}^2}} }}{{\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - {{y^2}})}^2}} }} $

(14)

MAE表示平均绝对误差, 该值越小, 模型越好; MSE表示均方误差, 该值越小, 模型越好; r2_score表示预测值和真实值的接近程度, 该值越接近1, 表示预测值和近似值越接近, 模型越好.

2)本文方法与传统方法的比较

表4为本文方法与传统方法的比较. 由表4可知, 相比于传统的砂当量试验和亚甲蓝试验, 本文的方法较为省时, 所需试剂较少. 相对于砂当量试验中求絮凝物和物质总高度之比和亚甲蓝试验中通过亚甲蓝试剂进行试纸色晕, 本文的方法都较为简单, 耗费人力较少.

3.3 本文算法LCH重要性

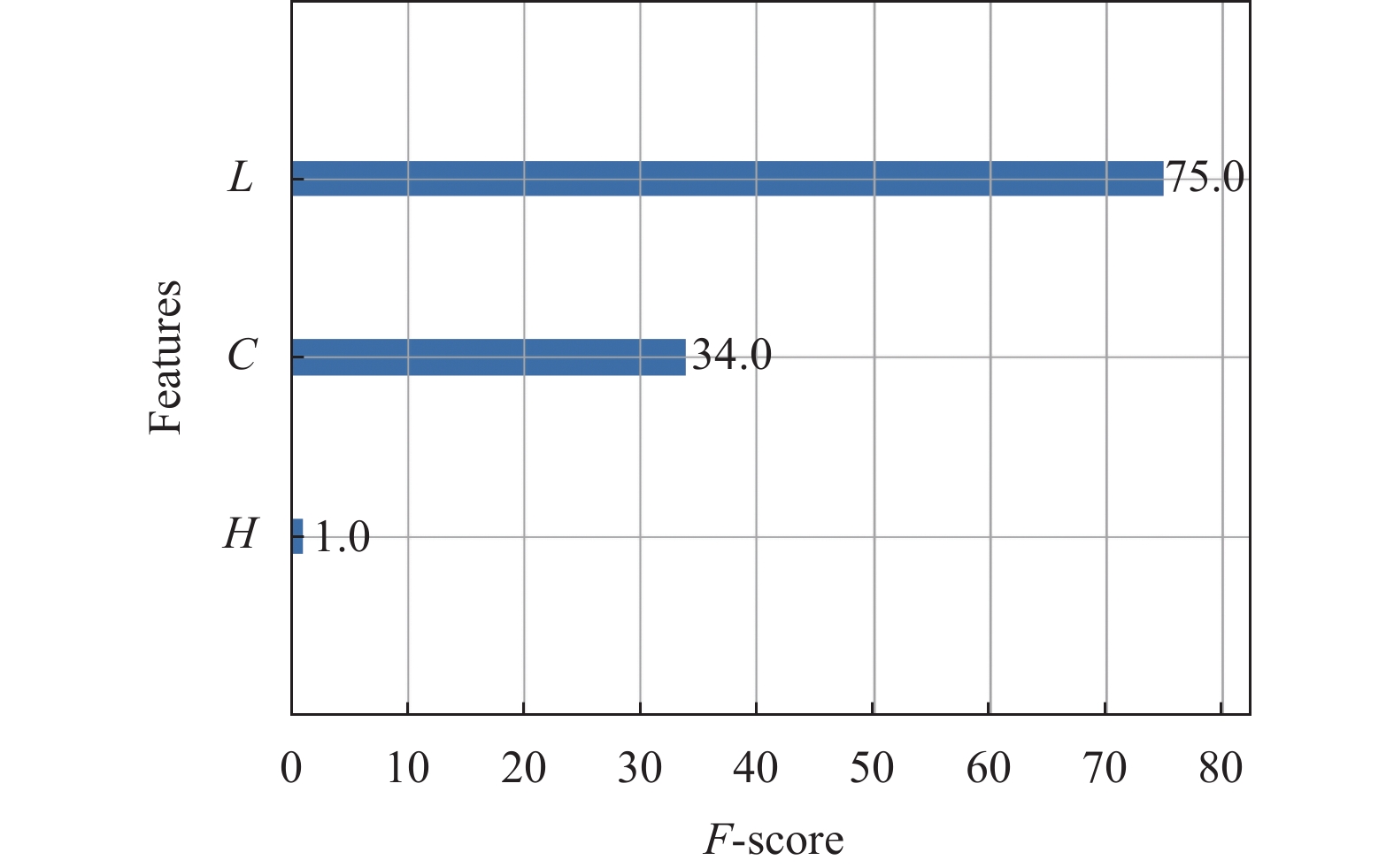
本文算法LCH重要性分布图如图18. 由图中可以看出, L,C, H这3个特征分量中, 亮度L的重要性最大, 饱和度C次之, 色相H最小. 因为溶液的细粉含量的多少直观地影响到溶液的明暗程度, 是细粉含量越大, 溶液越暗. 饱和度是指图片色彩的纯洁性, 色彩越纯洁, 饱和度越低, 在本试验中, 溶液的细粉含量对于饱和度的影响较弱, 说明即使溶液有细粉含量区别, 但是色彩纯洁性区别不大. 色相是包括红橙黄绿青蓝紫品8种色彩, 溶液的细粉含量对该特征的影响最小.

4 结论与展望

本文提出了一种基于机器学习XGBoost的机制砂溶液细粉含量检测系统, 通过对机制砂筛出小于0.075 mm的石粉和泥的量来表示细粉含量的多少. 实验过程要经历筛出、制成溶液、拍摄、预处理、模型预测等步骤, 实验步骤仅需十几分钟, 可以较快完成机制砂细粉含量定量预测分析. 本文通过贝叶斯优化对XGBoost参数进行多次迭代, 可以提高XGBoost的r2_score, 同时可以节省计算参数结果的时间. 通过实验表明, 该模型预测的r2_score可以达到0.967 762, 相比于传统的多元线性回归模型、BP神经网络模型、XGBoost模型的r2_score有所提高, 同时, 该模型的预测精度可以达到0.1, 在实际的生产应用中, 可以缩短细粉含量计算时间, 简化细粉含量计算实验流程, 有非常重要的价值. 在之后的机制砂研究中, 可以采用该实验方法进行细粉含量的预测, 该方法对于进行机制砂测量智能化高效化具有重要的意义.