近年来, 中国马拉松赛事发展迅速, 在中国田径协会注册的马拉松赛事经历了从2010年13场到2019年1828场的跨越式发展, 全国马拉松赛事参加人次从2013年的75万增长到2019年的712万, 马拉松已成为国内大众参与的热门赛事^[1]. 马拉松赛事的举办对凝练城市文化、提高城市软实力、城市经济发展以及民生问题的提升都有着积极的促进作用^[2]. 马拉松赛道路线一般由主办方根据地形图以及城市特色文化地标进行手动规划路线, 最后利用装有琼斯计数器的校准自行车进行赛道测量^[3]. 马拉松路线规划不仅需要耗费大量的资源, 而且人工规划的局限性也会导致规划的路线存在诸多安全隐患, 例如赛道拥挤、交通拥堵等^{[4, 5]}.

对于路线规划的问题, 常用的算法有贪心算法、回溯算法、Dijkstra算法、A*算法、蚁群算法等, 这类算法解决的是最优化问题, 例如求最短路径、最短时间等. 马拉松路线规划要满足距离为42.195公里, 且起终点之间的直线距离不得超过总距离的50%等要求^[6]. 针对马拉松路线规划, 黄鹤等提出改进的A*算法对马拉松路线进行规划^[3], 有效地简化了马拉松选线工作中的繁琐步骤, 使马拉松路线的选线更加高效、直观. 但A*算法是在两点间生成一条最短路径, 无法得到往返路径而实际路网需要考虑道路双向问题, 因而存在一定局限性.

本文结合城市路网、POI数据以及城市道路信息对城市马拉松路线规划进行研究, 以经纬度坐标点反应路网信息, 以道路交叉口作为路线转移节点, 可以充分考虑道路的双向问题和转弯角度情况, 减小算法生成路径时的计算成本. 同时, 基于贪心和回溯算法, 在每个路口处, 根据启发式预估策略获得路线局部最优解从而得到最终备选路线. 在此基础上, 提出一套评估体系对赛道路线进行评估. 最后通过规划路线与人工路线对比分析验证方法的有效性.

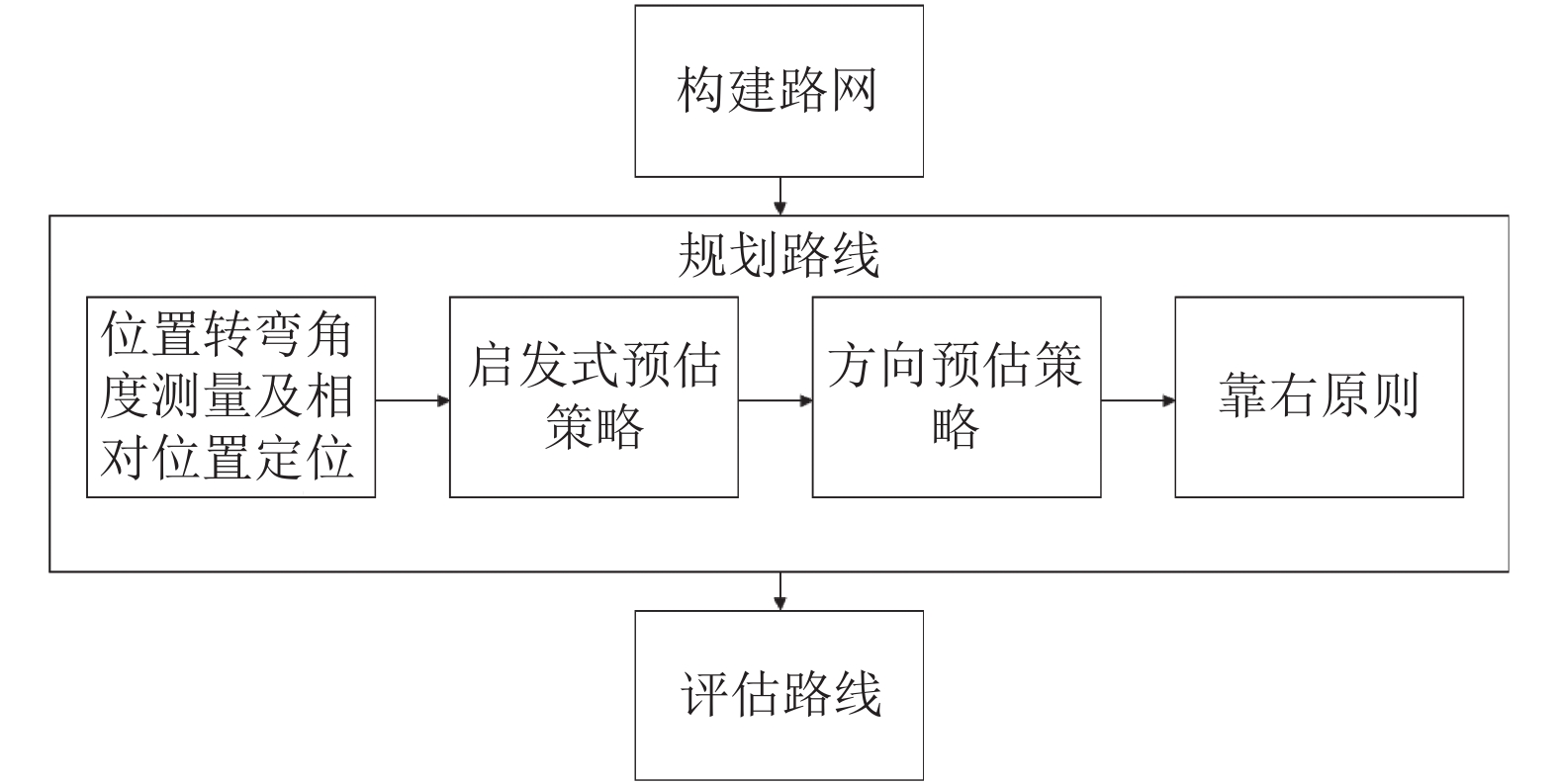
1 总体思路

城市马拉松路线规划必定满足以下必要条件: 1)从起点出发经过不重复的路段最终到达选定终点; 2)路线总距离为42.195公里. 但是在城市路网中从起点到终点之间存在诸多拓扑关系, 所以该问题的解空间庞大且无最优解. 为更快得出路线, 给出包括起终点在内的几个关键点, 将该问题近似的变成旅行商问题. 即使如此, 依旧存在42.195公里的限制, 且关键点与关键点之间不是最短路径的优化问题. 为了得到一个符合的路线, 在城市路网中利用贪心思想和回溯剪枝的手段得到局部最优解, 从而得到全局解^[7]. 如图1所示, 整个方法分为3个部分: 构建路网、规划路线和评估路线, 其中规划路线包括4个核心模块: 转弯角度测量及相对位置定位、启发式预估策略、方向预估策略和靠右原则.

通过分析城市路网信息可知整个路网由一个个经纬度坐标点根据拓扑关系连接而成, 每一条道路由多个路段组成, 每个路段由多个坐标点构成, 根据每个坐标点的连接情况, 将坐标点划分为单联节点、双联节点和多联节点, 如图2所示. 本文提出路线规划方案是根据坐标点遍历搜索法进行, 单联结点作为路线搜索回退标志, 双联节点作为路线折返标志, 多联结点作为路线转移标志和路线折返标志.

针对马拉松路线的特殊性, 需要满足一定的起跑距离以达到更好的赛事效果, 因此将搜索分为两个阶段: 起跑阶段和非起跑阶段^[8]. 规定从起点出发, 在起跑阶段选择直道路线并持续一定距离, 之后到达非起跑阶段. 如图3所示, 在非起跑阶段, 在当前路口节点处进行判断决定采用何种策略进行下一个坐标点的查找. 本方法给出3种启发式预估策略: 直接逼近策略、启发式远离策略和启发式靠近策略^[9].

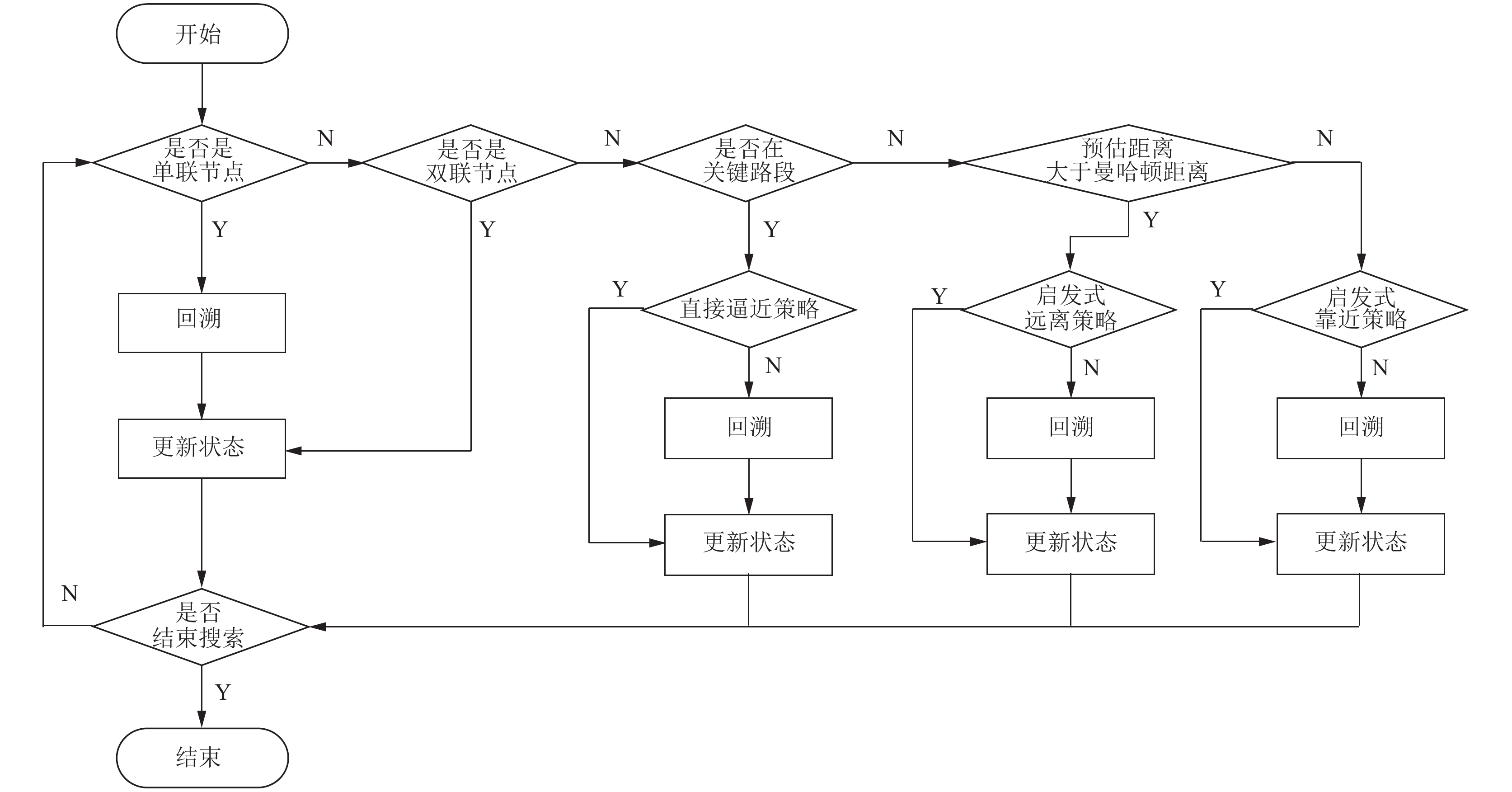
这3种策略每一个策略都要满足如下条件: 1)为保证规划舒适的赛道路线, 要确保下一个点转弯角度大于75°^[8]; 2)为避免路线交叉, 要确保不走已走过的坐标点; 3)为避免搜索提前结束, 要确保不提前进入终点所在路段. 满足以上条件则更新状态, 否则进行回溯, 回到上一个状态, 策略检查流程如图4所示.

2 路线规划 2.1 转弯角度测量及相对位置定位

本文中的路网是由一个个经纬度坐标点连接而成, 所以可以针对连续的3个坐标点, 通过计算其余弦值来反映转弯角度(假设3个坐标点在同一平面内), 这有助于在道路交叉口进行路线转移.

$ cos = \frac{{(x1 - x2)(x3 - x2) + (y1 - y2)(y3 - y2)}}{{\sqrt {{{(x1 - x2)}^2} + {{(y1 - y2)}^2}} \sqrt {{{(x3 - x2)}^2} + {{(y3 - y2)}^2}} }} $

(1)

其中, cos表示从坐标点(x1, y1)经坐标点(x2, y2)到坐标点(x3, y3)所形成的转弯角度的余弦值.

路网中的道路不都是横平竖直, 因此在规定路线方向时, 约束一定角度范围为某一固定方向, 通过计算两坐标点(假设两个坐标点在同一平面内)的斜率来反映两点形成的直线相对于横坐标轴的倾斜程度, 从而确定它们的相对位置, 这有助于判断在路口处是否右转. 相对位置以上、下、左、右、左上、左下、右下和右上表示.

$ tan = \frac{{y1 - y}}{{x1 - x}}, x1 \ne x $

(2)

其中, tan表示坐标点(x1, y1)与坐标点(x, y)的正切值, 即斜率.

2.2 启发式预估策略

直接逼近策略是当前坐标点在下一个关键点路段时为避免错过关键点而直接逼近的策略, 其预估方向为下一个关键点所在的方向; 启发式远离策略是在到下一个关键点前预估距离大于曼哈顿距离时而采取的策略, 此时为保证全程的距离接近42.195 km而选择远离关键点的方向; 启发式靠近策略是在到下一个关键点前预估距离小于等于曼哈顿距离时而采取的策略, 曼哈顿距离近似代表当前距离到达关键点最短距离. 在二维平面两点a(x1, y1)与b(x2, y2)的曼哈顿距离计算公式如下:

$ M(a, b) = \left| {x1 - x2} \right| + \left| {y1 - y2} \right| $

(3)

为实现有效的启发式靠近和远离策略, 需要动态的计算当前坐标点到下一个关键点剩余的曼哈顿距离和剩余预估距离. 路网中关键点拓扑示意图如图5所示.

图5中, q为起点节点, z为终点节点, a、b、c、d为关键点节点, n为当前节点. 当前点到下一个关键点剩余的曼哈顿距离计算公式如下:

$ \begin{split} &RestD = \\ &\frac{{\left[ {{D_{{\rm{sum}}}} - \displaystyle\sum\limits_{i = 0}^{j - 1} {D({K_i}, {K_{i + 1}}) - \displaystyle\sum\limits_{i = j}^{n - 1} {M({K_i}, {K_{i + 1}})} } } \right] \times M({K_j}, {K_{j + 1}})}}{{\displaystyle\sum\limits_{i = j}^{n - 1} {M({K_i}, {K_{i + 1}})} }} \\ &+ M({K_j}, {K_{j + 1}}) - D({K_j}, {K_{j + 1}}) \end{split} $

(4)

其中, n表示关键点的个数, j为当前关键点的位置, K_i为第i个关键点, D_sum表示总的路线距离, M(K_i, K_i+1)表示第i个关键点至第i+1个关键点的曼哈顿距离, D(K_i, K_i+1)表示第i个关键点至第i+1个关键点的已走距离, $\displaystyle\sum\nolimits_{i = 0}^{j - 1} {D({K_i}, {K_{i + 1}})} $ 表示从起点到当前关键点的已走距离, $\displaystyle\sum\nolimits_{i = j}^{n - 1} {D({K_i}, {K_{i + 1}})} $ 表示当前关键点至终点的曼哈顿距离. 当前坐标点至下一个关键点要走的剩余曼哈顿距离计算公式如下:

$ RestM = M(p, {K_{j + 1}}) $

(5)

其中, p为当前坐标点.

2.3 方向预估策略

通过启发式预估策略已经知道在路口处接下来是靠近还是远离下一个关键点, 但是到达一个路口时有多个方向可选, 对于方向的选择提出了方向预估策略, 根据当前坐标点与关键点的位置以及当前方向给出预估方向列表, 并按照优先级排序, 以确保局部最优. 对靠近和远离两种情况提出靠近原则和远离原则. 靠近原则优先推荐与关键点相同的方向, 其次推荐靠近关键点且与当前方向相同的方向, 最后推荐靠近关键点但与当前方向不同的方向; 远离原则优先推荐与关键点相反的方向, 其次推荐远离关键点且与当前方向相同的方向, 最后推荐远离关键点但与当前方向不同的方向.

如图6所示, 当前方向向下, 关键点位于当前点的左下方, 接下来有左, 右以及下3个方向可走. 根据方向预估策略, 若靠近关键点, 则预估方向列表为: 左下、下、左、左、下; 若远离关键点, 则预估方向列表为右上、上、右、上.

2.4 靠右原则

通过方向预估策略已经得出路线转移方向. 由于本方法充分考虑路网中道路双向的问题, 为避免路线搜索混乱, 本文约束对于一条道路选择前进右侧的路段, 即靠右原则.

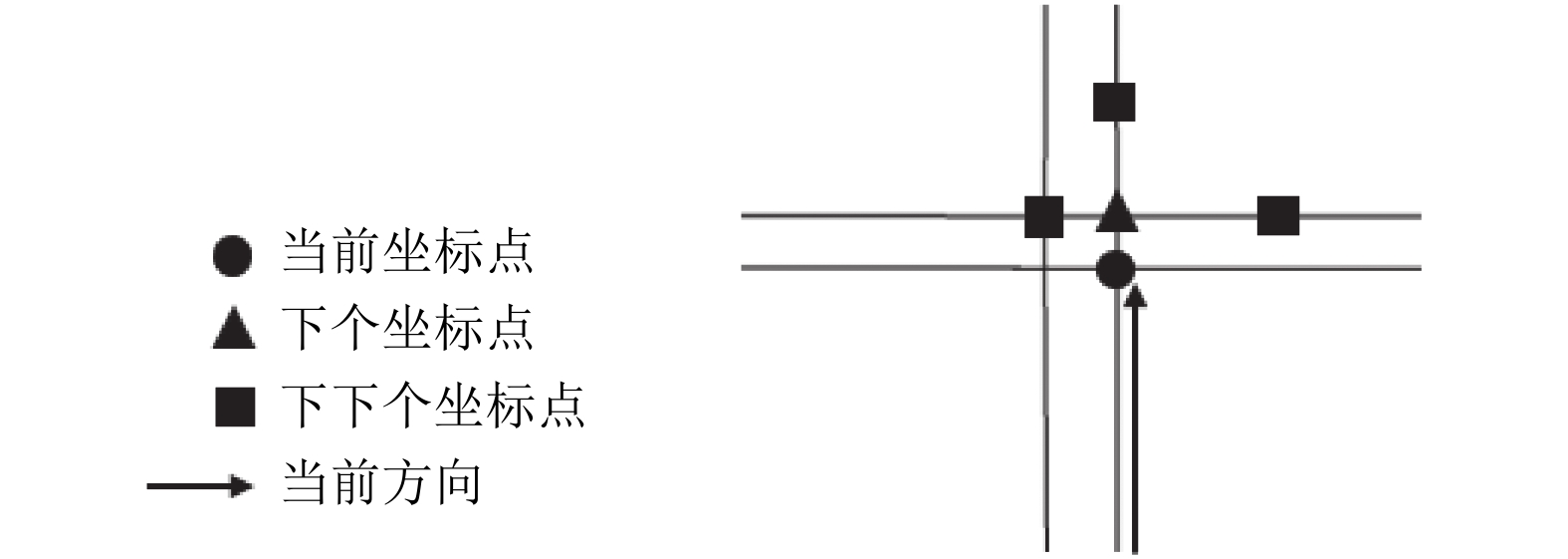
路口示意图如图7所示, 路口的具体控制策略流程图如图8所示, 采取的策略是通过当前方向找到下一个与当前方向相同的点并判断其是否是路口节点, 如果是路口节点则通过该节点进行转弯决策. 若决策是右转则不过该路口节点, 若决策是左转, 则穿过该路口节点.

3 评估体系

城市马拉松赛道是宣传一个城市文化、科技和经济的重要媒介^[10], 同时作为赛事的核心, 赛道要满足赛事要求, 为选手提供舒适安全的比赛环境, 也需降低对城市交通的影响. 根据国内外学者对马拉松赛道的分析和权威机构发布的文件^[11], 本文对每一条路线从POI热度值、道路宽度适宜度、路线畅通指数、过弯舒适度以及POI密集度5个维度进行综合评估, 其计算公式规定如下:

$ S = \frac{{({S_{\rm{poi}}} + {S_{\rm{road}}} + {S_{\rm{cross}}} + {S_{\cos }} + {S_{\rm{poin}}})}}{5} $

(6)

其中, S是路线的最终评估分数, S_poi是路线POI热度值得分, S_road是道路宽度适宜度得分, S_cross是路线畅通指数得分, S_cos是过弯舒适度得分, S_poin是POI密集度得分.

城市POI数据含有城市的地理、地貌以及人文特征, 能够凸显城市形象和赛道文化^[12]. 定义POI热度值为赛道路线附近的所有POI数据的热度值均值. 将每个POI数据定义初始值为100分, 先按照大类进行等次划分, 再按照小类进行等级划分, 进一步量化POI热度值, S_poi计算公式如下:

$ {S_{{\rm{poi}}}} = \frac{{\left(\displaystyle\sum\limits_{i = 1}^{{n_p}} {100 \times {G_i} \times {L_i}} \right)}}{{{n_p}}} $

(7)

其中, G_i表示第i个POI数据的等次所持比例, L_i表示第i个POI数据等级所持比例, n_p是路线所包含的POI数据数量.

关注POI质量的同时也关注POI数量. 本文对近几年国内著名马拉松路线研究^[13], 分析其赛道POI数量, 总结POI密集度得分S_poin计算公式如下:

$ {S_{{\rm{poin}}}} = \left\{ \begin{gathered} 0, \; {n_p} \lt 5 \\ 30, \; 5 \leqslant {n_p} \lt 10 \\ 60, \; 10 \leqslant {n_p} < 20 \\ 80, \; 20 \leqslant {n_p} < 30 \\ 90, \; 30 \leqslant {n_p} < 50 \\ 100, \; {n_p} \geqslant 50 \\ \end{gathered} \right. $

(8)

马拉松赛道宽是影响选手成绩和参赛体验的重要因素^[14]. 一条路线由多个路段组成, 规定每条路线的宽度初始值为100, 给不同宽度的路段分配不同的占比来量化宽度适宜度. 整个路线的宽度适宜度S_road计算公式如下:

$ {S_{{\rm{road}}}} = 100 \times \left( \frac{{{D_{ \geqslant 12}}}}{{{D_{{\rm{sum}}}}}} \times 100{\text{%}} + \frac{{{D_{ \geqslant 9\& < 12}}}}{{{D_{{\rm{sum}}}}}} \times 70{\text{%}} + \frac{{{D_{ < 9}}}}{{{D_{{\rm{sum}}}}}} \times 50{\text{%}} \right) $

(9)

其中, D_≥12为路线中宽度大于等于12的路段总长度, D_≥9&<12为宽度在[9, 12)区间的路段总长度, D_<9为宽度小于6的路段总长度.

进行马拉松赛事举办时, 需要进行交通管制, 对赛道进行封路, 这势必会对公众出行造成一定的影响^[15]. 路线畅通指数反应马拉松赛道给城市交通带来的影响. 规定每条路线的路线畅通指数初始值为100, 给不同拥堵程度的路段分配不同的占比来量化路线畅通指数. 整个路线的路线畅通指数S_cross计算公式如下:

$ \begin{split} &{S_{{\rm{cross}}}} =100 \times \\ &\left(\frac{{D{C_4}}}{{{D_{{\rm{sum}}}}}} \times 10{\text{%}} + \frac{{D{C_3}}}{{{D_{{\rm{sum}}}}}} \times 50{\text{%}} + \frac{{D{C_2}}}{{{D_{{\rm{sum}}}}}} \times 70{\text{%}} + \frac{{D{C_1}}}{{{D_{{\rm{sum}}}}}} \times 100{\text{%}} \right) \end{split} $

(10)

其中, DC₄是路线中拥堵级别为“严重拥堵”的路段总长度, DC₃是拥堵级别为“拥堵”的路段总长度, DC₂为拥堵级别为“缓行”的路段总长度, DC₁是拥堵级别为“畅通”的路段总长度, D_sum是路线所有路段总长度(道路的拥堵等级根据高德地图开放平台划分).

马拉松赛道中弯道路线是影响选手成绩的因素^[16], 因此把弯道舒适度作为评价指标之一, 规定每条路线的弯道舒适度初始值为100, 给不同弧度的弯道分配不同的占比来量化弯道舒适度, 整个路线的弯道舒适度得分S_cos计算公式如下:

$ \begin{split} {S_{\cos }} = & 100 \times \left(\frac{{{N_{ > 0}}}}{{{N_{{\rm{sum}}}}}} \times 0{\text{%}} +\frac{{{N_{ > - 0.5\& \leqslant 0}}}}{{{N_{{\rm{sum}}}}}} \times 50{\text{%}} \right. \\ &\left. + \frac{{{N_{ > - 0.93\& \leqslant - 0.5}}}}{{{N_{{\rm{sum}}}}}} \times 70{\text{%}} + \frac{{{N_{ \leqslant - 0.93}}}}{{{N_{{\rm{sum}}}}}} \times 100{\text{%}} \right) \end{split}$

(11)

其中, N_>0是路线中过弯角度小于90°的弯道数量, N_>−0.5&≤0是过弯角度大于等于90°且小于120°的弯道数量, N_{>−0.93&≤−0.5}是过弯角度大于等于120°且小于150°的弯道数量, N_≤−0.93是过弯角度大于等于150°的弯道数量, N_sum是路线中弯道总数量.

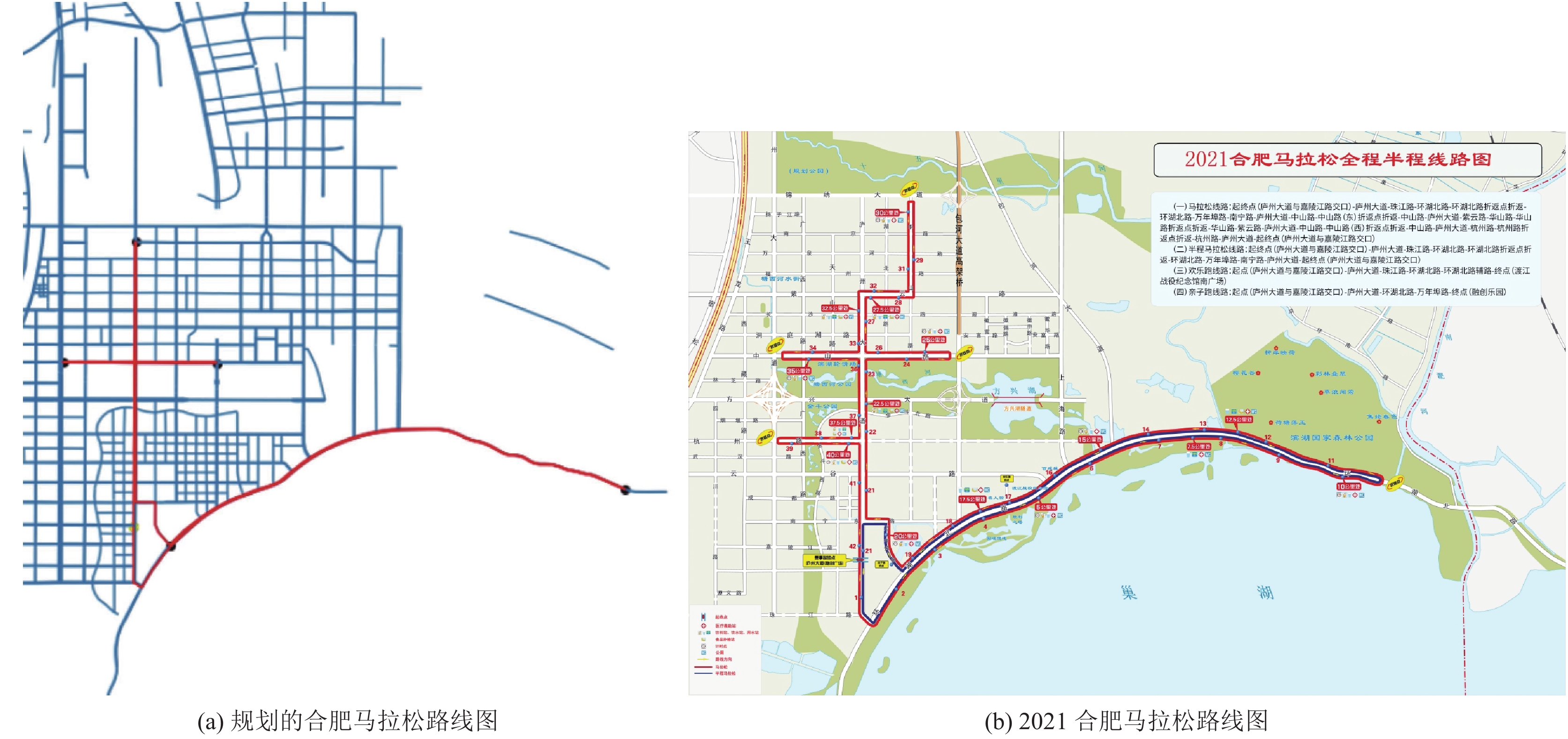
4 实验验证

在OpenStreetMap平台爬取了合肥市城市路网信息, 在合肥市路网中, 以嘉陵江路与庐州大道路口为起终点, 依次以环湖北路, 环湖北路与万年埠路路口, 中山路与包河大道路口, 庐州大道与扬子江路路口以及中山路为关键点进行路线搜索, 得到马拉松路线规划路线, 对比同样以嘉陵江路与庐州大道路口为起终点的2021合肥马拉松路线, 如图9所示. 通过对两张路线图评估和分析, 得到结果, 如表1所示.

两个路线相似度为92.94%, 所以两个路线的分值接近, 本方法规划的路线包含更长的庐州大道, 因此在宽度舒适度指标要多高于已有路线.

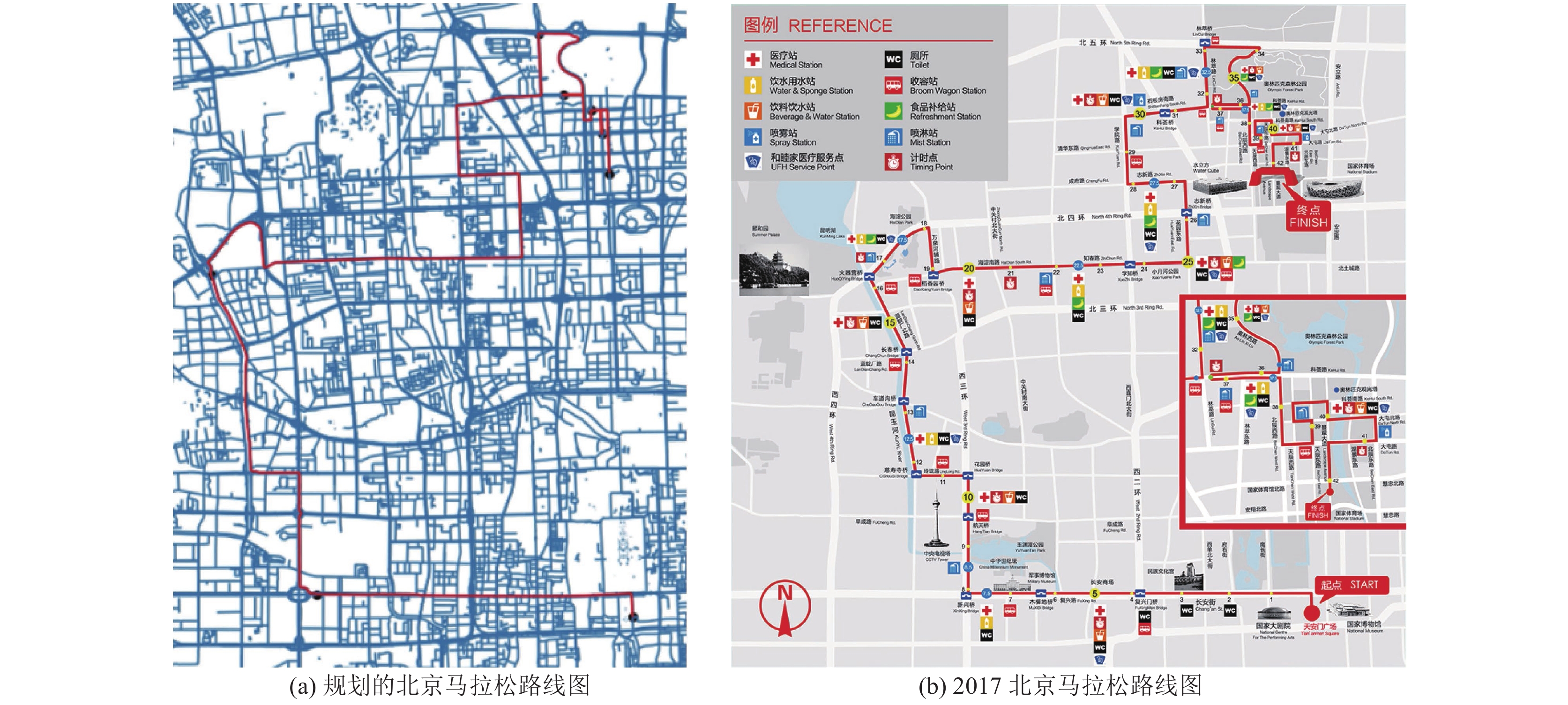
还以同样的步骤对北京路网进行处理, 并选择天安门广场东侧路作为起点路段, 奥林匹克公园的景观大道作为终点路段, 利用本方法得到马拉松路线规划路线, 对比同样以天安门广场东侧路作为起点路段、奥林匹克公园的景观大道作为终点路段的2017北京马拉松路线, 如图10所示. 通过对两张路线图评估和分析, 得到结果, 如表2所示.

两个路线相似度为97.04%, 其分值也非常相近, 二者主要差别在于弯道舒适度指标, 在路网中可以看到, 在快接近终点处, 规划路线的弯道角度更小, 因此分值低于已有路线.

通过两组对比分析, 表明用本研究可有效地规划出马拉松赛道路线, 并且规划路线与已有路线进行对比有较大的相似之处, 然而由于方法的程序化也导致与人工规划的路线存在个别差异.

5 结束语

本文采用贪心和回溯算法对城市马拉松路线规划进行实践与研究: 首先对路网数据进行裁剪; 其次在路网中根据关键点进行路线搜索, 在路口处利用启发式预估策略和方向预估策略进行方向转移, 再遵循路线靠右原则得到局部最优解; 最后根据局部最优解得到备选路线. 本研究考虑道路的双向问题, 规划的路线更接近真实道路情况, 通过实验和评估表明本研究可以对赛道路线进行快速高效智能规划, 为马拉松路线规划提供了新的思路, 对马拉松路线规划工作有重要指导意义.