正则表达式是描述字符序列模式的字符序列, 跟自动机一样同为正则语言模型中的一种^[1], 二者是等价的, 自动机可以转化为对应的正则表达式, 正则表达式也可以转化为对应的自动机^[2,3], 与自动机相比, 正则表达式具有强大的表达能力, 也具备简单性与易理解性, 目前已经成为搜索引擎、文字处理器和文本编辑器中最流行的模式设计语言, 此外, 正则表达式的使用正在多个不同的应用领域推广, 包括信息提取、网络安全、生物信息学等. 然而, 要想获得简洁、可读性强、高质量的正则表达式是不容易的, 如何快速高效的将有限自动机转化为高质量的正则表达式已经成为计算机理论研究中的重大课题.

目前把有限自动机转化为正则表达式的经典方法主要有状态削减法^[4]、Brzozowski代数法^[4]和传递闭包法^[5]: 状态消减法按照状态削减序列和状态削减规则, 不断地将状态从有限自动机中去除, 最终将有限自动机转换为只有终态和初态的表达式自动机, 从而得到正则表达式; Brzozowski代数法将自动机转化为正则表达式的问题规约为代数方程组求解, 通过代数消元后得到转化后的正则表达式, 传递闭包法根据状态的迭代顺序, 反复计算自动机的转移矩阵, 最后得到自动机对应的正则表达式, 在这3种方法中, 状态削减法会受到状态削减顺序的影响, Brzozowski代数法受到代数消元顺序的影响, 传递闭包法会受到状态迭代顺序的影响.

综上所述, 状态的排序方式对这3种经典的正则表达式生成算法有着十分重大的影响, 直接影响着生成的正则表达式的质量, 所以如何对状态的排序方式, 也就是状态序列进行优化, 是提高正则表达式质量的关键所在.

目前, 关于优化状态序列这方面的研究比较少, 主要是一些通过使用启发式算法来对状态序列进行优化的研究, 如McNaughton等提出的流量法^[5], 将自动机中每个状态的状态转移个数定义为流量, 从而将状态按照流量从小到大排序; Gruber等提出了度乘积法^[6]将状态初度和入度的乘积作为优化状态序列的依据, 要求度乘积大的状态排在状态序列的后面, 并且采用动态排列的方式, 即每削减一个状态后重新计算剩余状态的度乘积, 重新排序; Delgado等提出了权重法^[7], 把状态削减后有限自动机字符规模的增加量作为此状态的权重, 对状态进行排序, 得到状态削减序列; Moreira等提出了回路计算法^[8], 按照含有某个状态的回路数量作为此状态的依据, 完成状态序列的排序; Singh提出可以通过自动机中回路及其嵌套回路之间的关系寻找状态序列^[9].

在上述的这些使用启发式算法对状态序列进行优化的研究中, 虽然他们采用的方法不同, 但是本质上都是通过对状态序列的排序进行研究, 对状态进行优先级的排序, 缩小状态序列的搜索空间, 进而找到符合要求的状态序列, 这些方法虽然提高了搜索状态序列的效率, 但也使得它们在效果以及应用范围上受到了限制, 流量法、度乘积法、权重法根据不同的方式定义了评价每个状态的参数, 固然可以缩小状态序列的搜索空间, 但也正是因为对搜索空间进行了限制, 导致它们无法找到一些质量更高但是不满足状态优先级排序的状态序列, 通过寻找回路以及寻找回路和嵌套回路之前的关系来获得状态序列, 使得它们对有限自动机的结构有了一定的要求, 只适用于存在回路的有限自动机, 导致了算法的应用范围变窄, 普适性下降.

受到上述算法的启发, 为了缓解这一问题, 找到高质量的状态序列, 本文提出了基于食肉植物算法的状态序列搜索方法, 将食肉植物算法的核心理论和种群进化模型使用到状态序列的搜索中, 并结合了其他启发式算法进行设计与优化, 在扩大了状态序列的搜索空间的同时, 也能够找到较优的状态序列, 并且对自动机的结构也无特殊需求, 避免了算法应用范围变小的问题, 实验结果表明, 基于食肉植物算法的状态序列搜索方法找到的状态序列优于上述的启发式算法, 并且随着自动机阶数的增加, 算法的效果会愈发凸显.

1 预备知识

有限自动机主要分为确定有限自动机与非确定有限自动机两种类型, 本文主要研究的是最小确定有限自动机, 形式化的定义如下.

定义1. 确定有限自动机^[10]. 确定有限自动是一个五元组 $ A = (Q, \Sigma , \delta , s, f) $ , 其中, Q是自动机的状态集合, 状态的个数是有限的; $\Sigma $ 是自动机输入符号的集合, 也叫字母表; $\delta $ 是自动机的状态转移函数, 函数的输入是一个状态与一个输入符号, 输出是此状态接收输入符号发生转移后的状态, 若转移函数的输入状态 ${q_i} \in Q$ , 输入符号是 $k \in \Sigma $ , 输出状态 ${q_j} \in Q$ , 则 $ {q_j} = \delta \left( {{q_i}, k} \right) $ ; s是自动机的开始(初始)状态, 简称初态; f是自动机的终止状态, 简称终态.

定义2. 确定有限自动机最小化^[11]. 若确定有限自动机D中没有不可达状态(指不能从初态到达的状态), 且两两状态互不等价(指在同一输入串下不产生区别), 则称D为最小确定有限自动机.

定义3. 正则表达式. 字母表 $\Sigma $ 上的正则表达式定义如下.

$\phi $ 和 $\varepsilon $ 是正则表达式; $\phi $ 表示空集, $\varepsilon $ 表示空串.

每个字符 $\alpha \in \Sigma $ 是正则表达式.

若 $\alpha $ 和 $\;\beta $ 是正则表达式, 则它们的选择运算 $(\alpha + \beta )$ 和连接运算 $ (\alpha \cdot \beta ) $ 的结果也是正则表达式.

若 $\alpha $ 是正则表达式, 则 $ ({\alpha ^*}) $ 也是正则表达式, $ ({\alpha ^*}) $ 为 $\alpha $ 的克林闭包.

定义4. 正则表达式的长度. 将正则表达式 $\alpha $ 中除元字符外的字符个数定义为正则表达式的长度, 记为 $ |\alpha | $ ; 例如, 正则表达式 $(\alpha + \beta )$ 的长度为2.

在自动机转化为正则表达式的过程中, 根据状态序列的不同, 会导致生成的正则表达式的长度不同, 这也是本文研究的重点, 下面介绍状态序列的定义.

定义5. 状态序列. 状态序列是自动机中的除初态和终态以外的状态 ${q_i} \in Q$ 的有序排列, 定义状态序列s为 $ < {q_1}, {q_2}, {\text{ }} \cdots , {q_{n - }}_1, {q_n} > $ , 状态序列的长度记为 $|s| = n$ .

2 问题模型

状态序列的搜索问题可以归纳为排列组合的问题, 根据定义5可知, 状态序列就是自动机中除去初态和终态以外的状态的有序排列, 不同的排列方式代表着不同的状态序列, 这也是影响生成的正则表达式质量的关键因素.

为了研究如何快速高效地找到较优的状态序列, 本文选择了经典生成算法中的状态削减法作为生成正则表达式的方法, 并以生成正则表达式的长度作为评判状态序列优劣的标准, 给定自动机, 生成的正则表达式长度越短, 代表找到的状态序列质量越好.

2.1 状态削减法

状态削减法是一种经典的将自动机转化为正则表达式的方法, 接下来将以简单的例子为例, 介绍状态削减法的运行流程及原理^{[6, 12]}.

如图1所示, 确定有限自动机D1, 状态 $ {q_0} $ 是初态, 状态 $ {q_4} $ 是终态, 以状态序列 $ < {q_3}, {q_2}, {q_1} > $ 为例, 讲述有限自动机D1转化为正则表达式的过程. 首先, 削减状态 $ {q_3} $ , 与 $ {q_3} $ 相关的状态转移也同时被削减, 按照状态削减法定义的规则完成调整, 即将 $ {q_1} $ 到 $ {q_3} $ 与 $ {q_3} $ 到 $ {q_2} $ 的状态转移合并到 $ {q_1} $ 到 $ {q_2} $ 的状态转移中, 削减状态 $ {q_3} $ 后的自动机如图2所示, 接下来将削减状态 $ {q_2} $ , 将 $ {q_1} $ 到 $ {q_2} $ , $ {q_2} $ 到 $ {q_4} $ 的状态转移合并到 $ {q_1} $ 到 $ {q_4} $ 的状态转移中, 削减后的自动机如图3所示, 最后削减状态 $ {q_1} $ , 将 $ {q_0} $ 到 $ {q_1} $ , $ {q_1} $ 到 $ {q_4} $ 的状态转移合并到 $ {q_0} $ 到 $ {q_4} $ 的状态转移中, 结果如图4所示, 此时, 完成了状态削减的所有步骤, 初态 $ {q_0} $ 到终态 $ {q_4} $ 的状态转移便是确定有限自动机D1所对应的正则表达式.

使用状态削减法, 对确定有限自动机D1按照状态序列 $ < {q_3}, {q_2}, {q_1} > $ 进行状态削减后得到的正则表达式为nc*f|(a|eh*j)i, 长度为8, 若将状态序列修改为 $ < {q_2}, {q_3}, {q_1} > $ , 得到的正则表达式为nc*(f|ai)|(eh*ji), 长度为9, 则状态序列 $ < {q_3}, {q_2}, {q_1} > $ 优于状态序列 $ < {q_2}, {q_3}, {q_1} > $ .

综上所述, 寻找较优状态序列的问题转化为了排列组合问题, 在状态序列的搜索空间中, 尽可能地找到生成正则表达式较短的状态序列就是本文的研究目标.

3 基于食肉植物算法的状态序列搜索方法

食肉植物算法是马来西亚的Ong等2020年提出的一种元启发式算法^[13], 其灵感来源于模拟食肉植物在恶劣的生存环境中不断适应和进化的过程, 在求优化问题时有十分优良的表现, 为了在状态序列庞大的搜索空间中快速高效地找到较优解, 本文以食肉植物算法的理论为核心, 并对算法进行了设计与优化, 提出了基于食肉植物算法的状态序列搜索方法, 接下来将详细介绍关于算法的运行流程以及在各个环节的设计.

3.1 初始种群

在基于食肉植物算法的状态序列搜索方法中, 搜索空间中每个状态序列被视为独立的个体, 首先, 在湿地中随机初始化由食肉植物和猎物组成的n个个体, 食肉植物与猎物的数目分别记为nCPlant和nPrey, 要完成初始种群的构建, 构建种群的方式主要有两种.

(1)随机生成满足种群预设规模n的状态序列.

(2)随机生成一定数目的状态序列, 将其中最好的加入到初始种群中, 整个过程执行若干次, 直到满足种群预设规模n为止.

在经过初始种群构建的对比实验后, 发现这两种构建方式对本实验的结果影响甚微, 尤其在自动机的阶数较低时, 两种构建方式最后得到的状态序列生成的正则表达式长度是相等的, 因此最终采用了第1种方式来构建初始种群, 以降低算法的时间复杂度.

3.2 适应度函数

完成初始种群的构建后, 首先要计算个体的适应度, 适应度函数的定义如下:

$ Fitness[i] = Length[i] $

(1)

其中, $ Fitness[i] $ 是适应度函数, $ Length[i] $ 代表按照状态序列 $ Order[i] $ 经过状态削减法后得到的正则表达式长度, 适应度函数的值越小, 代表生成的正则表达式长度越短, 对应的状态序列质量就越高.

3.3 分类和分组

在完成种群中所有个体的适应度计算后, 开始对种群中的个体按照其适应度的值进行分类, 将得到的适应度值进行升序排列, 排在前nCPlant位的个体被视为食肉植物, 剩下的nPrey个个体被视为猎物, 其中nCPlant和nPrey满足如下关系:

$ n{\rm{Prey}}/n{\rm{CPlant}} \geqslant 2 $

(2)

分类完成后, 开始对种群进行分组, 分组过程要模拟每个食肉植物及其猎物的环境, 在分组过程中, 最佳适应度值即适应度值最小的猎物被分配给排名第一的食肉植物, 相似的, 适应度排在第2位和第3位的猎物被分配给排名第2和第3的食肉植物, 直到排名第nCPlant位的猎物被分配给排名nCPlant位的食肉植物, 排名nCPlant+1的猎物再分配给第1位的食肉植物, 反复循环, 直到完成分组.

3.4 增长

由于土壤缺乏营养, 食肉植物会吸引、捕获和消化猎物, 以促进其生长, 猎物被吸引到食肉植物上的同时, 也有可能陆续逃离魔爪, 这里引入了吸引率的概念:

对于每个分组后的小群体, 随机选择一个猎物, 若吸引率高于随机生成的数字, 则猎物被食肉植物捕获并消化, 来完成食肉植物的生长, 进化为新的食肉植物, 另一方面, 若吸引率低于随机值, 则猎物逃跑并继续生长, 进化为新的猎物个体, 在食肉植物算法中, 每组中只有一个食肉植物, 猎物数必须大于等于两个, 对大多数例子来说, 吸引率被设为0.8^[13].

假定状态序列s1 $ < {q_1}, {q_3}, {q_4}, {q_2} > $ 为食肉植物, 状态序列s2 $ < {q_2}, {q_4}, {q_1}, {q_3} > $ 为猎物, 当猎物被食肉植物捕获并消化后, 会进化为一个新的食肉植物, 具体的流程如算法1所示.

算法1. 产生新食肉植物/猎物
1) 先用随机数cut_idx确定序列s1产生变化的区域, 如cut_idx的值为2, 则保持序列s1的前两项不变, 从第3项开始产生变化, 即保持 $\scriptstyle {q_1} $ , $\scriptstyle {q_3} $ 位置不变, 改变 $\scriptstyle {q_2} $ , $\scriptstyle {q_4} $ 的顺序. 2) 扫描序列s2, 直到找到 $\scriptstyle {q_2} $ 或者 $\scriptstyle {q_4} $ , 将其添加到 $\scriptstyle < {q_1}, {q_3} > $ 的后面.3) 得到新的食肉植物/猎物, 即状态序列s3 $\scriptstyle < {q_1}, {q_3}, {q_2}, {q_4} > $ . 4) 若s3与s1或者s2相同, 则返回步骤1).

由于状态序列的有序性, 在产生新个体的算法设计上借鉴了遗传算法中交叉和变异的操作, 在产生新个体的同时也扩大的搜索空间, 使得搜索空间的状态序列都有机会被搜索到.

3.5 繁殖

完成生长过程的食肉植物开始进入繁殖阶段, 只有排名第一的食肉植物才被允许与其他的食肉植物进行繁殖操作, 在这一阶段, 引入了繁殖率 $ {p_r} $ , 选定一个食肉植物, 生成一个随机数, 若繁殖率高于生成的随机数, 则开始繁殖过程, 反之则不进行繁殖操作, 为了维持种群的稳定性与多样性, 对繁殖率进行了自适应设计, 让它根据参与繁殖的个体的适应度自适应调整, 具体的设计如下:

$ {p_r} = {p_{r2}} + ({p_{r1}} - {p_{r2}})(f - {f_{\min }})/({f_{{\rm{avg}}}} - {f_{\min }}) $

(3)

其中, $ {p_{r1}} $ 与 $ {p_{r2}} $ 为预定义的介于0和1之间的值, 并且 $ {p_{r1}} $ > $ {p_{r2}} $ , $ f $ 为被选定的食肉植物的适应度, $ {f_{\min }} $ 是排名第一的食肉植物的适应度, ${f_{{\rm{avg}}}}$ 为所有食肉植物的平均适应度. 通过对繁殖率的设计, 可以让适应度函数值与最佳食肉植物相差较大的个体有更大的机会参与繁殖, 增加种群的多样性, 让适应度函数值与最佳食肉植物相近的个体也有参加繁殖的机会, 维持种群的稳定性.

3.6 种群更新与合并

将新产生的所有食肉植物和猎物都加入到初始种群中, 所有个体根据适应度值重新排序, 将排在前n名的个体选为进入下一代的初始种群, 开始下一轮的迭代, 不断重复分类、分组、生长、繁殖等过程, 直到满足迭代次数或预定义的停止条件, 算法运行结束, 此时适应度函数值最小的个体, 就是找到的较优状态序列.

4 实验结果及分析

在这一节, 本文设计了对比实验, 将基于食肉算法的状态序列搜索方法与其他的启发式算法进行了对比, 验证了本文提出方法的可行性和有效性, 实验所用机器的CPU为AMD Ryzen 4800H, 主频为2.9 GHz, 配置内存为16.00 GB, 操作系统为Windows 10, 使用C#作为编程语言, 并以Visual Studio 2017作为实验平台.

实验方案如下: 按照自动机的阶数随机生成确定有限自动机1 000个, 主要包含的阶数为12, 14, 16, 18, 20, 以在每个数据集上得到的正则表达式长度作为评判标准, 对每个算法得到的状态序列质量进行评价和对比, 对比实验中主要包括的启发式算法有随机序列法(RA)、自然序列法(NA)、流量法(TR)、静态度乘积法(OA)、动态度乘积法(OB)、权重法(DM)、必经路径法(NE)、遗传算法(GA)和基于食肉植物算法的状态序列搜索方法(CPA), 其中遗传算法采用的是无放回随机选择算子、迭代次数为50, 种群规模为50, 基于食肉植物算法的状态序列搜索方法的参数为: 种群规模50, 迭代次数30, 吸引率0.8, $ {p_{r1}} $ =0.8, $ {p_{r2}} $ =0.6, 具体的实验结果如图5所示.

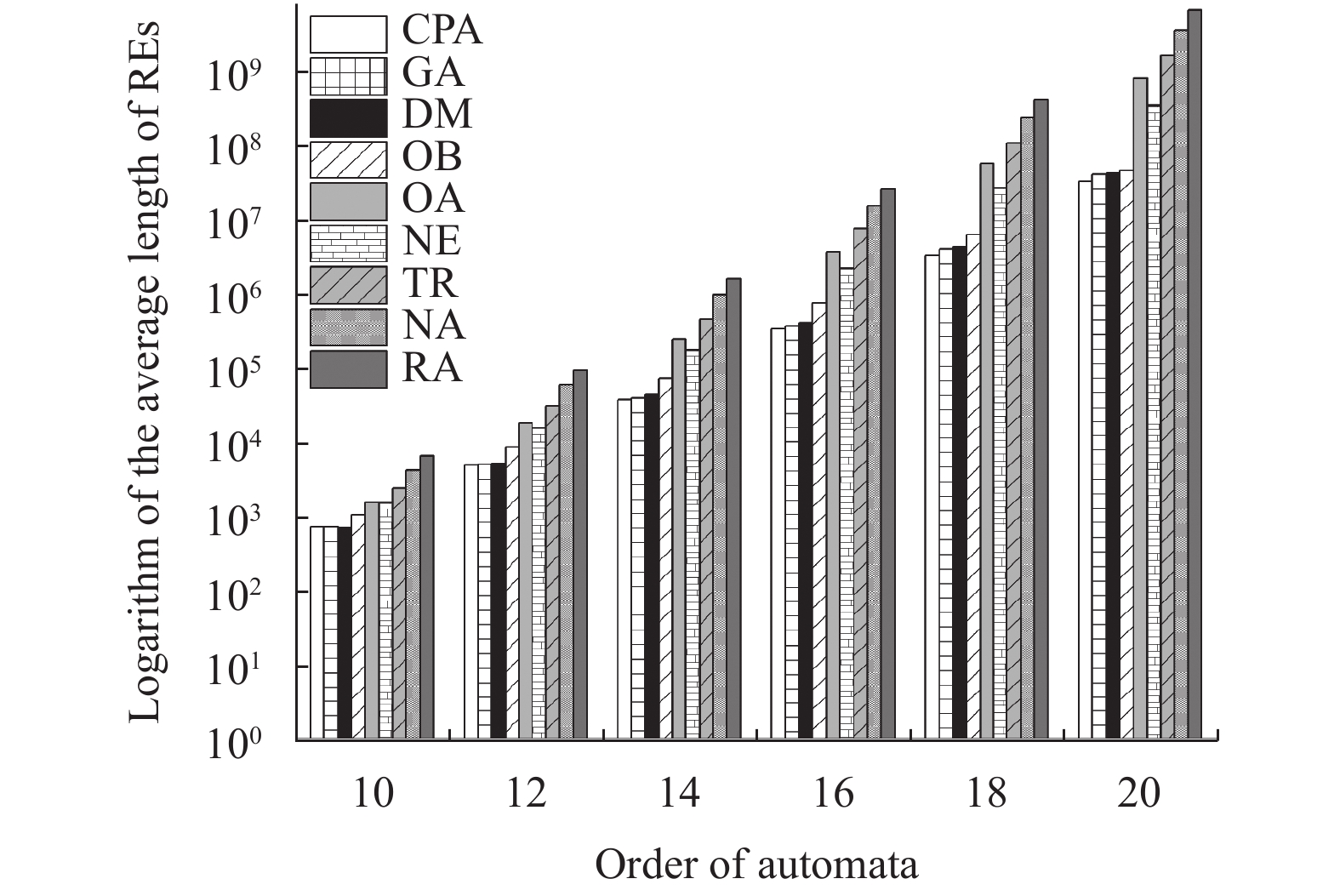
在图5中, 横坐标为自动机的阶数, 纵坐标是将算法在每个自动机数据集上得到的正则表达式平均长度取以10为底数的对数后得到的值, 可以看出, 基于食肉植物算法的状态序列搜索算法所得到的状态序列生成的正则表达式长度要短于其他启发式算法, 其中更是领先了随机序列法、自然序列法这些启发式算法多个数量级.

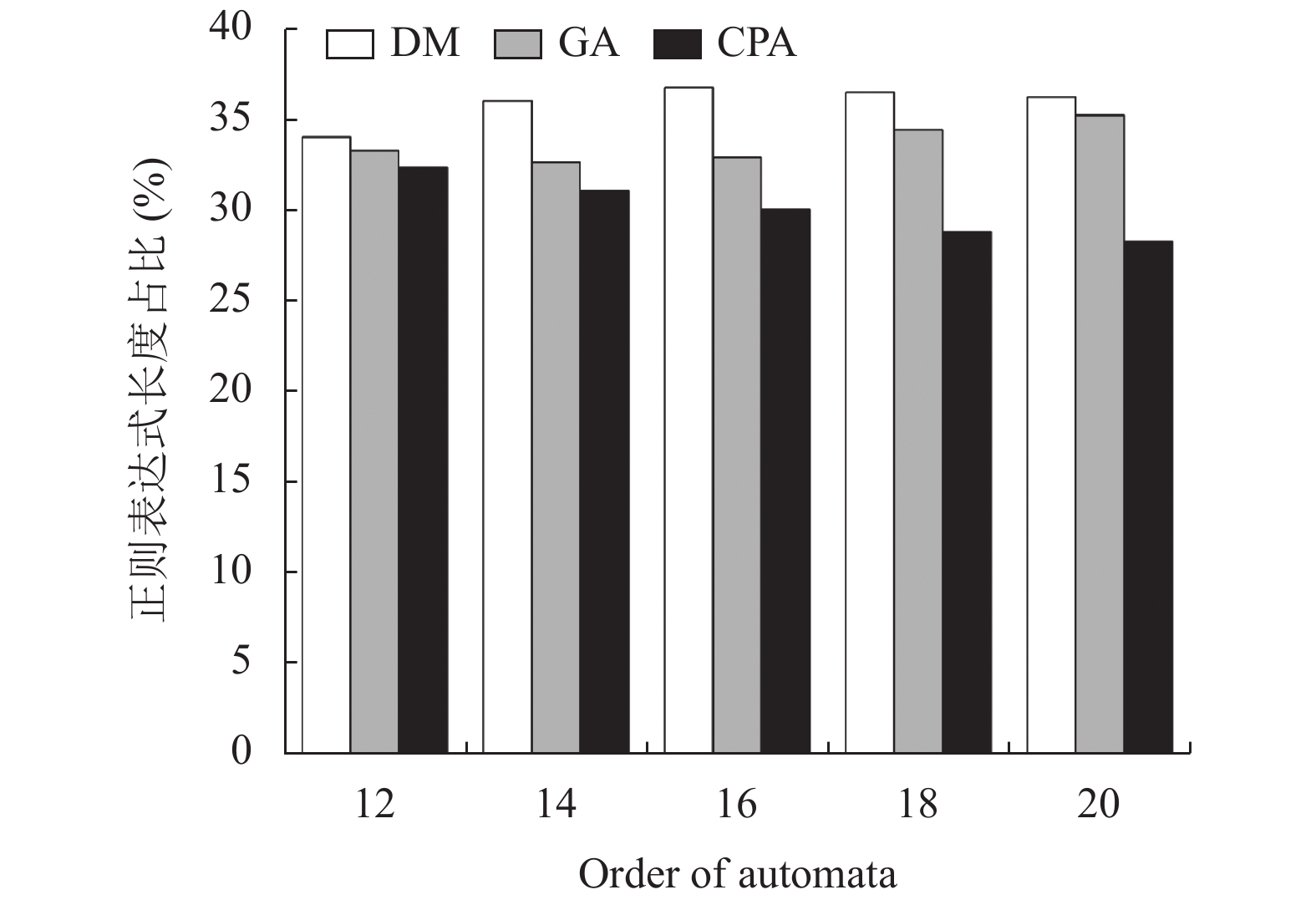
因为纵坐标轴刻度的设置, 使得GA、DM与CPA的差距在图5中不易体现, 因此, 为了进一步体现CPA的有效性, 进一步将这3个算法进行了对比, 实验结果如图6和图7所示.

在图6中, 横坐标为自动机的阶数, 纵坐标是每个算法得到的状态序列生成的正则表达式长度在总和中所占的百分比, 可以看出, CPA和GA的效果要优于DM算法, 尤其是CPA, 在3种算法中表现最好, 正则表达式的长度最短.

在图7中, 横坐标为自动机的阶数, 纵坐标是GA和CPA对比于DM算法在正则表达式长度方面缩短幅度的对比, 在同样的种群规模下, 随着自动机阶数上升GA的缩短幅度会呈现出先增后减的趋势, CPA的缩短幅度不断上升, 也就是说, CPA不仅在生成正则表达式的长度上有优势, 并且对于种群规模的需求还要更小, 这也进一步降低了算法的时间复杂度.

5 结论与展望

为了提高正则表达式的质量, 找到较优的状态序列, 本文提出了基于食肉植物算法的状态序列搜索方法, 并通过实验证明了算法的实用性和优越性, 此方法不仅扩大了状态序列的搜索空间, 也避免了对自动机结构存在需求的问题, 提高了算法的适用范围, 可以作为一个寻找较优状态序列的有效方法.

国内目前关于自动机和正则表达式的研究比较稀少, 在自动机生成正则表达式的过程中, 每个环节的改善, 都会对得到高质量的正则表达式起到关键作用, 本文重点研究了如何获得较优的状态序列, 并没有对正则表达式的化简以及生成正则表达式的方法等进行研究, 在未来的发展中, 可以进一步对这些方面进行研究, 从而提高生成正则表达式的效率与质量.