基于属性嵌入与图注意力网络的实体对齐算法

引用本文

苏谟, 步格格, 范秋枫, 刘凡力. 基于属性嵌入与图注意力网络的实体对齐算法. 计算机系统应用, 2023, 32(3): 202-208.http://www.c-s-a.org.cn/1003-3254/8967.html

Su M, Bu GG, Fan QF, Liu FL. Entity Alignment Algorithm Based on Attribute Embedding and Graph Attention Network. Computer Systems and Applications, 2023, 32(3): 202-208(in Chinese).http://www.c-s-a.org.cn/1003-3254/8967.html

基于属性嵌入与图注意力网络的实体对齐算法

苏谟^2,3, 步格格^1,2, 范秋枫², 刘凡力²

1. 中国科学院大学, 北京 100049;
2. 中国科学院沈阳计算技术研究所, 沈阳 110168;
3. 沈阳理工大学, 沈阳 110159

收稿日期：2022-07-26; 修改日期：2022-09-01; 采用时间：2022-09-14; csa 在线出版时间：2022-11-29

基金项目：沈阳市中青年科技创新人才(RC210393); 辽宁省“百千万人才工程”项目(2021921015)

通讯作者：步格格, E-mail: bgg1279@126.com.

摘要：实体对齐旨在找到位于不同知识图谱中的等效实体, 是实现知识融合的重要步骤. 当前主流的方法是基于图神经网络的实体对齐方法, 这些方法往往过于依赖图的结构信息, 导致在特定图结构上训练得到的模型不能拓展应用于其他图结构中. 同时, 大多数方法未能充分利用辅助信息, 例如属性信息. 为此, 本文提出了一种基于图注意力网络和属性嵌入的实体对齐方法, 该方法使用图注意力网络对不同的知识图谱进行编码, 引入注意力机制从实体应用到属性, 在对齐阶段将结构嵌入和属性嵌入进行结合实现实体对齐效果的提升. 在现实世界的3个真实数据集上对本文模型进行了验证, 实验结果表明提出的方法在很大程度上优于基准的实体对齐方法.

关键词: 实体对齐图注意力网络知识图谱属性嵌入对齐预测

Entity Alignment Algorithm Based on Attribute Embedding and Graph Attention Network

SU Mo^2,3, BU Ge-Ge^1,2, FAN Qiu-Feng², LIU Fan-Li²

1. University of Chinese Academy of Sciences, Beijing 100049, China;
2. Shenyang Institute of Computing Technology, Chinese Academy of Sciences, Shenyang 110168, China;
3. Shenyang Ligong University, Shenyang 110159, China

Abstract: Entity alignment aims to find equivalent entities located in different knowledge graphs and is an important step for knowledge fusion. Currently, mainstream entity alignment methods are those based on graph neural networks. However, they often rely too much on the structural information of graphs, as a result of which models trained on specific graph structures cannot be applied to other graph structures. Meanwhile, most methods fail to fully utilize auxiliary information, such as attribute information. In response, this study proposes an entity alignment method based on a graph attention network and attribute embedding. The method uses the graph attention network to encode different knowledge graphs, introduces an attention mechanism from entity application to attribute, and combines structure embedding and attribute embedding in the alignment stage to improve the effect of entity alignment. The proposed model is verified on three real-world datasets, and the experimental results show that the proposed method outperforms the benchmark methods for entity alignment by a large margin.

Key words: entity alignment graph attention network knowledge graph (KG) attribute embedding alignment prediction

知识图谱(knowledge graph, KG)将非结构化知识转化为清晰简洁的<头实体、关系、尾实体>三元组, 其中实体指的是现实世界中的唯一对象, 而关系则是描述连接这些对象的关系. 使用实体作为节点, KG中的三元组本质上是相互关联的, 从而组成了一个大的知识图谱, 以实现知识的快速响应. 目前KG已在多个领域构建和应用, 除了个性化推荐^[1]、问答^[2]和信息提取^[3]外, 在不同行业也有广泛应用, 例如医疗、金融和信息等行业. 现有的大多数知识图谱都是由不同的机构根据不同的数据源和需求进行构建的, 因此, KG存在异构性, 即使是在同一领域, 同一实体也可能以不同的形式存在于不同的知识库中. 为了处理KG的异构性问题并融合不同知识库中的知识, 必须进行知识图谱对齐, 即在不同知识图谱中找到相同的现实世界对象的实体, 这称为实体对齐. 实体对齐提供了一种有效的方法, 通过链接等效实体, 将这些知识库中的知识融合到一个统一的KG中, 从而更高效地使用KG进行应用.

实体对齐的早期方法通常需要人工参与的特征构建过程^[4]或依赖于他人构建的外部信息来克服KG之间的异质性, 例如机器翻译和外部词典^[5]. 最近的研究提出了一些新的实体对齐方法来减少人工参与, 可以将不同KG的实体嵌入到统一的向量空间中实现实体对齐.

1 相关工作 1.1 KG嵌入

知识图谱嵌入模型是实现知识图谱融合的重要方法之一, 是指将KG中的实体和关系嵌入到统一向量空间, 同时保留KG中的结构信息. 当前的KG嵌入模型主要分为翻译模型、语义匹配模型和神经模型. TransE^[6]是一种典型的翻译模型, 其基本思想是如果三元组 $ (h, r, t) $ 成立, 期望 $ \overrightarrow{h}+\overrightarrow{r}\approx \overrightarrow{t} $ 成立. 为了进一步提升对齐效果, 许多模型基于TransE作出了改进, 如TransH、TransR和TransD等. 与TransE相比, 这些模型将实体和关系嵌入到不同的向量空间, 使模型可以表达更加复杂的关系. 语义匹配模型使用基于相似性的评分函数来推断关系信息, 例如HolE^[7]中的循环相关.

神经模型利用深度学习技术进行KG嵌入, 图神经网络GNN最近已被用于各种自然语言处理任务, 例如分类任务、关系提取和机器翻译等. GNN在图结构上聚合信息, 主要通过递归聚合相邻节点的表示来学习目标节点的表示. GNN有许多变体, 包括图卷积网络(GCN)、图注意力网络(GAT)和关系图卷积网络(R-GCN). GCN能够提供强大的图结构建模能力, 而GAT对GCN采用了注意力机制, 其中每个节点根据其相邻节点获得一个注意力分数, 实现对相邻节点信息的聚合. R-GCN可以建模带有多种关系类型的图数据. 以上模型都关注关系结构, 可以对KG的结构信息进行编码.

1.2 实体对齐方法

基于嵌入的实体对齐方法一般分为嵌入学习阶段和实体对齐阶段. 嵌入学习阶段使用知识表示学习方法来学习KG的实体嵌入, 实体对齐阶段通过计算实体嵌入的相似度实现实体对齐. IPTransE^[8]和BootEA^[9]使用半监督学习来克服实体对齐的“种子对齐”的稀疏性, 将迭代过程中新的实体对齐添加到训练数据集中以优化后续进程. MtransE^[10]使用TransE模型来学习两个KG中实体的嵌入, 为每个实体向量表示计算出映射到其他嵌入空间中的变换.

基于图的模型是当前实体对齐的一种主流方法. GCN-Align^[11]是一种基于图卷积网络的模型, 它利用图卷积网络GCN根据实体的相邻节点信息对其进行建模. RDGCN^[12]结合门控机制和GCN网络将关系信息与相邻结构信息进行整合, 通过计算注意力权重来获取KG的复杂关系信息. MuGNN^[13]利用基于注意力的GNN模型为相邻节点分配不同的权重, 通过多个通道对KG进行编码实现对齐. KECG^[14]结合了图注意力网络和TransE模型来捕获图内结构和图间对齐信息, 通过生成联合训练模型来解决KG的结构异质性问题. AliNet^[15]采用了注意力机制突出有用的远邻节点并减少噪音, 用门控机制与远距离邻域信息直接聚合, 以端到端的方式缓解邻域结构的异构问题. Dual-AMN^[16]使用双重注意力匹配网络来捕获图内和跨图的双重关系信息, 同时引入归一化硬样本挖掘损失, 优化了基于嵌入方法的性能.

许多相关工作将KG中的其他信息与结构信息结合起来, 以提高实体对齐的性能. JAPE^[17]将两个知识图的结构信息共同嵌入到一个统一的向量空间中, 利用属性相关性来进一步完善. KDCoE^[18]使用协同训练方法, 利用实体描述作为补充来细化实体嵌入, 在KG结构信息和实体描述上迭代训练两个嵌入模型. AttrE^[19]将属性三元组 $ \left(h, a, v\right) $ 等同于关系三元组, 并类似TransE模型期望 $ \overrightarrow{h}+\overrightarrow{a}\approx \overrightarrow{v} $ 成立学习实体嵌入. MuitiKE^[20]提出组合策略, 结合名称、属性和结构3个视图进行嵌入学习实体表示. BiGCN-A^[21]将GCN结合双向对齐机制, 将关系表示和实体表示结合生成联合实体表示, 并融入属性信息进行训练. 本文从以上方法中得到启示, 属性信息是至关重要的信息, 之前的大部分工作都集中在实体的属性类型上, 本文对属性和属性值的重要程度进行研究, 充分利用属性信息.

2 问题描述

在本文中, 知识图谱(KG)被表示为六元组有向图 $ G=\mathrm{ }(E, R, A, V, {T}_{r}, {T}_{a}) $ , 其中, $ E\mathrm{、}R\mathrm{、}A $ 和 $ V $ 分别指的是实体、关系、属性和属性值. 其中 $ {T}_{r}=\mathrm{ }\left\{\right(h, r, t\left)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\right|h, t\in E, r\in R\} $ 是关系三元组的集合, ${T}_{a}=\mathrm{ }\{(e, a, v\left)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\right|e\in E, a\in A, v\in V)\}$ 是属性三元组的集合. 关系三元组描述实体之间的关系, 表示为 $\left({entity}_{1}, \; relation, \; {entity}_{2}\right)$ . 属性三元组描述了实体的属性, 它的形式表示为( $entity, \; attribute, value)$ . 实体对齐就是找到两个知识图谱 $ {G}_{1} $ 和 $ {G}_{2} $ 之间的映射, 即 $ \delta = \left\{\right({e}_{1}, {e}_{2}\left) \right|{e}_{1}\in {E}_{1}, {e}_{2}\in {E}_{2}\} $ , 其中 $ {e}_{1} $ 和 $ {e}_{2} $ 是两个存在等价关系的实体.

3 算法描述

本文采用基于属性嵌入与图注意力的实体对齐方法, 充分利用KG的结构信息和属性信息, 将实体嵌入到统一的向量空间中, 主要分为3个阶段, 分别是结构信息嵌入、属性信息嵌入和实体对齐预测. 首先, 模型利用引入注意力机制的GAT模型作为编码器来进行结构嵌入, 它能够通过忽略重要程度较低的相邻节点来减轻实体对齐过程中异构性产生的负面影响, 得到实体结构的全局特征; 同时, 设计一种属性信息编码器嵌入实体的属性信息, 从初始特征开始选择性地向目标实体聚合属性和属性值的特征; 最后, 在对齐阶段将结构嵌入和属性嵌入结合, 通过测量统一嵌入空间中实体之间的距离来进行对齐预测. 模型的整体框架如图1所示.

图 1 模型整体框架图

3.1 知识嵌入模块 3.1.1 结构嵌入

KG的结构信息为实体对齐提供了有力的帮助, 这表示具有相似相邻结构的实体对齐效果会更好. 给定两个知识图谱 $ {G}_{1} $ 和 $ {G}_{2} $ , 将 $ {G}_{1} $ 和 $ {G}_{2} $ 放在一起作为一个输入图 $ G $ . 为了学习KG结构嵌入, 模型利用GAT网络为实体聚合相似的相邻结构信息. 首先按照最近的研究工作对实体的语义信息进行编码, 使用预训练的词嵌入^[22]来初始化实体表示, 预训练的词嵌入是一种词表示方式, 旨在对单词的语义和句法意义进行捕捉, 将单词表示为词向量. 编码器的输入为实体嵌入矩阵 $ \mathit{Y}\in {\mathbb{R}}^{n\times {m}_{h}} $ , 其中 $ n $ 是 $ G $ 包含的实体数量, $ {m}_{h} $ 是实体嵌入的维度. GAT编码器由多个堆叠的图注意力层组成, 因此它可以包含更高程度的邻域节点信息, 每个图注意力层将一组节点特征作为输入, 并输出新的节点特征如下:

$ {\mathit{H}}^{(l+1)}=ReLU\left({\mathit{D}}^{\left(l\right)}{\mathit{H}}^{\left(l\right)}{\mathit{W}}^{\left(l\right)}\right) $

(1)

其中, $ {\mathit{H}}^{\left(l\right)}\in {\mathbb{R}}^{n\times {{m}_{h}}^{\left(l\right)}} $ 是第 $ l $ 层的输出节点特征, $ {\mathit{W}}^{\left(l\right)}\in {\mathbb{R}}^{{{m}_{h}}^{\left(l\right)}\times {{m}_{h}}^{(l+1)}} $ 为可训练权重矩阵, $ {\mathit{H}}^{\left(0\right)} $ 是随机初始化的实体嵌入矩阵, $ {\mathit{H}}^{\left(0\right)}=\mathit{Y} $ . $ {\mathit{D}}^{\left(l\right)}\in {\mathbb{R}}^{n\times n} $ 代表连通矩阵, $ {\mathit{D}}^{\left(l\right)} $ 所包含的元素 $ {d}_{ij}^{\left(l\right)} $ 代表实体 $ {e}_{i} $ 到实体 $ {e}_{j} $ 的权重, 通过对输入图 $ G $ 使用自注意力机制计算获得, 下面计算 $ {\mathit{D}}^{\left(l\right)} $ 的元素 $ {d}_{ij}^{\left(l\right)} $ :

$ {d}_{ij}^{\left(l\right)}={\textit{Softmax}}\left({c}_{ij}^{\left(l\right)}\right)=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({c}_{ij}^{\left(l\right)}\right)}{{\displaystyle\sum }_{k\in {N}_{i}}\mathrm{e}\mathrm{x}\mathrm{p}\left({c}_{ik}^{\left(l\right)}\right)} $

(2)

其中, $ {N}_{i} $ 是第i个节点的相邻节点的集合, $ {c}_{ij}^{\left(l\right)}\mathrm{是} $ 实体 $ {e}_{i} $ 到实体 $ {e}_{j} $ 的注意力系数. 注意力系数 $ {c}_{ij}^{\left(l\right)} $ 的计算如下所示:

$ {c}_{ij}^{\left(l\right)}=\sigma \left({\mathit{r}}^{{\rm{T}}}\left[{\mathit{W}}^{\left(l\right)}{\mathit{h}}_{i}^{\left(l\right)} \oplus {\mathit{W}}^{\left(l\right)}{\mathit{h}}_{j}^{\left(l\right)}\right]\right) $

(3)

其中, $ {\mathit{h}}_{i}^{\left(l\right)}\in {\mathit{H}}^{\left(l\right)} $ 和 $ {\mathit{h}}_{j}^{\left(l\right)}\in {\mathit{H}}^{\left(l\right)} $ 分别是 $ {e}_{i} $ 和 $ {e}_{j} $ 的隐藏状态, $ \sigma \left(\cdot \right) $ 是非线性激活函数LeakyReLU函数, ${\mathit{r}}^{{\rm{T}}}$ 是可学习参数 $ \mathit{r}\in {\mathbb{R}}^{2{{m}_{h}}^{\left(l\right)}} $ 的转置, $ \oplus $ 代表向量连接. $ L $ 代表编码器层数, 经过 $ L $ 次迭代, 实体及其相邻节点的特征融合后得到特征向量 $ {\mathit{H}}^{\left(L\right)} $ .

3.1.2 属性嵌入

KG的结构信息为表示实体提供了有用的信息. 然而, 仅使用结构嵌入很难区分相似度高的实体, 尤其是仅具有细微差异的实体. 为了提高实体对齐的效果, 消除相似实体的歧义, 本文引入属性嵌入来改进基于结构嵌入的实体表示.

属性嵌入的目标是将实体属性信息嵌入到一个统一的向量空间中. 在传统方法中, 需要手动匹配属性, 然后比较相应属性的值以获得实体之间的相似性. 由于KG的数据特性, 目标对齐实体的属性之间可能存在较大差异, 从而误导GAT训练. 为了解决以上问题, 同时, 为了提高嵌入精度, 使属性嵌入更适合GAT训练, 本文设计了一种属性信息编码器, 可以从初始特征开始选择性地向目标实体聚合属性和属性值的特征.

首先使用前文提到的预训练词嵌入来进行属性信息嵌入, 得到实体e的属性特征序列 $ \left\{{\mathit{a}}_{1}, \cdots , {\mathit{a}}_{n}\right\} $ 和值特征序列 $\{{\mathit{v}}_{1}, \cdots , {\mathit{v}}_{n}\}$ , 将属性三元组 $ \left\{\right(e, {a}_{1}, {v}_{1}), \cdots, (e, {a}_{n}, {v}_{n}\left)\right\} $ 的 $ e $ 作为输入. 将属性值看作是节点, 将属性看作边进行添加, 从而形成一个实体、属性和属性值相连的知识图. 为了将属性和属性值信息聚合到单一向量中, 引入注意力机制进行计算, 具体方式为计算属性和属性值的加权平均值. 实体 $ e $ 的隐藏状态 $ {\mathit{s}}_{e}^{\left(l\right)} $ 定义如下:

$ {\mathit{s}}_{e}^{\left(l\right)}=\phi \left(\sum _{k=1}^{{m}_{s}}{\alpha }_{k}{\mathit{W}}_{1}\left[{\mathit{a}}_{k};{\mathit{v}}_{k}\right]\right) $

(4)

$ {\theta }_{k}={\textit{Softmax}}\left({q}_{k}\right)=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({q}_{k}\right)}{{\displaystyle\sum }_{i=1}^{{m}_{s}}\mathrm{e}\mathrm{x}\mathrm{p}\left({q}_{i}\right)} $

(5)

$ {q}_{k}=\sigma \left({\mathit{u}}^{{\rm{T}}}\left[{\mathit{s}}_{e}^{0};{\mathit{a}}_{k}\right]\right) $

(6)

其中, $k\in \left\{1, \cdots , {m}_{s}\right\}, {m}_{s}$ 是属性嵌入的维度, $ \sigma (\cdot ) $ 是LeakyReLU函数, $ \phi (\cdot ) $ 是ELU激活函数, $ {\mathit{W}}_{1} $ 和 ${\mathit{u}}^{{\rm{T}}}$ 是可学习参数矩阵, $ {\mathit{s}}_{e}^{0} $ 是初始实体特征, $ {\theta }_{k} $ 表示 $ {\mathit{s}}_{e}^{0} $ 与属性 $ {a}_{k} $ 的相似度, $ {q}_{k} $ 表示注意力系数.

3.2 实体对齐模块

实体对齐通过减少等效实体之间的距离, 将每个输入图的等效实体汇聚到一个统一的向量空间中. 给定两个知识图谱 $ {G}_{1} $ 和 $ {G}_{2} $ , 它们首先基于GAT学习其结构嵌入, 以捕获每个图的关系信息, 然后经过属性信息编码器获得实体基于属性嵌入的特征向量. 由于每个图都有一个独特的嵌入空间, 因此模型通过测量统一嵌入空间中实体之间的距离来预测实体对齐. 对于 $ {G}_{1} $ 中的实体 $ {e}_{1} $ 和 $ {G}_{2} $ 中的实体 $ {e}_{2} $ , 对其距离进行计算:

$ \begin{split} F\left({e}_{1}, {e}_{2}\right)= &\tau \frac{f\left({\mathit{h}}^{\left(L\right)}\left({e}_{1}\right), {\mathit{h}}^{\left(L\right)}\left({e}_{2}\right)\right)}{{m}_{h}} \\ &+\left(1-\tau \right)\frac{f\left({\mathit{s}}^{\left(L\right)}\left({e}_{1}\right), {\mathit{s}}^{\left(L\right)}\left({e}_{2}\right)\right)}{{m}_{s}} \end{split}$

(7)

$ f\left(\mathit{a}, \mathit{b}\right)=\parallel \mathit{a}-\mathit{b}{\parallel }_{{L}_{1}}$

(8)

其中, $ {\mathit{h}}^{\left(L\right)}(\cdot ) $ 和 $ {\mathit{s}}^{\left(L\right)}(\cdot ) $ 分别代表实体的结构嵌入和属性嵌入, $ {m}_{h} $ 和 $ {m}_{s} $ 代表结构和属性嵌入的维度, $ \tau $ 是平衡两种嵌入的超参数.

在对齐阶段, 目标是将实体嵌入到相同的低维向量空间中, 其中等效实体彼此靠近. 为了使GAT能够在向量空间中尽可能近地嵌入等效实体, 使用负样本来训练模型, 正负样本中实体对之间的距离尽可能大, 通过最小化以下基于边际的排名损失函数来执行模型训练:

$ L=\sum _{({e}_{i}, {e}_{j})\in \mathbb{L}}\sum _{(e'_{i}{}, e'_{j}{})\in{\mathbb{L'}}{{}}}\mathrm{max}\left\{ \begin{array}{c}0, F\left({e}_{i}, {e}_{j}\right)+\gamma -F(e'_{i}{}, e'_{j}{})\end{array} \right\} $

(9)

其中, $ \gamma $ 是边距超参数, 对于一个对齐实体对, 使用k近邻算法获得其中一个的邻近实体进行替换作为负样本, 得到正负样本集合. $ \mathbb{L} $ 是正样本集合, ${\mathbb{L'}}{{}}$ 是 $ \mathbb{L} $ 的负样本集合, 采用自适应学习率优化算法(AdaGrad)来优化上述损失函数.

4 实验与结果分析 4.1 数据集

参考最近研究^{[23, 24]}与经典算法, 本文使用DBP15K数据集作为实验数据来评估模型. DBP15K数据集由文献[17]构建, 从包含不同语言版本之间丰富的语言间链接(ILL)的大型多语言知识库DBpedia生成, 包括3个子集DBP15K_ZH-EN、DBP15K_JA-EN和DBP15K_FR-EN. 每个子集包含15000个对齐的实体对, 采用两种语言版本的知识库. DBP15K数据集的信息如表1所示, 详细介绍了每个子集所包含的实体、关系及关系三元组、属性及属性三元组的数量.

表 1 DBP15K数据集

4.2 评价指标与参数设置

模型使用Hits@k和MRR (平均倒数排名)作为评估指标来评估模型和基准方法的性能, 这些指标在其他 KG对齐工作中被广泛使用. Hits@k衡量在前k个候选中排名正确的实体的比例, MRR是结果的倒数排名的平均值. 在本文中使用Hits@1、Hits@10、MRR作为评价指标, 更高的Hits@k和MRR意味着更好的性能.

对于参数设置, 两个GAT层都包含128个隐藏单元, 结构嵌入和属性嵌入的维度同样设置为128, 使用BERT模型对数据进行预训练词嵌入, 并进行最大池化操作得到一个固定长度的向量作为初始化的特征向量嵌入. 学习率设置为0.005, 损失函数中的阈值 $ \gamma $ 设置为3.0, 超参数 $ \tau $ 设置为0.9. 每50个epoch更新一次负样本, 总训练轮数设置为500.

4.3 实验 4.3.1 实验结果

本文将模型与最近提出的6种实体对齐基线模型进行比较, 并将其分为两类: 1)仅使用实体结构信息, MTransE、IPTransE以TransE为基础嵌入结构信息, RDGCN以GCN为基础引入注意力机制增强信息学习能力; 2)使用实体结构和属性信息, JAPE结合TransE和属性信息联合学习, GCN-Align用GCN作为基础模型结合属性信息, 结合属性结构的图卷积模型^[25](以下简称Dual-GCN)使用加强的双重GCN联合属性嵌入. 对于所有比较的方法, 随机拆分30%的数据作为训练数据集, 剩余的作为测试数据. 实体对齐的结果如表2所示.

表 2 实体对齐结果对比

实验结果表明, 本文模型性能在3个数据集上的所有指标都明显优于基准方法. 与同使用实体结构和属性信息的JAPE、GCN-Align和Dual-GCN相比, 本文模型性能取得了明显的提高, 说明选用GAT模型优于KG嵌入模型和GCN模型. 基于嵌入的模型对实体的约束相对不足, 所以对齐结果较差. 基于GCN模型的方法, 对结构差异很敏感, 很难缩小对齐的差异. 因此本文模型使用GAT作为基础模型, 改善了基于图的方法的缺点, 有效减轻了异构KG的负面影响, 成功地提高了实体对齐的效果. 在仅使用结构信息的方法MTransE、IPTransE和RDGCN中, RDGCN的各项指标是最高的, 与RDGCN相比, 本文模型在指标Hits@1、Hits@10、MRR分别提升了6%、5%、10%, 说明引入属性信息对实体对齐同样重要.

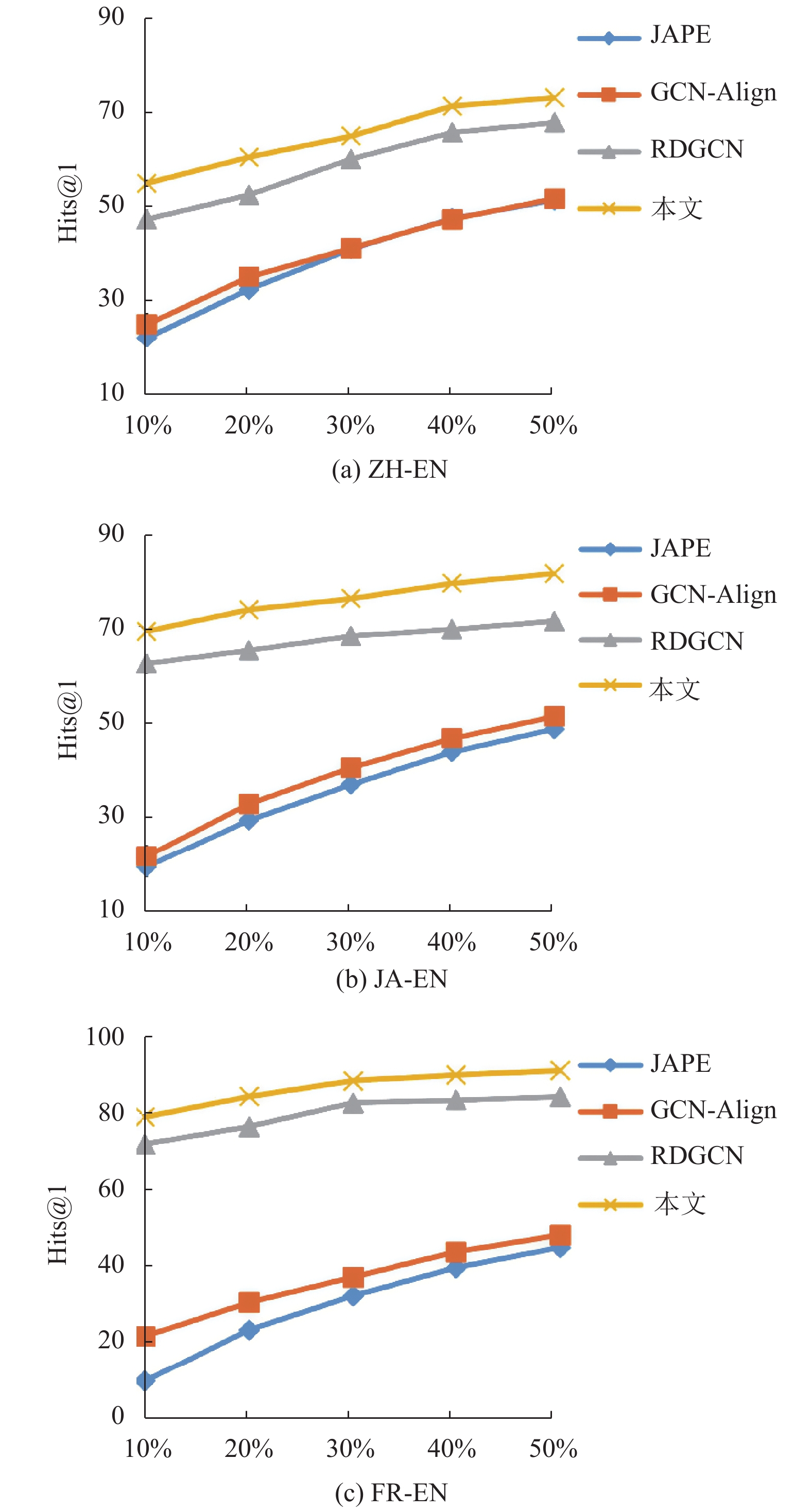
4.3.2 对齐种子敏感度实验

在本文中, 将模型与JAPE、GCN-Align、RDGCN进行比较, 将预对齐实体对的比例从10%开始, 以10%的步长增加到50%, 并将其余的对齐种子作为测试集.

实验结果如图2所示, 随着对齐种子比例的增加, 所有模型的性能在所有数据集上持续增加. 从图2可以看出, 本文所使用的模型始终以显著的优势优于基准方法, 说明了模型的稳健性.

图 2 不同比例种子集对齐敏感度对比结果 (横坐标为对齐种子的比例)

5 结论

本文提出了一种基于图注意力网络和属性嵌入的方法. 模型使用图注意力网络GAT对知识图谱进行编码, 引入注意力机制从实体应用到属性, 通过忽略一些重要程度较低的邻近节点来减轻对齐过程中异质性的负面影响, 同时设计一种属性信息编码器利用实体的属性信息, 在对齐阶段将结构嵌入和属性嵌入进行结合, 实现了实体对齐效果的提升. 模型在3个真实的数据集上进行评估, 结果显示所提出的方法优于其他6个基准方法. 本文工作只使用了属性信息, 还有一些额外信息如实体名称、关系路径等信息没有被充分利用. 在未来的工作中将研究如何通过这些辅助信息来进一步提高实体对齐的准确性.

参考文献

[1]	Wang X, Wang DX, Xu CR, et al. Explainable reasoning over knowledge graphs for recommendation. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 5329–5336.
[2]	Wang GY, Zhang W, Wang RX, et al. Label-free distant supervision for relation extraction via knowledge graph embedding. Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. Brussels: Association for Computational Linguistics, 2018. 2246–2255.
[3]	Zhang YY, Dai HJ, Kozareva Z, et al. Variational reasoning for question answering with knowledge graph. Proceedings of the 32nd AAAI Conference on Artificial Intelligence and 30th Innovative Applications of Artificial Intelligence Conference and 8th AAAI Symposium on Educational Advances in Artificial Intelligence. New Orleans: AAAI Press, 2018. 745.
[4]	Mahdisoltani F, Biega J, Suchanek FM. YAGO3: A knowledge base from multilingual Wikipedias. Proceedings of the 7th Biennial Conference on Innovative Data Systems Research. Asilomar: CIDR Conference, 2015. 1–11.
[5]	Wang ZC, Li JZ, Tang J. Boosting cross-lingual knowledge linking via concept annotation. Proceedings of the 23rd International Joint Conference on Artificial Intelligence. Beijing: AAAI Press, 2013. 2733–2739.
[6]	Bordes A, Usunier N, Garcia-Durán A, et al. Translating embeddings for modeling multi-relational data. Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2013. 2787–2795.
[7]	Nickel M, Rosasco L, Poggio T. Holographic embeddings of knowledge graphs. Proceedings of the AAAI Conference on Artificial Intelligence, 2016, 30(1): 1955-1961.
[8]	Zhu H, Xie RB, Liu ZY, et al. Iterative entity alignment via joint knowledge embeddings. Proceedings of the 26th International Joint Conference on Artificial Intelligence (IJCAI). Melbourne: AAAI Press, 2017. 4258–4264.
[9]	Sun ZQ, Hu W, Zhang QH, et al. Bootstrapping entity alignment with knowledge graph embedding. Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm: AAAI Press, 2018. 4396–4402.
[10]	Chen MH, Tian YT, Yang MH, et al. Multilingual knowledge graph embeddings for cross-lingual knowledge alignment. Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne: AAAI Press, 2017. 1511–1517.
[11]	Wang ZC, Lv QS, Lan XH, et al. Cross-lingual knowledge graph alignment via graph convolutional networks. Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. Brussels: Association for Computational Linguistics, 2018. 349–357.
[12]	Wu YT, Liu X, Feng YS, et al. Relation-aware entity alignment for heterogeneous knowledge graphs. Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: IJCAI, 2019. 5278–5284.
[13]	Cao YX, Liu ZY, Li CJ, et al. Multi-channel graph neural network for entity alignment. Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics. Florence: Association for Computational Linguistics, 2019. 1452–1461.
[14]	Li CJ, Cao YX, Hou L, et al. Semi-supervised entity alignment via joint knowledge embedding model and cross-graph model. Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP). Hong Kong: Association for Computational Linguistics, 2019. 2723–2732.
[15]	Sun ZQ, Wang CM, Hu W, et al. Knowledge graph alignment network with gated multi-hop neighborhood aggregation. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(1): 222-229. DOI:10.1609/aaai.v34i01.5354
[16]	Mao X, Wang WT, Wu YB, et al. Boosting the speed of entity alignment 10×: Dual attention matching network with normalized hard sample mining. Proceedings of the Web Conference 2021. Ljubljana: Association for Computing Machinery, 2021. 821–832.
[17]	Sun ZQ, Hu W, Li CK. Cross-lingual entity alignment via joint attribute-preserving embedding. Proceedings of the 16th International Semantic Web Conference. Vienna: Springer, 2017. 628–644.
[18]	Chen MH, Tian YT, Chang KW, et al. Co-training embeddings of knowledge graphs and entity descriptions for cross-lingual entity alignment. Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm: AAAI Press, 2018. 3998–4004.
[19]	Trisedya BD, Qi JZ, Zhang R. Entity alignment between knowledge graphs using attribute embeddings. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 297-304.
[20]	Zhang QH, Sun ZQ, Hu W, et al. Multi-view knowledge graph embedding for entity alignment. Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: IJCAI, 2019. 5429–5435.
[21]	车超, 刘迪. 基于双向对齐与属性信息的跨语言实体对齐. 计算机工程, 2022, 48(3): 74-80. DOI:10.19678/j.issn.1000-3428.0060540
[22]	Wu YT, Liu X, Feng YS, et al. Neighborhood matching network for entity alignment. Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. Association for Computational Linguistics, 2020. 6477–6487.
[23]	赵丹, 张俊. 基于双重注意力和关系语义建模的实体对齐方法. 计算机应用研究, 2022, 39(1): 64-69, 79. DOI:10.19734/j.issn.1001-3695.2021.04.0169
[24]	Yu DH, Yang YM, Zhang RH, et al. Knowledge embedding based graph convolutional network. Proceedings of the 2021 Web Conference. Ljubljana: Association for Computing Machinery, 2021. 1619–1628.
[25]	田江伟, 李俊锋, 柳青. 结合属性结构的图卷积实体对齐算法. 计算机应用研究, 2021, 38(7): 1979-1982, 1992. DOI:10.19734/j.issn.1001-3695.2020.10.0366