2. 大连交通大学 计算机与通信工程学院, 大连 116052
2. School of Computer and Communication Engineering, Dalian Jiaotong University, Dalian 116052, China
股票市场被认为是一个复杂的系统, 具有非线性特征, 受到经济、政治和心理因素的影响. 因此, 在这样一个市场中, 对股票波动的准确预测是非常重要的[1].
机器学习是一种高度复杂的非线性人工智能系统, 是对人脑抽象的人工模仿[2]. 具有分布式存储、自组织、并行处理和自我调整能力. 机器学习的上述特点使其更适合处理具有多种影响因素、不稳定和随机类型的复杂非线性问题. 因此, 各国学者纷纷将机器学习用于股票市场的数据分析和预测, 并取得了一定的研究成果.
传统的机器学习方法包括自回归模型(AR)[3]、移动平均模型(MA)[4]、自回归移动平均模型(ARMA)[5]和差分自回归移动平均模型(ARIMA)[6]. 但由于股票自身的非平稳与非线性特征, 这些方法不能在预测时达到较好的效果. 此外支持向量机[7]、随机森林[8]、遗传算法[9]、集成学习[10]等技术也已成功应用于从原始金融数据中提取特征并进行预测. 调查表明, 在金融行为建模中使用的变量的数量和类型方面, 这些方法各不相同. 而且对于最适合使用哪些输入变量并没有达成共识. 此外, 需要注意的是, 在实际应用中使用时, 所提出的方法的利润评估通常被忽略.
近年来随着人工智能的不断发展以及计算机运算能力的提升, 机器学习中的深度学习技术受到广泛关注. Hajiabotorabi等人[11]通过使用高效的离散小波变换对高频时间序列的预测进行了改进, 提出了BSd-RNN模型. 结果表明, BSd-RNN模型优于其他常见的DWT-RNN模型. Cao等人[12]将两种经验模态分解(EMD)与长短时间记忆网络模型(long short-term memory, LSTM)相结合, 形成两种混合预测模型分别对金融时间序列进行预测. Niu等人[13]提出了一种基于变异模式分解(VMD)和门控递归单元(gated recurrent unit, GRU)的新型混合模型, 并通过注意力机制来提高股票价格指数预测的准确性.
注意力机制是在计算机视觉领域首次提出的. Google Mind团队将注意力机制应用于循环神经网络模型(recurrent neural network, RNN)进行图像分类, 并取得了极高的准确率[14]. 它模仿人脑的信号处理机制, 将计算资源分配给更重要的任务. Chen等人[15]建立了一个基于注意力机制的LSTM模型并选择香港市场的股票来验证注意力机制的有效性. Qiu等人[16] 通过小波变换来处理股票数据, 使用基于注意力机制的LSTM神经网络来预测股票开盘价, 并与广泛使用的LSTM、GRU神经网络模型对比, 所提模型具有更好的拟合度. Chen等人[17]在此基础上提出了一种新型混合深度学习模型, 它整合了注意力机制、多层感知器和双向长短期记忆神经网络, 预测4种股票指数的收盘价.
与单个神经网络模型相比, 混合模型进行股票价格预测的例子相对较少. Lu等人[18]提出了一种基于CNN-LSTM的股票价格预测方法, 采用卷积神经网络(CNN)从数据中提取有效特征, 来预测股票价格, 结果表明, 混合模型对股票价格预测是可行的, 并且预测精度较高. 这种预测方法不仅为股票预测提供了一种新的研究思路, 也为学者们研究金融时间序列数据提供了实践经验. Kumar等人[19]提出了一种双混合方法, 即带有花粉算法的RNN-LSTM和带有粒子群优化的RNN-LSTM, 以开发一个最佳的深度学习模型来提高当天内股票市场的预测.
在神经网络模型中, LSTM网络因其独特的算法机制在时间序列预测领域占主导地位[20]. 虽然LSTM网络克服了传统的循环神经网络中的梯度消失问题, 但它仍然是一种依赖顺序的计算方法. 此外, 单层LSTM模型在每个时刻都平等地对待所有股票状态[21]. 基于以上文献讨论, 目前大部分对股票价格预测的模型都是基于单个神经网络, 部分混合模型也是单层相结合, 没有考虑过神经网络层数对预测结果的影响.
为了进一步减小股票价格的预测误差, 本文进行多次实验, 结合每种神经网络的优势, 对比挑选出由双层长短期记忆网络(LSTM)和双层门控递归单元(GRU), 并结合自注意力机制组成的新型混合神经网络模型(ATLG), 来对股票价格进行精确预测, 然后应用股票基本指标和技术指标来优化预测结果. 最后通过MACD指标进行回测, 将收益与同期沪深300作对比. 通过对比实验得出的结论, 本文所提出的模型在股票价格预测中取得了良好的成果.
1 股票价格预测基本原理与实现 1.1 LSTM、GRU神经网络模型LSTM是RNN的改进版, 广泛应用在时间序列分析、文件分类、声音和语音识别等领域. 它使记忆过去的数据变得更加容易, 同时解决了梯度消失的问题. LSTM的核心在于细胞状态以及“门”结构, 这样的设置有助于更新或删除信息. 其计算过程如下:
| ft=sigm(Wfxt+Ufht−1+bf) | (1) |
| it=sigm(Wixt+Uiht−1+bi) | (2) |
| ˜Ct=tanh(Wcxt+Ucht−1+bc) | (3) |
| ct=ft×ct−1+itטct | (4) |
| ot=sigm(Woxt+Uoht−1+bo) | (5) |
| ht=ot×tanh(ct) | (6) |
GRU是LSTM的简化变体, 它有控制单元内部信息流的门控机制, 而没有单独的存储单元. 所以它跟LSTM有相同的优点, 但是比LSTM的计算更简单, 更节省时间和算力. GRU的设计将遗忘门和输入门合并为一个单元, 命名为“更新门”, 并有一个额外的“重置门”来处理单元内的信息流. 其计算过程如下:
| zt=sigm(Wzxt+Uzht−1+bz) | (7) |
| rt=sigm(Wrxt+Urht−1+br) | (8) |
| ˜ht=tanh(Whxt+Uh(rt×ht−1)+bh) | (9) |
| ht=(1−zt)×ht−1+ztטht | (10) |
根据式(1)–式(6)中遗忘门(ft)、输入门(it)、细胞状态(ct)、输出门(ot)各部分功能结构, 推导出LSTM的简写模型, 如式(11)所示. 根据式(7)–式(10)中更新门(zt)、重置门(rt)各部分功能结构, 推导出GRU的简写模型, 如式(12)所示. 其中(xt)为输入向量, (ht–1)为前一单元的输出, W、U、b中的权重矩阵和偏执向量是在实验中逐步训练得出.
| (ht,ct)=LSTM(xt,ht−1,ct−1,W,U,b) | (11) |
| (ht,zt)=GRU(xt,ht−1,zt−1,W,U,b) | (12) |
注意力机制是一种通过加权方式来消除无用信息, 更有效地完成任务的方法. 在分析股票价格走势时, 利用注意力机制来计算不同时间段的股票价格数据的权重以便更好地预测股票价格的走势. 如图1(a)所示.
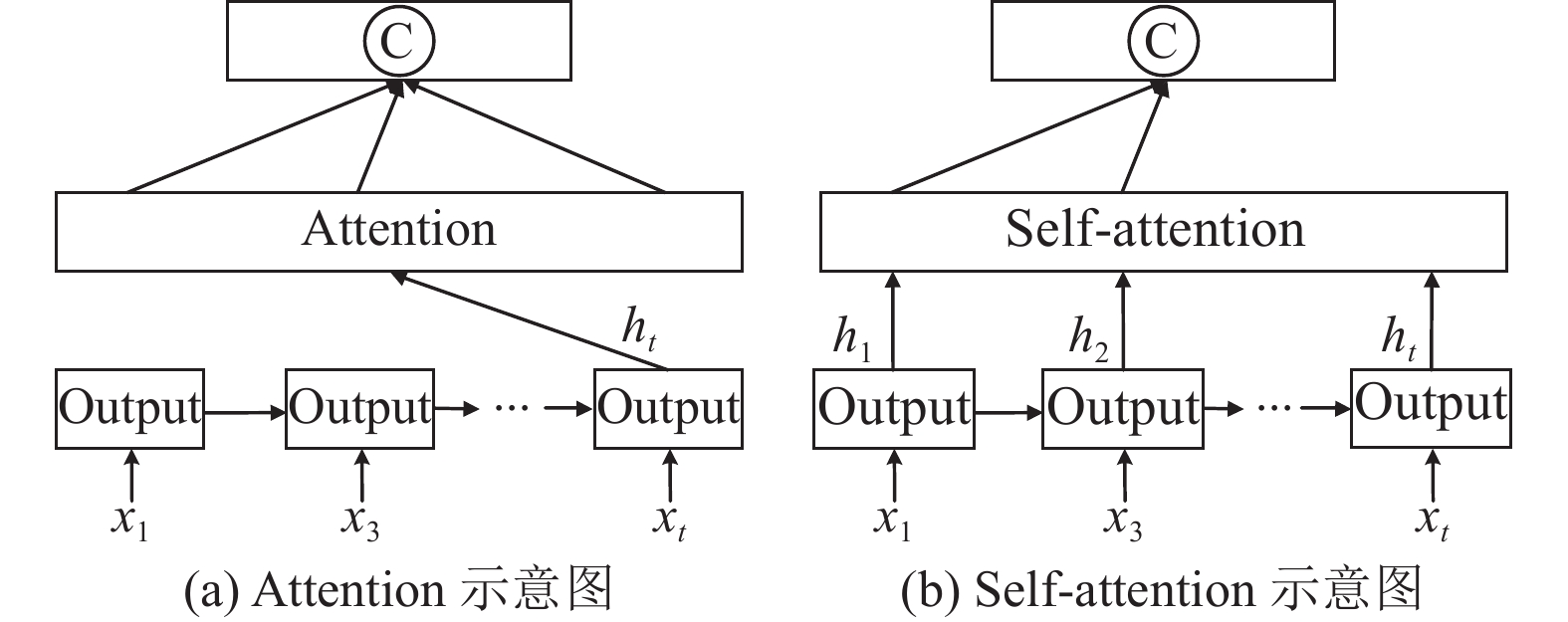
|
图 1 注意力机制示意图 |
本文所用的自注意力机制是注意力机制的变体, 其减少了对外部信息的依赖, 更擅长捕捉数据的内部相关性. 如图1(b)所示, 其本质思想如式(13)所示:
| Attention(Q,S)=Softmax(QKT√dk)V | (13) |
本文在结合LSTM和GRU这两种神经网络模型的基础上, 加入了self-attention机制, 使混合后的模型可以更好地从股票数据中提取有效信息, 抓住核心关键点. 所提出的ATLG混合神经网络模型融合了每种模型的优点, 即LSTM良好的顺序数据处理能力, GRU计算速度更快, 参数更少, 以及self-attention强大的获取长期依赖的能力. 为了建立一个稳定的数据处理模型, 采用了单层self-attention和双层LSTM以及双层GRU. 高级模型的结构如图2所示.

|
图 2 ATLG结构示意图 |
输入层: 本研究使用前T个交易日的数据来预测第(T+1)天的股价变化, 股票数据特征集的维度为15, 12个基本市场指标加上3类股票技术指标.
循环层: 循环层采用双层LSTM以及双层GRU模型的结构. 运用控制变量法, 在训练的过程中不断调整参数, 直至模型的预测效果最佳. 经过多次调参及优化, 最终确定, LSTM层搭建具有80个记忆体的循环层, GRU层设置为100个记忆体. 堆叠式的优点是可以在不同的时间步长内学习原始时间数据的特征, 而且可以减少内存容量, 使模型可以加速收敛. 堆叠的实验模型可以描述如下:
| (h1t,c1t)=LSTM1(xt,h1t−1,c1t−1,W1,U1,b1) | (14) |
| (h2t,c2t)=LSTM2(h1t,h2t−1,c2t−1,W2,U2,b2) | (15) |
| (h3t,z1t)=GRU1(h2t,h3t−1,z1t−1,W3,U3,b3) | (16) |
| (h4t,z2t)=GRU2(h3t,h4t−1,z2t−1,W4,U4,b4) | (17) |
自注意力机制层: RNN、LSTM、GRU和其他RNN在预测的每一步都使用相同的固定状态向量C. C是一个压缩的向量, 没有办法表达完整的序列信息, 之前输入的信息也会被后来的信息所覆盖. 引入自注意力机制可以更好地从股票数据中提取有效的信息, 抓住核心关键点.
输出层: 将通过第4个GRU层的输出数据
| yt=w×h4t+b | (18) |
其中, w是隐藏层到输出层的权重矩阵, b是偏置向量, yt是一个介于0–1之间的预测值. 另外, 为了防止模型过拟合, 在各层之间进行Dropout操作.
本文主要是针对股票价格的预测, 输出变量线性依赖于其先前的值, 因此是一个回归性问题. 实验使用大量数据来训练模型并估计回归方差的未知系数, 通过训练后的模型来预测股票的未来价格, 在实际价格和预测价格之间进行比较, 选用回归评价指标来量化模型的性能, 同时也将准确率作为比较模型的辅助指标.
所提出的ATLG模型的新颖性如下: (1) ATLG模型是一个深度的5层神经网络模型, 它弥补了传统神经网络中层数的不足, 提高了模型的准确性. (2)由于是对整个数据求self-attention的, 所以能抓取到当前数据和该股票所有数据的依赖关系强度. 这方面的能力显然比RNN的获取长依赖的能力强大得多. (3) ATLG模型结合了LSTM的良好数据呈现能力和GRU的易收敛能力, 因此克服了传统RNN的局限性, 提高了模型的性能.
3 实验 3.1 股票数据集的选择从股价反映市场的角度来看, 筛选出了能够代表市场的个股, 形成一个金融时间序列数据集. 为了选择代表市场的优质股票, 本文从tushare上获取了“上证50指数”成分加权表, 其中部分股票如表1所示. 本文选择了权重较高的前30只股票组成股票数据集. 股票数据集包括贵州茅台、招商银行、中国平安、兴业银行、上海浦东发展银行等.
| 表 1 上证50指数的部分权重表 |
3.2 股票市场基本数据
在筛选出要选择的股票后, 下一步是获得这30只股票的基本市场数据. 本文从tushare获取所有股票的基本数据, 时间是从2010年1月–2019年12月. 输入特征包含两类, 基本指标和技术指标.
基本指标包括: 开盘价、最高价、最低价、收盘价、涨跌额、涨跌幅、成交量、成交额、换手率、量比、市盈率PE、市净率PB等.
技术指标包括: (1)指数移动平均EMA: 价格跟随指标, 能准确反映近期价格的变化. 选择了5天、10天、20天、30天、60天的EMA值作为输入特征. (2)平滑异同移动平均线MACD: 表征当前的多空状态和股价可能的发展变化趋势. 指标包括MACD快速线(DIF)、慢线(DEA)和MACD柱. (3)个股资金流向: 小、中、大、特大单的买入卖出量以及买入卖出额, 以及净流入量和净流入额.
3.3 股票数据预处理(1) 数据集划分
本文选取2010年1月–2019年12月的30只股票组成原始数据集. 2010–2017年的数据用于训练, 2018年和2019年的数据用于测试. 这包括12个基本的市场数据和3类技术指标数据.
(2) 归一化处理
由于将股票的价格数据、交易量数据和资金流向数据等同时作为输入的特征参数, 而数值差异巨大, 为了消除指标间的量纲影响, 提升模型精度和收敛速度, 本文对数据进行了归一化处理. 由于数据集的不同项目处于不同的数量级, 因此需要进行数据规范化操作, 否则大数量级的项目会掩盖小数量级的情况, 导致小数量级项目的信息损失问题.
(3) 涨跌标签
“涨幅”为用来训练的标签, 定义为: (当日收盘价–昨日收盘价)/昨日收盘价; “涨幅正负”为用来验证准确率和精度的标签. 设定为当涨幅为正时, 则判定该股票的趋势为涨(label: 1); 当涨幅不为正时, 则判定该股票的趋势为跌(label: 0).
3.4 评价指标为了评估模型对股票价格的预测性能, 通过均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2) 这3种回归评价指标来量化模型的性能. RMSE和MAE越小, 预测值越接近真实值; 系数R2越接近1, 模型的拟合度越高, 4种指标总结为式(19)–式(21):
| MAE=1N∑Ni=1|xi−yi| | (19) |
| RMSE=√1N∑Ni=1(xi−yi)2 | (20) |
| R2=1−∑i=1((xi−yi)2)∑i=1((xi−ˉy)2) | (21) |
根据样本的真实结果和模型预测结果, 将样本分为4类: true positive (TP), 样本是正样本并且模型预测结果也是正样本的个数; false negative (FN)样本是正样本但模型预测结果是负样本的个数; false positive (FP)样本是负样本但模型预测结果是正样本的个数; true negative (TN)样本是负样本并且模型预测结果也是负样本的个数. 准确率用式(22)表示:
| Accuracy=TP+TNTP+TN+FP+FN | (22) |
移动平均线收敛和背离(MACD)指标是股票交易中的一个常见技术分析工具. MACD指标的设计是基于移动平均线的原理, 它是对收盘价进行平滑处理(计算加权平均)后的价格指标. MACD指标由一系列曲线和垂直条组成, 反映了股票波动周期的特点, 这些特点能够钻研出买卖股票的最佳时机. MACD的优势在于它消除了移动平均线(MA)所传递的频繁买入和卖出信号的缺点, 这增加了对信号传输的要求和限制. 它在实战中的使用比MA更稳定. 指数移动平均线(EMA)是当天的收盘价减去昨天的EMA, 乘以一个平滑系数, 然后再乘以昨天的EMA. 计算公式为:
| EMA=2N+1C+(1−2N+1)EMA′ | (23) |
| DIF=EMA(12)−EMA(26) | (24) |
| DEA(N)=2N+1DIF+N−1N+1DEA′ | (25) |
| MACD=2×(DIF−DEA) | (26) |
其中, N为所计算的天数, C为今日收盘价, EMA'表示昨日的EMA, DIF为离差值, DEA为离差平均值, DEA'为昨日DEA.
3.6 实验对比实验1. 在其他条件相同的情况下, 探索基础模型RNN、LSTM和GRU之间的性能差异.
实验2. 探讨自注意力机制对股票价格预测的影响. 分析和比较基础模型RNN、LSTM和GRU在加入自注意力机制后各项指标的变化.
实验3. 研究探讨神经网络层数对AT-RNN、AT-LSTM和AT-GRU模型的影响. 基于第2个实验基准模型, 循环层分别从1层升级为2层、3层或4层. 观察实验结果, 比较不同深度的循环层对实验结果的影响.
实验4. 基于第3个实验得出的结论, 得到了对模型影响的最佳层数. 在最佳层数的基础上对模型两两结合, 分别于基本模型、加入自注意力机制的模型做出对比, 评选出对股票预测的最优模型.
4 实验结果和分析 4.1 实验环境实验环境: Windows 10操作系统 16 GB内存; 开发工具: PyCharm 2020 TensorFlow 2.0; 显卡: NVIDIA GeForce MX450; CPU: Intel(R) Core(TM) i5-1135G7 @2.40 GHz.
4.2 探索RNN、LSTM、GRU之间的性能差异分别比较单层的RNN、LSTM、GRU模型对股票价格短期预测的效果. 使用Adam优化器, 损失函数定为均方差(mean squared error, MSE), 批处理大小(batch_size)设置为64. 对每个模型分别进行多次实验, 取多次结果的平均值, 得到最终的实验结果, 如图3和表2所示.

|
图 3 基础模型预测效果 |
| 表 2 基础模型的实验结果比较 |
从表2可以看出GRU的误差最低, 其次是LSTM, 而表现最差的是RNN. 就准确率而言, GRU的准确率最高为53.31%, 其次是LSTM达到52.93%, RNN最低只有50.54%. 这也验证了之前的分析, RNN难用梯度下降法来训练, 而且存在梯度消失和爆炸问题. 而LSTM和GRU很好地解决了这一问题. 并且GRU模型将LSTM中的遗忘门和更新门优化合并为重置门, 需要训练的参数更少且可以防止过拟合. 实验证明在相同参数时, GRU模型效果普遍好于RNN、LSTM模型.
4.3 探索加入自注意力机制对模型的影响如图4和表3所示, 可以看出AT-GRU的误差普遍小于AT-LSTM和AT-RNN. 在准确率方面, AT-GRU最好, 达到57.25%, 其次是AT-LSTM, 达到56.43%, 而准确率最低的是AT-RNN. 相对于基础模型, 加入self-attention机制的预测模型效果更优. 原因主要有两个: 第一, 未加入self-attention机制时, 模型对不同时间点编码向量关注度相同, 未能对重点信息的影响特征赋予更多注意力. 第二, 由于依靠self-attention机制进行加权, 可以适用不断变化股市波动规律, 泛化能力较强, 并且模型用自注意力机制来处理特殊时间段特征信息时, 所以可以关注重要时间点位置信息, 从而减小实验的误差.
4.4 探讨循环层的层数对预测模型的影响在加入self-attention机制的模型的基础上, 循环层分别增加到2层、3层和4层. 分析了循环层的层数对股票预测模型的影响. 对性能进行分析和评估后, 各个模型的预测结果的准确性如图5所示.

|
图 4 加入self-attention后模型预测效果 |
| 表 3 加入注意力机制后的模型实验结果比较 |

|
图 5 不同层数对实验结果的影响 |
就准确性而言AT-GRU的两层循环层模型结果最优, 达到57.5%, 而表现最差的是有着4层循环层的RNN, 准确率为54.2%. 普遍来看, 2层循环层表现得结果最为突出, 准确率普遍高于3层和1层, 4层循环层得准确率最低. 从实验结果中可以看出, 增加神经网络的层数在一定程度上可以增加模型的精度, 但是会出现过拟合的情况, 因此, 增加模型的层数, 要避免过拟合现象的产生, 并不是一味地增加网络层数就可以提高模型的精度.
4.5 探究混合模型对实验结果的影响第3个实验中, 得到了循环层数对预测模型的影响, 在其他条件相同的情况下, 2层循环层表现得效果最佳. 所以在最优层数的基础上对已有自注意力机制的模型两两结合, 搭建5层神经网络模型, 依次为自注意力机制层加双层RNN加双层LSTM (ATRL), 自注意力机制层加双层RNN加双层GRU (ATRG), 以及自注意力机制层加双层LSTM加双层GRU (ATLG). 进行多次对比实验, 评选出对股票价格预测的最优模型. 各个模型的预测结果的准确性如图6和表4所示, 通过实验结果可知自注意力机制层加双层LSTM加双层GRU的混合模型表现最好, 均方根误差为0.1515、平均绝对误差为0.1057、决定系数为0.9407. 就准确率而言ATLG的准确率达到62.84%, 优于其他两种组合模型, 实验并给出了ATLG的损失函数, 如图7所示.
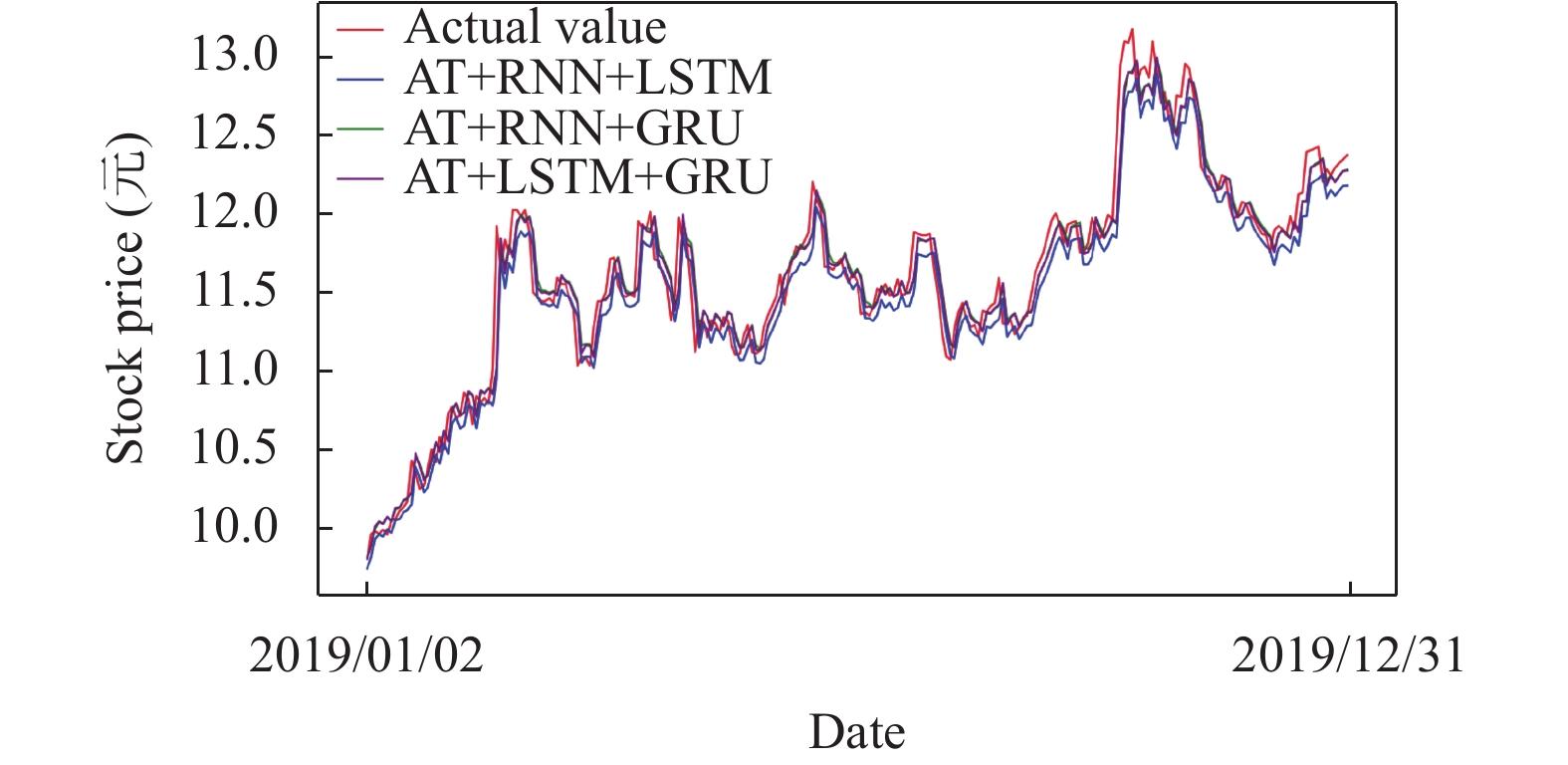
|
图 6 混合模型预测效果 |
| 表 4 混合模型实验结果 |
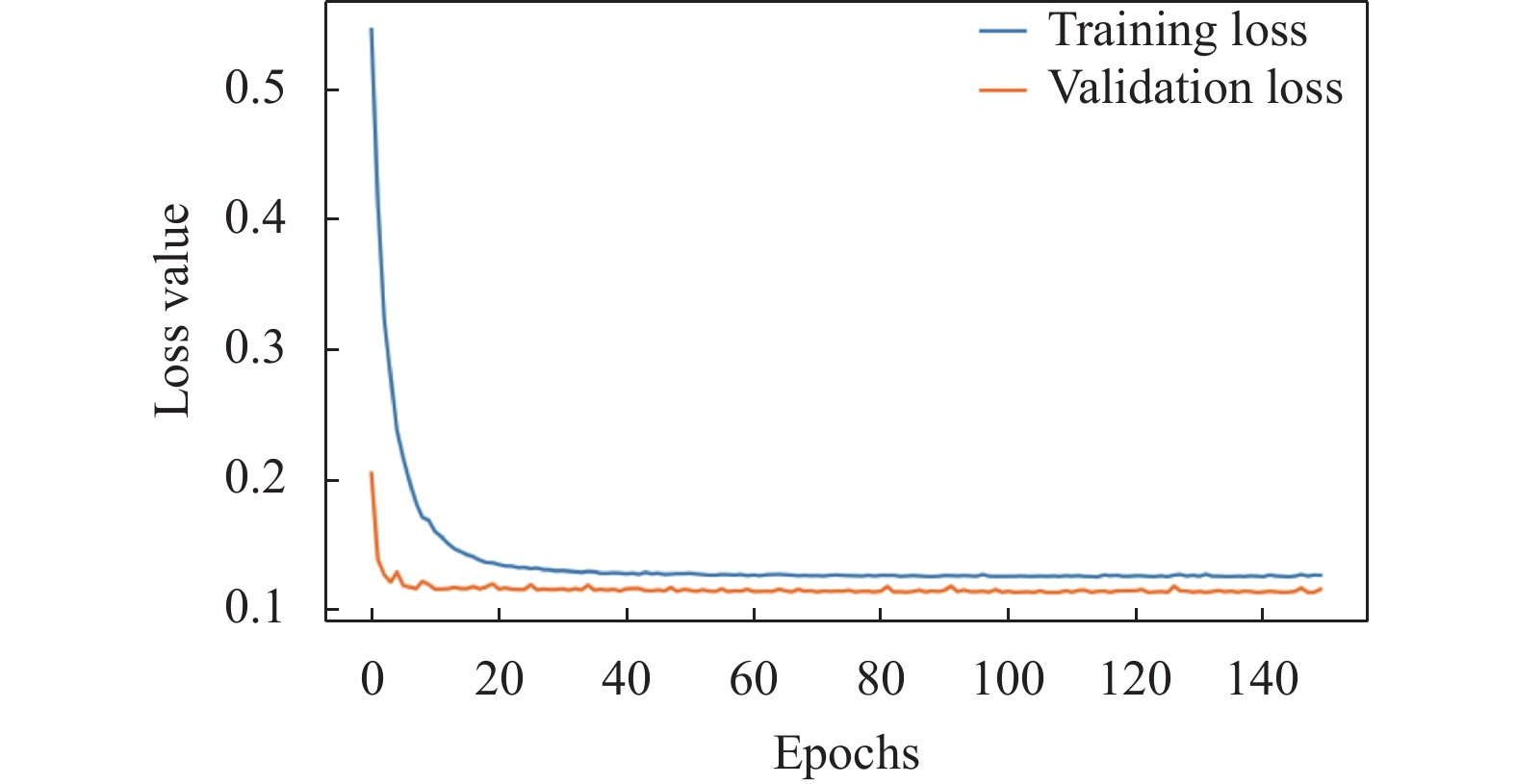
|
图 7 ATLG的损失函数 |
4.6 实验结果分析
为了验证本模型的先进性, 选取了一些最近流行的实验模型进行对比, 分别是, 2022年严冬梅等人[22]提出的一种结合自注意力机制和残差网络的生成式对抗神经网络模型(SAR-GAN); 2022年刘茜阳等人[23]提出的一种基于模糊K线的长短期记忆(LSTM)网络和支持向量回归多阶段混合模型(FCLSTM-vSVR); 2021年, 郑树挺等人[24]提出改进的self-attention模型; 以及2021年蒙懿等人[25]构建的基于CNN-BiLSTM和注意力机制的股价预测模型. 如表5所示.
| 表 5 实验结果分析 |
通过实验结果分析可知, 本文提出的ATLG模型在均方根误差、平均绝对误差、决定系数和准确率方面均优于其他对比模型, 仅在决定系数上略差于CNN-BiLSTM模型, 这表明该模型在股票价格预测上具有一定的有效性和实用性.
4.7 消融实验为了验证所提出的方法的每个组成部分对股票价格预测的有效性, 现删除模型中的一个组成部分, 探究每个组成部分对模型的影响. 结果如表6所示.
| 表 6 消融实验结果分析 |
从实验结果可以看出, 加入双层LSTM结构和双层GRU结构后, 模型准确率分别提升了4.38%和5.21%, 充分证明了LSTM模型可以很好地解决股票预测系统中股票数据难以预测及股票数据过长的问题, 以及GRU模型计算更简单, 更节省时间和算力的优点. 加入自注意力机制后, 模型准确率提升了8.03%, 同样可以验证自注意力机制能更好地从股票数据中提取有效的信息, 抓住核心关键点.
4.8 模型回测及投资收益通过实验得出了对股票预测得最优模型, 将模型对真实股票数据(以浦发银行为例)进行买卖点以及收益率的回测, 计算出收益并且和同期沪深300进行对比. 买卖的策略为, 假设初始资金为100000元, 当MACD从负数转向正数, 模型提示买入. 当MACD从正数转向负数, 模型提示卖出. 当MACD以大角度变化, 表示快的移动平均线和慢的移动平均线的差距非常迅速地拉开, 代表了一个市场大趋势的转变. 图8展示了浦发银行的部分K线及买卖点的提示图, 图中提示的买卖时间点是每日的刚开盘时间(即9:30). 为显示策略的可行性, 选取同期沪深300指数进行对比, 在所有买卖点之后, 浦发银行总收益为53146.687元, 收益率为53%, 同期沪深300总收益为142621.410元, 收益率为42%, 图9展示了浦发银行和沪深300的收益对比. 可以发现所提的模型可以提高收益率, 证明了所提出的ATLG模型可以用于真实股票预测.

|
图 8 浦发银行K线及买卖提示图 |
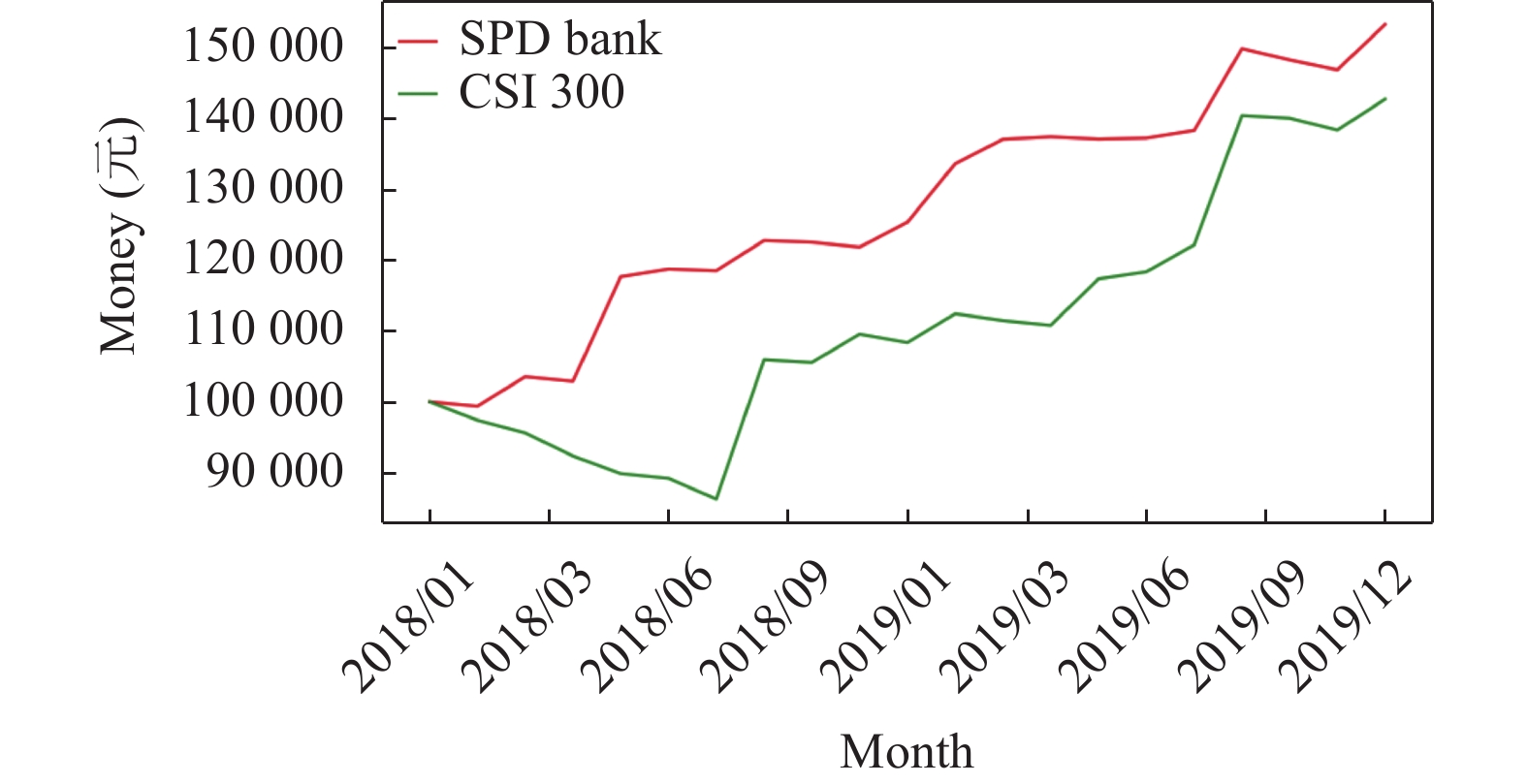
|
图 9 浦发银行和沪深300的收益对比 |
5 总结
本文提出了一个由双层LSTM、双层GRU和自注意力机制组成的混合ATLG神经网络模型, 用于股票价格的预测. 为了提高性能, 逐步探讨了加入自注意力机制后对基本模型的误差和准确率的影响, 探讨了神经网络中层数对模型的影响. 并且在得出最优层数的结论后, 将模型两两组合最终得出对股票价格预测的最优模型. 对比其他文献在各项指标上, 所提模型均有提高, 实验结果反映出ATLG模型可以适用于市场的股票价格预测.
此外, 本文进行了额外的基金模拟, 提出的框架可以产生可观的利润, 年化收益明显增加, 与市场表现相比, 这是一个显著的改进. 由于股价预测任务的不确定性和难度, 以及相当大的交易成本使得轻微的价格波动毫无意义, 因此, 关注更有可能成为高利润机会的重要交易点, 而不是预测每个时间点的趋势, 可以带来更多的利润. 在未来的工作中, 将继续研究深度学习投资组合构建技术, 更加关注中长期的预测, 还将通过纳入自然语言处理NLP技术来扩展预处理部分, 以捕捉社交媒体、新闻和谣言对股票市场价格的影响.
| [1] |
Wang L, Ma F, Liu J, et al. Forecasting stock price volatility: New evidence from the GARCH-MIDAS model. International Journal of Forecasting, 2020, 36(2): 684-694. DOI:10.1016/j.ijforecast.2019.08.005 |
| [2] |
Freeborough W, van Zyl T. Investigating explainability methods in recurrent neural network architectures for financial time series data. Applied Sciences, 2022, 12(3): 1427. DOI:10.3390/APP12031427 |
| [3] |
Taylor JW, Yu KM. Using auto-regressive logit models to forecast the exceedance probability for financial risk management. Journal of the Royal Statistical Society: Series A (Statistics in Society), 2016, 179(4): 1069-1092. DOI:10.1111/rssa.12176 |
| [4] |
Pradhan R, Bharadwaj K, Saxena A, et al. Stock trend prediction and analysis using LSTM neural network and dual moving average crossover algorithm. IOP Conference Series: Materials Science and Engineering, 2021, 1131: 012005. DOI:10.1088/1757-899X/1131/1/012005 |
| [5] |
Chen B, Buesser B, DiPietro K. Recurrent neural networks for autoregressive moving average model selection. IEEE International Conference on Big Knowledge. Beijing: IEEE, 2019. 33–41.
|
| [6] |
Bukhari AH, Raja MAZ, Sulaiman M, et al. Fractional neuro-sequential ARFIMA-LSTM for financial market forecasting. IEEE Access, 2020, 8: 71326-71338. DOI:10.1109/ACCESS.2020.2985763 |
| [7] |
赵澄, 叶耀威, 姚明海. 基于金融文本情感的股票波动预测. 计算机科学, 2020, 47(5): 79-83. DOI:10.11896/jsjkx.190400145 |
| [8] |
Khaidem L, Saha S, Dey SR. Predicting the direction of stock market prices using random forest. arXiv:1605.00003, 2016.
|
| [9] |
Hu Y, Liu K, Zhang XZ, et al. Application of evolutionary computation for rule discovery in stock algorithmic trading: A literature review. Applied Soft Computing, 2015, 36: 534-551. DOI:10.1016/j.asoc.2015.07.008 |
| [10] |
谢琪, 程耕国, 徐旭. 基于神经网络集成学习股票预测模型的研究. 计算机工程与应用, 2019, 55(8): 238-243. DOI:10.3778/j.issn.1002-8331.1807-0294 |
| [11] |
Hajiabotorabi Z, Kazemi A, Samavati FF, et al. Improving DWT-RNN model via B-spline wavelet multiresolution to forecast a high-frequency time series. Expert Systems with Applications, 2019, 138: 112842. DOI:10.1016/j.eswa.2019.112842 |
| [12] |
Cao J, Li Z, Li J. Financial time series forecasting model based on CEEMDAN and LSTM. Physica A: Statistical Mechanics and Its Applications, 2019, 519: 127-139. DOI:10.1016/j.physa.2018.11.061 |
| [13] |
Niu HL, Xu KL. A hybrid model combining variational mode decomposition and an attention-GRU network for stock price index forecasting. Mathematical Biosciences and Engineering, 2020, 17(6): 7151-7166. DOI:10.3934/mbe.2020367 |
| [14] |
Mnih V, Heess N, Graves A, et al. Recurrent models of visual attention. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2204–2212.
|
| [15] |
Chen S, Ge L. Exploring the attention mechanism in LSTM-based Hong Kong stock price movement prediction. Quantitative Finance, 2019, 19(9): 1507-1515. DOI:10.1080/14697688.2019.1622287 |
| [16] |
Qiu JY, Wang B, Zhou CJ. Forecasting stock prices with long-short term memory neural network based on attention mechanism. PLoS One, 2020, 15(1): e0227222. DOI:10.1371/journal.pone.0227222 |
| [17] |
Chen Q, Zhang WY, Lou Y. Forecasting stock prices using a hybrid deep learning model integrating attention mechanism, multi-layer perceptron, and bidirectional long-short term memory neural network. IEEE Access, 2020, 8: 117365-117376. DOI:10.1109/ACCESS.2020.3004284 |
| [18] |
Lu WJ, Li JZ, Li YF, et al. A CNN-LSTM-based model to forecast stock prices. Complexity, 2020, 2020: 6622927. DOI:10.1155/2020/6622927 |
| [19] |
Kumar K, Haider MTU. Enhanced prediction of intra-day stock market using metaheuristic optimization on RNN-LSTM network. New Generation Computing, 2021, 39(1): 231-272. DOI:10.1007/s00354-020-00104-0 |
| [20] |
Torres JF, Hadjout D, Sebaa A, et al. Deep learning for time series forecasting: A survey. Big Data, 2021, 9(1): 3-21. DOI:10.1089/big.2020.0159 |
| [21] |
Pang XW, Zhou YQ, Wang P, et al. An innovative neural network approach for stock market prediction. The Journal of Supercomputing, 2020, 76(3): 2098-2118. DOI:10.1007/s11227-017-2228-y |
| [22] |
严冬梅, 李斌. 基于生成式对抗神经网络的股票预测研究. 计算机工程与应用, 2022, 58(13): 185-194. DOI:10.3778/j.issn.1002-8331.2112-0005 |
| [23] |
刘茜阳, 宋燕, 张亚萌. 基于模糊K线的FCLSTM-vSVR模型的股票价格预测. 智能计算机与应用, 2022, 12(4): 54-60, 69. DOI:10.3969/j.issn.2095-2163.2022.04.010 |
| [24] |
郑树挺, 徐菲菲. 基于改进Self-Attention的股价趋势预测. 计算机技术与发展, 2021, 31(3): 33-38. DOI:10.3969/j.issn.1673-629X.2021.03.006 |
| [25] |
蒙懿, 徐庆娟. 基于CNN-BiLSTM和注意力机制的股票预测. 南宁师范大学学报(自然科学版), 2021, 38(4): 70-77. DOI:10.16601/j.cnki.issn2096-7300.2021.04.010 |
 2023, Vol. 32
2023, Vol. 32



