互联网及移动支付等技术的蓬勃发展给传统金融业带来了广泛影响, 网络借贷就是其催生的产物. 一方面, 由于网络借贷具备方便、灵活的融资属性, 越来越多的人选择其作为融资渠道. 另一方面, 由于网络借贷用户的信用水平难以准确识别, 这导致很高的违约率, 严重阻碍了网贷平台的健康发展. 因此, 构建一套广泛适用的个人信用预测模型对网络借贷的风险控制以及网贷平台的良性发展具有深远的意义.

近年来, 在信用风险预测模型的研究中应用了很多基于机器学习和统计学的方法, 例如支持向量机、神经网络、随机森林等方法. 国内外学者对此进行了大量探索研究, 但是在信用风险评估场景下, 样本中出现贷款违约的比例很低, 多数类样本和少数类样本比例相差极大. 使用这样的样本对模型进行训练, 严重影响了模型的预测能力^[1]. 针对此类数据集的预测问题, 目前学界主要集中在数据和算法两个层面.

(1)数据层面一般采用的方法是用欠采样或过采样方法对数据进行处理. Chen等^[2]在集成学习方法中引入参数扰动并将其与欠采样方法融合构建预测模型, 一定程度上解决了随机欠采样带来的信息遗失问题, 但是在处理多数类和少数类样本极不平衡的数据集时预测效果不够理想. Chawla等^[3]提出了 SMOTE算法, 该算法通过人工合成少数类样本使数据集样本分布平衡, 减少了出现过拟合的概率. Phetlasy等^[4]使用SMOTE方法对少数类样本进行过采样处理, 并提出一种组合多个分类器的方法, 该方法将未被正确分类的流量数据送入后续的分类器重新分类, 从而提高预测的灵敏度和准确率. 田臣等^[5]融合了随机森林算法和少数类过采样法构建信用预测模型, 预测效果较随机森林算法和朴素贝叶斯算法相比更好. 针对数据维度过高的问题, Cai等^[6]使用Pearson相关系数来衡量特征变量间的线性相关关系, 从而将相关性较小的特征变量进行筛除, Tibshirani^[7]提出了Lasso变量选择方法. Lasso方法增加L1范式函数作为惩罚项来压缩变量系数, 将相关性弱的变量系数压缩为0, 从而实现特征压缩和对应参数的估计.

(2)算法层面. 传统分类算法在处理正负样本类极不平衡的数据集时表现较弱, 为了解决这一问题, 学者们将损失函数或错误率引入模型中, 代表方法包括代价敏感学习、集成学习算法等^[8]. 代价敏感学习^[9]通过增加少数类样本分类错误的惩罚代价, 优化目标函数从而提升模型的分类准确度. 而集成学习算法^[10]集合了多个基分类器, 降低单个分类器对正负样本类比例相差很大的数据集进行预测时出现的偏差, 提升整体模型的分类准确度. 目前广泛使用的是融合数据采样方法与分类算法. Sun等^[11]提出一种对不平衡数据集进行分类的方法, 该方法将不平衡数据集分解为数个平衡的数据子集, 然后训练每个子集从而获得基分类器. 王俊红等^[12]提出一种融合了代价敏感学习算法和欠采样法的预测方法, 提升了处理样本不平衡数据集时的分类效果.

随着大数据时代的全面到来, 用户特征呈现高维度稀疏发展趋势, 从而导致分类模型难以正确区分个人信用数据的多数类和少数类. 同时高维度数据会导致维度灾难, 使算法的计算开销随着数据维度的上升出现指数增长. 因此, 维度灾难和样本类不平衡这两个难题^[13], 严重影响了个人信用评价问题.

综上所述, 本文针对高维度不平衡数据集进行预测的问题, 提出一种基于特征优化和集成学习的个人信用预测方法(PL-SmoteBoost). 主要贡献如下: 1)利用Pearson对数据进行初始化分析, 剔除冗余数据; 通过Lasso选取部分特征来减少数据维度, 降低高维风险. 2)通过SMOTE过采样方法对降维数据的少数类进行线性插值, 以解决类不平衡问题. 3)构建基于集成学习的个人信用评估模型, 以常用的处理二分类问题的算法作为对比方法, 采用从Kaggle和微软开放数据库上下载的数据集对算法进行测试, 证明该方法的有效性.

1 特征优化的理论与方法 1.1 Pearson相关系数

皮尔森(Pearson)系数^[14]具有去中心化、归一化等特点, 在反应目标值与特征值的相关性上有着出色表现, 因此广泛应用于衡量特征的线性相关程度上, 其公式如下:

$ r(x, y) = \frac{{\displaystyle\sum\limits_{i = 1}^n {({x_i} - \overline x )({y_i} - \overline y )} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - \overline x )}^2}} } \sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - \overline y )}^2}} } }} $

(1)

其中, 变量 $ x $ 为特征值, 变量 $ y $ 为信用分, Pearson相关系数即为上述2个变量的协方差除以其标准差的乘积. 其中系数 $ r(x, y) $ 的取值范围在−1至1之间, 值越接近1或−1则表示正负相关性越强, 值越接近0表示相关性越弱. 皮尔森系数在保留偏好特征方面表现良好, 能较好反映特征间的线性相关性, 因此适合用于信用评价中特征的筛选.

1.2 Lasso算法

Lasso 算法是一种基于线性回归模型的特征筛选办法, 通过对变量进行筛选和压缩来减少特征维度, 可以有效防止出现过拟合问题. Lasso 算法使用L1 范式构造惩罚函数, 在多元线性回归误差平方和最小的基础上, 对回归系数增加惩罚函数, 将与模型结果相关性较小的变量回归系数压缩至0, 从而删除这些特征变量, 达到减少特征维度的目的^[15].

Lasso 特征选择方法即为残差平方和最小化加上L1范式的惩罚项, 公式如下:

$ \mathrm{min}{\displaystyle \sum {e}_{i}^{2}+L1范式}=\mathrm{min}{\displaystyle \sum ({x}_{i}-{\hat{x}}_{i}}{)}^{2}+\lambda {\displaystyle \sum _{u=1}^{k}\left|{\hat{\beta }}_{u}\right|} $

(2)

其中, $ {x_i} $ 表示个体 $ i $ 的变量 $ x $ 的实际数值; $ {\hat x_i} $ 表示对个体 $ i $ 的变量 $ x $ 的估计值; $ {e_i} = {x_i} - {\hat x_i} $ , 代表了估计值与实际值之间的差值; $ \;\hat \beta $ =( $ \;{\hat \beta _1}, {\hat \beta _2}, \cdots, {\hat \beta _k} $ )为回归系数. $ \lambda $ 是预先设定好的非负数, 其大小决定了算法的选择能力, 如果 $ \lambda $ 过大则会导致无法删除任何特征, 通过将 $ \lambda $ 设定为一个合适的低值, 可以将与类相关性较低的特征变量系数降为 0, 从而删除这些特征, 突出与类相关性强的特征, 实现对数据集的特征筛选.

1.3 SMOTE算法

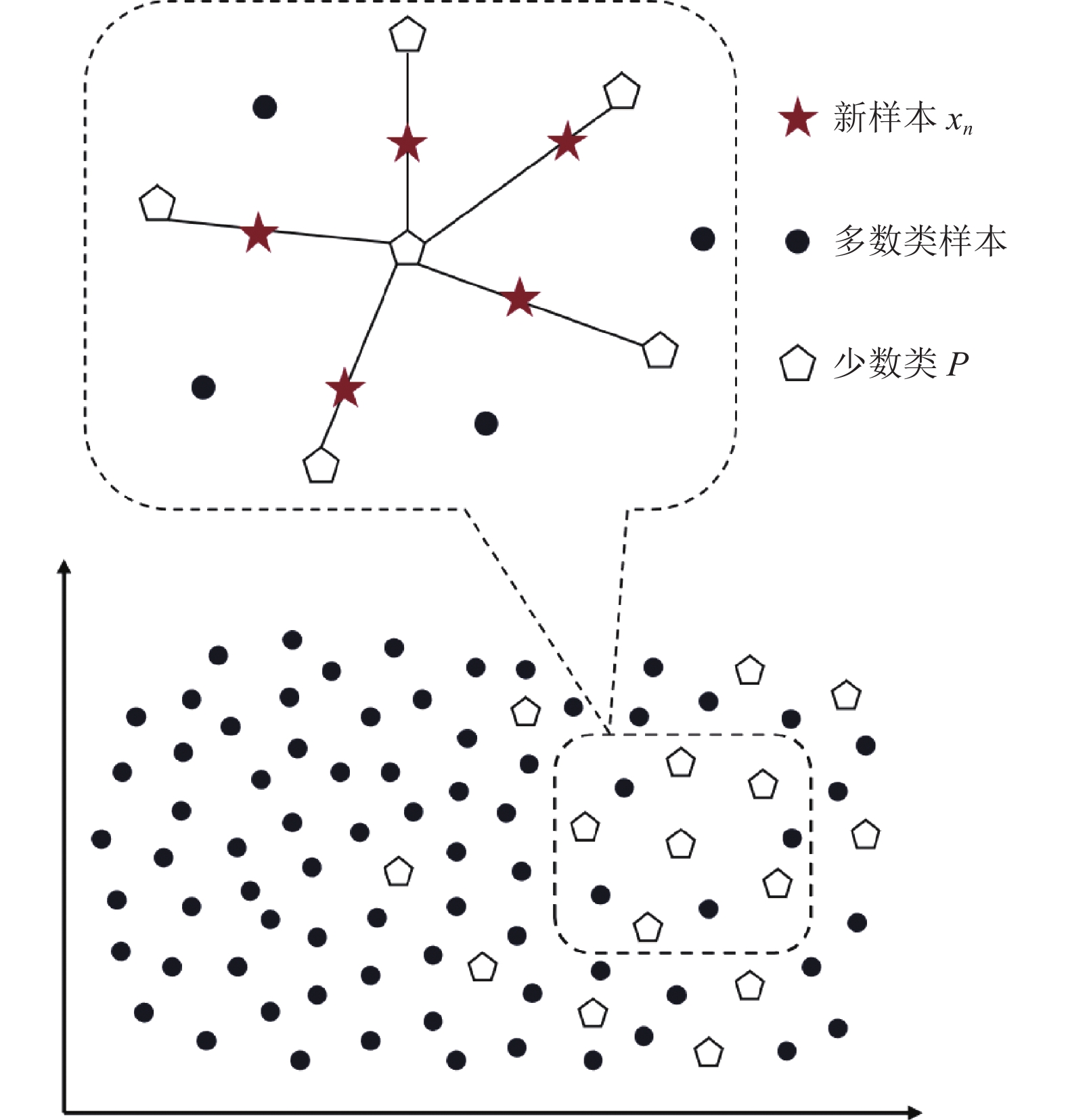
SMOTE合成少数类过采样技术是一种基于随机过采样法的改进方法. 它基于“线性插值”来合成新的少数类样本^[16], 以每个少数类样本的K个最近邻样本为参照, 随机的选择数个邻近点进行插值, 从而合成新的少数类样本. 因为特征空间上临近的样本特征具有相似性, 据此合成的新样本与老样本间特征也相似.

样本不平衡问题指正样本数量远高于负样本数量, 通过SMOTE技术合成少数类样本, 从而有效解决数据集的样本不平衡问题. 合成少数类样本的公式如下:

$ {x_n} = P + \lambda \times \left( {{K_i} - P} \right) $

(3)

其中, $ {x_n} $ 为新构造的少数类样本; $ P $ 为少数类中的每一个样本; $ \lambda $ 为区间(0, 1)内的随机数; $ {K_i} $ 为数据样本 $ P $ 中最近邻样本中的第n个样本; $ {{i}} $ =1, 2, …,k; 通过SMOTE技术构造少数类样本, 可以有效缓解数据集类不平衡问题.

SMOTE算法的合成实例如图1所示, 首先依次选择数据集中的每个少数类样本 $ P $ ; 然后从 $ P $ 的最近邻样本中选择n个, n一般为5; 依次在选择的n个最近邻样本中与少数类样本 $ P $ 使用式(3)进行线性插值, 从而获得新合成的少数类样本 $ {x_n} $ , 通过合成少数类样本, 使得数据集的正负样本数量趋于均衡, 提升模型预测准确度.

1.4 Boosting集成学习算法

XGBoost是一种基于传统梯度提升树(GBDT)进行改进的算法, 它使用预排序算法对树模型进行拟合, 在树生长的过程中遍历每一个切分点, 从而找到最优切分点对数据做叶子节点的切分, 获得各个叶子节点的分数, 将其加和得出样本的预测值. 并且XGBoost内置处理缺失值的规则, 支持并行计算, 灵活性很高, 能在消耗更少内存的情况下提供更快的运算速度^[17].

LightGBM算法基于XGBoost做了进一步改进. LightGBM使用基于叶子节点分割的树生长策略以及直方图算法, 大幅度降低了计算和内存消耗, 因而可以在维持模型精度的前提下提升训练速度^[18]. 并且LightGBM提升了树的最大深度限制, 一定程度可以规避按叶子节点分割所导致的过拟合问题.

CatBoost是以对称树为基学习器的算法, 在训练过程中处理类别特征时使用 Target-based 方式, 因而CatBoost适宜用来处理大部分特征都是类别特征的数据集. 另外CatBoost降低了对广泛的超参数优化的依赖, 一般情况下使用默认参数就能获得良好的效果, 有助于降低预测所需的时间, 规避过拟合问题^[19].

2 基于PL-SmoteBoost个人信用预测方法

为了解决面向高纬度、不均衡数据环境下的信用分预测问题, 提出一种基于特征优化和集成学习的个人信用预测方法(PL-SmoteBoost). 该模型分为3个部分, 各部分介绍如下.

(1)数据清洗部分. 数据集的数据来源多种多样, 例如人工录入、用户填写、爬虫爬取等, 因为用户填写不认真、爬虫程序不够智能、人工录入失误、存储设备故障等原因, 数据难以避免的会产生大量缺失值和异常值, 例如一条数据只有名字没有其他信息, 或者年龄一栏错填了性别等问题. 这使得数据集的预测能力大打折扣. 因此, 为了提升预测水平, 将获取的数据集进行缺失值填充、异常值删除等操作, 提高模型训练能力.

(2)模型构建部分. 分为数据模块和训练模块, 数据模块是通过统计学和机器学习等方法将原始的数据转换成可参与模型计算的形式. 训练模块采用集成学习中Boosting算法对模型进行训练.

(3)模型评估部分. 输出基于PL-SmoteBoost的个人信用评估方法的结果, 并以 AUC 值作为算法的评价指标.

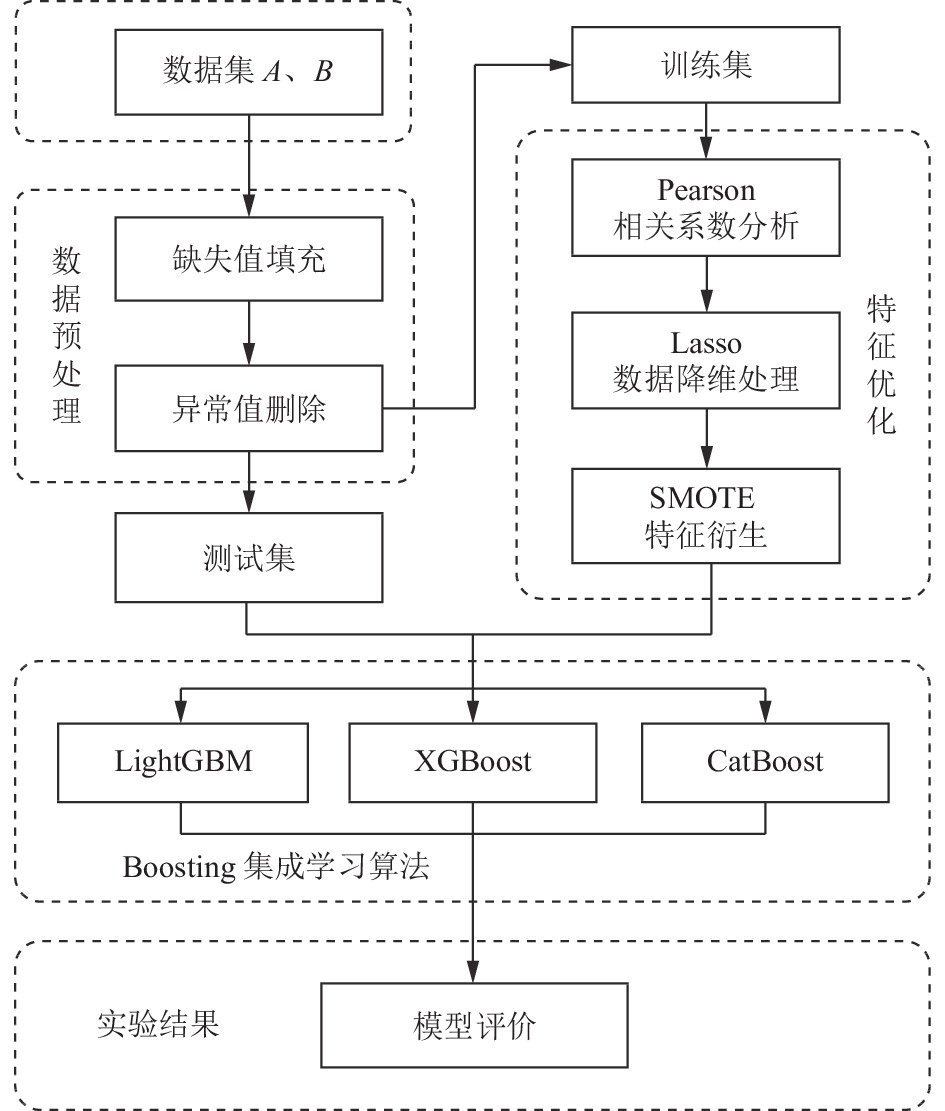
2.1 算法流程

基于特征优化和集成学习的个人信用预测方法(PL-SmoteBoost)的流程图如图2所示.

基于PL-SmoteBoost的个人信用预测模型的具体步骤如下.

第1步. 数据预处理. 对获取到的数据集A、B进行缺失值填充、异常值删除等操作, 得到数据集A₀、B₀, 使数据处于同一量纲下, 提升数据表达能力.

第2步. 使用Pearson系数分析特征与信用之间的关联性, 采用Lasso提取重要程度高的特征, 进行特征选择, 减少数据维度, 降低高纬风险.

第3步. 采用SMOTE过采样技术对不平衡数据进行衍生处理, 输出均衡数据集A₁、B₁.

第4步. 模型训练. 将经过特征处理后的数据A₁、B₁, 分别代入Boosting集成学习LightGBM、XGBoost、CatBoost算法进行模型训练, 得出预测结果.

第5步. 评分结果. 输出基于PL-SmoteBoost的个人信用评分模型的预测结果, 以常用的处理不均衡分类问题的算法作为对比方法进行测试, 以 AUC值作为算法的评价指标, 利用统计检验手段对实验结果进行分析得出结论, 基于PL-SmoteBoost的个人信用评分模型训练效果好, 适合应用于信用评分预测.

2.2 评价指标

评价一个分类器的好坏有许多标准, 一般情况下准确率高的分类器效果就好. 但是在多数类和少数类样本比例差别很大的情况下, 准确率高并不一定意味着分类器性能好. 例如对用户的信用情况进行预测, 因为信用良好的用户数量远比信用违约的用户数量高, 所以在大部分情况下, 任意模型预测客户的信用良好, 准确率都能达到 90%以上, 因此使用准确度对分类器的性能进行评价并不充分.

因此本文采用AUC值对分类器进行评价. ROC曲线是以真正率为坐标轴纵轴、假正率为坐标轴横轴的曲线, AUC值为ROC曲线和X轴围成的面积. ROC曲线越贴近坐标轴左上角则表明模型的性能越好^[20], 即AUC值越大越好. AUC值在样本数据失衡的情况下仍能较好地反应模型预测能力, 因此为了量化模型的好坏, 用AUC值来评价分类器的性能.

3 实验分析 3.1 数据清洗

本文使用两个数据集进行对照实验, 以增强模型证明力度. 数据为脱敏后的数据, 数据来源为在Kaggle下载的数据集A和微软开放数据库下载的数据集B.

本部分将以Kaggle数据集A为例详细描述对数据集的处理过程. 数据集A数据特征多达56个, 共分为5类, 其中包括用户基本信息、借贷行为、活跃行为、用户消费行为、违约情况.

(1) 缺失值处理

数据集A原始的56个特征中: 有42个特征含有缺失值, 有12个特征的缺失值比例在30%以上, 缺失值比例过大的特征直接整列删除, 4个特征采用固定值填充. 以工作年限这列特征为例, 统计可知其中有3376条缺失值, 原始数据集中用“n/a”表示, 本步采用其他样本的均值对其进行填充.

(2) 异常值检测

异常值是数据集中的非正常值, 其可能是不正确的“脏数据”, 也可能是正确的异常数据, 需要具体分析后, 对部分特征采用均值填充进行处理, 部分无法处理的数据做删除处理.

对缺失值、异常值处理后保留了 29个特征变量, 共计 6889个样本. 其中, 违约样本数量为682个, 未违约样本数量为 6207个. 本文建立如表1所示数据特征指标, 对个人信用风险进行识别.

3.2 特征优化

(1) Pearson相关系数分析

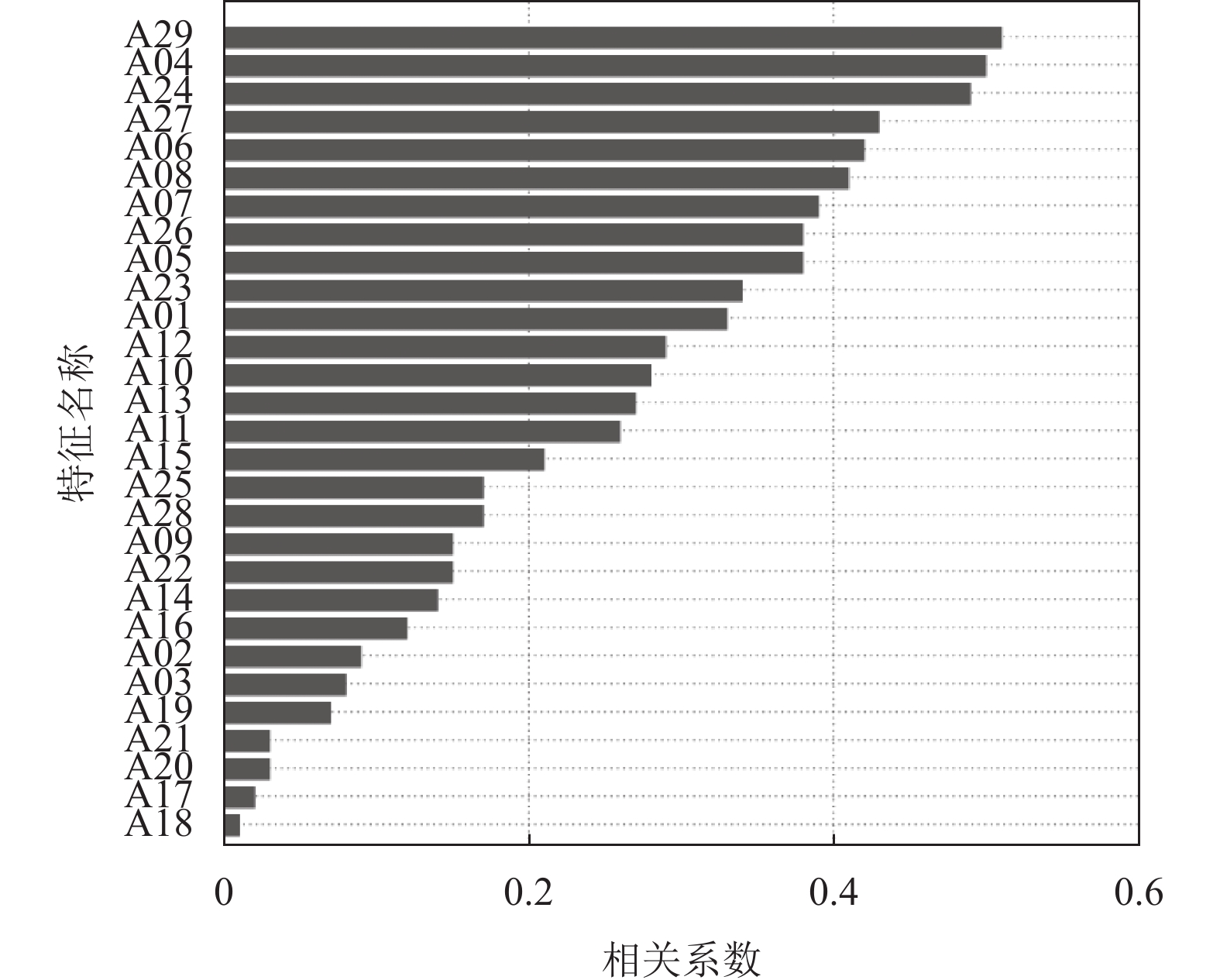
如图3所示, 为了降低数据集特征维度, 提高数据分析的准确性和高效性. 将经过预处理的特征变量输入模型算法中, 计算各个特征与信用预测之间的相关系数, 将其进行排序并输出为一个特征值与信用预测相关性的柱状图, 从图中可以发现部分特征与信用预测相关性较低, 将这些特征删除, 保留剩下的与信用预测相关性较高的特征变量. 本步骤剔除的是登录频率和用户使用APP时间、交往圈人数、社交频率4个低相关特征, 保留剩下的25个特征.

(2) Lasso特征选择

Lasso算法通过增加L1范式函数作为惩罚项, 将绝对值小于阈值的特征回归系数压缩至0, 即将这些特征变量对于分类结果的贡献忽略, 从而可以剔除这些变量. 在Lasso算法中, $ \lambda $ 的大小决定了算法的选择能力, 因此本步骤中微调其大小, 从中选择最合适的值. Lasso 中参数 $ \lambda $ 微调结果如表2所示.

当 $ \lambda $ 为0.01时, 模型存在欠拟合的情况, 25个特征变量中只保留了5个. 经过多次测试训练集与测试集得分, 在 $ \lambda $ 为0.005–0.0025之间时训练集与测试集分值相差较低. 当 $ \lambda $ 降至 0.0001 时, 训练集与测试集得分差值较高, 存在过拟合现象. 因此本文选择 $ \lambda $ =0.0025进行实验, 此时样本保留22个.

(3) SMOTE过采样

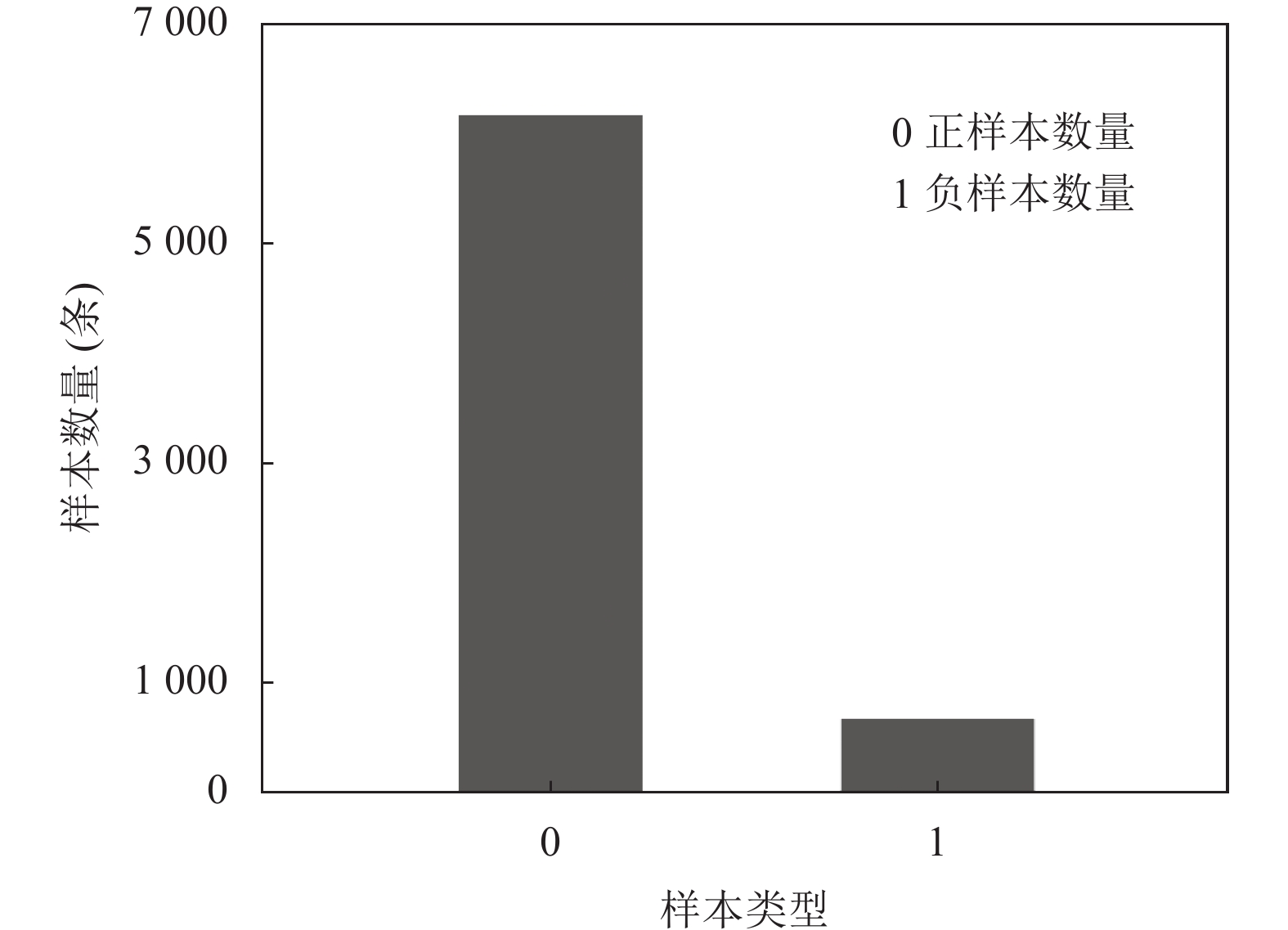
如图4所示, 本文采用的用户数据中正负样本不均衡, 正样本数目远大于负样本. 而大部分分类器会基于阈值输出结果, 如大于某值的为正例, 反之则为反例. 在样本数据不均衡时, 预先设定的阈值会导致模型输出结果倾向于数据多的类别. 为了解决这一问题, 本文采用SMOTE过采样技术合成少数类样本, 让正负样本数目一样多.

SMOTE算法步骤如算法1.

算法1. SMOTE算法

输入: 少数类样本 $\scriptstyle P $ , 向上采样倍率 $\scriptstyle N $ , 样本近邻数 $\scriptstyle k $

输出: 新合成的少数类样本 $\scriptstyle {x_n} $

步骤1. 计算得到少数类样本 $\scriptstyle {x_n}$ 的 $\scriptstyle k$ 个近邻样本

步骤2. 在 $\scriptstyle k$ 个近邻样本中随机选择一个为 $\scriptstyle {K_i}$

步骤3. 生成一个0到1之间的随机数 $\scriptstyle \lambda$

步骤4. 按照向上采样倍率 $\scriptstyle N$ 重复步骤2–3

步骤5. 合成新的少数类样本 $\scriptstyle {x_n}$

步骤6. 对新合成的少数类样本 $\scriptstyle {x_n}$ 做分类

步骤7. 输出分类后的结果

3.3 实验评估

经过数据清洗和特征优化后, 本文获得了数据集A₁、B₁. 为了验证PL-SmoteBoost模型对个人信用评分的预测能力, 使用Python 3.9.0开发环境, 进行如下两组实验.

实验1. 本轮实验为了验证特征优化对模型预测效果的影响, 实验采用仅经过数据清洗的数据集A₀、B₀以及特征优化后的数据集A₁、B₁进行对比, 分别使用SVM、LR、RF、BP四种算法进行实验对比分析.

表3为特征优化前后AUC值对比. 从实验结果可以看出, A、B两个数据集的4种模型的训练子集在经过特征优化后, AUC 值都有所提升, 提升的数值约在7.2%–9.6%之间, 说明本文特征优化处理后的数据对提升模型准确率有显著的效果, 其中RF算法的优化效果最好.

实验2. 本轮实验为了体现Boosting集成学习算法对个人信用预测的作用, 引入基于Boosting集成学习中的XGBoost、CatBoost、LightGBM和实验1中预测效果最优的RF算法进行对比, 采用五折交叉算法对数据集进行训练来减少随机性对分类结果的影响. 实验结果如表4、表5所示.

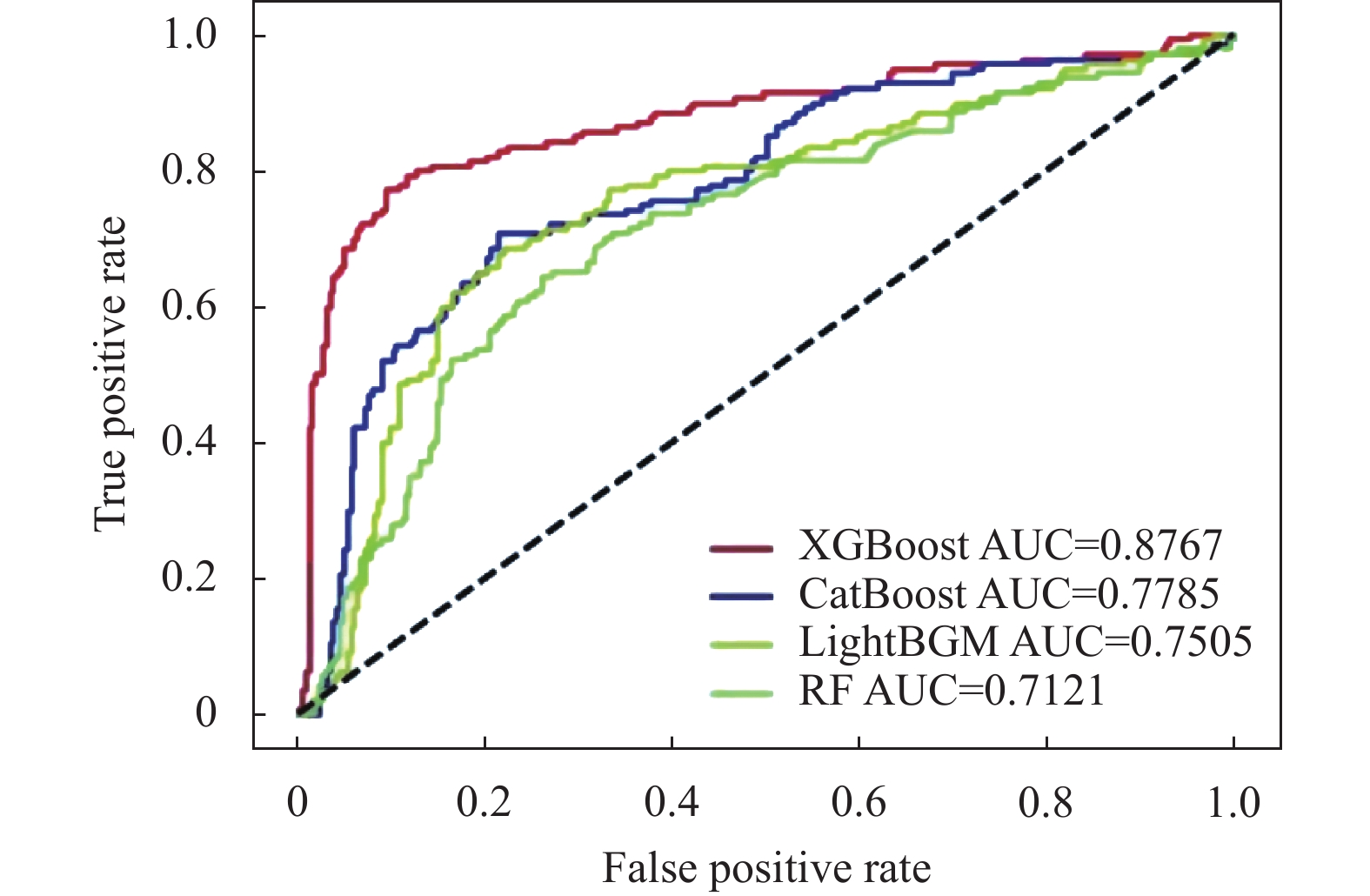
从表4、表5可以看出, 在4个评估模型中, 基于Boosting的3个模型效果都比RF好. 其中, XGBoost模型训练效果最好, A、B两组数据集的AUC 平均值分别为 0.877和0.864, 比RF模型的AUC平均值分别高出16.5%和14.3%, LightGBM的训练效果在3组Boosting算法中最差, 但其AUC平均值也比RF模型的AUC平均值分别高出3.8%和5.8%.

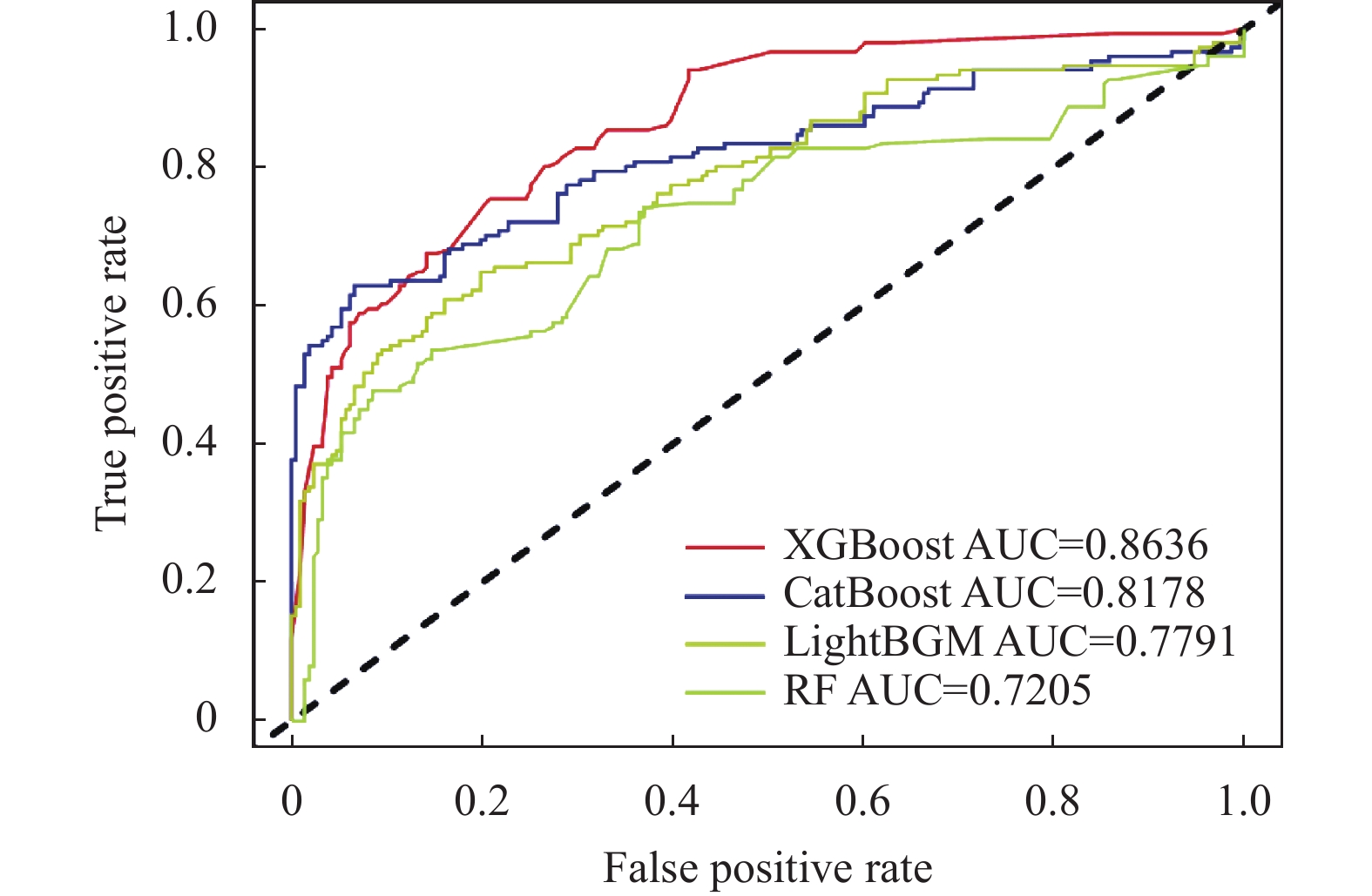
为了能够更直观的对比4种模型的训练效果, 本文使用ROC曲线对比图来呈现, 如图5、图6所示, ROC曲线是一条在不同阈值下分类结果的假正率和真正率所构成的曲线, 其中坐标轴横轴为假正率, 坐标轴纵轴为真正率, 曲线下的面积为AUC值, 即曲线越靠近左上方模型分类效果越好.

从图5、图6中4种模型的ROC曲线可以看出, XGBoost都在图中最上方, 训练效果最优; 而RF的ROC曲线都在最下方, 结果相比Boosting算法中的3个模型要差.

4 总结与展望

为了解决面向高纬度、不均衡数据环境下的信用分预测问题, 本文提出一种基于特征优化和集成学习的个人信用预测方法(PL-SmoteBoost). 该方法充分考虑了数据高纬度、不均衡等特点, 选取Pearson相关系数、Lasso、SMOTE等算法进行数据特征的优化, 考虑个人信用评分的特殊性, 采用对噪声敏感的Boosting集成学习算法对数据进行训练. 选用Kaggle和微软开放数据库上公开的数据集进行评估, 使用AUC值作为评估指标, 实验结果表明, PL-SmoteBoost算法性能优于其他算法, 适用于个人信用评分.

不足及未来展望: 本文采用SMOTE过采样方法, 虽然解决了数据不平衡问题, 但是还是存在一些问题: 比如合成样本的质量问题、模糊类边界问题、少数类分布问题. 这些都会影响模型最终的预测结果, 所以选取更加合适的数据平衡方法是需要进一步探讨的问题.