剩余可用寿命能够显示航空发动机未来的健康状态趋势, 提高操作的可靠性和安全性. 准确的RUL预测对航空发动机的预防性维修有重要指导作用, 可以保证发动机的良好工作条件, 降低故障发生的概率和发动机维护成本^{[1, 2]}. RUL预测方法, 一般可以分为基于模型和数据驱动两类^[3]. 基于模型的解决方案, 要求建立一个精确的航空发动机系统模型, 但是随着工业科技的不断发展, 航空发动机越来越精密, 系统内部之间的相互联系也越来越复杂, 这一解决方案难以实现. 数据驱动的解决方案, 不需要了解发动机的内部构造和系统之间的相互作用, 只需将各类传感器数据作为数据驱动算法的输入, 算法自动学习具有代表性的显著特征, 用于最后的RUL预测^{[4, 5]}.

数据驱动方法中, 深度神经网络基于其强大的自动特征学习能力和推理分析能力, 在RUL预测问题上展现出优异的性能. 因此, 基于深度神经网络的RUL预测方法受到越来越多学者的关注^[3]. Yang等^[6]提出了基于双卷积神经网络(CNN)的智能RUL预测方法, 双CNN分别用来识别初始故障点和进行RUL预测. Zhu等^[7]提出多尺度卷积神经网络(MSCNN)进行RUL预测, MSCNN可使全局和本地信息保持同步, 自动学习有助于RUL预测的显著特征. Shao等^[8]提出一种新型卷积深度信念网络(CDBN), 先将数据压缩降维, 然后使用CDBN网络来学习代表性特征用于最后的RUL预测.

上述文献中的前馈神经网络结构无法有效分析具有整体逻辑特征的时序输入, 然而航空发动机的各类传感器数据具有时序性, RUL预测是一个典型的时序问题. 循环神经网络(RNN)在网络结构中添加自反馈神经, 可以很好地处理时序输入. Aggarwal等^[9]提出深度Weibull模型(DW-RNN)和多任务学习(MTL-RNN). DW-RNN来学习潜在的故障动力学, MTL-RNN来学习底层分布.

RNN在反向传播的过程中会出现梯度爆炸或消失等问题, 很难处理长期依赖关系的时序输入. LSTM引入细胞状态来存储长期记忆, 可以很好地缓解梯度爆炸和消失的问题^[10]. Zheng等^[11]提出一种用于估计的LSTM方法, 性能明显优于传统的RUL估计方法以及RNN. Miao等^[12]设计了双任务深度LSTM, 用于联合学习航空发动机退化评估和剩余使用寿命预测.

Bi-LSTM可以从数据中捕捉到更多代表性显著特征, 得到更精确, 更可靠的预测结果^[13]. 车畅畅等^[1]建立一种基于一维卷积神经网络(1D-CNN)和 Bi-LSTM 的混合模型, 1D-CNN得到性能退化分析模型, Bi-LSTM进行RUL预测 . 牟含笑等^[14]提出基于CDBN与Bi-LSTM的剩余寿命预测方法, CDBN提取反应隐含深层次特征的健康指标, Bi-LSTM挖掘时序特征(TF)和退化趋势, 进行RUL预测. 但是上述深度神经网络都将重点放在最后一个时间步长得到的学习特征, 学习特征的利用率较低, 而且每个时间步长得到的学习特征对RUL预测有着不同的贡献. 同时一些手工特征(HF)和空间特征(SF)也可以为RUL预测提供额外信息, 提高模型预测精度.

综上所述, 本文建立了一种基于多特征融合的航空发动机RUL预测模型. 模型使用Bi-LSTM从特征数据中提取时序特征, 再采用Multi-attention为时序特征分配权重, 捕获时序特征相互关联信息的多重特征, 充分利用模型构建中学习到的特征, 提高学习特征的利用率. 设计Conv-LSTM模块将输入数据的简单特征通过卷积映射到更复杂的高维模式, 挖掘输入数据深层次非线性的时空特征. 提取特征数据的手工特征, 并使用Softmax函数分配权重, 为RUL预测提供不同重要程度的额外信息. 构建一个特征融合框架将时空特征, 时序特征和手工特征进行融合用于最终RUL预测.

1 RUL预测模型 1.1 模型总体结构

基于多特征融合的航空发动机RUL预测模型如图1所示.

如图1所示, 首先利用指数平滑法为原始数据降噪, 得到稳定性较高的特征数据. 然后通过滑动窗口方法将特征数据分割为输入时间窗时间序列. 提取各个时间窗的手工特征, 并使用Softmax函数为同一时间窗口下的手工特征赋予不同的权值; 设计Conv-LSTM提取每个时间窗的时空特征; 双层Bi-LSTM自动学习输入时间窗时间序列的时序特征, 学习到的时序特征序列作为Multi-attention的输入, Multi-attention为每个时序特征分配权重. 上述3种特征经过全连接网络获取抽象特征后, 通过特征融合框架实现融合. 最后融合特征作为全连接网络的输入, 通过全连接网络回归实现航空发动机RUL预测.

1.2 Bi-LSTM时序特征提取

航空发动机传感器数据属于时序数据, 因此利用航空发动机传感器数据进行RUL预测可以看作是时序数据预测问题. Bi-LSTM基于整个时间序列学习时序数据之间的双向长期依赖关系, 可以提取更加具有代表性的时序特征, 有利于提高RUL预测精度^{[2, 14]}, 所以本文采用Bi-LSTM进行时序特征提取.

Bi-LSTM内部节点与LSTM相同, 均由遗忘门, 输入门, 输出门3个门结构和一个用来存储长期记忆的细胞状态构成. 遗忘门 ${f_t}$ 决定前一时刻细胞状态 ${C_{t - 1}}$ 中信息的保留或丢弃. 输入门 ${i_t}$ 决定当前时刻输入 ${x_t}$ 和前一时刻隐藏输出 ${h_{t - 1}}$ 中的哪些信息可以被记录到细胞状态中. 遗忘门和输入门共同决定细胞状态 ${C_t}$ 的更新. 输出门 $ {o_t} $ 决定当前隐藏状态的输出 $ {h_t} $ ^[2]. 数学表达式如下^{[1, 15]}:

$ {f_t} = \sigma ({W_f} \cdot [{h_{t - 1}}, {x_t}] + {b_f}) $

(1)

$ {i_t} = \sigma ({W_i} \cdot [{h_{t - 1}}, {x_t}] + {b_i}) $

(2)

$ {\tilde C_t} = \tanh ({W_c} \cdot [h{}_{t - 1}, {x_t}] + {b_c}) $

(3)

$ {C_t} = {f_t} * {C_{t - 1}} + {i_t} * {\tilde C_t} $

(4)

$ {o_t} = \sigma ({W_o} \cdot [{h_{t - 1}}, {x_t}] + {b_o}) $

(5)

$ {h_t} = {o_t} * \tanh ({C_t}) $

(6)

其中, ${f_t}$ , ${i_t}$ , $ {o_t} $ 是一个0–1之间的数值, $ \sigma $ 代表Sigmoid函数, $ {\tilde C_t} $ 为新的状态候选向量, $ \tanh $ 代表 $ \tanh $ 函数. $ {W_f} $ , $ {W_i} $ , $ {W_c} $ , $ {W_o} $ 为权重项. $ {b_f} $ , $ {b_i} $ , $ {b_c} $ , $ {b_o} $ 为偏置项.

Bi-LSTM是在正时间输入的LSTM网络结构上又添加了一个独立的负时间输入的LSTM网络层. 时序信息以正时间输入到第1层LSTM中, 得到当前时刻的顺序信息 $h_t^R$ , 以负时间输入第2层LSTM中, 得到当前时刻的逆序信息 $h_t^L$ . 将两个输出信息进行结合后形成当前时刻的隐藏输出 ${h_t}$ . 所以当前时刻的输出就同时包括过去和未来的时序信息, 是上下文相关的. Bi-LSTM结构隐藏输出数学表达如下^{[1, 15]}:

$ h_t^R = {f^R}({W_1}{x_t} + {W_2}h_{t - 1}^R) $

(7)

$ h_t^L = {f^L}({W_3}{x_t} + {W_4}h_{t + 1}^L) $

(8)

$ {h_t} = f({W_5}h_t^R + {W_6}h_t^L) $

(9)

1.3 Multi-attention分配权重

Bi-LSTM每个时间步长都会有一个学习特征. 假设某个样本经过Bi-LSTM学习的特征表示为:

$ H = {\left\{ {\;{h_1}, {h_2},\cdots, {h_N}} \right\}^{\rm{T}}} $

(10)

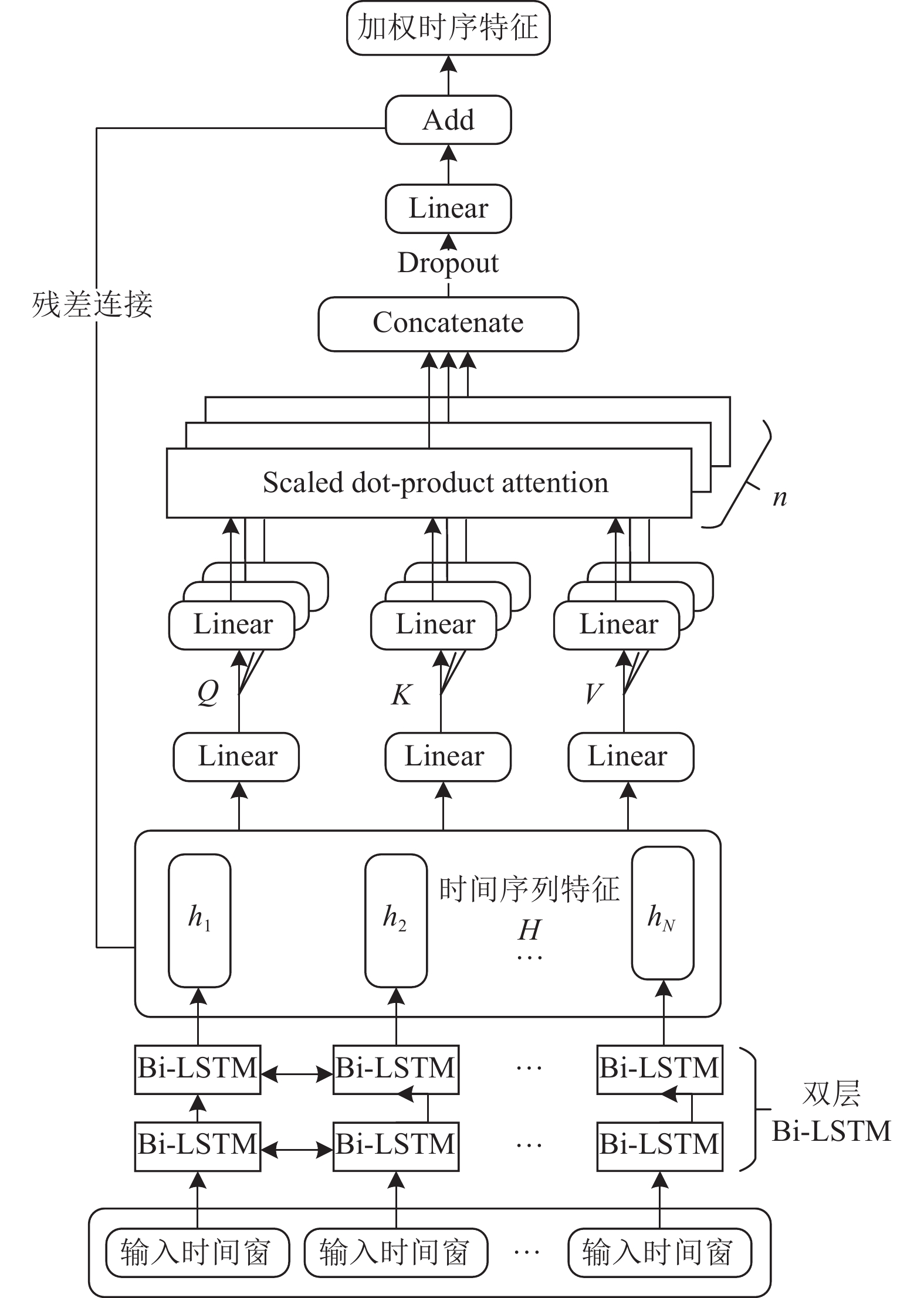
但是Bi-LSTM将重点放在最后一个时间步长上学习到的特征^[5], 存在对学习特征利用率较低的问题, 而且每个时间步长的学习特征对神经网络最后的结果都有着不同的贡献. 所以使用Multi-attention为Bi-LSTM各时间步长学习特征分配权重, 然后再与H进行残差连接得到加权时序特征. 充分利用每个时间步长的学习特征并解决权重矩阵退化问题, 进而提高RUL预测精度. 具体流程如图2所示.

图2中查询矩阵 $ Q $ , 键矩阵 $ K $ , 值矩阵 $ V $ 均为 $ H $ 的线性映射, $ n $ 为子空间个数. Scaled dot-product attention是Multi-attention的重要组成部分, 其数学表达式如下:

$ Attention({Q_ - }, {K_ - }, {V_ - }) = {\textit{Softmax}}\left(\frac{{{Q_ - }{K_ - }^T}}{{\sqrt {{d_{{k_ - }}}} }}\right){V_ - } $

(11)

其中, $ {Q_ - } $ , $ {K_ - } $ , $ {V_ - } $ 分别为 $ Q $ , $ K $ , $ V $ 的线性映射, $ K $ 的维度为 $ {d_k} $ .

Multi-attention将输入特征线性映射到多个不同的子空间, 然后计算每个子空间的注意力分数, 最后将这些注意力分数拼接到一起. 这使得模型可以共同关注不同位置的不同表示子空间的信息^[16], 数学表达式如下:

$ \begin{split} MultiHead\, (Q, K, V) = Concat\;(hea{d_1}, \cdots, hea{d_n}){W} \\ \;\;\;\;\;\;\;{\rm{where}}\;hea{d_i} = Attention\;({Q_-}W_i^{{Q_-}}, {K_-}W_i^{{K_-}}, {V_-}W_i^{{V_-}}) \\ \end{split} $

(12)

其中, $ hea{d_i} $ 表示第i个子空间的注意力分数. $ W_i^{{Q_ - }} $ , $ W_i^{{K_ - }} $ , $ W_i^{{V_ - }} $ 分别为第i个子空间下 $ {Q_ - } $ , $ {K_ - } $ , $ {V_ - } $ 的权重矩阵. $ {W^o} $ 为 $ n $ 个子空间计算结果拼接后对应的权重矩阵.

1.4 提取手工特征

手工特征是一种根据领域知识人为设计的特征, 它的每一维度往往都具有一定的物理或数学含义, 具有很强的针对性和可解释性. 本文提取的手工特征包括均值特征和趋势系数特征, 均值表示传感器参数量级的大小, 趋势系数代表传感器参数未来的退化潜力. 手工特征能够为RUL预测提供一些额外的有意义的信息, 可以提高RUL预测精度^[3]. 如图1所示, 手工特征经过激活函数ReLU后, 使用Softmax函数计算相应权重, 然后内积合并得到加权手工特征, 最后经过一层全连接网络提取更加抽象的特征. 数学表达式如下:

$ {{\boldsymbol{y}}_h} = {x_h} \otimes {\textit{Softmax}}({Re} LU({\kern 1pt} {x_h}\, )\;) $

(13)

$ {Y_h} = {W_h}{y_h} + {b_h} $

(14)

其中, ${y_h}$ 为加权手工特征, ${x_h}$ 为手工特征输入矩阵, $ \otimes $ 为矩阵内积操作. ${Y_h}$ 为全连接网络输出, ${W_h}$ 为权重矩阵, ${b_h}$ 为偏置项.

1.5 Conv-LSTM提取时空特征

如图3所示. 本文设计的Conv-LSTM模块主要由卷积神经网络和LSTM网络组成. 卷积神经网络包含两个一维卷积层, LSTM网络包含一个LSTM层. 卷积神经网络将输入数据映射到更复杂的高维模式进行空间特征提取, 提取到的空间特征作为LSTM层的输入进一步提取时序特征, 两种特征经过全连接层获取抽象特征后, 通过concatenate函数实现特征融合, 得到输入数据的时空特征. 不同于独立使用卷积神经网络和LSTM网络分别提取空间特征和时序特征, Conv-LSTM整体处理输入信息, 更有效地捕获时空特征, 有利于提高RUL预测精度.

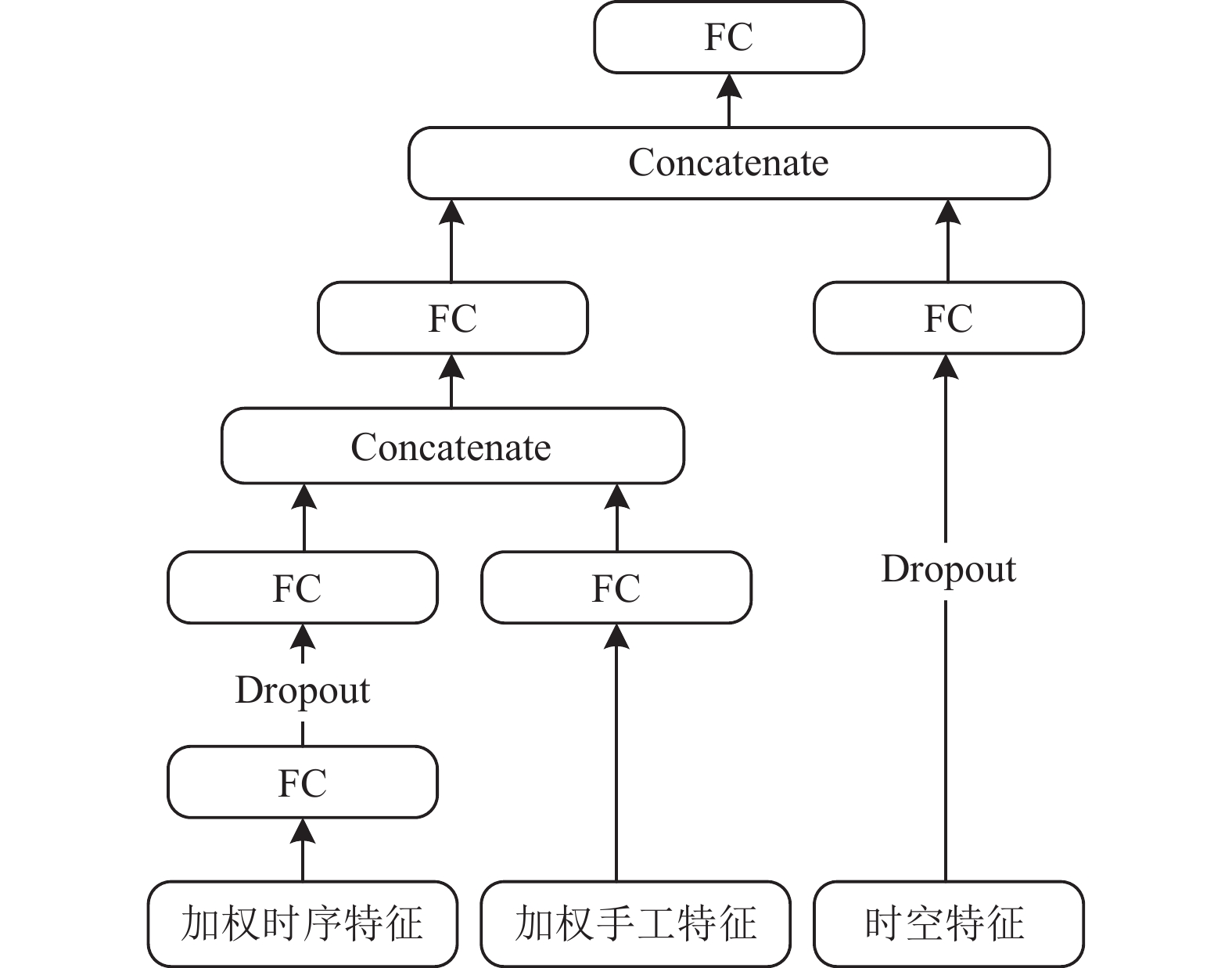
1.6 特征融合框架

本文构建的特征融合框架如图4所示. 加权时序特征和加权手工特征经过全连接网络获取抽象特征后通过concatenate函数实现特征融合, 然后融合特征再经过一层全连接网络来获取抽象特征. 时空特征通过一层全连接网络获取抽象特征后, 使用concatenate函数实现与时序特征和手工特征的融合.

2 实验及结果分析 2.1 数据集

模型使用由NASA提供的商用模块化航空推进系统仿真(C-MAPSS)数据集进行仿真验证. C-MAPSS数据集模拟了航天发动机的退化过程, 被广泛用于以往的RUL预测研究中^{[1, 3,12]}. C-MAPSS数据集由4个不同工作条件和故障模式下的子数据集组成, 每个子数据集又可以进一步分为训练集和测试集. 训练集记录了一定数量的航空发动机从正常到发生故障的全部飞行周期内的传感器状态参数. 测试集记录了一定数量的发动机在特定运行周期内的传感器状态参数, 测试集主要用于评估模型的RUL预测能力. C-MAPSS数据集基本信息如表1所示.

数据集中每条数据由发动机编号、当前飞行循环数、3个操作条件和的21个传感器状态参数组成. 传感器状态参数包括低压压缩机进气道总温度、高压压缩机出口处总压力、物理风机转速、核心机物理转速、高压压缩机出口静压等各种航空发动机状态信息.

2.2 数据预处理

对于21个传感器状态参数, 传感器编号为1, 5, 6, 10, 16, 18和19在运行到故障的全过程中具有恒定的值, 这些传感器状态参数与发动机退化无关, 所以将这些传感器状态参数移除^[17]. 剩余的14个传感器状态参数稳定性差, 噪声多, 使用指数平滑法对其进行降噪. 指数平滑法数学表达式如下^[18]:

$ \alpha = \frac{2}{{1 + s}} $

(15)

$ \left\{ {\, \begin{array}{*{20}{l}} {{y_0} = {x_0}, \quad \qquad\qquad\qquad t = 0 \quad } \\ {{y_t} = \frac{{\displaystyle\sum\limits_{i = 0}^t {{{(1 - \alpha )}^i}{x_{t - i}}} }}{{\displaystyle\sum\limits_{i = 0}^t {{{(1 - \alpha )}^i}} }}, \quad \quad t \gt 0} \end{array}} \right. $

(16)

其中, $ \alpha $ 为衰减因子, $ s $ 为范围跨度, $ {y_t} $ 为t时刻观测值, ${x_t}$ 为t时刻真实值, $ {y_{t - 1}} $ 为t−1时刻观测值.

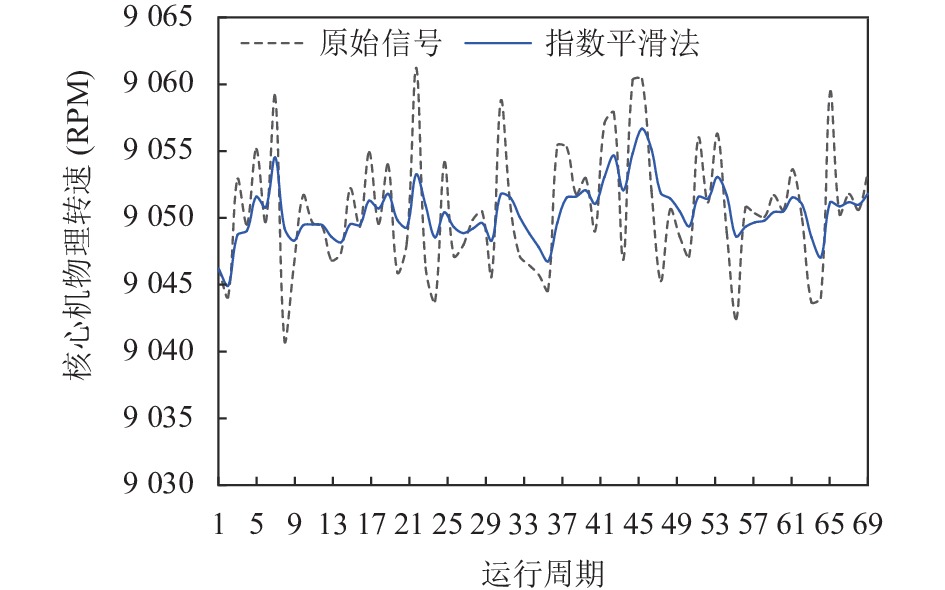
图5为指数平滑法效果图, 数据来源为FD001数据集中1号发动机的9号传感器前70次运行周期.

由图5可知, 指数平滑法不仅可以保留原始数据的变化趋势, 还可以对原始数据进行降噪平滑处理, 是一种有效的时序数据降噪技术^[18].

各类传感器状态参数具有不同的量纲, 会影响到RUL预测结果, 为了提高模型的收敛速度和预测精度, 使用max-min归一化法对传感器状态参数进行归一化处理. 采用窗口大小为30, 步长为1的滑动窗口方法对数据集进行数据分割得到输入时间窗序列^[3]. 然后为每个窗口添加RUL标签, 时间窗RUL标签定义为:

$ RUL_{{i}}^j = {\rm{min}}\, \left\{ {\, {m^j} - m_{{i}}^j\;, \;130\, } \right\} $

(17)

其中, $ RUL_i^j $ 代表第j个发动机的第i个窗口的剩余可用寿命, $ {m^j} $ 代表第j个发动机的整个生命周期, $ m_i^j $ 代表第j个发动机的第i个窗口的最后一周期. 由于早期航空发动机退化并不明显, RUL的最大值设置为130^{[3, 18]}. 计算每个窗口的手工特征并使用Softmax函数分配权重, 然后对其进行标准化处理.

2.3 评价指标和损失函数

本文采用两个常用的评价指标: 均方根误差(RMSE)和非对称评分函数 (Score)来评估模型的性能. 均方根误差可很好地反映预测的精密度. 数学表达式如下^{[19, 20]}:

$ {\textit{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {({{\hat r}_i} - {r_i})} } $

(18)

其中, $ N $ 为样本总个数, $ {\hat r_i} $ 为预测值, $ {r_i} $ 为真实值.

非对称评分函数是一个保守且安全的评价函数, 能够对早期预测和后期预测产生不同的惩罚结果. 如果预测RUL大于真实RUL, 惩罚将更大, 因为这种情况会导致更严重的后果. 相反, 当预测RUL小于真实RUL时, 惩罚会更小. 数学表达式如下^{[19, 20]}:

$ {\textit{Score}} = \left\{ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{{{i}} = 1}^N {({{\rm{e}}^{ - \frac{{{{\hat r}_i} - {r_i}}}{{13}}}} - 1)\;, \;\;\;\;\;{\rm{if}}\;\;{{\hat r}_i} - r \lt 0} } \\ {\displaystyle\sum\limits_{{{i}} = 1}^N {({{\rm{e}}^{\frac{{{{\hat r}_i} - r}}{{10}}}} - 1)\;, \;\;\;\;\;{\kern 1pt} \, {\rm{if}}\;\;{{\hat r}_i} - r \geqslant 0} } \end{array}} \right.\, $

(19)

本文采用的损失函数为MSE, MSE可以反映预测数据和真实数据之间的差异程度, 数学表达式如下:

$ {\textit{MSE}} = \frac{1}{N}\sum\limits_{{{i}} = 1}^N {({{\hat r}_i} - {r_i})} $

(20)

2.4 使用FD001数据集进行对照实验和消融实验

使用FD001数据集进行对照实验和消融实验, 训练集和测试集经过预处理后可以获得17 731个训练样本和100个测试样本.

本文模型通过提取特征数据的时序特征(TF), 手工特征(HF)和时空特征(TSF) 这3种特征来提高RUL预测精度. 不同的特征融合顺序对RUL预测结果有着不同的影响, 建立4种不同特征融合顺序模型进行对照实验, 实验结果如表2所示.

由表2可知, 4种不同特征融合顺序模型在第一次迭代时RMSE值和Score值差距较大, 但是最优结果差距相对较小. 对照实验1具有较高的RUL预测精度和较少的迭代次数, 所以将对照实验1的特征融合顺序确定为本文模型特征融合顺序.

为了更好地评价ES降噪模块, Multi-attention模块, Bi-LSTM模块和Conv-LSTM模块的有效性, 对本文模型进行消融实验, 实验结果如表3所示.

由表3可知5种模型预测精度差距较小, 均有着较高的预测精度. 通过模型之间对比可知, ES模块和Bi-LSTM模块可以显著减少模型构建所需的迭代次数, 提高了模型的收敛速度, 对提升模型预测精度具有积极意义. Multi-attention模块有利于提升模型的预测精度, 但是对于减少模型构建所需迭代次数的效果并不明显. Conv-LSTM模块不仅可以减少模型构建所需的迭代次数, 还可以提升模型预测精度.

使用FD001数据集对模型进行30次迭代训练, 模型训练过程中测试集RMSE值和Score值的变化情况如图6所示.

由图6可知, 测试集RMSE值在模型第8次迭代后获得最小值, 值为12.38, 在之后的迭代过程中虽有波动, 但总体趋于平稳. 测试集Score值在模型第18次迭代后获得最小值, 值为216.72, 在之后的迭代过程中变化较为曲折.

2.5 参数设置

模型中Conv-LSTM模块和Bi-LSTM模块的具体结构和参数设置如表4所示. 表4中K和N分别代表卷积核的大小和个数.

模型中使用的Multi-attention模块主要超参数设置如表5所示.

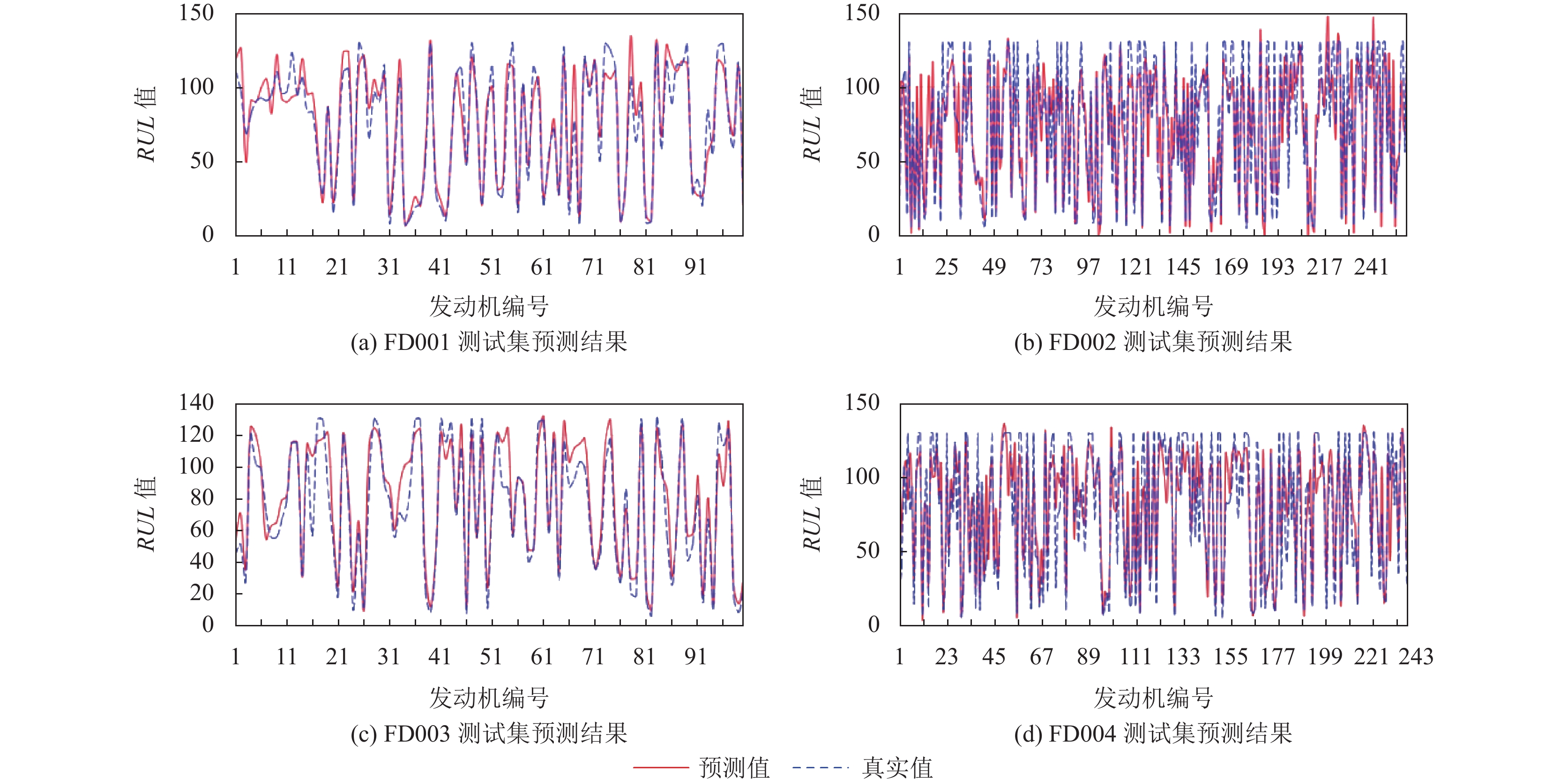
3 实验结果

图7展示了该模型在C-MAPSS的4个子集上的RUL预测结果对比. 如图7所示, 发动机RUL预测值分布在真实值附近, 预测精度较高. 尤其在RUL真实值较小的点, 预测值与真实值更加贴近, 差距更小. 这意味着当发动机临近故障时, 该模型能够更加充分的提取故障特征, 可以更准确捕捉到提前预测的相关特征, 具有较强的预测能力和较高的可行性.

对该模型进行10次实验, 获得 RMSE 和 Score 的平均实验结果, 然后与其他模型进行比较, 对比结果如表6所示. 由表6可知, 在FD001, FD002和FD004三个数据集中, 本文模型的RMSE和Score均要优于所有对比模型. 在FD002和FD004数据集上RMSE和Score有着显著降低, 这表明本文模型在复杂环境下仍然可以精确预测航空发动机RUL, 模型适应性更好. 在FD003子集中RMSE略差于MODBNE, Score差于Bi-LSTM, 但是模型仍表现出较高预测精度. 该模型通过对原始数据降噪平滑处理和引入Multi-attention提高学习特征的利用率, 减少了模型构建所需迭代次数, 缩短了模型训练时间, 得到误差较低, 精度较高的预测结果. 表明该方法能自适应学习航空发动机退化序列的特点, 提高航空发动机RUL预测准确性.

4 结论与展望

本文提出一种基于多特征融合的航空发动机RUL预测模型. 模型利用ES对原始数据进行降噪平滑处理, 提高了模型对航空发动机数据中显著特征的敏感性, 减少了模型迭代次数. 使用Multi-attention为Bi-LSTM各个时间步长中获得的学习特征分配权重, 充分利用模型构建中学习到的特征, 解决了学习特征利用率较低的问题. 设计Conv-LSTM模块挖掘高维模式下航空发动机数据的时空特征, 提高了模型RUL预测精度. 根据传感器数据特点进行预处理, 提取航空发动机数据的手工特征为RUL预测提供不同重要程度的额外信息. 使用C-MAPSS数据集对模型进行仿真验证, 并与其他模型进行比较, 实验结果表明该模型预测精度更高, 适应性更好, 综合性能优于其他模型, 有着更好的应用前景.

该模型虽然迭代次数较少, 但是每次迭代运行时间较长, 未来工作将在保证RUL预测精度的基础上, 通过简化模型缩减每次迭代运行时间, 并且尝试减少神经元之间复杂的共适应关系, 提高模型的泛化能力.