日益庞大、复杂、隐蔽的网络威胁严重影响着网络安全, 诸如入侵检测、恶意病毒检测等技术并不能够全面且有效地分析预测网络的安全发展趋势. 继1988年态势感知技术的提出, 网络安全态势感知技术也随之被提出, 后续由最初的军事应用逐渐推广到不同场景的网络安全防护应用中. 网络安全态势感知是一种利用网络安全要素分析与预测未来网络安全状态的方法, 广泛地应用于军事、政务部门、企业等网络的安全防护研究中. 网络安全态势感知基于网络环境中相关要素的属性、状态和动态等信息, 从全局视角分析与预测网络未来的安全趋势, 从而能够未雨绸缪, 实现防患于未然. 现在针对网络安全态势研究的方法非常多[1-5], 主流的有基于攻击图、博弈论、马尔可夫模型、深度学习和神经网络等网络态势研究[6-8]. 近年来又出现了基于生物流行病传播模型的网络安全态势感知研究, 经典的模型有SI、SIS和SIR模型[9-11].
现有基于生物流行病传播模型的网络安全研究中大部分是针对一类或指定计算机病毒进行探索, 并且在这些方法的模型中, 很多没有考虑实际网络中设备之间的差异性、攻击方法的多样性和网络动态变化的特征, 导致模型的动力学传播方程和模型的结构设计不够灵敏, 与实际情况贴合度不够. 针对上述问题本文提出了SIPM模型, SIPM模型支持多种病毒在网络中独立传播, 网络中每个节点都具备记忆存储空间, 用于记录不同攻击的详细信息和该节点的安全状态信息, 同时, 每个节点都可以设置独立的参数模拟病毒攻击取得成功的概率, 模型的攻击传播方程在考虑上述因素的基础上, 还将无标度网络的幂律特征考虑在内. 最后, 在一种典型的校园网网络拓扑上进行仿真实验, 实验结果证明了SIPM模型可以在指定时间内, 对网络中病毒的传播过程进行模拟, 实现网络安全态势的预测.
1 相关工作流行病传播模型是应用在复杂网络中, 专门研究生物传播、社交传播和数字传播的一种方法. 计算机网络系统是一种度分布符合幂律分布的复杂网络, 网络中的攻击属于数字传播的一种, 因而使用流行病传播模型分析网络的安全态势切实可行, 现已有一部分学者在这个方面展开了研究.
在国内相关研究中, 王刚等[12]研究了多操作系统异构网络中的病毒传播规律及安全性能优化策略, 在SIRS病毒传播模型中引入异构边比例参数, 通过系统平衡点求解和基数再生分析, 研究了异构边对单系统病毒传播和网络安全性能的影响, 在此基础上设计了非异构边随机中断、非异构边随机重连和单操作系统节点随机跳变3种网络安全优化策略. 王刚等[13]针对新型潜伏病毒的传播特性, 研究了潜伏机制下的网络病毒传播模型及其稳定性. 首先分析了处于潜伏状态的网络节点存在的3种转换模式, 提出了潜伏机制下的网络病毒传播模型, 其次运用劳斯稳定判据, 论证了网络病毒传播平衡点的局部稳定性, 最后给出了潜伏状态下3种转移参数对系统稳定性影响的仿真验证. 伍志韬等[14]针对电网中信息域的恶意攻击极有可能传播至物理域的问题, 基于电网CPS耦合架构框架研究了电网跨风险域传播的基本形式, 提出了一种基于复杂网络的电网风险传播模型, 并给出了风险评估指标. 通过构建IEEE-118总线系统为物理域的耦合电网场景, 仿真模拟该场景下遭受恶意攻击的风险传播模型, 同时讨论了风险扩散率、初始攻击点等因素对风险传播的影响. 李妍等[15]针对恶意软件对工控网络安全造成严重威胁的问题, 提出了应用于工控网络中3种不同的SUIR模型, 并对其无病平衡点和地方病平衡点的稳定性进行了推导证明. 在此基础上分别对3种模型进行了数值实验, 实验结果表明兼备打补丁和主动查杀功能的良性蠕虫具有最好的防御效果.
在国外相关研究中, Yao等[16]发现工业控制系统的可编程控制逻辑器(PLC)缺乏网络安全方面的考虑, 随着工业控制系统(ICS)网络攻击的爆发, 一种可以在Internet和ICS网络之间传播的PLC-PC蠕虫会对网络安全造成严重威胁. 针对此问题, Yao等[16]在SIR流行病传播模型基础上, 首次提出了一个研究PLC-PC蠕虫在PLC-PC耦合网络中传播行为的模型, 该模型理论分析了具备防御措施网络的“无病均衡”和“地方病平衡”特点, 模拟实验说明了该模型的有效性. Zhou等[17]发现恶意软件在无线传感器网络传播研究中, 传统的恶意软件传播模型较少考虑攻击和防御过程对恶意软件传播结果的影响, 针对此问题, Zhou等[17]从博弈论角度分析了恶意软件在无线传感器网络中传播的微观机理, 建立了无线传感器网络的攻防博弈模型, 推导了该模型的混合纳什均衡解, 并据此推导出恶意软件在无线传感器网络中的传播模型. 同时通过对理论模型的分析, 推导出稳态感染率与博弈参数之间的关系, 得到了恶意软件长期存在的条件. Masood等[18]发现可移动存储介质在向连接到关键网络的计算机传输数据时有传输病毒的风险, 因此建立了一个流行病传播模型, 该模型研究震网病毒(Stuxnet)在正常局域网和一个关键网络之间的传播. 在该模型基础上, Masood等[18]研究了无病平衡和地方病平衡的特点, 同时利用李雅普诺夫函数分析了无病平衡点和地方病平衡点的全局稳定性, 在数值模拟分析中验证了模型的准确性.
上述研究模型都是针对特定网络环境进行分析与设计, 在一般的传统网络中流行病模型也有相应研究. Upadhyay等[19]引入了攻击类和目标类两种不同的框架模型, 用基本再生数等价地讨论了平衡点的存在性和稳定性. 同时还引入了最优控制概念, 提出了一种控制病毒传播的措施, 在数值实验中, 通过敏感性分析得出了决定病毒在网络中传播的相关性参数. Da等[20]发现在网络攻击建模研究中, 大多数研究都没有考虑到同时或协同攻击, 而协同攻击实际上是现实网络中一种重要的攻击手段, 针对此问题, Da等[20]提出了一个可以容纳不同类型攻击同时进行攻击的新模型, 同时研究了流行病在网络上消亡的条件及消亡的上界, 验证了攻击强度和成功攻击概率异质性对攻击传播的影响. 这两类模型均针对网络攻击在一般传统网络中的传播, 对网络安全态势的影响进行了分析.
以上只是众多研究中较为典型的几类研究, 从这些研究中可以发现, 大多数研究都是在研究针对一类攻击的网络建模, 极少数研究会涉及几种类型攻击的网络建模, 本文在这些研究的基础上, 根据实际网络攻击状况进一步研究了不限攻击类型、可以同时进行攻击模拟的传播模型.
2 SIR模型介绍SIR流行病传播模型在1927年由Kermack等[21]发表, 后逐渐发展成为现在主流的传染病传播模型之一, SIR模型的研究对象通常为复杂网络, 在介绍SIR模型之前, 先对复杂网络进行介绍. 复杂网络是由真实系统通过高度抽象得到的具有复杂结构和特性的网络, 它是一种特殊的网络结构, 将复杂系统中的元素抽象为节点, 元素间的关系抽象成连边[22-24]. 钱学森对复杂网络给出的定义是: 具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络. 复杂网络需要满足3个特征.
(1) 小世界特性: 网络中点与点之间的特征路径长度值接近随机网络, 但网络的聚合系数接近规则网络.
(2) 无标度特性: 在网络中少数节点的度值会很大, 而大部分节点的度值很小, 节点的度值分布符合幂律分布规律.
(3) 社团结构特性: 复杂网络的节点通常呈现出集群特性, 社团区域内部节点之间的联系非常强, 而社团内节点与社团外节点的联系明显减弱.
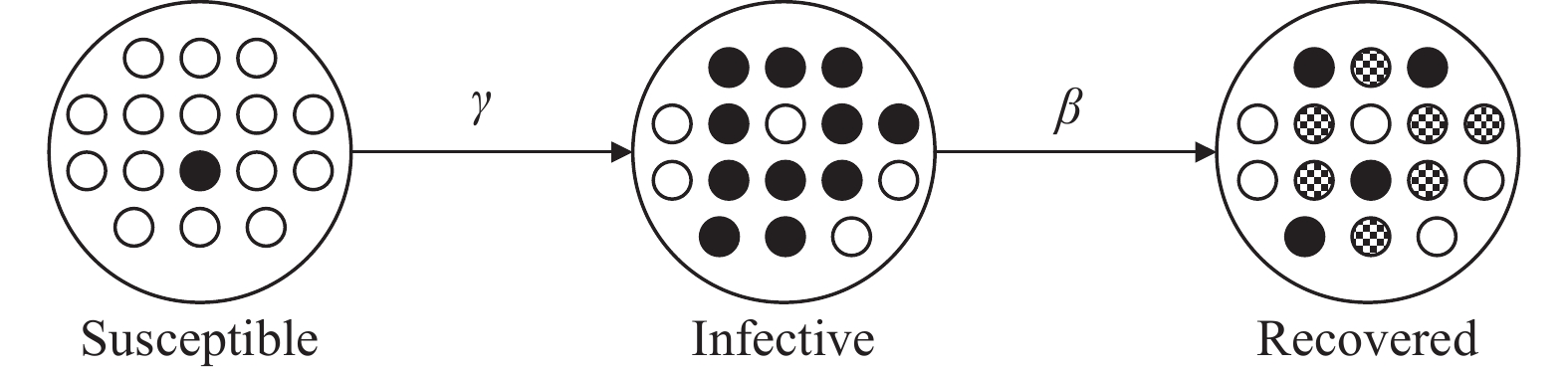
SIR模型是对流行病传播过程的模拟, SIR模型中根据个体感染病毒前后的不同状态, 将人群划分为3类: 未感染病毒但有概率被感染的人群(susceptible), 已经感染病毒并具有传染性的人群(infective), 感染病毒康复后具有免疫能力的人群(recovered)[25-28]. SIR模型如图1所示, 不同人群中, 白色圆形代表未感染病毒个体, 黑色圆形代表感染病毒个体, 内有实线填充圆形代表康复个体, 模型中有两个重要的假设条件:
(1) 假设1: 认为每个个体将以相同的概率接触已感染个体, 即任何人都可以感染其他人.
(2) 假设2: 从已感染状态恢复的个体将具备对病毒的永久免疫力, 即永久不会再次被感染.
|
图 1 SIR模型示意图 |
在不考虑个体之间差异的基础上, 引入病毒传播的感染系数γ和恢复系数β(通常称作感染率和康复率), 易感人群、已感人群和康复人群的数量分别用S,I和R表示, 可以建立起SIR的数学模型. 根据病毒传播过程中不同人群数量变化的关系, 可以得到式(1), 其中N为总的人群数量. 在Δt时间内, 易感人群数量的减少如式(2)所示, 康复人群数量的增加如式(3)所示, 感染人群数量的变化如式(4)所示:
| S+I+R=N | (1) |
| ΔS=−S×γΔt | (2) |
| ΔR=I×βΔt | (3) |
| ΔI=S×γΔt−I×βΔt | (4) |
在N恒定不变条件下, 使用无量纲参数
| dSdτ=−R0SI | (5) |
| dIdτ=R0SI−I | (6) |
| dRdτ=I | (7) |
从约化后的公式中可以得到一个重要的常量
通过上述介绍可以发现, SIR模型的关注点是某一类病毒的传播分析, 通过将感染人群划分为不同的安全状态, 研究分析不同状态群体的转换过程. 但该方法并不完全适用于计算机网络病毒传播研究中, 主要原因有3点: 首先, 计算机网络中设备的类型、属性等因素远比人类群体要多样化, 因此原模型安全要素的考量需要增加; 其次, 计算机网络中攻击类型多种多样, 要实现安全态势感知需要同时针对多目标进行跟踪分析, 故原模型的整体架构需要重新设计; 最后, 原模型认为人群个体具有同等性, 这并不符合计算机网络中的实际情况, 计算机网络不同设备具有不同的静态和动态属性, 并且计算机网络整体的运行状态也是动态的, 因此需要改进原模型的建模方程式, 使其更加贴近计算机网络实际情况.
计算机网络中病毒的传播与生物传染病传播类似, 不同设备都有一定的概率感染病毒, 也有一定的病毒查杀能力, 计算机网络的结构特性与传染病传播的生物网络结构特性具有相似性, 所以SIR模型同样适用于计算机网络, 用以分析病毒传播对网络安全态势造成的影响. 但在经典SIR模型中, 假设所有个体染病概率和康复概率都是相同的, 这并不符合实际情况, 实际中不同个体因为自身和环境因素, 染病概率和康复概率是不同的, 同时模型中也缺乏人为干预措施, 与实际情况相差较大. 所以该模型实现精确预测还需要对模型结构进行调整和创新, 使其尽可能符合实际应用场景.
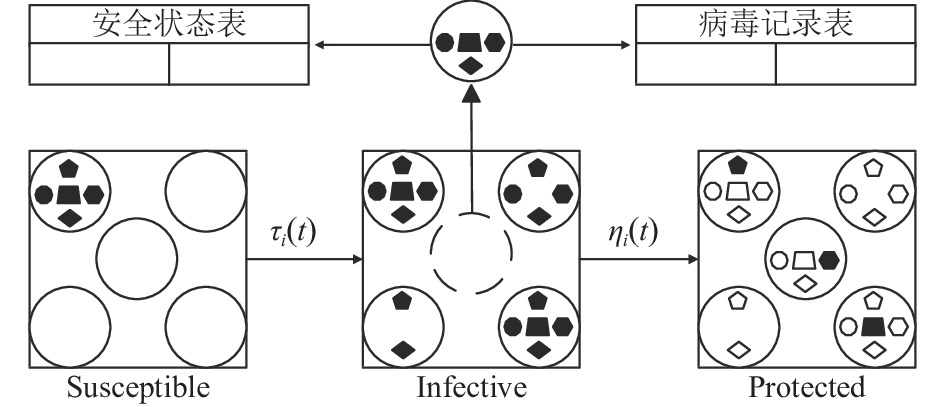
3 SIPM网络安全态势分析模型 3.1 模型设计本文提出的SIPM模型是基于SIR模型的改进, 模型架构如图2, 其中正方形内最大的正圆代表不同网络设备个体, 每个正圆中不同的图形代表不同病毒, 黑色表示该病毒处于存活状态, 白色表示该病毒已被消杀. 模型由3类群体组成: 未感染任意一种病毒但有概率被任意一种病毒感染的易感网络设备群体(suscep-tible)、感染了任意一种病毒的已感网络设备群体(infec-tive)、感染了一种及以上病毒并已经完成对至少一种病毒永久免疫的被保护网络设备群体(protected), 该模型还增加了对已感病毒的记忆功能(memory). 本文提出的模型具备以下3个特点.
|
图 2 SIPM模型架构图 |
(1) 模型支持多种病毒同时在网络中进行传播, 多种病毒的传播过程各自独立进行, 互不影响.
(2) 模型中每个设备个体不再被同等看待, 不同设备个体对同一种病毒的防御能力不同, 对不同种类病毒的防御能力也不同, 同时受设备的安全防护措施和所处环境的影响, 病毒对每个设备个体的感染能力各不相同.
(3) 模型中每个设备个体具有记忆功能, 可以记录所感染病毒的传播路径、存活状态等详细信息, 同时也可以记录设备个体实时的安全状态信息, 记录病毒详细信息的病毒记录表各表项内容如表1所示, 记录个体安全状态信息的安全状态表各表项内容如表2.
| 表 1 病毒记录表参数说明 |
| 表 2 安全状态表参数说明 |
受模型结构变化的影响, SIPM的数学模型也需要进行调整. 引入S表示易感群体设备的数量, I表示已感群体设备的数量, P表示受保护群体设备的数量, N表示计算机网络中设备的总数量, 病毒传播过程中不同群体数量的变化遵循式(8). SIPM模型中每个设备个体在t时刻具有不同的感染系数
| S+I+P=N | (8) |
| τi(t)=N∑m=1(−1)m+1Sm | (9) |
| ηi(t)=G∑k=1(−1)k+1Ik | (10) |
| Sm=∑1⩽m⩽NP(τ1iτ2i⋯τmi) | (11) |
| Ik=∑1⩽k⩽GP(η1iη2i⋯ηki) | (12) |
在一段时间Δt内, 根据式(9)和式(10), 可以推导出易感群体设备数量的减少如式(13)所示, 被保护群体设备数量的增加如式(14)所示, 已感群体设备数量的变化如式(15)所示, 其中S和I分别代表易感群体和已感群体的设备数量,
| ΔS=−∑S⌊N∑m=1(−1)m+1Sm+(1−ρ)⌋⋅Δt | (13) |
| ΔP=∑I⌊G∑k=1(−1)k+1Ik+(1−ϖ)⌋⋅Δt | (14) |
| ΔI=∑S⌊N∑m=1(−1)m+1Sm+(1−ρ)⌋⋅Δt−∑I⌊G∑k=1(−1)k+1Ik+(1−ϖ)⌋⋅Δt | (15) |
| dSdt=−∑S⌊N∑m=1(−1)m+1Sm+(1−ρ)⌋ | (16) |
| dPdt=∑I⌊G∑k=1(−1)k+1Ik+(1−ϖ)⌋ | (17) |
| dIdt=∑S⌊N∑m=1(−1)m+1Sm+(1−ρ)⌋−∑I⌊G∑k=1(−1)k+1Ik+(1−ϖ)⌋ | (18) |
最后, 根据上述模型公式的推导, SIPM模型中个体状态转换如下,
If
| Nti={NS,withprobability1−τi(t)NI,withprobabilityτi(t) | (19) |
If
| Nti={NI, with probability 1−ηi(t)NP, with probability ηi(t) | (20) |
If
| Nti=NP | (21) |
得益于SIPM模型对病毒的记忆功能, 可以根据病毒传播路径的长度C和传播时间, 对病毒的传播效率进行计算与评价, 此评价对应于设备节点病毒记录表的“evaluate”表项. 病毒传播效率评价如式(22)所示, 其中, V表示病毒传播的效率, C对应病毒记录表的“counter”表项, N是网络中设备节点的总个数, 病毒的传播时间等于当前节点病毒被发现并记录的时间
| V=CN⋅(ts−te⌈ts−te24⌉×24)−1 | (22) |
网络中单个设备节点的安全程度E的评估如式(23)所示, 在单个设备节点中, 存活的病毒越多说明该节点越容易遭受病毒的攻击, 用存活的病毒数
| E=nan⋅nsna=nsn | (23) |
网络安全态势的分析基础是不同设备节点的安全状态, 根据关注点不同, 可以从以下3个方面分析网络安全态势.
(1) 高危节点占比分析: 网络中个别高危(感染多种高传染性病毒)设备节点可以通过隔离或针对性查杀等手段, 消除其对全局网络的安全影响, 因而不会对整体网络安全造成严重影响, 当高危节点占比到达设定阈值
| θ=∑IiN | (24) |
| Ii={1,V⩾αandE⩾ε0,V<αandE<ε | (25) |
| SN={safe,θ<δdanger,θ⩾δ | (26) |
(2) 核心节点沦陷分析: 网络中有一些重要的核心设备节点, 如核心交换机、数据中心存放重要数据的服务器等(在设备节点安全状态表中以“imp_level”字段标识), 这些设备安全评估值E一旦达到设定阈值
| SD={safe,E<ψdanger,E⩾ψ | (27) |
(3) 网络鲁棒性分析: 因计算机网络近似服从幂律分布, 使用BA无标度网络的一些分析手段可以分析网络的鲁棒性. 网络中部分普通设备节点在通信过程中发挥着重要作用, 当这些节点感染病毒发生故障后, 可能会导致网络变为非连通状态等后果, 影响网络的鲁棒性能. 使用接近中心性C(u)衡量节点的重要程度, 计算公式如式(28)所示, u为待计算接近中心性的点, N为网络中所有节点, d(u, v)是节点v和节点u之间最短的距离, 在SIPM模型中是两个设备节点之间的跳数. 当一个设备节点的C(u)达到设定阈值
| C(u)=1∑Nv=1d(u,v) | (28) |
| SP={safe,C(u)<κ,E<ψdanger,C(u)⩾κ,E⩾ψ | (29) |
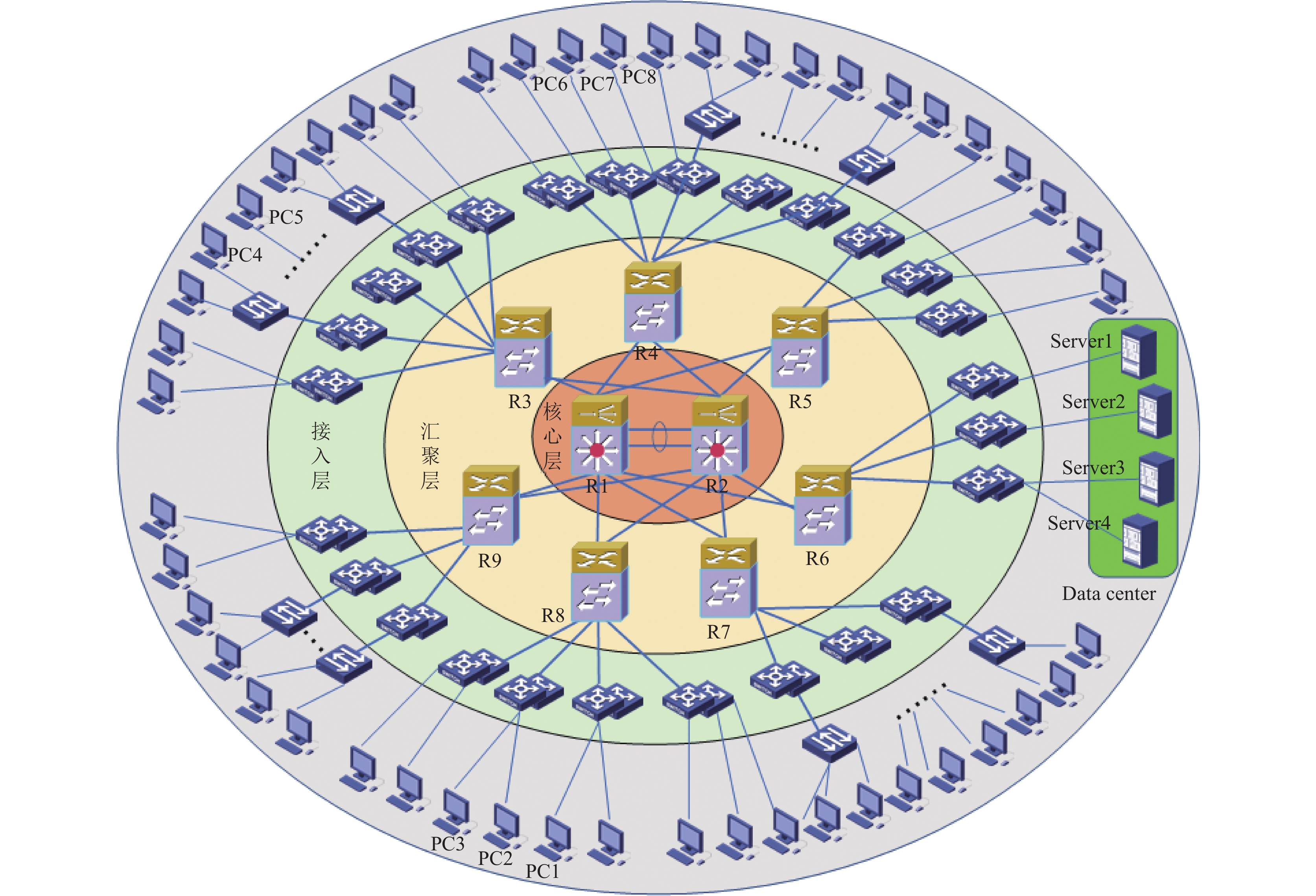
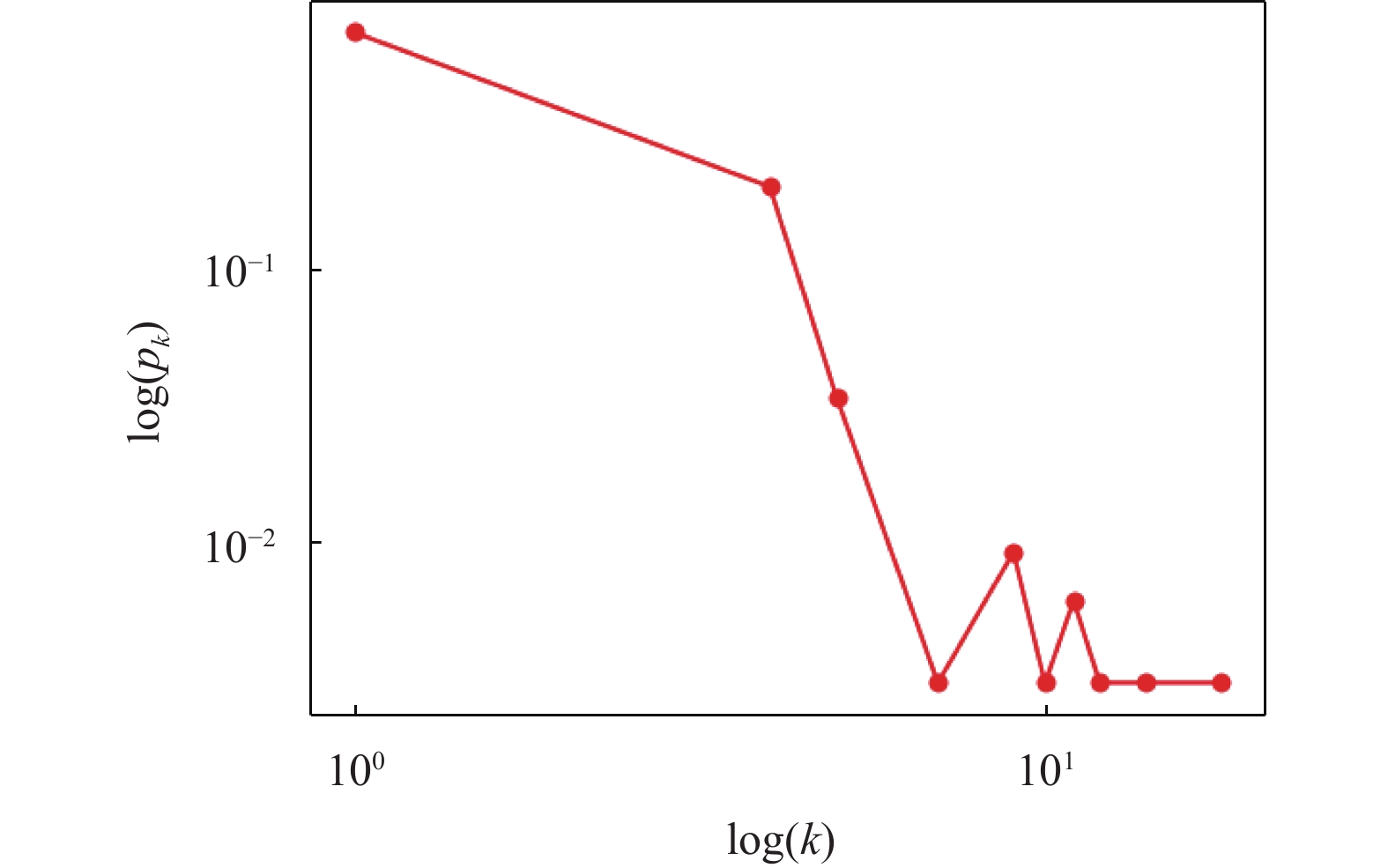
模拟实验采用了一个典型的校园网拓扑, 包含核心交换设备、校园运行所需重要机器设备和一些普通的设备, 如图3所示. 该网络中设备节点的度分布近似服从幂律分布, 可从图4的双对数坐标轴下度分布统计图看出, 横坐标代表网络节点度的对数形式, 纵坐标代表不同度在整个网络中占比的对数形式. 网络中不同节点的重要程度、安全防护系数等参数根据实际情况分别进行了设置, 部分重要节点的参数设置如表3所示, 其中“设备角色”代表设备在网络中所承担的任务, “imp_level”代表设备在网络中的重要程度, “pro_efficiency”代表设备有多大概率抵御不同病毒的攻击.
|
图 3 校园网络架构拓扑图 |
|
图 4 网络拓扑度分布统计图 |
实验中设置了6种病毒(分别以CIH、T-DDoS、T-Q34、W-aS、S.R、HCK表示)在网络中同时传播. 6种病毒在网络传播中部分重要节点参数的设置如表4所示, “病毒”列表示不同病毒在实验中的代号, “说明”列说明了具体病毒名称, “感染效率(
| 表 3 重要设备节点参数设置列表 |
| 表 4 病毒传播参数设置列表 |
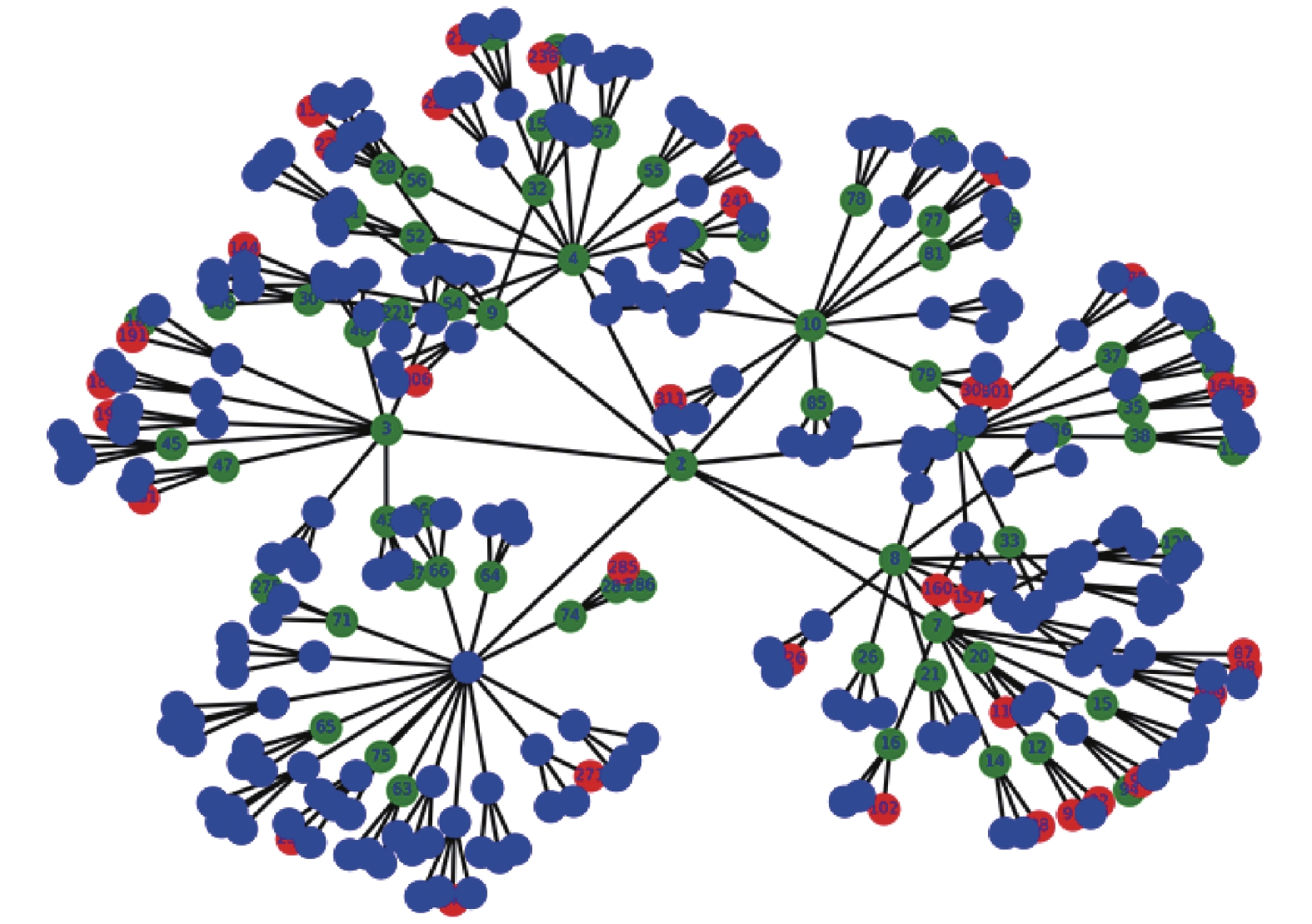
|
图 5 网络中无主动查杀措施安全态势预测图 |
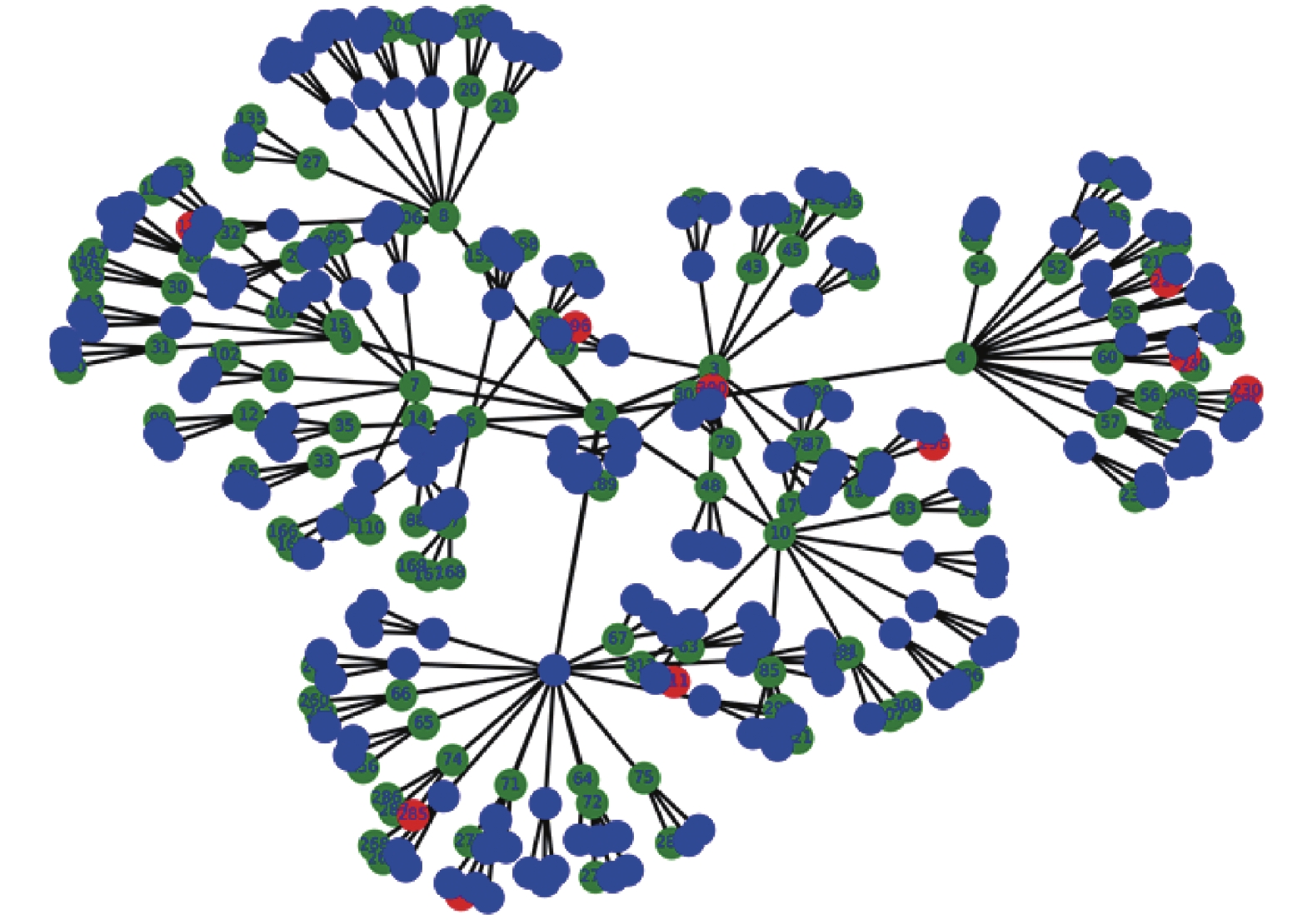
|
图 6 网络中有主动查杀措施安全态势预测图 |
4.2 高危节点占比分析
设置安全告警阈值
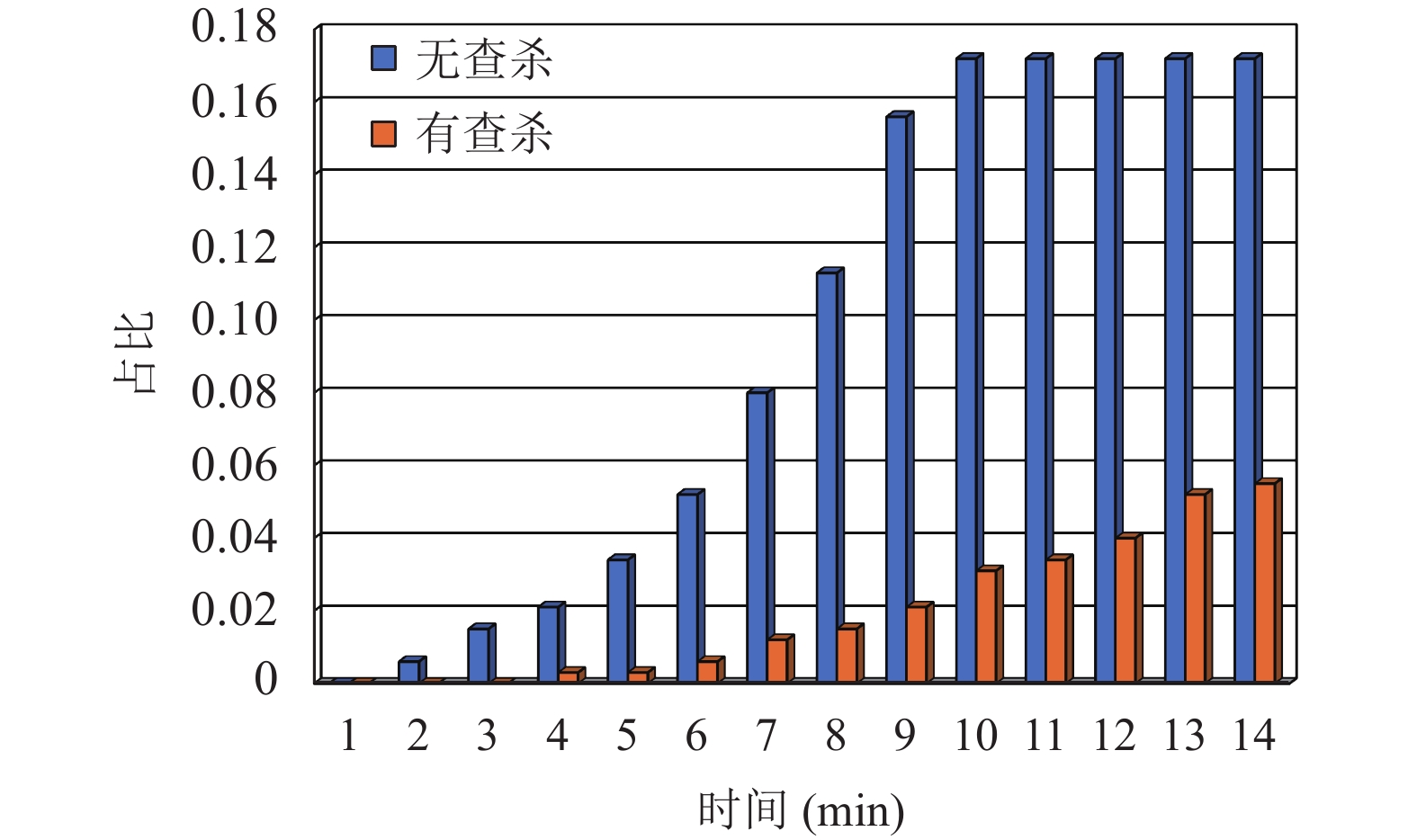
|
图 7 高危节点占比统计图 |
4.3 核心节点沦陷分析
设置阈值
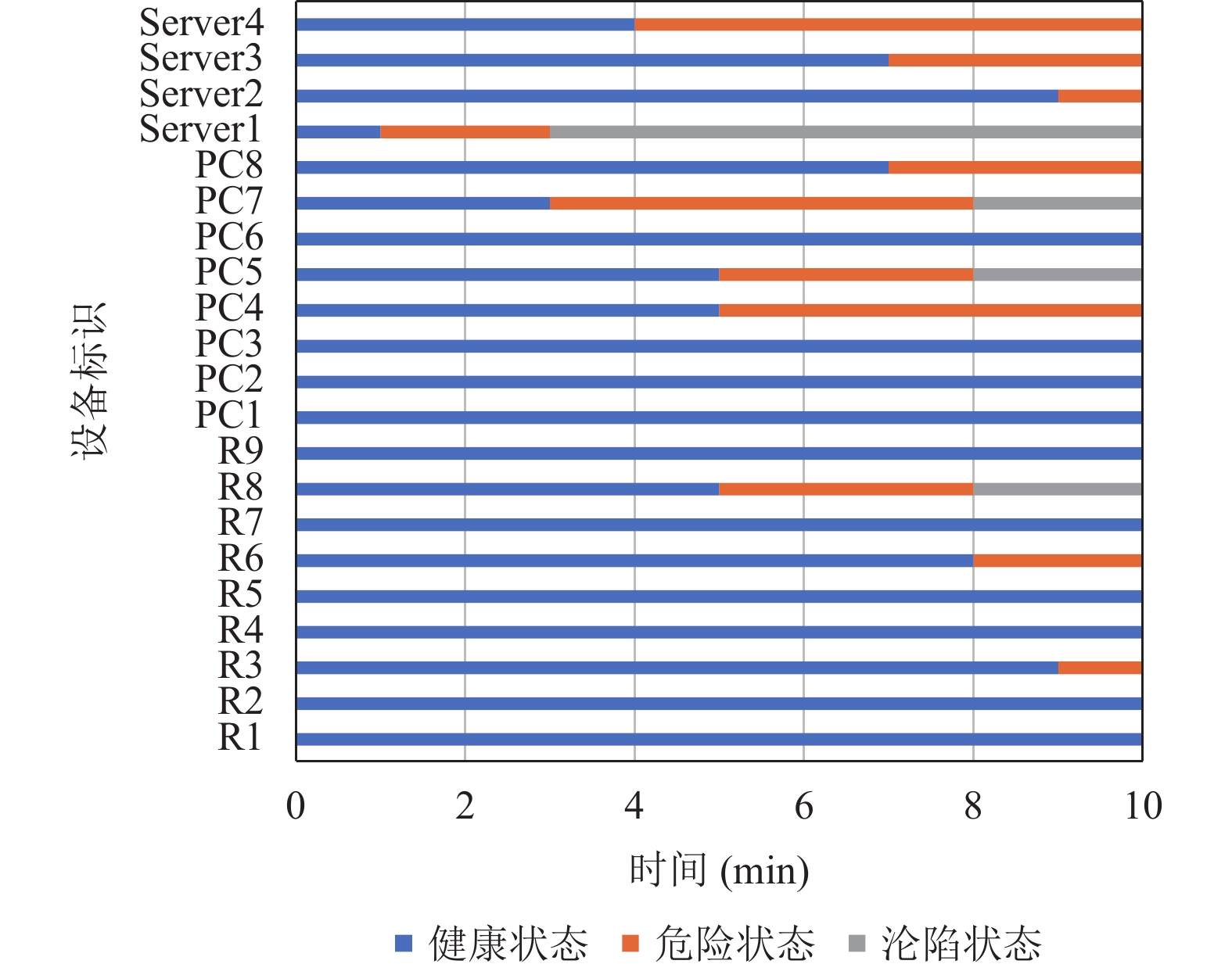
|
图 8 重要设备节点安全状态变化图 |
4.4 网络鲁棒性分析
设置阈值
| 表 5 C(u)>κ设备节点评估信息表 |
5 结论与展望
在本研究中, 主要研究了多种病毒在计算机网络中的传播过程及其对网络安全造成的影响. 在SIR模型基础上, 引入了记忆功能, 使得新模型可以同时容纳多个病毒在网络中传播, 同时改进了动力学传播方程, 支持病毒传播过程中节点的感染概率和病毒防御性能独立设置与变化. 通过仿真分析验证了本文提出的模型可以实现对网络安全态势的分析与预测, 同时数值模拟的结果表明, 合理的网络安全防护措施有助于延迟病毒的传播过程, 也有助于抑制病毒大范围地传播, 这一现象说明本文提出的模型有助于检验网络安全防护措施部署的合理性. 在后续研究中, 将在此基础上进一步研究网络安全的防护方案, 此外, 还将考虑在真实网络中继续提升相关理论模型与实际网络现状的贴合度.
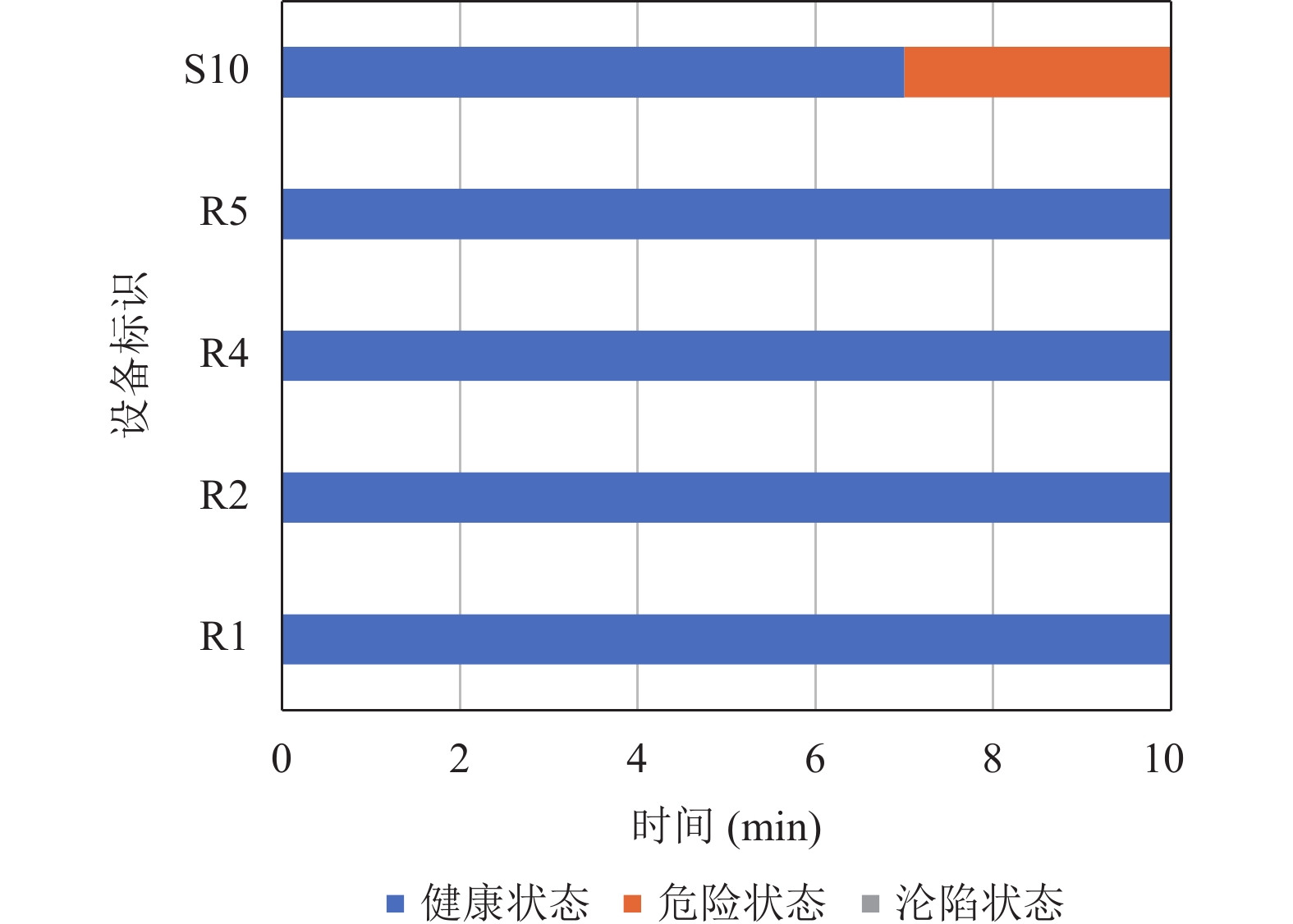
|
图 9 C(u)>κ设备节点安全状态变化图 |
| [1] |
Zaripova DA, Makhmudov AAU. Network security issues and effective protection against network attacks. International Journal on Integrated Education, 2021, 4(2): 79-85. DOI:10.31149/ijie.v4i2.1204 |
| [2] |
耿方方, 王昂. 基于量子遗传算法的网络安全态势感知研究. 计算机仿真, 2021, 38(8): 348-351, 491. DOI:10.3969/j.issn.1006-9348.2021.08.068 |
| [3] |
丁华东, 许华虎, 段然, 等. 基于贝叶斯方法的网络安全态势感知模型. 计算机工程, 2020, 46(6): 130-135. DOI:10.19678/j.issn.1000-3428.0055219 |
| [4] |
陆雨晶, 陈琳. 基于FAHP的网络安全态势感知风险评估技术研究. 计算机与数字工程, 2021, 49(5): 957-960, 976. DOI:10.3969/j.issn.1672-9722.2021.05.018 |
| [5] |
周莉, 李静毅. 基于决策树算法的联级网络安全态势感知模型. 计算机仿真, 2021, 38(5): 264-268. DOI:10.3969/j.issn.1006-9348.2021.05.054 |
| [6] |
Dass S, Datta P, Namin AS. Attack prediction using hidden Markov model. Proceedings of the IEEE 45th Annual Computers, Software, and Applications Conference. Madrid: IEEE, 2021. 1695–1702.
|
| [7] |
Ansari MS, Bartoš V, Lee B. GRU-based deep learning approach for network intrusion alert prediction. Future Generation Computer Systems, 2022, 128: 235-247. DOI:10.1016/j.future.2021.09.040 |
| [8] |
Prabakaran S, Ramar R, Hussain I, et al. Predicting attack pattern via machine learning by exploiting stateful firewall as virtual network function in an SDN network. Sensors, 2022, 22(3): 709. DOI:10.3390/s22030709 |
| [9] |
Li M, Liu RR, Lü LY, et al. Percolation on complex networks: Theory and application. Physics Reports, 2021, 907: 1-68. DOI:10.1016/j.physrep.2020.12.003 |
| [10] |
刘娜, 方洁, 邓玮, 等. 基于双层耦合网络的分数阶SIR传染病模型的稳定性分析. 数学的实践与认识, 2020, 50(20): 117-123. |
| [11] |
范如国, 王奕博, 罗明, 等. 基于SEIR的新冠肺炎传播模型及拐点预测分析. 电子科技大学学报, 2020, 49(3): 369-374. DOI:10.12178/1001-0548.2020029 |
| [12] |
王刚, 冯云, 陆世伟, 等. 多操作系统异构网络的病毒传播模型和安全性能优化策略. 电子与信息学报, 2020, 42(4): 972-980. DOI:10.11999/JEIT190360 |
| [13] |
王刚, 陆世伟, 胡鑫, 等. 潜伏机制下网络病毒传播SEIQRS模型及稳定性分析. 哈尔滨工业大学学报, 2019, 51(5): 131-137. DOI:10.11918/j.issn.0367-6234.201805136 |
| [14] |
伍志韬, 杜伟, 刘蕾蕾, 等. 恶意攻击下的电力耦合网络风险传播模型研究. 电网技术, 2020, 44(6): 2045-2052. DOI:10.13335/j.1000-3673.pst.2019.1426 |
| [15] |
李妍, 张宏宇. 工业控制网络中的良性蠕虫传播模型. 控制工程, 2020, 27(7): 1286-1292. DOI:10.14107/j.cnki.kzgc.20190564 |
| [16] |
Yao Y, Sheng C, Fu Q, et al. A propagation model with defensive measures for PLC-PC worms in industrial networks. Applied Mathematical Modelling, 2019, 69: 696-713. DOI:10.1016/j.apm.2019.01.014 |
| [17] |
Zhou HP, Shen SG, Liu JH. Malware propagation model in wireless sensor networks under attack-defense confrontation. Computer Communications, 2020, 162: 51-58. DOI:10.1016/j.comcom.2020.08.009 |
| [18] |
Masood Z, Samar R, Raja MAZ. Design of a mathematical model for the Stuxnet virus in a network of critical control infrastructure. Computers & Security, 2019, 87: 101565. DOI:10.1016/j.cose.2019.07.002 |
| [19] |
Upadhyay RK, Singh P. Modeling and control of computer virus attack on a targeted network. Physica A: Statistical Mechanics and Its Applications, 2020, 538: 122617. DOI:10.1016/j.physa.2019.122617 |
| [20] |
Da GF, Xu MC, Zhao P. Modeling network systems under simultaneous cyber-attacks. IEEE Transactions on Reliability, 2019, 68(3): 971-984. DOI:10.1109/TR.2019.2911106 |
| [21] |
Kermack WO, McKendrick, AG. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London, 1927, 115(772), 700–721.
|
| [22] |
Wen T, Cheong KH. The fractal dimension of complex networks: A review. Information Fusion, 2021, 73: 87-102. DOI:10.1016/j.inffus.2021.02.001 |
| [23] |
安沈昊, 于荣欢. 复杂网络理论研究综述. 计算机系统应用, 2020, 29(9): 26-31. DOI:10.15888/j.cnki.csa.007617 |
| [24] |
王强, 江昊, 羿舒文, 等. 复杂网络的双曲空间表征学习方法. 软件学报, 2021, 32(1): 93-117. DOI:10.13328/j.cnki.jos.006092 |
| [25] |
Acemoglu D, Chernozhukov V, Werning I, et al. A Multi-risk SIR Model with Optimally Targeted Lockdown. Cambridge: National Bureau of Economic Research, 2020.
|
| [26] |
喻孜, 张贵清, 刘庆珍, 等. 基于时变参数-SIR模型的COVID-19疫情评估和预测. 电子科技大学学报, 2020, 49(3): 357-361. DOI:10.12178/1001-0548.2020027 |
| [27] |
凡友荣, 杨涛, 孔华锋. 基于阶段式SIR-F模型的新冠肺炎疫情评估及预测. 计算机应用与软件, 2020, 37(11): 51-56, 62. DOI:10.3969/j.issn.1000-386x.2020.11.009 |
| [28] |
蒋建洪, 李倩倩. 基于模仿创造的网络流行语传播模型及仿真研究. 计算机应用研究, 2020, 37(7): 1940-1945. DOI:10.19734/j.issn.1001-3695.2018.11.0950 |
| [29] |
Chung KL. Generalization of Poincaré’s formula in the theory of probability. The Annals of Mathematical Statistics, 1943, 14(1): 63-65. DOI:10.1214/aoms/117773149 |
 2023, Vol. 32
2023, Vol. 32



