随着卫星技术的发展, 卫星视频中的目标跟踪成为新的研究领域. 而与普通视频相比, 卫星视频中的目标相对于背景只占少量像素, 这会使卫星视频中的目标跟踪更容易产生漂移现象.

目标跟踪分为基于相关滤波和基于深度学习的方法. 基于相关滤波的方法依赖手工特征通过相关计算进行目标的位置预测, 常见的相关滤波算法有MOSSE^[1]、CSK^[2]、KCF^[3]、CN^[4]等. 基于深度学习的孪生网络跟踪方法通过提取深度特征在精度和速度之间达到了平衡, 这种方法简单高效, 受到广泛学者的关注. Bertinetto等^[5]提出SiamFC算法, 该算法使用相同的网络结构提取模板和搜索区域的特征, 然后利用相关计算得到目标位置. Li等^[6]在SiamFC的基础上加入区域候选网络, 提出了SiamRPN算法, 有效解决了目标尺度变化问题. Li等^[7]在SiamRPN的基础上引入残差网络和通道互相关策略, 提出了SiamRPN++算法. Guo等^[8]在SiamRPN++的基础上将分类和回归并行计算, 提出了SiamCAR算法, 实现无先验框跟踪, 避免了很多先验框超参数的设置. Shi等^[9]在SiamFC的基础上增添一个新分支提出了TripFC算法.

这些方法主要针对传统视频的目标跟踪进行的改进, 但在卫星视频跟踪中还需要根据目标特征不明显的特点进行优化. Shao等^[10]在孪生网络中加入目标的像素级运动特征保证目标更精确的定位. Zhang等^[11]利用全卷积网络预测像素位置提高跟踪精度. Wu等^[12]引入慢特征和运动特征提高目标跟踪性能. Ruan等^[13]通过拟合目标运动轨迹缓解模型漂移问题. Song等^[14]在孪生网络中加入通道、空间和交叉注意力机制, 实现更精确的目标定位.

与上述算法不同, 本文以无锚框SiamCAR算法为基本框架, 将通道注意力模块和运动激励模块结合, 更多的关注得分较高的通道和运动位置, 并且添加相邻帧分支和卡尔曼预测分支形成四重网络, 提高算法在卫星视频中的目标跟踪能力. 我们的算法仅需额外训练注意力机制模块, 增添的相邻帧和卡尔曼预测模块不需要训练, 可以直接使用.

1 相关理论

SiamCAR将跟踪问题分解成分类和回归两个子问题, 以像素的方式进行求解. 该框架主要包括: 一个用于特征提取的骨干网络和一个用于边界框预测的分类回归子网.

1.1 特征提取

特征提取子网采用改进的ResNet-50网络^[15], 如图1, ResNet-50网络包含49个卷积层、1个全连接层, 第1部分结构主要对输入进行卷积、正则化、激活函数和最大池化计算, 第2–5部分结构中都增添了残差块, 解决了原CNN网络过深时准确率下降的问题.

改进的ResNet-50将后3层的特征进行拼接分别得到template patch的特征图 $ \varphi \left( Z \right) $ 和search region的特征图 $ \varphi \left( X \right) $ , 之后执行深度互相关计算获得响应图R:

$ R = \varphi \left( Z \right) \star \varphi \left( X \right) $

(1)

其中, $\star $ 表示深度相关. 然后将响应图R通过1×1的卷积层进行降维得到R*, 以减少模型参数量, 加快后续的计算.

1.2 边界框预测

将特征提取阶段得到的 $ R_{w \times h \times m}^ * $ 作为输入, 分类回归子网通过分类分支和回归分支输出, 其中分类分支输出分类特征图 $ A_{w \times h \times 2}^{cls} $ 和中心度特征图 $ A_{w \times h \times 1}^{cen} $ , 回归分支输出回归特征图 $ A_{w \times h \times 4}^{reg} $ . $ A_{w \times h \times 2}^{cls} $ 中每个点都包含一个二维向量, 该向量表示输入搜索区域中相应位置的前景和背景分数; $ A_{w \times h \times 4}^{reg} $ 中每个点都包含一个四维向量 $ t\left( {i, j} \right) = \left( {l, t, r, b} \right) $ , 该向量表示从相应位置到输入搜索区域中边界框四边的距离, 设 $ \left( {{x_0}, {y_0}} \right) $ 和 $ \left( {{x_1}, {y_1}} \right) $ 表示实际边界框的左上角和右下角, 并设 $ \left( {x, y} \right) $ 表示点 $ \left( {i, j} \right) $ 的对应位置, 则回归目标的公式为:

$ \tilde l = x - {x_0} $

(2)

$ \tilde t = y - {y_0} $

(3)

$ \tilde r = {x_1} - x $

(4)

$ \tilde b = {y_1} - y $

(5)

$ A_{w \times h \times 1}^{cen} $ 中每个点给出相应位置的中心度分数, 公式定义为:

$ C\left( {i, j} \right) = I\left( {{{\tilde t}_{i, j}}} \right) * \sqrt {\frac{{\min \left( {\tilde l, \tilde r} \right)}}{{\max \left( {\tilde l, \tilde r} \right)}} \times \frac{{\min \left( {\tilde t, \tilde b} \right)}}{{\max \left( {\tilde t, \tilde b} \right)}}} $

(6)

1.3 跟踪阶段

对于每个位置都会生成对应的6维向量 $ {T_{i, j}} = \left( {cls, cen, l, t, r, b} \right) $ , 其中 $ cls $ 表示分类的前景分数, $ cen $ 表示中心度分数, $ l + r $ 和 $ t + b $ 表示当前帧中目标的预测宽度和高度. 然后加入尺度惩罚 $ {p_{i, j}} $ , 将跟踪阶段的公式定义为:

$ q = \arg \mathop {\max }\limits_{i, j} \left\{ {\left( {1 - {\lambda _d}} \right)} \right.\left. {cl{s_{ij}} \times {p_{ij}} + {\lambda _d}{H_{ij}}} \right\} $

(7)

其中, H是余弦窗, $ {\lambda _d} $ 是平衡权重, q是最大分数像素对应的位置.

2 改进的卫星视频目标跟踪算法

将SiamCAR算法作为基本框架, 首先在特征提取模块中加入运动激励模块(ME)和改进的高效通道注意力(ECA)模块; 然后加入相邻帧模板和卡尔曼预测模板补充对象模板以形成四重网络结构.

2.1 特征提取模块

特征提取模块以改进的ResNet-50为基础, 在骨干网络的残差单元加入了运动激励模块和改进的高效通道注意力模块, 改进的残差单元结构如图2所示.

2.1.1 运动激励模块

运动激励模块^[16]将短距离运动建模与整个时空特征学习方法相结合, 激发特征的运动敏感通道, 以解决卫星视频中前景背景对比性低的问题. 首先输入形状为[N, T, C, H, W]的时空特征X, 其中N是批量大小, T和C分别表示时间维度和特征通道, H和W表示形状. 将输入特征X经过1×1的2D卷积得到信道压缩特征 $ {X^r} $ . 接着对 $ {X^r} $ 进行通道变换, 计算t时刻的运动特征为:

$ M\left( t \right) = con{v_{{\rm{trans}}}} * {X^r}\left( {t + 1} \right) - {X^r}\left( t \right),\; 1 \leqslant t \leqslant T - 1 $

(8)

其中, conv_trans是一个3×3的 2D通道卷积层.

接着, 连接所有运动特征得到最终运动矩阵M, 使用全局平均池层来总结空间信息得到 $ {M^s} $ , 将得到的空间信息进行1×1卷积, 并使用Sigmoid函数获得运动注意权重A:

$ A = 2{\textit{Sigmoid}}\left( {con{v_{\exp }} * {M^s}} \right) - 1,\; A \in {R^{N \times T \times C \times 1 \times 1}} $

(9)

最后, 将输入特征X与注意力权重A进行通道乘法, 得到了激励运动敏感通道和抑制静态背景信息的特征, 计算公式如下:

$ {X^o} = X + X \otimes A,\; {X^o} \in {R^{N \times T \times C \times H \times W}} $

(10)

其中, $ {X^o} $ 是运动模式被激发的输出, $ \otimes $ 表示通道乘法.

2.1.2 改进的高效通道注意力模块

高效通道注意力模块^[17]是在SE-Net通道注意力基础上采用无降维的局部跨通道交互策略的一种注意力机制, 该模块涉及少量参数, 通过增强有用信息的通道, 抑制信息较少的通道, 带来明显的性能增益. 卫星视频中目标相对于背景只占少量像素, 原ECA模块利用通道的全局平均值计算, 会带来很多与目标无关的背景信息, 因此本文加入全局最大值计算, 将全局平均值和全局最大值得到两个空间信息进行叠加优化成更好的通道注意力模块, 如图3所示.

首先将大小为 $ H \times W \times C $ 的输入特征分别进行全局最大池化和全局平均池化, 将两个结果进行叠加得到 $ 1 \times 1 \times C $ 的压缩特征, 然后进行自适应k相邻1维卷积获得局部跨信道交互信息, 自适应k值的计算公式如下:

$ k = {\left| {\frac{{\log _2{C}}}{\gamma } + \frac{b}{\gamma }} \right|_{{\rm{odd}}}} $

(11)

其中, C为通道数, $\gamma $ 和b为调节参数, ${\left| {f\left( x \right)} \right|_{{\rm{odd}}}}$ 为获取值的最近奇数.

最后, 使用Sigmoid函数将得到的结果转换成0–1之间的数值, 作为权值与输入的特征对应相乘, 得到带有通道注意力的特征图.

2.2 四重网络模型构建

SiamCAR使用初始帧作为对象模板, 在跟踪过程中, 通常会面临着遮挡、光照等影响, 此时初始帧模板中包含的信息不足以支持后续帧的跟踪. 为了提高跟踪器的性能, 我们加入了相邻帧模板和卡尔曼预测模板, 用来补充对象模板以形成四重网络, 如图4所示.

2.2.1 加入相邻帧模板

SiamCAR算法仅利用首帧模板进行目标跟踪, 当目标在后续跟踪中受到干扰时会导致模板信息不准确, 于是在SiamCAR的基础上添加一个相邻帧模板, 将初始帧和相邻帧的信息结合以增强模板特征的表达能力. 分别将初始帧模板和相邻帧模板与搜索区域进行深度互相关计算, 计算公式如下:

$ {R_1} = \varphi \left( {{Z_1}} \right) \star \varphi \left( X \right) $

(12)

$ {R_2} = \varphi \left( {{Z_2}} \right) \star \varphi \left( X \right) $

(13)

其中, $ {R_1} $ 和 $ {R_2} $ 的大小相同, 将两者进行叠加得到最终响应图, 计算公式如下:

$ {A_{cls}} = {\varphi _{cls}}\left( {{R_1}} \right) + {\varphi _{cls}}\left( {{R_2}} \right) $

(14)

$ {A_{cen}} = {\varphi _{cen}}\left( {{R_1}} \right) + {\varphi _{cen}}\left( {{R_2}} \right) $

(15)

$ {A_{reg}} = {\varphi _{reg}}\left( {{R_1}} \right) $

(16)

$ {P_{{\rm{score}}1}} = {A_{cls}} \times {A_{cen}} $

(17)

2.2.2 加入卡尔曼预测模块

由于卫星视频中目标相对于背景较小, 特征信息不明显, 于是在SiamCAR的基础上增添一个卡尔曼^[18]预测的模板分支, 对目标的运动轨迹进行预测, 将预测的目标位置与跟踪算法得到的目标位置进行最优值计算, 减少目标漂移问题, 提高目标的跟踪性能. 卡尔曼滤波器系统的状态方程和观测方程分别为:

$ {x_t} = {A_{t - 1}}{x_{t - 1}} + {w_{t - 1}} $

(18)

$ {{\textit{z}}_t} = {H_t}{x_t} + {v_t} $

(19)

其中, $ {A_{t - 1}} $ 是系统在t–1帧的状态转移矩阵, $ {H_t} $ 是系统在t帧的观测矩阵, $ {x_t} $ 和 $ {x_{t - 1}} $ 分别是系统t帧和t–1帧的系统状态的最佳值, ${{\textit{z}}_t}$ 是状态矩阵的观测量, $ {w_{t - 1}} $ 和 $ {v_t} $ 分别是均值为0、协方差矩阵为Q和R的高斯白噪声.

然后利用上一时刻运动状态预测此时刻的状态变量值, 如式(20)所示:

$ \hat x_t^ - = {A_t}{\hat x_{t - 1}} $

(20)

利用上一时刻误差协方差值预测此时刻的误差协方差值, 如式(21)所示:

$ P_t^ - = {A_{t - 1}}{P_{t - 1}}A_{t - 1}^{\rm{T}} + {Q_{t - 1}} $

(21)

使用卡尔曼增益系数作为权重, 如式(22)所示:

$ {K_t} = P_t^ - {H^{\rm{T}}}{\left( {HP_t^ - {H^{\rm{T}}} + {R_t}} \right)^{ - 1}} $

(22)

然后取状态变量预测值与观测值的加权和作为最终状态变量, 如式(23)所示:

$ {\hat x_t} = \hat x_t^ - + {K_t}\left( {{{\textit{z}}_t} - {H_k}\hat x_t^ - } \right) $

(23)

误差协方差值更新, 如式(24)所示:

$ {P_t} = P_t^ - - {K_t}{H_t}P_t^ - $

(24)

利用卡尔曼滤波预测的模板与搜索区域进行深度互相关计算, 计算公式如下:

$ {R_3} = \varphi \left( {{Z_3}} \right) \star \varphi \left( X \right) $

(25)

$ A_{cls}^ * = {\varphi _{cls}}\left( {{R_3}} \right) $

(26)

$ A_{cen}^ * = {\varphi _{cen}}\left( {{R_3}} \right) $

(27)

$ {P_{{\rm{score}}2}} = A_{cls}^ * \times A_{cen}^ * $

(28)

2.2.3 跟踪阶段

根据前两个阶段分别得到的响应图 ${P_{{\rm{score}}1}}$ 和 ${P_{{\rm{score}}2}}$ 进行最大值比较, 选取响应值最大位置作为目标跟踪的最终位置, 计算公式如下:

$ {P_{{\rm{score}}}} = \max \left( {{P_{{\rm{score}}1}}, {P_{{\rm{score}}2}}} \right) $

(29)

$ q = \arg \max \left( {{P_{{\rm{score}}}}} \right) $

(30)

3 实验结果分析 3.1 实验环境及配置

本文实验所使用的环境配置为Windows 11、CUDA 11.6. 硬件配置为Intel-CPU-i5-11260H处理器, 显卡为Nvidia GeForce RTX 3050Ti. 本文选取SatSOT卫星视频数据集^[19]里的10组数据作为本文实验的测试序列, SatSOT是第1个密集注释的卫星视频目标跟踪数据集, 覆盖了卫星视频中特定的移动目标类别, 包括汽车、火车、飞机和船舶. 为了验证本文算法的鲁棒性和有效性, 采取成功率和准确率作为跟踪评价标准, 将SiamCAR算法与本文算法进行对比.

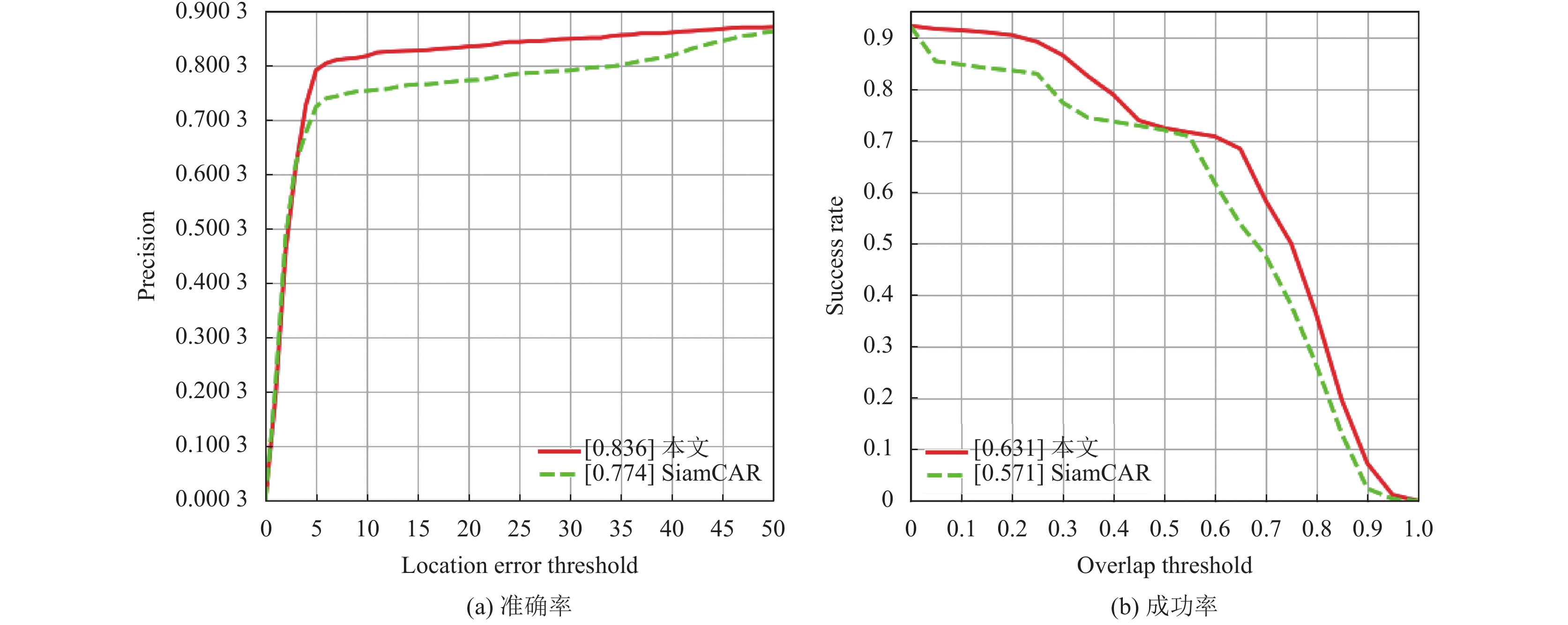
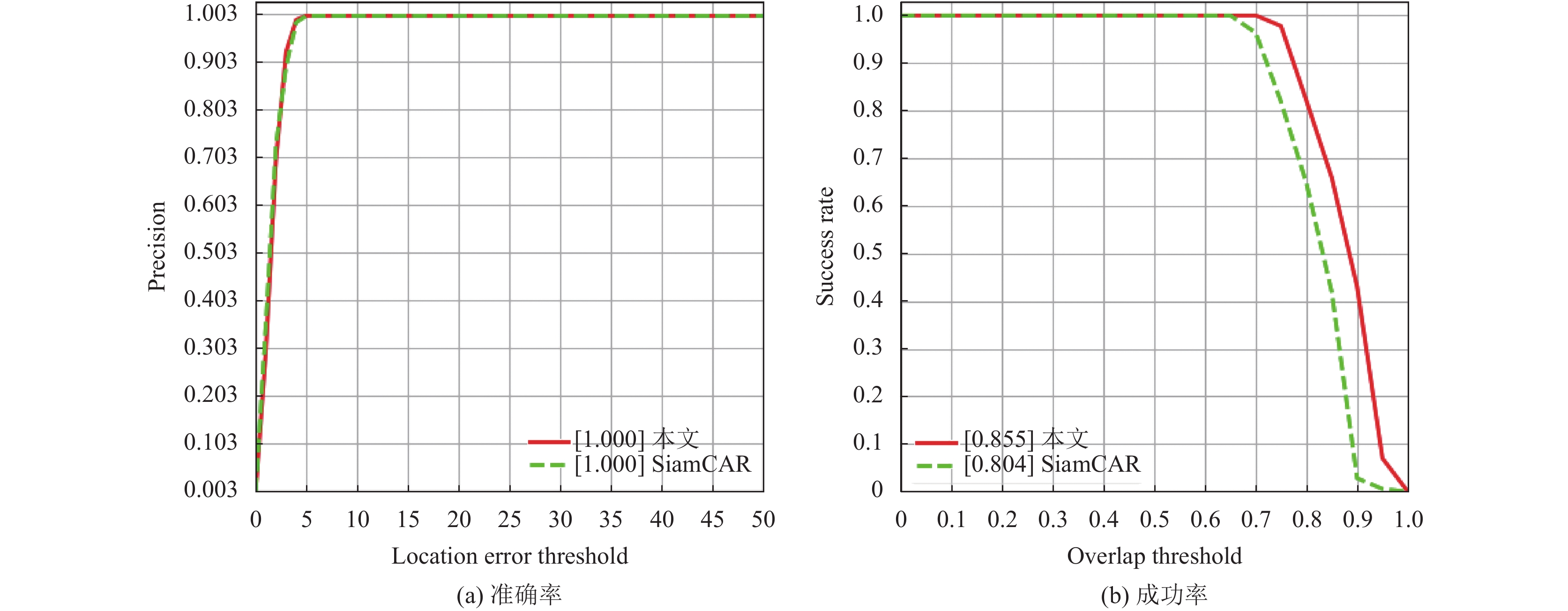
3.2 算法结果比较分析 3.2.1 定量分析

为了验证算法的跟踪性能, 在选取的10组数据集上测试了SiamCAR算法和本文算法. 表1为实验所得数据. 本文算法在10组数据集的准确率和成功率相比SiamCAR算法分别提高了6%和6.2%; 本文算法在plane_02序列中的准确率和成功率相比SiamCAR算法分别提高了0和45.1%; 本文算法在ship_01序列中的准确率和成功率相比SiamCAR算法分别提高了57.2%和5.1%; 本文算法在train_03序列中的准确率和成功率相比SiamCAR算法分别提高了3.3%和7.5%. 分别如图5–图8所示.

3.2.2 定性分析

为了更直观评估算法的跟踪性能, 将本文算法与SiamCAR算法分别在plane_04、ship_01和train_03视频序列上进行了对比实验, 如图9–图11所示. 其中红色框代表本文算法跟踪结果、蓝色框代表SiamCAR算法跟踪结果. 图9–图11表明, 在卫星视频目标跟踪中, 本文算法相比于SiamCAR算法可以更贴合目标的尺寸, 更好的跟踪目标.

4 结论

本文主要介绍了改进后的卫星视频目标跟踪算法网络, 针对卫星视频中存在的目标特征信息不明显、目标与背景对比性低等问题, 将运动激励模块和改进的高效通道注意力模块加入到骨干网络的残差单元, 激励目标的运动敏感通道和有用信息通道, 增强目标的特征提取信息; 并增加了相邻帧模板和卡尔曼预测帧模板与首帧模板和搜索区域形成四重网络结构, 补充目标的运动信息和外观信息. 实验表明, 改进后的算法网络有效地提高了目标跟踪的准确率和成功率.