异常检测[1-4]就是检测数据中不符合行为的异常数据, 异常数据也可以称之为离群点、污点、不一致点, 数据异常可以转化为各种应用领域中的重要可操作信息. 在大数据信息时代, 异常检测在许多领域都发挥着不可忽视的作用, 包括信用卡欺诈检测, 保险或医疗保健, 交通管理, 网络安全入侵检测, 安全攸关系统中的故障检测以及对敌方活动的军事监视等[5-8]. 异常检测技术的研究是当前机器学习与数据挖掘的热点研究领域之一, 具有非常重要的应用意义.
当前学术界也产业界已有很多异常检测方法的研究. Breunig等人提出了基于密度的LOF算法[9], 其基本原理是对数据点进行计算, 找出其k个近邻, 然后计算 LOF 得分, 得分越高则异常的可能性越大. LOF是一个比值, 其分子是k个近邻的平均局部可达密度, 分母则是该数据点局部可达密度. Chen等人提出了基于聚类的DBSCAN算法[10], 该算法通过将紧密相连的样本划为各个不同的类别, 最终得出聚类类别结果. K-means算法[11]假设距离最近的聚类结果较远的点为异常点. 该算法首先对数据进行聚类, 然后通过计算样本与所属聚类的两个距离, 一个是样本与所属聚类中心的距离, 一个是样本与所属聚类的类内平均距离, 通过两个距离的比值衡量异常程度. 在不同的异常检测算法中, isolation forest[12-14]是具有独特能力的方法, 该方法计算效率高, 易用于并行计算范式[15], 且已被证明在检测异常方面非常有效[16]. 该算法的主要优点是它不依靠构建模型来查找不符合此模型的样本; 而是利用了异常数据“少而不同”的特点, 通过理解异常来发现异常, 观察它们的属性并将它们与其余的正常数据样本隔离[17-19]. 在隔离森林中, 数据被子采样, 并以树状结构处理随机选择的值. 在数据被树状结构处理后, 那些走得更深的样本进入树枝, 也就是叶子节点的异常可能性较小, 而较短的分支表示该数据很快就被隔离至叶子节点, 有更大的概率是异常数据. 因此, 叶节点的深度即为度量每个给定点的异常或“异常分数”的关键因素. 然而, 隔离森林算法仍然存在一些问题. 事实证明, 虽然该算法在计算上行之有效, 但由于它固有的分支方式, 传统隔离森林算法存在很多局限性. 为了解决这些局限性, 诞生了一系列“改进版”隔离森林, 例如extended isolation forest[20], inne[21]等. 显然, 这些改进版的隔离森林算法解决了传统隔离森林算法的一些问题, 但是, 它们依然存在一些需要改进的地方. 大体来说, 这些算法仍然存在以下几点问题.
(1) 采用超平面来对空间进行随机切割和隔离, 不能充分利用数据中每个维度的信息, 可能导致大量维度信息没有被利用, 算法的可靠性较低.
(2) 当前的方法仅适应于一些分布比较常见、比较简单的数据, 由于其采用随机超平面进行空间的划分, 在处理不均衡数据集时存在一定程度的分类准确率低、误警率高的问题, 难以拥有稳定且良好的表现.
(3) 仅对全局的稀疏点、异常点敏感, 不善于处理局部的、内部的异常点.
针对以上问题, 本文提出了基于k近邻隔离森林(k-nearest neighbor based isolation forest, KNIF)的异常检测方法. KNIF方法具有不同的隔离机制, 先对数据空间进行多次采样, 构建一个个检测集合, 并由多个集合共同构成一片“森林”. 与隔离森林不一样, 本算法采用超球体作为隔离工具, 充分利用每个维度的信息. 在隔离区域中, 每个区域都是一个超球体, 其中心由来自子样本, 其边界由到该子样本的第n近邻的距离定义, 以便将每个实例与其余的数据空间隔离开来. 简而言之, 我们使用基于第n近邻的方法来执行隔离而不是原始的轴平行细分方法. 也采用兼具创新性的异常得分计算方法, 并确定每个隔离区域的隔离分数. 此方法在继承之前隔离森林系算法的优点的同时, 也由其创新性解决了之前算法存在的痛点, 是一种更高效、更稳定、更全面的算法. 本文的主要贡献及创新点如下.
(1) 使用所有可用属性将数据空间划分为隔离区域, 充分利用数据集中所有维度的信息, 而不是仅为其分区过程使用属性的子集. 因此, 新方法不存在子空间方法的缺点.
(2) 将隔离森林的集成学习方法与最近邻的方法有机结合起来, 并提出新颖的、有效的异常点界定方式.
(3) 相比于随机超平面的隔离划分, 超球体能更好地检测局部的、内部的异常, 在密集区域创建更小的超球体, 在稀疏区域创建更大的超球体, 每个球体的半径都是判断异常的关键依据, 能更好地适应和处理分布复杂且多样的数据, 提升分类准确率.
本文进行了充分的实验, 先采用人工合成数据生成的热力图来直观地展示本算法的优势. 且在4个高维真实数据集进行评估实验, 将实验结果与已有的数个异常检测算法作比较, 并使用AUC指标客观地评估各算法的表现, 以充分说明此算法的优越性. 本文第1节介绍隔离森林及其背景基础; 第2节给出本文的问题定义; 第3节提出了问题的解决方案; 第4节实验与结果分析; 最后是结论与展望.
1 隔离森林及相关基础隔离森林, 又名孤立森林, 不同于传统异常检测算法的思想, 其用隔离的方法将异常点与正常点区分开来, 通过利用数量稀少和不同的异常特性并测量个体的被隔离敏感度, 通过将特征空间划分区域来执行隔离. 这种方法充分利用了异常点的特性, 背后的思想是异常更容易被隔离.
隔离森林是由N个树构成的. 每棵树的学习过程非常随机: 它会随机抽取特征, 随机选取随机选择的真实值样本中所选属性的最小值和最大值之间的值来建立决策树, 从而将每一个样本分到一个独立的子节点上(取值相同的样本视为同一个样本). 从超空间的角度看, 这样就是不断地用随机选取的超平面切分样本点, 直到所有的样本点都被这些超平面“隔离”起来, 即与其他样本点分隔开.
隔离森林使用x落入的叶节点的路径长度来计算其隔离分数, 使用少量的平行轴来隔离具有很少数据点的区域分区. 实例x的路径长度h(x)基于x落入的叶节点定义.
隔离森林可以使用较小的样本来建立隔离模型. 与其他方法相比, 时间复杂度和空间复杂度都较低. 第一个隔离方法为 iForest, 构建了一个称为隔离的树集合树, 其中每个隔离树都是从随机选择的大小为ψ的子样本构建的. 隔离树是一棵二叉树, 其中在每个节点上, 对随机选择的一个节点执行随机分裂来自特征空间的属性. 分割点是随机选择的真实值样本中所选属性的最小值和最大值. iForest使用x落入的叶节点的路径长度作为其隔离分数, 其中直觉上, 可以使用少量的平行轴来隔离具有很少数据点的区上图就是对子样本进行切割训练的过程, 如图1所示, 图1(a)的
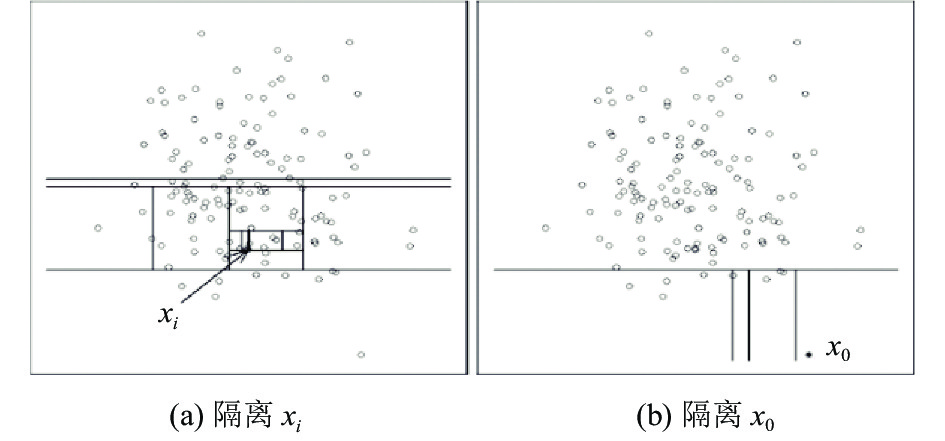
|
图 1 隔离森林切割过程 |
由于切割过程是完全随机的, 所以需要用整合的方法来使结果收敛, 即反复从头开始切, 整合全部隔离树的结果, 然后计算每次切分结果的平均值.
获得t棵隔离树后, 单棵树的训练就结束了. 接下来就可以用生成的隔离树来评估测试数据了, 即计算异常分数s. 对于每个样本x, 需要对其综合计算每棵树的结果, 通过式(1)计算异常得分:
| $ s\left(x, \psi \right)={2}^{\frac{E\left(h\left(x\right)\right)}{c\left(\psi \right)}} $ | (1) |
其中, h(x)为x在每棵树的高度,
如果异常得分接近1, 那么一定是异常点.
如果异常得分远小于0.5, 那么一定不是异常点.
如果异常得分所有点的得分都在0.5左右, 那么样本中很可能不存在异常点.
2 问题定义致力于提升隔离森林算法的鲁棒性和可靠性, 本文提出KNIF算法. KNIF基于k近邻构建超球体作为隔离工具. 定义1及定义2给出所使用的距离及第k近邻定义.
定义 1. 各实例之间的距离由欧氏距离来定义, N维欧氏空间中两点
| $ d=\sum _{i=1}^{N}\left({x}_{1i}-{x}_{2i}\right) $ | (2) |
定义 2. 第k近邻: 设x为空间上的点, 距离实例点p第k近的距离的点q即为第k近邻:
| $ q=\underset{{x}_{i}}{{{\rm{argmax}}}\{}d < p, {x}_{i} > \} , \; {x}_{i}\in {N}_{k}\left(x\right) $ | (3) |
其中,
作为KNIF重要的隔离工具, 基于k近邻构建的隔离球在充分利用各维度信息的同时. 适应复杂分布的数据. 其半径大小直接表达该区域的稀疏程度. 以k近邻的方法构建多个隔离球, 形成隔离树, 以覆盖数据集分布的区域, 用于单次异常检测. 多棵隔离树共同组成隔离森林, 进行多次异常检测. 定义3–定义6给出相关定义.
定义 3. 隔离球: 以实例点T为圆心, 以第k近邻的欧式距离为半径画出来的超球体即为隔离球c.
定义 4. 基于k近邻的隔离树: 由n个隔离球组成的集合, 即隔离树X={c1, c2, c3, …, cn}.
定义 5. 基于k近邻的隔离森林: 由m棵隔离树组成的集合, 即隔离森林F={X1, X2, X3, …, Xn}.
定义 6. 异常分数(异常值): 异常分数是判断一个实例异常与否的关键因素. 我们采用了非常明了且实用的方式来计算异常值: 排序. 以一棵隔离树为例, 我们将此隔离树中的n个隔离球以半径大小从小到大排序, 并以其位置赋予其异常值, 隔离球半径越小, 其位置越考前, 对应异常值也就越小. 最小值为0, 最大值为1. 因此, 每棵隔离球都会对应一个异常值, 为后续的检测奠定良好的基础. 实例点p的异常分数计算公式如下:
| $ S(x)=\frac{rank\left(p\right)}{n} $ | (4) |
根据异常分数, 我们可以得到以下结论.
(a) 如果异常值非常接近于1, 则说明该隔离球的半径很大, 其附近的点分布得很稀疏.
(b) 如果异常值非常小, 接近于0, 则说明改隔离球的半径很小, 其附近的点分布得很密集.
(c) 如果异常值非常接近于0.5, 则说明隔离球的半径适中, 其附近的点分布得比较均匀.
3 基于k近邻隔离森林的异常检测方法本节讨论并展示所提出算法的思想. 相比于基于超直线隔离的方法, KNIF以超球体来做隔离. 超球体的中心为实例点, 超球面的半径由实例点x与其KNN之间的距离决定(k值自设). 根据KNN的性质, 实例点在稀疏区域更可能形成大的超球体, 密集区域形成的球体会相对更小. 由于异常点更可能分布于稀疏区域, 正常区域实例更可能在密集区域分布, 根据密集稀疏程度可以直接用于异常的检测. 算法1为具体算法流程.
算法1. KNIF(X, t, v, n)
输入: X: input data; t: number of trees; v: subsampling size; k: k-th nearest neighbor输出: a set of KNBTrees
1. KNIF←Ø2. for i←1 to t do3. Si←RandomSample(X, v)4. Ti←Ø5. for all p∈Si do6. B(p)←build a NN hypersphere. centered at p7. Ti←Ti∪{B(p)} Give every B(p) a anomaly score by it’s rank in Ti8. end for9. KNIF←KNIF∪{Ti}10. end for11. return KNIF
如算法1所示, KNIF 算法有一个输入数据X, 3个输入参数: 分别是子采样大小v, 树的数量t和选定的第k近邻k: KNIF先从数据集中随机选取v个数据点构建v个隔离球, 根据半径大小给v个隔离球赋予异常值, v个带有隔离值的隔离球形成的集合为一颗隔离树. 重复上述流程, 构建t棵隔离树, t棵隔离树形成的集合为基于k近邻的隔离森林(KNIF)输入参数子采样大小v控制训练数据大小. 我们发现当v增加到一定值时, 无需进一步增加v的大小, 因为这只会徒增资源的消耗. 我们通常会把v设为27~29之间, 也就是128~512之间. 第k近邻k同理, 实验发现, 对于绝大多数的数据, 都可以在3~6之间获得理想的效果, 且能达到较低的时间复杂度. 参数t控制隔离树的数量. 通过实验发现树的数量t在100左右能得到较好的实验效果. 若无另外说明, 本文使用t=100作为实验中树的数量的默认值.
构建出了基于k近邻隔离森林之后, 对需要检测的数据进行异常值的计算. 算法2给出异常值计算的算法流程.
算法2. 异常值计算: anoScore(KNIF)
输入: X: input data; KF: KNIF; t: number of trees输出: AS: anomaly scores
1. for all q∈X do2. sumscore←Ø3. for i←1 to t do4. find the nearest point p of q in NFi, assign the score of B(p) to q5. sumscore+=scoreq6. end for7. ASq=sumscore/t8. end for9. return AS
数据点的异常值计算方法如算法2所示. 有两个输入数据, 第1个是待检测数据集X, 第2个是已构成的基于最近邻的隔离森林KF; 有一个输入参数t, t与算法KNIF一样, 控制隔离树的数量. 我们先在每棵树上找到离数据点q最近的点p, 再把由该点p形成的隔离球的异常值赋予数据点q, 最后把q点在每棵树上的异常值取平均值, 即得到了数据点q的异常值. 如果异常值越接近于1, 则表示该点越离群, 其异常的可能性也就越大; 如果异常值越接近于0, 则表示改点所处的区域越密集, 其异常的可能性越小. 经过实验证明, 此方法能取得非常好的效果.
4 实验分析本节以图文结合的方式展示实验结果. 首先, 使用人工合成的数据来直观地展示KNIF相对于现存隔离森林系算法的优势, 主要与两个算法进行比较: isolation forest和extend isolation forest. 除了展现检测出的异常点之外, 本文采用异常值构成热力图以直观地比较3种不同算法在面对不同数据集时得出的异常值分布. 之后, 采用数个高维真实数据集来比较各个算法的表现. 最后, 比较他们的时间复杂度. 在指标层面, 观察他们对应的ROC曲线, 比较他们的AUC值, 以客观地分析各个算法的有效性和可靠性.
4.1 异常点检测图检测实验以几组人工生成的数据为基础, 并选出一组最具代表性的数据以作展示. 如图2所示, 分别用3种算法对正弦函数分布数据进行检测, 每个算法都被要求标记出异常值最高的10个点. 在这种情况下, 数据具有正弦形状的固有结构, 从图2(a)和图2(b)可以看出标准隔离森林和扩展隔离森林的检测性能很差. 这些算法只能检测出全局的, 外部的相对异常点, 而对于局部的, 处于分布内部的数据, 其表现得差强人意. 而用KNIF算法进行检测时, 其不会对数据点分布的位置产生偏见, 检测出的异常点分布较为均匀.
4.2 异常值热力图给定一个数据集, 我们希望能够训练我们的隔离森林, 以便它可以为每个数据集分配一个异常分数数据点, 并对它们进行排名, 并帮助得出关于异常分布和标称点. 仔细观察 standard IF 和extend IF产生的分数, 能发现这些异常分数存在很多不合理的地方. 观察简单的数据集, 以直观地了解异常分数如何分布以及什么构成异常. 如图3–图5所示, 其横纵坐标均表示为数据点的值. 观察图3, 检测所用的数据集为一个人工生成的随机数据集, 其均值为(0, 0), 协方差为(1, 0), (0, 1), 颜色越亮代表该区域的异常值越低, 颜色越深代表该区域的异常值越高. 理所当然地, 一个数据点如果落在(0, 0)附近, 则应该将其视为正常点. 然而, 随着数据点远离源点, 他们的异常分数应该会增加. 所以我们希望看到一个随着源点距离增加, 其异常值也增加的异常分数图. 从图3(a)和图3(b)可以看出无论是标准隔离森林算法还是拓展隔离森林算法, 其对异常值的分布都存在偏见. 例如standard IF, 其对与x、y轴平行的数据宽容度较高, 会赋予其相对较低的异常值. 而从图3(c)看出, Nearest neighbor IF得到的热力图则可以比较完美地契合数据分布的形状.

|
图 2 异常点检测图 |
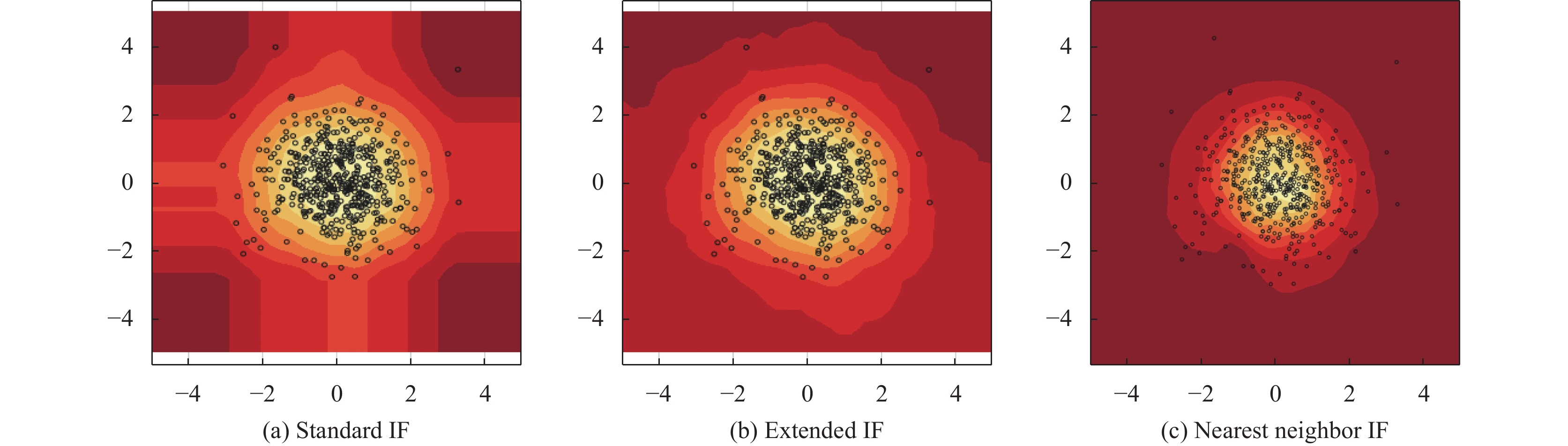
|
图 3 正态函数分布数据热力图 |
图4 比较了各算法对正弦函数分布数据的实验结果. 图4(a)展示了标准隔离森林算法等高线热力图, 其低异常值的等高线形成的形状接近矩形, 且由于隔离森林算法的分割方式为随机选择与坐标轴平行的直线来分割数据集, 其对与数据集平行的区域尤其宽容. 图4(b)展示了拓展隔离森林算法但等高线. 热力图拓展隔离森林的表现稍好, 但观察其等高线, 分布得比较散乱, 不能契合数据的分布. 图4(c)展示了KNIF算法等高线热力图, 等高线的分布很好地契合了数据在空间上的分布. 深色区域的数据表示脱离于数据整体分布的数据点, 其异常值很高, 可以轻易地把该区域的数据判定为异常数据点.

|
图 4 正弦函数分布数据热力图 |

|
图 5 Ionosphere数据集ROC曲线检测对比 |
热力图是数据的代表. 依据KNIF的检测结果, 显而易见, 其得分图比标准隔离森林和拓展隔离森林能更紧密地贴合正弦数据的分布.
4.3 真实数据集检测结果本节使用4个经典高维真实数据集进行评估实验, 将实验结果与已有的数个异常检测算法作比较, 使用ROC曲线和AUC指标客观地评估各算法的表现. ROC曲线也称“受试者工作特征曲线”, ROC曲线图是反映敏感性与特异性之间关系的曲线. 横坐标X轴假阳性率(误报率), X轴越接近零准确率越高; 纵坐标Y轴为真阳性率(敏感度), Y轴越大代表准确率越好. 根据曲线位置, 把整个图划分成了两部分, 曲线下方部分的面积被称为AUC (area under curve), 用来表示预测准确性, AUC值越高, 也就是曲线下方面积越大, 说明预测准确率越高. 曲线越接近左上角(X越小, Y越大), 预测准确率越高.
表1列举了我们使用数据的各方面信息, 表2展示3种算法处理不同数据集的AUC值.
| 表 1 数据集信息 |
| 表 2 AUC值对比 |
图5–图8 为ROC曲线, 为隔离森林、拓展隔离森林和KNIF对以上数据集的检测结果.
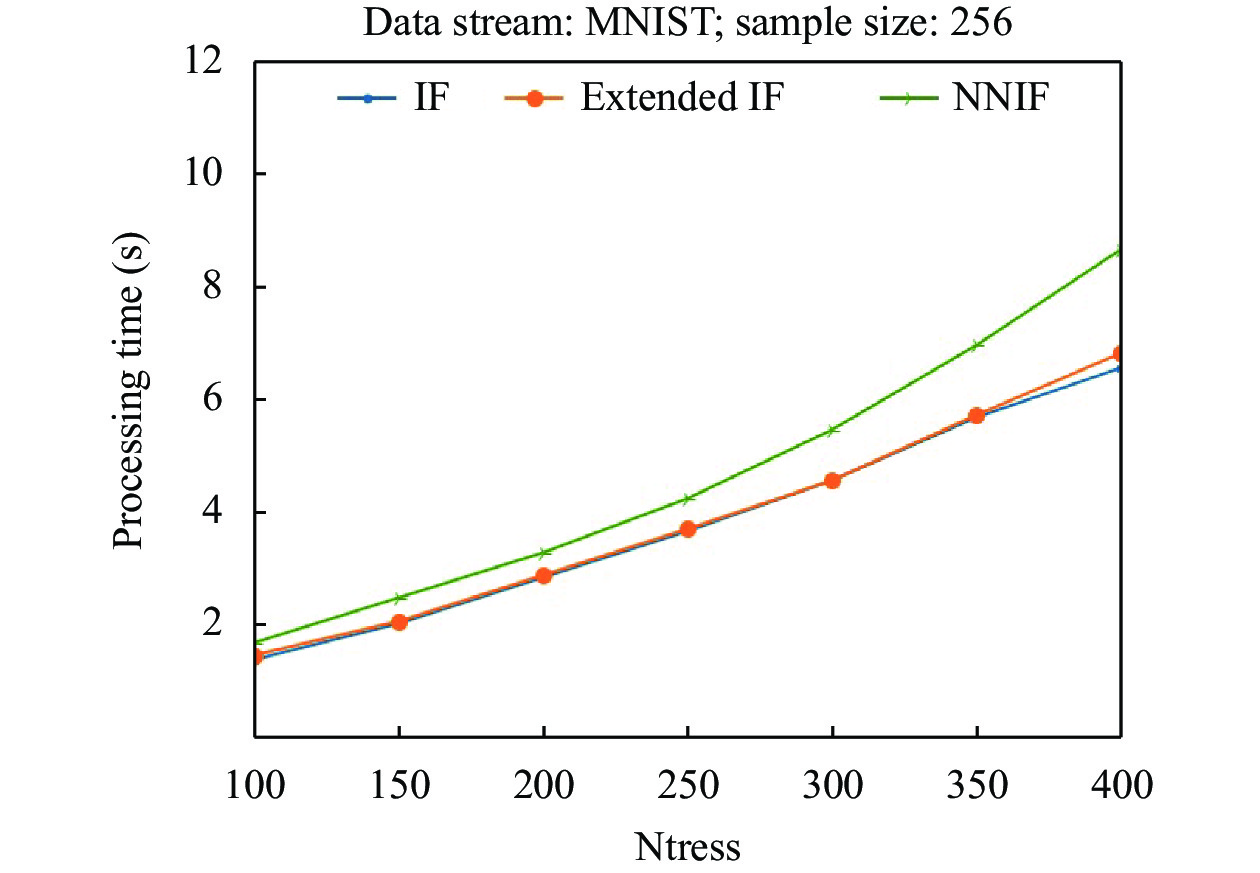
4.4 算法性能分析本节通过实验以比较IF、extended IF与NNIF算法的时间复杂度. 实验设计如下.
为了验证本文所提出的算法NNIF的时间复杂度, 本节设计了在不同树的数量下, NNIF算法与IF、extended IF算法处理时间的对比实验, 其中本实验采用的是经典数据集MNIST, 其具体参数详看表1. 实验设计如下.
本次实验子样本大小ψ的值固定在256, 比较3个不同算法在构建不同规模的森林(也就是不同数量的树)时检测异常所用的时间.
实验结果如图9所示, 横坐标为树的数量, 纵坐标为运行时间, 可以看出IF检测异常所用时间最少, extended IF的运行时间与IF很相近, 略逊于IF; NNIF的效率相对较差, 运行时间平均慢1–2 s, 但是从实验3中的图5–图8中可以看出, 这种以一定时间来换取算法的精确度以及可靠性的策略是可取的.

|
图 6 Vowels数据集ROC曲线检测对比 |
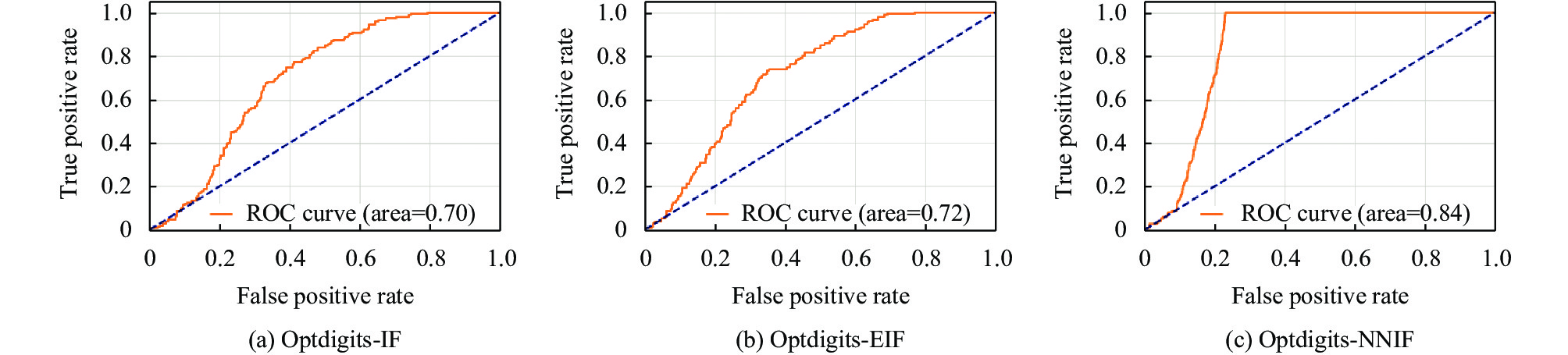
|
图 7 Optdigits数据集ROC曲线检测对比 |
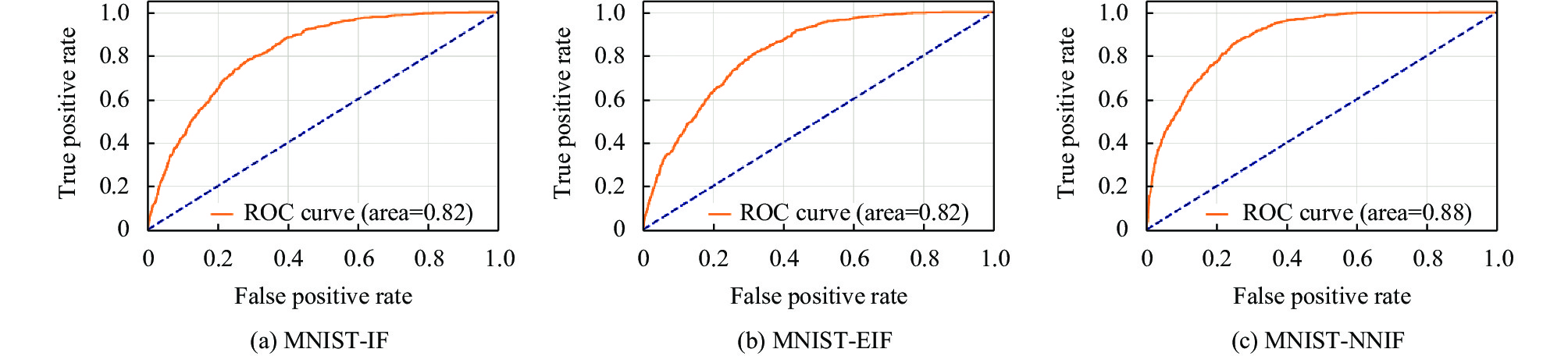
|
图 8 MNIST数据集ROC曲线检测对比 |
5 结论与展望
本文的工作建立在这个假设之上: 异常的点比较容易被隔离, 提出了一个基于最近邻隔离森林的异常检测的扩展算法KNIF. 该方法使用超球体作为隔离工具, 并使用基于距离的异常值计算方法. 无论是隔离森林, 亦或拓展隔离森林, 其算法效能会因所检测数据集分布和形状的不同而出现显著的差异, KNIF充分继承了隔离的思想, 并在隔离思想基础上提出新的改良工具, 显著提高了算法的稳定性和可靠性. 本文展示了异常点分布图, 以此来观察这3种算法对分布形状不同的数据的检测效果. 同时, 展示了不同算法对不同数据的等高线热力图, 表明了其对分布在不同区域数据集的检测结果, 以清晰地展示KNIF与其他隔离森林系算法的差异性. 最后, 我们对数个真实高维数据进行实验, 进一步验证KNIF算法的可靠性.
虽然KNIF算法具有一定的优点, 但是不可避免其还是存在弱点, 特别是由于KNIF算法结合了最近邻的方法, 在时间复杂度上会稍逊色于传统的隔离森林系算法. 进一步提高KNIF的效率, 将会是未来的研究方向之一.
|
图 9 算法性能对比 |
| [1] |
Nassif AB, Talib MA, Nasir Q, et al. Machine learning for anomaly detection: A systematic review. IEEE Access, 2021, 9: 78658-78700. DOI:10.1109/ACCESS.2021.3083060 |
| [2] |
王鑫, 张涛, 金映谷. 异常检测算法综述. 现代计算机, 2020(30): 21-26. DOI:10.3969/j.issn.1007-1423.2020.30.005 |
| [3] |
Sharma R, Guleria A, Singla RK. An overview of flow-based anomaly detection. International Journa of Communication Networks and Distributed Systems, 2018, 21(2): 220-240. DOI:10.1504/IJCNDS.2018.094221 |
| [4] |
Pang GS, Shen CH, Cao LB, et al. Deep learning for anomaly detection: A review. ACM Computing Surveys, 2021, 54(2): 38. |
| [5] |
Di Biase G, Blum H, Siegwart R, et al. Pixel-wise anomaly detection in complex driving scenes. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Virtual: IEEE, 2021. 16918–16927.
|
| [6] |
Mothukuri V, Khare P, Parizi RM, et al. Federated-learning-based anomaly detection for IoT security attacks. IEEE Internet of Things Journal, 2022, 9(4): 2545-2554. DOI:10.1109/JIOT.2021.3077803 |
| [7] |
Erhan L, Ndubuaku M, Di Mauro M, et al. Smart anomaly detection in sensor systems: A multi-perspective review. Information Fusion, 2021, 67: 64-79. DOI:10.1016/j.inffus.2020.10.001 |
| [8] |
Roth K, Pemula L, Zepeda J, et al. Towards total recall in industrial anomaly detection. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022. 14298–14308.
|
| [9] |
Breunig MM, Kriegel HP, Ng RT, et al. LOF: Identifying density-based local outliers. ACM SIGMOD Record, 2000, 29(2): 93-104. DOI:10.1145/335191.335388 |
| [10] |
Chen ZG, Li YF. Anomaly detection based on enhanced DBScan algorithm. Procedia Engineering, 2011, 15: 178-182. DOI:10.1016/j.proeng.2011.08.036 |
| [11] |
Lu W, Issa T. Unsupervised anomaly detection using an evolutionary extension of K-means algorithm. International Journal of Information and Computer Security, 2008, 2(2): 107-139. DOI:10.1504/IJICS.2008.018513 |
| [12] |
Liu FT, Ting KM, Zhou ZH. Isolation forest. Proceedings of the 8th IEEE International Conference on Data Mining. Pisa: IEEE, 2008. 413–422.
|
| [13] |
Marteau PF, Soheily-Khah S, Béchet N. Hybrid isolation forest-application to intrusion detection. arXiv:1705.03800, 2017.
|
| [14] |
Liu FT, Ting KM, Zhou ZH. Isolation-based anomaly detection. ACM Transactions on Knowledge Discovery from Data, 2012, 6(1): 3. |
| [15] |
Hariri S, Kind MC. Batch and online anomaly detection for scientific applications in a Kubernetes environment. Proceedings of the 9th Workshop on Scientific Cloud Computing. Tempe: Association for Computing Machinery, 2018. 3.
|
| [16] |
Susto GA, Beghi A, McLoone S. Anomaly detection through on-line isolation forest: An application to plasma etching. Proceedings of the 28th Annual SEMI Advanced Semiconductor Manufacturing Conference (ASMC). Saratoga Springs: IEEE, 2017. 89–94.
|
| [17] |
Chen G, Cai YL, Shi J. Ordinal isolation: An efficient and effective intelligent outlier detection algorithm. Proceedings of the 2011 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems. Kunming: IEEE, 2011. 21–26.
|
| [18] |
Das S, Wong WK, Dietterich T, et al. Incorporating expert feedback into active anomaly discovery. Proceedings of the 16th IEEE International Conference on Data Mining (ICDM). Barcelona: IEEE, 2016. 853–858.
|
| [19] |
Noto K, Brodley C, Slonim D. Anomaly detection using an ensemble of feature models. Proceedings of the 2010 IEEE International Conference on Data Mining. Sydney: IEEE, 2010. 953–958.
|
| [20] |
Hariri S, Kind MC, Brunner RJ. Extended isolation forest. IEEE Transactions on Knowledge and Data Engineering, 2021, 33(4): 1479-1489. DOI:10.1109/TKDE.2019.2947676 |
| [21] |
Bandaragoda TR, Ting KM, Albrecht D, et al. Isolation based anomaly detection using nearest-neighbor ensembles. Computational Intelligence, 2018, 34(4): 968-998. DOI:10.1111/coin.12156 |
 2023, Vol. 32
2023, Vol. 32


