工业报警的产生与报警阈值、过程测量信息和操作生效时间等因素相关, 其提供的报警信息可以辅助操作人员对相关异常进行处理, 保障生产安全, 达到工业系统稳定运行的效果. 随着报警变量配置技术不断进步, 使得其在工厂里的数量大幅增加. 理论上大量报警变量提供的报警信息能够帮助操作人员进行有效的防护措施, 但过多报警变量有可能会在短时间内产生大量警报, 产生“报警泛滥”问题, 这会给操作人员带来困扰, 影响操作人员的应急防护措施. 为了解决“报警泛滥”这一问题, 近年来提出了多种技术, 包括序列对比[1]、模块提取方法[2]等一系列方法, 由于其算法的复杂性导致其在实际中使用效果并不是很好, 无法有效帮助操作人员应对“报警泛滥”问题.
由于因果分析可以找到变量之间的关系, 使得在复杂工业过程中建立报警传播网络成为可能. 因此, 基于因果分析处理工业报警问题逐渐成为这一领域热点研究方向. 因果分析建模主要包括知识驱动和数据驱动两种方式, 在知识驱动方面, 通过分析已有的系统信息和专家知识等过程知识, 以获得报警变量之间的因果关联, 从而进一步建立因果关系模型. 其中, Mondal等人[3]通过一种新型的状态绝对平均偏差控制图和双层贝叶斯网络对过程进行监测和故障诊断. Tian等人[4]基于交叉映射构建因果网络, 利用得到的报警传播网络对节点状态进行分析. Dorgo等人[5]利用滑动窗口对数据进行预处理, 并使用决策树对故障进行监测. 基于可解释模型[6]、邻接矩阵[7]、贝叶斯网络[8]等方法也对报警传播网络构建做出了贡献. 但生产系统结构的智能化提升以及各类信息传递复杂度的增大, 使得单纯的基于知识驱动的建模方法不能满足这类系统的要求.
随着各种采集数据系统的成熟, 使得分析复杂信息传递关系成为可能. 数据驱动建模方法利用生产过程中产生的历史数据, 使用先进的数据挖掘算法进行变量之间的因果关系识别. 使用较多的算法包括有格兰杰因果分析[9]和传递熵[10], 相比较格兰杰因果分析方法, 传递熵无需考虑数据类型, 对线性数据和非线性数据均有优异的分析结果, 更加适用于工业过程的报警分析. 因此在工业领域, 相关专家学者致力于对传递熵的应用与性能进行优化. 例如: Yang等人[11]提出动态相异指数构建动态在线子块划分模型, 并使用传递熵进行故障变量识别. Ma等人[12]对典型变量分析进行检测, 然后利用广义重建选取部分故障变量完成传递熵的计算. 尽管传递熵在识别因果关系这一问题较其他方法具有一定的优越性, 但单独由传递熵构建的报警传递网络往往较为复杂, 无法有效定位报警发生的根本原因.
单独使用知识驱动或数据驱动的方式无法有效地构建报警传递网络, 使得越来越多的学者开始通过知识驱动与数据驱动相结合的方式获得更加准确的因果关系. Chen等人[13]利用多元非线性模式分解的方式来获得故障发生数据, 并利用多元格兰杰因果关系定位故障发生根本原因, Amin等人[14]利用主成分分析和贝叶斯网络相结合地方式来故障检测和诊断. 虽然上述方式可以有效判断出故障发生根本原因, 但现有方法中很少能够同时对因果传播模型、故障发生根本原因和间接关系进行分析, 本文提出的方法旨在丰富这一方面的研究.
由于贝叶斯网络可以通过图模型与概率相结合的方式, 充分展示过程变量间的强弱因果关系, 使得贝叶斯网络能充分应用于工业报警分析过程. 本文通过改进贝叶斯网络中的K2算法并与传递熵相结合, 来建立报警传播网络, 贡献主要有以下两点: 首先, 在K2评分函数中引入时间维度, 考虑每一节点在不同状态下所占时间比重K2评分函数进行改进, 以此来提出一种新的评分函数, 其次, 在利用传递熵与改进K2评分函数来构建报警传播网络时, 对报警变量状态按高低阈值做进一步细分. 剩余内容分为5节: 第1节对拟解决的问题进行描述和转化, 第2节对提出的方法进行详细介绍, 第3节利用田纳西伊斯曼过程对提出的方法进行验证, 第4节对结果进行分析, 第5节总结提出的方法.
1 问题描述及转化“报警泛滥”指的是在工业生产过程中, 某一个系统设备的异常波动就有可能导致多个报警, 而这些报警之间往往存在因果联系. 为了有效识别出报警通知之间的关联联系, 本文采用报警建模的方式, 建立报警事件传播模型, 确定异常信息的传播路径, 从而最终锁定故障发生的根本原因. 整个过程首先需要确定报警变量具体的报警阈值, 接着使用报警建模方法对报警变量进行分析, 进而确定报警根源. 为了得到报警事件传播模型, 利用数据驱动来对报警时序信息、设备节点信息进行分析, 来初步获得报警关联信息, 再使用知识驱动进行结构学习, 将建立报警传播模型转化成生成报警传播网络, 得到的网络节点表示各个报警变量, 节点之间的连线表示因果传递关系. 第2节详细介绍建立报警传播网络的过程.
2 报警传播网络构建方式 2.1 网络结构初始化对于报警过程产生的报警变量, 利用传递熵来识别报警变量之间的关系, 传递熵是信息熵[15]的扩展, 由于两两之间的传递熵具有不对称的特点, 因此可用于变量之间的因果关系判断. 传递熵[16]的计算公式如下:
| $ {T_{y \to x}} = \sum\limits_{{x_n}, {x_{n + h}}, {y_n}} {P({x_{n + h}}, {x_n}, {y_n})\log } \frac{{P({x_{n + h}}, {x_n}, {y_n})P({x_n})}}{{P({x_n}, {y_n})P({x_{n + h}}, {x_n})}} $ | (1) |
其中,
基于传递熵的特点, 利用如下判断方式进行因与果的判断, 若
算法1. 节点之间去环算法
输入: 节点祖先节点集合记为
1.
评分函数是结构学习中十分重要的一部分, 最终学习得到的结果就是评分最高的网络结构, 提出的改进K2算法较K2算法增加时间维度, 具体改进之后的公式如下:
| $ \begin{split} K(i, {\pi _i}) = &\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{{q_i}} {\left(\left(\log (\frac{{({r_i} - 1)!}}{{({N_{ij}}(D) + {r_i} - 1)!}}\right)\right)} }\\ & + \sum\limits_{k = 1}^{{r_i}} {\log ({N_{ijk}}(D)!)} ) \end{split} $ | (2) |
其中,
利用第2.1节得到的报警传播网络, 可以得到每个节点父节点的节点顺序, 以及每个节点与父节点之间的报警数据, 将以上信息作为改进K2算法的输入, 通过改进K2算法计算得到每一子节点的最佳父节点, 然后按照各个节点所选定的父节点以及节点之间的传递过程进行网络的重构, 选择得分最高的网络结构即为最终的报警传播网络. 算法2为网络结构学习算法.
算法2. 网络结构学习算法
输入:
1.
提出的方法通过田纳西伊斯曼(Tennessee Eastman process)过程[17]验证, 田纳西伊斯曼过程被广泛应用于报警和过程监控领域, 其流程图如图1所示. 田纳西伊斯曼过程在生产环境中主要可以分为3个模块, 进料和反应器在物理结构上直接相连, 可划分成同一模块; 反应器和气液分离器通过生成物冷凝器、循环压缩机等单元实现关联关系, 故此可以划分成同一模块; 最后气液分离器和汽提塔之间存在连接, 可视为同一模块.

|
图 1 田纳西伊斯曼过程 |
图1中第一子模块涵盖进料、反应器等重要单元, 且变量数量多, 结构复杂, 故选择以第一子模块进行分析, 表1对第一子模块过程变量进行描述.
| 表 1 第一子模块过程变量描述 |
第一子模块涉及进料之间的反应主要包括有: 在催化剂B作用下, A、C、D、E在反应器中发生放热反应, 产生生成物G与H以及副产物F, 反应器中部分没有反应的物料与产物一起输送到冷凝器, 冷凝器中反应生成的混合物进入气/液分离塔进行分离, 最后副产物从分离塔分离.
3.2 数据仿真与阈值处理在选择完实验模块之后, 以故障IDV(6), 即A进料发生缺失为例, 使用Matlab软件在Intel(R) Core(TM) i5-1035G1 CPU @1.00 GHz的条件下运行, 仿真72小时, 故障在系统运行12小时趋于稳定之后引入. 数据采样间隔为10分钟, 共360组数据. 考虑到前60组数据为正常状态, 故最终使用的数据为300组.
对于通过仿真得到的各变量过程数据, 为了减少后续计算资源的开销, 需要进一步处理转化成离散的报警数据. 同时为了将报警数据区分为高阈值报警和低阈值报警, 采用
| $ {L_a} = \left\{ {\begin{array}{*{20}{c}} {1, \; {V_p}(t) \geqslant \mu + 3\sigma } \\ {0, \; {V_p}(t) < \mu + 3\sigma } \end{array}} \right. $ | (3) |
| $ {H_a} = \left\{ {\begin{array}{*{20}{c}} {1, \; {V_p}(t) \geqslant \mu - 3\sigma } \\ {0, \; {V_p}(t) < \mu - 3\sigma } \end{array}} \right. $ | (4) |
其中,
| 表 2 过程变量的阈值设置 |
4 结果与讨论 4.1 构建报警传递网络
通过第3节的数据处理, 可获得16个离散时间序列. 接着使用获得的离散时间序列, 计算两两变量之间的传递熵, 对于得到的节点之间传递熵, 可进一步由节点之间的传递熵大小来确定两两节点之间的因果关系, 判断得到的结果如图2所示. 由图2可以看出, 该报警传播网络节点之间的关系十分复杂, 既无法有效确定报警根源, 同时也不能确定哪条路径为最有可能的传递路径. 为了进一步简化该报警流程图, 保留节点之间最相关的路径, 需要利用改进K2算法进行网络结构学习.
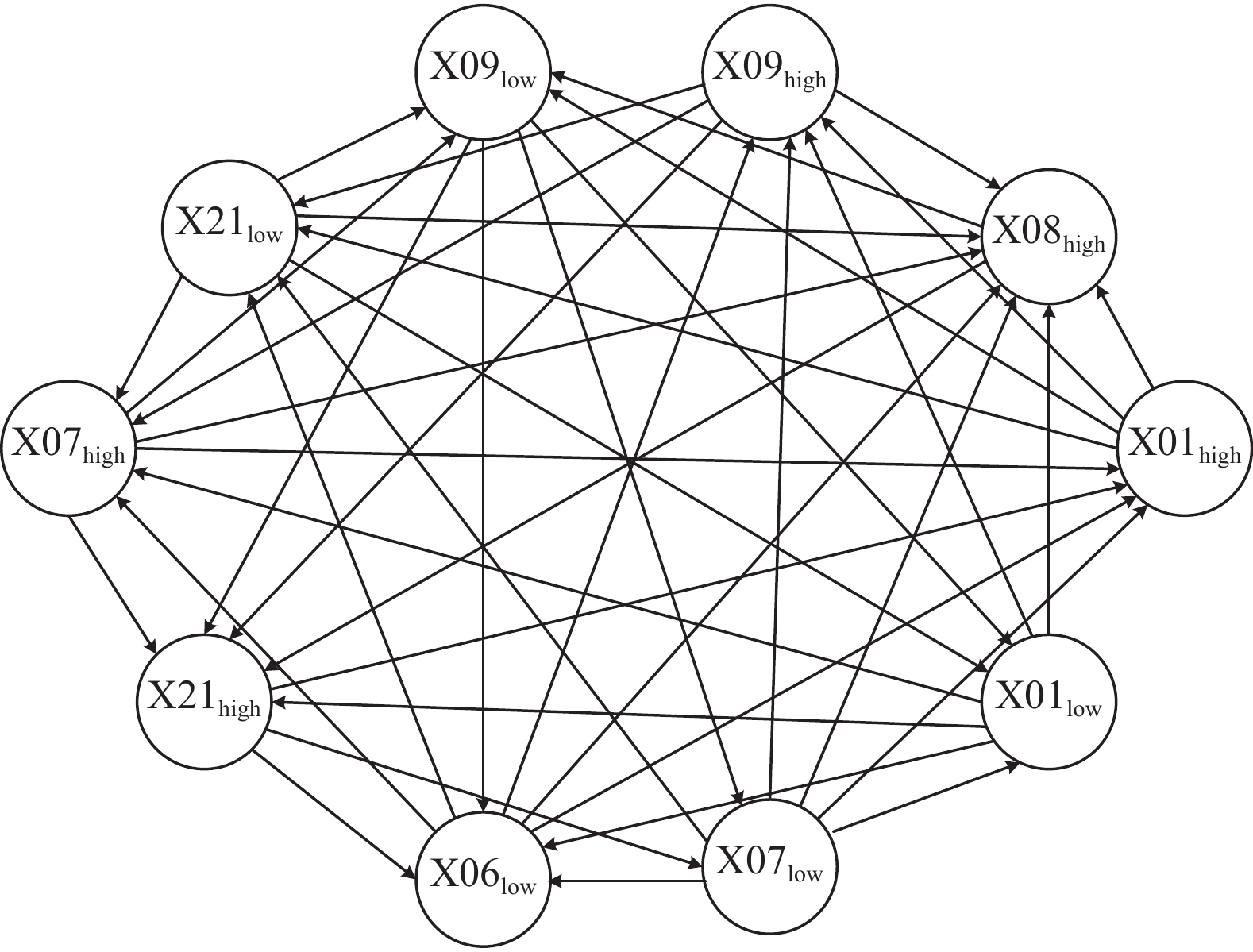
|
图 2 初步判断因果关系后得出的因果图 |
但改进K2算法无法对节点之间存在循环现象, 即节点之间成环的网络进行学习, 因此需要利用算法1对初步得到的因果图进行去环操作, 通过记录每个节点的子节点和祖先节点, 每次选择网络中节点之间传递熵最大的节点进行判断, 以此来保留网络之中传递可能性最大的边, 再判断节点的子节点是否为其祖先节点, 若是则舍弃该节点与子节点的关系, 反之则保留节点之间的关系. 重复以上操作之后, 得到无环因果图. 之后通过得到的无环因果图确定各个节点的父节点, 利用已知节点之间的报警数据与节点数, 由算法2对网络结构进行学习, 将得分最高的网络结构作为最终报警传播网络, 获得结果如图3所示.

|
图 3 最终得到的报警传播网络 |
图3较图2的复杂程度大大较低, 通过图3可以看出, 得到的报警传播网络准确地判断出导致故障发生的根本原因是由于A进料缺失, 即图中X01产生低阈值报警. 由于缺少A进料, 导致进料速度降低, 并且由于反应器所发生反应为放热反应, 当在短时间不再放热时温度下降会导致内部压力值降低, 为确保反应器温度维持在反应能够发生的温度, 势必会导致反应器内部温度升高和冷却水温度升高. 同时, 发生进料速度过慢的报警之后, 会提高A进料添加速度和反应器液位值升高, 而在进料速度到达高阈值之后, 又会导致冷却水出口温度下降, 通过上述分析得知该报警传播网络不仅准确定位出故障发生根本原因, 而且较好地学习得到关键的报警传播路径.
4.2 实验对比分析本节将本文提出的评分函数与不同评分函数求得报警传播网络进行对比, 主要比较每个评分函数对于各节点之间具有明显因果关系和网络整体的学习情况. 选择的第1种评分函数为BIC (Bayesian information criterion)[18], BIC通过测量网络对应的信息流得分来判断网络的结构, 学习得到的最终网络结构连接关系往往较为简单, 其计算结构的得分公式为:
| $ BIC = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{{q_i}} {\sum\limits_{k = 1}^{{r_i}} {{P_{ijk}} \log \left(\frac{{{P_{ijk}}}}{{{P_{ij}}}}\right)} } } - \frac{1}{2} \log (m)\sum\limits_{i = 1}^n {({r_i} - 1){q_i}} $ | (5) |
其中,
第2种评分函数为K2[19], K2需要预先知道节点之间的传递关系, 利用节点的传递关系来学习最终的网络结构, 其计算结构的得分公式为:
| $ K={\displaystyle \prod _{i=1}^{n}{\displaystyle \prod _{j=1}^{{q}_{i}}\frac{({r}_{i}-1)!}{({N}_{ij}+{r}_{i}-1)!}{\displaystyle \prod _{k=1}^{{r}_{i}}{N}_{ijk}!}}} $ | (6) |
其中,
第3种评分函数为TE[20], 和BIC一样通过测量网络对应的信息流得分来判断网络结构的优劣, 不同的是TE直接将传递熵的值作为评分准则, 其计算结构的得分公式为:
| $ TE = \sum\limits_{i = 1}^n {{T_{{x_{{i_p}}} \to {x_i}}} - \log ({q_i}({r_i} - 1))} $ | (7) |
其中,
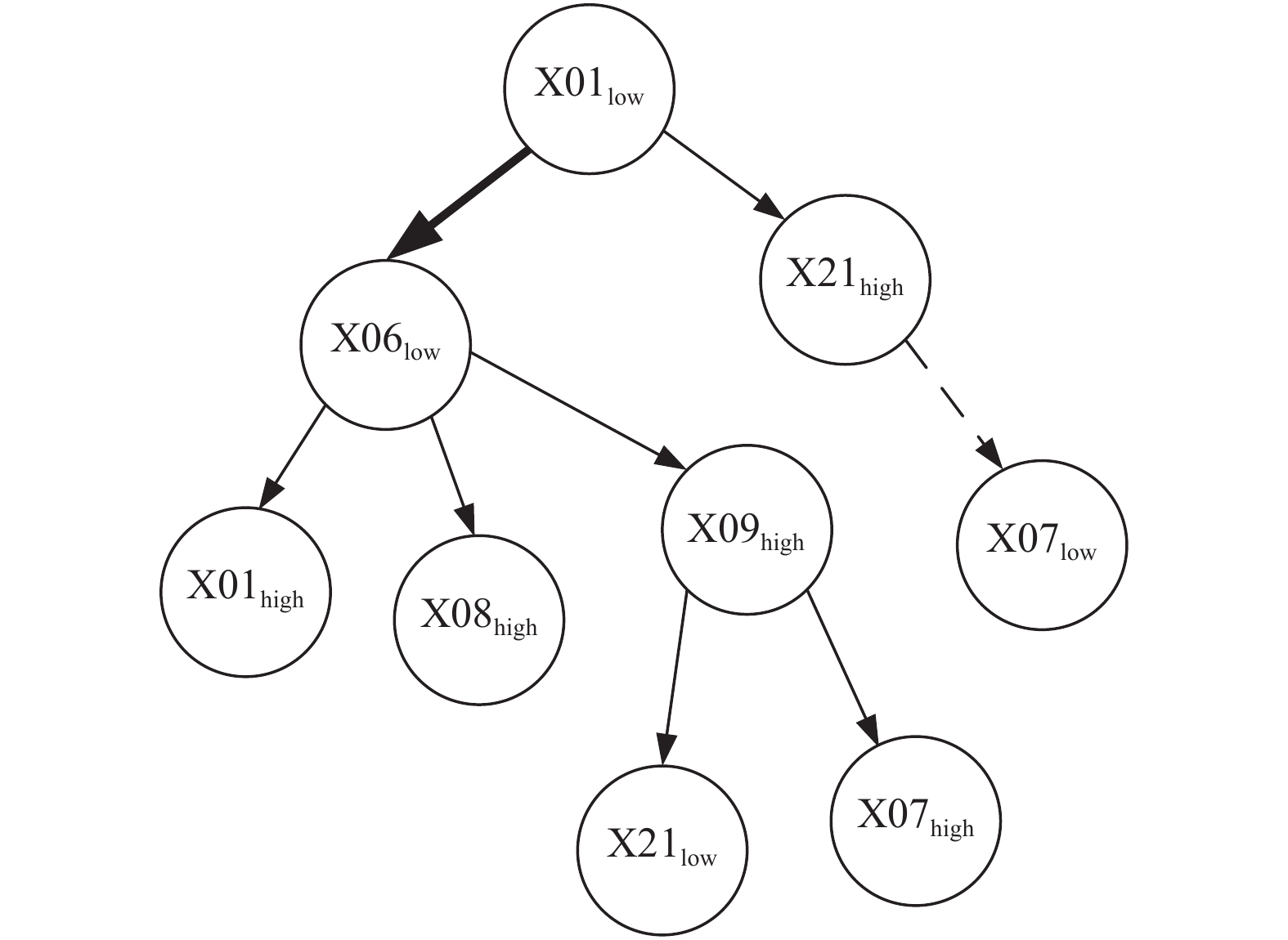
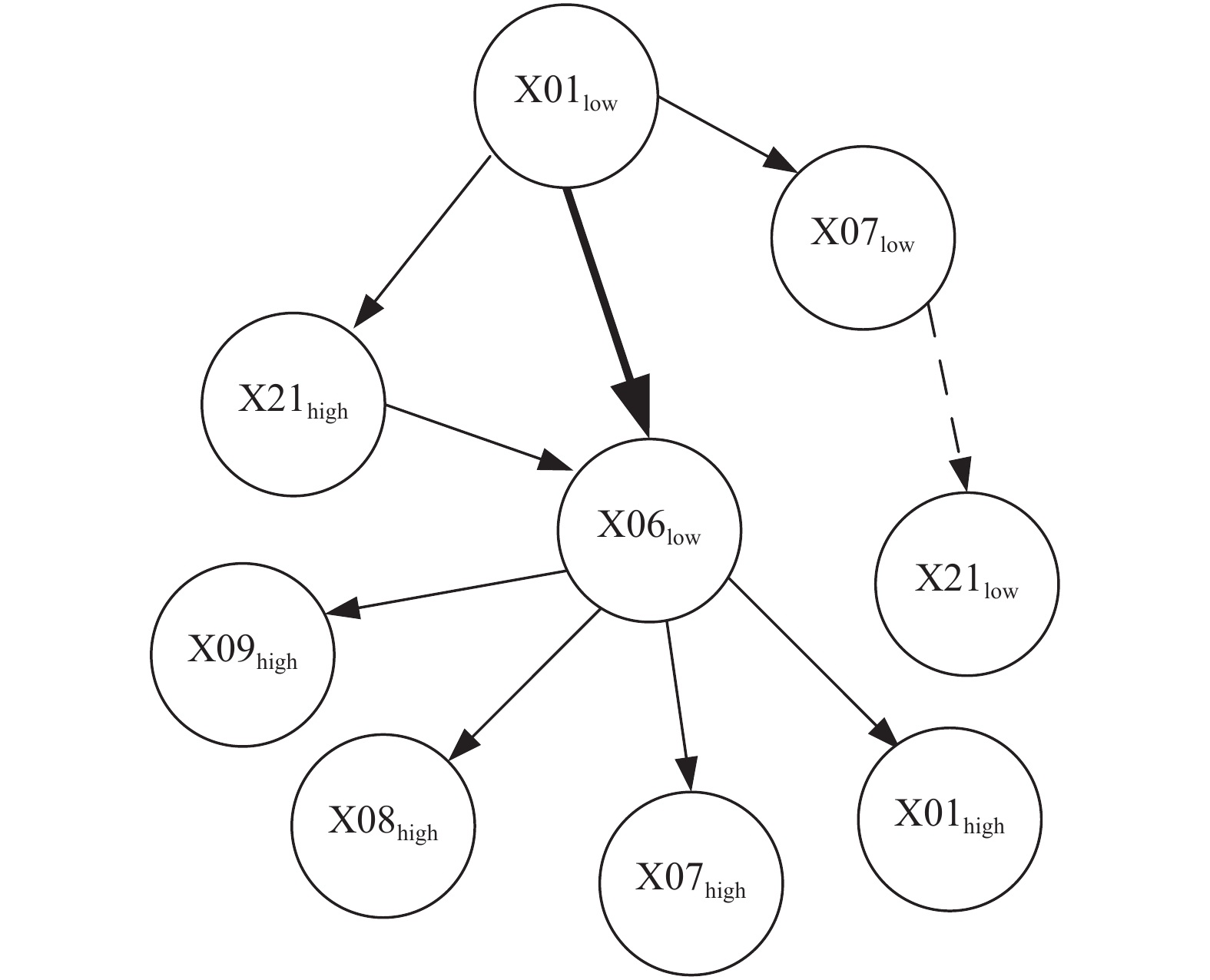
由上述评分函数的计算方式, 可分别得出4种不同的报警传播网络, 如图4–图7所示. 其中, 细实线代表学习得到的报警传播关系符合工业过程变量间关系, 虚线代表学习得到的报警传播关系不符合工业过程变量间关系, 粗实线代表未学习到的重要变量间关系. 表3罗列各个评分函数对于节点之间具有明显因果关系节点之间的学习情况, 表4对图4–图7进行整体分析, 分别统计了细实线, 粗实线和虚线的数量, 以及学习正确率.

|
图 4 BIC评分求得的报警传播网络 |
|
图 5 K2评分求得的报警传播网络 |
|
图 6 TE评分求得的报警传播网络 |
在表3中, Y表示变量间因果关系得到正确学习, N表示未能够正确学习变量间因果关系. 从表3中发现本文提出的方法对于节点之间所具有的明显因果关系可以进行准确地学习, 而对于其他评分函数, 并不能对明显的因果关系进行很好的学习. 尤其是TE评分函数, 其进行学习之后, 只能得到两对正确的因果关系. 在得到各评分函数对于明显因果关系的学习情况之后, 接下来对各评分函数所得到报警传播网络进行整体分析, 以确定其对各节点因果关系的学习情况.
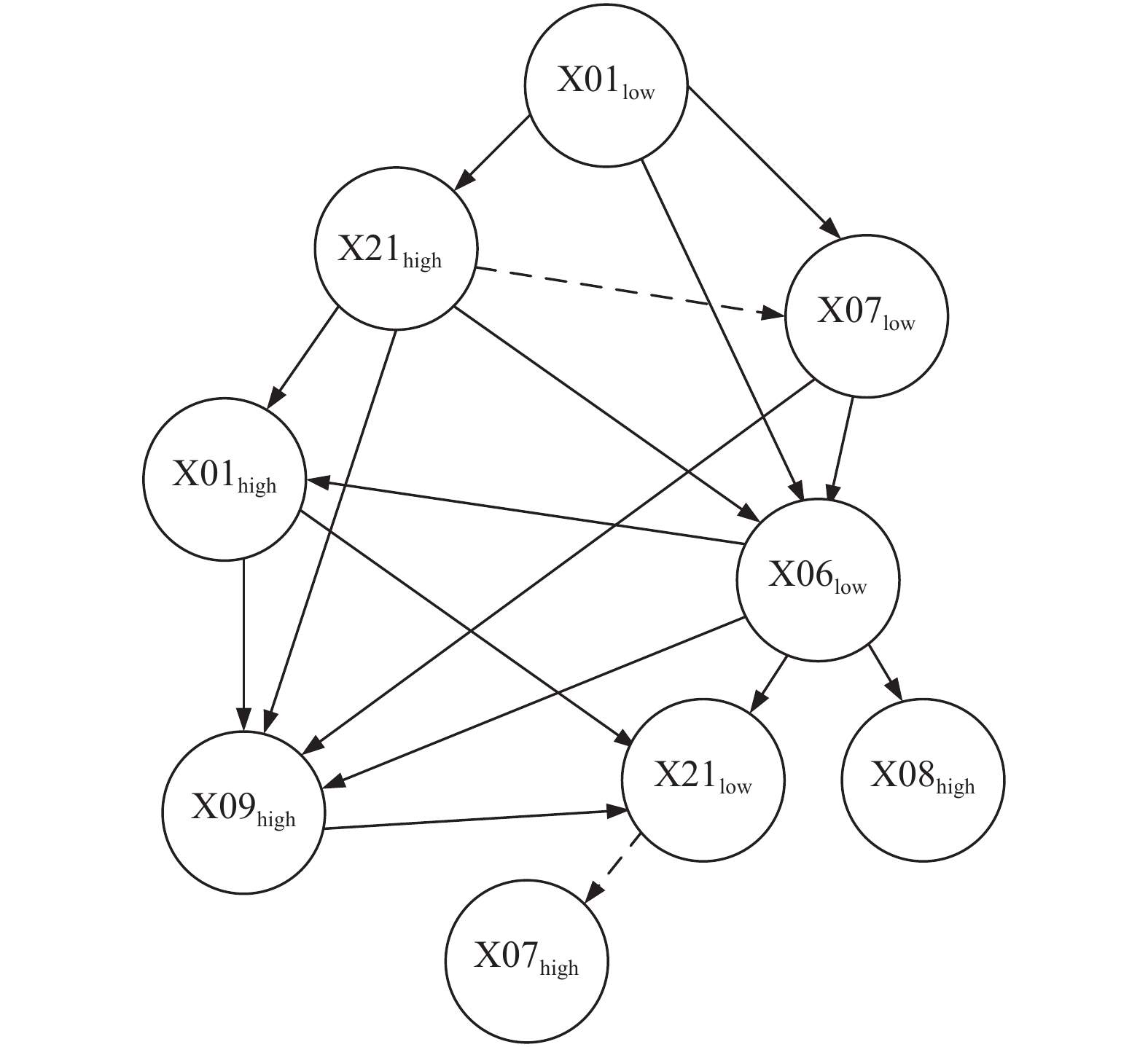
|
图 7 本文方法求得的报警传播网络 |
从表4可以看出, 对于网络整体的学习情况, 本文提出的方法不仅能够学习到较多的因果关系, 使得构建地报警传播网络较为完善, 而且对于每一个变量之间的因果关系都做出了较好地判断, 使得判断的准确率较高. 基于BIC评分求得的报警传播网络虽然能较好地定位到故障发生根本原因, 但对于很多重要的报警传播路径却没有判断出来, 同时没能够正确判断某些变量之间的关系, 使其获得的结构准确率最低. 基于TE评分求得的报警传播网络也存在类似于BIC评分的问题, 一方面没有学习到重要变量之间的关系, 另一方面对于某些变量之间的因果关系判断出错, 从而导致获得的结构准确率比较低. 而对于基于K2评分学习得到的传播网络, 虽然结构的准确率比其他两种学习方法要高, 但其网络结构却最为简单, 学习得到变量之间正确关系的条数最少, 尽管能够定位到故障发生的根本原因, 但不能够反映更多关于此次报警传递过程的信息, 也没办法进一步对报警做更多分析.
本文提出的方法以变量处于不同状态的时间作为权重, 对K2评分方法做出改进, 综合考虑各变量潜在父节点的排列组合, 保留得分最高的父节点和相应的子结构, 从而进一步确定网络结构. 得到的报警传播网络在准确定位故障发生根本原因的同时, 也能够对变量之间重要的传播关系做出判断, 有利于解决“报警泛滥”.
| 表 3 使用不同评分函数对具有明显因果关系节点检测结果比较 |
| 表 4 各评分方法网络结构学习结果统计 |
5 总结
本文提出了采用传递熵和改进K2算法解决工业生产环境上的“报警泛滥”问题, 改进K2算法的时间复杂度较K2算法的时间复杂度变动不大, 依旧为
| [1] |
张泽生, 李宏光, 杨博, 等. 基于置信规则库推理的过程报警预测方法. 控制工程, 2019, 26(4): 765-772. DOI:10.14107/j.cnki.kzgc.161267 |
| [2] |
员天佑, 王晓丽, 安宝冉, 等. 基于专家知识和模糊推理的大科学装置故障诊断方法. 计算机测量与控制, 2019, 27(2): 6-8, 42. DOI:10.16526/j.cnki.11-4762/tp.2019.02.002 |
| [3] |
Mondal PP, Ferreira PM, Kapoor SG, et al. Monitoring and diagnosis of multistage manufacturing processes using hierarchical Bayesian networks. Procedia Manufacturing, 2021, 53: 32-43. DOI:10.1016/j.promfg.2021.06.007 |
| [4] |
Tian C, Zhao CH, Fan HD, et al. Causal network construction based on convergent cross mapping (CCM) for alarm system root cause tracing of nonlinear industrial process. IFAC-PapersOnLine, 2020, 53(2): 13619-13624. DOI:10.1016/j.ifacol.2020.12.858 |
| [5] |
Dorgo G, Palazoglu A, Abonyi J. Decision trees for informative process alarm definition and alarm-based fault classification. Process Safety and Environmental Protection, 2021, 149: 312-324. DOI:10.1016/j.psep.2020.10.024 |
| [6] |
Ragab A, El-Koujok M, Poulin B, et al. Fault diagnosis in industrial chemical processes using interpretable patterns based on logical analysis of data. Expert Systems with Applications, 2018, 95: 368-383. DOI:10.1016/j.eswa.2017.11.045 |
| [7] |
Song PY, Zhao CH. Sparse adjacency forecasting and its application to efficient root cause diagnosis of process faults. IFAC-PapersOnLine, 2021, 54(3): 439-444. DOI:10.1016/j.ifacol.2021.08.281 |
| [8] |
Xu YZ, Wang JD, Yu Y. Alarm event prediction from historical alarm flood sequences based on Bayesian estimators. IEEE Transactions on Automation Science and Engineering, 2020, 17(2): 1070-1075. DOI:10.1109/TASE.2019.2935629 |
| [9] |
Liu Y, Chen HS, Wu HB, et al. Simplified granger causality map for data-driven root cause diagnosis of process disturbances. Journal of Process Control, 2020, 95: 45-54. DOI:10.1016/j.jprocont.2020.09.006 |
| [10] |
Lee HD, Kim C, Lim S, et al. Data-driven fault diagnosis for chemical processes using transfer entropy and graphical lasso. Computers & Chemical Engineering, 2020, 142: 107064. DOI:10.1016/j.compchemeng.2020.107064 |
| [11] |
Yang YH, Kang WQ, Liu XZ. Fault diagnosis based on online dynamic integration model and transfer entropy. Measurement, 2022, 193: 110946. DOI:10.1016/j.measurement.2022.110946 |
| [12] |
Ma L, Dong J, Peng KX, et al. A novel data-based quality-related fault diagnosis scheme for fault detection and root cause diagnosis with application to hot strip mill process. Control Engineering Practice, 2017, 67: 43-51. DOI:10.1016/j.conengprac.2017.07.005 |
| [13] |
Chen QM, Lang X, Lu S, et al. Detection and root cause analysis of multiple plant-wide oscillations using multivariate nonlinear chirp mode decomposition and multivariate Granger causality. Computers & Chemical Engineering, 2021, 147: 107231. DOI:10.1016/j.compchemeng.2021.107231 |
| [14] |
Amin MT, Khan F, Ahmed S, et al. A data-driven Bayesian network learning method for process fault diagnosis. Process Safety and Environmental Protection, 2021, 150: 110-122. DOI:10.1016/j.psep.2021.04.004 |
| [15] |
Yin YM, Duan XJ. Information transfer among the components in multi-dimensional complex dynamical systems. Entropy, 2018, 20(10): 774. DOI:10.3390/e20100774 |
| [16] |
Su JJ, Wang DZ, Zhang YN, et al. Capturing causality for fault diagnosis based on multi-valued alarm series using transfer entropy. Entropy, 2017, 19(12): 663-681. DOI:10.3390/e19120663 |
| [17] |
Jang K, Hong S, Kim M, et al. Adversarial autoencoder based feature learning for fault detection in industrial processes. IEEE Transactions on Industrial Informatics, 2022, 18(2): 827-834. DOI:10.1109/TII.2021.3078414 |
| [18] |
Watanabe S. A widely applicable Bayesian information criterion. Journal of Machine Learning Research, 2013, 14(1): 867-897. |
| [19] |
Aghdam R, Tabar VR, Pezeshk H. Some node ordering methods for the K2 algorithm. Computational Intelligence, 2019, 35(1): 42-58. DOI:10.1111/coin.12182 |
| [20] |
Yu J, Rashid MM. A novel dynamic Bayesian network-based networked process monitoring approach for fault detection, propagation identification, and root cause diagnosis. AIChE Journal, 2013, 59(7): 2348-2365. DOI:10.1002/aic.14013 |
 2023, Vol. 32
2023, Vol. 32


