2. 河北省地质矿产勘查开发局第六地质大队, 石家庄 050086
2. The Sixth Geological Brigade of Hebei Bureau of Geology and Mineral Exploration and Development, Shijiazhuang 050086, China
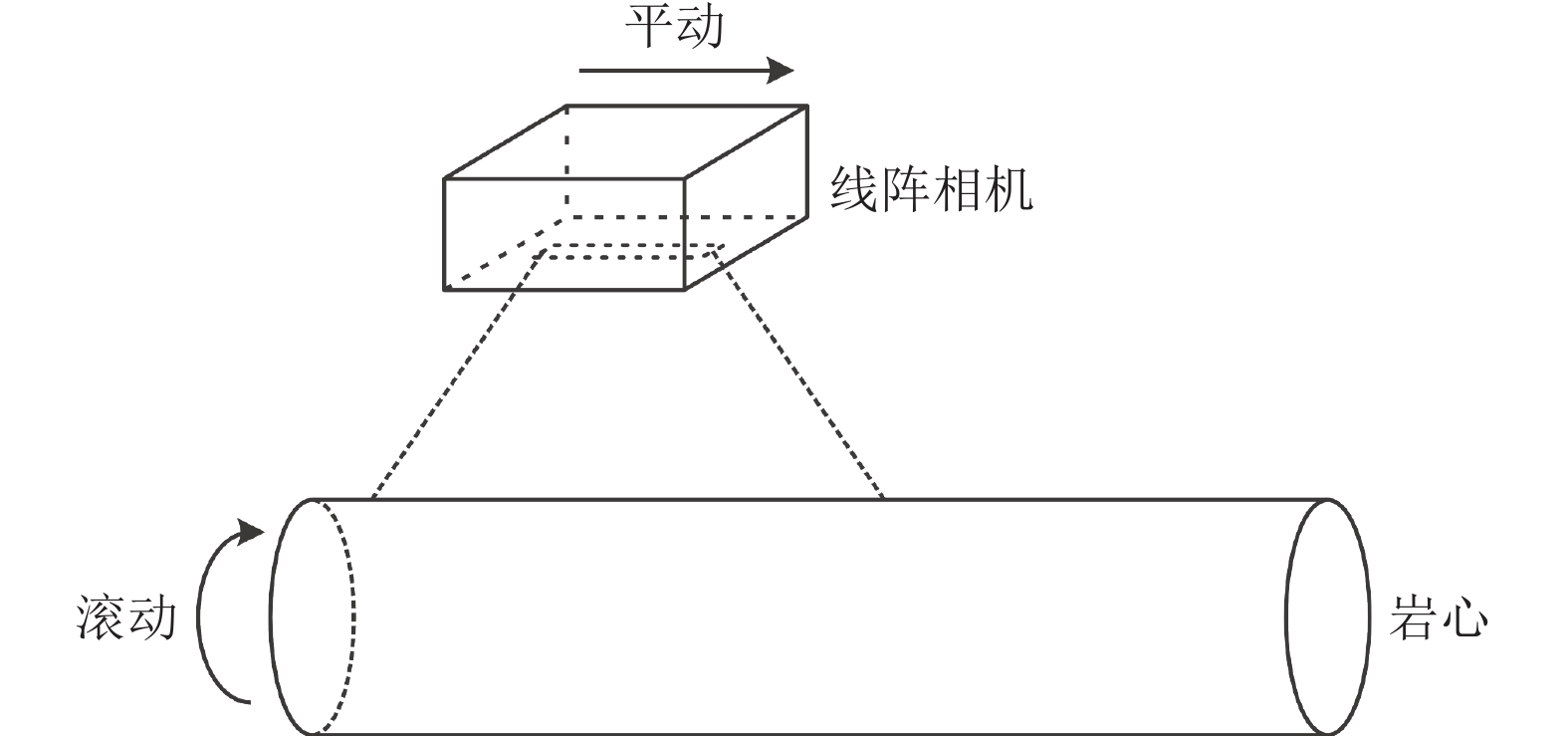
在地质勘探工作中, 科研人员利用特殊的取芯设备从地质层中取出圆柱状岩石样品, 即岩心. 为了解决大量岩心的存放和共享问题, 需要将岩心数字化保存[1]. 滚动扫描是采集岩心图像的方式之一, 通过线阵相机与岩心表面的相对运动来采集图像, 如图1所示. 由于相机视野的限制, 每一次只能采集一定长度的岩心图像, 为了得到完整的图像, 需要将多幅岩心图像拼接起来. 采用自动化的图像拼接技术能节省大量人工劳动, 同时提高图像拼接的准确性, 从而提高工作效率.
|
图 1 滚动扫描示意图 |
常见图像拼接流程包括图像预处理、图像配准以及图像融合[2], 其中不同的图像配准方法直接导致不同的时间复杂度和拼接准确性, 图像配准中最重要的是特征点提取与匹配, 常见的方法有SIFT (scale-invariant feature transform)算法[3]. SURF (speeded-up robust features)算法[4]和ORB (oriented FAST and rotated BRIEF)算法[5]. 由于岩心图像分辨率高, 可提取的特征点数量大, 使用ORB特征点能在满足特征点精度的同时保证提取速度, 从而减少了整个拼接过程的耗时. RANSAC算法是常见的特征点提纯算法, 但存在迭代次数多, 且由于随机性带来的不稳定性. 不同的图像融合方法导致拼接细节的差异性[6]. 常见的图像融合方法是渐进渐出加权平均算法, 根据此方法拼接之后的重合区域能实现平滑过渡[7]. 但是对于一些具有一定扭曲角度的岩心图像来说, 会在局部产生鬼影现象. 使用基于最佳缝合线[8]的金字塔融合方法能够避免鬼影的产生, 提升拼接图像的细节.
针对上述可能出现的问题, 本文提出一种应用于岩心图像的拼接方法, 首先使用ORB算法提取待拼接图像的特征点, 然后使用改进的RANSAC算法对提取的特征点进行提纯, 最后使用基于最佳缝合线的金字塔融合方法进行图像融合, 完成岩心图像的拼接. 该方法能在满足拼接速度与准确性的基础上, 减少图像拼接的鬼影问题, 实现较好的拼接效果.
1 相关工作本文提出的岩心图像拼接方法主要包括岩心图像的采集、灰度变换、特征点提取与匹配、图像配准与融合等步骤. 以下分别对步骤中常见的技术进行介绍.
1.1 特征点提取与匹配ORB算法使用图像中的关键点快速创建特征向量, 并使用这些向量来识别对象. ORB算法使用高效的FAST (features from accelerated segment test)算法[9]来进行特征点检测, 使用BRIEF (binary robust inde-pendent elementary features)算法[10]来描述每一个特征点, 搜索此描述符的时间短. 为了保证拼接的速度, 本文使用ORB算法来提取特征点.
由ORB算法提取的特征点中会有部分错误匹配的特征点, 如果使用这些错误的匹配点进行配准将会有很大的误差. 最常用的方法是使用RANSAC算法对两幅图像中匹配的特征点进行提纯, 这是一种迭代的估计方法, 能够从大量数据中估算出比较好的数据模型[11]. RANSAC主要有以下步骤.
(1) 在图像提取的特征点集中, 随机抽取4个样本, 计算其单应性矩阵, 并将其所对应参数记为模型M0, 确定好阈值.
(2) 以此模型为基准, 计算集合中所有点到M0的距离, 若距离小于设定阈值, 则将此特征点加入到内点集S0中.
(3) 如果当前内点集中的特征点数大于最优的内点集, 则更新最优内点集Sb为S0.
(4) 重复步骤(1)–(3), 直到迭代次数达到设定值, 或者最优内点集Sb元素数达到设定值, 此时Sb内特征点对应的是最可靠模型, 算法结束.
1.2 图像配准与融合经过提纯后的特征点反映了两幅岩心图像之间正确的变换关系. 岩心图像的采集方式决定了两幅岩心图像之间不会有较复杂的变换关系, 通常为平移关系. 并且岩心图像分辨率很高, 使用平移关系计算而非单应性矩阵计算使计算速度更快, 因此本文通过平移关系进行图像配准.
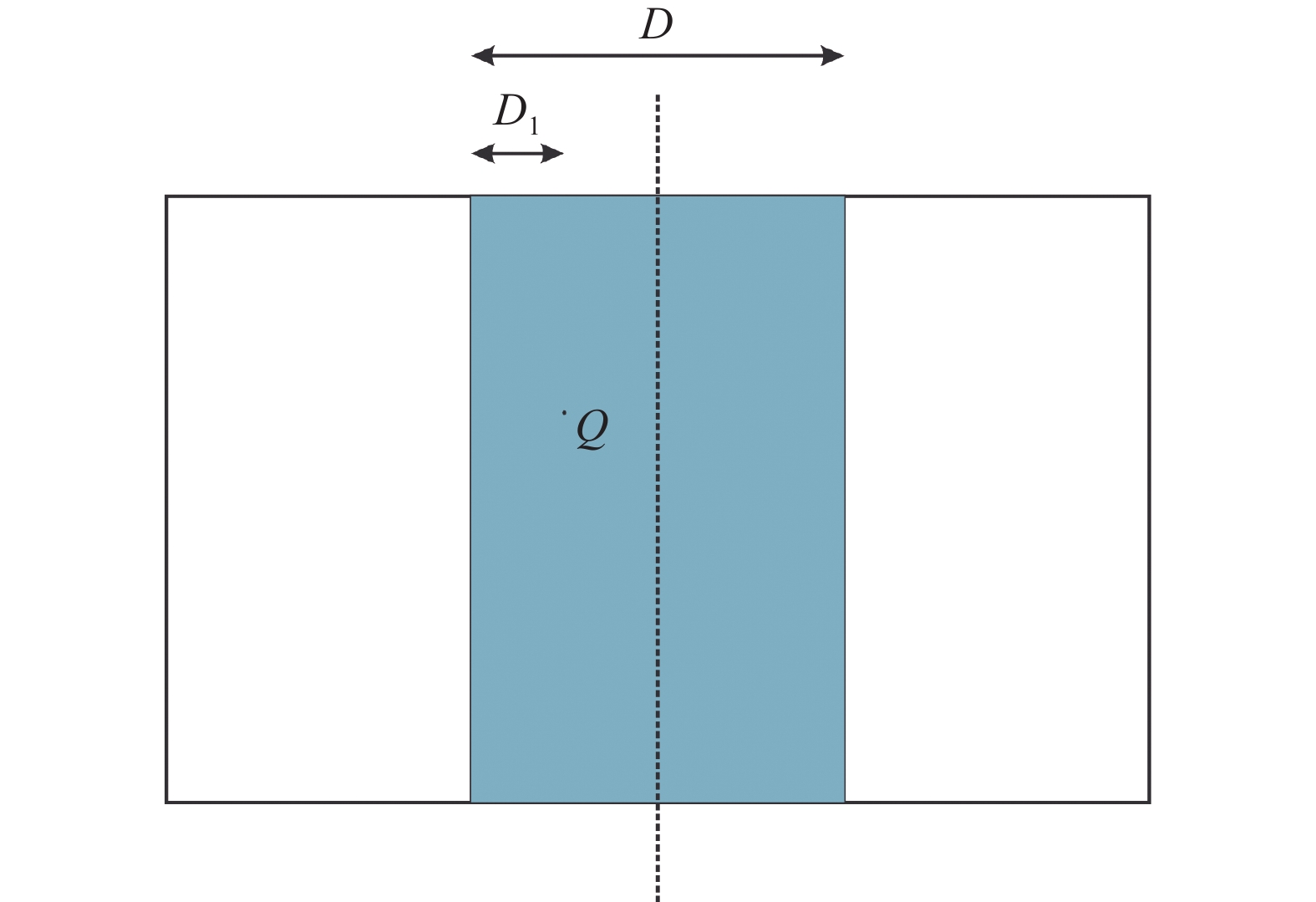
图像融合方法直接决定了岩心图像拼接的最终质量. 最简单的图像融合方法是将两幅图像重叠区域像素值求均值作为拼接图像对应位置的像素值. 简单融合会造成岩心图像拼接处有明显的亮度、色调差异, 使得拼接图像不自然, 从而影响岩心工作人员进行判断. 渐进渐出图像融合能在一定程度上解决简单融合带来的问题, 这是最常见的图像融合方法, 以两幅图像横向拼接为例, 如图2所示, 白色区域为非重叠区域, 可直接将左图和右图的对应点的像素值赋值给拼接图像. 对于有色重叠区域, 例如求Q点融合所得像素值, 则由左图和右图对应点像素值加权求和所得:
| $ I(x, y) = {W_1}{I_1}(x, y) + {W_2}{I_2}(x, y) $ | (1) |
其中, I(x,y)、I1(x,y)和I2(x,y)分别代表该点在拼接图像中的像素值、该点在左图中的像素值和该点在右图中的像素值. W1和W2分别是左图和右图中像素点的权重, 其计算方法为:
| $ \left\{ \begin{gathered} {W_1} = \frac{{D - {D_1}}}{D} \\ {W_2} = 1 - {W_1} \\ \end{gathered} \right. $ | (2) |
其中, D为重叠区域的总宽度, D1为Q点距离重叠区域左边界的宽度.
|
图 2 渐进渐出融合示意图 |
如图2所示, 渐进渐出图像融合将重叠区域的中间的虚线作为缝合线进行融合, 运算量小且简单, 因此被广泛使用.
使用以上方法, 能完成岩心图像的拼接. 但经过实际测试发现, 采用上述方法拼接速度不够理想, 且拼接处容易产生鬼影.
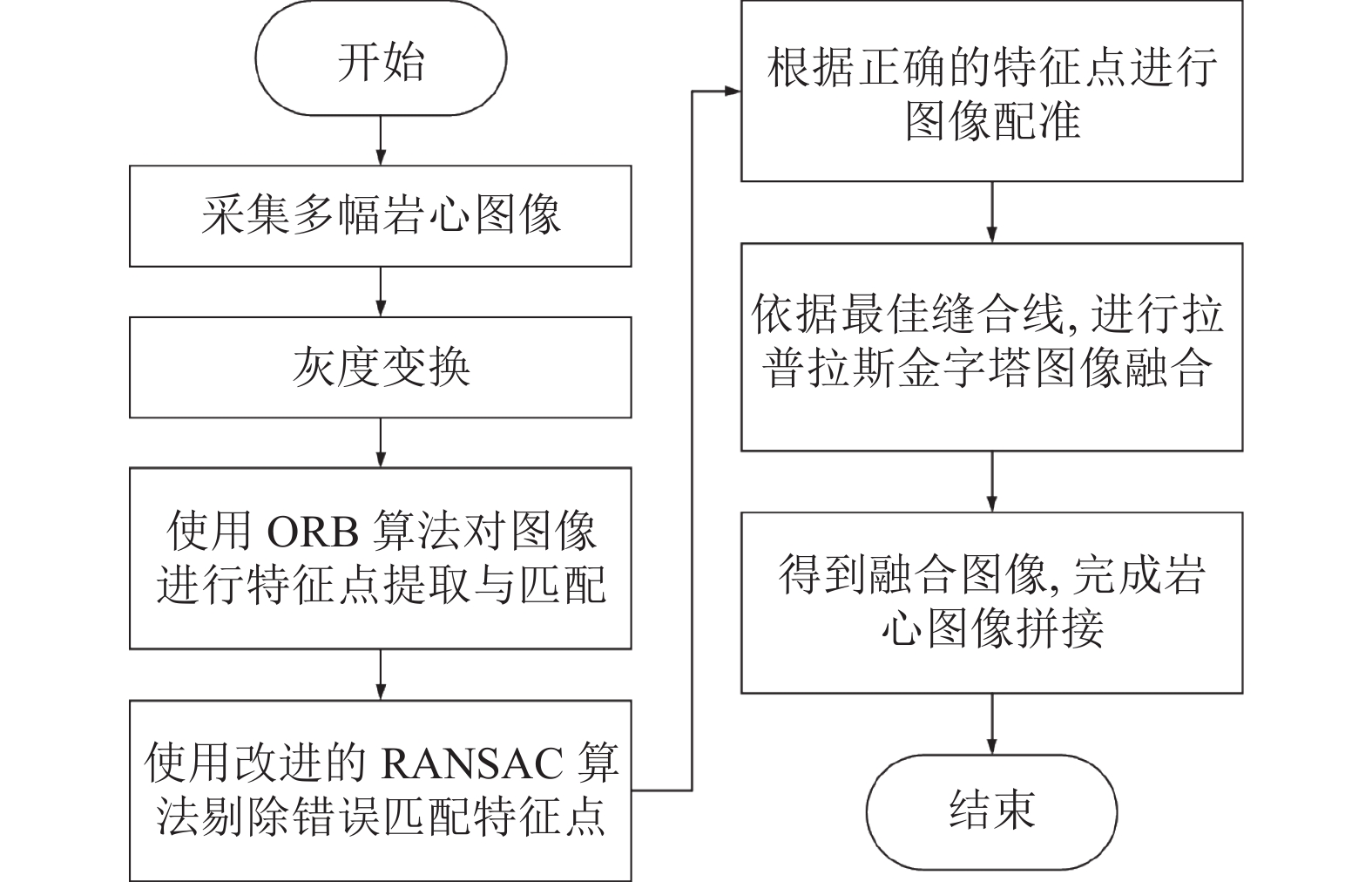
2 本文提出的方法本文提出的岩心图像拼接流程如图3所示. 首先对采集的多幅图像进行灰度变换, 以减少错误匹配点的数量. 使用ORB算法对灰度图像进行特征点的提取与匹配, 然后使用改进的RANSAC算法删除部分误匹配的特征点, 根据正确的特征点进行图像配准, 最后基于最佳缝合线进行拉普拉斯金字塔融合. 使用该方法进行岩心图像的拼接, 能在保证拼接实时性的同时保留更好的岩心图像纹理等细节. 以下分别对本文提出的改进RANSAC算法和结合最佳缝合线的拉普拉斯金字塔融合方法进行介绍.
|
图 3 岩心图像拼接流程 |
2.1 改进的RANSAC算法
理论上传统的RANSAC算法只要迭代次数足够, 就能够估算出最优内点集. 但由于下一次迭代与上一次迭代毫无关联, 其随机性可能导致在设定的迭代次数内无法找到内点集, 或找到的内点集元素数较少. 在迭代过程中, 下一次迭代取点不从全部特征点中选取, 而是从上一次迭代得到的最优内点集中选取, 这样能进一步加快迭代的速度. 同时, 在第一次迭代之前, 先对所有特征点对按其欧氏距离排序, 当最优内点集内元素数小于一定数量时, 要求随机点对在排序后的点对集合中下标之差不大于某设定值, 本文使用的设定值为全部匹配点对数量的10%. 这样能使算法快速进入有效迭代中, 且更快地达到迭代终止条件. 算法主要的步骤如下.
(1) 对匹配的特征点对按欧氏距离进行排序, 将排序后的特征点对存放在集合Ss中.
(2) 当最优内点集Sb元素数小于等于设定值时(本文设定为4), 从Ss中随机选取两对特征点对, 当这两对特征点对在Ss中的位置差大于Ss内元素总数的10%时, 重复步骤(2). 若Sb元素数大于设定值时, 则从Sb中随机选取两对特征点对.
(3) 根据选取的两对特征点对计算其单应性矩阵, 并将其所对应参数记为模型M0, 确定好阈值.
(4) 以此模型为基准, 计算集合Ss中的所有点到M0的距离, 若距离小于设定阈值, 则将此特征点加入到内点集S0中.
(5) 如果当前内点集S0中的特征点数大于最优的内点集, 则更新最优内点集Sb为S0.
(6) 重复步骤(2)–(5), 直到迭代次数达到设定值, 或者最优内点集Sb元素数达到设定值, 算法结束.
改进算法相比于原算法, 能在内点数较少时快速迭代到较多内点数的状态, 且在后续迭代过程中能以更快的速度达到迭代终止条件, 从而提升了原算法的速度.
2.2 结合最佳缝合线的拉普拉斯金字塔融合使用渐进渐出图像融合能完成岩心图像的融合, 但岩心图像细节较多, 在滚动扫描过程中岩心的滚动会导致该融合方法容易产生鬼影. 而且由于岩心采集设备的光照不均, 可能由于相机校色不准导致两幅岩心图像色彩不能很好过渡, 会导致拼接的岩心图像上在缝合线周围有较为明显的拼接缝. 针对这些问题, 本文提出结合最佳缝合线的拉普拉斯金字塔融合方法.
最佳缝合线[12]的核心思想是在重叠区域寻找最合适的拼接缝, 以解决融合后产生的鬼影现象. 一条理想的缝合线上的像素点在两幅图像上的颜色差异最小, 且在两幅图像上的几何结构最相近. 使用最佳缝合线能减小因岩心图像采集设备光照不均问题造成的色彩差异和岩心滚动过程中的晃动造成的轻微形变所造成的影响.
根据最佳缝合线位置, 将缝合线两边的像素值分别置为0和1, 可以得到拼接掩模图像. 掩模图像可用于后续的岩心图像融合, 它规定了待拼接图像的待拼接区域、权值等. 通过将掩模图像进行高斯模糊, 能够控制岩心图像拼接处的过渡效果. 待拼接岩心图像及对应掩模图像示例如图4所示.

|
图 4 待拼接图像及掩模图 |
进行图像融合之前, 需要对每幅图像构建拉普拉斯金字塔图像. 拉普拉斯金字塔的构建基于高斯金字塔. 在形成高斯金字塔的过程中, 下采样会造成图像的部分高频信息丢失, 为了保存这部分信息, 提出了拉普拉斯金字塔[13]. 通过拉普拉斯金字塔的构建, 能够将岩心图像的高频信息分解到多个不同的频带上, 在融合过程中同时考虑不同频段的信息, 保证了岩心图像融合后的细节保留.
本文提出结合最佳缝合线和拉普拉斯金字塔进行图像融合, 具体步骤如下.
(1) 计算最佳缝合线, 同时生成对应掩模图像.
(2) 两幅图像和掩模图像分别构建拉普拉斯金字塔.
(3) 对于每一层图像都使用掩模进行拼接, 此时可通过平滑掩模图像来控制拼接缝左右的亮度、色彩等差异.
(4) 每一层融合后得到融合图像的拉普拉斯金字塔, 进行图像重建即可得到所需融合图像.
通过本文的岩心图像融合方法, 保证了融合后的岩心图像的细节保留, 避免了鬼影的产生, 并且在融合区域实现了平滑的过渡, 使得融合后的图像更加符合人眼视觉特性.
3 实验结果与分析为了验证提出方法的效果, 本文进行了实验, 实验测试平台为Intel(R) Core(TM) i5-6500 CPU @ 3.20 GHz, 内存为8 GB, 开发环境为Visual Studio 2013. 本文使用3组待拼接的岩心图像进行测试, 每组都包含20幅(10对)待拼接的岩心图像, 每组岩心图像的尺寸分别为7404×9321、3700×4821和3700×4616, 以下实验结果均为每组实验结果平均值.
本文首先使用ORB算法对两幅待拼接岩心图像进行特征点提取. 在提取了特征点后, 需要将特征点进行匹配. 为验证文中使用的匹配特征点提纯方法的有效性, 将本文所提出的改进RANSAC算法与原RANSAC算法进行对比, 结果如表1所示. 实验结果表明, 本文提出的改进RANSAC算法在匹配点正确率变化微小的情况下, 大幅提升特征点匹配的速度.
| 表 1 匹配结果对比 |
文献[14]介绍了一种图像拼接质量评价方法DoEM(difference of edge map), 此方法基于图像边缘信息来评价拼接质量, 该文献中的实验证明此评价方法符合人眼视觉对图像的主观评价感受. 其计算方法为:
| $ DoEM = {{\rm{e}}^{ - \frac{{{\sigma ^2}}}{{{e_4}}}}}\left(\frac{{{\mu _e}{{\rm{e}}^{ - \frac{{{\mu _e}}}{{{c_1}}}}} + {\mu _a}{{\rm{e}}^{ - \frac{{{\mu _a}}}{{{c_2}}}}}}}{{{\mu _e} + {\mu _a}}}\right) + \left(1 + {{\rm{e}}^{\frac{{ - {\sigma ^2}}}{{{e_4}}}}}\right){{\rm{e}}^{\frac{{ - {\sigma ^2}}}{{{c_3}}}}} $ | (3) |
其中, μe为边缘差分谱过渡区域边界区均值, μa为过渡区域整体均值, σ2为过渡区域整体方差. 式中4个常量分别取值为c1=80, c2=50, c3=600, c4=256. 根据文献[14], DoEM值越大说明图像拼接效果越好.
以3组测试图为例, 将本文图像融合算法与渐进渐出融合和文献[15]的非线性权重图像融合算法进行比较, 以左图的待融合区域作为真实场景图, 使用3种客观评价指标对岩心图像融合部分进行评价, 对比结果如表2所示. 从客观评价指标的分数来看, 计算3组实验对象的平均值, 本文提出的融合方法优于另外两种方法, 相比渐进渐出融合在PSNR、SSIM和DoEM这3种指标上分别提升14.3%、5.6%和47.0%, 相比文献[15]在PSNR、SSIM和DoEM这3种指标上分别提升20.5%、4.4%和55.6%, 且本文算法更加符合人眼视觉特性.
| 表 2 不同图像融合方法对比 |
从3组实验对象中各取一张拼接图像的局部融合区域放大, 对比结果如图5所示. 可见图5(b)、图5(e)、图5(h)对应的图像有较为明显的鬼影现象, 而使用本文方法融合的岩心图像能避免鬼影现象. 使用本文方法拼接的最终结果示例如图6所示, 拼接结果图色彩过渡自然, 与真实场景更加相近, 符合人眼视觉特性.

|
图 5 图像融合效果对比 |

|
图 6 岩心图像拼接结果 |
4 结论
在采集岩心图像的过程中, 需要快速准确地实现多张岩心图像间的拼接. 本文提出了一种岩心图像自动拼接算法, 在特征点提取与匹配速度上较快, 能满足实时性要求. 使用本文的改进RANSAC算法能在较短时间内完成特征点匹配. 对于渐进渐出融合方法在岩心图像上产生的鬼影等问题, 本文提出结合最佳缝合线和拉普拉斯金字塔的图像融合方法, 使拼接后的图像质量和效果更好, 并在客观评价指标上获得了更高的分数. 本文所提出的方法具有一定的实际应用价值, 已在部分地质部门用于实际生产作业中.
| [1] |
陈春霞, 修连存, 高扬. 岩心光谱扫描仪数据处理应用研究. 光谱学与光谱分析, 2019, 39(5): 1630-1636. |
| [2] |
刘鹏飞, 高如新. 基于相位相关法与改进SURF算法的图像拼接方法. 软件导刊, 2019, 18(11): 157-160, 164. |
| [3] |
Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [4] |
Bay H, Ess A, Tuytelaars T, et al. Speeded-up robust features (SURF). Computer Vision and Image Understanding, 2008, 110(3): 346-359. DOI:10.1016/j.cviu.2007.09.014 |
| [5] |
Rublee E, Rabaud V, Konolige K, et al. ORB: An efficient alternative to SIFT or SURF. Proceedings of the 2011 International Conference on Computer Vision. Barcelona: IEEE, 2011. 2564–2571.
|
| [6] |
周华兵, 侯积磊, 吴伟, 等. 基于语义分割的红外和可见光图像融合. 计算机研究与发展, 2021, 58(2): 436-443. DOI:10.7544/issn1000-1239.2021.20200244 |
| [7] |
刘杰, 游品鸿, 占建斌, 等. 改进SIFT快速图像拼接和重影优化. 光学 精密工程, 2020, 28(9): 2076-2084. DOI:10.37188/OPE.20202809.2076 |
| [8] |
牟琦, 唐洋, 李占利, 等. 基于网格运动统计算法和最佳缝合线的密集重复结构图像快速拼接方法. 计算机应用, 2020, 40(1): 239-244. |
| [9] |
王柔, 冯冲, 张俊星, 等. 图像FAST角点检测算法的FPGA实现与系统集成. 单片机与嵌入式系统应用, 2021, 21(2): 55-58. |
| [10] |
刘欢蝶, 龚涛, 章庆伟, 等. 基于FAST和BRIEF的密度聚类图像匹配算法改进. 测绘与空间地理信息, 2020, 43(3): 54-57. DOI:10.3969/j.issn.1672-5867.2020.03.015 |
| [11] |
方林波, 石昊苏, 路雅宁, 等. 基于RANSAC的道路影像控制点选取方法研究. 电子设计工程, 2021, 29(6): 142-147. DOI:10.14022/j.issn1674-6236.2021.06.028 |
| [12] |
罗顺元, 苍岩, 乔玉龙. 一种改进的最佳缝合线算法. 应用科技, 2019, 46(6): 1-5. DOI:10.11991/yykj.201906015 |
| [13] |
江海军, 陈力. 拉普拉斯金字塔融合在红外无损检测技术中的应用. 红外技术, 2019, 41(12): 1151-1155. |
| [14] |
万国挺, 王俊平, 李锦, 等. 图像拼接质量评价方法. 通信学报, 2013, 34(8): 76-81. DOI:10.3969/j.issn.1000-436x.2013.08.010 |
| [15] |
徐启文, 唐振民, 姚亚洲. 基于改进SURF算法的图像拼接研究. 南京理工大学学报, 2021, 45(2): 171-178. DOI:10.14177/j.cnki.32-1397n.2021.45.02.006 |
 2023, Vol. 32
2023, Vol. 32


