如今的社会是一个互联网高速发展的社会, 大量互联网公司和政府部门每天运营中产生海量的数据^[1], 数据的价值和重要性不言而喻, 因此如何维护数据的可靠性和稳定性^{[2, 3]}是急需要解决的关键技术. 现有的集中式存储主要靠数据服务器和存储设备^[4]. 但是集中式存储, 设备价格昂贵, 而且需要大量的管理时间以及维护成本^[5]. 集中式存储一旦遭到破坏, 数据将永久毁灭. 相较于集中式存储, 具有可扩展、设备成本低、高性能、易用性的分布式存储系统成为目前主流存储系统^[6]. 分布式存储对数据的存储采用的策略是复制策略和纠删码策略^{[7, 8]}. 复制策略就是把需要存储的原始文件复制 $ n $ 份, 然后对复制的所有数据进行存储, 通过复制的副本数据来保障数据的可靠性, 当出现数据损坏, 可以直接复制副本数据快速修复, 整个过程简单易实施, 但复制策略的缺陷是存储开销大^[9].

与复制策略相比, 纠删码策略只需要存储少量的编码数据块. 使系统的存储开销得到有效地降低, 同时纠删码策略通过编码产生的校验数据块, 使系统具有更好的容错性. 但在分布式存储系统中通过纠删码对故障节点进行修复时, 系统需要消耗较大的修复带宽开销^[10]. 目前里所(reed-solomon, RS)码和磁盘阵列码^[11]等典型的纠删码被广泛应用于分布式存储系统中. 如图1所示为 RS编码和重构原理过程. 当其中任意一个数据块发生故障, 都可以通过解码恢复出故障数据块.

针对复制策略和纠删码策略等局限性^{[12, 13]}, 研究者通过研究发现在存储开销跟修复带宽开销之间折中, 提出简单再生码(simple regenerating codes, SRC)的编码方式^[14]. 简单再生码是通过大量的有限域运算编码构造^[15]. 不需要消耗大量的存储开销, 并且在修复故障节点时, 只需要连接相应节点就可以修复数据, 修复带宽开销较低. 但修复过程需大量解码运算, 使得修复过程非常复杂, 修复时间增多, 而且还需要连接多个节点进行修复, 因此修复局部性高^[16].

部分重复(fractional repetition, FR)码^[17]无需进行有限域运算, 同时也可以降低节点存储开销^[18]. 在对故障节点修复时, 具有较低的修复局部性和修复带宽开销^{[19, 20]}. 因此, 部分重复码被广泛研究. 目前主流的FR码构造方法有如下几种: 基于正则图、分组设计^[21]及可分解设计^[22], 但构造过程复杂, 且不能灵活选择部分重复码的构造参数, 不适应实际的存储系统^{[23, 24]}. 因此提出基于完全图图因子分解的部分重复(complete graph factorization based FR, CGFBFR)码的构造算法.

图 1

Fig. 1

图 1 RS编码和重构原理

图的因子分解是图分解的一种方法, 记图 $ G $ 表示为 $ G = (V, {\text{ }}E) $ , 图 $ H $ 为图 $ G $ 的子图, 满足 $ V(H) \subseteq V(G) $ 且 $ E(H) \subseteq E(G) $ , 记为 $ H \subseteq G $ . 若V(H)=V(G), 图 $ H $ 是图 $ G $ 的生成子图. 对于 $ n $ 阶完全图记为 $ {K_n} $ , 图 $ G $ 的阶就是图 $ G $ 所有的顶点个数.

如果图 $ G $ , 可以分解成生成子图 $ {F_1}, {F_2}, \cdots , {F_n} $ , 且 $ V({F_i}) = V(G) $ , 图 $ G $ 分解的每个生成子图满足 $ \bigcup\nolimits_{i = 1}^n {E({F_i}) = E(G)} $ , $ E({F_i}) \cap E({F_j}) = \phi {\text{ }}(i \ne j) $ , 称这些生成子图 $ {F_i} \; (i = 1, 2, \cdots , n) $ 为 $ G $ 的因子, 称为图 $ G $ 的因子分解. 若每个分解出来的因子都是 $ m $ 正则图时, 则称图 $ G $ 是可 $ m $ 因子分解的.

在 $(n, k, d)$ 分布式存储系统(distributed storage system, DSS)中, 其中 $ n $ 表示存储节点个数, 即分布式系统中存储数据的节点. $d \geqslant k$ 是修复故障节点时连接的节点个数, $k \lt n$ 表示恢复出原文件需要节点个数.

定义1. 在 $(n, k, d)$ 系统中^[25], $ (n, d, \theta , \rho ) $ 部分重复码可以由 $ n $ 个子集的集合 $ N = \{ {N_1}, \cdots , {N_n}\} $ 表示, $ \rho $ 是数据块的重复度, 每个子集中的符号均属于符号集 $[n] = \{ 1 , 2, \cdots , \theta \}$ . 该 $ (n, d, \theta , \rho ) $ 部分重复码的构造过程满足如下条件.

(1)每个节点存储 $d$ 个数据块, 即 $\left| {{N_i}} \right| = d{\kern 1pt} {\kern 1pt} {\kern 1pt} (1 \leqslant i \leqslant n)$ .

(2) $[n]$ 中的每个元素都出现于 $N$ 中 $\;\rho $ 个不同的子集.

在 $ (n, d, \theta , \rho ) $ FR码的构造过程中, 其中参数满足 $ \theta \rho = nd $ , 首先对原文件进行分割为 $ m $ 个数据块, 如图2所示, 分别为数据块m₀到m₈, 其次通过最大距离可分(maximum distance separable, MDS)码对m₀到m₈进行编码, 产生m₀到m₈、P₉等编码数据块, P₉为校验块数据块, 保护数据的可靠性. 然后采用复制策略, 对m₀到m₈、P₉等编码数据块复制 $\;\rho $ 份, 最后通过部分重复码的内部构造算法把所有的数据块存储在 $n$ 个节点里.

图 2

Fig. 2

图 2 部分重复码构造过程

本文提出一种新的部分重复码的构造算法, 通过完全图的因子分解进行构造, 构造过程简单, 同时也解决了传统FR码存在的不足. 具体构造步骤如下.

步骤1. 对完全图 $ {K_{2k}} $ 的图 $ G $ 做可1因子分解, 得到 $ {F_1}, {F_2}, \cdots , {F_l} $ , 图 $ G $ 中的每个顶点 $ {v_i} \; (1 \leqslant i \leqslant n) $ 视为分布式存储系统中需要存储的数据块 $ {d_i}\; (1 \leqslant i \leqslant n) $ , 其中 $ l $ 满足公式如下:

步骤2. 确定分布式存储系统中FR码构造过程每个数据块 $ {d_i} \; (1 \leqslant i \leqslant n) $ 的重复度 $ \;\rho {\text{ }}(1 \leqslant \rho \leqslant l) $ . 因为图 $ G $ 的所有顶点都包含于每个因子 $ {F_\sigma } \; (1 \leqslant \sigma \leqslant l) $ 之中, 因此可以构造 $\left( {_\rho ^{{\kern 1pt} l{\kern 1pt} }} \right)$ 种重复度为 $\; \rho $ 的FR码.

步骤3. 在分解的所有因子 $ {F_1}, {F_2}, \cdots , {F_l} $ 中, 根据数据块的重复度 $ \;\rho $ , 选择任意 $\; \rho $ 个因子的边分别编号为 $ {e_\mu }\left( {1 \leqslant \mu \leqslant n\rho } \right) $ .

步骤4. 构造数据矩阵, 通过数据矩阵 ${m_{\mu , i}} \; ( 1 \leqslant \mu \leqslant n\rho , 1 \leqslant i \leqslant n )$ 对部分重复码进行构造, $ {m_{\mu , i}} $ 的横坐标代表部分重复码的存储节点 $ {N_\mu }\left( {1 \leqslant \mu \leqslant n\rho } \right) $ , 在数据矩阵 $ {m_{\mu , i}} $ 中, 对矩阵中相应数字为1的编码数据块 $ {d_i} \; (1 \leqslant i \leqslant 2n) $ 进行存储, 其中 $ {m_{\mu , i}} $ 数据矩阵构造公式如下:

具体地, 可以对 $ {K_6} $ 进行因子分解, 然后构造一个重复度为 $ \;\rho {\text{ }}(1 \leqslant \rho \leqslant 15) $ 的FR码. 如果取重复度 $\; \rho = 3 $ , 因此可以在 $ {F_1}, {F_2}, \cdots , {F_{15}} $ 所有因子中任选3个进行构造数据矩阵, 这里我们在15个因子中选取 $ {F_1}, {F_2}, {F_3} $ , 然后对选中 $ {F_1}, {F_2}, {F_3} $ 因子的边进行依次编号为 $ {e_\mu }\left( {1 \leqslant \mu \leqslant 9} \right) $ , 如图3所示.

图 3

Fig. 3

图 3 $ {K_6} $ 的部分因子分解

通过图2, 我们可根据式(2)求出数据矩阵 $ {m_1} $ 如下:

基于完全图因子分解的部分重复码如图4所示, 部分重复码的存储节点 $ {N_\mu }\left( {1 \leqslant \mu \leqslant 9} \right) $ 为数据矩阵 $ {m_1} $ 的横坐标, 对标记为1数据块 $ {d_i} \; (1 \leqslant i \leqslant 6) $ 进行存储. 利用 $ {K_6} $ 的可1因子分解, 重复度 $\; \rho = 3 $ 的FR码的构造方法总共有 $\left( {_{{\kern 1pt}{\kern 1pt} 3}^{15}} \right)$ 种. 因此, CGFBFR码具有灵活的参数选择性, 而且有多种构造方法.

图 4

Fig. 4

图 4 基于 $ {K_6} $ 因子分解的CGFBFR码

对基于完全图 $ {K_{2k}} $ 可1因子分解构造的CGFBFR码与目前分布式系统主要研究的RS码、SRC以及最新的循环可变部分重复(variable fractional repetition, VFR)码性能进行分析.

表1给出了SRC、RS码、三副本、以及VFR码与CGFBFR码几种编码方案性能的分析. 为了便于比较, 文件大小取 $ M{\text{ = 2}}000\;{\text{Mb}} $ , $ t $ 为单位时间内寻址时间, SRC的子文件数 $ f = 3 $ , 且CGFBFR码外部编码采用 $ (k + 3, {\text{ }}k) $ 码.

表 1(Table 1)

表 1 编码方案的性能分析 编码方案 (n, k, f)SRC (n, k)RS CGFBFR 三副本 VFR 存储开销 $ (f + 1)M/k $ $ M/k $ $ 2M/k $ M $ 3M/k $ 修复复杂度 $ (f - 1)(f + 1) $ $ {k^2} + k $ 0 0 0 寻址时间 $ (f - 1)(f + 1)tM $ $ \left( {{k^2} + k} \right)tM $ $ tM $ $ tM $ $ tM $

表 1 编码方案的性能分析

在修复故障节点时下载的数据量就是修复带宽开销. 当单节点故障时, 如表2所示, 若采用 $ (n, k, f) $ SRC, 因为SRC每个节点存储的数据块为 $ f + 1 $ , 每一个数据块的大小是 $ {M \mathord{\left/ {\vphantom {M {fk}}} \right. } {fk}} $ , 修复时需要从其他数据节点下载 $ f $ 个数据块, 因此 $ (n, k, f) $ SRC修复单节点故障的带宽开销为 $ {{(f + 1)M} \mathord{\left/ {\vphantom {{(f + 1)M} k}} \right. } k} $ ; $ (n, {\text{ }}k) $ RS码修复时需要靠原文件修复故障节点, 所以带宽开销为 $ M $ ; 对于VFR码, 单节点故障时, 修复带宽开销为 $ 3M/k $ . 对于CGFBFR码, 每个节点存放的数据块大小为2, 数据块每个的大小为 $ {M \mathord{\left/ {\vphantom {M k}} \right. } k} $ , 因此CGFBFR码修复带宽开销为 $ {{2M} \mathord{\left/ {\vphantom {{2M} k}} \right. } k} $ .

当两个节点发生故障时, 如表2所示, (n, k)RS编码在修复数据时仍需要通过原文件来修复故障节点, 因此修复带宽开销仍为 $ M $ . 对于(n, k, f)SRC, 修复带宽开销为 $ M $ . VFR码的两节点故障时修复带宽开销也为 $ M $ . 对于CGFBFR码, $ {{2M} \mathord{\left/ {\vphantom {{2M} k}} \right. } k} $ 为单个存储节点存储开销, 因此 $ {{4M} \mathord{\left/ {\vphantom {{4M} k}} \right. } k} $ 是两节点故障时的修复带宽开销. 图5给出了4种编码方式的修复带宽开销, 显而易见, CGFBFR码的修复带宽更低.

表 2(Table 2)

表 2 编码方案的性能分析 编码方案 (n, k, f)SRC (n, k)RS CGFBFR VFR 修复带宽开销 单节点故障 $ (f + 1)M/k $ $ M $ $ 2M/k $ $ 3M/k $ 两节点故障 $ M $ $ M $ $ 4M/k $ $ M $ 修复局部性 单节点故障 $ 2f $ $ k $ $ 2 $ $ 2 $ 两节点故障 $ k $ $ k $ $ \max \{ 4\} $ $ \left\lceil {\dfrac{k}{3}} \right\rceil + 1 $

表 2 编码方案的性能分析

图 5

Fig. 5

图 5 单节点故障的修复带宽开销对比

当分布式存储系统中出现单节点故障时, 如图6所示. 对于(n, k, f)SRC需要 $ 2f $ $ (2f \leqslant n) $ 个节点修复故障节点, 因此(n, k, f)SRC系统中修复局部性为 $ 2f $ ; 对于 $ (n, {\text{ }}k) $ RS码的修复局部性是 $ k $ ; VFR码单节点故障故障修复局部性为2; 采用CGFBFR码, 修复故障节点需要连接的节点数为2, 因此CGFBFR码修复局部性为2.

图7给出了两节点故障时, 4种不同的编码修复局部性. 对于(n, k, f)SRC, 恢复原文件需要 $ k $ 存储节点, 通过原文件对故两节点故障进行修复, 因此(n, k, f)SRC修复局部性是 $ k $ ; 对于 $ (n, {\text{ }}k) $ RS码需要连接 $ k $ 个节点恢复原文件, 然后再对两故障节点进行修复, 所以 $ (n, {\text{ }}k) $ RS码的修复局部性也是 $ k $ ; VFR码的两节点修复局部性为 $ \left\lceil {K/3} \right\rceil + 1 $ . 对于CGFBFR码的修复局部性最大4.

图 6

Fig. 6

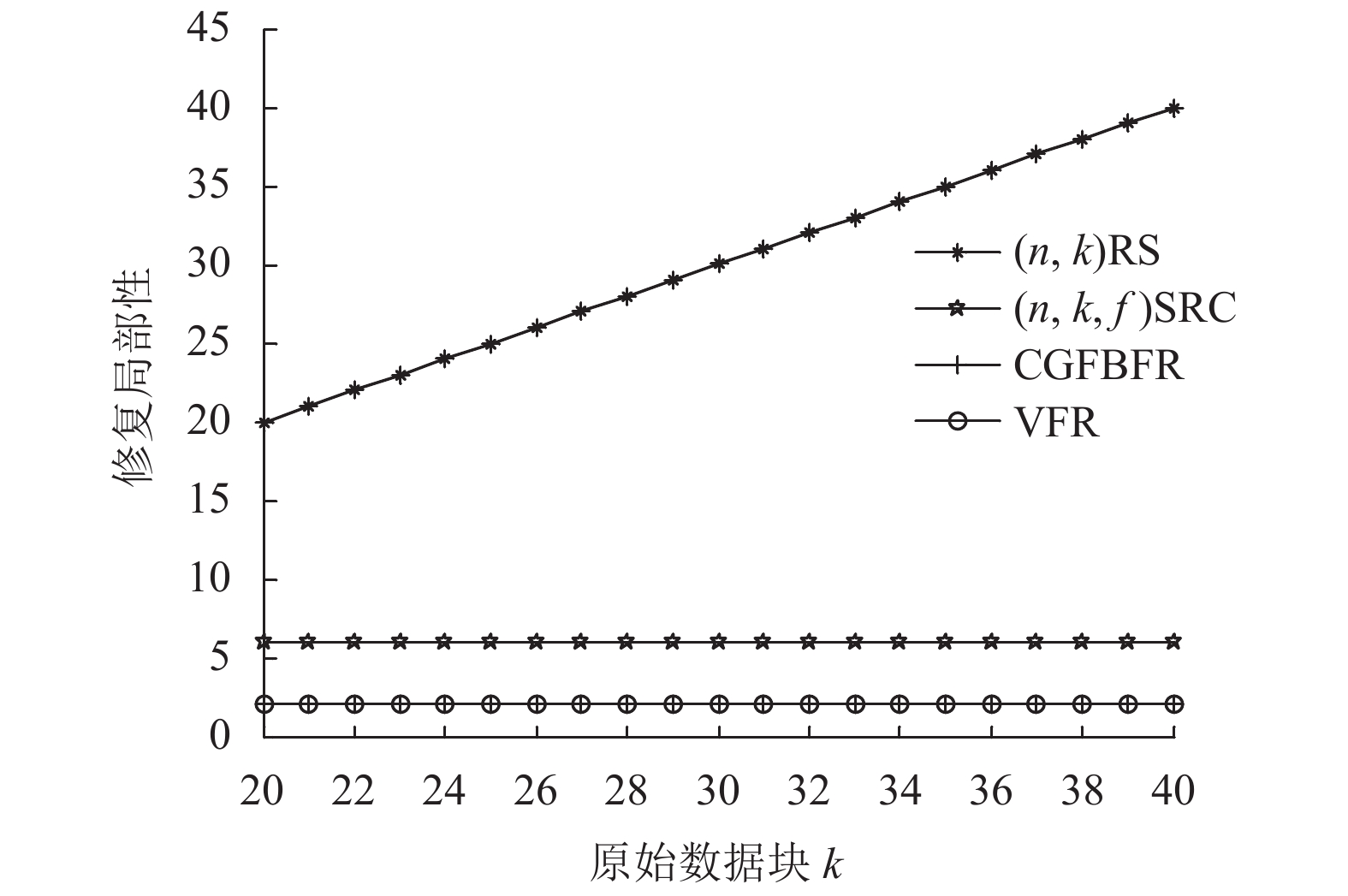
图 6 单节点故障修复局部性

图 7

Fig. 7

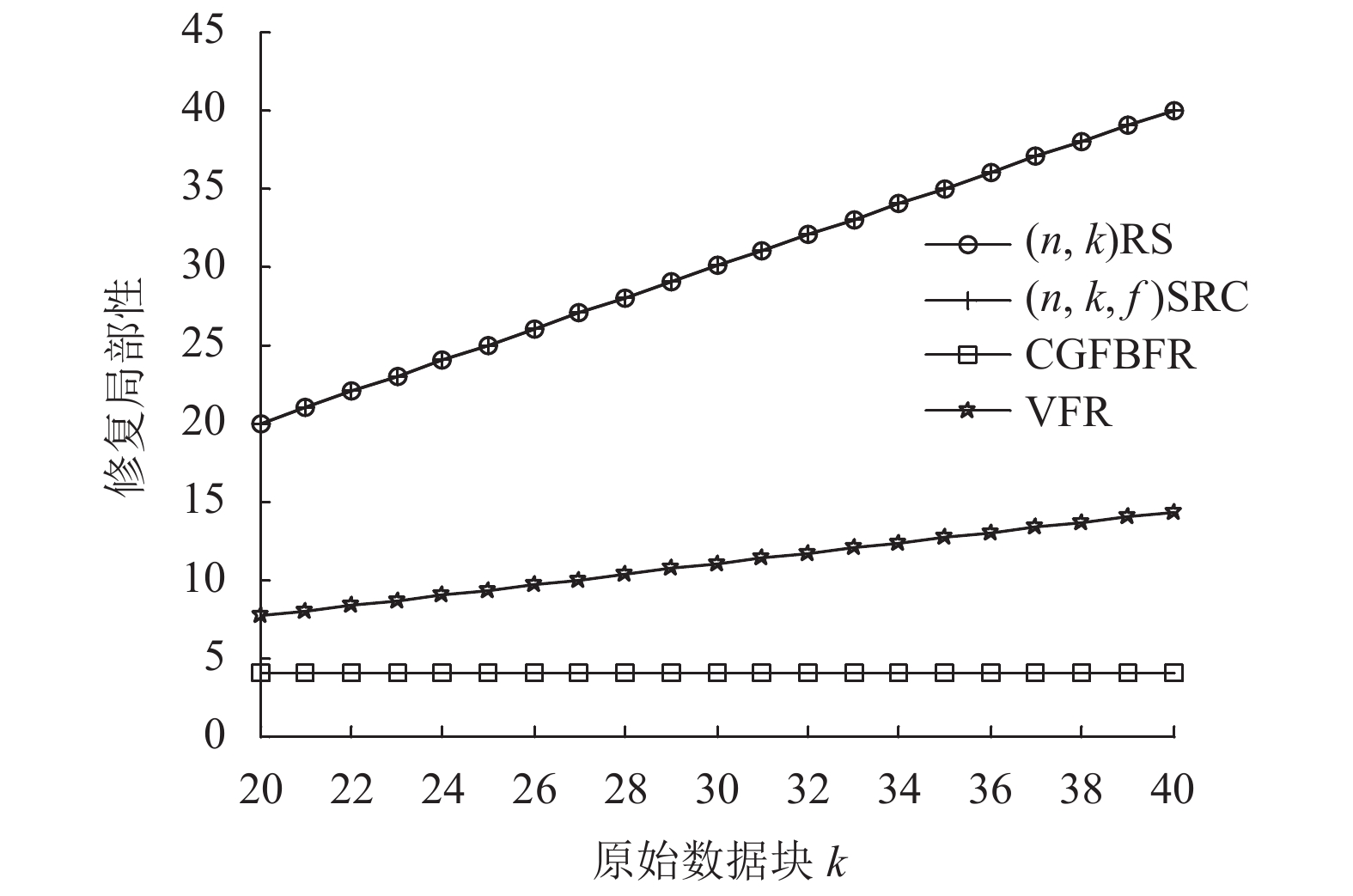
图 7 两节点故障修复局部性

对于RS码, 在分布式存储系统中修复故障节点时, 系统需要经过 $ {k^2} - 1 $ 次有限域加法运算, $ {k^2} + k $ 次有限域乘法运算, 因此RS码在修复单节点的故障时它的修复复杂度为 $ {\rm{O}}\left( {2{k^2} + k - 1} \right) $ . 对于SRC, 系统需要执行 $ (f - 1)(f + 1) $ 次异或运算, 所以SRC的修复复杂度为 ${\rm{O}}\left( {{f^2} - 1} \right)$ . 对于CGFBFR码, 不需要经过有限域运算和异或运算, 直接通过复制数据就可以进行修复, 因此CGFBFR码相比于RS码和SRC具有较低修复复杂度, 能够快速修复故障节点, 降低修复时间.

本文提出一种CGFBFR码能够满足分布式存储系统的实际需求, 提高了分布式存储系统中故障节点的修复效率, 并且能够灵活的选择构造参数. 在修复故障节点时, CGFBFR相较于分布式存储系统中其他编码, 在修复局部性、修复复杂度、修复带宽开销都有较大的性能提升. 更加具有发展的前景和应用背景.