数据分析过程中, 总是存在一些与其他数据大相径庭的非正常对象, 这种异常现象影响着数据挖掘的准确性, 甚至对其应用领域造成巨大的损失. 异常的产生可能会表现为人为错误、技术或机械方面的故障、噪声、系统变化和欺诈行为等^[1]. 比如: 顾客的某次消费明显不同于以往正常的花销记录; 中转设备发生故障时, 通信或数据的传输出现错误; 路由器在短时间内突然收到大量交换包^[2]. 为了避免这些异常的现象对数据挖掘的影响, 异常检测技术得到广泛应用. 虽然, 大部分的异常检测方法在技术上基本相同, 但是, 它们会有许多不同的名字, 比如离群值检测、异常值检测、新颖值检测、噪声检测或异常挖掘等^[3]. 异常检测是数据挖掘中的一个重要问题, 目的是把那些与其他数据点显著不同的独特或不寻常的数据对象检测出来^[4].

异常检测的算法可以大致分为4大类: 基于统计的异常检测算法^{[5, 6]}、基于距离的异常检测算法^[7–9]、基于密度的异常检测算法^[10–12]和基于聚类的异常检测算法^[13–16]. 基于统计的异常检测算法分为有参数和非参数两大类检测算法, 与之前的算法相比, 提升了异常检测的性能. 但是, 其数据分布需要提前确定, 基于距离的异常检测算法弥补了这一缺点, 不需要考虑数据分布. 基于距离的异常检测算法主要是基于目标对象邻域的稀疏状态与其异常状态之间的相关性假设^[9]. 基于密度的异常检测算法根据数据点的密度检测异常, 如果某个数据点的密度低于其周围邻居的密度, 那么该数据点就是异常点^[12]. 基于密度的异常检测算法主要从局部的角度来考虑异常情况, 可以识别更多有意义的局部异常数据点.

聚类作为一种无监督的方法, 根据相似度度量对数据进行分组, 其目标是获得高的簇内相似性(即类簇内的数据是相似的)和低的簇间相似性(即来自不同类簇的数据是不同的)^[13]. 那么, 基于聚类的异常检测算法是根据数据点之间的相似性将数据集中的数据点分类为多个聚类, 异常值是指不位于任何聚类中或离最近聚类的质心很远的数据点^[17]. DBSCAN (density-based spatial clustering of applications with noise)^[14]可以发现任意形状的簇, 将数据有效的分开, 能够在低密度区域中识别噪声, 即噪声数据的密度必定低于簇的密度. Huang等^[15]提出了一种新的基于聚类的异常检测算法(relative outlier cluster factor, ROCF), 不需要提前指定异常值的个数, 只需要一个参数k表示邻居的数量, ROCF也可以通过构造决策图自动计算出数据集的离群率. 整体而言, ROCF检测算法在获取离群值和离群值簇时更加倾向于自适应性. 为了提升大规模数据集中的异常检测性能, Nozad等^[16]提供了基于批处理的异常检测算法, 是一种利用聚类方式检测异常的算法, 在此过程中通过密度实现聚类, 该算法对具有相关性或不相关性特征的高斯簇的检测效果表现更好, 同样适用于遵循任意分布的凸形簇.

本文提出了一种基于二阶近邻的异常检测算法, 通过二阶近邻获取相似性矩阵完成聚类过程, 利用每个簇中的数据点与其所属簇中心的关系捕捉异常情况. 该算法的相关假设是: 正常的数据点更加靠近所属簇中心, 远离簇中心的数据点则表现为异常; 一般情况下, 异常数据点的密度比正常数据点低. 基于二阶近邻的异常检测算法主要分为两阶段: 聚类阶段和异常检测阶段. 在聚类阶段, 通过二阶近邻的方式获取相似性矩阵, 这一过程捕获到了数据在聚类过程中的全局结构. 第二阶段考虑了每个簇中的数据点与其所属簇中心之间的关系, 根据正常数据点与簇中心关系更加紧密, 异常数据点与簇中心相距较远这个假设, 计算每个簇中所有的数据点与其所属簇中心之间的距离; 根据密度较小的数据点更有可能成为异常点的假设, 计算每个数据点的密度. 结合距离值与密度值, 最终获取每个数据点的异常值分数.

本文的主要贡献有以下两点.

(1) 提出了一种基于二阶近邻的异常检测算法, 利用二阶近邻获得相似性矩阵, 综合考虑数据的局部性和全局性结构信息, 深入挖掘数据点与数据点之间的关系, 增强了捕获它们之间的相似性的能力, 对于较稀疏的数据集会有更好的性能;

(2) 在异常检测阶段, 根据簇中的数据点与所属簇中心之间的关系判断异常情况, 同时考虑到簇与簇之间的临界处可能会存在数据点较密集的情况, 根据密度较小的数据点更有可能成为异常点的假设, 利用数据点的局部密度排除边界情况, 减少错误识别异常值的可能性.

1 相关概念

如果近邻图中任意两个顶点 $ {x_i} $ 和 $ {x_j} $ 之间由一条边连接, 即边上的权值 $ {W_{ij}} \gt 0 $ , 那么这两个点则为一阶近似^[18]. 一阶近似描述了顶点之间的成对相似性, 意味着图中由一条边连接的顶点往往是相似的. 例如, 观看同一场音乐会的两个人必定有相似的兴趣点. 因此, 保持图节点之间的一阶近似性非常必要. 图1中的顶点E和顶点F之间存在一条边连接, 它们之间则为一阶近似. 但是, 现实世界中的信息网络一般比较稀疏, 许多相似的点往往并不存在直接相连的边. 一阶近似只考虑到了局部结构, 二阶近邻^[18]则可以捕获全局网络结构, 弥补一阶近似的不足. 设 $ {A_i} = {\text{\{ }}{a_{i, 1}}, {a_{i, 2}}, {a_{i, 3}},\cdots, {a_{i, |V|}}{\text{\} }} $ 表示顶点 $ {x_i} $ 与其他顶点之间的一阶近似性. 由邻域 $ {A_i} $ 和 $ {A_j} $ 的相似性来确定二阶近邻. 有许多共同邻居的两个顶点为二阶近邻, 即使它们之间没有一阶近似性, 但仍具有相似性. 例如, 一般情况下, 有许多共同朋友的两个人往往也是朋友. 二阶近邻作为一种定义两个顶点的相似性的良好度量工具, 表征数据的全局结构, 可以高度丰富顶点之间的关系, 达到深度挖掘数据的目的. 图1中的顶点E和顶点G之间并不存在相连的边, 但是, 它们共享邻居顶点A、顶点B、顶点C和顶点D, 因此, 顶点E和顶点G之间是二阶近邻, 存在相似性.

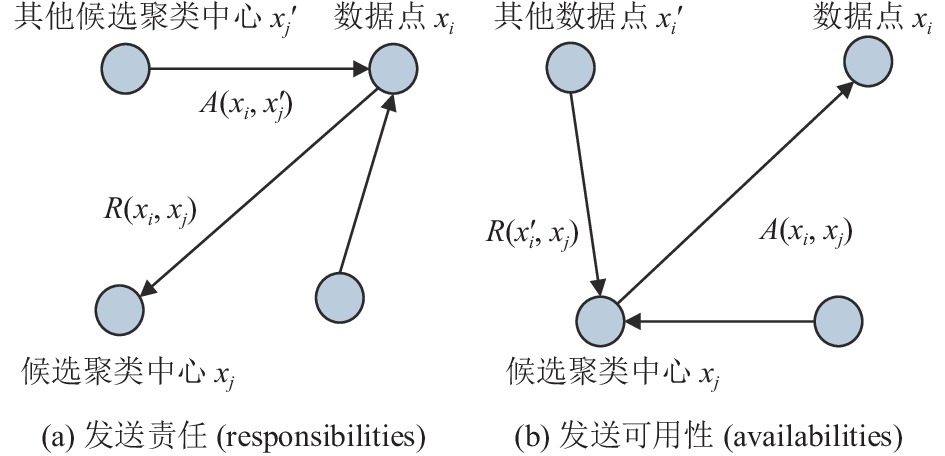
基于亲和传播的聚类(affinity propagation, AP)^[19]是在2007年被提出的一种重要的聚类算法, 主要结合相似性和消息传递进行聚类, 将数据点对之间的相似性作为消息传递的一个输入度量. 真实值消息在数据点之间交换, 直到最优候选范例和相应的集群逐渐出现. 具体的消息传递过程如图2所示. 图2(a)表示的责任(responsibility) $ R{\text{(}}{x_i}, {x_j}{\text{)}} $ 是从数据点 $ {x_i} $ 发送到候选聚类中心 $ {x_j} $ , 指出每个数据点选择候选聚类中心 $ {x_j} $ 而不是其他候选聚类中心的强烈程度. 图2(b)表示的可用性(availability) $ A{\text{(}}{x_i}, {x_j}{\text{)}} $ 是从候选聚类中心 $ {x_j} $ 发送到数据点 $ {x_i} $ , 指出候选聚类中心 $ {x_j} $ 成为数据点 $ {x_i} $ 的聚类中心的可能程度. AP算法在聚类时不需要事先初始化聚类中心, 每个数据点都有可能成为聚类中心, 消息传递的过程经过不断迭代可以自动确定聚类中心. 但是, 原始的亲和传播聚类算法仅使用数据样本的欧几里得距离作为相似度计算的唯一标准, 增加了算法在高维稀疏性数据集上的局限性.

2 算法描述

基于二阶近邻的异常检测算法通过二阶近邻获得相似性矩阵实现聚类, 以聚类结果为基础, 根据簇中的点与簇中心的关系, 计算每一个簇中的所有的点与该簇中心的距离, 捕获异常情况. 同时考虑每个数据点的局部密度, 避免在簇与簇之间的边界处错误识别异常值的情况. 基于距离值和局部密度值得到每个数据点的异常值分数, 并根据异常值分数排序, 取其值较大的数据点作为异常点. 该算法的流程图如图3所示.

2.1 聚类阶段

本节主要对整个数据集中的数据进行聚类. 在此过程中联合一阶近似性和二阶近邻捕获相似性, 深入探究数据点与数据点之间的紧密关系, 然后经过消息传递过程实现聚类. 这是异常检测的初始阶段.

2.1.1 二阶近邻求相似性

相似性表示数据点与数据点之间的密切程度, 聚类往往通过相似性度量所有数据点之间的关系, 对于数据的分布则没有太大的要求. 聚类过程中将相似性较高的那些数据点聚集在一起形成一个簇, 而相似性较低的数据点之间则处于一个远离的状态, 据此可以很好地将不同类的数据分别聚集成不同的簇. 计算相似性的方式有很多种, 此处将数据点 $ {x_i} $ 和数据点 $ {x_j} $ 之间的初始相似性 $ S({x_i}, {x_j}) $ 用欧几里得距离表示, 即:

$ S({x_i}, {x_j}) = - ||{x_i} - {x_j}|{|^2} $

(1)

欧几里得距离原本是正值, 但是两个数据点之间的距离越远, 它们的相似性越小, 因此在距离值前面加上了一个负号, 使得初始相似性为负值. 所有数据点之间的初始相似性存放在相似性矩阵 $ S $ 中, 矩阵 $ S $ 中的值所表示的是数据点与数据点之间的一种成对近似性, 即是所谓的一阶近似性, 能够很好地表示数据的局部信息, 因此, 矩阵 $ S $ 也被称为一阶近似性矩阵. 因而, 为了更进一步刻画不同数据点之间的相近性水平, 通过使用更高阶的近似性来探究数据集内部的数据点与数据点的紧密程度. 在这里, 利用每个数据点的邻域关系, 通过二阶近邻来描绘一阶近似性矩阵 $ S $ 中拥有共同邻居的数据点, 增强这些数据点与其二阶近邻之间的相似性. 即以一阶近似性矩阵为基础, 通过向数据点周边的邻居进行扩展, 根据数据点与数据点之间共享邻居的程度, 获取它们之间的近似性并存入到二阶近邻矩阵中. 二阶近邻弥补了一阶近似性的不足, 充分地捕获了数据的全局结构信息. 因此, 联合一阶近似性和二阶近邻重构相似性矩阵, 能够更深入地度量数据点之间的相似性. 在基于随机游走的概率集合中, 一阶和二阶近邻分别是1步和2步随机游走的概率转移矩阵^[18], 因此二阶近邻矩阵由2步随机游走的概率转移矩阵所表示, 即 $ {S^2} = S \times S $ , 那么一阶近似性矩阵和二阶近邻矩阵的联合信息则可以通过如下方式计算:

$ S = \alpha \times S + (1 - \alpha ) \times {S^2} $

(2)

通过为一阶近似性矩阵和二阶近邻矩阵分配合适的权值, 重新构造相似性矩阵 $ S $ , 综合考虑了数据的局部性和全局性结构信息. 其中, $ \alpha $ 是一个参数, 表示一阶近似性矩阵的权值, $ {\text{(}}1 - \alpha {\text{)}} $ 则是为二阶近邻矩阵所分配的权值, $ \alpha $ 的取值范围一般是(0.5, 1), 参数 $ \alpha $ 的值越大, 一阶近似性矩阵的权重就越大. $ \alpha \times S $ 表示相似性矩阵的一阶近似性, $ {\text{(}}1 - \alpha {\text{)}} \times {S^2} $ 表示的是相似性矩阵的二阶近邻. 为了保证一阶近似性矩阵和二阶近邻矩阵中的数据具有相同的分布形式, 提高聚类的精确度, 重新构造相似性矩阵之前, 需要对一阶近似性矩阵和二阶近邻矩阵进行归一化处理, 在这里使用的是按行归一化方式, 并始终保持矩阵原来的对称性.

2.1.2 消息传递

把通过二阶近邻获得的相似性矩阵传入到消息传递过程中, 不断更新迭代得到最后的聚类结果. 最初数据集中的每一个数据点都可以被看作候选聚类中心, 即需要向消息传递过程中输入一个表示数据点 $ {x_j} $ 的 $ S{\text{(}}{x_j}, {x_j}{\text{)}} $ , $ S{\text{(}}{x_j}, {x_j}{\text{)}} $ 的值越大, 数据点 $ {x_j} $ 越有可能成为一个聚类中心. $ S{\text{(}}{x_j}, {x_j}{\text{)}} $ 的值被称为偏好值, 用P表示, 评估了数据集中的每一个点成为聚类中心的可能性. 它可以取所有数据点之间的相似性的最小值, 也可以取所有数据点之间的相似性的平均值等.

责任 $ R{\text{(}}{x_i}, {x_j}{\text{)}} $ 和可用性 $ A{\text{(}}{x_i}, {x_j}{\text{)}} $ 作为消息传递中的两种消息交换, 在数据点之间的消息更新过程中起着至关重要的作用. $ R{\text{(}}{x_i}, {x_j}{\text{)}} $ 反映的是数据点 $ {x_j} $ 适合成为数据点 $ {x_i} $ 的候选聚类中心的累积证据, 考虑到了其他有可能成为数据点 $ {x_i} $ 的候选聚类中心的数据点. $ A{\text{(}}{x_i}, {x_j}{\text{)}} $ 反映的是数据点 $ {x_i} $ 选择数据点 $ {x_j} $ 作为自己的候选聚类中心的累积证据, 考虑到了其他有可能选择数据点 $ {x_j} $ 作为候选聚类中心的数据点. 更新之前, 可用性值初始化为0, 即 $ A{\text{(}}{x_i}, {x_j}{\text{)}} = 0 $ . 责任计算方式如下:

$ R({x_i}, {x_j}) = S({x_i}, {x_j}) - \mathop {\max }\limits_{x'_j \; {\rm{s.t.}} \; {x_j} \ne x'_j} \{ A({x_i}, x'_j) + S({x_i}, x'_j)\} $

(3)

在第一次迭代中, 因为可用性为0, $ R{\text{(}}{x_i}, {x_j}{\text{)}} $ 表示为数据点 $ {x_i} $ 和候选聚类中心 $ {x_j} $ 之间的输入相似性减去数据点 $ {x_i} $ 与其他候选聚类中心之间的最大相似性. 在之后的迭代中, 当一些数据点被分配给其他候选聚类中心时, 它们的可用性将根据更新规则降到0以下. 当 $ {x_i} = {x_j} $ 时, $ R{\text{(}}{x_j}, {x_j}{\text{)}} $ 设置为表示数据点 $ {x_j} $ 可能成为聚类中心的输入偏好值 $ S{\text{(}}{x_j}, {x_j}{\text{)}} $ 减去数据点 $ {x_i} $ 与其他候选聚类中心之间的最大相似性. $ R{\text{(}}{x_j}, {x_j}{\text{)}} $ 也被称为自我责任(self-responsibility), 反映了数据点 $ {x_j} $ 成为一个聚类中心的累积证据.

在上述责任更新过程中, 所有的候选聚类中心竞争同一个数据点的所有权, 即成为这个数据点的聚类中心. 而可用性的更新则来自那些数据点中是否每一个候选聚类中心都可以成为一个更好的聚类中心的证据:

$ A({x_i}, {x_j}) = \min \{ 0, R({x_j}, {x_j}) + \sum\limits_{x'_i \; {\rm{s.t.}} \; x'_i{} \notin \{ {x_i}, {x_j}\} } {\max \{ 0, R(x'_i, {x_j})\} \} } $

(4)

$ A{\text{(}}{x_i}, {x_j}{\text{)}} $ 为 $ R{\text{(}}{x_j}, {x_j}{\text{)}} $ 加上候选聚类中心从其他数据点获取到的正的责任的和. 自我可用性(self-availability) $ A{\text{(}}{x_j}, {x_j}{\text{)}} $ 的更新有所不同:

$ A({x_j}, {x_j}) = \sum\limits_{x'_i \; {\rm{s.t.}} x'_i \ne {x_j}} {\max \{ 0, R(x'_i, {x_j})\} } $

(5)

这个消息基于其他数据点发送给数据点 $ {x_j} $ 的正的责任, 反映了数据点 $ {x_j} $ 成为聚类中心的累积证据.

$ R{\text{(}}{x_i}, {x_j}{\text{)}} $ 和 $ A{\text{(}}{x_i}, {x_j}{\text{)}} $ 消息更新之后, 数据点 $ {x_i} $ 的聚类中心可以通过以下方式来确定:

$ E({x_j}) = \arg \mathop {\max }\limits_{{x_j}} \{ R({x_i}, {x_j}) + A({x_i}, {x_j})\} $

(6)

消息传递的过程中通过不断迭代更新, 在形成簇的同时自动确定了每个簇的中心点, 即聚类中心, 完成了聚类.

2.2 异常检测阶段

本节主要是根据第2.1节得到的聚类结果进行异常检测. 文中所提出的算法的相关假设中提到正常的数据点更加靠近所属簇中心, 而异常的数据点在所属簇中会距离簇中心较远. 基于上述假设, 那些紧密围绕在簇中心的数据点通常是正常值, 而异常的数据点则稀疏地围绕在簇的边界处. 由此说明正常的数据点往往与所属簇的簇中心有着密切的关系. 因此, 每个数据点的异常情况都可以很好地通过它本身与所属簇中心的距离近似表示. 假设第2.1节中基于二阶近邻得到的聚类结果为 $\left\{{C_1}, {C_2}, {C_3}, \cdots, {C_m}\right\}$ , $ {C_m} $ 表示的是第m个簇, ${C_m} = \left\{{x_{1m}}, {x_{2m}}, {x_{3m}}, \cdots, {x_{km}} \right\}$ 表示第m个簇中包含k个数据点, 那么, 每个簇中的每个数据点与该簇中心的距离为:

$ dist({x_{km}}, {c_m}) = ||{x_{km}} - {c_m}|| $

(7)

其中, $ {x_{km}} $ 表示的是第m个簇中的第k个数据点, $ {c_m} $ 表示第m个簇的簇中心. $ dist{\text{(}}{x_{km}}, {c_m}{\text{)}} $ 的值越大, 数据点 $ {x_{km}} $ 越有可能成为一个异常值. 但是, 每个簇与簇之间的边界处可能会存在一些较密集的数据点, 如果只考虑距离问题, 则极有可能会使正常的数据点被误认为是异常点, 极大地影响到异常检测的准确度. 为了排除这种边界情况, 减少错误识别率, 基于密度较小的点更有可能成为异常点的假设, 同时把数据点的密度考虑进去. 最初, 数据点的密度一般是指其特定范围内所包含的数据点的个数. 在基于密度的聚类的定义中, 每一个簇都是由一组密集的数据点所构成, 不同的簇则被那些数据点较稀疏的区域划分开. 因此, 数据点周围越密集, 其密度越大, 越不可能成为异常值. 但是, 这种仅仅考虑数据点周围的邻居个数作为其密度的方式, 只在数据点较密集的情况下比较适用. 为了更好地适应不同类型的数据集, 文中通过采用基于高斯核函数的方式生成数据点的局部密度, 数据点 $ {x_i} $ 的局部密度 $ {\rho _i} $ 可以通过以下公式来计算:

$ {\rho _i} = \sum\limits_{{x_i} \ne {x_j}} {{{\rm{e}}^{ - {{(dist({x_i}, {x_j})/{d_c})}^2}}}} $

(8)

其中, $ dist{\text{(}}{x_i}, {x_j}{\text{)}} $ 表示数据点 $ {x_i} $ 和数据点 $ {x_j} $ 之间的距离, $ {x_j} $ 表示整个数据集中除了数据点 $ {x_i} $ 的每一个数据点. $ {d_c} $ 为截断距离, 一般根据经验从所有升序排序的距离值中取一个合适的值作为截断距离. 那么, 作为异常检测过程中的一个重要判断依据, 数据点 $ {x_i} $ 的异常值分数则可以通过以下公式来获得:

$ score({x_i}) = \frac{{dist({x_{km}}, {c_m})}}{{{\rho _i}}} $

(9)

数据点 $ {x_i} $ 即为数据点 $ {x_{km}} $ , 其异常值分数与距离 $ dist{\text{(}}{x_{km}}, {c_m}{\text{)}} $ 成正比, 与密度 $ \;{\rho _i} $ 成反比. 即与所属簇中心的距离越远, 且其局部密度越小的数据点更有可能被识别成为异常点. 最后把所有数据点的异常值分数按从大到小的顺序进行排序, 异常点则为异常值分数值较大的数据点.

2.3 总的算法框架

文中所提出的基于二阶近邻的异常检测算法的实现步骤的详细描述如算法1所示. 该算法主要分为聚类(步骤1–5)和异常检测(步骤6–8)两个阶段. 聚类阶段, 计算数据点与数据点之间的相似性构造初始相似性矩阵 $ S $ , 按行归一化相似性矩阵 $ S $ 以及该矩阵的平方 $ S \times S $ , 并保持 $ S $ 和 $ S \times S $ 原来的对称性, 在此基础上, 通过一阶近似性和二阶近邻对初始相似性矩阵重新构造; 然后, 把最终构造好的相似性矩阵 $ S $ 、参数 $ \alpha $ 、偏好值参数P传入到消息传递的过程中, 计算责任和可用性的值并重复迭代直到收敛, 获取最终聚类结果, 得到不同的簇. 异常检测阶段, 根据数据点与簇中心的距离关系以及对数据点的密度大小的考虑, 计算每个数据点与所属簇中心的距离值以及该数据点的局部密度, 得到每一个数据点的异常值分数, 对异常值分数按照降序排序, 取异常值分数较大的数据点作为异常点.

算法1. 基于二阶近邻的异常检测算法
输入: 数据集, 参数 $\scriptstyle \alpha $ , 偏好值参数P输出: 异常值分数score, 异常数据点
阶段1. 聚类1. 通过式(1)计算数据点之间的相似性并构造初始相似性矩阵 $\scriptstyle S $ ; 2. 通过式(2)以二阶近邻的方式重新构造初始相似性矩阵 $\scriptstyle S $ ; 3. 通过式(3)–式(5)实现消息传递; 4. 重复步骤3直至收敛得到最后的责任值和可用性值; 5. 利用式(6)确定最后的聚类中心, 获取聚类结果 $\scriptstyle \left\{{C_1}, {C_2}, {C_3}, \cdots, {C_m} \right\}$ ; 阶段2. 异常检测6. 通过式(7)计算每个簇中的每个数据点与该聚类中心的距离为 $\scriptstyle dist \scriptstyle{\text{(}}{x_{km}}, {c_m}{\text{)}} $ ; 7. 利用式(8)计算每个数据点的局部密度 $\scriptstyle \;{\rho _i} $ ; 8. 由式(9)得到异常值分数 $\scriptstyle score{\text{(}}{x_i}{\text{)}} $ , 把所有数据点的异常值分数按从大到小的顺序进行排序, 输出其中值较大的作为异常点.

基于二阶近邻的异常检测算法中取偏好值参数P为−0.2, 参数 $ \alpha $ 的取值范围一般为(0.5, 1), 为达到最优的结果, 在该算法中取参数 $ \alpha $ 为0.9. 在消息更新的过程中, 某些情况下会受到数值振荡的影响, 为了避免这种影响, 每种消息都表示为 $ \lambda $ 乘以上一次迭代得到的值, 加上 $ 1 - \lambda $ 乘以当前更新得到的值, 影响因子 $ \lambda $ 的取值范围为(0, 1), 为获得较好的结果, 在这里取 $ \lambda $ 的值为0.9.

算法1的计算复杂度主要体现在两个阶段: 聚类阶段(步骤1–5)和异常检测阶段(从步骤6–8), 第1阶段中, 步骤1和步骤2计算数据点之间的相似性并构造相似性矩阵需要花费 ${\rm{O}}{\text{(}}N \times N{\text{)}}$ , $ N $ 表示的是数据集中的数据点的个数, 从步骤3到步骤5的消息传递过程, 需要不断迭代更新, 需要花费更多的时间, 其复杂度为 ${\rm{O}}{\text{(}}{N^2} \times T{\text{)}}$ , $ T $ 表示的是消息传递过程的迭代次数, 而 ${\rm{O}}{\text{(}}N \times N{\text{)}}$ 远低于 ${\rm{O}}{\text{(}}{N^2} \times T{\text{)}}$ , 因此构造相似性矩阵的时间复杂度可以忽略, 聚类阶段的时间复杂度为 ${\rm{O}}{\text{(}}{N^2} \times T{\text{)}}$ ; 异常检测阶段中, 步骤6计算簇中的数据点与所属簇中心的距离时应考虑到簇的个数和每个簇中的数据点的数量, 需要花费 ${\rm{O}}{\text{(}}N - M{\text{)}}$ , $ M $ 为聚类过程形成的簇的个数, 步骤7计算数据点的局部密度的时间复杂度为 ${\rm{O}}{\text{(}}N \times N{\text{)}}$ , 步骤8需要计算每一个数据点的异常值分数, 因此时间复杂度仅为 ${\rm{O}}{\text{(}}N{\text{)}}$ , ${\rm{O}}{\text{(}}N - M{\text{)}}$ 和 ${\rm{O}}{\text{(}}N{\text{)}}$ 与 ${\rm{O}}{\text{(}}N \times N{\text{)}}$ 相比, 可以忽略不计, 因此这一阶段的时间复杂度应为 ${\rm{O}}{\text{(}}N \times N{\text{)}}$ . 总的时间复杂度为 ${\rm{O}}{\text{(}}{N^2} \times T{\text{)}} + {\rm{O}}{\text{(}}N \times N{\text{)}}$ , 忽略较低的 ${\rm{O}}{\text{(}}N \times N{\text{)}}$ , 最后的时间复杂度应为 ${\rm{O}}{\text{(}}{N^2} \times T{\text{)}}$ .

3 实验分析 3.1 实验数据集与实验设置

为了验证文中提出的异常检测算法的有效性, 我们基于10个真实的数据集做了一系列的比较实验. 这些数据集包括WPBC、Ovarian、Wholesale、ForestTypes、Haberman、Ionosphere、Leaf、MUSK、SHS、TAE. 除了Ovarian数据集( https://github.com/therneau/), 其他数据集都来自于UCI机器学习仓库( http://archive.ics.uci.edu/ml/). 所有数据集的信息的简要描述如表1所示, 其中“异常标记”表示数据集中的数据点被看作是异常值的标签, 不同数据集有其各自的异常标记信息. 比如, WPBC 数据集中的47个被标记为“R”的数据点、Wholesale数据集中被标记为“Channel 2”的142个数据点和Ovarian数据集中被标记为“Yes”的162个数据点都被看作是异常值.

实验的过程中将基于二阶近邻的异常检测算法与6种经典的异常检测算法进行比较, 这些算法分别为随机离群值选择异常检测算法SOS (stochastic outlier selection)^[20]、主成分分析异常检测算法PCA (principal component analysis)^[21]、基于偏差的线性离群值检测方法LMDD (linear method for deviation-based outlier detection) ^[22]、子空间离群值检测算法SOD (subspace outlier detection)^[23]、一级支持向量机异常检测算法OCSVM (one-class support vector machines)^[24]、局部相关积分异常检测算法LOCI (local correlation integral) ^[25]. 在SOS算法^[20]中, 一个数据点与另一个数据点之间的关系, 可以通过亲和性来量化. PCA算法^[21]作为一种线性降维方法, 将样本在所有特征向量上的投影距离的和作为其异常值分数, 据此确定异常值. LMDD算法^[22]把平滑因子的概念用到了异常检测中, 该概念表明通过从数据集中删除一个元素的子集, 可以减少一定的差异. SOD算法^[23]是子空间离群值检测方法, 能够根据数据对象与子空间的邻居的偏离程度来检测高维特征空间中不同子空间中的离群值. OCSVM算法^[24]是支持向量算法对无标记数据情况的自然扩展, 是一种无监督的异常检测算法. LOCI算法^[25]提供了一个自动的、数据指定的截断来确定某个点是否为异常值. 以上6种异常检测算法的源码皆来自于pyod工具包( https://pyod.readthedocs.io/en/latest/)^[26].

每个异常检测算法一般会需要设置不同的参数, 它们的取值会对异常检测的性能产生影响, 因此, 为参数分配适当的值非常重要. 为了保证合理性, 在实验过程中, 各种异常检测算法的参数都会设置为pyod工具包中推荐的值. 基于二阶近邻的异常检测算法中的参数设置在算法描述部分中会有详细的说明. 整个实验是在环境为64位、8 GB内存、Intel(R) Core(TM)i7-8550U CPU@1.80 GHz 2 GHz的Win10上进行的.

为了评估不同异常检测算法的性能, 文中采用了3种常用的度量指标, 分别是平均精度AP (average precision)、 $ {F_1} $ 的最大值 $ \max {F_1} $ 和接受者操作特性曲线ROC (receiver operating characteristic)下的面积AUC (area under curve)^[2]. 假设 $ {G_h} $ 和 $ {G_q} $ 分别表示真实值和q个候选异常值. 精度则为真实异常值在候选异常值中所占的比例:

$ P(q) = \frac{{|{G_h} \cap {G_q}|}}{q} $

(10)

平均精度AP就是所有 $ P{\text{(}}q{\text{)}} $ 的值的平均值. 召回率则为:

$ R(q) = \frac{{|{G_h} \cap {G_q}|}}{{|{G_h}|}} $

(11)

很容易可以看出, $ P{\text{(}}q{\text{)}} $ 显示了候选异常值中的真实异常值的存在情况, $ R{\text{(}}q{\text{)}} $ 则为真实异常值中被检测出来的异常值的情况. 那么, $ {F_1}{\text{(}}q{\text{)}} $ 的值则可以通过 $ P{\text{(}}q{\text{)}} $ 和 $ R{\text{(}}q{\text{)}} $ 这两个值来获得, 它是 $ P{\text{(}}q{\text{)}} $ 和 $ R{\text{(}}q{\text{)}} $ 的调和平均数:

$ {F_1}(q) = \frac{{2P(q)R(q)}}{{P(q) + R(q)}} $

(12)

$ \max {F_1} $ 是指q个候选异常值的 $ {F_1}{\text{(}}q{\text{)}} $ 中的最大值.

接受者操作特性曲线ROC是一个由真阳性率和假阳性率构成的图形图, AUC度量的是ROC曲线下的面积, 它作为一种衡量性能优劣的评价指标, 用来表示比较检测性能的数值结果. 它的值总是保持在[0, 1]区间内, 而且, 其值越大越好, 平均精度AP和 $ \max {F_1} $ 的值也是如此.

3.2 实验结果与讨论

我们分别在10个真实数据集上将基于二阶近邻的异常检测算法(anomaly detection based second-order proximity, SOPD)和其他的异常检测算法进行了性能测试和评估, 得到不同的实验结果. 在每个异常检测算法中, 每个数据集中的数据点的异常值分数都是自动生成, 根据异常值分数按从大到小的顺序对数据点进行排序, 取前q个数据点作为预测的异常值, q表示为真实异常值的个数. 根据生成的异常值分数、预测的标签和真实的标签, 计算每个异常检测算法在不同数据集下的平均精度AP 、 $ \max {F_1} $ 和AUC, 评估它们的检测异常的性能.

表2记录了SOPD算法与其他6种异常检测算法的平均精度AP, 其中粗体表示实验结果中每个数据集所对应的最高的AP值. 从表中可以看出, SOPD算法仅仅在SHS数据集上低于SOD算法的平均精度值, 其他数据集上, SOPD算法的平均精度都高于另外6种异常检测算法. 尤其是在Ionosphere数据集上, SOPD算法的平均精度高达0.92. 除此之外, Ovarian数据集上, OCSVM算法的平均精度和PCA算法、SOD算法一样都是0.70, 为6种异常检测算法中最高的, 这是因为OCSVM算法可以捕获到不同数据集的分布情况, 尤其是在维度较高的大样本数据集上, 事先并不知道数据的分布状况, 此种情况下OCSVM算法有较强的检测能力, 而SOPD算法的AP值为0.73, 比OCSVM算法更高, 因此, SOPD算法在未知数据分布的情况下, 对高维度数据集的异常检测性能也较好.

为了再次验证SOPD算法的优异性, 通过使用 $ \max {F_1} $ 进行性能度量, 具体实验比较结果如表3所示. 表3的比较结果显示, 在Ovarian数据集、SHS数据集和TAE数据集上, SOPD算法的 $ \max {F_1} $ 和另外6种异常检测算法中的最高值一样, 除此之外, SOPD算法在其他数据集上的 $ \max {F_1} $ 都高于那些异常检测算法. 比如, Leaf数据集中, SOPD算法的 $ \max {F_1} $ 为0.33, 而其他检测算法的最高的 $ \max {F_1} $ 仅为0.26, SOPD算法的结果仍较高. MUSK数据集上, PCA算法的 $ \max {F_1} $ 为0.75, 是6种异常检测算法中最高的, 但SOPD算法的 $ \max {F_1} $ 仍比PCA算法高. 因此, SOPD算法在所有数据集上都有较高的 $ \max {F_1} $ 值, 尤其是在Wholesale数据集、ForestTypes数据集和Ionosphere数据集上, SOPD算法的性能明显优于其他异常检测算法. SOPD算法主要是同时考虑了数据的局部性和全局性结构信息.

实验过程中通过使用AUC准则衡量算法的性能, 根据AUC的评价度量, 再次证明了SOPD算法的优越性. 图4描绘了不同异常检测算法的AUC, 图4一共有10个柱形图, 分别表示SOPD算法和6种异常检测算法在10个数据集上的AUC值的比较结果, 其中每个柱形图中的不同颜色的长条代表不同的异常检测算法, SOPD算法由最后一个长条所表示, 通过图4可以清晰地看出同一个数据集上不同异常检测算法的性能差异. SOPD算法的AUC只在SHS数据集上较低于SOS算法和SOD算法, 即使在TAE数据集上, SOPD算法的AUC也与6种异常检测算法中的最高值一样. 除此之外, 在其他数据集上, SOPD算法的性能明显比另外6种异常检测算法较优越, 特别是在ForestTypes数据集、Ionosphere数据集、Leaf数据集上, SOPD算法的AUC分别为0.91、0.93和0.91, 表现出了良好的性能. 因此, 由图4可以看出, SOPD算法的准确性总体上较好.

4 结束语

本文提出了一种基于二阶近邻的异常检测算法, 利用二阶近邻将数据全局结构考虑进去, 并利用数据点与所属簇中心之间的关系捕获异常情况. 总体来说, 该算法主要包括聚类和异常检测两个阶段. 在聚类过程中利用一阶近似和二阶近邻综合考虑局部性和全局性信息, 对数据的初始相似性矩阵进行重新构造, 提高聚类的性能. 之后, 在聚类结果的基础上, 同时考虑每个簇中的数据点与该簇中心之间的距离和数据点本身的密度, 得到异常值分数, 根据异常值分数判断数据点的异常情况. 我们在10个真实数据集上进行了比较实验, 其结果表明, SOPD算法与经典的异常检测算法相比具有一定的优越性. 下一步的研究方向是减少算法的时间复杂度, 并进一步增强算法对异常值的敏感度.