增强工业绿色发展水平是当今中国乃至今后较长时间实现经济可持续发展和生态文明建设的重要环节. 目前, 国内外对工业绿色发展水平的评价方法主要分为绿色GDP核算[1]、全要素生产率法[2]、基于多指标测度综合指数法[3]这3类. 但这3类评价方法都是基于效率的核算, 若要拓展工业绿色发展内涵, 则需构建绿色发展综合指标体系[4]. 然而, 什么样的多指标测度方法既能反映工业绿色发展水平的总体情况, 又能体现工业绿色创新能力呢?
为解决这类问题, 何静等[5]构建了绿色经济评价指标体系并运用因子分析法对中国30个地区历年的绿色经济进行了比较和评价. 田亚鹏等[6]采用超效率SBM-DEA模型测算陕西省地级市的绿色发展效率. 李兰冰等[7]研究了技术创新、节能减排与城市绿色发展之间的影响效应和路径机制. Zou等[8]研究了环境监管体系是否推动了中国污染密集型产业的绿色发展. 王韶华等[9]运用粗糙集和前沿函数模型对京津冀地区的工业绿色发展进行了研究. 但以上研究并没有从多维视角来分析工业绿色发展水平整体中的绿色投入要素和绿色产出效益间的相互影响与制约关系. 基于此, 在中国当前环境和资源等约束条件下建立基于混合多维云模型的多指标综合测度方法, 不仅可以反映工业绿色发展整体水平的高低, 也能精确计算出各指标贡献度, 从而判断其是否具有工业绿色创新能力; 同时为协调推动各地区工业绿色发展进程提供实质性参考建议和理论决策依据.
1 集结综合属性值的工业绿色发展水平指标体系构建当前工业绿色发展矛盾表现在资源能源消耗大、利用率低、环境污染严重、绿色发展能力和绿色创新能力不高. 因此本文借鉴四部委发布的《绿色发展指标体系》及在以往学者们[10-19]相关研究的基础上, 从绿色投入要素和绿色产出效益维度构建了集结综合属性值的工业绿色发展多指标评价体系如表1所示.
| 表 1 集结综合属性值的工业绿色发展水平指标体系 |
2 基于混合多维云模型的区间多属性测度方法的构建
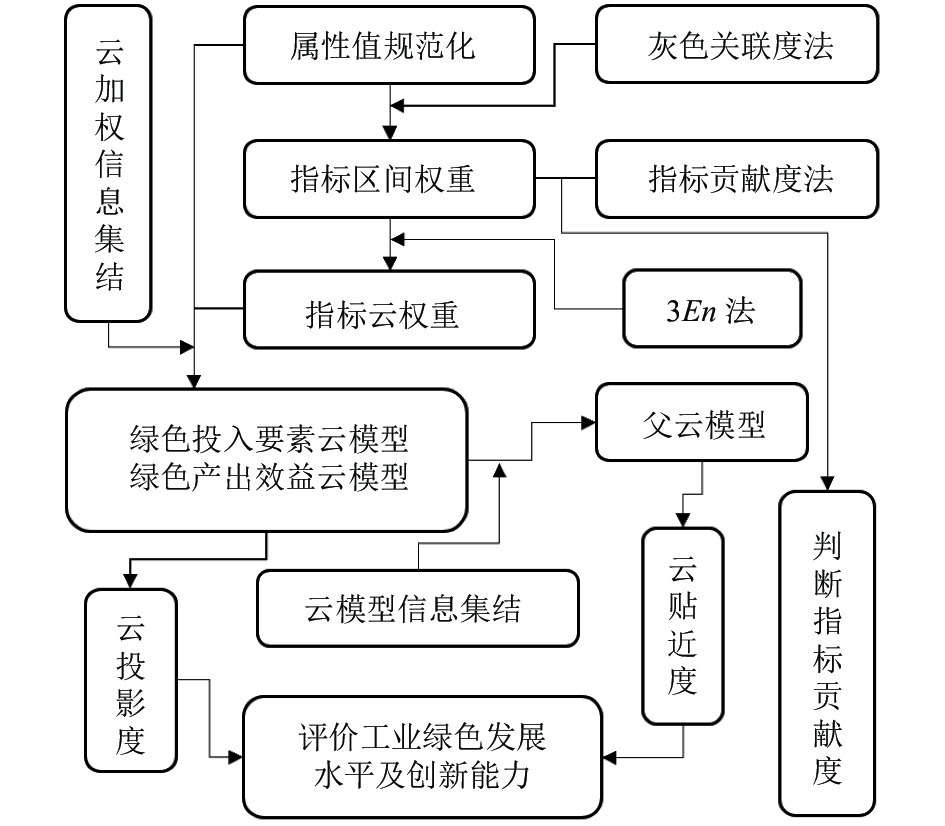
工业绿色发展水平指标阈值的衡量具有模糊性和不确定性, 对各指标权重界定常采用的主/客观赋权法缺陷比较明显. 因为对不同属性指标而言, 依赖主观意识、依赖足够样本数据和实际问题域的赋权法会导致权重与属性的实际重要程度相差较大, 进一步加剧指标数据量化评估权重的失真. 相比之下, 基于数据统计属性本身的云权重[20]在属性指标值不确定、属性权重完全未知时, 能通过期望、熵、超熵数字特征有效解决系统过程中的随机性和模糊性, 实现定性与定量间的双向认知转换, 最大程度地减少属性权重失真问题. 当权重值不精确时, 可通过区间权重的标准化来确定属性的权值问题, 提高指标评价的效率和准确性. 因此, 本文将构建基于混合多维云模型的区间多属性决策方法来测度工业绿色发展水平的高低, 并判断各地区是否具有工业绿色创新能力. 本研究针对工业绿色发展水平的测度模型具体流程见图1所示.
2.1 多属性多维云模型在工业绿色发展水平评价过程中, 其发展水平的高低由多个内在相互联系和共同影响的指标决定. 由此可将一维正态云模型推广至多维云模型, 通过多个维度来描述工业绿色发展水平指标属性的概念. 设
| $ {\mu _i}\left( {{x_1}, {x_2}, \cdots, {x_n}} \right) = \exp\left[ { - \sum\limits_{j = 1}^n {\frac{{{{({x_{ij}} - E{x_{ij}})}^2}}}{{2{{(E{n_{ij}}^\prime )}^2}}}} } \right] $ |
|
图 1 工业绿色发展水平测度模型图 |
|
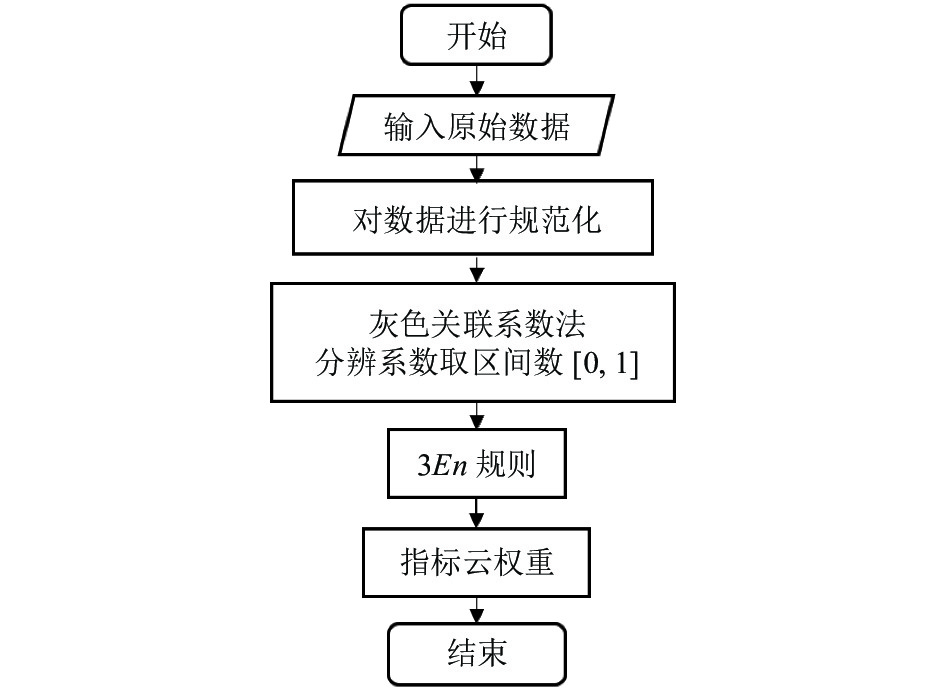
图 2 云权重算法流程图 |
因此, 多维正态云模型可用期望Ex、熵En、超熵He三个数字特征表示n维论域中的某个定性概念, 且云滴分布服从期望为Ex, 方差为En2+He2的随机变量. 其中, Ex是云滴在论域空间分布中的数学期望, 反映定性概念云滴群的云重心. En表示定性概念不确定性的度量, 反映了云滴的离散程度和论域范围内云滴的取值范围. He是对En的不确定性度量, 反映了云滴的厚度. 研究表明, 超熵越大, 云的离散程度越大, 隶属度的随机性也随之增大, 云的厚度也越厚.
2.2 多指标多属性规范化决策矩阵由于工业绿色发展水平指标属性的单位并不完全一致, 不能直接对多指标体系进行相互比较和信息集成. 为此, 对指标多属性决策矩阵进行无量纲化处理. 假设有m个待评价方案, 每个待评价方案
| $\left\{ { \begin{split} &y_{i j}=\frac{x_{i j}-x_{\text {min }}}{x_{\text {max }}-x_{\text {min }}}( { 效益型属性 })\\ &y_{i j}=\frac{x_{\text {max }}-x_{i j}}{x_{\max }-x_{\text {min }}}( { 成本型属性 }) \end{split}} \right. $ | (1) |
其中,
区间权重不同于精确实数属性权重, 其更能表达决策评价过程中的模糊性, 贴近实际的决策问题.
已知区间数
由于该区间权重不能直接映射属性权重的隶属度, 本文结合灰色关联系数法和
设规范化后母序列为
| $ \left\{ {\begin{array}{l} {\omega }_{j}={\lambda }_{0j}/{\displaystyle {\sum }_{i=1}^{n}{\lambda }_{0j}}\text{, }{\omega }_{j}=[{\omega }_{j}^-, {\omega }_{j}^+]\\ i=1, 2, \cdots, m;j=1, 2, \cdots, n\end{array} } \right.$ | (2) |
若正态分布
| $\left\{ {\begin{gathered} N_j^\omega = \left( {Ex_j^\omega , En_j^\omega , He_j^\omega } \right) = \left( {\frac{{\omega _j^ - + \omega _j^ + }}{2}, \frac{{\omega _j^ + - \omega _j^ - }}{{2.355}}, \frac{{\omega _j^ + - \omega _j^ - }}{{2.355 \times 10}}} \right) \\ \;j = 1, 2, \cdots , n \\ \end{gathered} } \right.$ | (3) |
其中,
本文从工业绿色发展的绿色投入要素和绿色产出效益这两个维度构建评价指标体系, 对属性间的信息集结也将从这两个维度构建工业绿色发展水平的多维云模型.
已知代表第
| $ \left\{ \begin{gathered} {N_{ik}} = {y_{ij}}N_j^\omega = \left( {E{x_{ik}}, E{n_{ik}}, H{e_{ik}}} \right), k = 1, 2 \\ E{x_{ik}} = \sum\limits_{j = 1}^n {{y_{ij}}Ex_j^\omega } \; \\ E{n_{ik}} = \sqrt {\frac{1}{n}\sum\limits_{j = 1}^n {{y_{ij}}En{{_j^\omega }^2}} } \; \\ H{e_{ik}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{y_{ij}}He{{_j^\omega }^2}} } \\ \end{gathered} \right. $ | (4) |
对于第
| $ \begin{split} {N_i}& = {N_{i1}} + {N_{i2}} = \left( {E{x_i}, E{n_i}, H{e_i}} \right) \\ & = \left( {E{x_{i1}} + E{x_{i2}}, \sqrt {\frac{{En_{i1}^2 + En_{i2}^2}}{2}} , \sqrt {\frac{{He_{i1}^2 + He_{i2}^2}}{2}} } \right) \end{split} $ | (5) |
各待评价方案的多维云模型用于判断自身是否具有工业绿色创新能力, 父云即用来比较工业绿色发展整体水平.
2.5 基于混合多维云模型的贴近度和云投影度测定在多维云模型中, 如何判断各云模型与父云之间的相似程度或接近程度, 可用贴近度进行度量. 本研究通过计算各待评价方案的父云模型, 找出正理想云模型和负理想云模型, 并计算各待评价方案与正理想云模型和负理想云模型的云相似度, 从而得到各待评价方案与正、负理想云模型的接近程度即贴近度. 具体计算过程如下.
将各地区的工业绿色发展水平的多维云模型凝聚为更高一级的父云
| $ \left\{ {\begin{array}{*{20}{l}} {{N_{\max/\min}} = \left( {E{x_{\max/\min}}, E{n_{\max/\min}}, H{e_{\max/\min}}} \right)} \\ {{N_{\max}} = \left( {\max E{x_i}, \min E{n_i}, \min H{e_i}} \right)} \\ {{N_{\min}} = \left( {\min E{x_i}, \max E{n_i}, \max H{e_i}} \right)} \end{array}} \right. $ | (6) |
其中, 基于云模型方差的形状相似度
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{Sim}}_{si}^{ + / - }\left( {{N_i}, {N_{\max/\min}}} \right) = \dfrac{{\min\left( {\sqrt {En_i^2 + He_i^2} , \sqrt {En_{\max/\min}^2 + He_{max/min}^2} } \right)}}{{\max\left( {\sqrt {En_i^2 + He_i^2} , \sqrt {En_{\max/\min}^2 + He_{\max/\min}^2} } \right)}} \\ {\mathit{Sim}}_{di}^{ + / - }\left( {{N_i}, {N_{\max/\min}}} \right) = \dfrac{1}{{\sqrt {{{\left( {E{x_i} - E{x_{\max/\min}}} \right)}^2} + {{\left( {E{n_i} - E{n_{\max/\min}}} \right)}^2} + {{\left( {H{e_i} - H{e_{\max/\min}}} \right)}^2}} }} \\ {{\mathit{Sim}}_i^{ + / - } = {\textit{Sim}}_{si}^{ + / - } \times {\textit{Sim}}_{di}^{ + / - }, \;i = 1, 2, \cdots, m} \end{array}} \right. $ | (7) |
则第
| $ {\gamma _i} = \frac{{{\mathit{Sim}}_i^ + }}{{{\mathit{Sim}}_i^ + + {\mathit{Sim}}_i^ - }},\; {i = 1, 2, \cdots, m} $ | (8) |
贴近度只能反映区域工业绿色发展水平的整体情况, 工业绿色发展水平是否具有绿色创新能力可通过云投影法来测度, 即将各待评价方案的绿色产出效益云模型投影到绿色投入要素云模型上来反映待评价方案内部的相互制约和影响关系.
云投影法是一种解决多维度、非线性问题的新统计方法, 通过计算反映将多维云模型数据投射到低维云模型子空间的投影度, 从而达到分析混合多维云模型数据的目的. 本研究中将各待评价方案的绿色产出效益云模型投影到绿色投入要素云模型上来反映待评价方案内部的相互制约和影响关系. 即将绿色产出效益云模型和绿色投入要素云模型的数字特征看作是两个向量, 运用向量投影法将绿色产出效益云模型投影到绿色投入要素云模型上, 则可以得到云模型间的云投影度
| $ Pr{j_{{N_{i1}}}}\left( {{N_{i2}}} \right) = \frac{{\sqrt {{{\left( {E{x_{i2}}} \right)}^2} + {{\left( {E{n_{i2}}} \right)}^2} + {{\left( {H{e_{i2}}} \right)}^2}} }}{{\sqrt {{{\left( {E{x_{i1}}} \right)}^2} + {{\left( {E{n_{i1}}} \right)}^2} + {{\left( {H{e_{i1}}} \right)}^2}} }} $ | (9) |
一般地,
考虑各项指标对工业绿色发展水平和工业绿色创新能力的影响存在差异, 可从区域视角找出长板指标和短板指标, 因地制宜地重点增强短板指标和持续稳定地发展长板指标, 最后实现各个指标的贡献度基本一致, 实现指标间的均衡协调发展. 其中, 对第
| $ \left\{ \begin{gathered} {a_{ij}} = {[a_{ij}^ - , a_{ij}^ + ]_{1 \times n}} = {y_{ij}} \times [\omega _j^ - , \omega _j^ + ] \\ p\left( {{a_{ij}} \geqslant {a_{i\left( {j + 1} \right)}}} \right) = \frac{{\min\{ {l_{{a_{ij}}}} + {l_{{a_{i\left( {j + 1} \right)}}}}, \max(a_{ij}^ + - a_{i\left( {j + 1} \right)}^ - , 0)\} }}{{{l_{{a_{ij}}}} + {l_{{a_{i\left( {j + 1} \right)}}}}}} \\ {v_j} = \frac{1}{{n(n - 1)}}\left(\sum\nolimits_{j = 1}^n {{p_{ij}}} + \frac{n}{2} - 1\right) \\ {\alpha _j} = \frac{{{\gamma _j}}}{{\displaystyle\sum\nolimits_{j = 1}^n {{\gamma _j}} }}, \;j = 1, 2, \cdots, n \\ \end{gathered} \right. $ | (10) |
由
根据排序向量可以确定各指标对工业绿色发展水平的初始贡献度
| $\left\{ { \begin{split} & \max\;[\mu \sum\nolimits_{j = 1}^n {{{({\beta _j}{\gamma _j})}^2}} - \left( {1 - \mu } \right)\sum\nolimits_{j = 1}^n {{\beta _j}} \ln{\beta _j}] \\ & {\rm{s.t.}}\left\{ \begin{gathered} \sum\nolimits_{j = 1}^n {{\beta _j}} = 1 \\ {\beta _j} \geqslant \eta , \;0 < \mu < 1, \;j = 1, 2, \cdots, n \\ \end{gathered} \right. \end{split} } \right.$ | (11) |
比较优化贡献度
在工业绿色发展水平评价指标体系及方法研究基础上, 本文拟对中国30个地区的工业绿色发展水平进行测度研究. 指标数据主要通过各政府官方网站公布的统计数据及历年中国各地区的《统计年鉴》《中国环境统计年鉴》《国民经济和社会发展统计公报》等获取.
工业绿色发展水平指标体系原始数据先由式(1)进行规范化处理, 再由式(2), 式(3)对属性进行赋权得到各个属性的区间权重, 再将区间权重转化为含隶属度的多维云权重, 如表2所示, 其处理模糊性和随机性的能力较强, 可减少信息缺失.
通过Matlab编制云正向发生器可直观展示各属性的云权重. 集结综合属性值的工业绿色发展水平指标体系的多维云权重如图3所示.
按照信息集结式(4)将云权重和规范化数据进行集结得到各地区的综合属性值, 即从绿色投入要素和绿色产出效益两个维度集结为工业绿色发展水平的多维云模型
通过式(5)将代表各地区工业绿色发展水平的多维云模型凝聚为更高层次的父云Ni, 式(6)确定正/负理想云模型, 式(7)计算出各地区的父云分别与正/负理想云模型的距离、形状相似度以及综合相似度, 再由式(8)算出各地区工业绿色发展水平的贴近度, 具体结果见表4. 由表4可知: 天津和北京分别位列第一、第二, 广东位列最后. 说明天津的工业绿色发展整体水平最高, 北京次之, 广东最低.
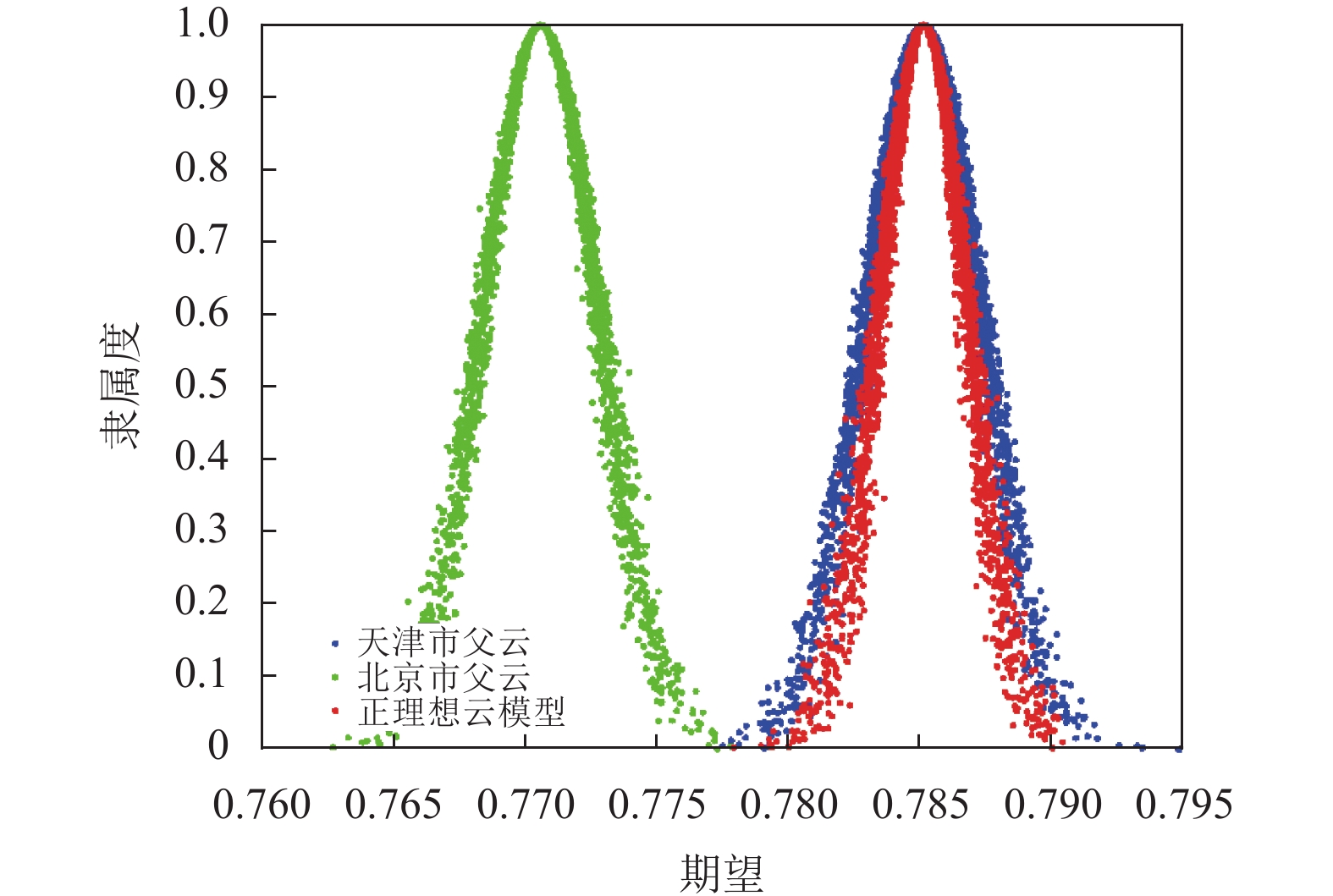
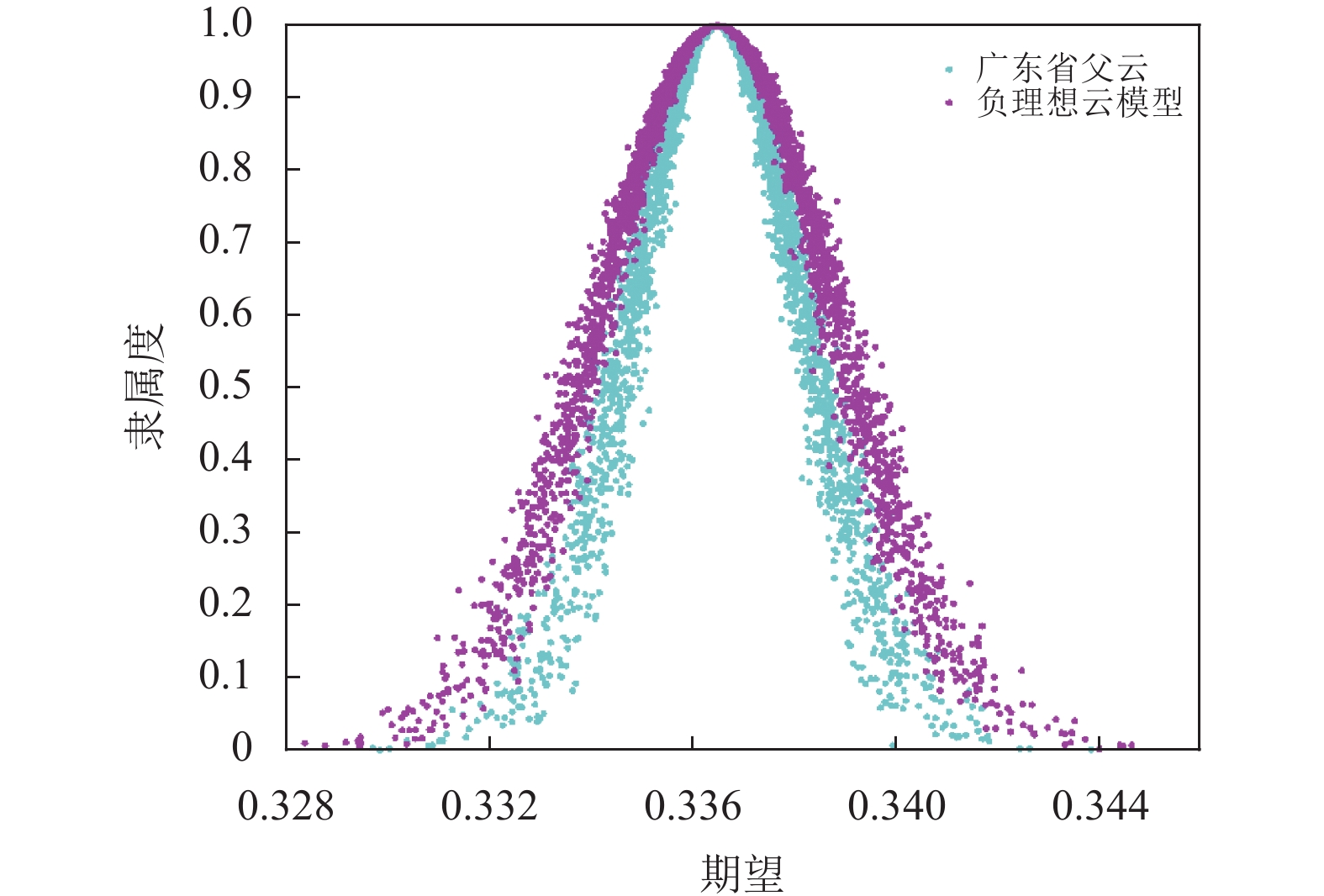
天津父云和北京父云与正理想云模型如图4所示; 广东父云与负理想云模型如图5所示. 由图可知, 天津作为工业绿色发展水平最高的省, 其父云与正理想云模型的贴近度非常高, 其次是北京; 广东的发展水平整体差距很大, 表现在父云与负理想云模型的贴近度高, 究其原因, 广东作为科技创新沿海地区, 在绿色投入要素C12、C14、C16、C17和C18指标上投入了大量的人力、资源和科技; 从原始数据来看, 原始属性值大多比其他省份高出一个数量级, 进行规范化后的属性值为0, 这导致了其工业绿色发展水平整体情况位列全国最低.
| 表 2 区间权重和多维云权重 |

|
图 3 工业绿色发展水平指标云权重图 |
| 表 3 各地区工业绿色发展水平的多维云模型 |
多维云模型中将绿色产出效益云模型投影到绿色投入要素云模型上, 通过式(9)计算云投影度(见表5)来判断各地区是否具有工业绿色创新能力.
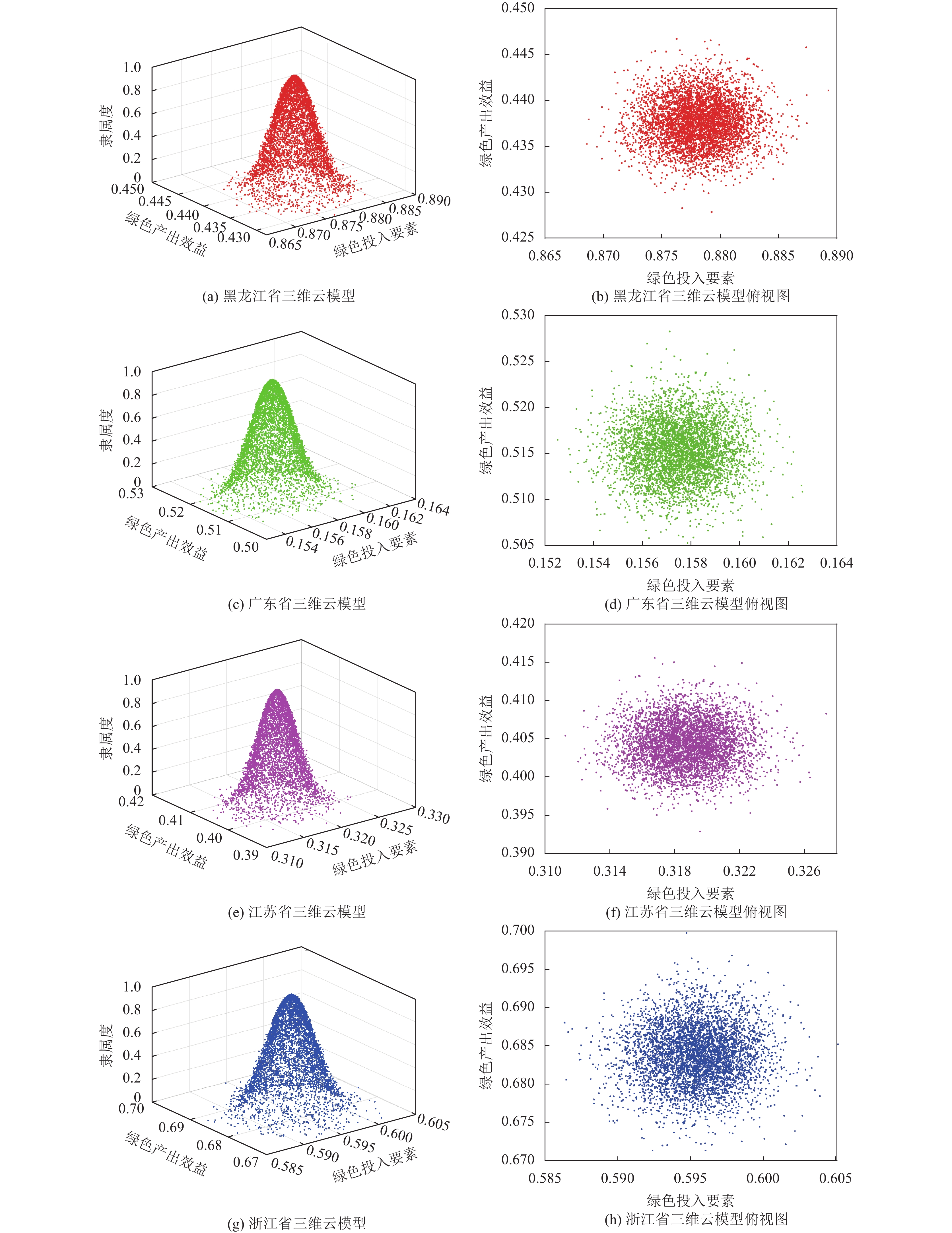
从云投影度排名来看, 广东是最具有工业绿色创新能力的地区, 江苏、浙江和上海次之, 都属东部沿海发达地区; 黑龙江位列最后, 说明其绿色创新能力不足. 从代表黑龙江的工业绿色发展水平多维云模型数据((0.8782, 0.0027, 0.0003), (0.4377, 0.0025, 0.0003))可知, 黑龙江的绿色投入要素云模型的期望要比绿色产出效益云模型的期望大得多, 是典型的投入多产出少. 反观广东工业绿色投入要素云模型(0.1575, 0.0014, 0.0001), 绿色产出要素云模型(0.5154, 0.0030, 0.0003), 其绿色产出效益云模型的期望比绿色投入要素的云模型的期望要大得多. 其中广东、黑龙江、江苏和浙江的多维云模型图如图6所示.
由图6可知黑龙江的工业绿色投入要素云模型的期望要远大于工业绿色产出效益, 云投影度仅为0.498, 位列最后一名, 但其工业绿色发展水平的贴近度排名15.
这就是典型的只由一个综合指数来评价工业绿色发展水平, 而忽略了整体中的部分指标被弱化和忽视, 特别是以资源环境大量被开发破坏而带来的工业绿色发展高水平的假象. 广东作为最具有工业绿色创新能力的地区, 云投影度为3.273, 远远大于1, 但贴近度位列最后一位. 为解释这种差异, 现以广东为例, 深入研究各指标对其工业绿色发展水平的贡献度, 以期为广东进一步实现工业绿色发展提供理论建议和参考. 由式(10)计算得广东工业绿色发展水平各个指标的区间数表达, 利用区间可能度得到排序向量, 并计算出各指标对广东工业绿色发展水平的初始贡献度(见表6).
再根据二次优化贡献度模型式(11)用LINGO软件求解贡献度差值, 得到广东工业绿色发展水平的各个指标初始贡献度与优化后的贡献度的距离
由表7可知, 指标C25、C11和C24为广东工业绿色发展的整体水平提供了较大的贡献度, 其初始贡献度就已经大于二次优化后的贡献度, 属于长板指标; 而指标C12、C14、C16、C17和C18的距离为负值, 属于短板指标, 并且这5个指标全都属于绿色投入要素这一维度, 为此有关管理部门需要着重注意与思考. 针对这一结果, 广东有关部门可依据此评价方法和结果对工业绿色发展水平的各类指标进行继续优化长板指标并对短板指标进行重点监管和发展, 使其短板也向长板指标发展, 最后实现指标间的协调均衡发展, 为工业发展由粗放式发展到高质量发展再到绿色发展提供有效贡献.
4 结论与管理建议基于工业绿色发展理念, 本文从绿色投入要素和绿色产出效益两个维度构建了工业绿色发展水平指标体系. 在传统多指标综合指数评价法的基础上引入多维云模型和区间数理论, 探讨了一种新的基于混合多维云模型的工业绿色发展水平测度方法对工业绿色发展水平的总体情况及创新能力进行判断, 避免了传统的多指标综合指数评价法只用一个综合指数来评估工业绿色发展水平, 而忽略了工业绿色创新能力的评估; 并采集2020年的相关数据对中国30个地区的工业绿色发展进行了验证, 进一步说明了模型构建的有效性.
| 表 4 各地区工业绿色发展水平贴近度 |
|
图 4 天津和北京父云与正理想云模型 |
|
图 5 广东父云与负理想云模型 |
| 表 5 各地区云投影度 |
|
表 6 可能度矩阵
|
| 表 7 广东省工业绿色发展水平指标贡献度距离 |
|
图 6 4个地区多维云模型图 |
同时, 本文的研究方法和研究结果对区域工业绿色发展有着重要的管理建议: (1)各地区应注重工业绿色创新能力的培养与发展. 工业绿色发展水平的高低一般只能反映工业绿色发展的综合情况, 并没有着重关注于工业绿色创新能力的培养与发展, 容易造成以资源环境大量浪费破坏为代价带来的工业绿色发展水平的虚高, 各地区应关注工业创新能力的提高, 加大各类资源综合利用率, 促进工业企业向科技化绿色化方面发展, 为工业绿色全生命周期过程提供有力的支持. (2)发挥长板指标优势, 补缺短板指标劣势. 参考指标的初始贡献度和优化贡献度, 各管理部门应找出影响该区域工业绿色发展的长短板指标, 取长补短. 发挥独特的优势指标能力, 对短板指标进行有针对性的监管和重点投入, 实现各类指标协调综合发展, 加大工业绿色发展的力度, 培育独具优势的工业绿色创新能力, 加大人才引进与科技发展, 缩小各省份间工业绿色发展水平的差距. (3)促进区域工业协调发展. 京津冀、长三角、珠三角和成渝等城市群的协调发展战略为工业绿色发展提供了历史性的机遇, 为此, 各地区可以联动周围城市群实现产业结构调整和科技成果转化, 进一步为工业发展绿色发展提供坚实基础.
| [1] |
王燕, 刘邦凡, 郭立宏. 基于SEEA-2012我国绿色GDP核算体系构建及时空格局分析. 生态经济, 2021, 37(9): 136-145. |
| [2] |
Brandt L, Tombe T, Zhu XD. Factor market distortions across time, space and sectors in China. Review of Economic Dynamics, 2013, 16(1): 39-58. DOI:10.1016/j.red.2012.10.002 |
| [3] |
栗欣如, 姜文来, 冯欣. 我国水利绿色发展水平测算分析. 中国农业资源与区划, 2021, 42(1): 7-17. |
| [4] |
He LY, Sun YM, Xia YF, et al. Construction of a green development performance index of industrial enterprises: Based on the empirical study of 458 listed industrial enterprises in China. Ecological Indicators, 2021, 132: 108239. DOI:10.1016/j.ecolind.2021.108239 |
| [5] |
何静, 李战江, 苏金梅. 基于R聚类-灰关联优势分析的绿色经济评价指标体系构建. 科技管理研究, 2018, 38(10): 90-98. DOI:10.3969/j.issn.1000-7695.2018.10.013 |
| [6] |
田亚鹏, 柳晓艺. 基于超效率SBM-DEA和空间分析的区域绿色发展效率评价. 统计与信息论坛, 2021, 36(8): 56-65. DOI:10.3969/j.issn.1007-3116.2021.08.006 |
| [7] |
李兰冰, 李焕杰. 技术创新、节能减排与城市绿色发展. 软科学, 2021, 35(11): 46-51. DOI:10.13956/j.ss.1001-8409.2021.11.08 |
| [8] |
Zou H, Zhang YJ. Does environmental regulatory system drive the green development of China’s pollution-intensive industries? Journal of Cleaner Production, 2022, 330: 129832.
|
| [9] |
王韶华, 刘晔, 张伟, 等. 基于粗糙集与未确知模型的京津冀工业绿色发展的差异性与协调性分析. 运筹与管理, 2021, 30(5): 200-207. |
| [10] |
李俊, 许家伟. 河南省工业用水效率的动态演变与分解效应——基于LMDI模型视角. 经济地理, 2018, 38(11): 183-190. DOI:10.15957/j.cnki.jjdl.2018.11.021 |
| [11] |
张治河, 焦贝贝, 李怡, 等. 科技资源匮乏地区创新驱动发展路径研究. 科研管理, 2018, 39(2): 46-59. DOI:10.19571/j.cnki.1000-2995.2018.02.006 |
| [12] |
Ghofrani A, Zaidan E, Abulibdeh A. Simulation and impact analysis of behavioral and socioeconomic dimensions of energy consumption. Energy, 2022, 240: 122502. DOI:10.1016/j.energy.2021.122502 |
| [13] |
徐严, 陈雨玮, 刘程军. 长三角城市群绿色化演化特征及其门槛效应研究. 管理现代化, 2021, 41(6): 28-32. DOI:10.19634/j.cnki.11-1403/c.2021.06.008 |
| [14] |
张丽君, 巩蓉蓉, 袁伟伦. 公共服务差距与区域间收入不平等的形成——基于2000–2019年省级面板数据的分析. 公共管理评论, 2020, 2(4): 50-81. |
| [15] |
黄群慧. “新常态”、工业化后期与工业增长新动力. 中国工业经济, 2014(10): 5-19. |
| [16] |
傅志华, 赵福昌, 李成威, 等. “创新、平衡、联动、包容、协同”是东部地区实现财经稳定发展的重要支撑. 经济研究参考, 2017(2): 49-63. DOI:10.16110/j.cnki.issn2095-3151.2017.02.005 |
| [17] |
左朝晖, 李绍康, 杨津津, 等. 基于GA-BP神经网络的页岩气开发区域水资源承载力研究. 环境工程技术学报, 2021, 11(1): 194-201. DOI:10.12153/j.issn.1674-991X.20200081 |
| [18] |
丁镭, 刁贝娣. 空间计量经济学视角下的浙江工业大气污染物排放及社会影响因素. 环境污染与防治, 2021, 43(1): 132-138. DOI:10.15985/j.cnki.1001-3865.2021.01.024 |
| [19] |
Wang HR, Cui HR, Zhao QZ. Effect of green technology innovation on green total factor productivity in China: Evidence from spatial durbin model analysis. Journal of Cleaner Production, 2021, 288: 125624. DOI:10.1016/j.jclepro.2020.125624 |
| [20] |
龚艳冰, 徐绪堪, 刘高峰. 基于正态云期望和方差距离的语言型多属性决策方法研究. 统计与信息论坛, 2021, 36(10): 12-19. DOI:10.3969/j.issn.1007-3116.2021.10.002 |
 2023, Vol. 32
2023, Vol. 32


