在实际工程应用中, 当发现路面存在损伤时, 基于对应无损路面图像有助于分析路面损伤演化细节, 且与相关结构工程理论知识结合更可辅助预测路面寿命或分析路面损伤演化趋势, 为下一步的养护管理提供决策支持. 而实测条件下采用多功能道路检测车采集到的路面受损图像难以获知其原始状态, 需采用图像修复技术对路面图像受损区域进行修复以得到对应的无损路面图像. 沥青路面常见的损伤主要包括开裂、车辙、沉陷、冻胀及水损[1]等, 其中裂缝作为最常见的路面损伤[2], 研究其相应的修复方法具有重要意义与实用价值.
图像修复是对图像中的受损区域进行重建, 或去除图像中多余物体的一门技术[3]. 它可分为传统方法和基于深度学习的方法两类.
传统方法依据修复思想的不同可分为基于扩散的方法和基于样本块的方法[4]. 基于扩散的图像修复方法是利用数学中的偏微分方程, 将图像中已知区域的像素平滑传播到缺失区域中来修复破损图像[4]. Bertalmio等人[5]最早在图像修复任务中引入(partial differential equation, PDE)思想, 提出了沿着等光线方向利用图像中已知信息采取平滑传播方式来修复缺失区域的BSCB(Bertalmio-Sapiro-Caselles-Ballester)模型, 但其无法修复具有大面积缺失或纹理较为复杂的图像; 受此启发, Shen等人[6]采用各向异性扩散思想, 提出整体变分(total variation, TV)模型, 使用最小化能量泛函的方式来进行图像修复; 随后他们继续对其进行改进, 提出基于曲率驱动扩散思想的CDD (curvature driven diffusion)模型[7], 解决了TV模型[6]采用直线修复的缺陷, 但同时存在修复时间较长的问题. 基于样本的图像修复方法通过计算并搜索破损图像缺失区域与已知区域相似度最高的样本, 并将其复制粘贴到缺失区域以修复破损图像[4]. Efros等人[8]最早提出了基于马尔可夫随机场的非参数纹理合成修复方法, 但存在部分纹理填充错误及修复速度较慢等缺陷; 在此基础上, Criminisi等人[9]提出了通过将已知区域的结构和纹理信息进行复制并传播到破损图像的缺失区域的方法, 但其所用的计算相似度的函数相对不稳定从而导致样本填充次序错误; 张申华等人[10]通过引入曲率和梯度信息, 获得了更加可靠的样本修复次序, 从而解决了Criminisi算法[9]填充次序不准确的问题, 但同样存在计算时间过长的问题.
基于深度学习的图像修复方法依据模型结构的不同可分为基于卷积神经网络(convolutional neural networks, CNN)和基于生成对抗网络(generative adversa-rial network, GAN)的方法[11]. Liu等人[12]提出了一种编码器-解码器网络架构, 结合多尺度思想共同修复图像的结构和纹理信息, 能有效去除破损区域周围的模糊和伪影现象; 但存在计算成本大的问题; Hong等人[13]提出了一种U-NET网络架构, 将融合块作为自适应模块, 通过把图像中的缺失区域与原始图像相结合, 使得图像的结构和纹理信息能够自然的从已知区域传播到缺失区域中, 从而避免了边缘出现不一致的现象, 但有时会出现语义混乱的情况; Yeh等人[14]采用预训练的深度卷积GAN (deep convolution GAN, DCGAN)[15], 并将先验知识和上下文损失结合起来, 共同预测图像缺失区域内容, 但存在预训练的GAN不稳定、容易坍塌等问题; Xiong等人[16]通过深度模型来学习图像的前景特征, 并用它预测轮廓信息, 同时引入了PatchGAN[17]构成的轮廓鉴别器来鉴别预测轮廓, 并充分利用预测轮廓信息来引导破损图像的修复过程, 它能够生成自然轮廓信息但易产生纹理伪影现象. 综上所述, 传统的图像修复算法修复效果差且持续时间长, 而一般的基于深度学习的图像修复算法网络模型较深会导致训练时间过长并且需要大量数据进行训练.
本文针对上述问题提出了一种基于深度图像先验[18]的无监督路面裂缝图像修复算法. 利用鲁棒主成分分析(robust principal component analysis, RPCA)算法[19]去除路面裂缝图像表面的竖状条纹噪声并采用最大类间方差(Otsu)法[20]和形态学处理, 从而提取出裂缝区域的掩码图像, 然后运用本文所提算法对路面裂缝图像修复得到对应的无损路面图像. 整个过程不仅耗时短, 且仅需单张图像便可实现修复. 最后通过实验验证了本文所提算法的有效性.
1 裂缝区域分割裂缝区域掩码流程示意图如图1所示.
路面裂缝图像数据集通过安装在多功能道路检测车上的线阵相机采集而来, 在采集过程中由于相机上的LED强照明系统补光的原因, 不可避免地会产生竖状的条纹噪声, 而其会影响后期裂缝区域的分割, 因此需要将此类噪声去除. 本文采用RPCA算法[19]去除竖状条纹噪声(低秩成分), 对保留下来的路面裂缝图像(稀疏成分)处理, 首先运用灰度变换, 进而采取Otsu阈值分割算法[20]并取反得到裂缝区域的初步掩码图像, 然后对其进行形态学处理: 首先标记连通域, 根据其面积大小舍去一些孤立噪点, 然后对剩余的裂缝主体部分进行形态学膨胀, 将断裂的裂缝区域连接起来, 最后保留取反后的二进制图像作为裂缝区域的最终掩码图像.
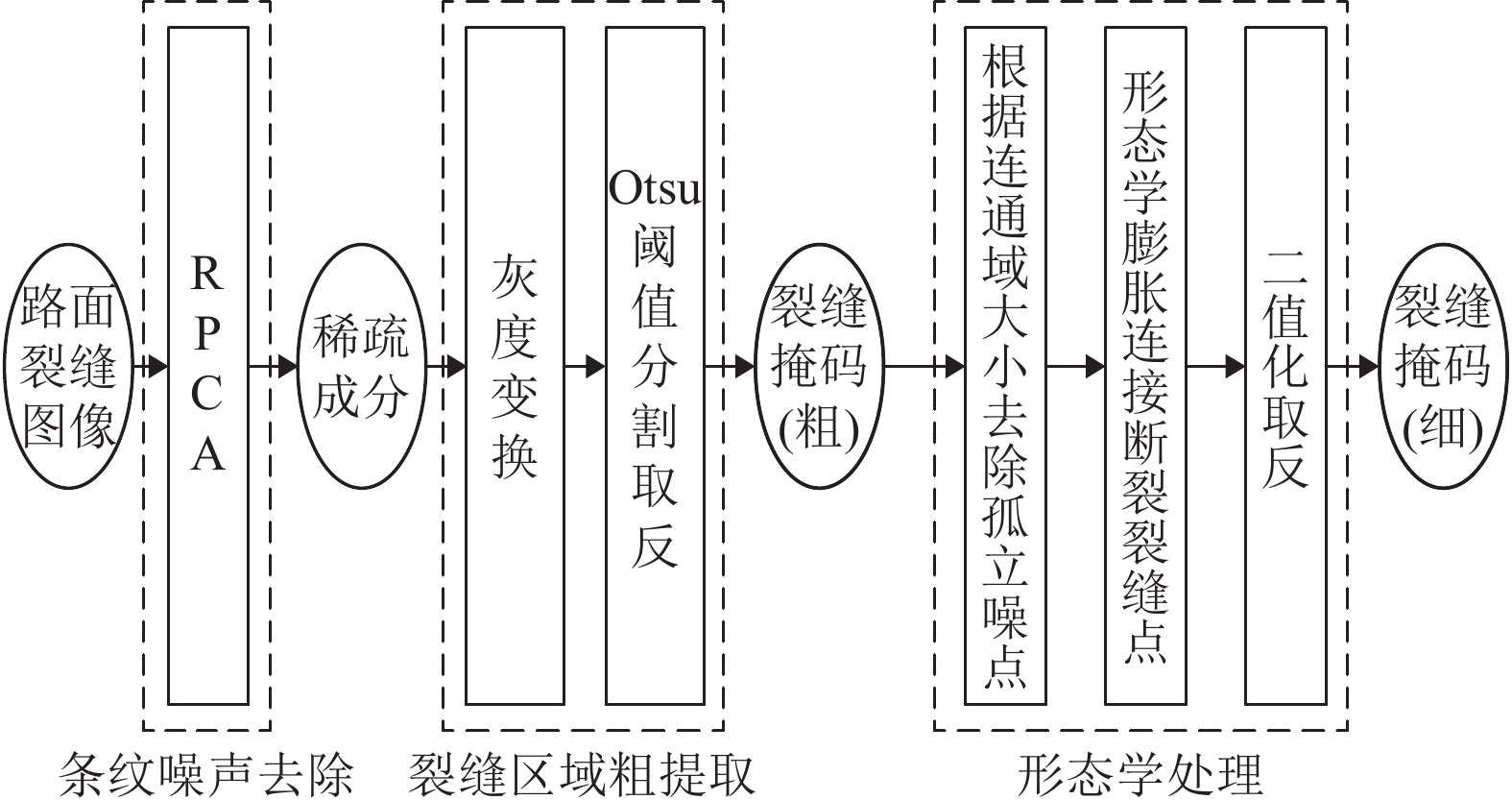
|
图 1 裂缝区域分割流程示意图 |
1.1 条纹噪声去除
RPCA算法[19]可以用来进行矩阵恢复和降噪等, 本文采用其去除路面裂缝图像中的竖状条纹噪声, 公式化描述如式(1):
| $ D = A + Q $ | (1) |
其中,
| $ A = U\Lambda {V^{\rm{T}}} = \sum\limits_{i = 1}^r {{\sigma _i}{u_i}v_i^{\rm{T}}} $ | (2) |
其中,
式(1)中的矩阵分解可通过求解凸优化问题来实现[21]:
| $\left\{ { \begin{array}{*{20}{c}} {\min}&{{{\left\| A \right\|}_ * } + \lambda {{\left\| Q \right\|}_1}} \\ {{\rm{s.t.}}}&{D = A + Q} \end{array}} \right. $ | (3) |
其中,
本文采用增广拉格朗日乘子法(augmented Lag-range method, ALM)求解上述的凸优化问题, 该算法可以有效地把
路面裂缝区域的提取主要采用最大类间方差(Otsu)法[22]. 它依据图像灰度特征来分割图像, 且将目标灰度值与背景灰度值的方差最大值定义为最佳分割阈值. 图像中裂缝区域与背景区域灰度值方差越大, 分割效果就越好, 裂缝就能尽可能完整地被分割出来.
假设图像的灰度级用
| $ N = \sum\limits_{i = 0}^{L - 1} {{n_i}} $ | (4) |
| $ \begin{array}{cc}{P}_{i}={n}_{i}/N, & {P}_{i}\geqslant 0且{\displaystyle \sum _{i=0}^{L-1}{P}_{i}}=1\end{array} $ | (5) |
若通过阈值
| $ {w_1} = \sum\limits_{i = 0}^t {{P_i}} $ | (6) |
| $ {w_2} = \sum\limits_{i = t + 1}^{L - 1} {{P_i}} = 1 - {w_1} $ | (7) |
因此目标和背景的灰度均值
| $ {u_1} = \sum\limits_{i = 0}^t {i{P_i}} /{w_1} = \frac{{u(t)}}{{{w_1}}} $ | (8) |
| $ {u_2} = \sum\limits_{i = t + 1}^{L - 1} {i{P_i}/{w_2}} = \frac{{{u_T} - u(t)}}{{1 - {w_1}}} $ | (9) |
其中,
| $ {u_T} = \sum\limits_{i = 0}^{L - 1} {i{P_i}} $ | (10) |
| $ u(t) = \sum\limits_{i = 0}^t {i{P_i}} $ | (11) |
综上可得:
| $ {u_T} = {w_1}{u_1} + {w_2}{u_2} $ | (12) |
假设图像中目标与背景两类的类间方差用
| $ \begin{split} {\sigma^2 _b} =& {w_1}{({u_1} - {u^2_T})} + {w^2_2}{({u_2} - {u_T})^2} \\ =& {w_1}({u^2_1} + {u^2_T}) + {u^2_T}({w_1} + {w_2}) \\ & - 2({w_1}{u_1} + {w_2}{u_2}){u_T} \\ =& {w_1}{w_2}{({u_1} - {u_2})^2} \end{split} $ | (13) |
让
形态学处理主要包括膨胀、标记连通域等数字图像处理技术中常见的操作. 由于Otsu阈值分割后的裂缝存在局部断裂的情况, 因此需要通过膨胀将距离较近的裂缝连接起来; 而标记连通域是为了根据连通区域面积大小来去除孤立噪点, 从而保留裂缝主体部分.
2 裂缝区域修复在获取裂缝区域掩码图像后, 需通过图像修复算法对路面裂缝区域进行修复, 最终得到对应的无裂缝图像. 本文采用深度图像先验算法进行修复, 它与一般的深度学习算法不同, 即无需成对的数据进行训练, 而是仅通过输入单张路面裂缝图像及对应掩码图像便可得到无损路面图像.
2.1 算法过程一般来说, 图像修复问题可用如下函数表示:
| $ {x^ * } = \mathop {\min }\limits_x E(x;{x_0}) + R(x) $ | (14) |
其中,
神经网络结构自身可以捕获大量低级的图像先验信息[18]. 本文中选择采用卷积神经网络来实现图像修复任务, 将卷积神经网络捕捉到的隐含先验用来代替正则项
| $ {\theta ^ * } = \mathop {{\text{argmin}}}\limits_\theta E(({f_\theta }({\textit{z}}));{x_0}), {x^ * } = {f_{{\theta ^ * }}}({\textit{z}}) $ | (15) |
其中,
神经网络对噪声具有高阻抗性, 对自然信号具有低阻抗性. 也就是说, 它首先会学习并拟合出自然的图像, 其次才会学习并拟合那些不规则噪声[18]. 因此自然图像会最先恢复出来, 不自然的图像则会慢很多. 依据神经网络的这种特性, 给定一张路面裂缝图像, 在其恢复过程中首先会恢复出自然图像(无损路面), 然后才会恢复出不自然的部分(含有裂缝).
对于路面裂缝图像修复问题来说, 路面裂缝图像
| $ E(x;{x_0}) = ||(x - {x_0}) \odot M|{|^2} $ | (16) |
其中,
本实验构建了一种编解码器架构形式的网络模型. 编码器和解码器均由6个模块组成, 具体的网络结构如图2所示.
图2中,
本文中网络损失函数如式(17)所示:
| $ {l_{loss}} = \min E(x, {x_0}) = \min|(x - {x_0}) \odot M{|^2} $ | (17) |
从式(17)可以看出, 损失函数在计算过程中去除了裂缝区域像素值的参与. 也就是说, 最初网络的输入为随机噪声矩阵
由于本文目的是为了获取路面裂缝图像对应的无损路面图像, 理想的结果为: 只需改变路面裂缝图像中裂缝区域的像素值, 而路面背景区域的像素值应当保持不变. 因此本文将重建后的图像中的路面背景区域用路面裂缝图像的路面背景区域替代, 具体的变换公式如式(18)所示:
| $ S = {x_0} \odot M + x \odot (1 - M) $ | (18) |
其中,
对应的变换过程如图3所示.
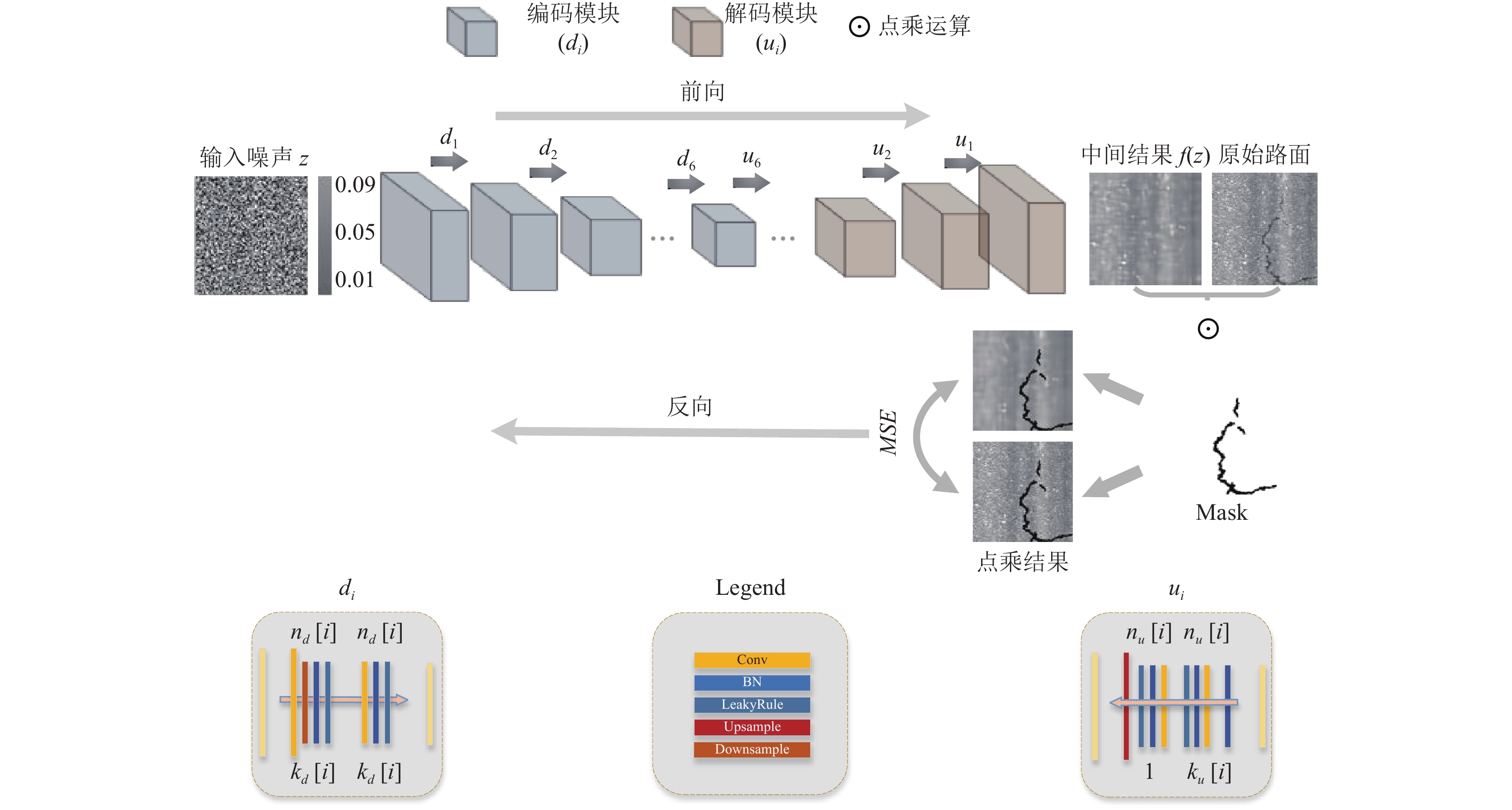
|
图 2 网络结构图 |

|
图 3 无损路面变换示意图 |
3 实验分析 3.1 实验环境
本实验的硬件环境为一台Dell塔式服务器, 主要配置为2个E5-2650V4 CPU, 64 GB内存, 480 GB固态硬盘和4 TB机械硬盘, 包含4 块 GTX 1080 Ti GPU, 且每一块GPU显存大小均为12 GB. 操作系统为Ubuntu 18.04. 实验的整个网络在PyTorch 1.1环境下运行.
3.2 数据集原始数据为安装在多功能道路检测车上的线阵相机采集到的200张路面裂缝图像, 且分辨率为2048×2944 . 首先将每一张原始图像裁剪成512×512的子图, 然后从中选取300张含裂缝的图像构成本实验所需数据集. 图4展示了本文实验中所用的部分路面裂缝图像. 由于本文所提方法是通过单张路面裂缝图像进行修复的, 网络的训练和测试是同时完成的, 因此每次只需输入一张路面裂缝图像即可.

|
图 4 实验数据集展示图 |
为定量评价图像的修复质量, 且考虑到第4.3节所引入的评价指标计算中涉及到真值图像, 因此本文借助Photoshop (PS)软件对路面裂缝图像中裂缝区域进行了自动填充操作, 即将路面受损区域像素值用周围路面背景像素值代替, 使整张图像构成无损路面, 并把它当做真值图来进行定量评价. 图5展示了部分路面裂缝图像PS前和PS后的效果对比图, 其中第1行分别为PS处理前的原始路面裂缝图像, 第2行分别为第1行中对应的每张图像经过PS后的效果图.

|
图 5 PS前后效果对比图(按列一一对应) |
3.3 评价指标
本文采用峰值信噪比(peak signal to noise ratio, PSNR)[24]和结构相似性 (structural similarity, SSIM)[25]两个计算指标来定量评价图像修复效果. PSNR和SSIM用以衡量两张图像的相似程度, 其值越大, 修复效果越好.
(1)峰值信噪比(PSNR)
给定一张原始干净图像
| $ {\textit{MSE}} = \frac{1}{{mn}}\sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {{{[I(i, j) - K(i, j)]}^2}} } $ | (19) |
PSNR定义为式(20):
| $ {\textit{PSNR}} = 10 \times {\log _{10}}\left(\frac{{{\textit{MAX}}_I^2}}{\textit{MSE}}\right) $ | (20) |
其中,
(2)结构相似性(SSIM)
在SSIM的计算中, 给定一张原始干净图像x和一张处理后图像y, 它是通过亮度、对比度、结构3个方面来计算图像相似度的. 其计算公式如式(21)所示:
| $ {\textit{SSIM}}(x, y) = \frac{{(2{\mu _x}{\mu _y} + {c_1})(2{\sigma _{xy}} + {c_2})}}{{({\mu _x}^2 + {\mu _y}^2 + {c_1})({\sigma _x}^2 + {\sigma _y}^2 + {c_2})}} $ | (21) |
其中,
在RPCA算法去除竖状条纹噪声的实验中, 需对原始数据进行预处理, 即将原始图像矩阵按列进行等量划分, 然后再进行矩阵重构. 本文原始图像矩阵大小为512×512, 将其按列等分为16份, 即分成16个512×32的矩阵. 然后将这些矩阵按行拼接, 则重构后的矩阵为8192×32. 算法迭代计算完成后, 再分别把得到的低秩矩阵和稀疏矩阵恢复成512×512. 恢复出来的低秩矩阵即为要去除的竖状条纹噪声, 稀疏矩阵为去除条纹噪声后保留的路面图像. 实验正则化参数
在图像修复实验中, 网络中设置的超参数如表1所示. 其中网络输入
| 表 1 网络超参数表 |
4 实验结果 4.1 RPCA去除竖状条纹噪声实验
实验中采用了RPCA算法对路面裂缝图像表面的竖状条纹噪声进行去除. 图6为采集车采集到的原始路面裂缝图像, 图中红色框代表在本文实验中经过裁剪得到的路面裂缝图像. 图7为采用RPCA算法处理后得到的结果. 其中第1列为裁剪后的路面裂缝图像, 第2列为路面裂缝图像剥离出来的竖状条纹噪声(低秩部分), 第3列为去除此类噪声后保留的路面裂缝图像(稀疏部分). 从图7中可以看出, 竖状条纹噪声几乎被完全去除, 且路面图像也不存在失真现象. 由此可见RPCA算法取得了良好的效果.
4.2 掩码生成实验实验中采用了数字图像处理相关方法实现对裂缝区域的分割, 实验效果展示如图8所示. 其中图8(a)为去除竖状条纹噪声后的路面裂缝图像, 对其执行灰度变换后得到图8(b), 图8(c)为采用Otsu阈值分割算法取反后的结果, 图8(d)为去除孤立噪点后的结果, 图8(e)为对图8(d)进行形态学膨胀后的结果, 图8(f)为对图8(e)取反后最终得到的裂缝区域掩码图像. 由图8(f)可知, 路面裂缝区域较为完整地被提取出来.

|
图 6 原始路面裂缝图像 |

|
图 7 RPCA算法去除竖状条纹效果图 |

|
图 8 裂缝区域掩码提取 |
4.3 图像修复实验
本文设置了Criminisi算法[9]、快速行进算法(fast marching method, FMM)[26]、流体力学算法(fluid dynamics method, FDM)[5]和本文所提算法4组修复路面裂缝图像的对比实验, 从自采集数据集中随机选择4幅图像, 结果如图9所示, 从上至下依次记为I–IV. 其中第1列为原始的路面裂缝图像, 第2列为利用本文所提方法得到的裂缝区域掩码图像, 第3、4、5、6列分别为采用传统Criminisi算法、FMM算法、FDM算法以及本文所提算法修复所得结果图像. 从第3、4、5、6列结果对比来看, 从全局的角度难以很好地评估这几种算法修复结果的好坏.
为了更直观的评估这几种算法的修复结果, 本文进一步以路面图像I和II为例, 对I和II中局部区域修复结果进行对比, 以红色框标志选定区域, 效果展示如图10所示. 第1、2、3、4列分别为采用Criminisi算法、FMM算法、FDM算法以及本文所提算法修复后裁剪的小块区域. 通过对比可以看出, 采用FMM算法和FDM算法修复的路面图像存在较为严重的模糊情况, 缺失区域与非缺失区域在纹理上也存在明显差异. 而另外两种修复算法相比, 采用本文所提算法结构和纹理修复的更好, 而采用Criminisi算法修复的结果存在语义混乱的情况. 由图9中对比结果可以看出, 路面图像I–III采用本文所提算法修复得到的结果无论是在纹理上还是语义上都恢复得更好, 看上去更加连贯自然, 因为它是依据图像本身具有的局部自相似性, 借助神经网络对噪声具有高阻抗性, 对自然信号具有低阻抗性的特性, 通过设置合理的迭代优化次数来优化网络参数, 进而恢复出无损路面图像. 而Criminisi算法图像待修复区域边缘上选取优先权最高的像素点, 然后以该为中心构造一个n×n大小的像素块, 然后在完好区域寻找与该模板块最相似的样本块, 并用找到的样本块更新模板块中的待修复信息, 最后更新已修复块块中像素点的置信度, 并开始下一次迭代修复, 直至修复完成. 它是基于样本块匹配的原理, 在图像全局上具有一个较好的修复效果, 但是在图像修复区域的局部细节处存在语义混乱的情况, 因为每个样本块的边界出并不十分连续, 因此其修复结果更加模糊. 从图像Ⅳ修复结果可以看到, 采用本文所提算法修复后的图像中存在细小的修复痕迹, 如图像中用蓝框标出的部分. 这是由于裂缝区域像素值本身处于未知状态, 修复结果并不局限于某一种情况, 当然如果能与周围区域完全融合是最好的. 本文算法修复的结果虽然看上去有细小的修复痕迹, 但其也可代表修复成功之后的一种状态.

|
图 9 路面裂缝图像修复效果图 |

|
图 10 修复区域局部放大对比 |
此外, 本文采用PSNR和SSIM两个定量评价指标对传统的Criminisi算法、FMM算法、FDM算法和本文所提算法修复效果进行了定量评价. 表2和表3分别为修复后路面图像的PSNR值和SSIM值. 从表2和表3中两项数据对比可以看出, 除图像III外, 采用本文所提算法的图像的PSNR值均高于其他3种传统修复算法. 而4幅图像中, 采用本文所提算法图像的SSIM值均高于其他3种修复算法. 综合来看, 本文所提出的算法更加有效.
| 表 2 修复后路面图像的PSNR (dB) |
| 表 3 修复后路面图像的SSIM |
图11给出了路面裂缝图像I在修复过程中网络损失函数随着迭代次数增加而变化的曲线图. 由曲线图可以看出, 损失函数随着迭代次数增加总体呈现下降的趋势, 在一开始曲线下降速度较快, 之后呈现小幅下降趋势, 在迭代次数达到最大值6 000时(这个6 000是依据经验值人工设置的), 曲线基本达到收敛状态. 此时网络重构出来的路面背景区域与原始路面裂缝图像的背景区域误差达到最小, 此时的网络参数即为最优参数, 利用这组参数, 输入和原始路面图像尺寸一样的随机噪声z, 网络就可以恢复出无损路面图像.

|
图 11 误差损失曲线图 |
为了验证本文所提算法的高效性, 本文分别采用Criminisi算法与所提算法对图像I–IV进行修复, 并将修复过程所耗费的时间进行了对比, 由于另外两种对比算法FMM与FDM算法在Python官方库中已经集成好了, 因此本文直接调用了集成好的这两种算法, 并未统计这两种算法的时间效率. 从表4中两项数据对比来看, 路面图像裂缝区域越大, Criminisi算法修复速度就越慢, 且差异明显; 而本文所提算法对4幅图像的修复速度相差均不大. 同时对比在4幅图像上的表现, 本文所提算法的修复速度远高于传统的Criminisi算法. 因此本文所提算法表现得更加高效.
| 表 4 4种方法修复时间对比(s) |
由于上述实验结果只列出了4张路面裂缝图像作为样例来进行展示. 为了更具说服力, 表5给出了300张实验中用到的所有测试图像的PSNR、SSIM以及算法消耗时间的平均值. 其中第1列为算法名称, 第2列为PSNR平均值, 第3列为SSIM平均值, 第4列为每张图像修复消耗时间平均值. 由第2列和第3列结果对比可知, 本文所提算法的PSNR和SSIM平均值更高, 说明其修复效果更好. 由第4列结果对比可知, 本文所提算法的平均时间效率远高于Criminisi算法, 因此综合修复效果与修复效率, 本文所提算法既能保证修复速度又能兼顾修复质量.
| 表 5 所有测试图像评价指标平均值 |
5 结论与展望
本文提出了一种路面裂缝图像的修复方法. 一方面, 为了获取裂缝区域的掩码图像, 首先去除了路面裂缝图像中的竖状条纹噪声, 然后通过数字图像处理的相关方法得到了裂缝区域掩码图像. 另一方面, 在得到裂缝区域掩码图像后, 通过本文所提算法对裂缝区域进行修复得到了最终的原始无损路面图像. 针对传统修复算法的图像局部细节恢复不理想的情况, 本文所提算法修复的结果视觉效果更自然, SSIM和PSNR值更高, 且修复速度更快. 但当路面图像中裂缝宽度过大时, 该方法不能达到较好的修复效果, 会出现模糊现象. 在下一步的研究工作中, 会继续对网络结构进行改进, 以满足更宽裂缝及不同路面的修复需求.
| [1] |
王晓峰. 沥青路面结构的疲劳损伤和寿命估算研究. 建材技术与应用, 2021(5): 29-32. DOI:10.3969/j.issn.1009-9441.2021.05.009 |
| [2] |
张金喜, 张嘉, 曹丹丹. 沥青路面裂缝问题研究现状综述. 市政技术, 2021, 39(11): 17-23, 34. DOI:10.19922/j.1009-7767.2021.11.017 |
| [3] |
廖晓芳. 破损图像丢失区域自适应优化修复方法仿真. 计算机仿真, 2019, 36(6): 388-392. DOI:10.3969/j.issn.1006-9348.2019.06.080 |
| [4] |
罗海银, 郑钰辉. 图像修复方法研究综述. 计算机科学与探索, 2022, 16(10): 2193–2218.
|
| [5] |
Bertalmio M, Sapiro G, Caselles V, et al. Image inpainting. Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. New Orleans: ACM, 2002. 417–424.
|
| [6] |
Shen CJ. Mathematical models for local nontexture inpaintings. SIAM Journal on Applied Mathematics, 2002, 62(3): 1019-1043. DOI:10.1137/S0036139900368844 |
| [7] |
Chan TF, Shen JH. Nontexture inpainting by curvature-driven diffusions. Journal of Visual Communication and Image Representation, 2001, 12(4): 436-449. DOI:10.1006/jvci.2001.0487 |
| [8] |
Efros AA, Leung TK. Texture synthesis by non-parametric sampling. Proceedings of the 7th IEEE International Conference on Computer Vision. Kerkyra: IEEE, 2002. 1033–1038.
|
| [9] |
Criminisi A, Perez P, Toyama K. Region filling and object removal by exemplar-based image inpainting. IEEE Transactions on Image Processing, 2004, 13(9): 1200-1212. DOI:10.1109/TIP.2004.833105 |
| [10] |
张申华, 王克刚, 祝轩. 局部特征信息约束的改进Criminisi算法. 计算机工程与应用, 2014, 50(8): 127-130. DOI:10.3778/j.issn.1002-8331.1308-0414 |
| [11] |
Barnes C, Shechtman E, Finkelstein A, et al. PatchMatch: A randomized correspondence algorithm for structural image editing. ACM Transactions on Graphics, 2009, 28(3): 24. |
| [12] |
Liu HY, Jiang B, Song YB, et al. Rethinking image inpainting via a mutual encoder-decoder with feature equalizations. Proceedings of the 16th European Conference. Glasgow: ACM, 2020. 725–741.
|
| [13] |
Hong X, Xiong PF, Ji RH, et al. Deep fusion network for image completion. Proceedings of the 27th ACM International Conference on Multimedia. Nice: ACM, 2019. 2033–2042.
|
| [14] |
Yeh RA, Chen C, Lim TY, et al. Semantic image inpainting with deep generative models. Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 6882–6890.
|
| [15] |
Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv:1511.06434, 2015.
|
| [16] |
Xiong W, Yu JH, Lin Z, et al. Foreground-aware image inpainting. Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 5833–5841.
|
| [17] |
Isola P, Zhu JY, Zhou TH, et al. Image-to-image translation with conditional adversarial networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 1125–1134.
|
| [18] |
Lempitsky V, Vedaldi A, Ulyanov D. Deep image prior. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 9446–9454.
|
| [19] |
Candès E, Li XD, Ma Y, et al. Robust principal component analysis? Journal of the ACM, 2011, 58(3): 11.
|
| [20] |
Otsu N. A threshold selection method from gray-level histograms. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62-66. DOI:10.1109/TSMC.1979.4310076 |
| [21] |
Yang YC, Nagarajaiah S. Blind denoising of structural vibration responses with outliers via principal component pursuit. Structural Control & Health Monitoring, 2014, 21(6): 962-978. |
| [22] |
Lin ZC, Liu RS, Su ZX. Linearized alternating direction method with adaptive penalty for low-rank representation. Proceedings of the 24th International Conference on Neural Information Processing Systems. Granada: ACM, 2011. 612–620.
|
| [23] |
Lin ZC, Chen MM, Ma Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv:1009.5055, 2010.
|
| [24] |
Al-Najjar YAY, Soong DC. Comparison of image quality assessment: PSNR, HVS, SSIM, UIQI. International Journal of Scientific and Engineering Research, 2012, 3(8): 1-5. |
| [25] |
Wang Z, Bovik AC, Sheikh HR, et al. Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |
| [26] |
Telea A. An image inpainting technique based on the fast marching method. Journal of Graphics Tools, 2004, 9(1): 23-34. DOI:10.1080/10867651.2004.10487596 |
 2023, Vol. 32
2023, Vol. 32


