由于对道路路面缺乏及时与适当的维护, 会导致路面表面恶化, 路面价值贬值. 因此, 为了保持路面的良好状态, 必须对路面破损进行一定程度的评估, 依据评估情况对路面状况进行准确的监测. 从20世纪中期开始, 路面健康监测在路面管理中起着关键作用, 一直是交通研究的热点. 大多数路面恶化的前期表现为路面裂缝, 而路面裂缝可能威胁道路安全, 需要尽早修复. 如果不及时处理受损路面, 由于环境或人为因素, 路面的恶化可能会更严重. 根据相关的统计数据表明, 因为天然气候的影响和通行车辆荷载的要求, 部分地区道路路面裂缝类病害占沥青路面病害甚至高达85%以上^[1]. 所以, 路面裂缝被认为是路面破损的一个重要组成部分. 路面裂缝的形式、严重程度等是评价沥青路面质量的重要因素. 而道路路面裂缝也是公路质量的重要评价指标之一, 对于不同类型的路面裂缝, 关系着制定特定的养护政策, 以及评价养护工作的重要程度^[2]. 因此对不同类型的路面裂缝进行及时以及准确分类, 并根据分类结果对路面养护措施进行针对性的安排, 成为了当下交通行业的关注重点^[3].

1 裂缝图像分类方法

近些年来, 国内外研究学者将深度学习相关的方法与技术应用到了路面裂缝分类的领域, 成为了研究的热点, 许多学者取得了很好的效果. 现阶段利用深度学习相关的方法实现裂缝分类, 通常的方法是先将每类裂缝图像标注相应的标签, 通过人工标注的标签在深度学习网络中进行学习, 得到每个裂缝的特征, 从而实现分类. 有监督的方法需要人工标注信息, 而大量数据的精准标注, 需要耗费大量的人力物力资源^{[4, 5]}. 而通过人工标注的方法, 不仅需要大量的人力物力的支持, 而且要耗费大量的时间, 从而影响到道路养护决策的时效性, 阻碍了养护措施的实施; 另一方面, 通过人工标注的数据会受到人为主观因素的影响, 导致自动性较低^[6]. 所以设计一个自监督的分类方法成为了一个需要解决的问题.

2021 年, 章天杰等^[7]提出了一种基于语义分割的沥青路面裂缝快速分类方法, 首先, 获取沥青路面图像, 建立沥青路面原始图像集; 其次, 使用数据清洗算法对采集到的裂缝图像进行数据清洗, 构建沥青路面裂缝图像样本数据集; 再次, 在清洗后的沥青路面裂缝图像样本数据集基础上采用人工分割标注, 并用数据增广为模型提供充足的训练数据; 最后, 使用Unet网络进行裂缝图像语义分割, 最终输出裂缝信息. 但过程复杂不利于大批量检测分类. 2018 年, 马晓丽等^[8]根据图像灰度作为分类的特征, 引入神经网络实现了裂缝图像的分类. 首先对原始裂缝图像使用图像掩膜的方法进行降噪, 并统计出子块灰度方差的最值差、方差的最值差超过设定阈值的子块数量以及子块灰度熵的最值之差, 最后以统计出的3个数据为特征量进行分类. 但是该算法受待分类数据集的限制, 对不同数据集的分类效果不同, 无法满足实际工程任务需求. 2018 年, 宋俊芳等^[9]提出一种利用卷积神经网络模型进行裂缝分类的方法, 该模型在卷积层后选取 ReLU 激活函数实现简单输入到复杂输出的映射, 并在连续的卷积层之间加入最大池化层达到降低维度的目的, 最后利用 Softmax 分类器将裂缝分为横向裂缝、纵向裂缝以及复杂裂缝. 但该模型针对网状和龟裂裂缝的准确率较低, 无法非常精准的识别. 2018 年, Hoang 等^[10]提出了一种协同使用包括非局部均值, 可控滤波器, 投影积分和图像阈值处理在内的图像处理技术对裂缝图像进行特征提取. 并且通过建立了包含多类支持向量机和人工蜂群优化算法的机器学习模型来进行路面裂缝分类. 基于特征分析, 发现从图像投影积分导出的一组特征可以显著增强预测性能, 并且分类准确率较高. 2019 年, Hoang等^[11]首先利用图像的投影积分和用于图像阈值处理等图像处理方法对裂缝图像进行特征提取, 然后尝试使用不同的特征融合方案来创建路面裂缝图像特征数据集. 然后利用这些特征数据集对支持向量机(SVM), 人工神经网络(ANN)和随机森林(RF)进行训练. 最终使用训练好的模型和算法对路面裂缝图像进行分类. 实验结果表示理想的特征数据集可以起到优化分类效果的作用. 2018, Hoang等^[10]研究建立了一种自动识别路面裂缝形态的智能方法. 该方法中构建了一个包含多类支持向量机和人工蜂群优化算法的路面裂缝分类机器学习模型. 在特征分析的基础上, 从图像投影积分中提取出一组特征, 可显著提高预测性能. 实验证明提出的图像处理与机器学习模型集成的分类准确率高达 96%以上.

综上所述, 国内研究主要使用传统的图像处理方法, 根据不同裂缝类型的差异, 利用图像处理方法对裂缝特征进行表示学习, 最终通过统计方法或者分类器进行分类, 达到对裂缝进行分类的目的. 但路面裂缝的多样性与裂缝图像质量的不稳定会干扰分类的准确性. 国外路面裂缝图像分类技术主要是结合深度学习了技术进行处理. 通过深度学习, 不断进行学习训练, 提取出更高维、抽象的特征, 虽然解决了人工提取特征和分类器选择的不足. 但受数据本身的影响较大, 且泛化性较差.

根据以上提出的内容, 为解决有监督方法中的大量数据的精准标注问题、人工标注导致的时效性与自动性降低的问题, 以及模型的泛化性能问题, 提出一个自监督的深度学习路面裂缝分类方法成为了一个解决方向. 本文实现一个充分利用无标注数据的自监督训练模型, 学习图像本身的特征, 从而实现道路裂缝图像分类任务. 本文的研究工作主要包括以下几个方面: 路面裂缝数据的采集与预处理, 确保模型的分类精度, 对图像进行了裁剪与缩放等预处理操作; 通过数据增强方式对数据的特征进行学习, 从而达到自监督训练的目的; 对数据增强后的数据进行特征提取, 针对道路裂缝图像的特点进行多尺度的特征提取; 对不类型的路面裂缝数据进行采集, 并进行训练, 提高了模型的泛化能力.

2 对比学习分类方法

对比学习的提出, 主要为了解决有监督深度学习受标注样本制约的问题, 属于无监督学习的一种. 对比学习主要通过自然存在的大量无标注数据, 利用图像本身的先验知识, 学习图像本身的特征表示. 传统的自监督方法主要依赖于图像的颜色、空间位置等单一维度特征, 无法进行其他维度迁移^{[12, 13]}. 为了解决传统自监督方法所存在的问题, Chen 等^[14,15]提出了一种新的对比学习框架 SimCLR, 通过多重的数据增强方式, 利用图像多个维度的特征, 学习到更加通用的特征, 能够迁移到多种不同的下游任务中. 在ImageNet 图像分类的实验中, 该方法与有监督训练的ResNet50 的结果类似, 实现了 top-1 的无监督分类准确率. 为解决对比学习训练过程中的模型退化问题, He 等^[16]提出了新的对比学习框架MoCo, 该方法在内存中维护一个查询队列, 使用动量方法更新网络参数, 在 ImageNet 任务上的表现超过了 SimCLR. 此后也出现了很多类似于SimCLR 和 MoCo 的对比学习方法^[17-19].

本文基于SimCLR对比学习框架, 并对特征提取模块进行了改进, 提高了分类的准确率, 并加速了训练过程. 本文算法结构为图1所示, 算法结构主要包括4个部分: ① 数据增强部分, 采用不同的数据增强方式, 将任意图像转换为两个具有相关性的视图; ② 特征提取部分, 对数据增强后的视图进行特征提取, 采用改进的ResNet结构并加入了多尺度的卷积块; ③ 多层感知机部分, 通过小型的神经网络对提取到的特征向量进行映射, 降低向量维度; ④ 对比损失函数部分, 通过将映射的特征向量通过余弦相似度计算相似性, 使用归一化温度标度的交叉熵损耗进行优化.

2.1 数据增强

对于数据的增强方式已经广泛地应用于有监督与无监督的任务中, 在有监督学习中, 应用于扩充数据样本, 学习到数据本身的特征, 提高模型的泛化能力. 而在自监督学习中, 数据增强方式主要用于自然图像当中^[20]. 如图1所示, 对于裂缝图像 ${{x}}$ 通过数据增强得到两张图像 ${{{x}}_i}$ 与 ${{{x}}_j}$ . 本文图像的数据增强方式分为两种, 如图2 所示, 一种为空间几何变换, 主要包括翻转(Flip), 如水平翻转(HorizontalFlip)、垂直翻转(VerticalFlip)等, 另一种为颜色空间的变换(Colorjitter), 如颜色下降变换(Colorjitter Down)、颜色上升变换(Colorjitter Up)等. 设 $ x \in X $ 为输入的图像, 则对任意图像:

$ \begin{split} \\ {{{t}}_1}(x) = rand(Colorjitter, Flip)\;\; \end{split} $

(1)

$ {{{t}}_2}(x) = rand(Colorjitter, Flip)\;\; $

(2)

其中, $ rand() $ 为随机函数, 在训练时, 随意挑选大小为 $ N $ 的数据, $ \left\{ {{x_k}} \right\}_{k = 1}^N $ , $k \in \left\{ {1, 2, 3, \cdots , N} \right\}$ , 通过随机数据增强函数, 得到共 $ 2N $ 个数据, 表示为 $ \left\{ {{x_{2k}}} \right\}_{k = 1}^N $ 与 $ \left\{ {{x_{2k - 1}}} \right\}_{k = 1}^N $ , 其中 $ {x_{2k}} = {t_1}({x_k}) $ , $ {x_{2k - 1}} = {t_2}({x_k}) $ . 产生的一对数据为正样本, 剩余的 $ 2(N - 1) $ 为负样本.

2.2 特征提取

原本的对比学习框架中使用ResNet50进行特征提取, 由于裂缝图像的特殊性, 为对细小裂缝进行较为完整的特征提取, 本文通过重建了普通的ResNet架构的Bottleneck block, 用分层架构取代了标准的1-3-1的CNN布局, 并对ResNet50的结构进行了改进, 使得对裂缝特征的表达能力更强. 本文算法框架如图1所示.

如图3(a), 首先将原先ResNet50旧的 $ 7 \times 7 $ 的卷积核替换为3个 $ 3 \times 3 $ 堆积的主干, 激活函数从ReLU更改为Mish, 并更改批处理归一化与激活函数的顺序, 通过之前研究表明, 更改后对特征提取有积极影响^[19,21].

如图3(b), 更改后的Bottleneck block在经过1×1卷积得到的结果, 在保持其尺度不变的条件下, 将特征图进行均匀的分割得到新的特征子图 $ {x_1} $ , $ {x_2} $ , $ {x_3} $ , $ {x_4} $ , 每个特征子图具有相同的空间大小, 但只包含原特征图部分的信息. 特征图 $ {x_1} $ 不经过变换得到 $ {y_1} $ , $ {x_2} $ 经过 $ 3 \times 3 $ 卷积操作后, 得到 $ {y_2} $ , 将 $ {y_2} $ 与 $ {x_3} $ 拼接后的特征图进行 $ 3 \times 3 $ 卷积操作得到 $ {y_3} $ , 将 $ {y_3} $ 与 $ {x_4} $ 拼接得到的特征图进行同样的操作 $ 3 \times 3 $ 卷积操作得到 $ {y_4} $ , 得到了不同尺度的特征图 $ {y_1} $ , $ {y_2} $ , $ {y_3} $ , $ {y_4} $ , 进行拼接后经过 $ 1 \times 1 $ 卷积操作进行不同尺度的特征融合.

2.3 多层感知机与损失函数

经过特征提取后, 使用多层感知机(MLP), 即一个小型的神经网络, 将提取到的特征向量表示映射至可被对比的空间, 便于损失函数的计算. 主要使用两个单层全连接神经网络, 在每个全连接层后进行批处理归一化处理. 在第一个全连接层归一化处理结束后, 使用ReLU激活函数, 更好地对相关特征进行挖掘, 加快拟合的过程. 通过多层感知机将提取到的1×1×2048维特征向量降低到1×1×128维度, 通过减少计算量来提高损失函数的计算效率.

本文通过余弦相似度判断各个特征之间的相似程度. 相比较于距离度量, 余弦相似度更能体现两个向量在方向上的差异, 是较为常见的相似函数^[22]. 通过多对数据进行损失计算, 称为多类N对损失, 提出的目标函数允许多个反例进行联合计算, 得到最终的损失函数. 与其他损失函数相比, 在目标识别、分类以及检索方面有更好的效果, 在其他论文中均有应用^[23–25].

通过特征提取部分 $ f(\cdot) $ , 对全部数据增强得到的 $ 2N $ 个数据进行特征提取, 得到对应的特征向量 $ {h_{}} $ :

$ {h_{2k - 1}} = f({x_{2k - 1}}),\; {h_{2k}} = f({x_{2k}}) $

(3)

再通过多层感知机 $ g(\cdot) $ , 将提取到的特征向量投影到向量空间, 得到投影向量 $ {\textit{z}} $ :

$ {{\textit{z}}_{2k - 1}} = g({h_{2k - 1}}),\; {{\textit{z}}_{2k}} = g({h_{2k}}) $

(4)

在向量空间中, 即可通过余弦相似度判断各个向量之间的相似程度, 对于每一对 $ (i, j) $ , 其中 $i \in \left\{ {1, 2, 3, \cdots , N} \right\}$ , $j \in \left\{ {1, 2, 3, \cdots , N} \right\}$ , 计算余弦相似度 $ sim({{\textit{z}}_i}, {{\textit{z}}_j}) $ , 其中:

$ sim({{\textit{z}}_i}, {{\textit{z}}_j}) = {{\textit{z}}_i}^{\rm{T}}{{\textit{z}}_j}/(\left\| {{{\textit{z}}_i}} \right\|\| {{{\textit{z}}_j}} \|) $

(5)

一对正例(i, j)之间的交叉熵损失函数 $ {l_{i, j}}(i, j) $ 定义为:

$ {l_{i, j}} = - \log \frac{{\exp (sim({{\textit{z}}_i}, {{\textit{z}}_j})/\tau )}}{{\displaystyle\sum\nolimits_{k = 1}^{2N} {{1_{\left[ {k \ne i} \right]}}\exp (sim({{\textit{z}}_i}, {{\textit{z}}_j})/\tau )} }} $

(6)

其中, $ {1_{\left[ {k \ne j} \right]}} \in \left\{ {0, 1} \right\} $ 为归一化到1的指示函数, $ \tau $ 为可调节的参数. 最后的损失 $ Loss $ 是通过计算样本内所有的正例对, 包括 $ (i, j) $ 与 $ (j, i) $ 得到的:

$ Loss = \frac{1}{{2N}}\sum\nolimits_{k = 1}^N {\left[ {l(2k - 1, 2k) + l(2k, 2k - 1)} \right]} $

(7)

其中, $ N $ 为batchsize大小, $ l $ 为式(6)中的交叉熵损失函数.

3 实验分析

实验使用的数据集为Crack500数据集, 据集中包括500张手机拍摄的, 大小为 $ 2000 \times 1000 $ 的图片, 多种类型的路面, 有利于提高模型泛化能力. 由于原始数据过大, 将原图中包含的裂缝区域进行裁剪, 大小为 $ 256 \times 256 $ . 将裁剪得到的裂缝数据包含2 000张图像, 其中1 000张为训练集, 200张为验证集, 800张为测试集. 裁剪后的裂缝图像如图4所示.

3.1 实验参数与评价指标

模型训练过程优化器使用随机梯度下降法, 学习率设置为 lr×BatchSize/256, 基础学习率 lr设置为0.05, BatchSize为512, epoch次数为300. 实验采用基于Linux系统下搭建的TensorFlow深度学习框架, 硬件使用两个RTX2080ti进行多卡训练.

由于本文中的自监督方法的特殊性, 使用准确率(Acc)对路面裂缝自监督多分类结果进行评价. 基于本文中的多分类问题, 在本文路面裂缝多分类实验中以上4个指标的真实概念: TP: 属于该类而且被分为该类的裂缝个数; TN: 不属于该类而且没有被分为该类的裂缝个数;FP: 不属于该类却被分为该类的裂缝个数; FN: 属于该类却被分为其他类的裂缝个数. 基于以上的4个参数, 分类结果评价指标计算方式如式(8)所示:

$ A{{cc = }}\frac{{TP + TN}}{{TP + TN + FP + FN}} $

(8)

3.2 数据增强实验

对不同的数据增强方式对分类准确率的影响进行了比较. 实验结果表明, 空间与颜色变换组合的数据增强方式的效果要好于单一的数据增强方式. 在进行随机数据增强函数设计时, 确保每次都能将空间变换与颜色变换相结合, 使得分类效果更好. 表1为不同数据增强方式对分类结果的影响.

3.3 特征提取实验

为了证明本文设计的特征提取部分对裂缝图像可以提取到更细粒度的特征, 将原始ResNet50网络经过一层残差模块的特征图, 即图5(a), 与改进后的网络经过一层残差模块的特征图, 即图5(b)进行比较, 结果如图5所示. 可以看到, 加入了多尺度与对Cov1部分的改进后, 对裂缝的特征更敏感, 在特征图中裂缝的特征轮廓更加清晰, 对后续的分类任务有较大的提升.

3.4 裂缝分类对比实验

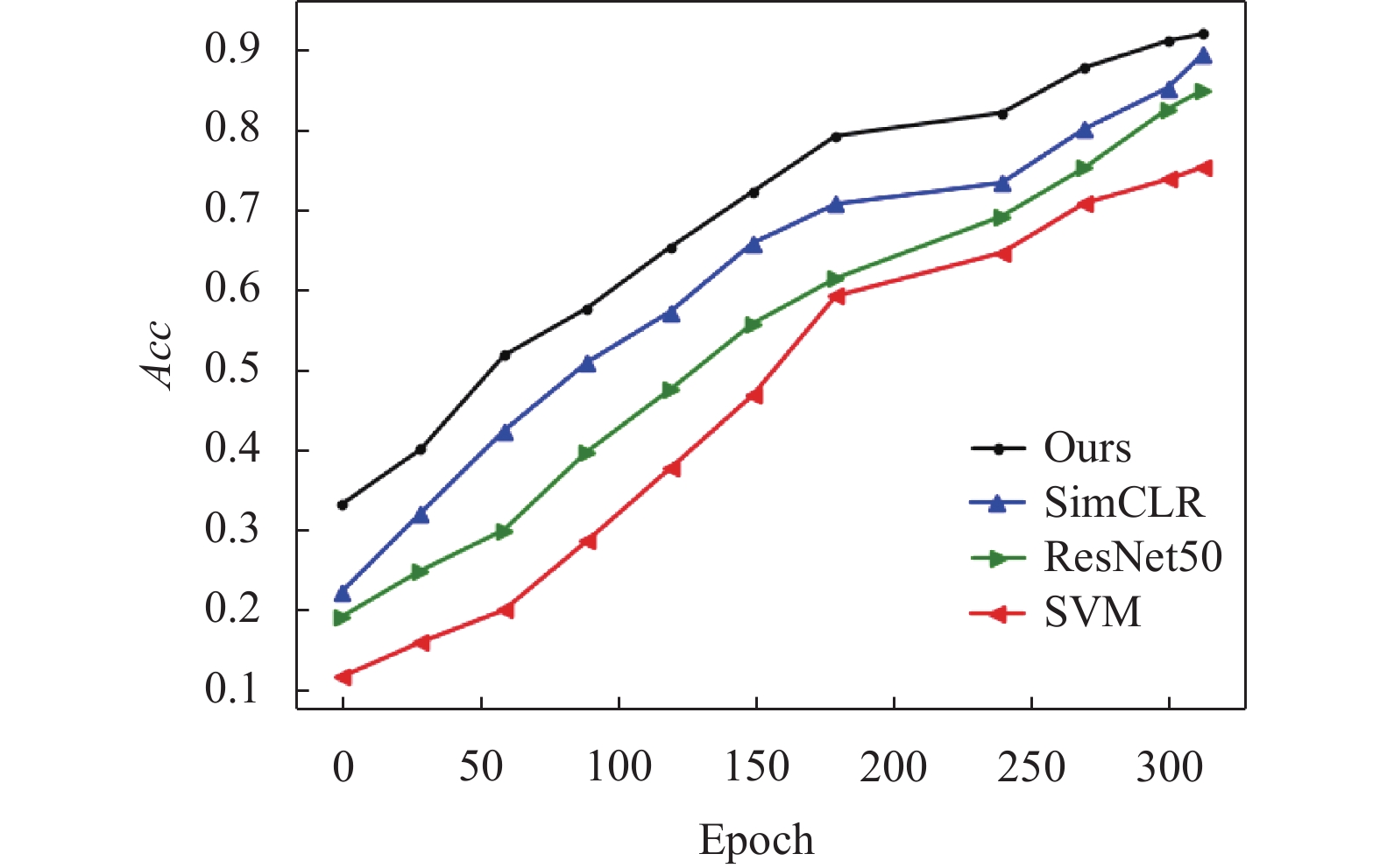
本节对几种分类方法对裂缝图像分类结果进行了对比, 主要包括支持向量机(SVM)^[26], ResNet50以及SimCLR, 分类准确率如图6所示, 具体的准确率如表2所示. 对于SVM方法, 当数据量比较大时, 分类准确率较低, 而ResNet50对各种裂缝的分类准确率较高, SimCLR方法准确率高于ResNet50, 而在本文中对SimCLR方法特征提取部分进行改进后, 分类准确率有所提升.

4 总结

为解决人工标注耗时长、效率低等问题, 本文提出了基于对比学习的道路裂缝图像分类方法. 通过实验发现, 对比学习在道路裂缝图像分类的任务中有较好的效果, 可以达到好的分类准确率. 通过实验结果表明, 不同的数据增强方式对分类准确率也有影响. 而通过对特征提取部分的改进, 也使得模型对细小裂缝的特征更加敏感, 对后续的分类任务有很大贡献. 而通过MLP对特征进行降维处理也简化了计算过程. 在3类道路裂缝的分类任务中, 达到了92.1%的平均分类准确率, 分类结果较为理想. 而本文方法仍存在一些不足, 如训练耗时较长, 训练时收敛较慢等, 仍需要对模型进行改进. 针对训练耗时较长问题, 可选择更高效的特征提取网络进行改进, 而针对训练时收敛较慢的问题, 可通过对损失函数进行调整使得收敛速度加快, 可在后续的研究中加以改善.