2. 南京邮电大学 现代邮政学院, 南京 210003
2. School of Modern Posts, Nanjing University of Posts and Telecommunications, Nanjing 210003, China
精确的SOC预测作为电池管理系统中极其重要的一环, 可以保障电池免受过充过放带来的损害. 然而, 锂离子电池是一个非常复杂的非线性系统, 它的荷电状态无法直接测量, 只有通过可直接测量的电池端电压、充放电电流和电池表面温度来对其进行估计. 此外, 电池的健康状态、自放电行为都会对SOC预测带来不利影响. 因此, 如何准确预测锂离子电池的荷电状态是一个值得研究问题.
SOC是电池中所存储能量的相对度量, 定义为特定时间点可从电芯提取的电荷量与总容量之比[1]. 目前用来预测SOC的方法主要有4种: 安时计数法, 开路电压法, 基于模型的方法和基于数据驱动的方法. 安时计数法是使用最广泛的SOC预测方法, 它的原理很简单, 用电流的积分代表电量, 这种方法的缺陷也很明显: 如果电流测量不准, 计算误差会随着时间不断增加, 需要不断的校准[2]; 开路电压法的原理是电池SOC与电池开路电压有着单调的对应关系[3], 但是开路电压的测量需要先将电池静置2 h以上, 因此该方法不适合实时预测SOC[4]. 基于模型的方法是指建立电池的状态空间模型, 常见的有卡尔曼滤波器及其变体[5, 6], 粒子滤波器[7], H无穷滤波器[8]. 基于模型的方法可以获得较好的预测效果, 但是这些模型需要大量的计算来进行参数辨识, 而且在不同的环境下, 模型也要改变[9, 10].
神经网络可以通过智能算法自动学习网络参数并从中获取电池输入数据和SOC之间的关系. 近年来进行SOC估计的神经网络结构主要有径向基函数神经网络(radial basis function neural network, RBFNN)[11], 反向传播神经网络(back-propagation neural network, BPNN)[12]等. 为了提升神经网络的预测精度, 需要进行大量实验去寻找最优参数, 采用布谷鸟搜索, 粒子群优化等算法可以快速寻找到神经网络相关参数的最优值[13].
为了解决传统神经网络中存在的梯度消失、过拟合等问题, 基于深度学习的SOC预测方法引起了学者们的广泛关注. 常用于电池SOC估计的深度学习模型有卷积神经网络(convolutional neural network, CNN)和循环神经网络(recurrent neural network, RNN)[14, 15], 其中, RNN的发展, 尤其是对门控循环单元(gated recurrent units, GRU)和长短期记忆网络(long short-term memory, LSTM)的研究, 为解决时间序列预测问题提供了新的方向[16-19].
Chemali等人使用LSTM训练了一个单一的网络模型, 该模型可以准确预测不同环境温度下的SOC, 在固定的环境温度下, 模型的MAE为0.573%, 在环境温度从10℃上升到25℃的数据集上, MAE为1.606%, 证明了该深度学习模型是SOC预测的强力工具[20]. 倪水平等人提出了一种基于一维卷积神经网络与长短期记忆网络结合的电池荷电状态预测方法, 该方法首先通过一层一维卷积层从样本数据中提取出高级数据特征, 之后再使用一层LSTM来预测SOC结果[21]. Bian等人在LSTM的基础上引入了双向循环结构和多层隐藏层, 构建了SBLSTM模型, 该模型可以完全利用电池的时间信息来预测SOC[22].
数据和特征决定了机器学习的上限, 而模型和算法只是逼近了这个上限而已. 然而, 现有的基于深度学习的SOC预测研究大多把研究重心放在模型的选择以及模型参数的优化上, 却忽视了数据本身的作用. 对深度学习来说, 海量的适配数据通常较难获得, 因此文中通过其他途径来优化数据, 继而提高预测的性能. 最常见的优化数据方法有特征选择和数据增强. 特征选择的目的是找到和预测目标关联性最强的特征, 这样可以极大的提升模型的预测效果[23]. 数据增强也叫数据扩增, 意思是在不实质性增加数据的情况下, 让有限的数据产生等价于更多数据的价值.
因此, 本文在选定了双向长短时记忆网络(Bi-LSTM)作为预测模型的基础上, 又采用了两种数据优化的方法: 使用PI特征选择算法来选择特征, 使用加入高斯噪声的方法来增强原始数据. 实验结果表明, 本文提出的PI特征工程和高斯数据增强方法可以进一步提升电池荷电状态预测模型的精度. 本文的剩余部分组织如下: 第1节介绍本文使用到的模型和方法: Bi-LSTM模型、PI算法、高斯数据增强. 第2节介绍了电池数据的获取以及实验步骤. 第3节是实验结果与分析. 第4节作为总结.
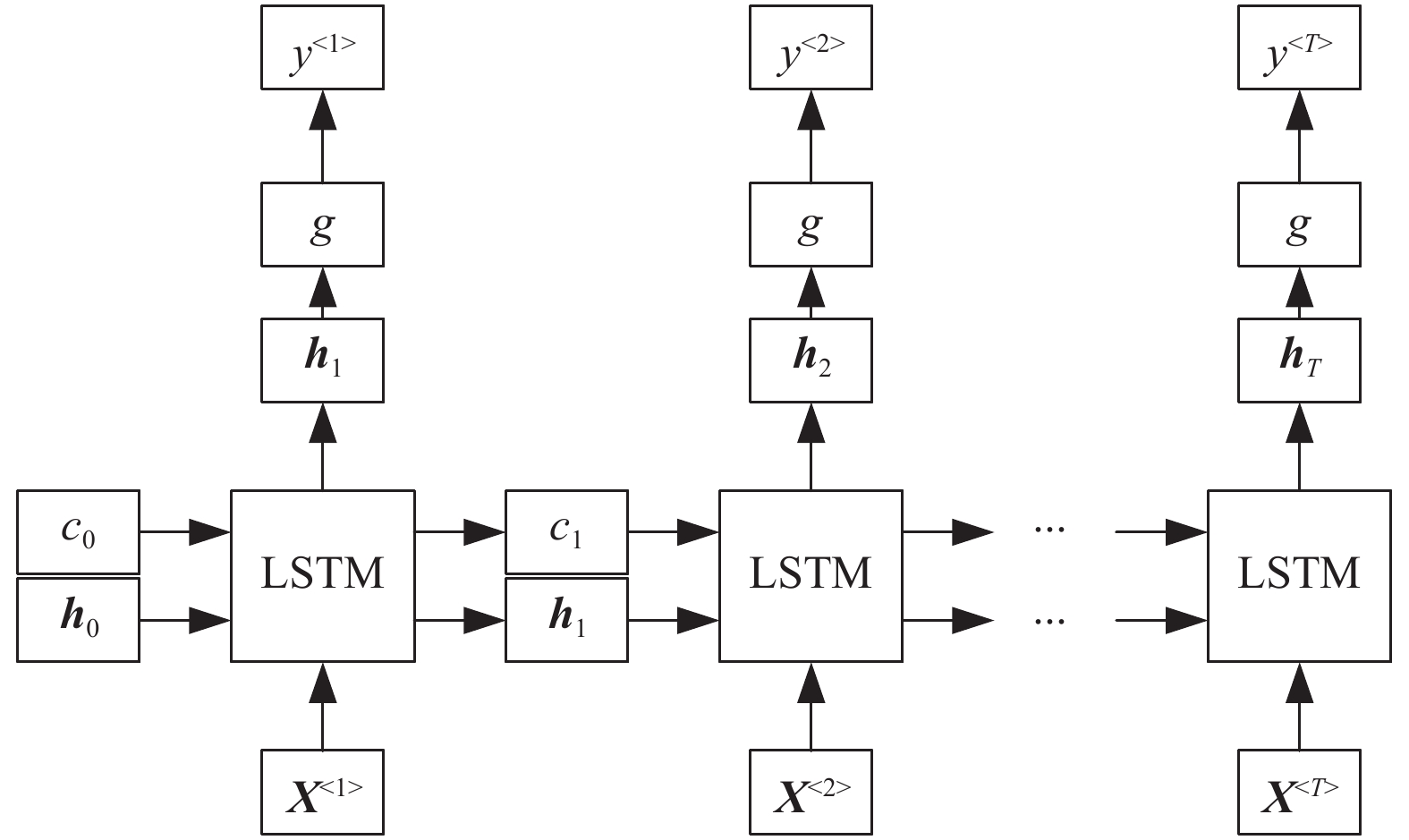
1 所用模型与方法介绍 1.1 Bi-LSTM模型 1.1.1 LSTM结构传统的前馈神经网络缺乏使用历史信息的能力, 历史信息在时间序列的数据中是非常重要的, 电池的充放电数据就是很典型的时间序列数据. 因此, 建立一个可以有效利用历史信息的神经网络模型来预测电池的荷电状态是很有必要的. 循环神经网络 RNN满足这一要求, 但是普通的RNN由于反向传播时的梯度消失问题, 无法捕捉长期的依赖信息. 为了解决该问题, Hochreiter等通过添加存储单元结构, 提出了LSTM循环神经网络[24]. LSTM循环神经网络的结构如图1所示.
|
图 1 LSTM循环神经网络 |
LSTM的输入是一条序列S={X<1>, X<2>, …, X<T>}, 长度为T, 序列中每一个元素是一个样本点X=[x1, x2, …, xn], n是样本的维度即特征个数. 在电池荷电状态预测中, 每个样本数据包含电流、电压、温度等n个特征, T个连续的样本构成一条序列, 序列中最后一个元素对应的 SOC 值就是该条序列的标签. h和c是隐藏层状态, 每个X对应一个输出y, y的计算公式为:
| $ {y^{ \lt i \gt }} = g({{\boldsymbol{W}}_{{{hy}}}} \times {{\boldsymbol{h}}_{{i}}} + {b_y}) $ | (1) |
其中, g是激活函数, 根据具体情况选择使用哪个激活函数; Why, by是输出层的权重与偏置矩阵. 在电池荷电状态预测中, y<T>是这条序列对应的最终预测值.
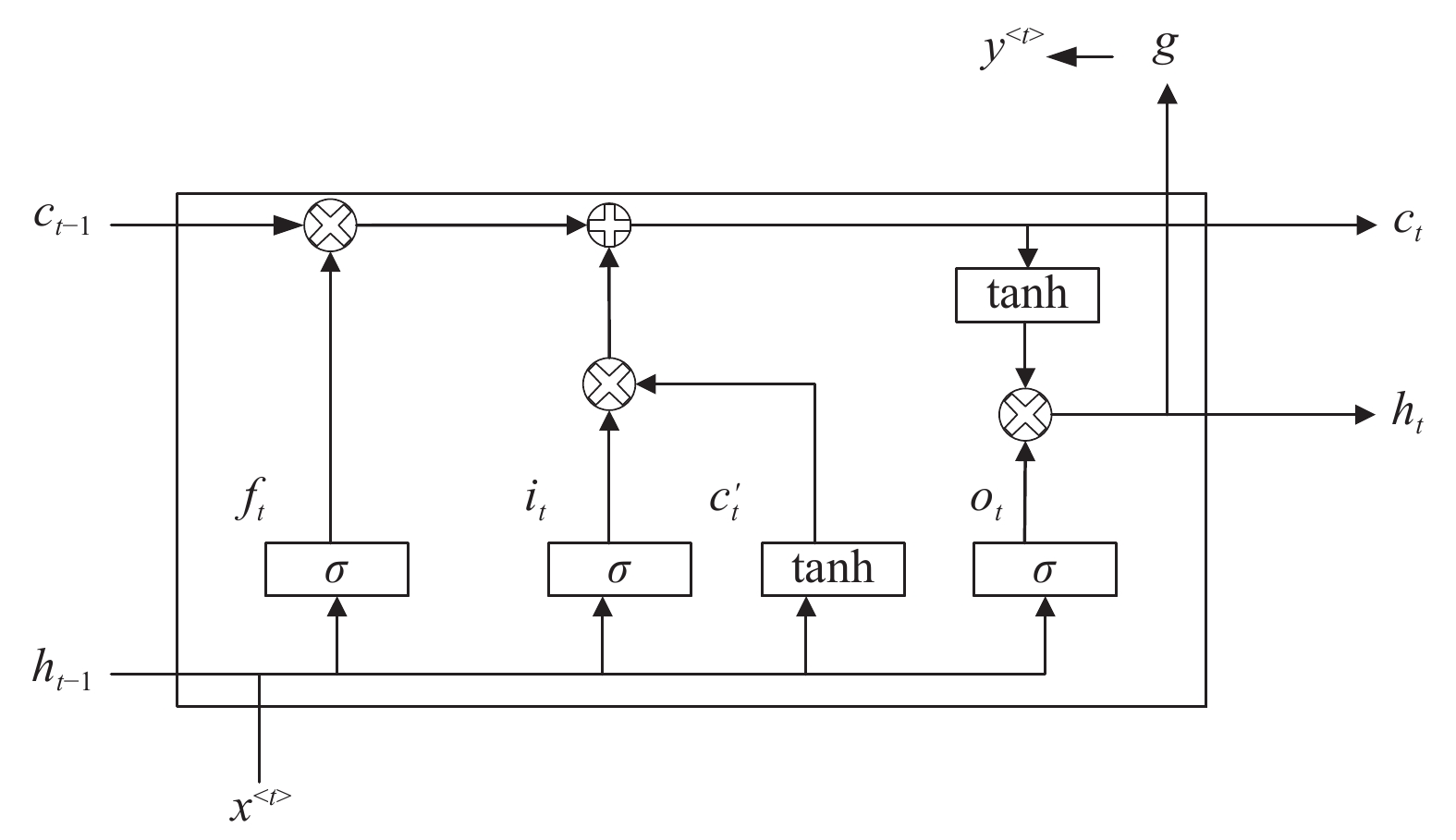
一个LSTM由一个保存历史信息的记忆单元和控制信息流动的门控机制组成. 图2显示的是一个LSTM单元的结构, 其中包括输入门、遗忘门、更新门和输出门. 输入门决定了当前输入的哪些信息可以被记忆下来, 它的计算公式为:
| $ {{\boldsymbol{i}}_{{t}}} = \sigma ({{\boldsymbol{W}}_{{{xi}}}}{{\boldsymbol{X}}^{{{ \lt t \gt }}}} + {{\boldsymbol{W}}_{{{hi}}}}{{\boldsymbol{h}}_{{{t - 1}}}} + {{\boldsymbol{b}}_{{i}}}) $ | (2) |
遗忘门会根据过去的记忆信息来决定当前输入的哪些信息是可以被忽略的, 其计算公式为:
| $ {{\boldsymbol{f}}_t} = \sigma ({{\boldsymbol{W}}_{{{xf}}}}{{\boldsymbol{X}}^{ \lt t \gt }} + {{\boldsymbol{W}}_{{{hf}}}}{{\boldsymbol{h}}_{{{t - 1}}}} + {{\boldsymbol{b}}_{{f}}}) $ | (3) |
更新门用来控制LSTM单元的状态信息c的更新, 更新方式如下:
| $ {\boldsymbol{c}'_t} = \tanh ({{\boldsymbol{W}}_{{{xc}}}}{{\boldsymbol{X}}^{{{ \lt t \gt }}}} + {{\boldsymbol{W}}_{{{hc}}}}{{\boldsymbol{h}}_{{{t - 1}}}} + {{\boldsymbol{b}}_{{c}}}) $ | (4) |
| $ {{\boldsymbol{c}}_{\boldsymbol{t}}} = {{\boldsymbol{f}}_{{t}}} \odot {{\boldsymbol{c}}_{{{t - 1}}}} + {{\boldsymbol{i}}_t} \odot {\boldsymbol{c}'_t}$ | (5) |
最后通过输出门得到的输出与ct一起计算得到ht, 计算公式如下:
| $ {{\boldsymbol{o}}_{{t}}} = \sigma ({{\boldsymbol{W}}_{{{xo}}}}{{\boldsymbol{X}}^{{{ \lt t \gt }}}} + {{\boldsymbol{W}}_{{{ho}}}}{{\boldsymbol{h}}_{{{t - 1}}}} + {{\boldsymbol{b}}_{{o}}}) $ | (6) |
| $ {{\boldsymbol{h}}_{{t}}} = {{\boldsymbol{o}}_{{t}}} \odot \tanh ({{\boldsymbol{c}}_{{t}}}) $ | (7) |
在式(2)–式(7)中,
|
图 2 LSTM单元结构 |
1.1.2 双向LSTM结构
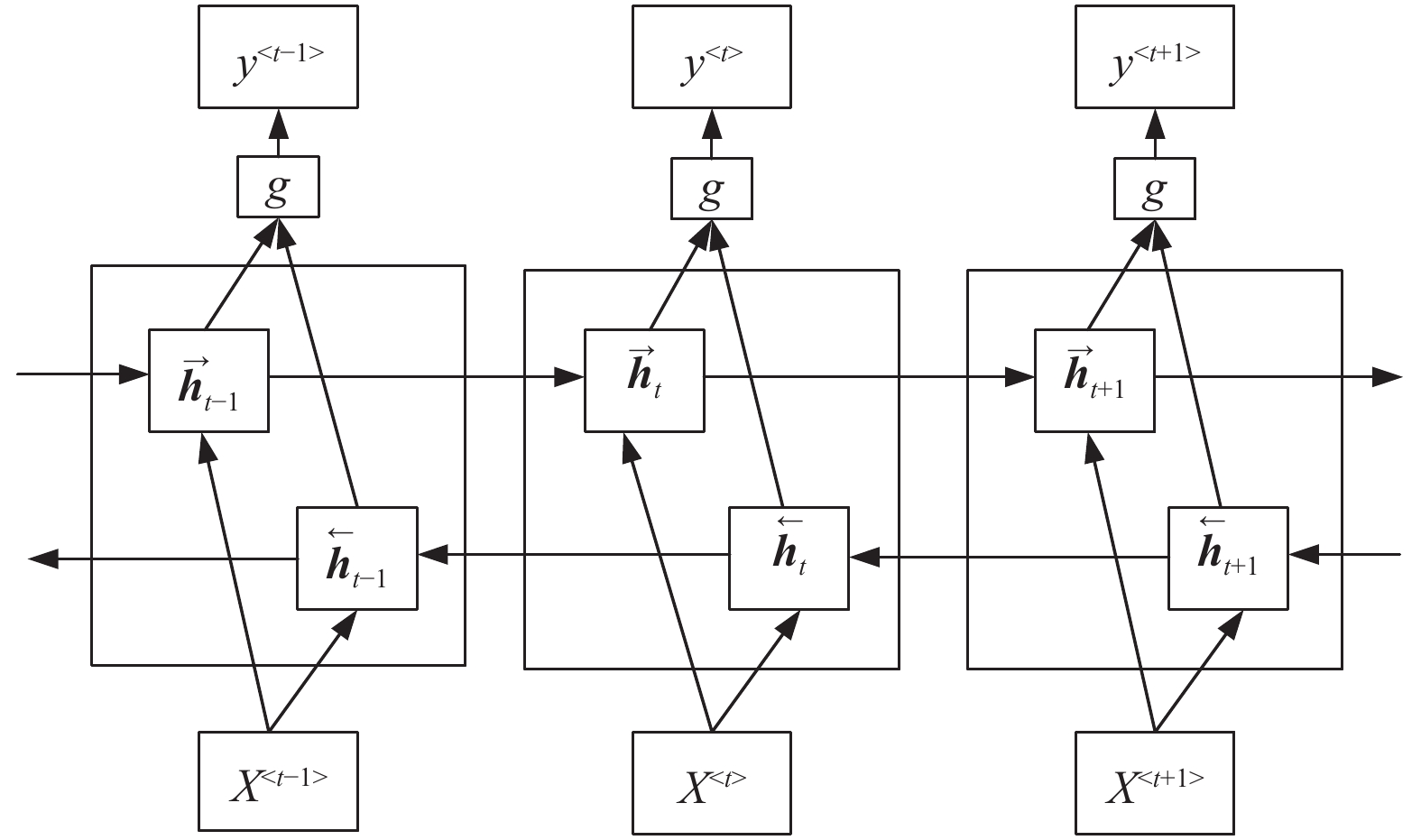
RNN和LSTM都是单向的, 这意味着他们只能访问正时间方向的输入时间序列. 与单向RNN不同, 双向RNN (BRNN)由两个独立的循环隐藏层组成, 一个用于正向输入序列, 另一个用于反向输入序列, 如图3所示. 其中
| $ y^{\lt t \gt}=g\left(\overrightarrow{\boldsymbol{h}}_t, \overleftarrow{\boldsymbol{h}_t}\right) $ | (8) |
|
图 3 双向RNN结构 |
使用这种特殊的结构, BRNN能够以向前和向后的方式捕获序列数据的时间依赖性, 然后将它们反馈到同一输出层. BRNN可以使用与单向RNN相同的算法进行训练, 因为前向层和后向层之间没有交互作用. 通过将双向结构应用于LSTM, 可以构造双向LSTM (Bi-LSTM).
1.2 排列重要性(permutation importance, PI)使用神经网络方法来做回归任务时, 特征工程是极其重要的一个环节, 有效的特征可以帮助神经网络模型捕捉到输入与输出之间的关系. 锂离子电池是一个复杂的非线性系统, 然而电池充放电实验中可以获取到的原始数据只有电压、电流和温度, 仅仅有这些是不够的. 此时就需要通过特征工程来根据原始数据构造新的特征, 然而, 并不是所有的特征都能提高模型的预测精度, 这就需要一种方法去找出对SOC预测最重要的几个特征. 本文使用PI方法来寻找重要特征, 使用该方法寻找重要特征的步骤如下.
Step 1. 用上全部特征训练一个模型.
Step 2. 在验证集上验证模型效果, 计算损失lossraw.
Step 3. 将验证集的一个特征f对应的数据打乱, 再次预测并得到损失lossf.
Step 4. 将上述得分做差即可得到特征f对预测的重要性: impf=|lossf–lossraw|.
Step 5. 依次将每一列特征按上述方法做, 得到每个特征对预测的重要性.
Step 6. 最后根据计算得到的重要性来选取适合的特征.
Step 7. 使用选出的特征再次训练一个模型, 并在测试集上验证其效果.
该方法中的特征重要性计算是在模型训练好后进行的, 所以不需要再训练其他的模型, 这大大节省了时间. 将一个特征的数据随机打乱会降低模型在测试集上的预测效果, 因为打乱后的数据就没有任何实际意义了. 被打乱的特征越是重要, 那么预测的结果就越差, 而那些对预测效果影响不大的特征被打乱后, 模型的预测效果也不会受到太大影响, 因此通过计算打乱数据后的模型预测损失lossf与原损失lossraw的差值所得到的impf可以表征特征f对模型预测的重要性.相对于PCA和EMD等特征选择方法来说, PI方法有两个优点, 一是该方法可以获得每个特征对模型重要性的数值度量, 让研究者可以直观地知道哪个特征重要以及为什么重要. 二是在选出重要的几个特征后, 以后在对新数据进行预测时, 只要将需要的特征制作出来就可以直接进行预测了, 而PCA方法则每次都需要制作出所有特征再进行降维处理才能进行预测.
1.3 高斯数据增强在训练神经网络时, 往往会遇到过拟合的问题, 即网络可以学习特定的输入示例及其关联的输出, 而不是学习从输入到输出的一般映射. 这将导致模型在训练数据集上表现良好, 而在新数据上表现不佳, 即泛化能力很差.
目前解决过拟合的方法主要有两个方向. 一是对神经网络做改动, 例如减少神经元个数、减少隐藏层层数和降低学习率等, 这类方法是通过限制网络学习训练数据的能力来增强泛化能力, 虽然有效, 但却无法充分利用神经网络强大的学习能力.
二是对训练数据做改动, 最理想的方式是获取更多更全面的数据, 但往往不容易实现. 一种合理的解决方案是通过给训练数据添加噪声从而增加数据量. 添加噪声意味着网络无法记住训练样本, 因为它们一直在变化, 从而导致网络权重更小且网络更健壮, 泛化误差更低. 噪声意味着从已知样本附近的域中抽取新样本, 从而平滑了输入空间的结构. 这种平滑意味着训练数据更易于网络学习, 从而导致更好, 更快的学习. 高斯噪声常常用来增强训练数据, 高斯噪声是概率密度函数服从高斯分布的一类噪声, 它的平均值为0, 标准差为1, 概率密度函数为:
| $ f(x) = \frac{1}{{\sqrt {2\pi } }}{{\rm{e}}^{\left( - \frac{{{x^2}}}{2}\right)}} $ | (9) |
在对训练数据添加噪声前会将训练数据进行归一化, 本文使用最大最小值方法将训练数据的每一特征列归一化到[0, 1]之间. 之后在每一轮迭代训练开始前对训练数据添加高斯噪声, 添加的高斯噪声的幅度要合理的设置, 太小则新数据与原数据几乎相同达不到数据增强的效果, 太大则新数据可能是现实情况中不可能出现的数据, 这种数据是无效的. 在实验过程中需要不断对噪声幅度进行调整来寻找最佳的幅度值.
2 电池数据获取与实验步骤 2.1 电池数据介绍本文使用Panasonic 18650PF数据集[20]来验证所提方法的有效性. 所使用的电池的详细参数如表1所示. 电池采用恒流恒压的方式进行充电, 一开始电流为1C (2.9 A), 电压为4.2 V, 当电流降到50 mA时停止充电, 此时电池的SOC为1. 然后, 使用驱动循环功率模式(drive cycle power profiles, 后称工况)对电池进行放电, 直到电压降至2.5 V. 在试验中使用了9种工况, 包括循环1、循环2、循环3、循环4、洛杉矶92 (Los Angeles 92, LA92)、公路燃油经济性驾驶计划(highway fuel economy test, HWFET)、补充联邦测试程序驾驶计划(supplemental federal test procedure driving schedule, US06)、城市测功机驾驶计划(urban dynamometer driving schedule, UDDS)、神经网络(neural networks, NN). 循环1–4包括US06、HWFET、UDDS和LA92的随机混合. NN由US06和LA92驱动循环的部分组合而成, 其设计具有一些额外的动力学特性, 有助于训练神经网络. 每种工况分别在3个不同的环境温度下(0℃, 10℃, 25℃)进行放电实验并获取相应的数据, 用来验证本文所提方法在不同环境温度下的有效性.
| 表 1 电池信息 |
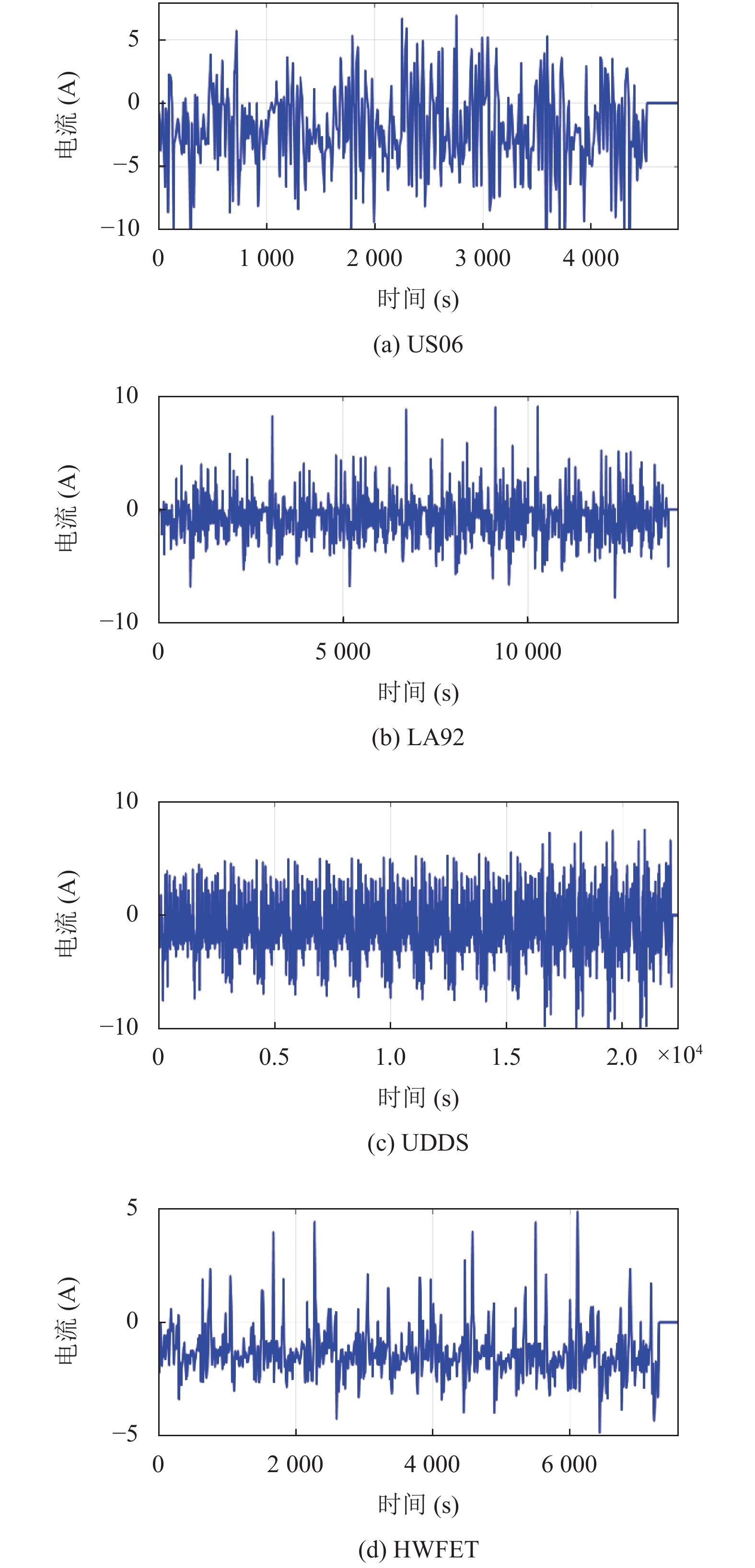
各种工况都是模拟现实中电动汽车在不同情况下的行驶特点, 不同工况的区别具体体现在电池放电时端电流的曲线不同, 最终获取的电池数据中, 电流数据是固定的, 只有电压和温度是在放电过程中实时测量获得的. 记录数据的时间间隔为1 s, 在不同的工况下, 放电所需时间大约在6000 s到10000 s之间. 图4显示了US06、LA92、UDDS和HWFET这4种工况在25℃下的电流曲线. 从图4可以看出, 各个工况下的电流曲线都表现出了极强的非线性.
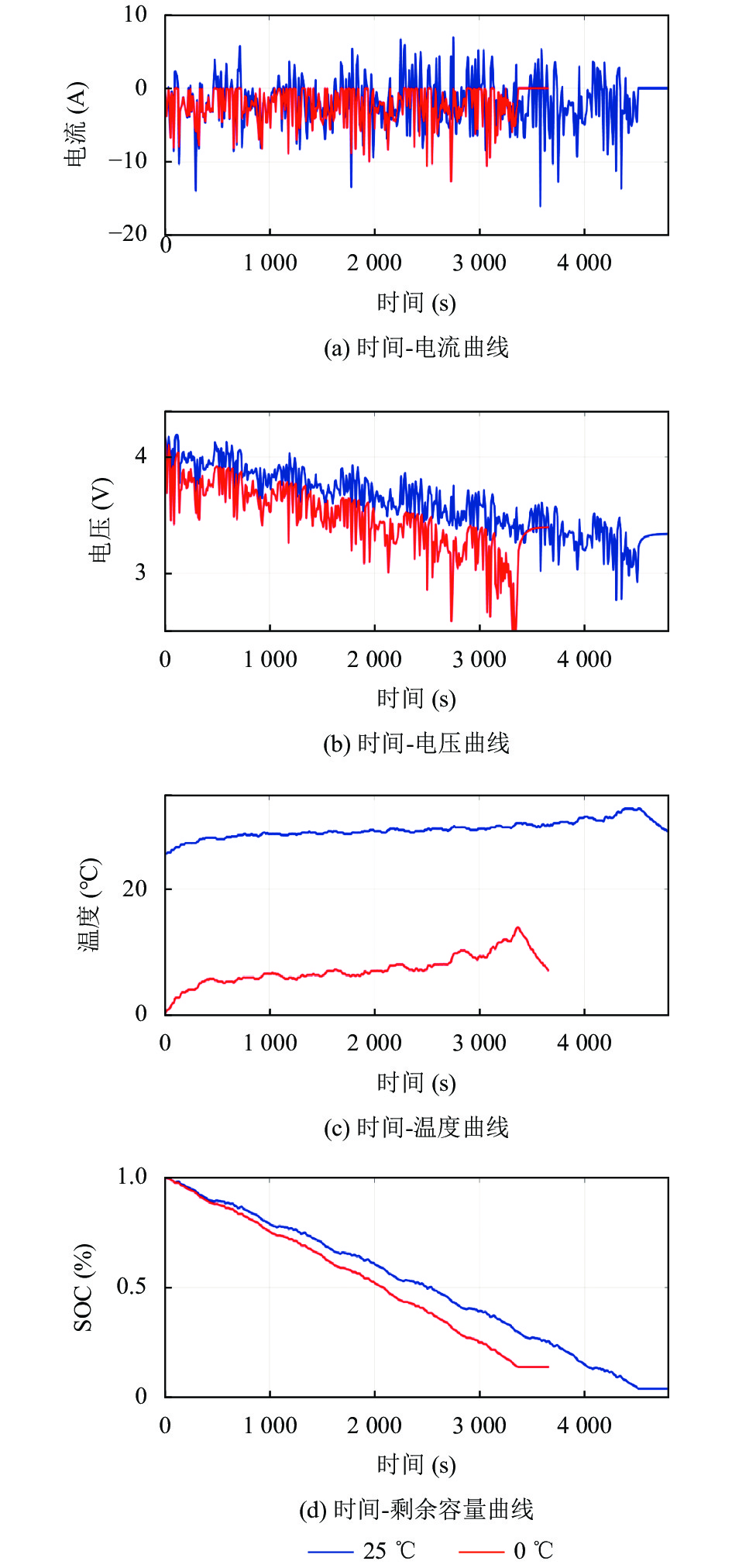
Panasonic 18650PF数据集中的9种工况并不能涵盖现实中电动汽车的所有行驶情况, 为了能让本文提出的模型能应用于现实, 本文选取NN工况下的数据作为验证集, 包含11698条数据, US06工况和HWFET工况下的数据作为测试集来验证模型效果, 分别包含4806和7595条数据, 其余6种工况下的数据作为训练集, 共有80924条数据. 图5显示了US06工况在0℃和25℃下, 电流(图5(a))、电压(图5(b))、温度(图5(c))和电池剩余容量(图5(d))随时间的变化曲线. 在25℃的情况下, 放电过程中是存在再生制动的, 而0℃的情况下没有出现, 这是因为当温度低于10℃时进行充电会对电池造成较大伤害.
|
图 4 不同工况下的电流曲线 |
2.2 实验步骤 2.2.1 数据处理与特征工程
原始数据包括电压、电流和温度, 数据的采集间隔为1 s, 每个温度下的数据总量大约为100000条. 根据采集的数据进行特征工程, 共制作n个特征[f1, f2, …, fn]. 此后还要将每个特征分别进行归一化, 本文采用最大最小值归一化方法, 计算方法如下:
| $ {x_{{\rm{norm}}}} = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $ | (10) |
其中, x, xmin, xmax, xnorm分别代表原始值、该特征的最小值、该特征的最大值和归一化后的值. 最后要构造时间序列数据, 本实验设定一条序列的时间跨度为50 s, 所以序列长度Nseq为50.
|
图 5 US06工况在25℃和0℃下测得的电池放电数据 |
2.2.2 实验环境和Bi-LSTM模型设置
本文使用Python的PyTorch库搭建Bi-LSTM模型, 模型的各个相关参数设置如表2所示. 实验硬件设施使用AMD Ryzen 7 5800U CPU @3.2 GHz, Windows 11 64位操作系统, 16 GB运行内存和500 GB硬盘. 编程 软件为Jupyter Notebook.
| 表 2 Bi-LSTM模型参数设置 |
2.2.3 模型训练
本文使用NN工况下测得的数据作为验证集, US06和HWFET工况下测得的数据作为测试集, 其余数据作为训练集. 每次训练都要将所有训练数据迭代100次, 每次迭代训练包括以下3个步骤.
Step 1. 读入所有训练数据并加入噪声, 这样可以保证每次迭代训练的数据都不同.
Step 2. 模型训练.
Step 3. 在测试集上验证此时模型的效果, 计算各个性能指标.
100次迭代结束后, 取最后10次迭代的MAE、RMSE、MaxE的平均值作为该模型最终的效果.
3 实验结果与分析本文使用平均绝对误差MAE, 均方根误差RMSE和最大误差MaxE来衡量模型预测的效果, 它们的计算公式分别为:
| $ {\textit{MAE}} = \frac{1}{N}\sum\limits_{k = 1}^N {|{y_k} - {{\hat y}_k}} | $ | (11) |
| $ {\textit{RMSE}} = \frac{1}{N}\sum\limits_{k = 1}^N {\sqrt {{{({y_k} - {{\hat y}_k})}^2}} } $ | (12) |
其中, N是样本总数,
本文一共根据原始数据制作了14个特征, 主要分为3类, 原始数据特征[v, i, temp]和charge、导数类特征[dv, di, dtemp, d2v, d2i, d2temp]和历史统计特征
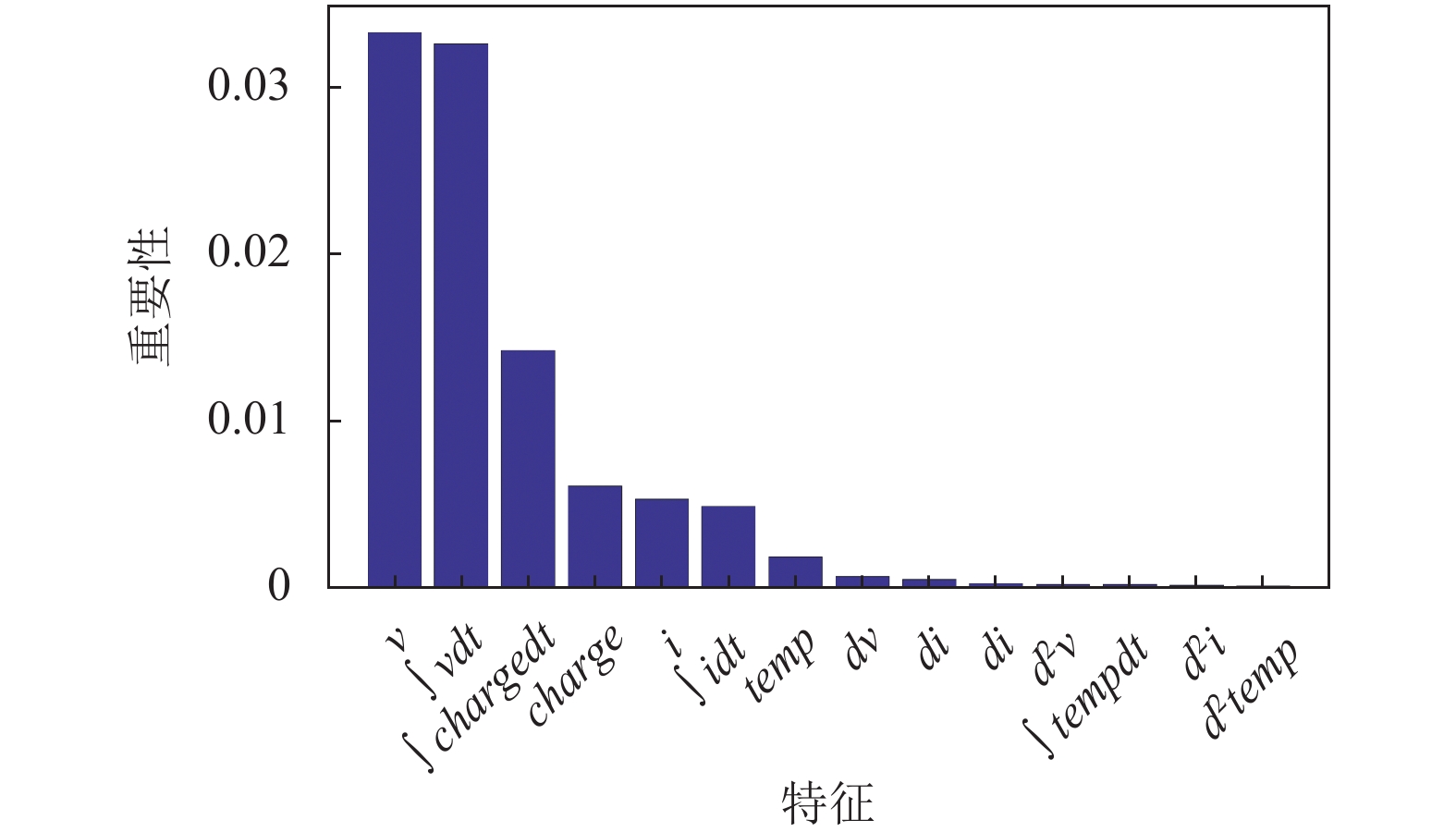
之后根据PI算法计算每个特征的重要性, 如图6所示. 从图中可以看出, 最重要的特征是
|
图 6 各个特征的重要性 |
3.2 高斯数据增强对模型预测的影响
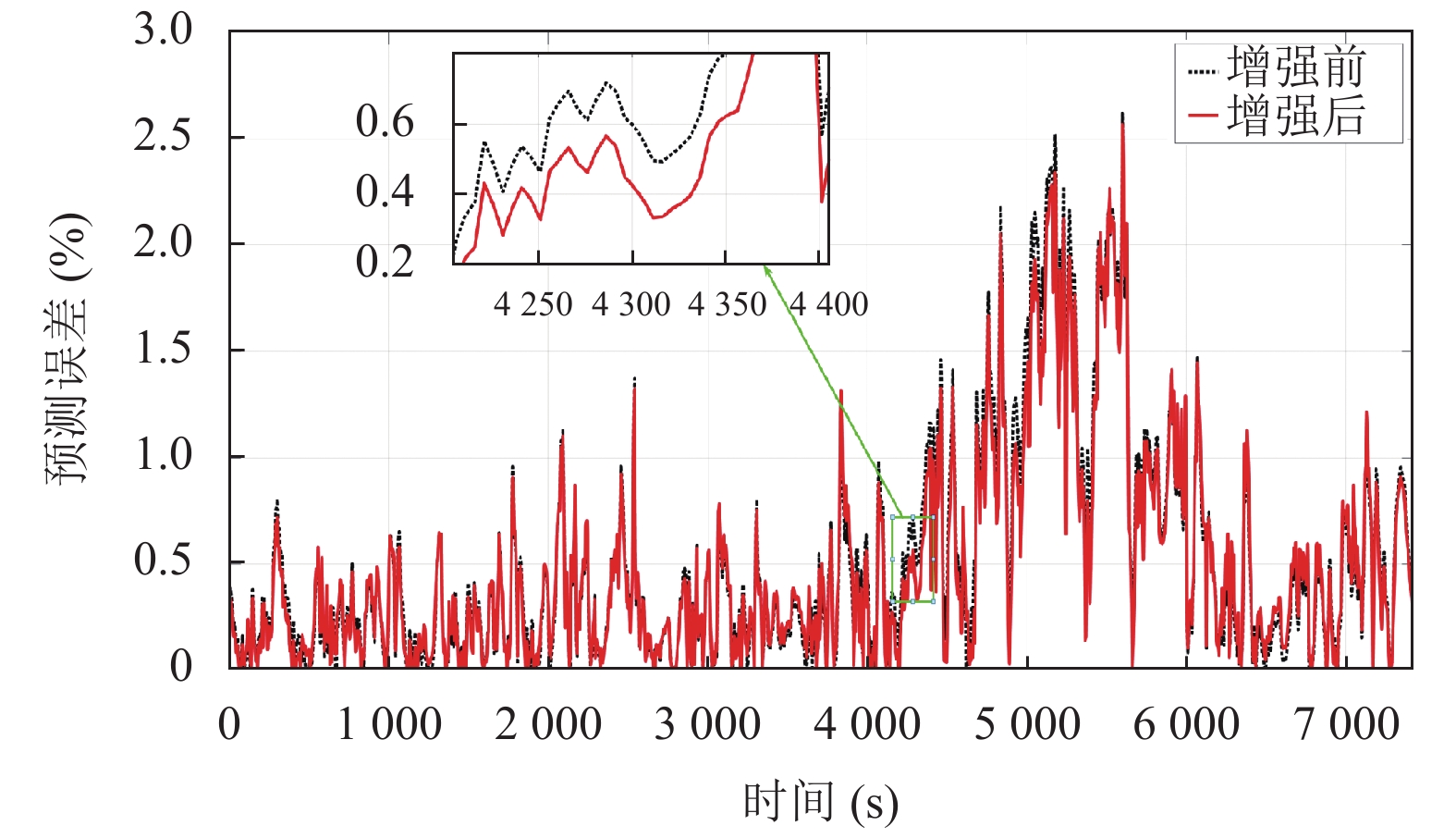
本文中给训练数据加的高斯噪声服从标准正态分布, 平均值为0, 标准差为1. 训练时, 在每一个epoch开始前都要重新读取数据并加入高斯噪声, 这样训练集数据总量相当于原来的100倍. 加入了高斯噪声后模型的预测结果如表4和图8所示. 从表4中可以看出, 加入噪声的幅度不同, 对模型预测效果的影响也不同.噪声幅度为0.001时, 模型预测效果并无明显提升, 这是因为新数据和原数据几乎一样, 这并没有达到数据增强的目的, 相当于将一样的数据迭代100次, 这与寻常的训练方式并无区别. 噪声幅度为0.005时, 模型的预测效果有了较大提升, MAE值和RMSE值分别为0.47%和0.68%, 相较于没有噪声的情况下提升了9.6%, 6.8%, 这说明通过添加适当的高斯噪声得到的大量额外数据可以弥补原始训练数据过少的缺点, 从而提升Bi-LSTM模型的预测效果. 当噪声幅度增大到0.01时, 模型的预测效果反而变差, 这说明加入的噪声幅度不能过大, 这样会导致获取到的新数据失去现实意义, 这种数据相当于异常数据, 会对模型预测产生负面影响.
| 表 3 不同特征下模型的预测结果 (%) |
|
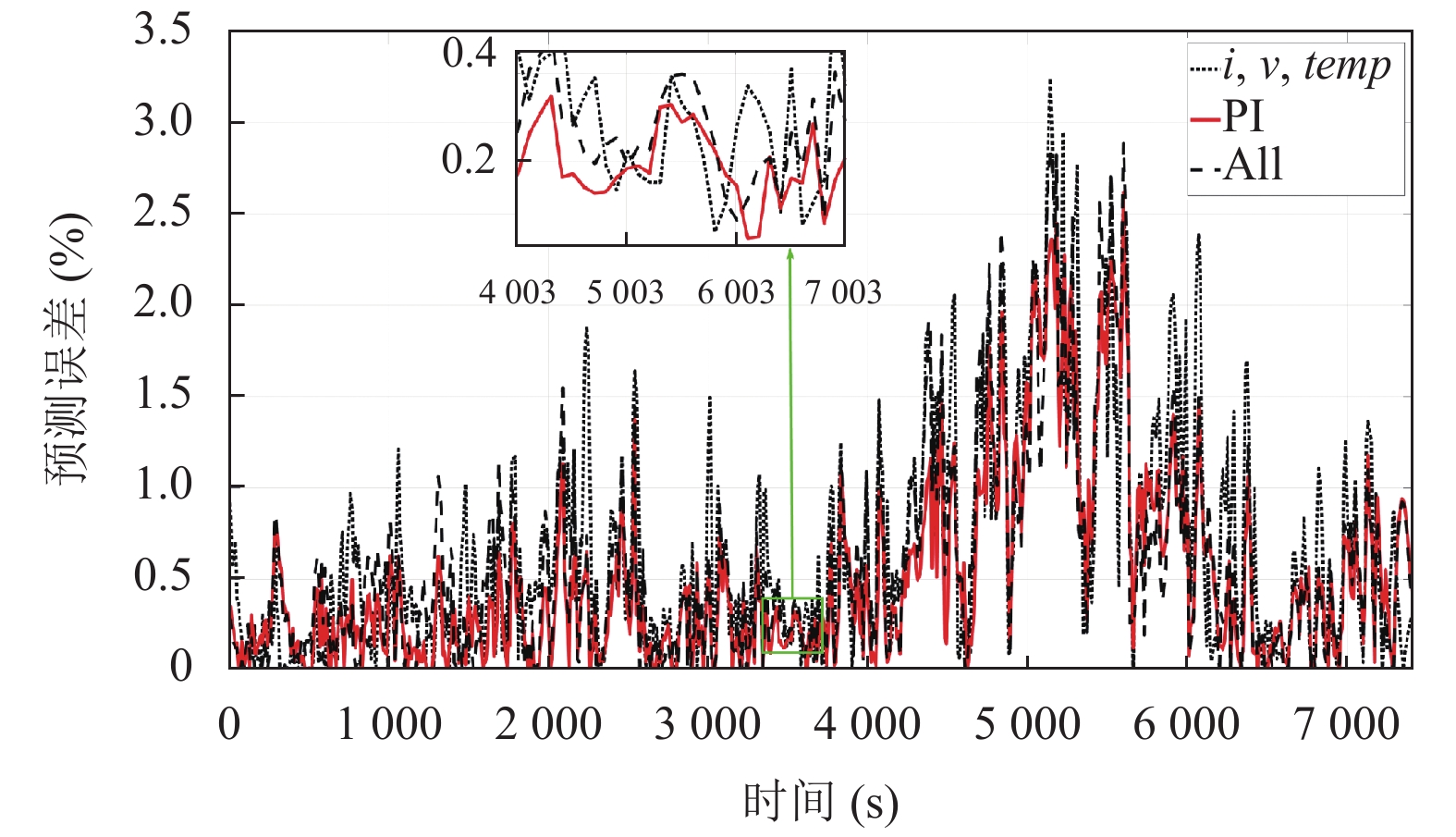
图 7 不同特征下模型的预测误差 |
| 表 4 高斯数据增强后的预测效果 |
|
图 8 数据增强后的模型预测误差 |
此外, 考虑到现实情况中电动汽车上的电流、电压和温度传感器的精度会随着使用时间下降, 这将导致各项数据无法准确测量. 所以进行了额外的实验: 给测试集也加上高斯噪声来验证Bi-LSTM模型的鲁棒性. 给测试集加的高斯噪声的幅度较大, 包括[0.01, 0.05, 0.1], 因为数据集的数据已经归一化到0到1之间, 所以加入噪声就相当于测量精度为[1%, 5%, 10%], 测试结果如表5所示.
| 表 5 测试集有噪声时的预测效果 |
从表5中可以看出, 测试集加入高斯噪声后, 模型在测试集上的预测效果有所下降, 当高斯噪声的幅度在0.05以内时, 模型预测的MAE维持在1%以内, 最大误差在5%左右, 这是一个可以接受的值. 但当高斯噪声的幅度达到0.1后, 即测量精度只有10%, 模型在测试集上的预测效果很差, 最大误差达到了8%. 由此可见, 在实际情况下, 即使锂离子电池的各项数据不能准确测量, 但只要把精度控制在5%以内, 使用本模型来预测SOC都能达到较好的效果.
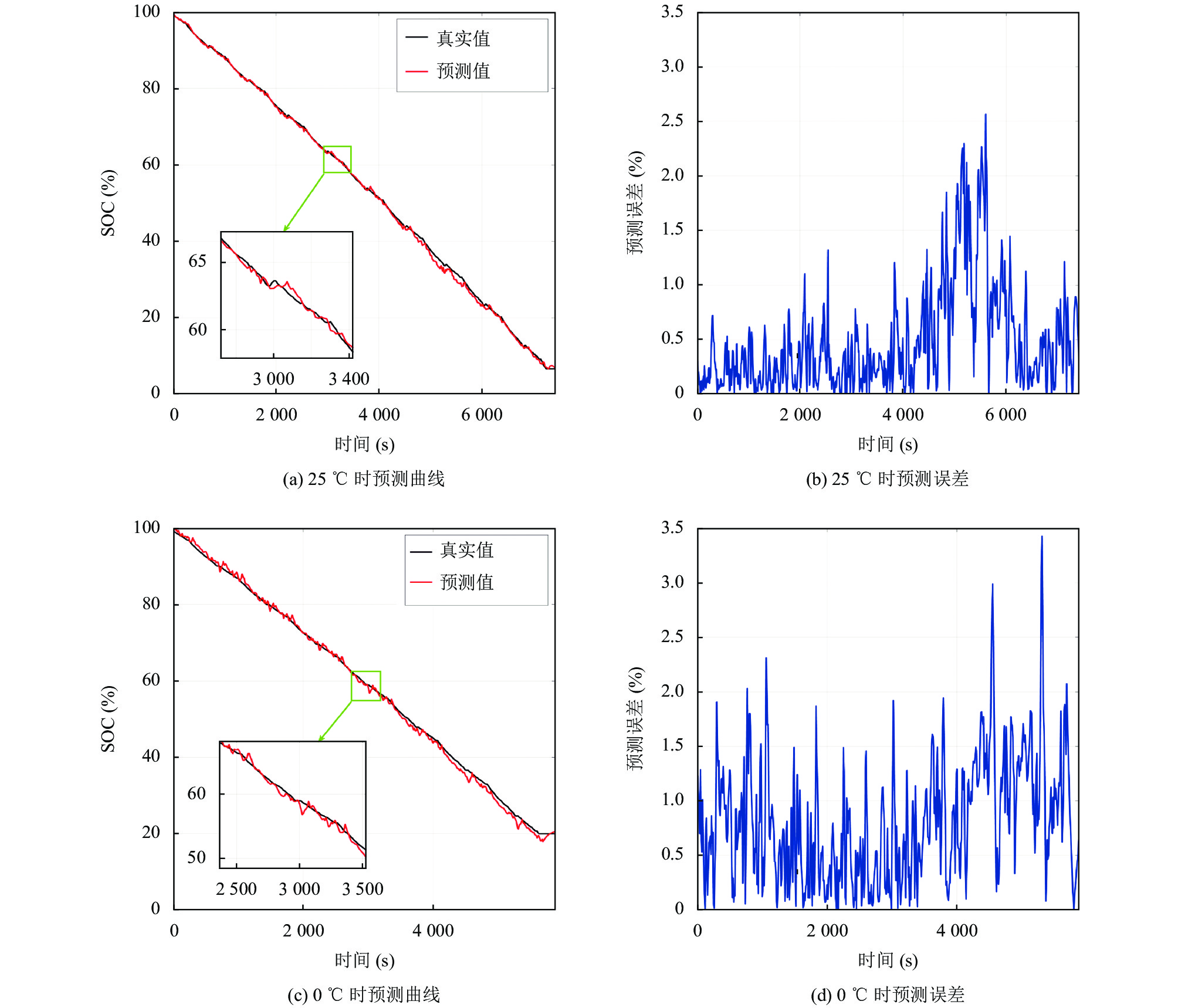
3.3 不同环境温度下的SOC预测温度对锂离子的电池荷电状态预测有着极大的影响, 当环境温度固定时, 电池在充放电过程中表面温度会随时间变化, 但整体上不会与环境温度相差太大. 电池表面温度一方面可以作为Bi-LSTM的一个输入特征来预测SOC, 此外电池表面温度还影响电池的充放电策略, 比如当电池表面温度过低时给电池充电会对电池造成损害, 因此应当避免在低温下进行充电. 本文研究了模型在3个固定的环境温度下的预测效果, 分别是0℃, 10℃, 25℃. 预测效果如表6所示, 预测曲线和误差曲线如图9所示. 从表6中可以看出, 模型在3个不同温度下的预测效果有所不同, 在HWFET工况下, MAE分别为0.47%, 0.84%, 0.80%, MaxE分别为2.61%, 4.05%, 3.61%. 由此可见, 温度对模型预测效果有着一定影响, 模型在低温(0℃, 10℃)下的预测精度要低于常温(25℃)下的预测精度. 作为对比, 文献[20]中的LSTM神经网络在相同的数据集下的预测结果分别是0.774%, 0.782%, 2.088%和3.692%, 4.047%, 6.687%. 本文提出的方法获得了更好的预测效果.
| 表 6 不同环境温度下模型的预测结果 |
4 结论
本文提出了一种基于特征选择和高斯数据增强的锂离子电池SOC预测方法. 该方法的贡献主要有3个方面. 1)根据原始电池数据设计了大量额外的特征, 并使用PI特征选择算法选出最有效的7个特征, 它们是v,
|
图 9 HWFET在25℃和0℃下模型的预测曲线和误差曲线 |
| [1] |
张照娓, 郭天滋, 高明裕, 等. 电动汽车锂离子电池荷电状态估算方法研究综述. 电子与信息学报, 2021, 43(7): 1803-1815. DOI:10.11999/JEIT200487 |
| [2] |
Truchot C, Dubarry M, Liaw BY. State-of-charge estimation and uncertainty for lithium-ion battery strings. Applied Energy, 2014, 119: 218-227. DOI:10.1016/j.apenergy.2013.12.046 |
| [3] |
Shen P, Ouyang MG, Lu LG, et al. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Transactions on Vehicular Technology, 2018, 67(1): 92-103. DOI:10.1109/TVT.2017.2751613 |
| [4] |
Barai A, Widanage WD, Marco J, et al. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells. Journal of Power Sources, 2015, 295: 99-107. DOI:10.1016/j.jpowsour.2015.06.140 |
| [5] |
郝世宇, 殷会飞, 杨茹, 等. 基于AEKF的锂离子动力电池荷电状态估计. 国外电子测量技术, 2021, 40(9): 49-53. DOI:10.19652/j.cnki.femt.2102842 |
| [6] |
朱奕楠, 吕桃林, 赵芝芸, 等. 基于并行卡尔曼滤波器的锂离子电池荷电状态估计. 储能科学与技术, 2021, 10(6): 2352-2362. DOI:10.19799/j.cnki.2095-4239.2021.0169 |
| [7] |
Bartlett A, Marcicki J, Onori S, et al. Electrochemical model-based state of charge and capacity estimation for a composite electrode lithium-ion battery. IEEE Transactions on Control Systems Technology, 2016, 24(2): 384-399. |
| [8] |
Aung H, Low KS, Goh ST. State-of-charge estimation of lithium-ion battery using square root spherical unscented Kalman filter (Sqrt-UKFST) in nanosatellite. IEEE Transactions on Power Electronics, 2015, 30(9): 4774-4783. DOI:10.1109/TPEL.2014.2361755 |
| [9] |
骆凡, 黄海宏, 王海欣. 基于电化学阻抗谱的退役动力电池荷电状态和健康状态快速预测. 仪器仪表学报, 2021, 42(9): 172-180. DOI:10.19650/j.cnki.cjsi.J2107637 |
| [10] |
武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述. 电工技术学报, 2022, 37(7): 1703-1725. |
| [11] |
张森. 基于径向基函数网络的MH/Ni电池荷电状态预测. 化工学报, 2006, 57(9): 2162-2166. DOI:10.3321/j.issn:0438-1157.2006.09.029 |
| [12] |
唐豪, 张振东, 吴兵. 基于BP神经网络的HPPC低温SOC优化估计. 计算机系统应用, 2021, 30(6): 293-299. DOI:10.15888/j.cnki.csa.007955 |
| [13] |
Lipu MSM, Hannan MA, Hussain A, et al. Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with PCA feature selection. Journal of Renewable and Sustainable Energy, 2017, 9(6): 064102. DOI:10.1063/1.5008491 |
| [14] |
Shin HC, Roth HR, Gao MC, et al. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Transactions on Medical Imaging, 2016, 35(5): 1285-1298. DOI:10.1109/TMI.2016.2528162 |
| [15] |
Sherstinsky A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Physica D: Nonlinear Phenomena, 2020, 404: 132306. DOI:10.1016/j.physd.2019.132306 |
| [16] |
Xiao B, Liu YG, Xiao B. Accurate state-of-charge estimation approach for lithium-ion batteries by gated recurrent unit with ensemble optimizer. IEEE Access, 2019, 7: 54192-54202. DOI:10.1109/ACCESS.2019.2913078 |
| [17] |
Yang FF, Li WH, Li C, et al. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy, 2019, 175: 66-75. DOI:10.1016/j.energy.2019.03.059 |
| [18] |
Chinomona B, Chung C, Chang LK, et al. Long short-term memory approach to estimate battery remaining useful life using partial data. IEEE Access, 2020, 8: 165419-165431. DOI:10.1109/ACCESS.2020.3022505 |
| [19] |
李超然, 肖飞, 樊亚翔. 基于循环神经网络的锂电池SOC估算方法. 海军工程大学学报, 2019, 31(6): 107-112. DOI:10.7495/j.issn.1009-3486.2019.06.020 |
| [20] |
Chemali E, Kollmeyer PJ, Preindl M, et al. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6730-6739. DOI:10.1109/TIE.2017.2787586 |
| [21] |
倪水平, 李慧芳. 基于一维卷积神经网络与长短期记忆网络结合的电池荷电状态预测方法. 计算机应用, 2021, 41(5): 1514-1521. |
| [22] |
Bian C, He HL, Yang SK. Stacked bidirectional long short-term memory networks for state-of-charge estimation of lithium-ion batteries. Energy, 2020, 191: 116538. DOI:10.1016/j.energy.2019.116538 |
| [23] |
Chandrashekar G, Sahin F. A survey on feature selection methods. Computers & Electrical Engineering, 2014, 40(1): 16-28. |
| [24] |
Graves A. Long short-term memory. Supervised Sequence Labelling with Recurrent Neural Networks. Berlin: Springer, 2012. 37–45.
|
 2023, Vol. 32
2023, Vol. 32


