2. 广东浩迪创新科技有限公司, 佛山 528299
2. Hodi Technology Co. Ltd., Foshan 528299, China
电力负荷预测是依据历史负荷信息以及相应的外部影响因素(如当地的天气状况和温度等), 对未来一段时间内负荷需求进行预判[1-3], 其对维持智能电网经济、安全以及稳定运行具有重大意义[4, 5]. 近年来, 伴随着“碳中和”的全面推进以及智能电网的全面建设, 分布式电网逐渐在各地开始部署, 各种清洁能源(风能、光伏)也开始以微电网的方式接入电网之中[6], 这极大地提高了负荷的不确定性. 由于确定性预测的方法难以分析和处理这种不确定性, 而概率负荷预测能够捕获更多关于未来负荷不确定的信息, 可以帮助决策层更全面地分析电力系统中潜在的风险[7, 8], 所以概率预测成为现今研究的热点领域[5].
目前, 负荷概率预测大致可以分为区间预测[9]、概率密度预测[10]和分位数预测[5, 7,8]. 如Li等人[9]提出一种基于ForecastNet的区间预测模型; Afrasiabi等人[10]提出了一种基于深度混合网络直接预测负荷的概率密度函数. 但是不论原始分布是何种类型, 分位数回归皆能解释随机变量之间的关系[5, 11], 因此备受关注. 如Yang等人[11]为有效地分析负荷之中的不确定性, 提出了一种联合高斯过程的分位数回归方法.
因为分位数回归是基于线性回归的, 难以直接分析具有非线性和较强复杂性的数据, 为了提高模型的非线性映射能力, 研究者们开始将机器学习与分位数回归相结合. 如He等人[12]为提高模型的非线性映射能力, 提出了一种基于支持向量机的分位数回归模型; He等人[13]提出了一种基于变分模态分解(variational modal decomposition, VMD)分解的分位数回归树模型; Lin等人[14]将深度学习与分位数回归相结合, 提出了一种基于双阶段注意力机制长短时记忆网络(long and short-term memory network, LSTM)分位数回归模型用于负荷概率预测.
尽管基于机器学习和分位数回归的预测模型在解决非线性映射问题方面具备显著的优越性, 但上述模型也都存在一个比较明显的亟待解决的问题, 即分位数交叉问题, 当样本空间有限时, 会存在不同分位点下的回归曲线交叉的现象, 这违背了分位数回归的基本原理, 即随着分位点增大, 其相应的回归值就越大[15]. 为解决这个问题, Chen等人[16]利用时间卷积网络(temporal convolutional network, TCN)同时对所有的分位点进行估计, 并构造了一种新的损失函数来防止分位数交叉, 这在一定程度上可以缓解分位数交叉, 但是无法从根本上解决这个问题; Huang等人[17]是首先使用卷积神经网络(convolutional neural network, CNN)进行确定性负荷预测, 然后使用线性规划的方式进行分位数预测, 并将分位数交叉的问题作为线性规划的约束. 这种方式可以很好地解决分位数交叉的问题, 但是随着训练数据的增加, 线性规划的约束也会增加, 导致线性规划的规模逐渐增大, 从而使得该线性规划问题难以解决; Cannon[18]提出了一种具有单调性的神经网络MCQRNN, 其利用单调性可以保证高分位点的回归值一定大于低分位点的回归值, 既保证了问题的可解性, 也解决了分位数交叉问题, 但是MCQRNN是基于多层感知机, 无法进一步地分析负荷中的序列信息和其内在规律性.
为了解决上述问题, 本研究融合了可以提取时序信息的因果卷积网络以及MCQRNN, 提出了一种既可以防止分位数交叉, 又能充分分析数据之中的时序信息的分位数回归网络, 即具有约束性的复合膨胀因果卷积网络(MCQRDCC). 为了验证MCQRDCC的有效性, 本研究选取了德国巴登符腾堡州的真实负荷数据进行了实验, 实验结果表明MCQRDCC不仅仅能有效地防止分位数交叉, 还能充分分析负荷之中的时序信息和内在规律, 准确地预测负荷变化的趋势, 提高负荷概率预测的精度.
1 理论基础 1.1 膨胀因果卷积网络因果卷积网络(causal convolutional networks, CCN)是一种用于时序分析的卷积网络[19, 20], 它相较于LSTM等循环神经网络, CCN没有循环机制, 能够并行运行, 所以它具备较快的训练速度[20]. CCN中的各层之间存在因果关系, 即当前层第i个神经元的值(Fi)只与上一层第i个神经元之前的值(xi–j)存在联系[19, 20], 其公式如式(1)所示:
| Fi=K−1∑j=0Wkjxi−j | (1) |
其中, K为卷积核的大小, Wk为卷积核的权重矩阵. 然而, 当输入的时序长度过长时, 需要堆叠多层网络来扩大神经网络的感受野, 但这会导致网络过深而难以训练的问题. 为解决上述问题, 膨胀因果卷积引入膨胀机制来扩大每一层网络的感受野, 以此减少网络的深度[19, 20], 其公式如式(2)所示:
| Fi=K−1∑j=0Wkjxi−jd | (2) |
其中, d为膨胀因子.
1.2 分位数回归分位数回归即分析输入变量与预测值的条件分位数之间的关系, 分位数线性回归的模型如式(3)所示:
| Yτ=X′β(τ) | (3) |
其中, τ为分位点(0<τ<1),Yτ为τ分位点下的预测回归值, X是输入变量, 表示影响预测值的各种因素β(τ)为参数向量[5], 该向量的求解可转化为如下优化问题[5]:
| min∑ρτ(Y−X′β(τ)) | (4) |
其中,
| ρτ(x)=max(τx,(1−τ)x) | (5) |
MCQRNN是由Cannon[18]融合MMLP (monotone multi-layer perceptron)[21]和CQRNN (composite quantile regression neural network)[22]提出的一种用于防止分位数交叉的神经网络[15, 18]. MCQRNN将输入分为约束输入与非约束输入, 当非约束输入不变, 约束输入增大时, 其输出随之增大, 其输入层的输出公式如式(6)所示:
| h=f(xmexp(Wm)+xuWu+bi) | (6) |
其中, h代表输入层的输出, f()代表非递减的激活函数, xm和xu分别代表约束输入与非约束输入, Wm和Wu分别代表约束权重与非约束权重, bi为输入层偏置.
其输出层的输出公式如式(7)所示:
| ˆy=f(hexp(Wh)+bh) | (7) |
其中,
| loss=1QNQ∑q=1N∑t=1ρτq(yt−ˆyτqt) | (8) |
其中, Q代表分位点的数目, N代表训练集的规模,
原始的MCQRNN是基于全连接神经网络的, 其无法较好地分析电力负荷中内部的周期性以及时序性. 为解决上述问题, 本研究将MCQRNN与DCC相结合, 提出一种既能解决分位数交叉又能充分地分析和处理电力负荷中的时序信息的分位数回归网络MCQRDCC(如图1所示).
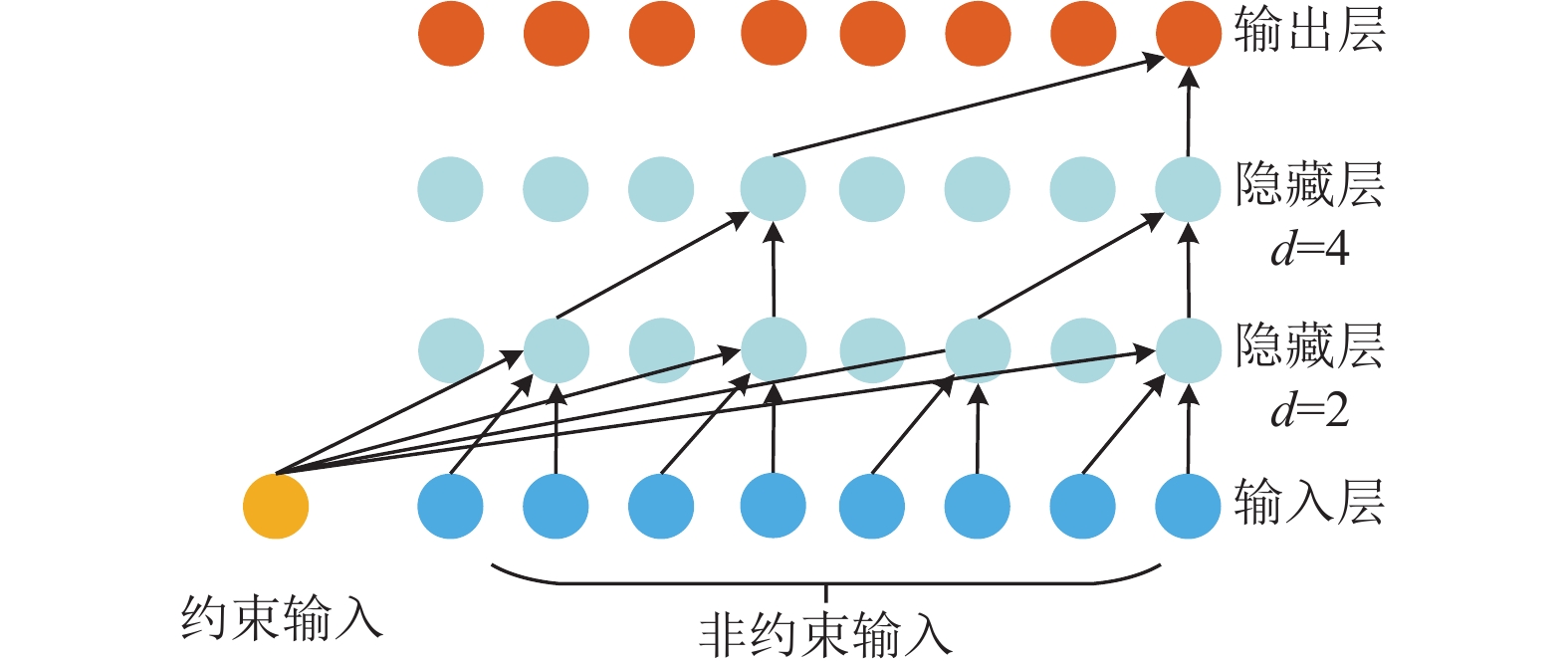
|
图 1 MCQRDCC模型 |
此外, 原始的MCQRNN使用指数函数对MCQRNN中的约束权重矩阵进行转化, 如图2所示, 当原始权重大于0时, 较大的梯度只会使得该权重进行微小的变化, 当原始权重小于0时, 细小的梯度变化可能引起原始权重较大的改变, 会极大地影响训练的质量. 为解决这一点, 本研究使用ReLU函数代替指数函数, 并使得初始权重大于0, 这样既可以解决上述问题, 也可以使小于0的权重自动失活, 以防止过拟合, 提高模型的泛化能力.
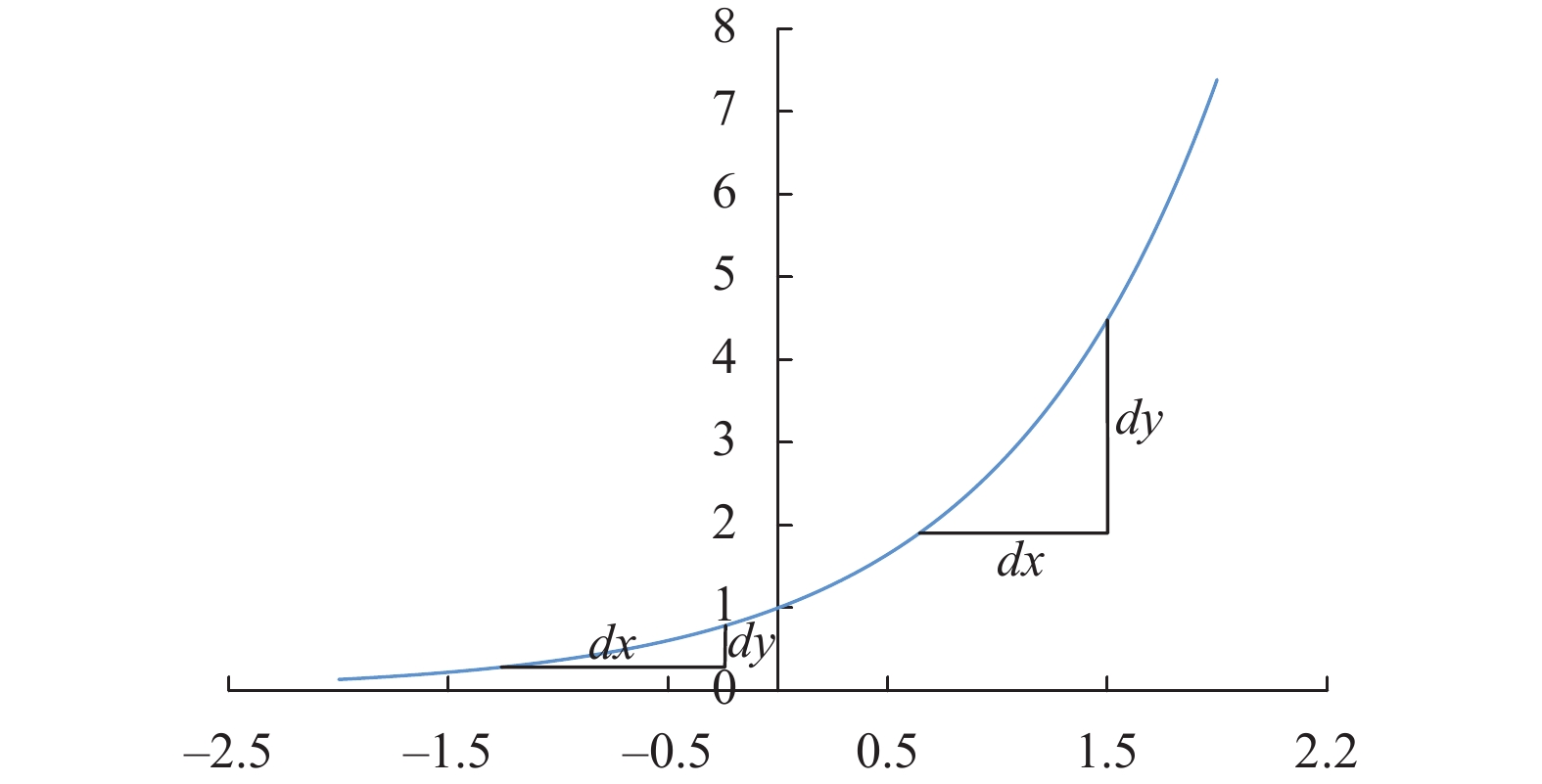
|
图 2 指数函数 |
MCQRDCC的输入层公式如式(9)所示:
| H(2)i=f(xmReLU(Wm)+K−1∑j=0Wkjxu(i−jd)) | (9) |
其中,
| H(l+1)i=f(K−1∑j=0ReLU(Wkj)H(l)i−jd) | (10) |
本研究选取的数据集来自于德国的巴登符腾堡州, 为全州2019年全年的负荷数据, 其采样间隔为15 min, 即一天96个时序点. 因为负荷数据具有较强的日周期性(图3), 本研究选择前一日的数据, 即预测点前的96个数据作为输入. 本研究选取最后一月的数据作为测试集, 其余作为训练集.
|
图 3 巴登符腾堡州负荷曲线 |
2.2 评价指标
本研究选取平均Pinball (average Pinball, APinball) 损失(式(8)), 区间覆盖率(PI coverage probability, PICP), 区间归一化平均宽度(PI normalized averaged width, PINAW)作为评价指标. 除此之外, 为了综合评价覆盖率以及预测区间的宽度, 本研究还选取CWC(coverage width-based criterion)以及平均区间分数(average interval score, AIS), 除PICP与AIS以外, 其他所有指标越小说明模型精度越高 . 其公式如式(11)所示:
| PICP(α)=1NN∑i=1ci | (11) |
其中,
| ci={1,yi⩾Liandyi⩽Ui0,others | (12) |
其中,
| PINAW(α)=1NTN∑i=1(Ui−Li) | (13) |
其中, T为y中最大值与最小值的差值.
| CWC(α)=PINAW(1+γe−η(PICP−α)) | (14) |
其中,
| γ={1,PICP<α0,PICP⩾α | (15) |
其中,
| AIS(α)=1NN∑i=1ISi(α) | (16) |
其中,
| ISi(α)={−2α(Ui−Li)−4(Li−yi),ifyi<Li−2α(Ui−Li)−4(yi−Ui),ifyi>Ui−2α(Ui−Li),others | (17) |
为了验证本研究提出的MCQRDCC模型的性能, 除了选取MCQRNN[15]作为对比模型以外, 本研究还选取如下算法作为对比模型.
(1)基于Huber函数的TCN概率预测方法(HTCN)[23], 该方法将分位数回归与TCN相结合, 提出一种基于TCN的分位数回归网络, 并使用Huber近似优化损失函数, 使得损失函数可导, 该方法针对每一个分位数都建立一个模型进行预测.
(2) 基于LSTM的概率预测模型(QLSTM)[24], 该模型将分位数回归与LSTM相结合, 该模型同时预测所有分位点的回归值, 所以只需要创建一个模型即可.
除上述外, 为了进一步探究本研究改进模型的优越性, 本研究还进行了如下对照试验.
(1) MCQRNN-ReLU, 使用ReLU函数代替指数函数对约束矩阵和隐藏层权重矩阵进行处理, 其余与MCQRNN一致.
(2) MCQRDCC-exp, 使用指数函数对约束矩阵和隐藏层权重矩阵进行处理, 其余与MCQRDCC一致.
3.2 实验环境与参数设置本研究全部实验是采用Python 3.9完成的, 深度学习框架是TensorFlow 2.9, 实验硬件平台使用Intel Core i5-11260H CPU, 采用NVIDIA GeForce GTX 3060进行加速.
经过参数优化, 各个模型的超参数设置如下.
HTCN采用两层残差块连接, 第1块的通道数为4, 第2块的通道数为8, 全连接网络的神经元数为8, 迭代次数为200, batch size为2 048, 学习率为0.01.
QLSTM是一层LSTM网络和一层全连接网络, 其中LSTM的神经元数为32, 全连接的神经元数为32, 迭代次数为200, batch size为2 048, 学习率为0.03.
MCQRNN与MCQRNN-ReLU全采用双层网络, 第1层的神经元数为4, 第2层的神经元数为2, 迭代次数为100, batch size为2 048, 学习率为0.01.
MCQRDCC与MCQRDCC-exp全采用两层网络, 第1层的通道数为4, 步长为1, 扩展因子为1, 第2层的通道数为4, 步长为2, 扩展因子为1, 迭代次数为100, batch size为2 048, MCQRDCC的学习率为0.001, MCQRDCC-exp的学习率为0.006.
3.3 实验结果和分析 3.3.1 对比实验结果如表1所示, 与本实验所选用的对比实验进行对比, 除PICP相对较小以外, MCQRDCC的其他指标要优于其他模型.
|
表 1 对比模型的实验结果(
|
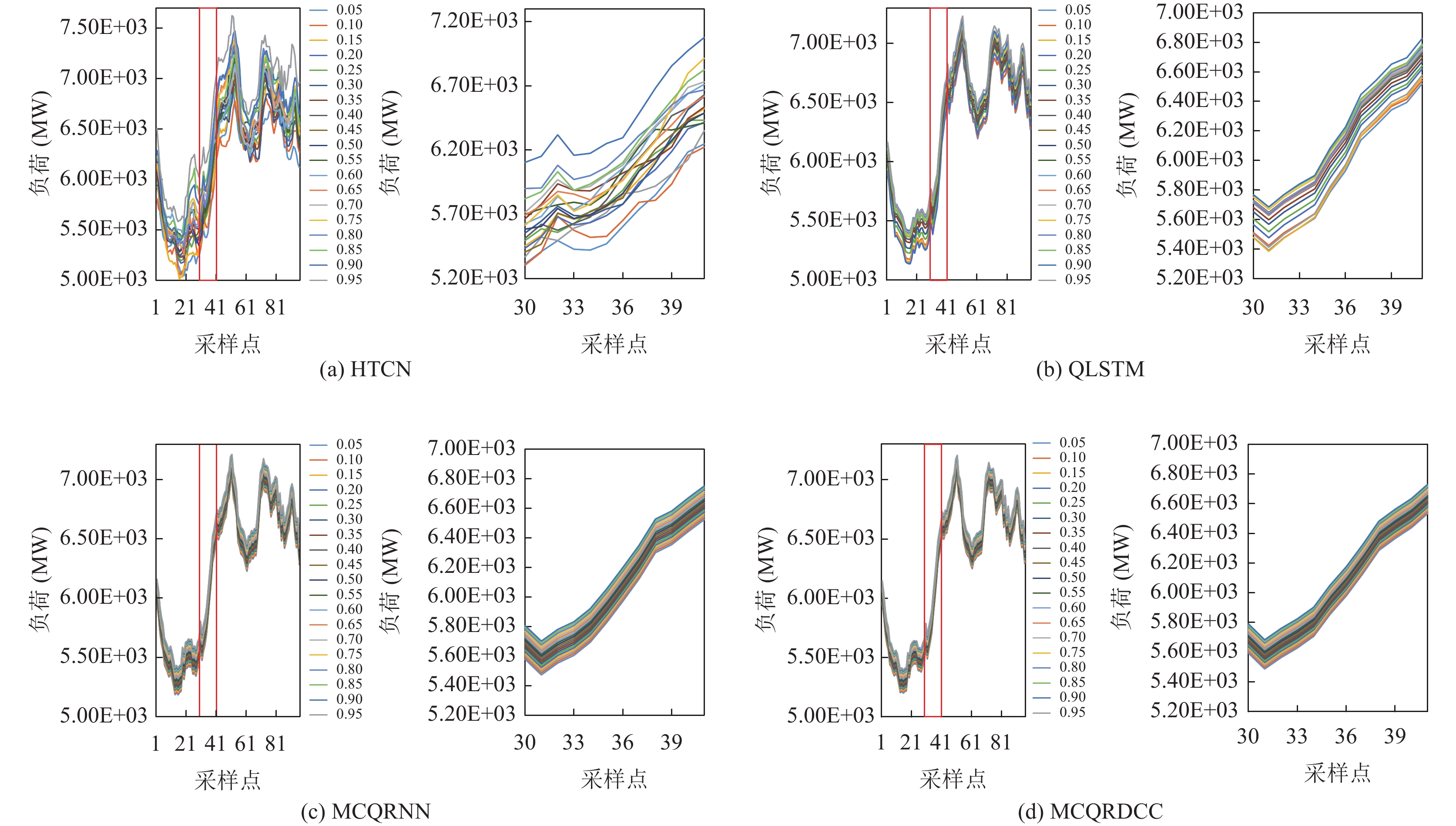
|
图 4 各个模型在各个分位点下的预测曲线 |
(1)相较于HTCN, MCQRDCC的APinball, NWPIW以及CWC分别降低了44.64%, 67.95%以及28.21%, AIS提升了63.90%, 表明MCQRDCC的预测精度远高于HTCN, 这是可能因为HTCN针对每一个分位点都建立一个模型进行预测, 导致各个模型无法全面分析整体的分位数分布, 所以其预测精度低于其他模型. 而HTCN的PICP高于MCQRDCC, 是因为HTCN具有较高的NWPIW, 说明相较于MCQRDCC, HTCN更关注覆盖率而忽视了预测区间的宽度.
(2)相较于QLSTM, MCQRDCC和MCQRNN的整体性能优于QLSTM, 这是因为QLSTM尽管可以全面分析各个分位数的总体分布, 但是QLSTM没有对各个分位数下的回归预测值进行约束, 所以导致其整体预测精度相对较低.
(3)相较于MCQRNN, MCQRDCC的APinball, NWPIW及CWC分别降低了2.11%, 13.79%以及9.31%, AIS提升了10.51%, 说明相较于MCQRNN, MCQRDCC能进一步分析负荷之中的时序信息, 以此提高预测的精确度. 而MCQRDCC的PICP低于MCQRNN的原因在于MCQRDCC比MCQRNN更能拟合负荷变化趋势, 使得预测区间的宽度更狭窄, 从而导致MCQRDCC的覆盖率相对更低.
(4) 图4为各个模型在各个分位点下预测的巴登符腾堡州12月1日负荷曲线, 每个子图中的右图是左图中红色区域的局部放大图, 从图4中, 可以明显发现HTCN的各个分位点下的预测回归值相互交叉, 这也进一步论证了HTCN无法全面分析各个分位数的整体分布; 通过细节图可以发现QLSTM也存在分位数交叉的问题, 这是因为其没有对各个分位点下的预测值进行合适的约束; 而MCQRNN与MCQRDCC对分位数进行了合适的约束, 所以这两种模型不存在分位数交叉的问题.
3.3.2 不同权重处理方式的影响从表2可以发现, 相较于使用指数函数处理权重的MCQRDCC-exp, MCQRDCC的APinball, NWPIW以及CWC分别降低了12.96%, 17.58%以及15.15%,AIS提高了15.62%. 这说明相较于指数函数, 利用ReLU函数处理约束权重的方式能更好地调整MCQDCC之中的约束权重和隐藏层权重矩阵, 以此有效地提高预测的精确度.
|
表 2 对照实验结果(
|
3.3.3 不同网络结构的影响
从表2的实验结果可以发现, 相较于基于全连接网络的MCQRNN-ReLU, 基于DCC的MCQRDCC的APinball, NWPIW以及CWC相对更低, AIS相对更高, 说明相较于全连接网络, DCC能更充分地分析电力负荷之间的时序信息以及内部规律性, 使得预测结果更加符合负荷的变化趋势以及分布范围.
4 结论与展望为了防止分位数交叉, 并充分分析和处理负荷数据之中的时序信息以及其内在规律性, 本研究融合MCQRCC与DCC提出了MCQRDCC模型. 该模型通过将输入划分为约束输入与非约束输入, 并将分位数值设为约束输入, 使得模型的输出随着分位数值的增大而增大, 因此可以防止分位数交叉, 同时, 借助DCC的结构, 使得该模型能较好地分析负荷数据之中的时序信息, 以此进一步提高预测精度. 在真实的负荷数据集上进行了对比实验, 实验结果表明, 相比于对比模型, MCQRDCC的预测精度相对更优, 而且可以防止分位数交叉. MCQRDCC模型虽然取得了相对更优的结果, 但是该模型只选用了历史负荷信息作为输入, 存在一定的局限性, 在未来的工作中, 可能会进一步分析外部因素, 如天气、温度, 对负荷变化趋势的影响, 以此进一步提高预测的精度.
| [1] |
余波. 短期电力负荷预测方法的研究与应用[硕士学位论文]. 南昌: 南昌大学, 2018.
|
| [2] |
王增平, 赵兵, 贾欣, 等. 基于差分分解和误差补偿的短期电力负荷预测方法. 电网技术, 2021, 45(7): 2560-2568. |
| [3] |
Guefano S, Tamba JG, Azong TEW, et al. Forecast of electricity consumption in the Cameroonian residential sector by grey and vector autoregressive models. Energy, 2021, 214: 118791. DOI:10.1016/j.energy.2020.118791 |
| [4] |
Tao XF, Lu Y, Yang XL. Short-term power load probability density forecasting based on a double-layer LSTM-attention quantile regression. Proceedings of the 2021 IEEE 21st International Conference on Communication Technology. Tianjin: IEEE, 2021. 1046–1051.
|
| [5] |
李丹, 张远航, 杨保华, 等. 基于约束并行LSTM分位数回归的短期电力负荷概率预测方法. 电网技术, 2021, 45(4): 1356-1363. |
| [6] |
Kong XY, Li C, Wang CS, et al. Short-term electrical load forecasting based on error correction using dynamic mode decomposition. Applied Energy, 2020, 261: 114368. DOI:10.1016/j.apenergy.2019.114368 |
| [7] |
Hu JM, Heng JN, Wen JM, et al. Deterministic and probabilistic wind speed forecasting with de-noising-reconstruction strategy and quantile regression based algorithm. Renewable Energy, 2020, 162: 1208-1226. DOI:10.1016/j.renene.2020.08.077 |
| [8] |
Zhang S, Wang Y, Zhang YT, et al. Load probability density forecasting by transforming and combining quantile forecasts. Applied Energy, 2020, 277: 115600. DOI:10.1016/j.apenergy.2020.115600 |
| [9] |
Li YP, Guo XF, Gao Y, et al. Short-term power load probabilistic interval multi-step forecasting based on ForecastNet. Energy Reports, 2022, 8: 133–140.
|
| [10] |
Afrasiabi M, Mohammadi M, Rastegar M, et al. Deep-based conditional probability density function forecasting of residential loads. IEEE Transactions on Smart Grid, 2020, 11(4): 3646-3657. DOI:10.1109/TSG.2020.2972513 |
| [11] |
Yang YD, Li SF, Li WQ, et al. Power load probability density forecasting using Gaussian process quantile regression. Applied Energy, 2018, 213: 499-509. DOI:10.1016/j.apenergy.2017.11.035 |
| [12] |
He YY, Liu R, Li HY, et al. Short-term power load probability density forecasting method using kernel-based support vector quantile regression and Copula theory. Applied Energy, 2017, 185: 254-266. DOI:10.1016/j.apenergy.2016.10.079 |
| [13] |
He FF, Zhou JZ, Mo L, et al. Day-ahead short-term load probability density forecasting method with a decomposition-based quantile regression forest. Applied Energy, 2020, 262: 114396. DOI:10.1016/j.apenergy.2019.114396 |
| [14] |
Lin J, Ma J, Zhu JG, et al. Short-term load forecasting based on LSTM networks considering attention mechanism. International Journal of Electrical Power & Energy Systems, 2022, 137: 107818. |
| [15] |
Zhang WY, He YY, Yang SL. Day-ahead load probability density forecasting using monotone composite quantile regression neural network and kernel density estimation. Electric Power Systems Research, 2021, 201: 107551. DOI:10.1016/j.jpgr.2021.107551 |
| [16] |
Chen YT, Kang YF, Chen YX, et al. Probabilistic forecasting with temporal convolutional neural network. Neurocomputing, 2020, 399: 491-501. DOI:10.1016/j.neucom.2020.03.011 |
| [17] |
Huang Q, Wei SY. Improved quantile convolutional neural network with two-stage training for daily-ahead probabilistic forecasting of photovoltaic power. Energy Conversion and Management, 2020, 220: 113085. DOI:10.1016/j.enconman.2020.113085 |
| [18] |
Cannon AJ. Non-crossing nonlinear regression quantiles by monotone composite quantile regression neural network, with application to rainfall extremes. Stochastic Environmental Research and Risk Assessment, 2018, 32(11): 3207-3225. DOI:10.1007/s00477-018-1573-6 |
| [19] |
陈霖, 周宇. 基于T2VNN模型的阀冷系统进阀温度预测. 计算机系统应用, 2022, 31(6): 132-140. DOI:10.15888/j.cnki.csa.008529 |
| [20] |
赵洋, 王瀚墨, 康丽, 等. 基于时间卷积网络的短期电力负荷预测. 电工技术学报, 2022, 37(5): 1242-1251. |
| [21] |
Zhang H, Zhang Z. Feedforward networks with monotone constraints. Proceedings of the International Joint Conference on Neural Networks. Washington, DC: IEEE, 1999. 1820–1823.
|
| [22] |
Xu QF, Deng K, Jiang CX, et al. Composite quantile regression neural network with applications. Expert Systems with Applications, 2017, 76: 129-139. DOI:10.1016/j.eswa.2017.01.054 |
| [23] |
Zhang ZY, Chen HR, Huang YX, et al. Quantile huber function guided TCN for short-term consumer-side probabilistic load forecasting. Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia. Weihai: IEEE, 2020. 322–329.
|
| [24] |
Wang Y, Gan DH, Sun MY, et al. Probabilistic individual load forecasting using pinball loss guided LSTM. Applied Energy, 2019, 235: 10-20. DOI:10.1016/j.apenergy.2018.10.078 |
 2023, Vol. 32
2023, Vol. 32



