图像分辨率作为评估图像质量的重要指标, 其决定了图像纹理细节的精细度. 图像分辨率越高, 意味着图像的纹理细节更清晰, 越有利于后续对图像的分析与处理. 然而, 受限于硬件设备、外部环境、压缩技术等客观条件, 无法获得分辨率非常高的图像, 图像超分辨率技术能有效地解决上述问题. 图像超分辨率技术旨在将低分辨率图像恢复为高分辨率图像, 近年来, 已被广泛应用于公安安防[1]、医学成像[2]和卫星遥感[3]等现实领域, 因此对图像超分辨率技术研究具有显著的意义. 图像超分辨率技术可以分为单幅图像超分辨率重建、多帧图像超分辨率重建和视频超分辨率重建3类, 本文主要研究的是单幅图像超分辨率重建技术.
传统单幅图像超分辨率算法可以分为3类.
(1) 基于插值的算法, 是通过利用核函数根据已知邻近像素的值, 计算出待插入像素的值. 最常用插值算法为双三次(Bicubic)[4]插值算法, 当放大倍数较小时, 利用Bicubic插值算法高效且稳定, 但是放大倍数较大时, 重建图像往往会因为细节的丢失存在明显的模糊失真问题.
(2) 基于重构的方法, 通过利用图像的一些先验知识, 例如图像的局部平滑性、非局部自相似性、稀疏性等特征来构成约束条件, 然后迭代优化估计出最接近低分辨率图像成像模型的逆过程, 从而重建高分辨率图像. 常见的方法有最大后验概率法[5]、迭代反向投影法[6]、凸集投影法[7]等, 相比于插值法, 重构法引入了更多额外信息获得了更好的重构效果, 但是对先验知识利用的不充分或者无法获得足够的先验知识, 所重建的图像存在平滑过度的问题.
(3) 基于学习的方法, 通过利用提前在训练集上训练学习到的低分辨率图像与高分辨率图像间的映射关系来重建高分辨率图像. 常见的有领域嵌入[8]、流形学习[9]、稀疏表示[10]等方法, 在对人脸、文本等图像重建, 这些方法表现出良好的重构效果, 但是其特征提取过程依赖于人工设计, 十分复杂.
近年来, 基于深度学习的方法通过卷积神经网络能够提取丰富的特征, 取得了很好的重建效果, 但目前大多数的超分模型注重加深网络而忽略了对特征信息的区别处理, 使得模型无法有效地恢复图像的纹理细节等高频信息. 同时, 随着网络深度的增加, 特征信息容易在向后传播过程中被削弱或丢失. 此外, 学习LR到HR的映射函数通常是一个不适定问题, 存在无穷多的HR图像可以下采样到相同的LR图像. 因此, 映射函数的解空间可能非常大, 学习到一个性能优异的映射函数非常困难.
本文提出的基于对偶回归和残差注意力机制的图像超分辨率重建网络. 通过对偶回归学习方法, 在原始回归任务基础上引入额外约束, 缩小映射空间. 融合通道和空间注意力机制构造的残差注意力模块能够对不同特征通道信息和相同特征通道不同空间位置信息进行自适应调节, 使网络专注于高频信息的学习. 此外, 融入密集特征融合模块, 增强了特征信息的流动性, 使特征信息在网络传播过程中更不易丢失.
2 相关工作 2.1 基于深度学习的图像超分辨率技术近年来, 随着深度学习技术的快速发展, 利用深度学习技术的图像超分辨率研究取得了显著进展. 2015年Dong等人[11]提出SRCNN (super resolution convolutional neural network), 首次将卷积神经网络(convolutional neural network, CNN)应用到图像超分领域, 结合稀疏编码的方法让CNN网络直接学习HR与LR间的端到端映射, 取得了不错的重构效果. 随后, Dong等人[12]对SRCNN做出改进, 提出FSRCNN (Fast-SRCNN)模型. FSRCNN引入反卷积层, 不需要对原始低分辨率输入图像进行双三次插值, 减少了计算量和输入误差且能够通过改变反卷积层实现不同尺度放大, 同时改变了卷积核大小和网络深度, 使FSRCNN模型获得了更快的收敛速度和更好的重构效果. Lim等人[13]证明了批处理归一化层(batch normalization, BN)丢失了图像的尺度信息, 于是去除了残差块中的BN层提出了EDSR(enhanced deep super-resolution)模型, 节省内存资源的同时在相同的计算资源下能堆叠更多的网络层, 并在每一层提取更丰富的特征信息, 从而提高重建图像质量. Ledig等人[14]首次将生成对抗网络应用到超分辨率重构领域, 提出超分辨率生成对抗网络(super-resolution using a generative adversarial network), 同时提出一种感知损失函数代替均方误差(mean square error, MSE)损失函数, 通过对抗训练, 重构得到的图像更符合人类视觉感知. Haris等人[15]基于迭代反投影方法提出了DBPN (deep back-projection networks)模型, 利用迭代升降采样, 为每个阶段提供误差反馈机制. Zhang等人[16]提出了RCAN (residual channel attention network)模型, 提出了一种通道注意力机制来自适应调节通道特征. Dai等人[17]提出了SAN (secondary-order attention network), 通过使用二阶特征统计量对图像特征信息进行自适应提取.
2.2 通道注意力机制大多数基于CNN的SR模型对LR图像的特征提取过程存在以下两个问题.
(1) 不同特征通道所包含的信息存在一定差异, 采用平等处理的方式不利于重建图像高频细节.
(2) 卷积层中每个滤波器的卷积核仅能使用一个特征通道的局部感受野, 无法利用其他通道的感受野信息.
针对这两个问题, 通道注意力机制利用特征通道之间的相互依赖关系来自适应地对特征通道的权重进行调整, 其结构如图1所示.
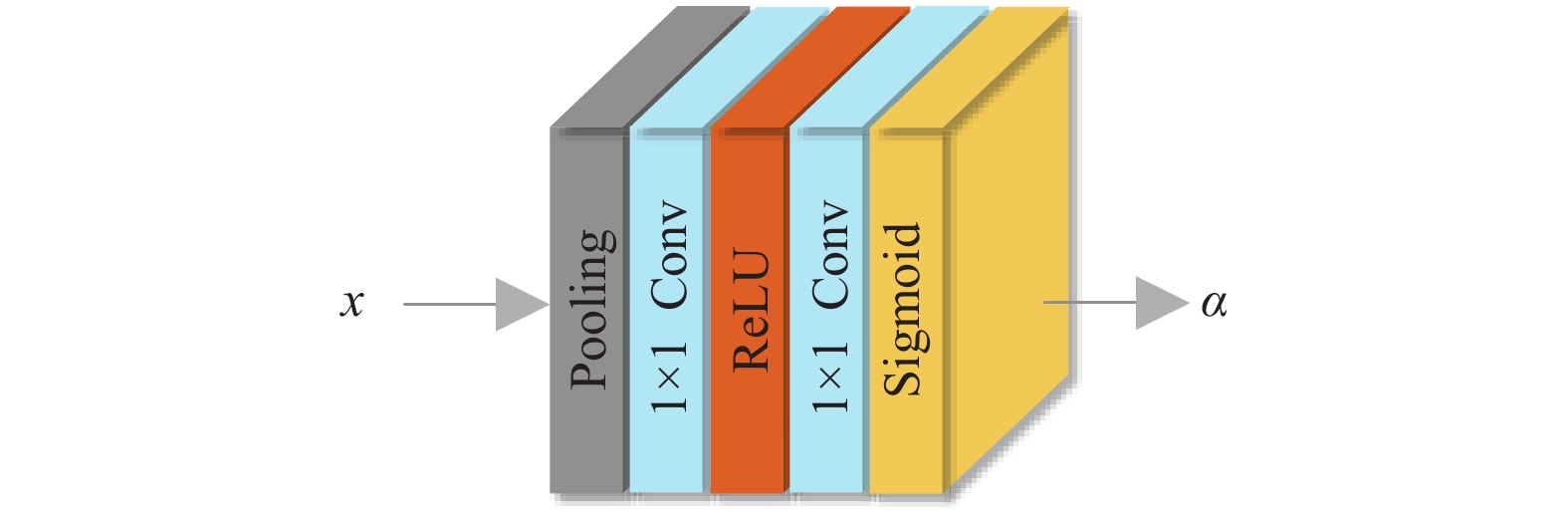
|
图 1 通道注意力模块 |
| zc=HGP(xc)=1H×WH∑i=1W∑j=1xc(i,j) | (1) |
其中,
经过池化层后, 利用Sigmoid激活函数来获取不同特征通道间的依赖关系, 计算方式如式(2)所示:
| α=f(WUδ(WDz)) | (2) |
其中,
最后, 利用
| UCA(x)=α⋅x | (3) |
其中,
同一特征通道所包含的信息因空间位置的不同而不同. 例如, 边缘或纹理区域通常含有更多的高频信息, 而平滑区域则含有更多的低频信息. 为了恢复图像的高频细节, 应该对高频区域给予更多的关注. 受此启发, 空间注意力模块将同一特征通道的低频信息与高频信息分离至不同的滤波器, 使得网络能更专注的学习高频信息, 重建图像具有丰富的高频细节. 其结构如图2所示.
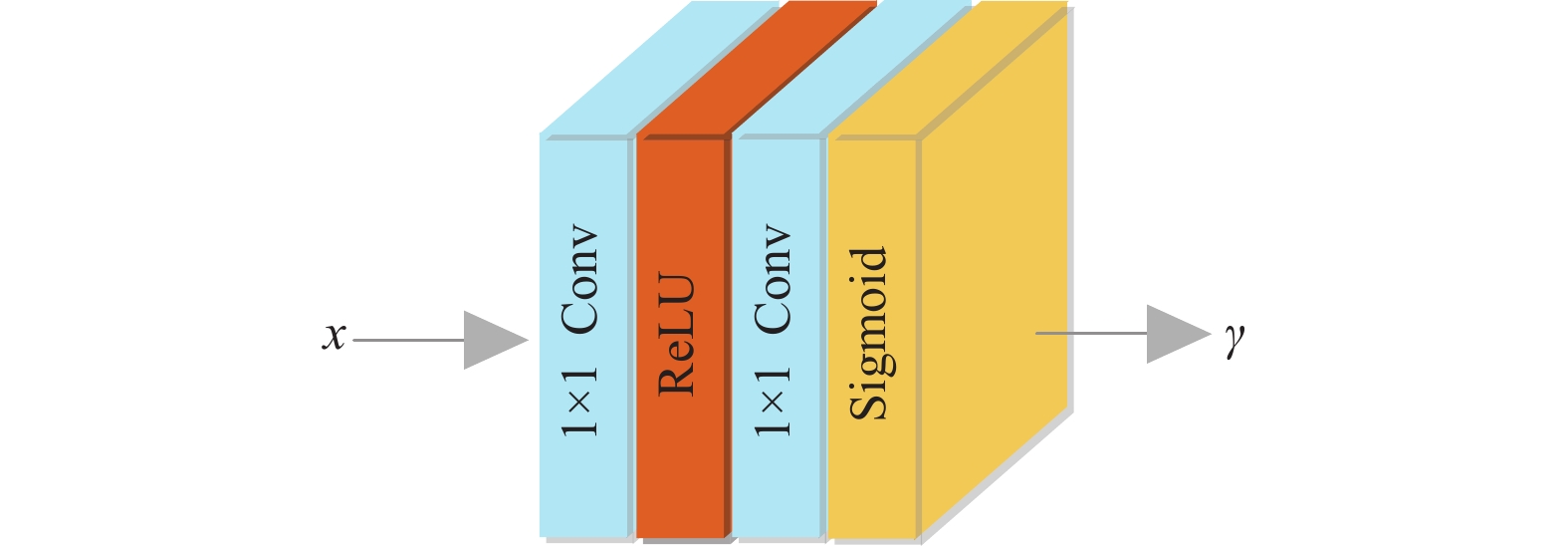
|
图 2 空间注意力模块 |
同样使用
| γ=σ(W2SAδ(W1SA(x))) | (4) |
其中,
最后, 利用
| USA(x)=x⋅γ | (5) |
其中,
本文所设计的网络总体结构基于U-Net网络[18], 网络结构图如图3所示, 整体网络结构分为两个部分: 原始回归网络和对偶回归网络, 原始回归网络是一种渐进上采样结构, 首先经过log2(s)次下采样, 进行初始特征提取, s表示超分任务的比例因子, 接着经过log2(s)次上采样, 进行深层特征提取, 上采样过程中通过融合下采样过程生成的同尺寸特征图, 再次进行特征提取, 有效增强了网络的学习能力. 最后将重建的超分辨率图像输入至对偶回归网络, 对偶回归网络将重建的超分辨率图像进行下采样操作后与原始LR图像进行对比. 该过程为LR-HR的映射学习引入了额外约束, 有效约束了映射空间.
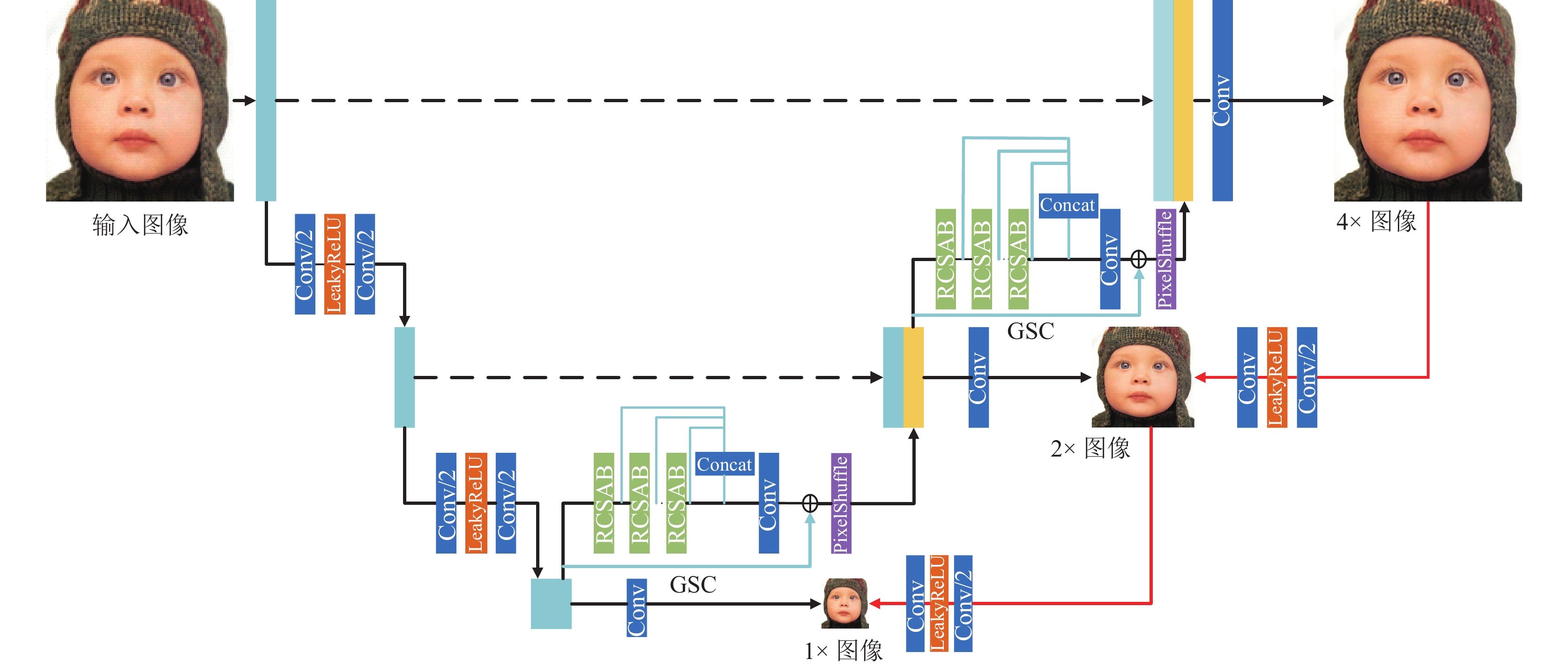
|
图 3 整体网络结构 |
3.2 原始回归网络
原始回归网络(图3中的黑线部分)由上采样和下采样两个模块组成, 下采样基本块由步长为2的
对偶回归[19]学习在语言翻译任务中首次被提出, 简单有效地提高了翻译效果. 随后应用于图像翻译[20]、图像处理[21]等监督学习任务中, 学习模型的性能均得到一定程度的提升.
对偶回归学习通过对偶模型学习与原始模型的相反映射, 使得原始模型和对偶模型形成一个闭环, 二者将生成的信息互相反馈来进行训练. 模型框架如图4所示.
在图像超分辨率任务中, 原始模型用于预测生成SR图像, 对偶模型用于对生成的SR图像进行下采样, 利用对偶模型生成的图像
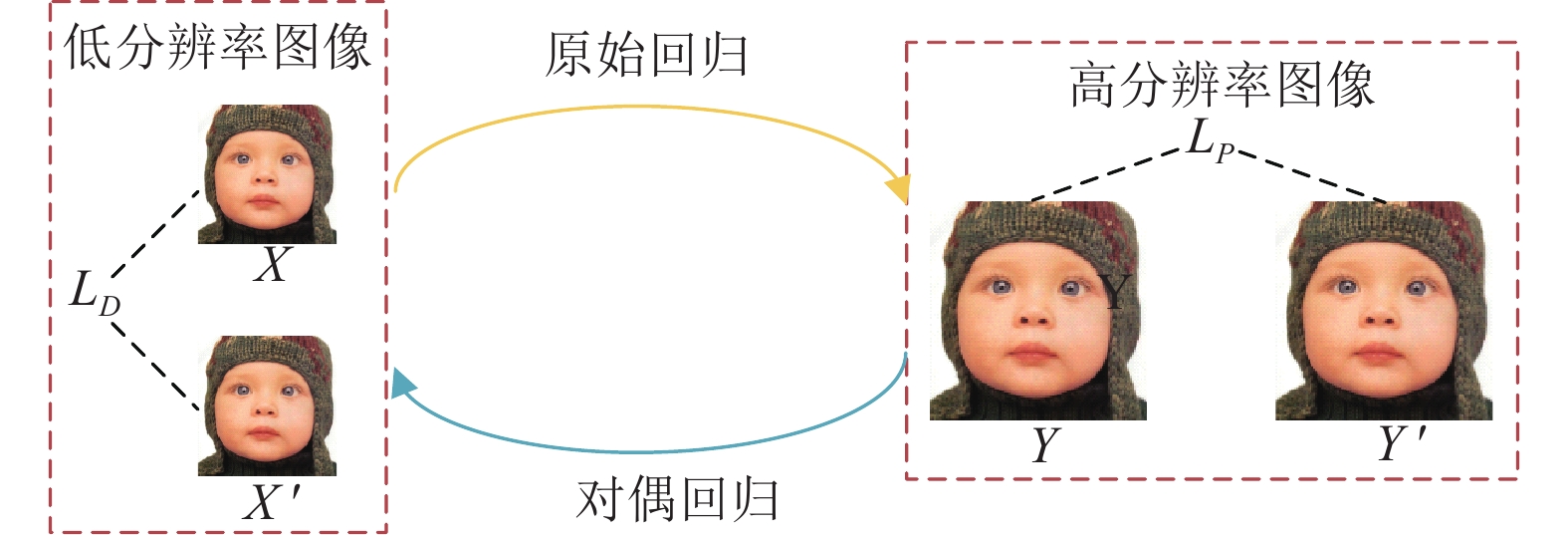
|
图 4 对偶回归模型 |
对偶回归网络(图3中的红线部分), 主要任务是学习下采样操作, 原始模型利用原始任务训练过程中学习到的信息和对偶模型提供的反馈信息迭代优化. 对偶模型的下采样基本块和原始模型下采样基本块结构相同, 由步长为2的
随着网络层数的加深, 网络可以进行更加复杂的特征提取, 但同时伴随着模型容易过拟合和梯度消失与爆炸等问题的出现, 针对这些问题, He等人[22]提出残差网络结构, 由于残差网络结构所需要学习的特征映射只是输入与输出的残差, 与不引入残差学习的网络结构所要学习特征映射相比更加简单, 大大提升了深层次网络模型的性能.
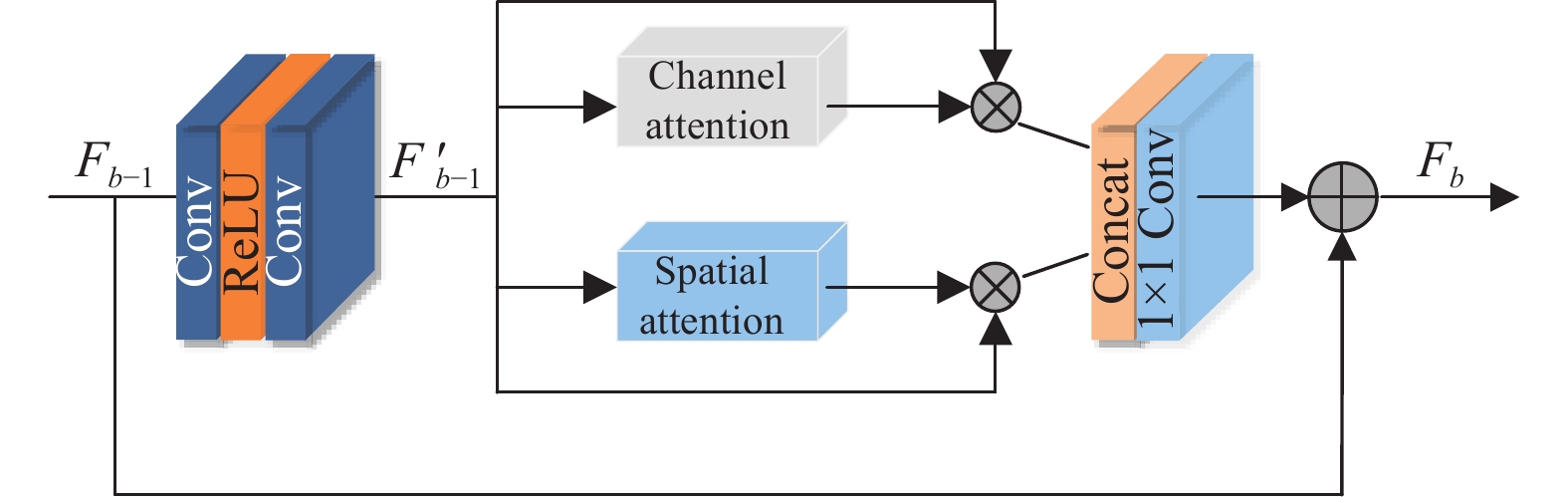
残差学习最初是针对分类、检测等高级计算机视觉任务提出, 直接应用超分辨率等低级计算机视觉任务效果不佳. 本文基于EDSR模型中使用的残差模块并融合了通道和空间注意力机制, 构建了RCSAB, 有效提取特征图像中的高频信息, 其结构如图5所示.
|
图 5 RCSAB模块 |
第
| Fb=Hb(Fb−1) | (6) |
其中,
首先, 将
| F′b−1=W2Rδ(W1R(Fb−1)) | (7) |
其中,
其次, 将
| Fb=Wc[UCA(F′b−1),USA(F′b−1)]+Fb−1 (8) $ | (8) |
其中,
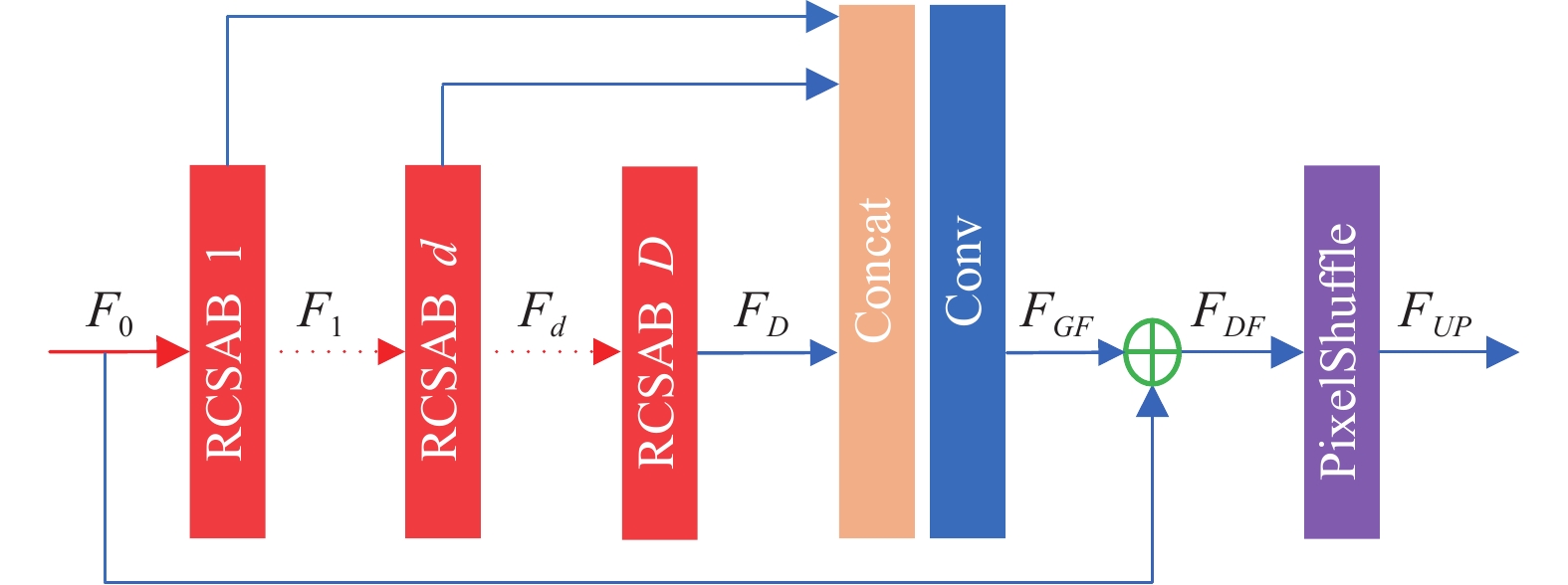
经过观察, 通过简单地堆叠更多地残差注意力模块不能获得更好的重建性能, 为了解决这一问题, 设计了一种密集特征融合模块. 其结构如图6所示, 该模块通过融合所有特征信息来提取全局特征, 有效地解决了特征信息在传播过程中的丢失问题, 提高了网络学习效率.
|
图 6 密集特征融合模块 |
首先, 将所有RCSAB的输出进行拼接融合, 对融合后的特征进行特征提取获得全局特征
| FGF=WGF([F1,⋯,Fd,⋯,FD]) | (9) |
其中,
接着, 经过全局残差连接获得最终输入至亚像素卷积层的特征
| FDF=F0+FGF | (10) |
其中,
损失函数主要由原始重建网络的损失及对偶回归网络的损失两部分组成. 给定一组
| L=N∑i=1LP{P(xi),yi}+λLD{D(P(xi)),xi} | (11) |
其中,
实验采用DIV2K和Flickr2K数据集组成的DF2K数据集作为训练集. 通过随机截取RGB输入低分辨率图像的48×48大小的图像块和对应的高分辨率图像块配对作为训练数据. 测试集采用Set5, Set14, BSD100, Urban100此外, 本文使用数据增强技术[23] , 将训练数据随机旋转90°, 180°, 270°以及平移和翻折.
评价指标采用单幅图像超分辨率方法常用的两种客观评价指标, 分别是峰值信噪比(peak signal-to-noise ratio, PSNR)和结构相似性(structure similarity, SSIM).
PSNR是有损变换中最常用的重构质量度量指标之一. 对于图像的超分辨率, PSNR是通过图像间的最大像素值和均方误差来定义, 计算方式如式(12)所示:
| PSNR=10⋅lg(L2MSE) | (12) |
其中,
SSIM基于亮度、对比度和结构的比较, 计算方式如式(16)所示:
| Cl(U,V)=2μUμV+C1μU2+μV2+C1 | (13) |
| Cc(U,V)=2σUσV+C2σU2+σV2+C2 | (14) |
| Cs(U,V)=σUV+C3σUσV+C3 | (15) |
| SSIM(U,V)=Cl(U,V)×Cc(U,V)×Cs(U,V) | (16) |
其中,
本文的实验基于PyTorch框架, 使用2块 NVIDA GeForce 2080Ti 显卡进行网络训练, 每块显存容量为10 GB. 优化器采用 Adam 优化器,
为了研究对偶回归损失权重对网络模型性能的影响, 在×4模型中分别将
|
表 1 |
从表1可以看出,
为了研究残差注意力模块和密集特征融合模块的有效性, 将残差模块融合不同注意力模块和密集特征融合模块进行对照实验. 实验数据如表2所示. 其中Baseline为没有融合任何模块的残差模块.
| 表 2 残差注意力模块与密集特征融合模块对照实验数据 |
从表2前4列或后4列可以看出, 融合了通道与空间注意力模块的残差模块测得的PSNR数值最高, 组3相比于Baseline提升了0.24 dB, 组7相比于组4提升了0.23 dB, 证明了本文的残差注意力模块的有效性. 对比前4列和后4列可以看出, 融入密集特征融合模块后, 对于×4模型虽然参数量提升了2.21 M, 但是PSNR值均得到了很大提升, 以组7和组3为例, 组7相较于组3的PSNR值提升了0.12 dB, 验证了密集特征融合模块的有效性.
4.4 与已有算法的对比在相同实验设置下选取了Bicubic、ESPCN、SRCNN、FSRCNN、SRGAN、EDSR、DBPN、RCAN、SAN与本文算法进行对比, 在Set5、Set14、BSD100、Urban100 四种基准数据集上进行测试, 放大倍数分别为: ×4, ×8. 实验结果如表3所示.
从表3可以看出, 在4倍尺度放大时, 本文算法所重建图像的客观评价指标具有明显优势, 在8倍尺度放大时, 虽然由于尺度因子的增加各算法性能均有所下降, 但从客观结果表明, 本文算法性能仍优于其他算法.
同样从主观视觉角度进行对比, 本文分别从Set5、Set14以及Urban100数据集选取了3张图片并对特定区域进行放大, 结果如图7–图9所示.
| 表 3 不同算法的PSNR和SSIM数值比较 |

|
图 7 “Set5-butterfly” ×4主观视觉效果对比 |

|
图 8 “Set14-zebra” ×4主观视觉效果对比 |

|
图 9 “Urban100-Img005” ×4主观视觉效果对比 |
从图7和图8看出, 本文方法构建的图像相较于其他方法更加清晰, 色彩与纹理细节更贴近真实图像. 此外, 观察图9可以看出, 相较于Bicubic插值算法, SRCNN算法准确地预测了窗沿方向, 但存在严重的伪影问题, FSRCNN有效减轻了伪影现象, 但混淆了窗沿平行线方向, 其他对比算法也均存在不同程度的混淆现象与伪影问题, 相比较而言, 本文算法预测的窗沿方向最准确, 同时有效解决了伪影问题.
5 结论与展望本文设计了一种基于对偶回归和残差注意力机制的单幅图像超分辨率网络结构, 对偶回归学习策略为LR-HR的映射学习引入了额外约束, 减少了可能的映射空间. 通过融合通道注意力模块和空间注意力模块至残差模块中对特征信息进行全局和局部调节, 有效提取了特征信息中的高频信息. 最后, 密集特征融合模块增强了特征信息流动性, 有效解决了网络传播过程中特征信息的丢失问题. 实验结果表明, 无论从客观指标评价还是主观视觉效果对比, 本文算法的重建效果均优于对比算法.
| [1] |
Kouame D, Ploquin M. Super-resolution in medical imaging: An illustrative approach through ultrasound. Proceedings of 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Boston: IEEE, 2009. 249–252.
|
| [2] |
Masutani EM, Bahrami N, Hsiao A. Deep learning single-frame and multiframe super-resolution for cardiac MRI. Radiology, 2020, 295(3): 552-561. DOI:10.1148/radiol.2020192173 |
| [3] |
Zhang L, Nie JT, Wei W, et al. Deep blind hyperspectral image super-resolution. IEEE Transactions on Neural Networks and Learning Systems, 2020, 32(6): 2388-2400. |
| [4] |
Keys R. Cubic convolution interpolation for digital image processing. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1981, 29(6): 1153-1160. DOI:10.1109/TASSP.1981.1163711 |
| [5] |
Irani M, Peleg S. Motion analysis for image enhancement: Resolution, occlusion, and transparency. Journal of Visual Communication and Image Representation, 1993, 4(4): 324-335. DOI:10.1006/jvci.1993.1030 |
| [6] |
Yang X, Zhang Y, Zhou DK, et al. An improved iterative back projection algorithm based on ringing artifacts suppression. Neurocomputing, 2015, 162: 171-179. DOI:10.1016/j.neucom.2015.03.055 |
| [7] |
Stark H, Oskoui P. High-resolution image recovery from image-plane arrays, using convex projections. Journal of the Optical Society of America A, 1989, 6(11): 1715-1726. DOI:10.1364/JOSAA.6.001715 |
| [8] |
Rahiman VA, George SN. Single image super resolution using neighbor embedding and statistical prediction model. Computers & Electrical Engineering, 2017, 62: 281-292. |
| [9] |
江俊君. 基于一致流形学习的人脸超分辨率算法研究[博士学位论文]. 武汉: 武汉大学, 2014.
|
| [10] |
Yang JC, Wright J, Huang T, et al. Image super-resolution as sparse representation of raw image patches. Proceedings of 2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008. 1–8.
|
| [11] |
Dong C, Loy CC, He KM, et al. Image super-resolution using deep convolutional networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307. DOI:10.1109/TPAMI.2015.2439281 |
| [12] |
Dong C, Loy CC, Tang XO. Accelerating the super-resolution convolutional neural network. Proceedings of 14th European Conference on Computer Vision. Cham: Springer, 2016. 391–407.
|
| [13] |
Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu: IEEE. 2017. 136–144.
|
| [14] |
Ledig C, Theis L, Huszár F, et al. Photo-realistic single image super-resolution using a generative adversarial network. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 105–114.
|
| [15] |
Haris M, Shakhnarovich G, Ukita N. Deep back-projection networks for super-resolution. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 1664–1673.
|
| [16] |
Zhang YL, Li KP, Li K, et al. Image super-resolution using very deep residual channel attention networks. Proceedings of the 15th European Conference on Computer Vision (ECCV). Munich: Springer, 2018. 294–310.
|
| [17] |
Dai T, Cai JR, Zhang YB, et al. Second-order attention network for single image super-resolution. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 11057–11066.
|
| [18] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation. Proceedings of 18th International Conference on Medical Image Computing and Computer-assisted Intervention. Cham: Springer, 2015. 234–241.
|
| [19] |
Zhu S, Cao RS, Yu K. Dual learning for semi-supervised natural language understanding. IEEE/ACM Transactions on Audio, Speech and Language Processing, 2020, 28: 1936-1947. |
| [20] |
Zhu JY, Park T, Isola P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks. Proceedings of the 2017 IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 2242–2251.
|
| [21] |
Wang L, Li D, Zhu YS, et al. Dual super-resolution learning for semantic segmentation. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 3773–3782.
|
| [22] |
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [23] |
Li Z, Yang JL, Liu Z, et al. Feedback network for image super-resolution. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3862–3871.
|
 2023, Vol. 32
2023, Vol. 32



