比特币(Bitcoin)[1]是许多现有分布式账本系统中最典型的例子, 其背后被称作“区块链(blockchain)”的分布式共识技术也成为了学界及工业界研究的目标. 其核心目的是让用户在没有可信第三方的情况下, 就公共账本信息达成共识. Nakamoto共识, Bitcoin的核心共识算法, 使用工作量证明(PoW)算法使节点参与Bitcoin系统并执行哈希计算操作来确保整个系统共识的安全性. Nakamoto共识宣称只要系统中恶意矿工的算力不超过全网总算力的50%, 那么该系统就是有效安全的, 不过后来的工作揭示了Nakamoto共识的一些缺点和潜在的攻击方案, 例如, 自私挖矿、顽固挖矿、日蚀攻击等[2-6].
除了这些攻击和漏洞之外, Nakamoto共识的可用性相较于当前的线上交易需求来说也很差——其平均每秒钟只能处理7笔交易, 且平均交易确认延迟高达1小时[7]. 另外, PoW型区块链还面临去中心化的挑战. PoW的leader选举已经显现出明显的“中心化倾向”与“不公平”(例如, 前4大Bitcoin矿池公司的总算力已超过全网算力的50%[8]), 过度的中心化也非常容易导致一些安全性问题. 传统的Byzantine fault tolerance (BFT)类协议则是完全去中心化的[9], 但它们限制节点自由加入或退出系统, 并且很容易被distributed denial of service(DDoS)攻击破坏. 目前, 许多高性能的共识协议都是基于以上两大类共识算法(PoW与BFT), 然而它们都或多或者存在一些缺陷和不足, PoW类方案则是把系统效率和安全性过度耦合造成性能瓶颈; 而BFT则无法适用于大网络多节点共识环境, 且需要额外的节点验证机制才能防止例如DDoS、Sybil类型的恶意攻击.
为了解决上述问题, 本文介绍PoM共识算法及基于PoM的第一个分布式账本协议——Achain. PoM将PoW共识和leader选举解耦, 大大削弱了安全性和出块间隔间的相互约束, 提高了系统吞吐量, 降低了交易延迟. 并且在相同的网络环境下, Achain与Bitcoin一样安全.
Achain的核心算法——PoM机制主要分为两部分: leader选举和消费节点PoW. 在leader选举中, 消费节点通过向他支持的候选节点提交合法交易数据来表示他在leader选举中支持此候选节点, 其中, 合法交易数据将被视为“选票(vote)”. 只有收集了预定数量的vote的候选节点才能成为leader节点. 在消费节点生成vote时, 其必须执行相应的消费节点PoW, 否则此vote将是非法的. Achain协议提供了一组激励机制来匹配PoM使得恶意的攻击在统计学意义上是无利可图的. 此外, 即使有不理智的攻击者坚持攻击, 他的攻击也不会比攻击相同设置(例如, 相同的PoW难度和自然分叉率)下的PoW型区块链的难度要小, 因为PoW和PoM具有相同的防御机制和防御特性. 而且Achain协议拥有比PoW类区块链更大的可控空间(例如, 可以通过调整PoM的一些参数来抑制自然分叉率). 总的来说, PoM实现了PoW型区块链的安全性, 其还可以有效抑制区块传输延迟对区块间隔和安全性的约束, 进而优化了Achain协议的吞吐量、交易延迟、去中心化、公平性以及能耗. 同时体现了消费节点和市场在leader选举方面的影响(而非完全的数学意义上的随机化). 并且我们还提供了一种针对Achain的优化方案——FastAchain, 其降低了系统节点的存储成本, 提升了系统的可扩展性和去中心化程度.
此外, 本文通过omnetpp模拟了一个p2p实验网络, 其具有30 Mb/s的带宽和100 ms的平均延迟, 并包含超过1000个分布式对等节点. 实验检测了协议的各个参数对Achain 性能的影响. 结果表明, 在大多数参数设置下, Achain可以实现出色的吞吐量和交易延迟(超过4000 TPS以及10–40 s的交易延迟). 在相似的网络环境下, Achain的吞吐量达到了10倍于Bitcoin-NG[7]、5倍于ByzCoin[10]以及4倍于Algorand[11]的水平, 交易延迟也达到了与Algorand相同的水平, 并且只有Bitcoin-NG和ByzCoin的一半. Achain系统中上链的交易在等待3个区块后的回滚率为0%, 且几乎没有高度超过1的分叉, 这说明该方案具有较高的安全性和可靠性. 并且Achain在所有参数设置下都保持了出色的去中心化水平.
1 相关工作及与Achain的对比不可否认, 当前的区块链设计还存在诸多难题, 其中讨论最多的便是可扩展性(scalability)问题. 为此, 学界和工业界还提出了许多解决方案, 例如Bitcoin-NG[7]和ByzCoin[10]. Bitcoin-NG引入了“key block”和“microblock”的概念, key block使用经典PoW算法进行leader选举, microblock用于存储交易. 并且为了防止双花攻击, Bitcoin-NG引入了“毒药交易”机制. ByzCoin则是基于Bitcoin-NG和practical Byzantine fault tolerance (PBFT)协议[9]的进一步改进. 它将leader选举和交易确认分开, 并使用 PBFT委员会的认证来立即确认交易. ByzCoin实现了与Paypal相当的吞吐量, 确认延迟为15–20 s. 然而, 它们仍然将PoW与leader选举联系耦合起来, 并且引入了除PoW外的复杂共识机制(例如, PBFT), 这将在极端情况下大大降低系统效率. 此外, 对PoW的一些修改(例如, proof-of-stake (PoS)、delegated proof-of-stake (DPoS)[12])并没有改变PoW的本质. 相反, Achain的PoM机制虽然仍然需要执行PoW操作, 但PoM将PoW操作分散到消费节点级别, 这解耦了系统的安全性和效率, 使两者均得到了提升.
Algorand[11]中则首次采用了VRF&BFT机制, 它使用可验证的随机数来确保leader节点选举的数学公平性. 类似地, 随后也有很多混合共识协议被提出[13-15], 它们大都基于PBFT算法, 并融合了RAFT[16]、分片(sharding)等技术, 以此实现扩展性的提升. 与上述协议不同的是, 本文的PoM并未使用复杂的混合共识机制, 而是基于新型PoW算法辅以激励策略在候选节点之间实现了激励相容, 并考虑到市场因素和消费节点的偏好.
还有许多学者提出了完全不同于PoW的新型共识算法设计, 例如PoB (proof-of-burn)[17]和PoR (proof-of-reputation)[18]. 虽然两者都实现了可观的性能表现, 但前者要求节点将代币(token)发送到一个“不可使用的(unspendable)”交易地质进行“销毁”, 这浪费了太多的算力和虚拟代币, 后者则以中心化为代价实现了对于“超过51%恶意算力攻击”的抵御.
区块链可扩展性的最终目标是“无限扩展(scale-out)”——网络规模扩大到任何程度都不会影响系统的性能, 甚至系统性能可以随着验证节点的增加而提升. 目前有两种主要类型的解决方案: 链下解决方案和分片[19-23]. 前者是利用区块链的特性, 提出不同应用场景下可行的链下解决方案. 然而, 这样的解决方案本质上超出了共识算法的控制范围, 且其安全性不受到共识算法的保护. 分片技术源于分布式数据库的思想, 它通过牺牲部分一致性来提升可扩展性. 因此, 这两种方案也都没有完全突破性能、安全性和去中心化的三角.
2 模型与问题定义在本节中, 首先对系统模型进行描述, 然后对要解决的问题进行定义.
2.1 模型(1)系统模型: 本文假设hash函数作为随机预言机(oracle), 任何节点都可以进行PoW操作, 并且这个过程在单位时间内的所有消耗(例如电力消耗、设备折旧、时间成本等)对于任何节点都是均等的, 任何节点都可以用同样的资金购买获得同等质量的“PoW计算服务”. 本文的系统具有标准密码学假设(例如, 公钥签名、集体签名等). 任何节点都可以获得正确且合法的创世区块. 系统中的任何节点都有一个固定的身份: 消费者(或称消费节点)或候选者(或称候选节点). 消费节点产生交易并提交给候选节点, leader选举将在候选节点中选出一个当前轮的leader (如果没有分叉). 然后leader节点打包并广播合法区块. 此外, 所有节点也根据属性(诚实和恶意)分为诚实节点和恶意节点.
(2)网络模型: 网络中共有
(3)威胁模型: 协议容忍所有恶意节点的计算能力不到全网的
(4)消费节点偏好模型: 消费节点对于候选节点的选择都有一定的偏好(这是其他区块链协议没有考虑的). 并记
在第2.1节的模型下, 本文的协议方案需要实现高吞吐量、低交易延迟、一定的可扩展性、低候选阈值(利于去中心化)、简单性、有效性和安全性, 具体说明如下.
(1)有效性和安全性: 诚实消费节点的交易最终会得到Achain区块链的确认; Achain可以抵御双花攻击(又称51% 攻击)、Sybil攻击以及single point of failure (SPOF)类攻击.
(2)吞吐量: 当网络的规模(即节点数)、带宽等系统参数确定后, 将单位时间内系统确认的平均交易数定义为系统的吞吐量. Achain的目标则需要最大限度地提高系统吞吐量.
(3)交易延迟: 当网络的规模、带宽等系统参数确定后, 交易延迟定义为从交易产生(即消费节点发起交易)起直到交易最终在区块链上被确认所经过的时间. Achain的目标则需要尽可能地减少交易延迟.
(4)可扩展性: Achain目标需要解决PoW型共识中安全性和可扩展性之间的冲突和耦合, 并保证在不牺牲安全性的情况下尽可能提高可扩展性. 此外, 方案应该能够嵌入其他分片协议和第2层协议(例如闪电网络[24]).
(5)候选节点门槛和去中心化: 在Achain中, 候选节点承担验证者的义务, 这里的候选节点的门槛意味着加入共识机制的条件(例如, 加入许可的区块链需要所有其他成员的批准). Achain需要尽可能降低此门槛以实现更高度的去中心化, 同时确保不牺牲安全性.
(6)消费节点偏好: 令
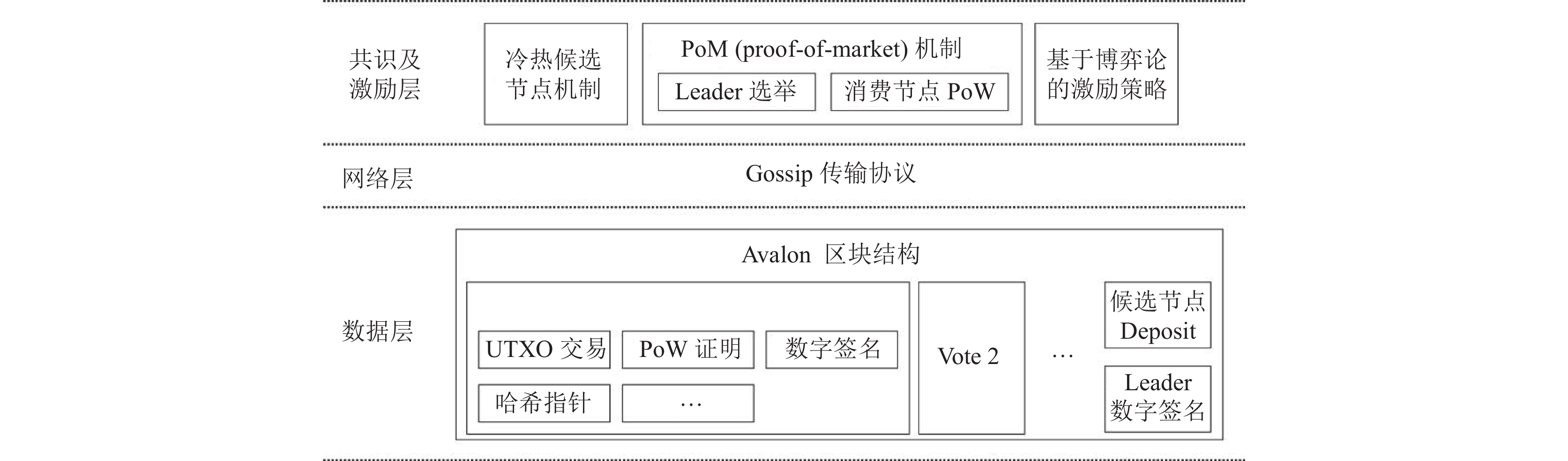
本节详细介绍Achain协议方案的设计内容, 图1展示了Achain的分层系统架构. 在数据层, Achain的区块链的数据结构和传统的Bitcoin类似, 但原本的交易信息被vote信息替代. Achain区块链由一个个Achain区块构成, Achain区块则包括vote信息、候选节点deposit信息、leader数字签名等, 其中vote信息还包括: unspent transaction outputs (UTXO)交易信息、消费节点PoW证明、消费节点数字签名、前块哈希指针等. 在网络层, Achain采用了Gossip传输协议, 保证消息在分布式网络中的可靠广播. 在共识和激励层, PoM机制作为Achain的核心共识算法被提出, 并辅以基于博弈论的激励策略以及冷热候选节点机制完成了共识激励的任务.
|
图 1 Achain系统架构图 |
各层级模块之间的关系如下, 系统中的所有候选节点运行Achain的leader选举模块; 同时消费节点执行消费节点PoW模块, 消费节点PoW需要输入UTXO交易信息, 其可输出合法的vote信息, 消费节点将合法的vote信息提交给相应的候选节点(此过程中, 博弈论激励模块和冷热候选节点机制也在同时起作用, 激励节点执行完成上述步骤); leader选举结束后成为leader的节点, 将收集到的vote信息整合为合法的Achain区块数据, 并调用Gossip传输协议广播此区块. 至此, 一个新的合法Achain区块在系统中被各节点达成共识.
3.1 市场证明(PoM)机制本节将介绍PoM共识机制, 它包括vote机制、leader选举和区块广播. 消费节点的PoW构成了vote机制. 与经典的leader选举不同, 这里采用了“一票多投(one voter for multiple investments, OVMI)”机制, 其消除了PoW机制对于系统吞吐量的限制并简化了Achain协议. 消费节点使用他们提交的交易数据作为vote来选择他们最喜欢的候选节点作为leader节点, 而消费节点PoW产生的成本可以过滤掉恶意节点.
3.1.1 候选节点的leader选举图2展示了Achain系统中的选举过程, 具体内容如下.
1) 首先, 在一轮leader选举中, 所有参加选举的候选节点“冻结”其本地账本中的一定数量的数字资产
2) 候选节点可以在前一轮leader节点广播区块后立即进行下一轮leader选举, 并将其deposit的
在leader选举中隐藏了很多细节, 这里, 首先描述候选节点需要收集的交易金额阈值, 记其为

|
图 2 Achain的leader选举过程示意图 |
3.1.2 消费节点PoW方案
当候选节点在执行leader选举时, 消费节点则需要通过消费节点PoW输出相应的vote数据, 并在leader选举中提交给特定的候选节点, 以此保证Achain系统中leader选举过程的正常执行. 具体内容如下.
(1) 消费节点提交给候选节点的消息结构为: 消费节点的数字签名、交易信息、最新区块的哈希信息(用于防止节点预先执行消费节点PoW)、支持的候选数量和随机数
(2) 消费节点必须对其vote进行PoW操作, 具体地, 调整随机数
(3) 一票多投(OVMI): Achain系统允许消费节点在一轮选举中将不同的vote提交给多位候选节点, 只要他们提交的vote是合法的.

|
图 3 消费节点的合法vote结构图 |
这里解释一下消费节点PoW难度, 记其为
定义1. 消费节点PoW难度, 记为
例如, 如果一笔交易的金额是10单位代币, 并且
与PoW型区块链一样, Achain 中消费节点的算力也会不断变化, 因此
实际上, PoM机制将挖矿与leader节点选举脱钩, 避免了算力的中心化和恶性的挖矿竞争.
3.2 激励机制消费节点PoM不足以使Achain系统是激励相容的, 因此需要引入配套的激励机制. 运用博弈论是设置合理的激励机制的关键, 本节介绍Achain协议的整体激励机制.
除了前面提到的交易金额的阈值
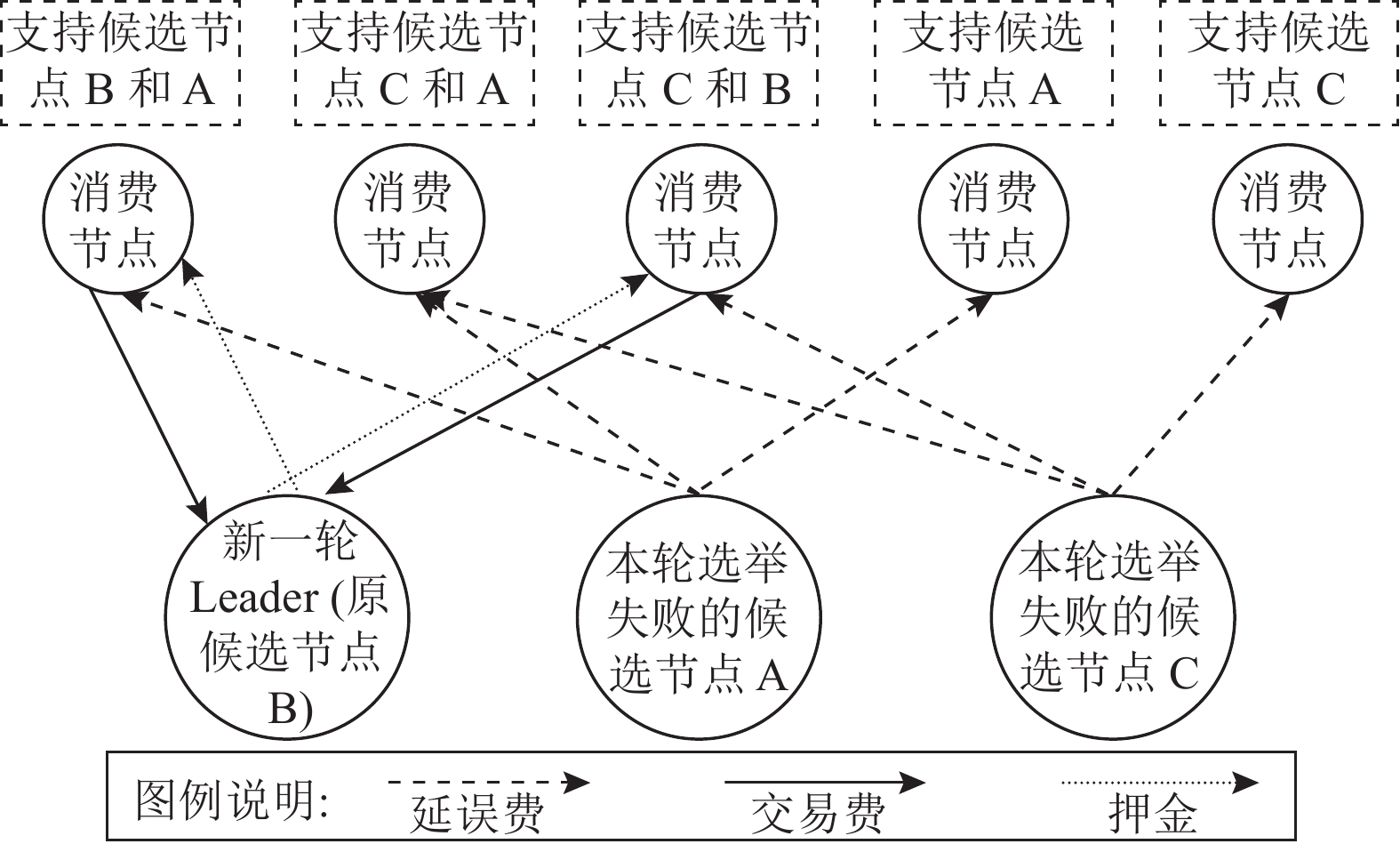
|
图 4 Achain的激励机制示意图 |
(1) 交易费率
(2) 延误费率
(3) 这里的
| $ (n - 1){k_d} + \frac{{{S_0}}}{{f({S_0})}} < {k_t} < \frac{{n(n + 1)}}{{n - 1}}{k_d} + \frac{{{S_0}}}{{f({S_0})}} $ |
以及:
| $ {k_d} < \frac{1}{{{d_c}}} $ |
其中,
交易费和延误费按照以下规则支付.
(1) Achain协议要求候选节点在决定参加选举时向全网广播带有签名的deposit信息. 如果候选节点获胜, 则立即将收集到的交易打包, 并按交易金额的比例向每个支持此leader的消费节点支付相应的deposit, 否则此交易集被视为非法的.
(2) 由于全网对失败候选节点收集的交易并不会达成共识, Achain协议采用“索赔”机制来分配延误费. 合法vote本身可以被视为一种“支票”, 当此“支票”在未来被用于支付时, 相应的金额将从相应的失败候选帐户中自动扣除.
(3) 为防止候选节点资金短缺而无法支付延误费, Achain协议规定候选节点在每次选举中必须冻结一定数额的“预付延误费”. 如果候选节点获胜, 则解冻, 否则等待几轮后自动解冻. 但只要候选节点处于选举状态, 那么就必须保持一定数额的“预付延误费”.
为了让延误费对Achain有正向的激励作用, 恶意节点不能从延误费中获利, 这就要求节点在消费节点PoW上的成本(投资)的数学期望大于他可以获得的延误费, 即,
在前面对Achain的描述中, 所有候选节点都可以同时参与leader选举. 但是, 这种方法分散了消费节点的计算能力, 并可能削弱Achain的安全性. 因此, Achain协议引入热冷候选节点机制.
(1) Achain系统的运行过程按照时间
(2) 在每个周期
(3) 消费节点只能向热候选节点提交合法交易, 除非消费节点判断热候选节点是恶意的或离线的.
(4) 当消费节点判断热门候选节点是恶意的或离线时, 消费节点可以提交合法vote给冷候选节点.
这里解释一下冷热候选方案的一些细节. 首先, 每轮只选出3个热门候选, 以确保所有消费节点PoW算力都集中在这3个候选上. 因此, 只要恶意节点的算力不超过全网算力(所有消费节点算力)的1/3, 他就无法进行双花攻击. 随机选择热门候选节点的过程在Algorand[11]的委员会选举方案中有详细说明, 该方案使用全局不可伪造且可验证的随机数来防止作弊. 关于消费节点发现候选离线的方法: 由于消费节点PoW的完成时间满足指数分布, 随着时间的增加, 热候选节点出块的概率会不断接近1. 如果等待足够长的时间还没有热候选节点发布新块, 则消费节点可以确定热候选节点均已离线.
3.4 Gossip传输协议Achain协议在网络传输层采用的Gossip协议是一种典型的分布式消息传输协议, 其底层一般采用UDP协议, 其可以同时实现低负载, 高可靠和可扩展性等性能, 且简单而易于实现. Gossip协议内容大致如下: 首先消息传输由一个种子节点发起, 此种子节点先随机挑选出若干个邻居节点, 并将需要同步的消息发送给它们. 收到消息的节点则成为新的种子节点并重复上述过程, 直到网络中的所有节点均接收到此消息. Gossip协议具有最终一致性, 因此, 在理论上, 总会存在一个时间节点, 系统内所有节点在此节点之后均收到了需要同步的消息.
3.5 分叉本节首先介绍Achain区块链的链接规则: 一个区块内的所有交易必须指向同一个父区块. 因此, 当分叉发生时, 所有消费节点都需要选择合适的父区块, 而候选节点也必须选择合适的消费节点(以确保其区块内的交易指向同一个父区块, 否则区块将被视为非法的).
当系统中产生分叉, 并且不同的网络分区产生不同的共识时, Achain使用与Bitcoin相同的解决方案——选择最长的链. 区块间隔的缩短可能会导致分叉的增加. 并且由于PoM的机制, 分叉的概率在更大程度上取决于市场情况. 例如, 如果有一个“超级候选节点”, 具有很强的吸引vote的能力(通过优惠策略、优质服务等), 那么分叉的概率非常低, 因为其他候选节点很难与他几乎同时发布合法块. 在最坏的期间下, 如果有多个相同受欢迎的候选节点, 那么分叉的概率会增加.
尽管如此, 与Bitcoin不同的是, 在这种情况下, Achain仍然可以通过调整参数来影响分叉率. 例如, 可以调整
本节在算法1中使用伪代码来阐明Achain的运行过程.
算法1. Achain主算法
输入: 交易金额阈值
(1) 对于任意候选节点
算法1中的CPoW函数(即消费节点PoW操作)的内容如算法2中所示.
算法2. 函数CPoW (消费节点PoW)
输入: 消费节点
步骤1. 产生随机数
为了进一步优化Achain的性能, 我们提出了FastAchain, 其提供一种基于默克尔树的新型链结构并采用账户模式记录交易信息, 帮助节点节省存储空间, 提升系统的可扩展性和去中心化程度. 详细内容如下.
Achain节点存储的块信息中包含了自创世块以来的所有交易记录, 这是因为UTXO交易结构需要对每笔交易进行溯源. Achain节点会随着系统的运行而不断地存储更多的交易, 这会造成区块链可扩展性的瓶颈, 并且高昂的存储成本也必然会导致中心化的加剧. 为此, FastAchain允许Achain节点对稳定的Achian块进行“快照”处理, 具体地, Achain节点只保存稳定的Achian块中的块头、所有交易的哈希信息、节点签名、交易金额这些主要数据, 而并不存储UTXO交易的主体内容. 并且采用账户(account)模式记录每个消费节点的当前余额状态. 其中, 所有交易的哈希信息采用默克尔树(Merkle trees)结构进行存储, 如图5所示. FastAchain中交易的默克尔树结构主要分为3层: 根哈希、节点哈希和交易哈希, 根哈希是此Achain块的所有交易的总哈希, 节点哈希是此Achain块中某个消费节点提交的所有交易的哈希, 每个交易哈希则对应着具体的某个UTXO交易.

|
图 5 FastAchain中交易的默克尔树结构示意图 |
采用FastAchain方案, 节点则无需存储绝大多数Achain块中的具体交易信息, 只需存储它们的默克尔树并维护一个消费节点的account列表即可. 在对热候选者节点广播的新块中的交易进行验证时也仅需验证其余额的合法性, 即, 此节点是否有足够的余额支付此笔交易.
FastAchain方案使得节点只需花费远小于Achain方案的存储空间就可以达到同样的共识效率, 由于默克尔树的存储成本极低且固定, 因此, FastAchain的链上数据容量增长是非常缓慢的, 且受网络规模扩大交易数量增多等因素的影响较小. 这进一步提升了Achain协议的可扩展性. 此外, 随着节点存储成本的减少, 系统的准入门槛也会降低, 这也有助于提升Achain协议的去中心化程度.
4 Achain有效性及安全性分析 4.1 有效性分析Achain的有效性分析在本质上与Bitcoin是一样的, 因为PoM本质上也是一种PoW机制. 换句话说, 文献[25]中对于Bitcoin主干协议的分析中的许多属性, 例如公共前缀(common prefix)和链质量(chain quality), 都可以“移植”到Achain. 下面我们尝试通过比较Bitcoin和Achain的一个变体来说明其有效性.
在前面的描述中, Achain的每一个消费节点似乎都是一个矿工, 他们需要不断地“挖矿”来使自己的交易合法化以提交给候选节点. 考虑另一种类似的情况(即Achain的变体): 消费节点不是“挖矿”的实际执行者, “挖矿”过程是交给候选节点的(例如: 消费节点不具备挖矿的硬件条件, 但是候选节点具有强大的计算能力). 消费节点仍然需要支付挖矿的消耗和成本, 他们可以自己选择委托哪个候选节点进行挖矿. 在这种情况下, Achain和Bitcoin已经非常相似, 仅有的区别是以下两点: 挖矿成本由不同方承担(在Bitcoin中, 由矿池承担; 在Achain中, 由消费节点承担); 挖矿工作是离散的, 但总工作量保持不变(在Bitcoin中, 挖矿工作是一个整体; 在Achain中, 挖矿工作根据交易离散化).
这里一个可能的疑问是: Achain挖矿的获胜条件看起来和Bitcoin不同. 但其实它们本质上是一样的: 因为Achain挖矿的获胜条件是达到一定交易金额, 而Achain的挖矿难度是成正比与金额门槛的. 因此, 两者的综合效果与Bitcoin的挖矿难度相同. Achain的变体和Bitcoin之间的差异不影响在Bitcoin主干协议[25]中获得的关于安全性和有效性的结论. 并且对于Achain变体的分析也适用于原始Achain. 因此, Bitcoin的有效性和安全性结论同样适用于Achain.
4.2 安全性分析本节主要讨论Achain在主流区块链攻击下的安全性.
(1)双花攻击(51% Attack): 双花攻击是指攻击者使用相同的UTXO在不同的交易中花费. 当攻击者拥有全网50%以上的算力时, 他可以创建一个高度大于原链的新链来回滚旧链上的交易(即, 创建一个分叉), 从而删除之前已被确认的交易, 达到双花的目的.
根据第4.1节的有效性分析, 当恶意节点控制的算力不超过总算力的50%时, Achain区块链与Bitcoin区块链相同, 确认上链的区块是不可篡改的. 唯一可能存在的问题是, Achain的分叉率可能会高于Bitcoin, 这需要消费节点等待更多的区块来确认他的交易. 幸运的是, 与Bitcoin相比, Achain有更高的自由度通过设置系统参数(例如:
(2)女巫攻击(Sybil attack): Sybil攻击是指具有多个身份的节点通过控制系统内的大部分其他节点来削弱冗余备份的作用. 在没有身份验证的p2p网络中, Sybil攻击很容易使数据备份失效并破坏共识. 因此, 大多数共识算法需要对加入系统的节点进行身份验证, 以确保它们不是Sybil节点.
Achain与Bitcoin一样, 允许节点自由进出系统, 这使其暴露在女巫攻击的威胁之下. 然而, Achain也有像Bitcoin一样防止Sybil攻击的机制. 当一个恶意节点打算制作多个恶意候选节点副本时, 他将面临延迟费的“惩罚”; 当一个恶意节点打算制作多个恶意消费节点副本时, 他将面临消费节点PoW的成本和消耗. Achain通过合理的系统参数设置使得这两种作恶的收益在数学期望上都是小于零的. 因此, Achain具有良好的抗Sybil攻击的能力.
(3) SPOF攻击: SPOF是指如果系统中的某个特定节点发生故障(例如, 遭受DDoS攻击), 系统将无法继续运行. 在分布式共识算法中, 如果leader选举是有规律且可预测的, 那么攻击者就可以连续不断地破坏这些leader节点, 从而导致整个系统完全瘫痪.
然而, Achain的领导者选举是随机的. 即使攻击者使用SPOF瘫痪了几个热门候选节点, 其他候选节点仍然可以正常运行并产生区块, 并且它们成为leader的顺序是不可预测的.
5 Achain原型实验及结果分析本节将评估Achain的性能, 包括: 交易的吞吐量、交易的确认延迟、交易的回滚率、链的收敛性和去中心化(详细解释见表1). 此外, 两个重要的变量是领导人选举的阈值
| 表 1 Achain实验参数及其说明表 |
5.1 Achain原型实验设置
本实验通过omnetpp在模拟的p2p网络中实现了Achain的原型. 为了模拟真实的全局分布式网络, 节点之间所有连接的带宽被限制为30 Mb/s, 并在所有通信链路上施加100 ms的延迟(这一设置类似于之前协议的实验[10, 19]). 并且为了模拟消费节点的交易, 本实验的交易池收集了Bitcoin区块链中所有真实交易的集合, 其来自高度从500000到505000的区块, 且每笔交易的容量大小也根据采集到的真实数据进行模拟(在150 KB到250 KB之间). 本实验原型共模拟了1003个消费节点, 每轮的热候选者节点也将随机地从这1003个节点中产生. 每个消费节点每秒产生5个原始交易(为了平衡实验的性能, 网络规模被控制为1003个节点, 但这已经可以接近很多了经典的区块链原型, 例如Bitcoin-NG、ByzCoin等).
5.2 交易吞吐量(TT)本节研究了
Achain的平均TCD实验结果如图8和图9所示. 注意这里的TCD是基于等待6个区块确认交易的时间, 即, 使用与Bitcoin相同的标准交易确认模型.

|
图 6 参数TAT与Achain系统的吞吐量之间的关系实验图 |
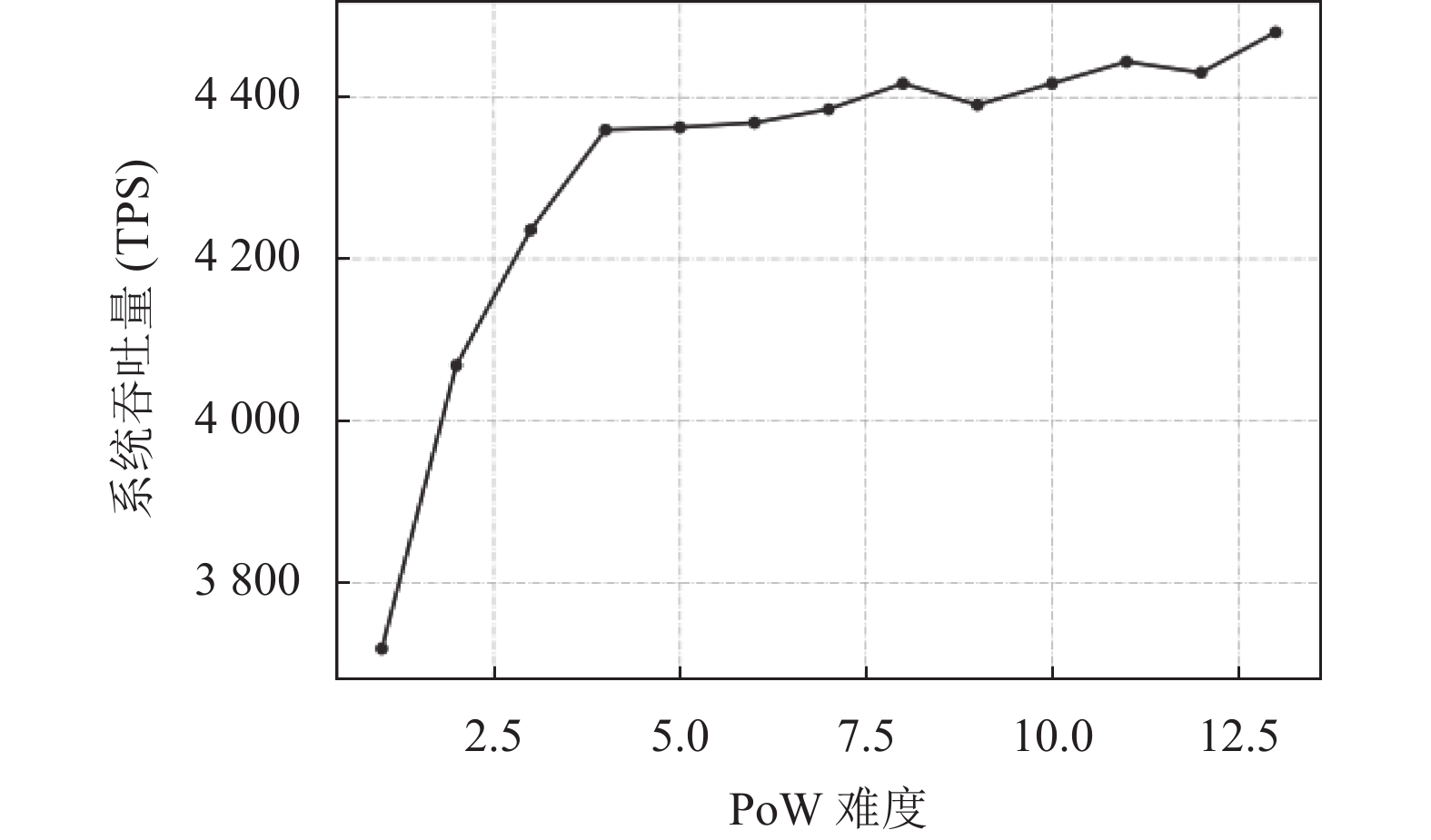
|
图 7 参数
|

|
图 8 TAT与交易确认延迟的关系实验图 |

|
图 9 |
总的来说, Achain的TCD远远超过了Bitcoin区块链的水平, 与目前主流的区块链协议相当, 这说明Achain在达到了高实用性的同时, 其延迟也是完全可以接受的.
5.4 交易回滚率(TRR)回滚率是衡量区块链协议的重要指标, 直接关系到系统的安全性. PoM本质上是一种PoW型共识, 因此Achain具有PoW型区块链的收敛性, 这使得提交的交易在被确认后是不可变的. 表2和表3为相关实验结果, 其中数据均取自高度超100的区块链.
| 表 2 TAT与交易回滚率的关系实验表 |
5.5 区块链的收敛性(CC)
Achain链的收敛实验通过记录分叉的数量和高度来判断区块链的安全性. 实验结果如表4和表5所示. 一般情况下, 大多数分叉的高度为1, 只有少数分叉达到高度2. 增加
|
表 3 |
| 表 4 TAT与分叉数量和高度的关系实验表 |
|
表 5 |
5.6 去中心化
去中心化实验检验了Achain的公平性和安全性. 如果区块间隔的过度缩小会使得节点每轮开始PoW操作的时间不同, 那么系统的安全性将受到极大威胁. 实验结果如表6和表7所示, 其中所有实验数据均至少稳定运行3次获得, 结果表明Achain在不同的
| 表 6 热候选节点的胜率(出块率)与阈值TAT的关系表 |
|
表 7 热候选节点的胜率(出块率)与消费节点PoW难度
|
6 结论与展望
总结来说, 本文提出了一种基于新型PoM共识的区块链协议——Achain, 它综合考虑了效率、公平性、去中心化和节能, 并试图打破经典区块链面临的诸多限制. PoM本质上是一种新型的PoW共识, 但它将“挖矿”操作从区块生产者转移到消费节点上. 再加上合理的激励机制, Achain使得恶意节点的攻击无利可图. 在理性攻击者的假设下, Achain 具有更好的性能和去中心化性, 并充分考虑了消费节点的意愿. 由于目前的Achain只是分布式账本系统, 并不是图灵完备的(turing completeness), 因此进一步的研究将拓展PoM共识机制的适用范围, 研制基于PoM的智能合约系统.
致谢感谢中国科学技术大学苏州高等研究院陈蔚林博士、陈柄任博士对本文Achain协议设计及实验的讨论和帮助.
| [1] |
Nakamoto S. Bitcoin: A peer-to-peer electronic cash system. Decentralized Business Review, 2008: 21260.
|
| [2] |
Eyal I, Sirer EG. Majority is not enough: Bitcoin mining is vulnerable. Proceedings of the 18th International Conference on Financial Cryptography and Data Security. Christ Church: Springer, 2014. 436–454.
|
| [3] |
Gervais A, Ritzdorf H, Karame GO, et al. Tampering with the delivery of blocks and transactions in Bitcoin. Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. Denver: ACM, 2015. 692–705.
|
| [4] |
Heilman E, Kendler A, Zohar A, et al. Eclipse attacks on Bitcoin’s peer-to-peer network. Proceedings of the 24th USENIX Conference on Security Symposium. Washington: USENIX Association, 2015. 129–144.
|
| [5] |
Karame GO, Androulaki E, Capkun S. Double-spending fast payments in Bitcoin. Proceedings of 2012 ACM Conference on Computer and Communications Security. Raleigh: ACM, 2012. 906–917.
|
| [6] |
Nayak K, Kumar S, Miller A, et al. Stubborn mining: Generalizing selfish mining and combining with an eclipse attack. Proceedings of 2016 IEEE European Symposium on Security and Privacy. Saarbruecken: IEEE, 2016. 305–320.
|
| [7] |
Eyal I, Gencer AE, Sirer EG, et al. Bitcoin-NG: A scalable blockchain protocol. Proceedings of the 13th USENIX Conference on Networked Systems Design and Implementation. Santa Clara: USENIX Association, 2016. 45–59.
|
| [8] | |
| [9] |
Castro M, Liskov B. Practical byzantine fault tolerance. Proceedings of the 3rd Symposium on Operating Systems Design and Implementation. New Orleans: USENIX Association, 1999. 173–186.
|
| [10] |
Kokoris-Kogias E, Jovanovic P, Gailly N, et al. Enhancing Bitcoin security and performance with strong consistency via collective signing. Proceedings of the 25th USENIX Conference on Security Symposium. Austin: USENIX Association, 2016. 279–296.
|
| [11] |
Gilad Y, Hemo R, Micali S, et al. Algorand: Scaling byzantine agreements for cryptocurrencies. Proceedings of the 26th Symposium on Operating Systems Principles. Shanghai: ACM, 2017. 51–68.
|
| [12] |
Wood G. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Project Yellow Paper, 2014, 151(2014): 1-32. |
| [13] |
Crain T, Natoli C, Gramoli V. Red belly: A secure, fair and scalable open blockchain. Proceedings of 2021 IEEE Symposium on Security and Privacy. San Francisco: IEEE, 2021. 466–483.
|
| [14] |
Li CL, Zhang J, Yang XM. Scalable blockchain storage mechanism based on two-layer structure and improved distributed consensus. The Journal of Supercomputing, 2022, 78(4): 4850-4881. DOI:10.1007/s11227-021-04061-3 |
| [15] |
Yang J, Jia ZH, Su RG, et al. Improved fault-tolerant consensus based on the PBFT algorithm. IEEE Access, 2022, 10: 30274-30283. DOI:10.1109/ACCESS.2022.3153701 |
| [16] |
Ongaro D, Ousterhout J. In search of an understandable consensus algorithm. Proceedings of the 2014 USENIX Conference on USENIX Annual Technical Conference. Philadelphia: USENIX Association, 2014. 305–320.
|
| [17] |
Karantias K, Kiayias A, Zindros D. Proof-of-burn. Proceedings of the 24th International Conference on Financial Cryptography and Data Security. Kota Kinabalu: Springer, 2020. 523–540.
|
| [18] |
Yu JS, Kozhaya D, Decouchant J, et al. RepuCoin: Your reputation is your power. IEEE Transactions on Computers, 2019, 68(8): 1225-1237. DOI:10.1109/TC.2019.2900648 |
| [19] |
Kokoris-Kogias E, Jovanovic P, Gasser L, et al. OmniLedger: A secure, scale-out, decentralized ledger via sharding. Proceedings of 2018 IEEE Symposium on Security and Privacy. San Francisco: IEEE, 2018. 583–598.
|
| [20] |
Liu CC, Guo HC, Xu MH, et al. Extending on-chain trust to off-chain—Trustworthy blockchain data collection using trusted execution environment (TEE). IEEE Transactions on Computers, 2022.
|
| [21] |
Zheng PL, Xu QQ, Luo XP, et al. Aeolus: Distributed execution of permissioned blockchain transactions via state sharding. IEEE Transactions on Industrial Informatics, 2022.
|
| [22] |
Zamani M, Movahedi M, Raykova M. RapidChain: Scaling blockchain via full sharding. Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security. Toronto: ACM, 2018. 931–948.
|
| [23] |
Kiayias A, Russell A, David B, et al. Ouroboros: A provably secure proof-of-stake blockchain protocol. Proceedings of the 37th Annual International Cryptology Conference on Advances in Cryptology. Santa Barbara: Springer, 2017. 357–388.
|
| [24] |
Poon J, Dryja T. The Bitcoin lightning network: Scalable off-chain instant payments. https://lightning.network/lightning-network-paper.pdf.
|
| [25] |
Garay J, Kiayias A, Leonardos N. The Bitcoin backbone protocol: Analysis and applications. Proceedings of the 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques on Advances in Cryptology. Sofia: Springer, 2015. 281–310.
|
 2023, Vol. 32
2023, Vol. 32


