随着具有GPS定位功能的移动设备和车载传感装置的普及, 海量的车辆时空轨迹数据被收集. 对车载终端采集的时空轨迹数据进行挖掘和分析能够给商业机构、交通管理部门、法律信息查询机构以及基于位置的服务部门等提供相应的数据支持[1, 2]. 轨迹数据是移动对象运动过程中产生的离散采样位置点, 包括时间戳、经度、纬度、速度、高度等, 这些采样点根据采样时间顺序构成了轨迹数据[3]. 停留点是离散的轨迹数据中在某些位置停留时间达到一定程度的数据点, 合理地对轨迹数据进行挖掘与研究, 获取数据背后蕴含的有价值的内容, 根据挖掘的信息预测人们的行为, 能够为人们的生产生活提供便利, 同时也能提供新的商业运作方式和科研工作方法.
然而, 随着信息化的不断发展以及近些年信息泄露导致的违法行为发生, 人们逐渐认识到了隐私保护的重要性. 当人们将个人轨迹数据上传至第三方服务器来获取位置服务时(服务器一般是不可信的), 攻击者很容易获取到轨迹数据并进行恶意挖掘, 严重泄露用户隐私比如工作单位、家庭住址等敏感信息. 敏感信息的泄漏可能会给用户带来不可估量的损失, 进而导致越来越多的用户由于担心信息泄露而拒绝使用相关的服务, 这样会阻碍国内基于位置的相关服务的良性发展. 我国“十三五”规划中曾提及要重视位置信息隐私安全建设, “十四五”规划中也再次对网络安全建设提出了新的要求[4]. 车辆停留信息中一般包含用户的诸多隐私信息, 现有的车辆轨迹停留点挖掘技术较多关注停留点的识别算法研究, 考虑到隐私保护问题的研究较少. 有效挖掘车辆停留信息同时保护用户的隐私不被侵犯是未来基于位置信息的服务行业持续良性发展的重要保障, 同时也是响应国家“十四五”规划的要求. 因此, 如何有效挖掘车辆停留信息同时保护用户的隐私不被侵犯成为亟待解决的问题.
目前, 针对轨迹数据停留点挖掘的隐私保护还是一个新兴的研究热点, 存在两个主要问题亟待解决: (1) 如何有效挖掘出停留点. (2) 如何保证在挖掘停留点的过程中不泄露用户隐私.
针对上述问题, 本文提出一种融合隐私保护的车辆轨迹数据停留点挖掘方法, 主要工作为: (1) 结合密度聚类算法, 设置时间阈值、距离阈值和速度阈值的判定条件, 缩小停留点的筛选范围, 有效挖掘出相关停留点. (2) 基于差分隐私机制, 对挖掘出来的停留点添加拉普拉斯噪声. 传统的添加噪声方法是对整个轨迹序列加噪, 不仅会消耗隐私预算还会降低数据可用性. 本文是有针对性地对停留点添加噪声, 能够减少隐私预算的消耗, 提高数据可用性. (3) 在真实重型卡车轨迹数据集上进行了实验, 以验证本文方法的有效性.
1 研究现状随着大数据的发展, 时空轨迹数据挖掘逐渐成为学者的研究重点. 时空轨迹数据在一定程度上反映了移动对象的性质、类别、状态等信息. 时空轨迹数据挖掘指对人们的历史轨迹进行大数据分析, 挖掘针对某些特定研究对象的新颖有价值的信息或者根据过去的轨迹数据对未来做出预测等. 目前轨迹数据的挖掘方法主要有统计分析、轨迹聚类、轨迹孤立点识别、遗传算法、神经网络算法等[5]. 轨迹聚类是目前比较经典的数据挖掘技术之一. 通过车辆轨迹数据聚类, 可以发现轨迹的相似行为, 挖掘车辆的出行模式, 停留信息等, 可用于城市建设、交通规划、智能交通、区域规划等. 按照聚类模型的不同, 聚类分为密度聚类、划分聚类、网格聚类、模型聚类以及层次聚类等[6].
Cao等人[7]基于GPS轨迹数据提出了一个轨迹模式挖掘系统, 结合K-means聚类匹配用户相似性轨迹, 能够发现城市的密集区域. Enami等人[8]利用PrefixSpan和BIDE的序列模式挖掘算法, 能够基于大量轨迹数据提取出频繁轨迹模式来预测对象未来轨迹的移动性. Cheng等人[9]考虑轨迹的时间和空间特征, 采用密度聚类的方法研究出租车的运动模式. 在轨迹停留点挖掘方面, Zhou等人[10]提出了DJ-cluster聚类算法, 结合轨迹的空间特征筛选轨迹邻域点数, 将不符合邻域最小点数的点标记为噪声, 但轨迹属性较为单一, 没有考虑轨迹的时间特性. Gao等人[11]设置时间阈值来判断停留点, 用滑动窗口方法筛选停留点, 提高了识别效率, 但该方法对数据采用频率以及数据实时性要求较高. Niu等人[12]提出了一种基于属性选择的轨迹的停止和移动挖掘算法, 能够在缺乏详细地理数据的基础上, 结合特征选择挖掘出轨迹聚类的核心属性, 提高了位置挖掘的准确性, 但没有考虑轨迹的隐私保护问题.
在此基础上, 部分学者关注到轨迹的隐私保护问题. Wang等人[13]结合位置相似性度量将轨迹采样位置分成不同的等价概率类, 采用假位置生成的方法对这些等价概率类中的轨迹进行重组, 满足了采样轨迹的隐私保护要求. Mahdavifar等人[14]采用匿名的方式保护轨迹隐私, 根据移动对象的不同而分配不同的隐私级别, 使得具有一定背景知识的攻击者无法识别特定轨迹. Peng等人[15]考虑到用户之间的位置信息相关性, 提出了一种数据发布机制来抵抗推断攻击并自适应地保护用户相关的位置信息. Ning等人[16]考虑到网络传输中的数据包含大量的图结构数据, 而加权图中的边权重可能会带来隐私泄露的风险, 提出了一种基于加权图的隐私保护算法, 通过对整个图集添加噪声以及为边权重分配隐私预算的方式实现对数据的隐私保护.
此外, 部分学者也关注到了轨迹挖掘与隐私保护相结合的研究方向. Han等人[17]通过指数机制, 将同一时间的位置集快速准确地划分为不同的分区, 输出更准确的位置点分区和轨迹计数组, 可以安全快速地进行数据挖掘工作, 同时将拉普拉斯噪声添加到轨迹数据中保护隐私. Zhao等人[18]将拉普拉斯噪声添加到集群的轨迹位置计数中以加强数据保护, 然后, 将受约束的拉普拉斯噪声加入到聚类中的轨迹位置数据中, 根据噪声位置数据和噪声位置计数, 得到聚类中的噪声聚类中心, 之后使用差分隐私技术增强隐私保护能力, 该方法具有良好的聚类效果同时兼具隐私保护功能. Xu等人[19]制定了轨迹混淆问题, 以选择与原始轨迹序列差异最小的最优轨迹序列, 为了防止隐私泄露, 他们分别在位置混淆矩阵生成和轨迹序列函数生成阶段将拉普拉斯噪声和指数噪声添加到输出中, 该方法可以较为准确地挖掘社区轨迹信息, 同时防止数据泄漏. 王豪等人[20]在传统的聚类和差分隐私中加入了二维拉普拉斯噪声, 并将噪声转换坐标系由直角坐标系转换为极坐标系, 将其融入到原始轨迹数据中. 赵书鹏[21]将AP轨迹聚类算法与豪斯多夫距离相结合, 提出一种新的基于聚类的差分隐私保护方法, 该方法受轨迹集合密集程度和范围变化的影响较小. 赵濛[22]将ε-差分隐私技术与幂迭代聚类算法相结合, 该算法根据目标的不同添加不同的噪声函数, 做到了数据挖掘和隐私保护相统一, 但是该算法本身过于复杂且在小数据集上效果不佳.
多数研究工作中里采用的是轨迹点密集的人类移动数据集, 较少考虑经纬度跨度大的车辆轨迹数据集. 在轨迹隐私保护过程中, 部分研究会忽略攻击者的背景知识, 没有考虑位置服务提供商(location service provider, LSP)的不可信性. 因此, 本文重点考虑LSP不完全可信的情况下, 如何在车辆轨迹数据挖掘的过程中, 保护其隐私信息不被泄露.
2 融合隐私保护的车辆轨迹数据停留点挖掘方法近年来, 融合隐私保护的数据挖掘得到了广泛关注[23]. 常见的隐私保护技术有数据加密、匿名、差分隐私等[24]. 数据加密技术通过密码学原理将数据加密成不可读的信息, 需要通过某种解密机制来获取数据的原始信息. 这种技术具有可靠性高、数据不易丢失等特点, 但加密过程需要较高的运算成本, 且运算效率较低. 匿名技术通常是对数据进行抽象化的描述, 使数据挖掘者无法在公开数据集中关联到隐私个体. 这种技术可以有效保护用户隐私, 但无法抵御背景知识攻击. 差分隐私是Dwork[25]在2006年首次提出的一种基于数据扰动的隐私保护模型, 由于该模型具有严格的数学定理证明, 能够抵御攻击者的背景知识攻击进而提供有效的隐私保护, 成为当下隐私保护领域的研究热点.
基于此, 本节针对车辆停留点挖掘过程中可能产生的隐私泄露问题, 通过引入差分隐私技术, 提出了一种融合隐私保护的车辆停留点挖掘方法: dp-STV-DBSCAN. 首先通过密度聚类完成对停留点的提取, 其次结合差分隐私机制对停留点位置进行扰动处理, 之后重构轨迹序列, 从而实现对车辆轨迹数据的隐私保护.
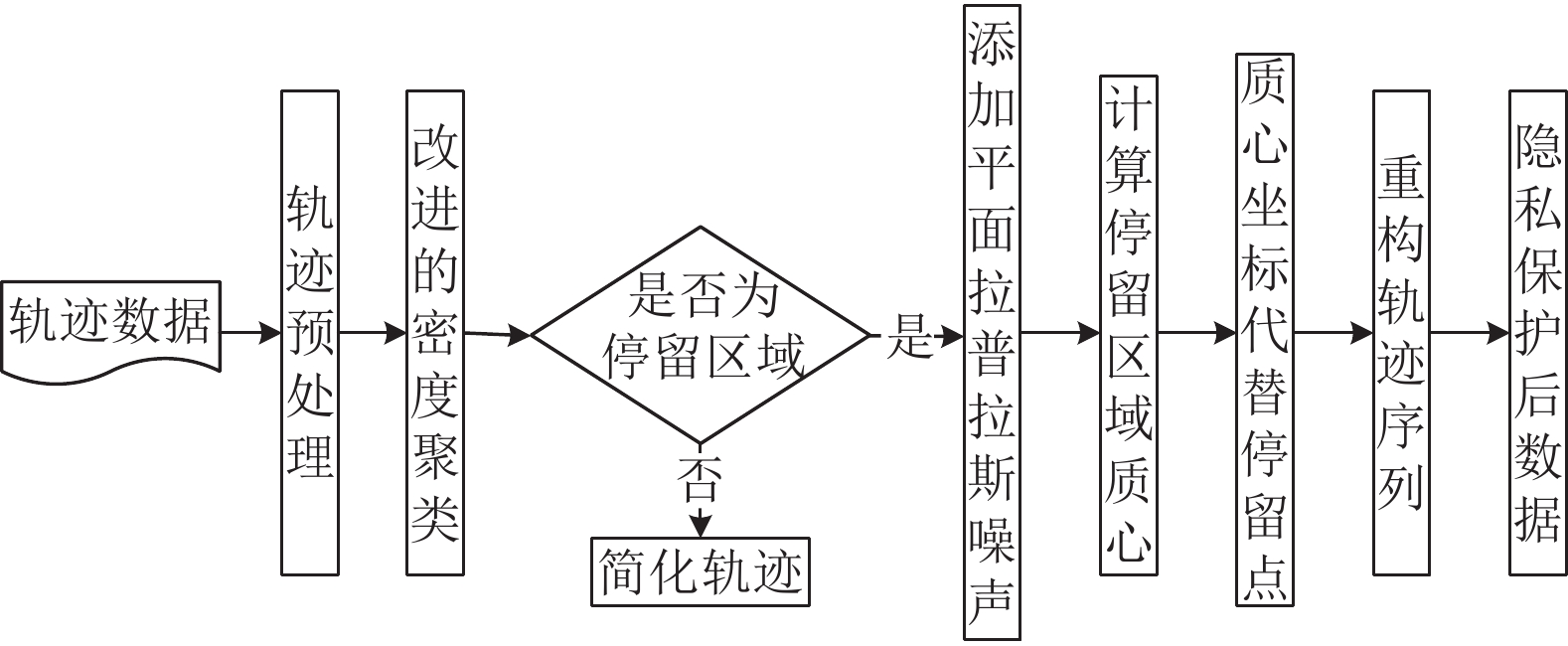
本文算法框架图如图1所示.
|
图 1 算法流程框架图 |
2.1 基于ST-DBSCAN改进的停留点挖掘算法
DBSCAN算法是比较经典的一种密度聚类算法, 它可以发现任意形状的聚类, 如凹形、线形、椭圆形等, 与K-means[26]等聚类算法相比, 它不需要预先确定聚类的数量, 而且能识别出噪声点, 对离群点也有较好的鲁棒性. 但DBSCAN算法仅支持一维空间数据, 使用一个距离参数Eps来衡量一维空间数据的相似性, 不适用于经纬度轨迹这类二维空间数据. Birant等人[27]提出了一种新的基于密度的聚类算法ST-DBSCAN, 包括两个距离度量Eps1和Eps2, 可支持二维空间数据. 其中, Eps1用于测量空间值, 即地理上两点的相似程度, Eps2用于测量非空间的相似性, 如温度、时间等. 但对于车辆轨迹数据来说, 一定间隔时间采样出来的轨迹数据经纬度跨度较大, 仅有距离阈值和时间阈值挖掘出来的停留点不够准确. 本节在ST-DBSCAN的基础上进行改进, 提出STV-DBSCAN聚类算法, 加入了轨迹速度变量, 设置轨迹时间阈值、距离阈值和速度阈值, 实现对车辆轨迹数据的聚类.
首先介绍密度聚类涉及到的相关定义.
定义1. 原始轨迹点. 表示一定采样频率下的连续采样点Pi={Xi, Yi, Ti}, 其中Xi表示轨迹点Pi在Ti时刻的纬度坐标, Yi表示轨迹点Pi在Ti时刻的经度坐标.
定义2. 原始轨迹. 表示一定采样频率下的连续采样点Pi的集合x={P1, P2, …,Pn}.
定义 3. 原始轨迹集. 表示由采样点集合 x 组成的对象集合D={x1, x2, …, xn}.
定义4. ϵ邻域. 表示以对象p为中心, 半径为ϵ的区域, 称为p的ϵ邻域[28].
定义5. MinPts. 表示ϵ邻域内的最小领域点数.
定义6. 核心对象. 如果对象p的ϵ邻域内的样本点数大于等于MinPts, 则p为核心对象[29].
定义7. 直接密度可达. 给定对象集合D, 存在对象p和对象q, 如果对象p为核心对象, 且q在p的ϵ邻域内, 则称p到q直接密度可达[29].
定义8. 密度可达. 给定对象集合D, 存在对象p1, p2, …, pn, p=p1, q=pn,
定义9. 噪声. 不属于任意一个集群的点就标记为噪声点.
本节算法首先根据轨迹时间阈值、距离阈值和速度阈值筛选出轨迹候选停留点集合. 之后将该集合内的邻域点数目与MinPts作比较, 筛选出符合要求的停留点, 得到最终停留点集合C={c1, c2, …, cn}. 首先介绍STV-DBSCAN算法.
算法1. 基于ST-DBSCAN改进的停留点挖掘算法
Input: D={x1, x2, …, xn}, Eps, T, MinPtsOutput: C={c1, c2, …, cn}
1. Calculate the average speed of set D: Avgspeed;2. clusterindex = 0;3. for xi in D: 4. if xi is not in a cluster:5. call algorithm 2;6. return X; 7. if Len(X) < MinPts:8. xi is a noise;9. else: 10. clusterindex += 1; 11. assign clusterindex labels to
速度计算: 轨迹点pi(lati, lngi, Ti),
| $ spee{d_{{ij}}} = \frac{{\left| {d\left( {{P_i}, {P_j}} \right)} \right|}}{{{T_j} - {T_i}}} $ | (1) |
其中, d(Pi, Pj)表示轨迹点Pi和Pj之间的距离.
平均速度: 轨迹集D整体轨迹点的平均速度Avgspeed可由所有轨迹点的速度之和与轨迹点数目N的比值得到, 计算方式如下:
| $ Av{g_{{\rm{speed}}}} = \frac{{\displaystyle\sum\limits_{i = 1}^n {spee{d_i}} }}{N} $ | (2) |
ST-DBSCAN算法[27]在停留点识别过程中, 如果距离阈值设置过大, 容易误将相距较近的停留点间的移动点也识别成停留点. 与ST-DBSCAN算法相比, STV-DBSCAN算法在筛选轨迹邻域点时, 增加了轨迹速度变量的判断条件. 通过计算轨迹整体平均速度, 在给定的速度阈值筛选之下, 进一步判断停留点, 缩小了停留点的识别范围, 能够使停留点有更好的划分.
如算法1所示, 算法输入为由轨迹经纬度、时间戳和速度组成的轨迹数据集D. 首先步骤1–2, 计算轨迹集D整体轨迹点的平均速度Avgspeed, 初始化集群索引标签为0. 从轨迹点x1开始, 按照时间顺序, 对所有轨迹点进行遍历, 如果当前轨迹点(xi)不属于任何集群, 则转到算法2. 算法2根据设定的距离阈值(Eps)、时间阈值(T)和速度阈值 (Avgspeed×u) (
算法2. 筛选邻域点方法
1. neighbors = [];2. fitter point xi by time;3. Ti= points{time(xi, xk) < T};
4. for x inTi:5. if not x:6. dxk, xi = haversine(xk, xi) ;7. if dxk, xi < Eps:8. if Vxk<Avgspeed×u9. X=neighbors.Append(xk) ;10. end if11. end if12. end if13. return X;
算法2是算法1中涉及到的根据条件阈值筛选核心对象邻域点[30]的描述. 具体过程为: 首先按照时间阈值进行过滤, 当轨迹点xi与轨迹点xk的时间距离小于时间阈值T, 则调用距离函数haversine计算两点之间的距离; 若两点之间距离小于距离阈值Eps, 则继续筛选速度变量, 若轨迹点xk的速度小于速度阈值Avgspeed×u, 则将xk添加到轨迹点xi的候选停留点集合X.
算法3. haversine函数
Input: Lata, Lnga, Latb, LngbOutput: d(a, b)
1. a=radians(a), b=radians(b); //将轨迹点a和b转换成弧度表示2.
算法2中提到的haversine函数是计算轨迹间距离的公式, 算法3为具体伪代码描述.
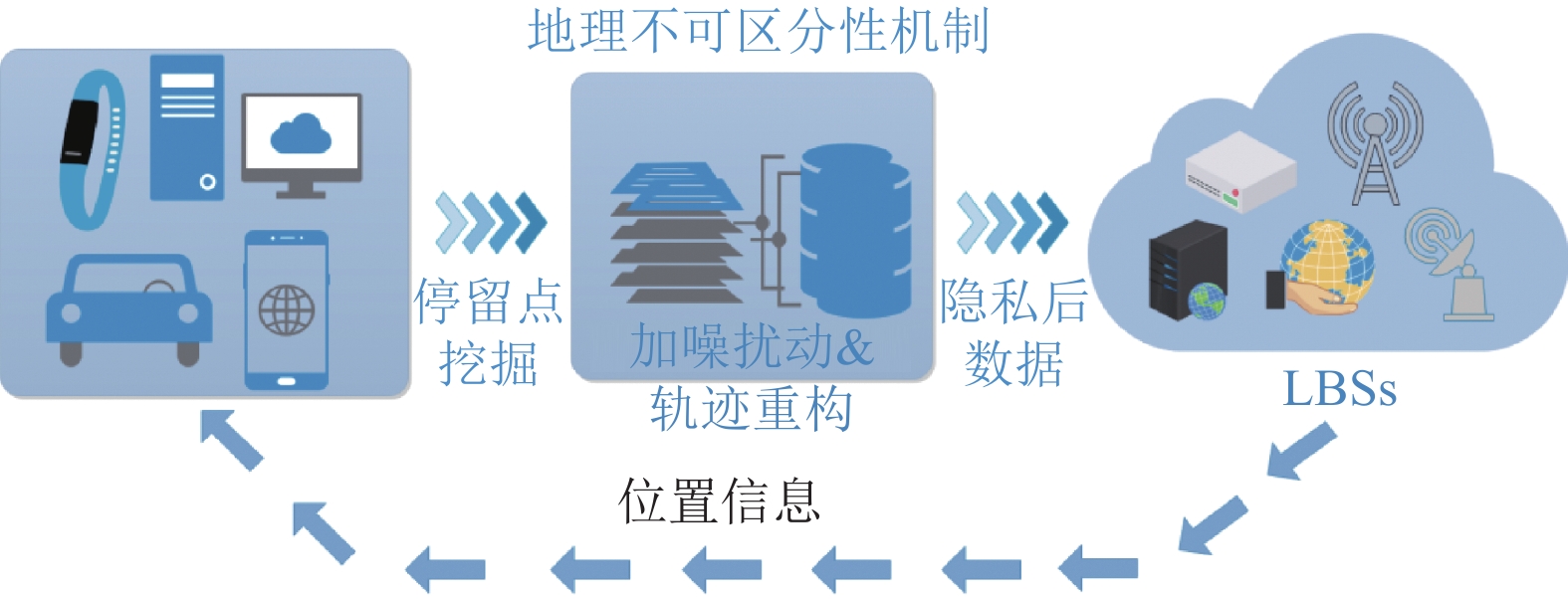
2.2 融合隐私保护的车辆停留点挖掘算法轨迹停留点中通常包含着许多有价值的信息, 直接发布这些轨迹数据会造成用户隐私泄露, 带来一系列安全问题. 本节提出的融合隐私保护的车辆停留点挖掘算法在停留点识别完成之后, 会根据轨迹特征引入差分隐私技术对轨迹进行保护. 隐私保护模型如图2所示.
|
图 2 隐私保护模型 |
差分隐私是Dwork[25]在2006年首次提出的一种基于数据扰动的隐私保护模型, 保护机制主要分为指数机制和拉普拉斯机制两种. 其中, 指数机制主要用于对非数值型数据的查询, 而拉普拉斯机制适用于对数值型数据的隐私保护[31]. 其基本思想为向数据集添加服从拉普拉斯分布的噪声, 并将产生的随机噪声加入到原始数据中, 从而实现差分隐私保护. 拉普拉斯分布的概率密度函数为:
| $ p(x) = \frac{1}{{2b}}{\rm{exp}}\left( - \frac{{\left| {x - u} \right|}}{b}\right) $ | (3) |
其中, u表示位置参数, b表示尺度参数. 称随机变量x服从参数为b和u的拉普拉斯分布.
拉普拉斯机制的定义为[32]: 给定一个数据集D, 设 f: D→Rd 是一个敏感度为Δf的函数:
| $ M\left( D \right) = f\left( D \right) + Y\;\; $ | (4) |
其中,
轨迹数据属于数值型数据, 所以应用拉普拉斯机制更为合适. 传统的拉普拉斯机制主要是对一维数据添加噪声, 这对于轨迹二维空间数据来说, 加噪效果并不理想. Andrés等人[33]提出了一个满足差分隐私的保护轨迹数据的模型, 将拉普拉斯分布从一维空间扩展到了二维空间, 得到平面拉普拉斯分布. 它的主要思想是: 对于半径r内的所有轨迹数据点, 如果任意两个轨迹点之间的距离小于一定阈值, 则这两个轨迹点是不可区分的, 反过来, 如果这两个轨迹点之间的距离大于一定阈值, 则攻击者能够对这两个轨迹点进行区分.
假定x是真实位置, y是发布位置, Andrés等人[33]提出的最终的发布位置y可以表示为:
| $ y = x + \left( {r \cdot {\rm{cos}}\theta , r \cdot {\rm{sin}}\theta } \right) $ | (5) |
其中, r表示极坐标下, 真实位置点x与发布位置点y之间的距离, θ表示直线xy与笛卡尔坐标系中的x轴之间的夹角.
直接对轨迹数据添加噪声, 不仅会消耗隐私预算还会降低数据可用性, 针对这一情况, 本节提出了一种融合隐私保护的车辆停留点挖掘算法: dp-STV-DBSCAN. 在第3.2节中, 挖掘出轨迹停留点后, 得到停留点集合:
算法4 为融合隐私保护的停留点挖掘算法, 旨在防止停留点挖掘过程中产生的隐私泄露问题. 由式(5)可知, 发布位置y的坐标值主要取决于r值的大小, 而r服从gamma分布, r值的大小取决于ε的大小. 如果r取值过大, 那么对原轨迹数据即停留点坐标的扰动越大, 造成发布位置与真实位置差距过大, 数据可用性极低, 会失去隐私保护的意义. 因此, 算法4在对停留点位置添加噪声的过程中, 会先设定一个区域半径s, 然后根据设定的隐私参数ε计算出的r, 计算加噪后的停留点Cm' 与原始停留点Cm之间的距离dist(Cm, Cm'), 如果dist(Cm, Cm')小于指定的区域半径s, 说明加噪后的停留点位置在合理区域范围之内, 将符合条件的加噪后的停留点添加到集合C'={C1', C2', …, Cn'}中, 反之, 则重新计算r. 之后重新计算该区域内轨迹点的质心, 将质心轨迹坐标替换原来的停留点坐标, 然后构成新的轨迹序列, 最后发布重构后即隐私保护后的轨迹数据.
算法4. 融合隐私保护的车辆停留点挖掘算法
Input: C={c1, c2, …, cn }, D={x1, x2, …, xn}, ε, sOutput: Y={y1, y2, …, yn}
1. r ~ gamma(2, 1/ε);2. θ ~ U(0, 2π);3. for m = 1:n do4. find the location of the stop pointCm;5. Cm' = Ci + (r×cosθ, r×sinθ);6. ifdist(Cm, Cm' ) < s:7. add Cm' toC'={C1', C2', …, Cn'}8. else:9. repeat steps 1–6;10. end if11. calculate the centroid Pm of the cluster where Cm' is located12. replaceCm with Pm;13. reconstructed trajectory sequence; 14. out ofY={y1, y2, …, yn};
如算法4所示, 算法输入为原始轨迹数据集D={x1, x2, …, xn}, 隐私参数ε, 指定的区域半径s以及由算法1得到的轨迹停留点集合C={c1, c2, …, cn}. 首先设置隐私参数ε, 根据gamma分布和均匀分布计算出半径r和角度θ. 其次, 遍历轨迹停留点集合, 找到每个停留点所在的轨迹及轨迹位置. 之后, 比较加噪后的停留点Cm'和原始停留点Cm之间的距离dist(Cm, Cm')与指定的区域半径s的大小, 若dist(Cm, Cm')小于指定的区域半径s, 则计算停留点Cm的噪声轨迹点Cm', 并添加到集合C'中, 否则重新计算r, 直到产生的噪声轨迹数据点落在指定的区域半径s内. 最后, 重新计算噪声轨迹点Cm'所处簇的质心Pm, 将质心Pm代替原来的停留点Cm, 然后构建轨迹序列, 最后得到隐私保护后的轨迹数据集Y={y1, y2, …, yn}.
3 算法实现与性能评估为了评估本文提出的融合隐私保护的停留点挖掘算法的有效性, 采用Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz处理器, 采用Python语言实现算法, 并与近年来的基线算法进行了对比实验.
为了说明算法的有效性, 本文选用重卡数据集进行验证.
该数据集包含了2018年8月14日–8月20日陕西省内360辆重型卡车的轨迹数据. 轨迹数据集中每条记录包括数据发生时间、数据接收时间、经度、纬度、海拔高度、方向等, 该数据集中大约包含3000万个轨迹点的记录.
3.1 聚类算法评估为了验证本文提出的基于ST-DBSCAN改进的聚类算法, 本文采用了轮廓系数(silhouette coefficient)和戴维森堡丁指数(Davies Bouldin index)两个评价指标[34], 通过与基线算法ST-DBSCAN[27]以及近年来提出的K_Medians[35]算法作对比实验, 来评估本文提出算法的聚类效果. 经过多次对比实验, 取平均值作为最终的实验结果.
(1)轮廓系数(SC)
| $ SC\left( o \right) = \frac{{b\left( o \right) - a\left( o \right)}}{{\max \left\{ {a\left( o \right), b\left( o \right)} \right\}}} $ | (6) |
其中, a(o)表示簇内距离, b(o)表示簇间距离. SC(o)的取值范围在[−1, 1]之间,SC(o)越接近1, 说明同类样本相距越近, 不同样本相距越远, 则聚类效果越好.
(2)戴维森堡丁指数(DBI)[36]
对于m个时间序列, 将这些时间序列聚类后得到n个簇, 将m个时间序列设为输入矩阵X, n个簇为N作为参数传入算法, 计算公式如下:
| $ DBI = \frac{1}{N}\sum\limits_{i = 1}^N {\mathop {\max }\limits_{j \ne 1} } \left(\frac{{{{\bar s}_i} + {{\bar s}_j}}}{{\parallel {\omega _i} - {\omega _j}\parallel 2}}\right) $ | (7) |
其中, DBI的取值范围为[0, 1], 值越小说明聚类效果越好.
3.1.1 参数选择本文使用基于ST-DBSCAN改进的聚类算法进行停留点挖掘. 算法1 需要的参数有距离阈值Eps, 时间阈值T, 邻域内最小点数MinPts和速度阈值V. 在实验过程中, 需要不断调整这些参数以获得最优结果.
由于本文经过轨迹数据预处理后, 将360辆车同一天的轨迹数据合并到了一起, 之后选取轨迹特征点集合作为实验数据集, 因此轨迹点前后的采样时间会相对大些(原始轨迹采样时间间隔为几秒钟一次, 处理过后数据点采样时间间隔为几分钟一次). 因此在实验过程中, 时间阈值会设置的比较大. 经过多次实验得出参数值如表1所示, Eps值设为500 m, 时间阈值T设为30 min, 邻域内最小点数MinPts设为2, 速度阈值V设置为0.2倍车辆平均速度时, 聚类效果最佳.
具体参数设置说明如表1.
| 表 5 参数说明 |
3.1.2 实验结果
(1)轮廓系数(SC)
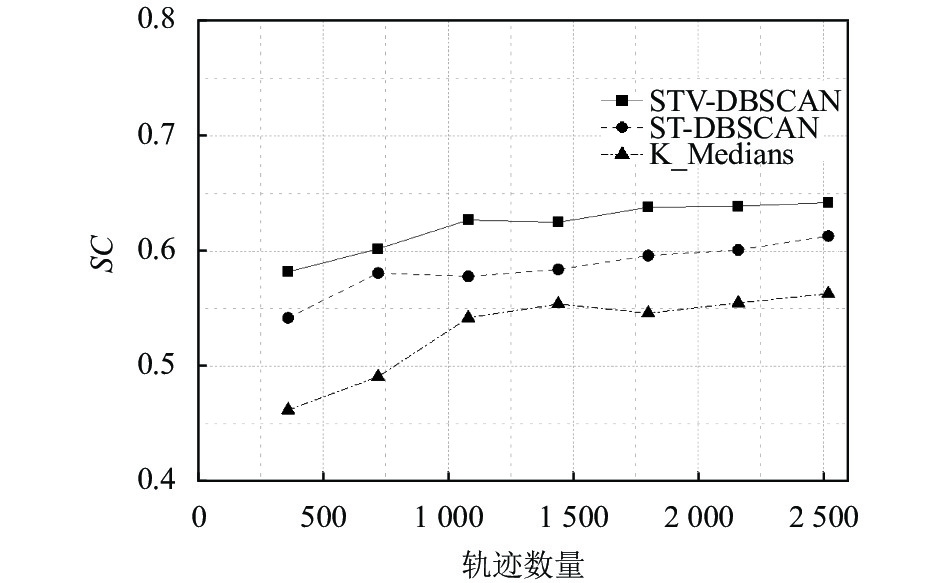
在重卡数据集上对算法1停留点聚类算法进行了实验验证, 实验结果如图3所示. 从图3可以看出, 本文提出的算法轮廓系数SC保持在0.62左右, 基线算法ST-DBSCAN的SC值保持在0.60以下, 对比算法K_Medians的SC值保持在0.55以下. 随着轨迹数量的增加, 本文提出的算法SC的值变化趋势依然保持稳定. 对产生的结果进行分析如下: (1)与基线算法ST-DBSCAN对比, 本文提出的算法增加了速度变量, 因此在筛选停留点时增加了一个判断条件, 使得聚类之后的样本对象更符合它所在的簇, 同时保证了轨迹簇间的距离相距更远. (2)对比算法K_Medians在聚类前要事先指定聚类的个数, 聚类个数的不同产生不同结果的簇, 导致簇内各节点之间的距离并不稳定, 因此聚类的迭代结果不理想.
(2)戴维森堡丁指数(DBI)
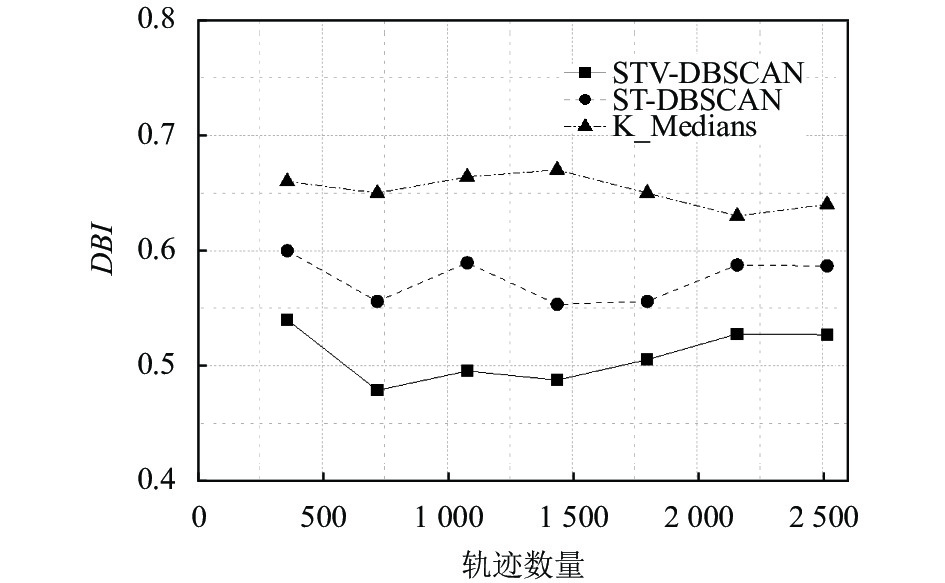
在重卡数据集上对算法1停留点聚类算法进行了实验验证, 实验结果如图4所示. 从图4可以看出, 本文提出的算法的DBI值保持在0.55以下, 基线算法ST-DBSCAN的DBI值保持在0.56以上, K_Medians算法的DBI值保持在0.65左右. 随着轨迹数量的增加, 本文提出的算法DBI的结果值逐渐保持稳定. 对产生的结果进行分析如下: (1)与基线算法ST-DBSCAN相比, 本文算法在密度聚类的过程中增加了车辆速度的条件, 能够识别出基线算法没有识别到的停留点, 因此簇内节点更加紧密. (2)对比算法K_Medians聚类前要事先指定聚类的个数, 导致迭代结果不稳定.
|
图 3 重卡数据集上SC的比较 |
|
图 4 重卡数据集上DBI的比较 |
(3)停留点可视化展示及语义描述
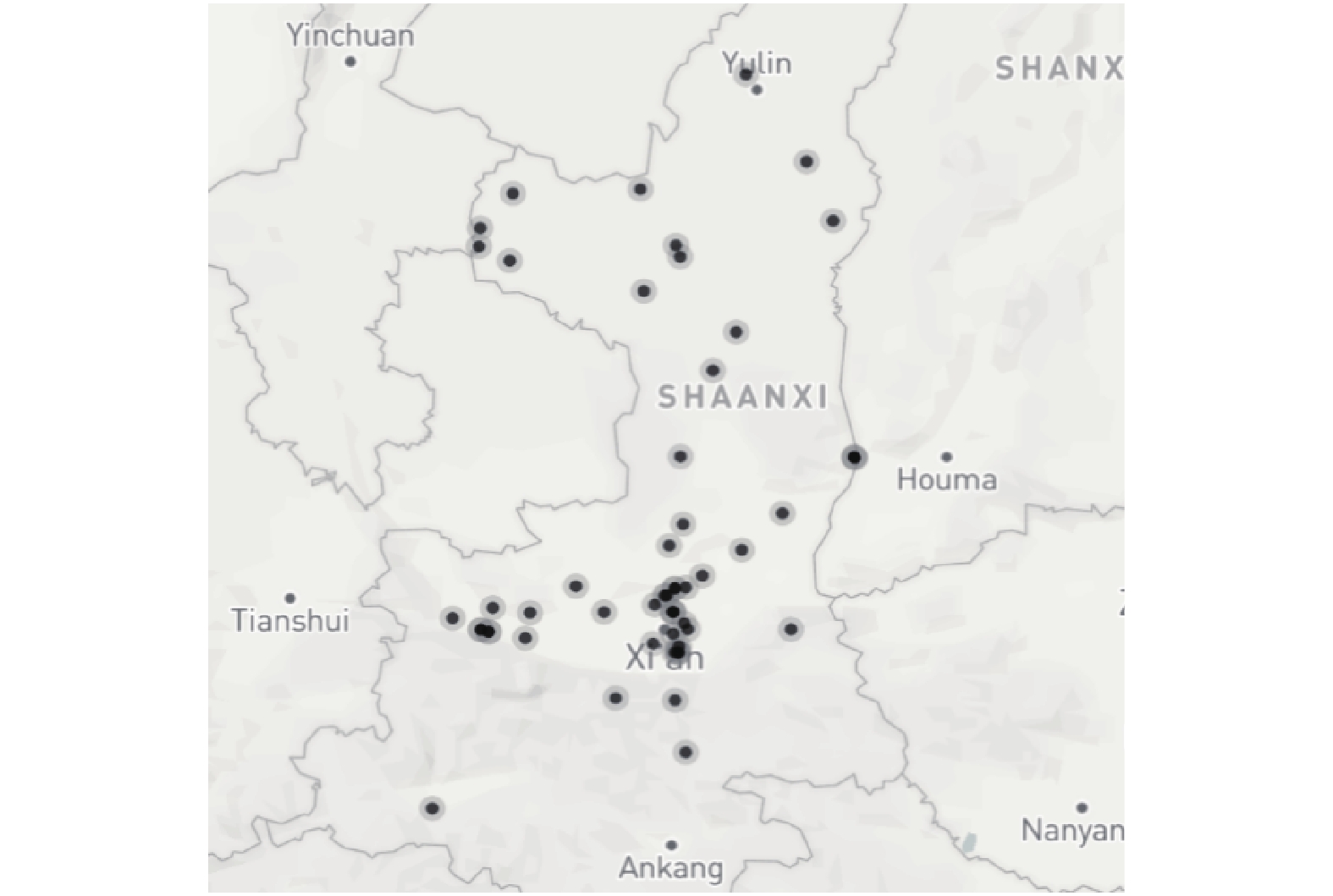
本节将挖掘出的部分停留点在地图上作了可视化处理. 图5展示了挖掘出的陕西省内的重卡车辆的停留点, 用黑色圆点表示. 可以看到, 西安市的停留点较为聚集, 陕西省其他市的停留点较为分散.
|
图 5 停留点的可视化展示 |
结合反向地理编码技术对图5中的部分停留点提取语义信息如表2所示.
| 表 6 停留点语义描述 |
重卡在车辆服务行业中承担着运输的重任, 是国家经济发展不可缺少的一部分. 由表2挖掘出的停留点区域语义化描述可知, 多数停留点在村庄或者公司附近, 结合重卡真实停留点来看, 挖掘出的停留点也是比较符合实际的.
3.2 隐私算法评估(1)停留点间距离: 轨迹点之间的距离可由算法3 haversine函数得到. 本节将停留点隐私保护前后的轨迹点间距离进行计算, 距离越大, 表示隐私保护效果越强.
(2)轨迹失真度: 轨迹失真度表示原始轨迹与隐私保护后轨迹的相似程度, 本节用最长公共子序列(longest common subsequence, LCSS)[37]来衡量轨迹间相似性. 轨迹之间的相似性越大, 轨迹失真度越低; 相反, 轨迹之间的相似性越小, 轨迹失真度越高.
3.2.1 参数选择由Laplace概率密度函数可知, 轨迹隐私保护程度与ε有关. ε越大, 代表加入的噪声越小, 隐私保护程度越低[22] . ε越小, 代表加入的噪声越大, 对原轨迹的扰动越大, 隐私保护程度越高, 但数据可用性会变差.
本文分别选取了ε=5, ε=20, ε=100时, 展示停留点间距离的变化.
3.2.2 实验结果(1)停留点间距离
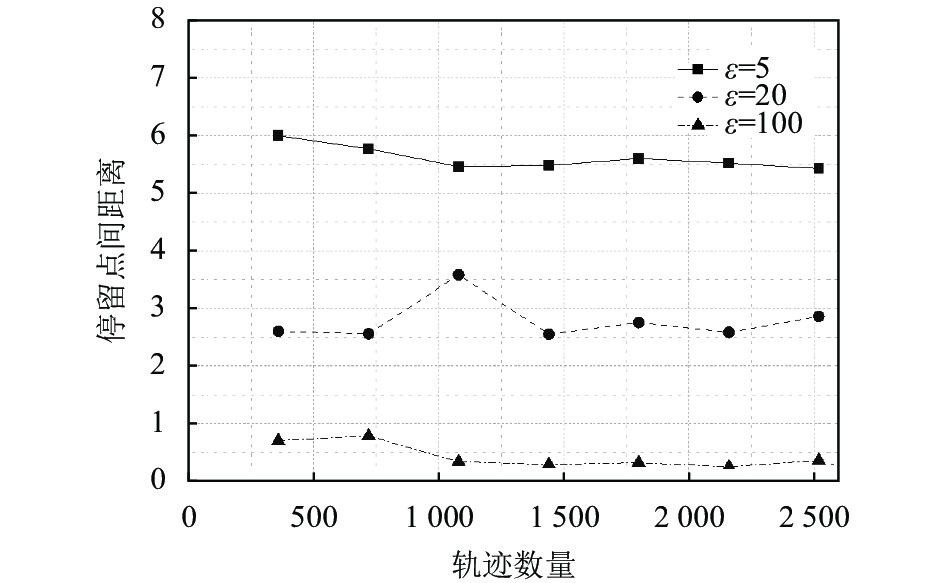
如图6, 展示了不同的ε值, 有着不同的隐私保护效果. 指定区域半径s=10 km, 选取不同值的参数ε, ε越小, 停留点间距离越大, 隐私保护效果越好. 由算法4可知, r ~ gamma(2, 1/ε), 而发布位置点的坐标与r有关, ε越小, r越大. 本文将加噪半径限制在了10 km以内, 即若隐私保护前后轨迹点之间的距离大于10 km, 则重新计算r. 经过多次实验取平均值可以看到, ε=5时, 停留点隐私保护前后的距离在5.5 km左右, 此时隐私保护效果较强; ε=20时, 停留点隐私保护前后的距离在2.6 km左右; ε=100时, 停留点隐私保护前后的距离在1 km以内. 用户在向服务器发送自己的位置时, 可以根据自身的隐私需求选择不同的隐私参数ε.
(2) 轨迹失真度
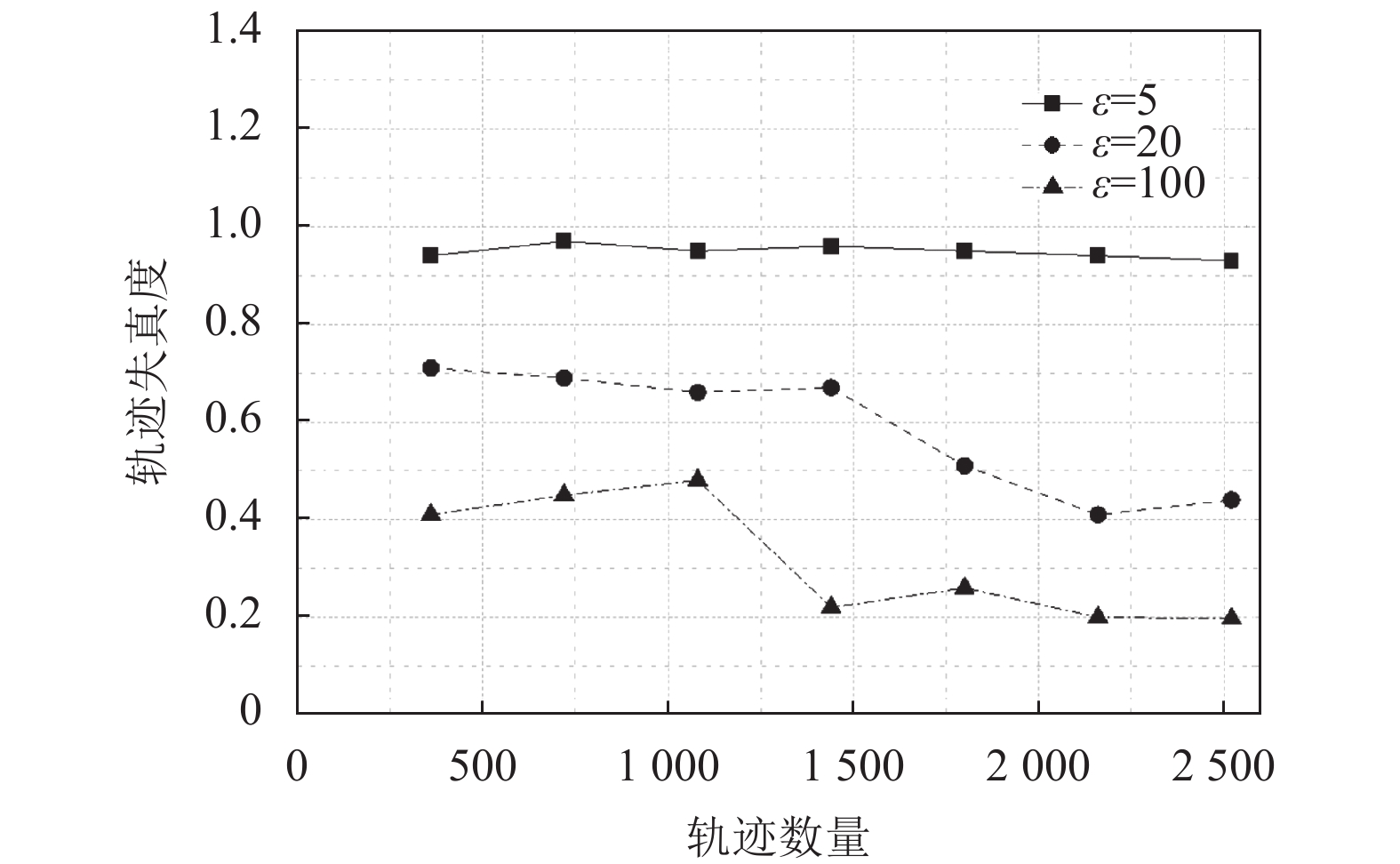
由于对停留点添加噪声数据之后, 又进行了轨迹重构, 那么重构之后的轨迹会与原始轨迹序列之间有一定偏差, 因此用轨迹失真度来衡量这个偏差. 如图7所示, 展示了不同的隐私参数ε下, 轨迹失真度的差别. 隐私参数ε越小, 轨迹失真度越大, 轨迹间相似性越小. 经过多次实验取平均值可以看到, ε=5时, 轨迹失真度在0.9以上; ε=20时, 轨迹失真度在0.75以下; ε=100时, 轨迹失真度在0.5以下. 随着轨迹数量的增长, 轨迹失真度大小呈下降趋势.
|
图 6 隐私保护前后停留点间距离 |
|
图 7 不同隐私参数下的轨迹失真度 |
4 结论
本文提出了一种融合隐私保护的车辆轨迹停留点挖掘方法进行轨迹隐私保护, 该方法将车辆轨迹停留点挖掘与差分隐私保护有效地结合起来, 重点考虑在第三方位置服务商不完全可信的情况下, 如何保护停留点位置的隐私不被泄露. 在停留点挖掘过程中, 采用的是基于密度的聚类方法, 为了有效识别出车辆停留点, 在聚类过程中加入了速度约束; 在隐私保护方面, 依据差分隐私机制对挖掘出来的停留点半径阈值内的点添加拉普拉斯噪声, 之后重新计算该区域内轨迹点的质心, 将质心轨迹坐标替换原来的停留点坐标, 然后构成新的轨迹序列, 达到隐私保护的目的.
| [1] |
李昇智. 基于GPS轨迹数据的位置预测方法研究[博士学位论文]. 沈阳: 东北大学, 2018. 1–2.
|
| [2] |
Atluri G, Karpatne A, Kumar V. Spatio-temporal data mining: A survey of problems and methods. ACM Computing Surveys, 2019, 51(4): 83. |
| [3] |
沈逸文. 面向实时数据流的轨迹数据分析平台[硕士学位论文]. 杭州: 浙江工商大学, 2017. 1–2.
|
| [4] |
王冬. 面向位置服务的差分隐私保护方法研究[博士学位论文]. 武汉: 武汉大学, 2021.
|
| [5] |
徐腾鹏. 基于轨迹数据的聚类算法和差分隐私保护算法研究[硕士学位论文]. 长春: 吉林大学, 2022.
|
| [6] |
陈新泉, 周灵晶, 刘耀中. 聚类算法研究综述. 集成技术, 2017, 6(3): 41-49. DOI:10.3969/j.issn.2095-3135.2017.03.004 |
| [7] |
Cao Y, Yuan JL, Xiao S, et al. TPM: A GPS-based trajectory pattern mining system. Proceedings of 2019 6th International Conference on Behavioral, Economic and Socio-cultural Computing (BESC). Beijing: IEEE, 2019. 1–4.
|
| [8] |
Enami S, Shiomoto K. Spatio-temporal human mobility prediction based on trajectory data mining for resource management in mobile communication networks. Proceedings of the 2019 IEEE 20th International Conference on High Performance Switching and Routing (HPSR). Xi’an: IEEE, 2019. 1–6.
|
| [9] |
Cheng ZY, Jiang L, Liu DS, et al. Density based spatio-temporal trajectory clustering algorithm. Proceedings of 2018 IEEE International Geoscience and Remote Sensing Symposium. Valencia: IEEE, 2018. 3358–3361.
|
| [10] |
Zhou CQ, Frankowski D, Ludford P, et al. Discovering personally meaningful places: An interactive clustering approach. ACM Transactions on Information Systems, 2007, 25(3): 12-es. DOI:10.1145/1247715.1247718 |
| [11] |
Gao ZG, Huang YC, Zheng LL, et al. Protecting location privacy of users based on trajectory obfuscation in mobile crowdsensing. IEEE Transactions on Industrial Informatics, 2022, 18(9): 6290-6299. DOI:10.1109/TII.2022.3146281 |
| [12] |
Niu XZ, Wang SM, Wu CQ, et al. On a clustering-based mining approach with labeled semantics for significant place discovery. Information Sciences, 2021, 578: 37-63. DOI:10.1016/j.ins.2021.07.050 |
| [13] |
Wang YF, Li MZ, Luo SS, et al. LRM: A location recombination mechanism for achieving trajectory k-anonymity privacy protection
. IEEE Access, 2019, 7: 182886-182905. DOI:10.1109/access.2019.2960008 |
| [14] |
Mahdavifar S, Deldar F, Mahdikhani H. Personalized privacy-preserving publication of trajectory data by generalization and distortion of moving points. Journal of Network and Systems Management, 2022, 30(1): 10. DOI:10.1007/s10922-021-09617-5 |
| [15] |
Peng ZL, An J, Gui XL, et al. Location correlated differential privacy protection based on mobile feature analysis. IEEE Access, 2019, 7: 54483-54496. DOI:10.1109/ACCESS.2019.2912006 |
| [16] |
Ning B, Sun YH, Tao XY, et al. Differential privacy protection on weighted graph in wireless networks. Ad Hoc Networks, 2021, 110: 102303. DOI:10.1016/j.adhoc.2020.102303 |
| [17] |
Han QL, Xiong ZB, Zhang KJ. Research on trajectory data releasing method via differential privacy based on spatial partition. Security and Communication Networks, 2018, 2018: 4248092. |
| [18] |
Zhao XD, Pi DC, Chen JF. Novel trajectory privacy-preserving method based on prefix tree using differential privacy. Knowledge-Based Systems, 2020, 198: 105940. DOI:10.1016/j.knosys.2020.105940 |
| [19] |
Xu CQ, Zhu L, Liu Y, et al. DP-LTOD: Differential privacy latent trajectory community discovering services over location-based social networks. IEEE Transactions on Services Computing, 2021, 14(4): 1068-1083. DOI:10.1109/TSC.2018.2855740 |
| [20] |
王豪, 徐正全. 面向轨迹聚类的差分隐私保护方法. 华中科技大学学报(自然科学版), 2018, 46(1): 32-36. DOI:10.13245/j.hust.180107 |
| [21] |
赵书鹏. 一种基于聚类的交通轨迹差分隐私保护数据发布方法. 现代计算机, 2021, 27(23): 29-35, 42. DOI:10.3969/j.issn.1007-1423.2021.23.006 |
| [22] |
赵濛. 基于差分隐私的幂迭代聚类方法[硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [23] |
Mendes R, Vilela JP. Privacy-preserving data mining: Methods, metrics, and applications. IEEE Access, 2017, 5: 10562-10582. DOI:10.1109/ACCESS.2017.2706947 |
| [24] |
Lu ZJ, Qu G, Liu ZL. A survey on recent advances in vehicular network security, trust, and privacy. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(2): 760-776. DOI:10.1109/TITS.2018.2818888 |
| [25] |
Dwork C. Differential privacy. Proceedings of the 33rd International Colloquium on Automata, Languages and Programming. Venice: Springer, 2006. 1–12.
|
| [26] |
Pavan KK, Rao AA, Rao AVD, et al. Single pass seed selection algorithm for K-means. Journal of Computer Science, 2010, 6(1): 60-66. DOI:10.3844/jcssp.2010.60.66 |
| [27] |
Birant D, Kut A. ST-DBSCAN: An algorithm for clustering spatial-temporal data. Data & Knowledge Engineering, 2007, 60(1): 208-221. DOI:10.1016/j.datak.2006.01.013 |
| [28] |
石陆魁, 张延茹, 张欣. 基于时空模式的轨迹数据聚类算法. 计算机应用, 2017, 37(3): 854-859, 895. DOI:10.11772/j.issn.1001-9081.2017.03.854 |
| [29] |
张文元, 谈国新, 朱相舟. 停留点空间聚类在景区热点分析中的应用. 计算机工程与应用, 2018, 54(4): 263-270. DOI:10.3778/j.issn.1002-8331.1608-0255 |
| [30] |
蔡小路, 曹阳, 董蒲. 基于速度的轨迹停留点识别算法. 计算机系统应用, 2020, 29(4): 214-219. DOI:10.15888/j.cnki.csa.007367 |
| [31] |
徐启元, 陈珍萍, 付保川, 等. 基于差分隐私的混合位置隐私保护. 计算机应用与软件, 2019, 36(6): 296-301. DOI:10.3969/j.issn.1000-386x.2019.06.054 |
| [32] |
兰微, 林英, 包聆言, 等. 融入兴趣区域的差分隐私轨迹数据保护方法. 计算机科学与探索, 2020, 14(1): 59-72. DOI:10.3778/j.issn.1673-9418.1901007 |
| [33] |
Andrés ME, Bordenabe NE, Chatzikokolakis K, et al. Geo-indistinguishability: Differential privacy for location-based systems. Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security. Berlin: ACM, 2013. 901–914.
|
| [34] |
胡学钢, 李慧宗, 潘剑寒, 等. 联合主题模型的标签聚类方法. 模式识别与人工智能, 2017, 30(5): 403-415. DOI:10.16451/j.cnki.issn1003-6059.201705003 |
| [35] |
Moshkovitz M, Dasgupta S, Rashtchian C, et al. Explainable K-means and K-medians clustering. International Conference on Machine Learning. PMLR, 2020. 7055–7065.
|
| [36] |
Wang W, Xia F, Nie HS, et al. Vehicle trajectory clustering based on dynamic representation learning of internet of vehicles. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(6): 3567-3576. DOI:10.1109/TITS.2020.2995856 |
| [37] |
Cheng L, Ng R. On the marriage of Lp-norms and edit distance. Proceedings of the 30th International Conference on Very Large Data Bases. Toronto: VLDB Endowment, 2004. 792–803.
|
 2023, Vol. 32
2023, Vol. 32


