基于云模型和余弦跳跃权重的改进蛙跳算法

引用本文

刘耿旗, 张旭秀, 马洪源. 基于云模型和余弦跳跃权重的改进蛙跳算法. 计算机系统应用, 2023, 32(2): 207-216.http://www.c-s-a.org.cn/1003-3254/8933.html

Liu GQ, Zhang XX, Ma HY. Improved Shuffled Frog Leaping Algorithm Based on Cloud Model and Cosine Leap Weights. Computer Systems and Applications, 2023, 32(2): 207-216(in Chinese).http://www.c-s-a.org.cn/1003-3254/8933.html

基于云模型和余弦跳跃权重的改进蛙跳算法

刘耿旗, 张旭秀, 马洪源

大连交通大学自动化与电气工程学院, 大连 116021

收稿日期：2022-06-24; 修改日期：2022-07-25; 采用时间：2022-08-09; csa 在线出版时间：2022-11-16

基金项目：辽宁省自然科学基金(2019-zd-0108)

通讯作者：刘耿旗, E-mail: flag0328@163.com.

摘要：标准蛙跳优化算法(SFLA)有寻优精度低和易陷入局部收敛区域的缺点, 为提高其性能, 提出一种基于云模型局部搜索和余弦跳跃权重更新位置的改进蛙跳算法(CSFLA). 首先通过Tent混沌映射和反向学习生成种群, 使种群的分布更均匀, 利用云模型的正态特性对子群中的优秀个体的所在区域进行探索. 同时, 对种群中其他个体引入基于余弦函数的跳跃步长权重, 使该权重在整个迭代过程中由高以不同的速率下降, 提高种群的全局搜索能力. 最后, 将CSFLA与多个优化算法在不同类型的测试函数上进行了比较. 结果表明, CSFLA具有更好的收敛速度和精度, 能有效找出全局最优解. 并且将改进算法应用至旅行商问题, 该算法可以找到总路程更短的路线.

关键词: 蛙跳算法反向学习云模型余弦跳跃权重混沌映射

Improved Shuffled Frog Leaping Algorithm Based on Cloud Model and Cosine Leap Weights

LIU Geng-Qi, ZHANG Xu-Xiu, MA Hong-Yuan

School of Automation and Electrical Engineering, Dalian Jiaotong University, Dalian 116021, China

Abstract: The standard shuffled frog leaping algorithm (SFLA) for optimization has the shortcomings of low optimization accuracy and easy falling into a local convergence area. To improve its performance, this study proposes an improved SFLA (CSFLA) based on local search with a cloud model and cosine leap weight update position. First, Tent chaotic mapping and backward learning are performed to generate a population so that the population has a more uniform distribution. The area where the best individuals in the subpopulation are located is explored by taking advantage of the normal property of the cloud model. Then, the leaping step size weight based on the cosine function is introduced to other individuals in the population, which makes the weight decrease from a high level at different rates throughout the iterations to improve the global search ability of the population. Finally, CSFLA is compared with multiple optimization algorithms on different types of test functions. The results show that CSFLA has a better convergence speed and accuracy and can find the global optimal solution effectively. The improved algorithm is applied to the traveling salesman problem and proved able to find shorter routes.

Key words: shuffled frog leaping algorithm (SFLA) opposition-based learning cloud model cosine leap weights chaotic mapping

群智能优化算法是一种新的迭代式搜索算法, 其灵感来源于自然界中以社会方式生活的动物寻找复杂问题解决方案的活动, 它可用于求解旅行商问题(traveling salesman problem, TSP)、多处理机调度问题和可靠性优化问题^[1].

TSP是经典组合优化问题之一^[2], 可以描述为: 在所有城市只有一个业务员的情况下, 业务员如何在每个城市只访问一次的前提下走遍所有城市, 并返回出发点. 同时也被证明是一个NP完全问题.

SFLA (shuffled frog-leaping algorithm)是Eusuff等人^[3]在2003年提出的一种混合启发式搜索算法. SFLA的参数很少, 因此实现起来很容易. 目前, 它已被广泛应用于多目标优化问题, 本研究将改进蛙跳算法应用于TSP, 用于检验算法的运行效果和效率.

文献[4]采取基于记忆的种群划分方法, 根据各组个体质量的优劣, 对种群进行分组, 不同类型的子群以不同的搜索次数采用不同的搜索策略, 充分地促进各子群间的信息交互. 文献[5]结合邻近矩阵初始化种群, 并使用定义的远离矩阵对青蛙个体进行局部搜索, 提高了算法的收敛精度并将其应用于多约束车辆路径模型. 文献[6]采用新颖的贪心算法进行种群初始化, 同时提出新的个体的重建策略, 提升了算法全局搜索效率. 文献[7]提出了一种基于解空间反向跳跃和强化子群间信息交互的个体更新方式, 降低了算法后期产生劣解的概率, 防止算法早熟. 文献[8]提出自主选择进化策略的更新方式, 使个体位置更新时从4种进化策略种选择, 提升了算法寻优速度.

文献[9]提出了一种改进的SFLA, 在局部搜索中使用levy flight公式控制跃迁步长, 并在全局洗牌中加入交互式学习规则, 提高了局部搜索和全局信息交换能力. 文献[10]将对立学习应用到种群初始化和个体位置更新中, 增强种群多样性, 克服了算法易早熟的缺点. 文献[11]结合粒子群算法和SFLA, 利用全局反馈, 改进了种群个体的位置更新方式, 避免了算法陷入局部最优. 文献[12]设计基于临近信息的个体生成算子, 并加入子组最优解的变异, 使算法不会过早收敛于非最优解. 文献[13]利用逆向学习算法进行初始化, 并在局部搜索中引入交叉因子, 提高了算法的性能.

此外, SFLA 以其卓越的全局优化能力和少量参数被广泛应用于各种工程问题^[14], 使用惩罚函数将多个目标转换为单个目标. 然后将 SFLA 与改进的局部搜索策略和全局洗牌机制一起应用于社交网络中的影响最大化问题. 文献[15, 16]将改进的蛙跳算法用于QoS的路由优化问题. 文献[17]将改进的算法用于传感器的任务分配. 文献[18]采用了改进的SFLA来优化网络的一些参数, 从而提高了货币汇率预测模型的准确性. 文献[19]提出了一种有效的离散SFLA, 设计新的个体位置更新公式, 有效提升搜索效率.

结合上述学者对蛙跳算法的分析和改进, 本文首先采用基于Tent混沌映射生成种群, 然后根据反向学习来生成最终的种群, 增加了种群的多样性和随机性, 同时在个体位置更新过程中引入基于余弦变化的跳跃权重, 并设立精英组, 用云模型变异对精英个体进行局部搜索. 最后对算法进行收敛性分析, 并通过实验仿真和具体应用证明算法的有效性.

1 标准混洗蛙跳算法

蛙跳算法将模因演化算法的信息交换和粒子群算法的位置更新相结合, 模拟了青蛙种群寻找食物的行为, 拥有更强的搜索能力.

蛙跳算法分为全局搜索和局部搜索两大部分, 在全局搜索中, 先对青蛙种群进行随机初始化, 并且按照适应度函数对青蛙个体将进行排序并完成分组操作, 然后进行局部搜索阶段(也被称为模因进化).

根据适应度值排序, 选择种群最优个体— $ X_g $ 、局部最优个体— $ X_{b} $ 和局部最差个体— $ X_{w} $ , 用于位置更新.

对于算法中的局部搜索阶段, 首先在每一个子群中采用轮盘赌选择算法挑选出数量为q的亚群, 然后对每个亚群中最差个体进行位置更新. 在所有子群的最差个体位置完成更新后, 对种群进行重新排序、分组. 位置更新公式如下:

$ X_{{{\rm{new}}}}=S+X_{w} $

(1)

其中, S是个体跳跃的步长, 该步长计算分为3步, 首先根据 ${{X}}_{{b}}$ 和 ${{X}}_{{w}}$ 的差值进行计算, 如果得到的新位置不如原来的, 则采用 ${{X}}_{{g}}$ 和 ${{X}}_{{w}}$ 的差值进行计算步长; 如果得到的新位置仍然不如原来的位置, 则随机选取一个新位置. 步长计算公式如下:

$ S = {\rm{min}} \{ {\mathop{ int}} [rand({X_b} - {X_w})], {S_{{\rm{max}} }}\} $

(2)

$ S={\rm{min}} \{{int}[{rand}(X_{g}-X_{w})], S_{{\rm{max}} }\} $

(3)

其中, $ rand $ 是一个在[0, 1] 范围内的随机数, $ S_{\max } $ 是个体跳跃时的最大步长, 步长的维度等于决策变量的数量, 即需要优化问题的维度.

虽然 SFLA 相对于其他算法收敛更快, 但由于位置更新公式过于依赖 $ X_{b} $ , $ X_{g} $ 和 $ X_{w} $ , 使得种群搜索区域过于片面, 进而导致算法易陷入局部最优. TSP随着问题规模的增大, 其可行解集的规模呈指数增长, 不可避免地导致“组合爆炸”现象, 标准蛙跳算法容易陷入局部最优解, 进而无法找到路程更短的路线.

2 改进的混洗蛙跳算法 2.1 基于混沌映射与反向学习的种群初始化 2.1.1 混沌映射

在进化算法的实际运行中, 如果对进化算法的初始化方式进行优化, 使其产生的种群个体更具有随机性、遍历性, 这更有利于算法找到最优个体, 在一定程度上减少算法的运行时间.

本算法首先使用Tent映射生成种群. Tent映射是一个分段的线性映射, 它可以在初始化时使种群较为均匀地分布在更大的搜索区域上, 进而提高算法的全局搜索能力.

$ x_{n+1}=\left\{\begin{array}{ll} \dfrac{x_{n}}{\alpha}, & x_{n} \in[0, \alpha) \\ \dfrac{\left(1-x_{n}\right)}{1-\alpha}, & x_{n} \in[\alpha, 1] \end{array}\right. $

(4)

其中, $ 0< \alpha<1 $ , 本文取 $ \alpha=0.5 $ .

2.1.2 反向学习

反向学习是Tizhoosh^[20]于2005年提出的一种用于扩大生成解的范围, 进而加强算法寻优和收敛能力的新方法. 主要思想是: 在求解问题时, 同时考虑可行解以及其相对解, 并通过具体问题的适应度函数从两个解中选取更为优质的解.

$ X_{{\rm{opp}}}=L b+U b-X_{i} $

(5)

本文在初始化中引入基于反向学习的思想. 在经过Tent混沌初始化后, 通过采用反向学习生成种群的反向解, 增加种群的多样性, 在初始化时将种群数量翻倍. 然后再根据个体的优秀程度, 选择前 $ N $ 个体作为本算法的真正初始种群.

2.2 基于余弦函数的跳跃权重

根据种群中个体的优劣程度对个体进行排序, 并将种群划分为 $ { m } $ 个拥有 $ n $ 只个体的子群, 即满足 $ N= n \times m $ . 分组方式按照标准蛙跳算法分组方法, 前 $ m $ 只个体作为每组的第一位, 即每个子群的局部最优个体, 依次类推, 将种群中的个体均匀分配到每个子群.

在子群的局部搜索阶段, 受到文献[21]的启发, 提出一种基于余弦函数和当前迭代次数的跳跃距离权重. 使个体在位置更新时不仅参考最优个体和最差个体, 而是增加了对上次更新的位置的参考, 避免算法过早陷入局部最优. 使算法在初始阶段进行更大范围的全局搜索; 在中间阶段平稳地过渡到对最优位置附近区域进行局部搜索; 在算法后期能更快地收敛到精确的最优解.

该权重迭代公式如式(6)、式(7)所示. 其中 $\omega_{ {{\rm{ini}} }}$ 和 $\omega_{ {{\rm{fin}} }}$ 是余弦跳跃惯性权重的初始值和最终值, 本文中 $\omega_{ {{\rm{ini}} }}$ =0.9, $\omega_{ {{\rm{fin}} }}$ =0.4, $ t_{\max } $ 是算法的最大迭代次数, $t $ 是算法的当前迭代次数.

$ \omega_{{{\rm{cos}}}}(t)=\dfrac{(\omega_{{{\rm{ini}}}}+\omega_{ {{\rm{fin}} }})}{2}+ \dfrac{(\omega_{{{\rm{ini}}}}-\omega_{{\rm{fin}} })}{2} \times \cos \left(\dfrac{I(t)}{t_{\max }} \pi\right) $

(6)

$ I(t+1)=\left\{\begin{array}{l} I(t)+1.5, \; I(t) \leqslant \dfrac{t_{\max }}{6} \\ I(t)+5, \; \dfrac{t_{\max }}{6} \lt I(t) \leqslant \dfrac{5 t_{\max }}{6} \\ I(t)+\dfrac{2}{9}, \; \dfrac{5 t_{\max }}{6} \lt I(t) \leqslant t_{\text {max }} \end{array}\right. $

(7)

$ S=\omega_{\cos }(t) \times S+{rand}\left({X}_{{b}}-{X}_{{w}}\right) $

(8)

$ S=\omega_{{{\rm{cos}}}}(t) \times S + {rand}\left({X}_{{g}}-{X}_{{w}}\right) $

(9)

基于余弦变化和迭代次数的权重随迭代次数的变化曲线如图1所示.

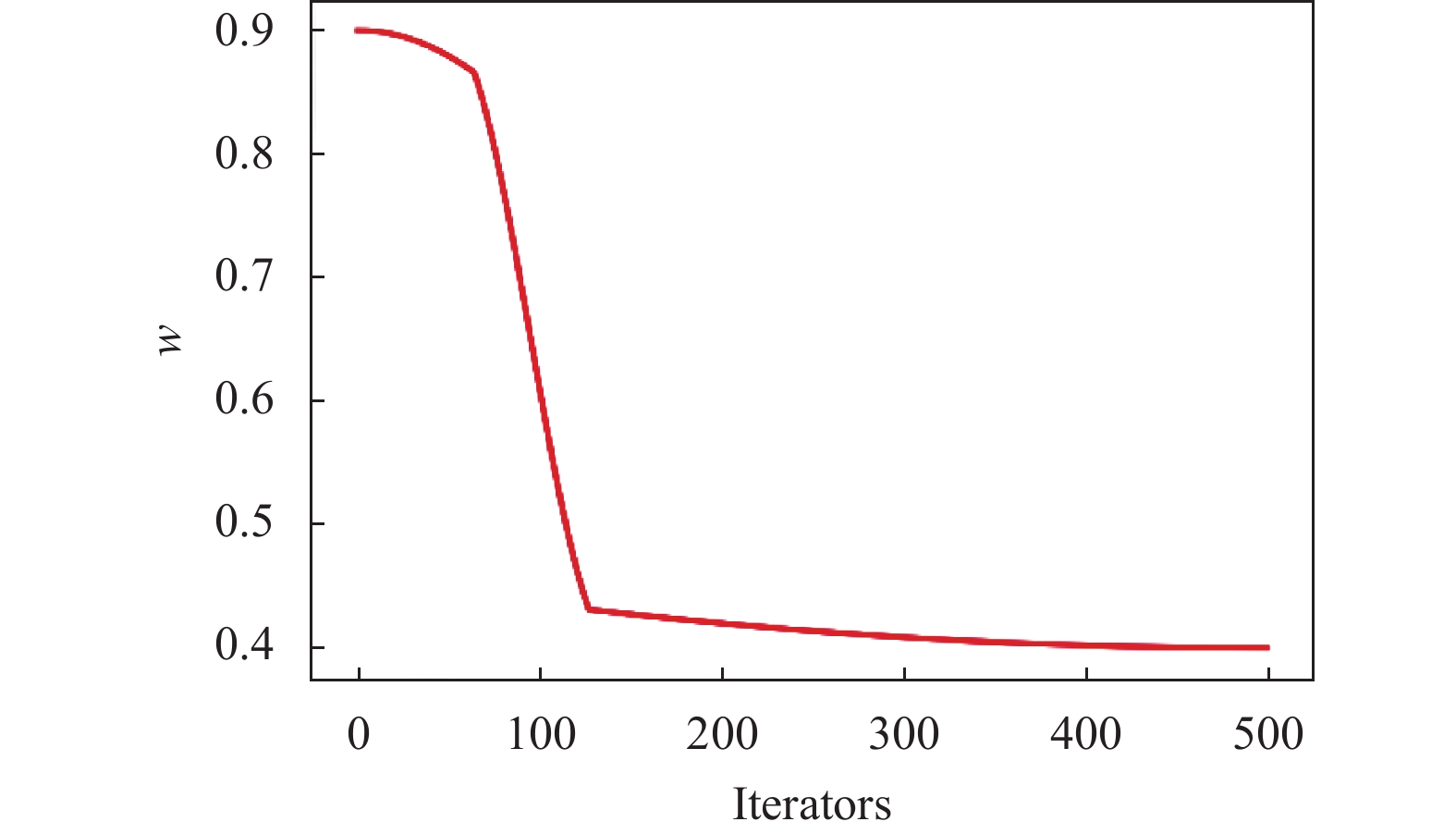
图 1 权重随迭代次数变化图

2.3 基于云模型的精英搜索

在一般情况下, 优质解的附近会分布同样优质甚至更为优质的解, 基于该思想, 本文定义精英组的概念. 精英组中的个体是种群中适应度值前 $ m $ 的个体. 并采用云模型的方法对精英组内的个体一定范围的区域进行探索, 寻找更为优质的可行解. 同时防止算法陷入局部最优.

更新时用到的云模型是李德毅等人^[22]在1995年提出的一种数学模型. 本文采用基于正态分布的云模型生成器, 可以更好地对精英组个体进行改善, 其隶属度函数如下:

$ \mu(x)=\exp \left[-\frac{\left(x-E_{x}\right)^{2}}{\left(2\left(E_{n}^{\prime}\right)^{2}\right)}\right] $

(10)

精英组位置更新公式如下:

$ X_{{{\rm{new}}}}={{Gnc}}\left(X_{b}, {E_n}, {H_e}, {Num}\right) $

(11)

其中, $ E_{x} $ 为期望代表了中心位置, 在本文为 $ X_{b} $ ; $ E_{n} $ 为云模型的熵, 代表了云的宽度, 本文取0.1; $ H_{e} $ 为超熵, 表示生成个体的聚集程度, 取0.04; $ { Num } $ 为生成个体数, 本文取5.

对精英组个体位置的每一次更新将生成 $Num$ 个新位置, 并采取其中最优秀的位置, 若新位置适应度值劣于精英组个体位置, 则保持原有位置.

综上所述, 本文提出了一种基于云模型和余弦跳跃权重的改进蛙跳算法(CSFLA), 流程图如图2所示.

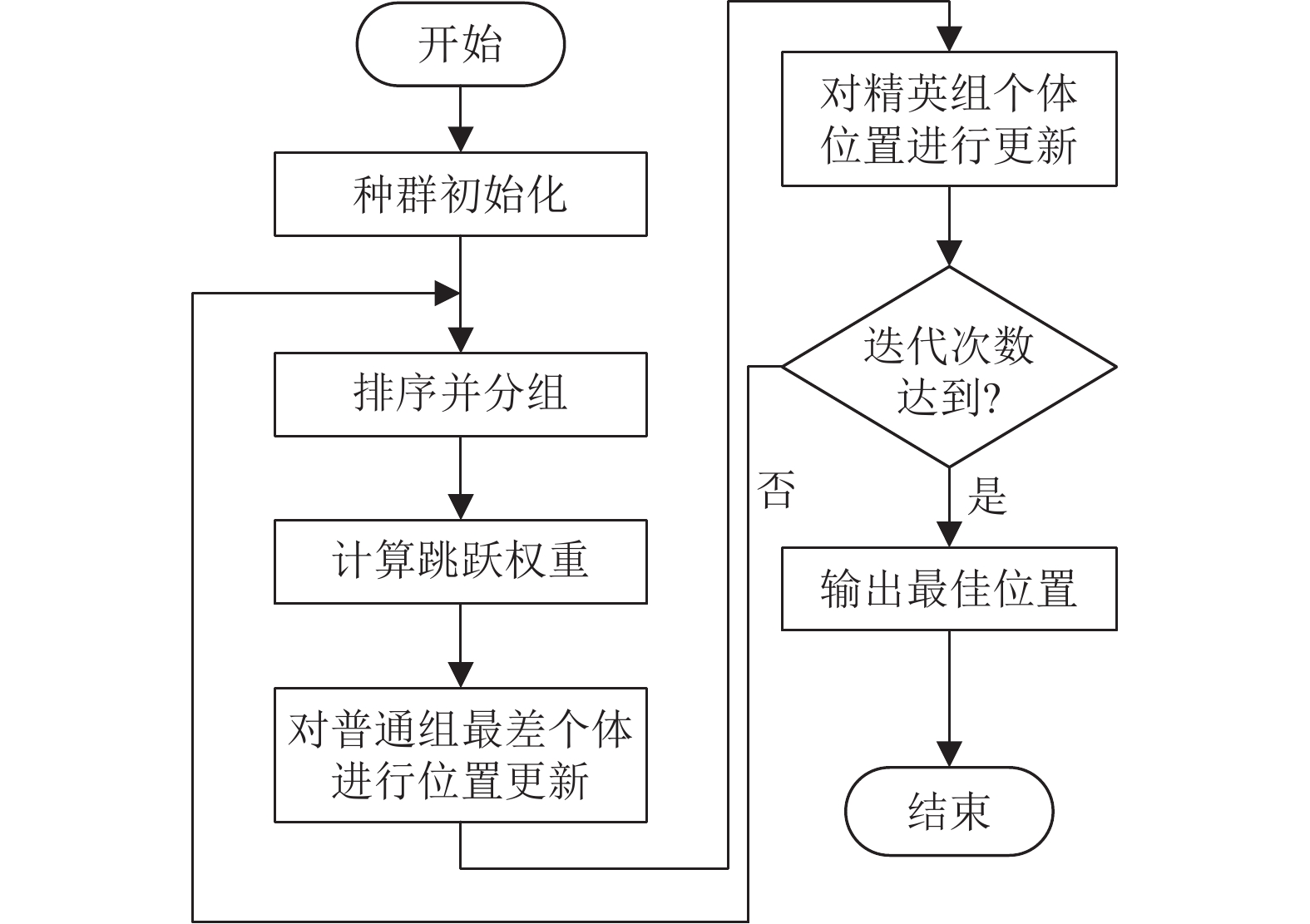
图 2 CSFLA算法流程图

3 收敛性分析

在本节中, 设子群中的最优个体为全局的最优个体, 即 $ X_{b} $ = $ X_{g} $ , 并且为了加大新解的产生范围, 将式(1)、式(8)和式(9)进行以下扩展.

第 $ k $ 次迭代:

$ X_{{w}}^{k}=\alpha X_{{w}}^{{k-1}}+\beta\left(X_{{t}}^{k-1}-X_{{w}}^{k-1}\right) $

(12)

第 $ k+1 $ 次迭代:

$ X_{{w}}^{k+1}=\alpha X_{{w}}^{k}+\beta\left(X_{{b}}^{k}-X_{{w}}^{k}\right) $

(13)

其中, $ \alpha $ 和 $\; \beta $ 为随机数, 由步长 $ S $ 和0–1的随机数经过计算组成. 由式(12)和式(13)可得:

$ X_{{w}}^{k+1}-X_{{w}}^{k}=(\alpha-\beta)\left(X_{{w}}^{k}-X_{{w}}^{k-1}\right)-\beta\left(X_{{t}}^{k}-X_{{t}}^{k-1}\right) $

记 $ \Delta X^{k+1}=X^{k+1}-X^{k} $ , 因此式(13)可以整理为:

$ \Delta X_{w}^{k+1}=\alpha \Delta X_{w}^{k}+\beta\left(\Delta X_{{w}}^{k}-\Delta X_{w}^{k}\right) $

进而可得:

$ \frac{\Delta X_{{w}}^{k+1}}{\Delta X_{{w}}^{k}}=\alpha+\beta\left(\frac{\Delta X_{{b}}^{k}}{\Delta X_{{w}}^{k}}-1\right) $

令 $l=\dfrac{\Delta X_{{b}}^{k}}{\Delta X_{{w}}^{k}}-1$ , 那么可知 $ \Delta X_{w}^{k} $ 是以 $ q=(\alpha+\beta l) $ 为公比的等比数列.

定理1. 若 $ 0<|q|<1 $ , 则 $ \Delta X_{w}^{n} $ 逐渐收敛于0, 并且 $ X_{w}^{n} $ 最终收敛于稳定值.

证明: $ \Delta X_{w}^{k} $ 是以 $ q $ 为公比的等比数列, 由等比数列的性质可知, 若 $ 0<|q|<1 $ , 则 $\lim \Delta {{X}}_{w}^n=0$ .

由数列极限的归并原理知子数列 $ \left\{\Delta X_{m}^{n_{k}}\right\} $ 的极限也为0, 因此 $X_{{w}}^{2}=X_{{w}}^{1}+\Delta X_{{w}}^{1}$ 有上确界, $X_{{w}}^{3}=X_{{w}}^{2}+\Delta X_{{w}}^{2}$ 也有上确界. 因此, $ X_{w}^{n}=X_{w}^{n-1}+\Delta X_{w}^{n-1} $ 亦有上确界, 故 $ X_{w}^{n} $ 收敛得证.

定理2. CSFLA的收敛速度和精度与 $ \alpha $ 和 $ \;\beta $ 在迭代时的大小有关. 因此合理地调整 $ \alpha $ 和 $ \;\beta $ 可以提高CSFLA的收敛速度和精度, 使其具有更强的全局搜索能力和平衡全局与局部的能力.

证明: 由定理1可知: 若 $ 0<|q|<1 $ , 则算法绝对收敛, 局部收敛能力很强. 由式(1), 式(8)和式(9)可知 $ X_{w}^{n} $ 的上确界与 $ X_{b} $ 和 $ X_{g} $ 有关, 但可能陷入局部最优解. 由式(6)–式(9)可知, $ \alpha $ 和 $ \;\beta $ 与 $ \omega_{\cos} $ 有关, 进而与迭代次数t有关. 由第2.2节可知 $ \omega_{\cos} $ 由0.9非线性递减至0.4, 使得在算法前期 $ \omega_{\cos} $ 在算法的早期阶段较大, 在后期阶段较小. 因此, CSFLA同时具有良好的全局搜索能力和对局部进行精细探索的能力.

综上所述, CSFLA满足收敛条件, 且拥有较好的平衡全局与局部搜索的能力

4 仿真与实验

本文中, 所有的实验均使用Python 3.8实现, 编译器为VS Code实验环境为Windows 10 64位操作系统, Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz, 8 GB内存.

在本节中, 设计了3组测试实验来测试CSFLA对不同类型的测试函数(单峰、多峰和固定维)的收敛精度和收敛速度, 并对测试结果的收敛速度和准确度进行分析. 为了形成对比, 与3种其他群体智能优化算法和原始蛙跳算法, 即PSO、CA、GWO和SFLA 与CSFLA进行了比较. PSO是较早提出的群体智能算法, 更是蛙跳算法的灵感来源之一, 已在众多具体项目中得到广泛应用. 之所以选择CA和GWO, 是因为这两个算法是近10年提出的, 具有很强的优化性能, 是经典的群智能算法, 并在工程中得到了一定的应用.

同时设计了城市数量为70的TSP环境, 并将SFLA和CSFLA运用至该环境, 将结果进行对比.

在实验中, CSFLA和SFLA种群数量为50, 其中每个子群中的个体数量为10; 为保证比较的公平性, 规定其他算法的总个体数为500, 与蛙跳算法的总个体数一致; 同时实验中所有算法的总迭代次数均为100次.

4.1 单峰测试函数

单峰测试函数的信息如表1所示, 单峰函数的只有一个极值点, 便于验证CSFLA的收敛速度和精度.

在本节中, 将CSFLA与其他算法在上述的测试函数上进行比较, 测试函数的结果如表2所示, 算法在上述单峰函数的适应度变化曲线如图3所示.

表 1 单峰测试函数信息

函数	函数表达式	搜索维度	范围	最优解
F₁	${F_1}\left( x \right) = \displaystyle \mathop\sum \limits_{i = 1}^n x_i^2$	20	[−100, 100]	0
F₂	${F_2}\left( x \right) =\displaystyle \mathop \sum \limits_{i = 1}^n \left\| {{x_i}} \right\| + \mathop \prod \limits_{i = 1}^n \left\| {{x_i}} \right\| $	20	[−10, 10]	0
F₃	${F_3}\left( x \right) =\displaystyle \mathop \sum \limits_{i = 1}^n {\left( {\mathop \sum \limits_{j = 1}^i {x_j}} \right)^2} $	20	[−100, 100]	0
F₄	${F_4}\left( x \right) = {{\rm{max}}_i}\left\{ {\left\| { {x_i} } \right\|1 \leqslant i \leqslant n} \right\}$	20	[−100, 100]	0
F₅	${F_5}\left( x \right) = \displaystyle \mathop \sum \limits_{i = 1}^{n - 1} \left[ {100 \times {{\left( {{x_{i + 1}} - x_i^2} \right)}^2} + {{\left( {{x_i} - 1} \right)}^2}} \right] $	20	[−2.028, 2.048]	0
F₆	${F_6}\left( x \right) = \displaystyle \mathop \sum \limits_{i = 1}^n {\left( {\left[ {{x_i} + 0.5} \right]} \right)^2} $	20	[−100, 100]	0
F₇	${F_7}\left( x \right) = - 0.0001{\left( {\left\| {{\text{sin}}\left( {{x_1}} \right){\text{sin}}\left( {{x_2}} \right){\text{exp}}\left( {\left\| {100 - \sqrt {x_1^2 + x_2^2} /\pi } \right\|} \right)} \right\| + 1} \right)^{0.1}}$	2	[−10, 10]	−2.06261
F₈	${F_8}\left( x \right) =\displaystyle \mathop \sum \limits_{i = 1}^n {\left\| {{x_i}} \right\|^{i + 1}} $	20	[−1, 1]	0
F₉	${F_9}\left( x \right) =\displaystyle \mathop \sum \limits_{i = 1}^n ix_i^2 $	20	[−5.12, 5.12]	0

表 1 单峰测试函数信息

表 2 单峰函数测试结果

算法	值	F₁	F₂	F₃	F₄	F₅	F₆	F₇	F₈	F₉
CSFLA	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	−2.06E–00	0.00E–00	0.00E–00
	最佳值	2.91E–90	3.81E–45	1.49E–91	5.93E–45	0.00E–00	0.00E–00	−2.06E–00	4.39E–11	5.21E–93
	平均值	5.68E–86	2.15E–37	5.46E–82	1.53E–38	5.49E–02	3.32E–04	−2.06E–00	4.87E–08	1.54E–89
SFLA	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	−2.06E–00	0.00E–00	0.00E–00
	最佳值	1.02E–03	6.46E–03	1.71E–08	1.32E–02	5.98E–03	2.75E–03	−2.06E–00	1.44E–02	9.48E–10
	平均值	5.98E–02	5.48E–02	5.12E–05	5.48E–01	4.47E–01	1.58E–02	−2.06E–00	5.79E–01	5.16E–07
CA	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	−2.06E–00	0.00E–00	0.00E–00
	最佳值	1.88E–01	9.28E–02	6.57E–05	2.54E–02	2.84E–00	1.23E–02	−2.05E–00	5.48E–02	4.21E–05
	平均值	0.97E–00	4.68E–01	4.68E–03	1.28E–01	5.23E+02	8.45E–01	−2.0100	1.65E–01	2.84E–04
PSO	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	−2.06E–00	0.00E–00	0.00E–00
	最佳值	1.39E–05	5.33E–12	3.91E–05	1.71E–16	8.32E–02	1.22E–06	−2.02E–00	5.41E–05	3.92E–04
	平均值	5.87E–03	4.87E–07	2.54E–03	5.13E–12	1.54E–00	7.45E–04	−1.87E–00	8.46E–03	5.13E–03
GWO	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00	−2.06E–00	0.00E–00	0.00E–00
	最佳值	3.11E–05	5.85E–07	2.11E–05	2.18E–05	1.63E–02	7.97E–07	−2.06E–00	2.82E–07	3.31E–24
	平均值	5.47E–03	1.58E–05	1.25E–03	5.64E–03	0.87E–00	5.65E–04	–2.06E–00	1.58E–05	5.46E–20
注: 加粗数据为该测试函数的最好结果

表 2 单峰函数测试结果

由图3可知, CSFLA的收敛速度在F₂、F₄、F₆和F₈函数的测试结果中收敛速度略低于PSO算法, 但根据表2的测试结果, 最后的收敛结果明显优于其他4个算法; 在函数F₇的测试结果中CSFLA的收敛精度并没有明显优于其他, 只是略微提高, 但从图3中可以看到收敛速度比其他3种算法快; 在函数F₁、F₃、F₅和F₉测试结果中, FLA的收敛速度和精度都明显优于其他4个算法.

图 3 单维测试函数结果收敛曲线

4.2 多峰测试函数

由于多峰测试函数具有多个局部极值的特点, 算法容易陷入局部收敛. 因此, 多峰测试函数可以用来测试CSFLA的跳出局部极值和全局探索的能力. 5个多峰测试函数的公式、初始化间隔、全局最优值和测试维度如表3所示.

表 3 多峰测试函数信息

针对多维度测试函数的结果如表4所示, 上述测试函数的适应度变化曲线如图4所示. 由图4可知, 在F₁₀、F₁₃和F₁₄的测试结果中, CSFLA的收敛结果明显优于其他4种算法, 且收敛速度也更快; 在函数F₁₁的测试结果中, CSFLA的收敛速度不如PSO, 但是PSO在结果到4.07E–13就收敛, 而CSFLA的收敛结果为0; 在函数F₁₂中, CSFLA的收敛速度比其他算法快, 但是最终收敛结果的精度不如PSO算法精确, 说明CSFLA在处理F₁₂这类函数的能力还有待进步.

表 4 多峰测试函数结果

算法	值	F₁₀	F₁₁	F₁₂	F₁₃	F₁₄
CSFLA	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	0.00E–00	0.00E–00	0.29E–00	0.00E–00	1.49E–32
	平均值	1.12E–26	0.00E–00	6.48E+01	0.00E–00	5.65E–19
SFLA	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	4.11E–04	8.62E–02	2.97E+00	4.81E–05	8.51E–05
	平均值	5.67E–03	8.01E–02	1.67E+01	5.84E–03	5.96E–02
CA	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	2.49E–03	4.34E–01	1.63E+02	9.25E–03	3.92E–03
	平均值	1.58E–03	3.15E–01	5.12E+03	4.64E–02	1.98E–01
PSO	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	5.65E–20	4.07E–13	2.05E–01	2.39E–38	1.97E–03
	平均值	5.61E–15	3.78E–10	8.45E–01	4.30E–23	1.84E–02
GWO	理论值	0.00E–00	0.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	3.34E–09	1.51E–08	7.01E–00	7.21E–11	5.04E–07
	平均值	3.44E–04	8.57E–06	1.43E+01	7.96E–05	1.37E–03
注: 加粗的数据该测试函数的最好结果

表 4 多峰测试函数结果

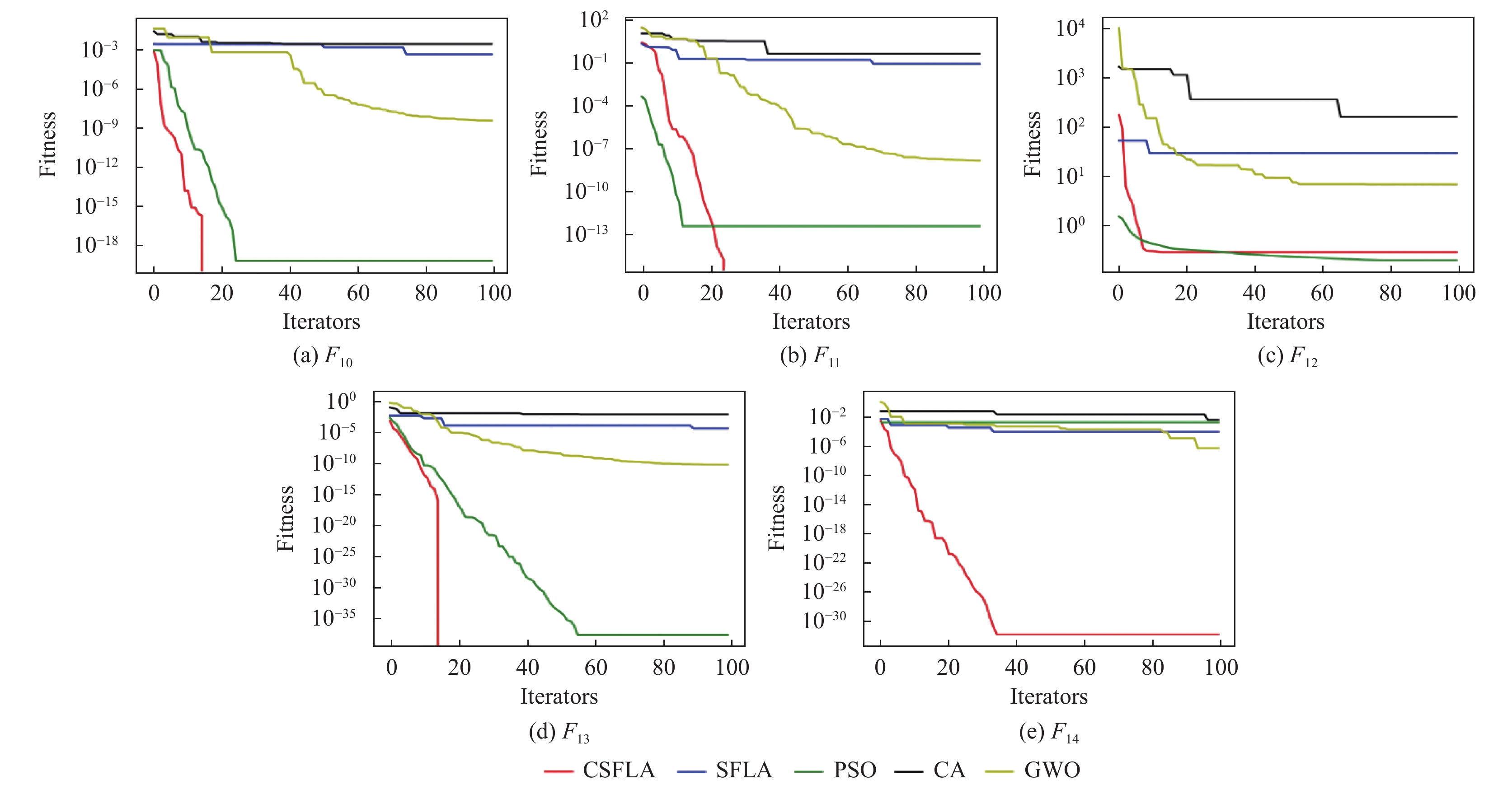
图 4 多维测试函数结果变化曲线

4.3 固定维数测试函数

为了更全面地测试CSFLA在寻找函数最优值方面的性能, 本节选择了4个固定维度的测试函数来进一步验证CSFLA在对函数进行寻优时的收敛速度和收敛精度. 表5列出了固定维度测试函数的公式, 初始化间隔, 全局最优值和测试维度.

对表5中列出的固定维度的测试函数进行测试, 得到的结果如表6所示, 算法的收敛曲线如图5所示.

表 5 固定维数测试函数信息

表 6 固定维测试函数结果

算法	值	F₁₅	F₁₆	F₁₇	F₁₈
CSFLA	理论值	−1.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	−1.00E–00	0.00E–00	1.09E–87	0.00E–00
	平均值	−9.86E–01	0.00E–00	1.94E–75	5.64E–98
SFLA	理论值	−1.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	−9.90E–01	1.59E–07	1.71E–05	4.81E–05
	平均值	−9.02E–01	4.86E–06	1.12E–05	3.54E–04
CA	理论值	−1.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	−9.68E–01	4.79E–05	1.01E–02	9.25E–03
	平均值	−9.12E–01	4.21E–05	8.54E–01	5.25E–02
PSO	理论值	−1.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	−9.36E–01	4.97E–06	6.61E–04	2.39E–38
	平均值	−7.80E–01	4.12E–05	6.02E–04	1.64E–30
GWO	理论值	−1.00E–00	0.00E–00	0.00E–00	0.00E–00
	最佳值	−9.36E–01	1.37E–10	1.85E–09	7.21E–11
	平均值	−7.98E–01	1.59E–08	1.24E–09	5.64E–09
注: 加粗的数据为该测试函数的最好结果

表 6 固定维测试函数结果

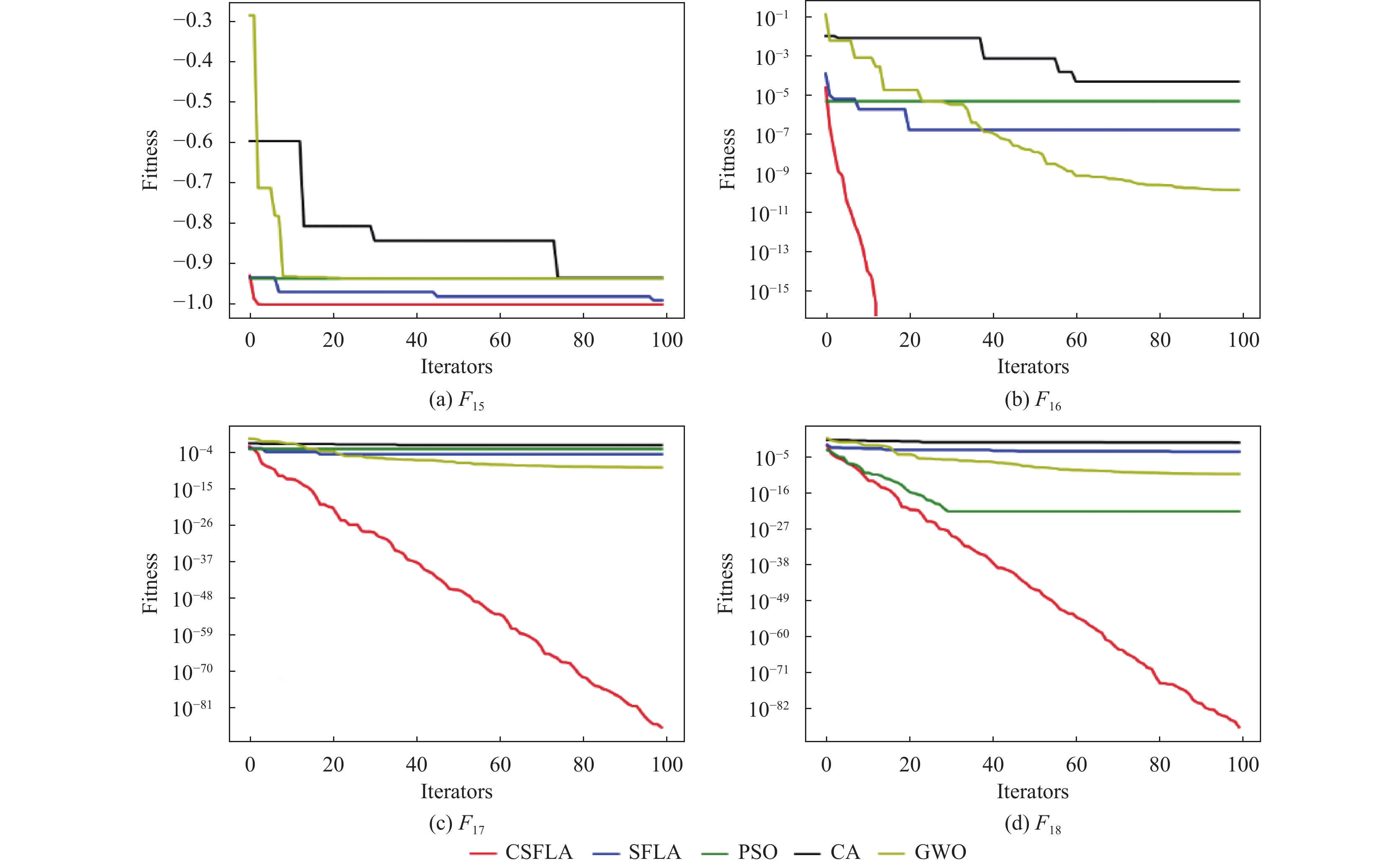
图 5 固定维数测试函数结果收敛曲线

由图5可知, CSFLA在4个固定维度的测试函数上的表现均是最优的, 且在F₁₆和F₁₇的测试结果的收敛精度明细优于其他4个算法; 在函数F₁₈测试结果中, 刚开始和PSO的收敛精度不相上下, 但随着迭代次数的增加, CSFLA的收敛精度逐渐远远优于PSO.

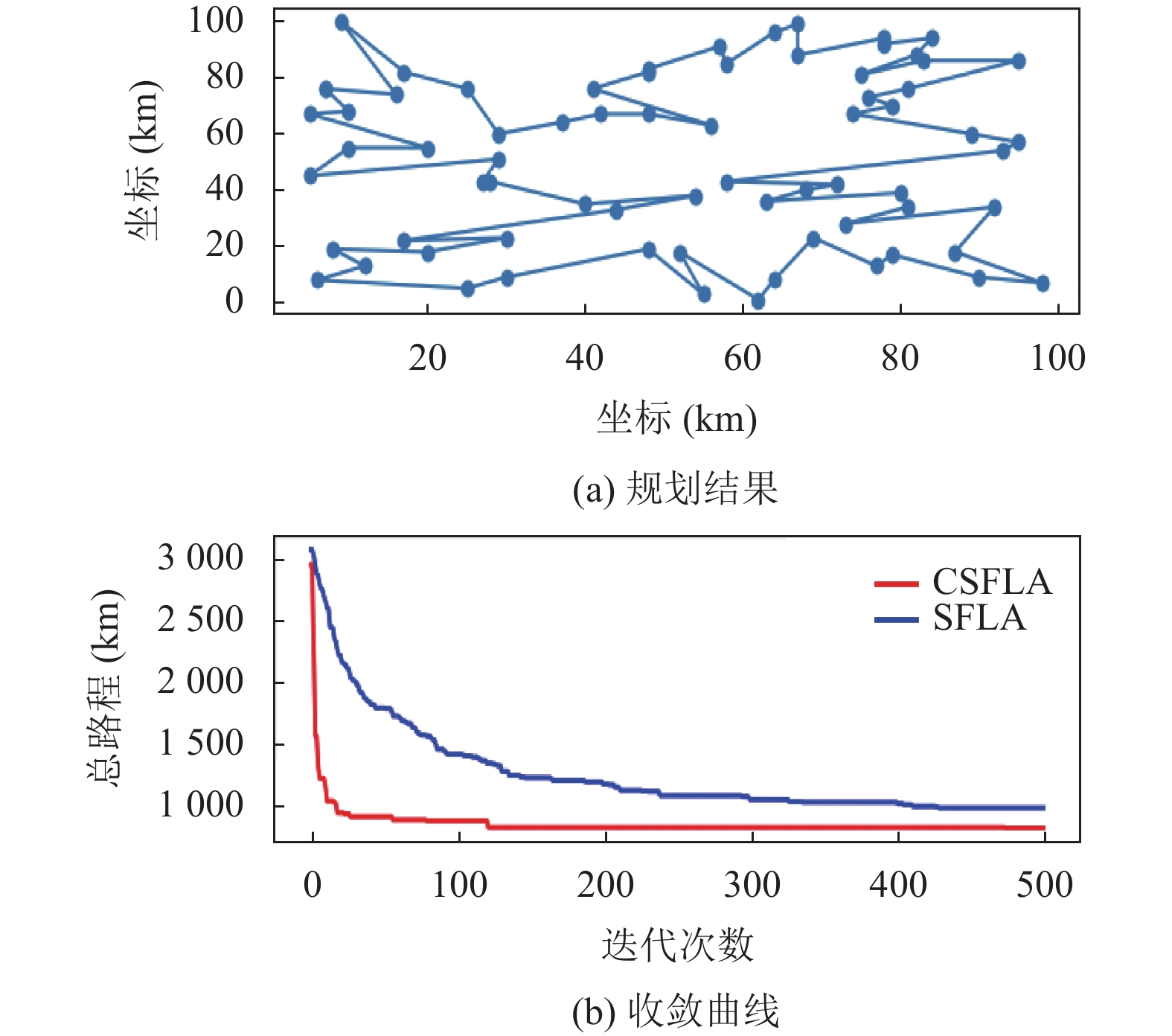
4.4 TSP测验

本节建立城市数为70的TSP环境, 并应用SFLA和CSFLA进行实验, 迭代次数均为500次, 个体数均为200, 组数为10, 子群内个体数为20.

实验结果如图6所示, 可以看到CSFLA无论是在初始化个体的优劣程度优于SFLA; 同时CSFLA的收敛速度更快, 在20次左右的迭代内, 适应度值快速下降, 在迭代120次后达到收敛, 而SFLA的收敛速度较慢, 在420次左右才达到收敛; CSFLA最终收敛结果为693, 而SFLA的族中结果为1142, 相比来看, CSFLA拥有更好的收敛精度.

图 6 TSP 测试结果

5 结论与展望

本文在SFLA基础上引入基于余弦变换和迭代次数的跳跃权重, 使跳跃权重可以随迭代次数以不同的下降速率下降, 平衡了全局搜索能力和局部搜索能力, 同时对原有初始化加入Tent混沌序列和反向学习策略, 并且设立精英组, 对精英组个体采用云模型变异进行更新. 通过对3类不同维度的函数进行测试, 给出CSFLA的收敛性分析. 从最终的收敛结果和收敛曲线来看, 所提出的CSFLA在几乎所有的测试函数中拥有更好的收敛精度和速度, 并且大大增强了跳出局部最优的能力, 但在处理个别多维函数问题时仍有进步空间. 并将CSFLA应用至70个城市规模的TSP环境, 实际结果表明比SFLA更好的收敛精度和速度.

后续的研究将通过使用CSFLA优化移动边缘环境下的多个边缘节点之间的协同卸载问题, 进一步验证CSFLA在具体应用中的优化效果及稳定性.

参考文献

[1]	林诗洁, 董晨, 陈明志, 等. 新型群智能优化算法综述. 计算机工程与应用, 2018, 54(12): 1-9. DOI:10.3778/j.issn.1002-8331.1803-0260
[2]	赵鑫, 杨雄飞, 钱育蓉. 改进的蚁群优化算法求解旅行商问题. 计算机工程与设计, 2022, 43(4): 962-968. DOI:10.16208/j.issn1000-7024.2022.04.009
[3]	Eusuff M, Lansey K, Pasha F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Engineering Optimization, 2006, 38(2): 129-154. DOI:10.1080/03052150500384759
[4]	雷德明, 王甜. 基于改进蛙跳算法的分布式两阶段混合流水车间调度. 控制与决策, 2021, 36(1): 241-248. DOI:10.13195/j.kzyjc.2019.0472
[5]	鲁建厦, 翟文倩, 李嘉丰, 等. 基于改进混合蛙跳算法的多约束车辆路径优化. 浙江大学学报(工学版), 2021, 55(2): 259-270. DOI:10.3785/j.issn.1008-973X.2021.02.006
[6]	徐俊, 项倩红, 肖刚. 基于改进混合蛙跳算法的云工作流负载均衡调度优化. 计算机科学, 2019, 46(11): 315-322. DOI:10.11896/jsjkx.181001866
[7]	申晓宁, 黄遥, 游璇, 等. 基于解空间反向跳跃和信息交互强化的新型混合蛙跳算法. 控制与决策, 2021, 36(1): 105-114. DOI:10.13195/j.kzyjc.2019.0719
[8]	张强, 李盼池. 进化策略自主选择的改进混洗蛙跳算法. 哈尔滨工程大学学报, 2019, 40(5): 979-985. DOI:10.11990/jheu.201803086
[9]	Tang DY, Yang J, Dong SB, et al. A lévy flight-based shuffled frog-leaping algorithm and its applications for continuous optimization problems. Applied Soft Computing, 2016, 49: 641-662. DOI:10.1016/j.asoc.2016.09.002
[10]	Sharma TK, Pant M. Opposition based learning ingrained shuffled frog-leaping algorithm. Journal of Computational Science, 2017, 21: 307-315. DOI:10.1016/j.jocs.2017.02.008
[11]	周林, 陶冠宏, 王佩. 一种基于混合蛙跳和粒子群融合的改进优化新算法. 电子信息对抗技术, 2019, 34(6): 27-31. DOI:10.3969/j.issn.1674-2230.2019.06.007
[12]	Huang Y, Shen XN, You X. A discrete shuffled frog-leaping algorithm based on heuristic information for traveling salesman problem. Applied Soft Computing, 2021, 102: 107085. DOI:10.1016/j.asoc.2021.107085
[13]	Ning B, Gu Q, Wang Y. Research based on effective resource allocation of improved SFLA in cloud computing. International Journal of Grid and Distributed Computing, 2016, 9(3): 191-198. DOI:10.14257/ijgdc.2016.9.3.20
[14]	Elattar EE. Environmental economic dispatch with heat optimization in the presence of renewable energy based on modified shuffle frog leaping algorithm. Energy, 2019, 171: 256-269. DOI:10.1016/j.energy.2019.01.010
[15]	卢毅, 徐梦颖, 周杰. 基于改进的免疫克隆蛙跳算法的多约束QoS路由优化研究. 通信学报, 2020, 41(5): 141-149. DOI:10.11959/j.issn.1000-436x.2020102
[16]	Malathi A, Sreenath N. Improved shuffled frog-leaping algorithm based QoS constrained multicast routing for VANETs. Wireless Personal Communications, 2018, 103(4): 2891-2907. DOI:10.1007/s11277-018-5976-y
[17]	Xiao J, Liu Y, Zhang Y, et al. A novel sensor task allocation method based on quantum elite shuffled frog leaping algorithm in IWSNs. Journal of Physics: Conference Series, 2021, 1924: 012031. DOI:10.1088/1742-6596/1924/1/012031
[18]	Dash R. Performance analysis of a higher order neural network with an improved shuffled frog leaping algorithm for currency exchange rate prediction. Applied Soft Computing, 2018, 67: 215-231. DOI:10.1016/j.asoc.2018.02.043
[19]	Tang JX, Zhang RS, Wang P, et al. A discrete shuffled frog-leaping algorithm to identify influential nodes for influence maximization in social networks. Knowledge-based Systems, 2020, 187: 104833. DOI:10.1016/j.knosys.2019.07.004
[20]	Tizhoosh HR. Opposition-based learning: A new scheme for machine intelligence. International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06). Vienna: IEEE, 2005. 695–701.
[21]	Zhang J, Sheng JN, Lu JW, et al. UCPSO: A uniform initialized particle swarm optimization algorithm with cosine inertia weight. Computational Intelligence and Neuroscience, 2021, 2021: 8819333. DOI:10.1155/2021/8819333
[22]	李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器. 计算机研究与发展, 1995, 32(6): 15-20.