2. 国网江苏省电力有限公司电力科学研究院, 南京 210019;
3. 国电南瑞科技股份有限公司, 南京 211106
2. Electric Power Research Institute of State Grid Jiangsu Electric Power Co. Ltd., Nanjing 210019, China;
3. NARI Technology Co. Ltd., Nanjing 211106, China
近几年, 电动汽车因其环保、清洁、节能的优势在我国各个省市大力推广, 逐渐普及[1]. 电动汽车充电设施作为电动汽车推广过程中的重要组成成分, 也发展迅速[2]. 目前, 电动汽车充电设施内部结构逐渐精细, 功能也越来越多, 智能化也在逐渐增强[3]. 但是, 在充电过程中, 相关的故障还是时有发生. 充电设施的安全问题, 不仅关乎着电动汽车的推广, 更关乎着电动汽车用户的安全[4]. 充电设施的故障诊断与预测是保障充电安全的重要措施, 也是电动汽车整个行业关切的问题.
充电设施根据不同用户的需求分为直流快充桩与交流慢充桩, 用户可根据自身需求进行选择[5]. 充电设施运行环境复杂, 涉及各方面人员. 由于运维服务体系的不完善, 故障率较高阻碍了电动汽车的推广发展[6]. 因此, 提高充电设施使用率, 减少充电设施故障发生率是需要解决的关键问题[7]. 目前, 充电设施的故障检测方面更多是人工检测建立分析模型, 或者充电设施自身的过压、过流等保护装置进行判断[8]. 其诊断精度与效率还够高. 传统一些充电设施运行状态和故障检测方法存在一定的缺陷. 根据相似性传播聚类算法无需先设置聚类中心与个数的特点, 江南大学学者利用基于距离的相似性传播聚类处理区间数据[9], 因此能够较为快速的识别数据中心, 但是在实际的故障诊断过程中由于数据信息冗杂, 影响因素较多, 造成设备的故障诊断准确率不高. 在过去的10年里, 马尔克夫模型在多个领域被广泛使用, 其中隐马尔克夫模型在故障诊断与预测中的使用逐渐活跃[10]. 隐马尔克夫模型是属于一种不确定性概率模型, 是通过一个隐藏的马尔可夫链生成随机不可观测序列, 然后由各个不可观测状态生成一个可观测随机序列的过程[11]. 其过程与故障发生的演变过程具有相似之处. 随着近些年来, 深度学习已成为研究领域的热点[12, 13], 在故障诊断与预测方面也有所应用. 其中, CNN是一种广泛应用在图像处理相关问题上[14], 具有强大的特征提取优势. 循环神经网络(recurrent neural network, RNN)自提出以来, 被广泛应用在随着时间序列变化的特征参数当中[15].
文章利用深度学习算法的优势, 基于GRU网络模型, 提出一种改进的GRU算法对充电设施进行故障预测. GRU模型本身是基于RNN网络基础上改进的网络模型, 解决了RNN学习过程中反向传播长时间滞后导致梯度爆炸或减小的问题. 文中利用粒子群算法对GRU网络初始参数进行优化, 并利用SVM优化网络输出, 最优利用算例结果表明, 该模型提高了充电设施的故障预测准确率.
1 直流充电桩故障分析及数据扩充直流充电桩主要包括AC-DC和DC-DC充电模块、辅助电源模块、非车载控制器模块、充电接口模块(充电枪部分). 充电桩输入电压为380 V, 经过AC-DC和DC-DC, 变换为电动汽车所需的充电电压, 具体输出电压由电动汽车电池最高电压和充电桩最高输出电压的最小值决定, 该过程由车载控制器与非车载控制器进行通信对充电模块进行控制实现. 而充电过程中故障的发生严重影响了充电设施、电动汽车以及人员的安全.
1.1 充电故障分析充电桩故障状态类型可分为充电时故障以及非充电时故障, 而绝大多数故障发生在故障过程中, 非充电时故障原因主要是由于环境影响以及运维服务的欠缺造成, 存在较大的不确定性, 主要解决方案为定期检修排查. 文中主要研究的充电桩故障为充电时故障. 某地区直流充电桩故障的统计, 在充电过程中, 充电机输出过压占比37.54%; 通信超时故障发生占比10.32%, 直流输出短路故障占比7.31%; 充电模块过温占比6.75%、输出欠压故障占比4.48%; 输出过流占比3.89%; 充电枪故障占比3.01%; 绝缘异常故障占比2.87%; 其他故障占比23.83%. 输出过压故障占比最高, 该故障影响不可忽视.
通信故障包括通信超时故障与通信中断故障, 发生通信超时故障时, 控制器控制开关断开, 10 s内停止充电; 若通信中断, 则所有开关全部断开, 10 s内停止充电. 正常情况下相关设备并不会损坏. 但对于发生充电机输出过压故障, 输出短路故障等, 虽然充电设施内的断路器能够在一定时间内进行断开处理, 这些故障已经对充电模块以及其他电路造成影响, 如果多次发生类似故障, 将同时对电动汽车的电池产生损坏.
因此, 亟需在故障即将发生时, 判断出故障并预测出故障类型, 提前采取措施, 避免故障发生带来的不必要的损坏. 文中主要研究充电设施输出过压、输出欠压、充电模块过温、输出过流、直流输出短路以及绝缘异常的故障预测. 由于从实际充电设施中获取的具体故障类型的数据量有限, 因此需要对原始数据样本进行扩充处理, 增加样本量以便用于后续的深度学习网络训练与测试.
1.2 充电故障分析数据扩充处理的方法有多种, VAE是一个不受数据格式影响的通用性很强的数据增强方法[16, 17]. VAE是由编码器与解码器构成, 其中编码器通过对原始充电过程采样的训练数据X进行编码得到隐藏层的隐向量Z, 设置Z分布的均值和方差, 依据生成的隐藏变量Z的变概率分布, 最后利用解码器生成近似于原始数据的X'. 基本框架见图1.
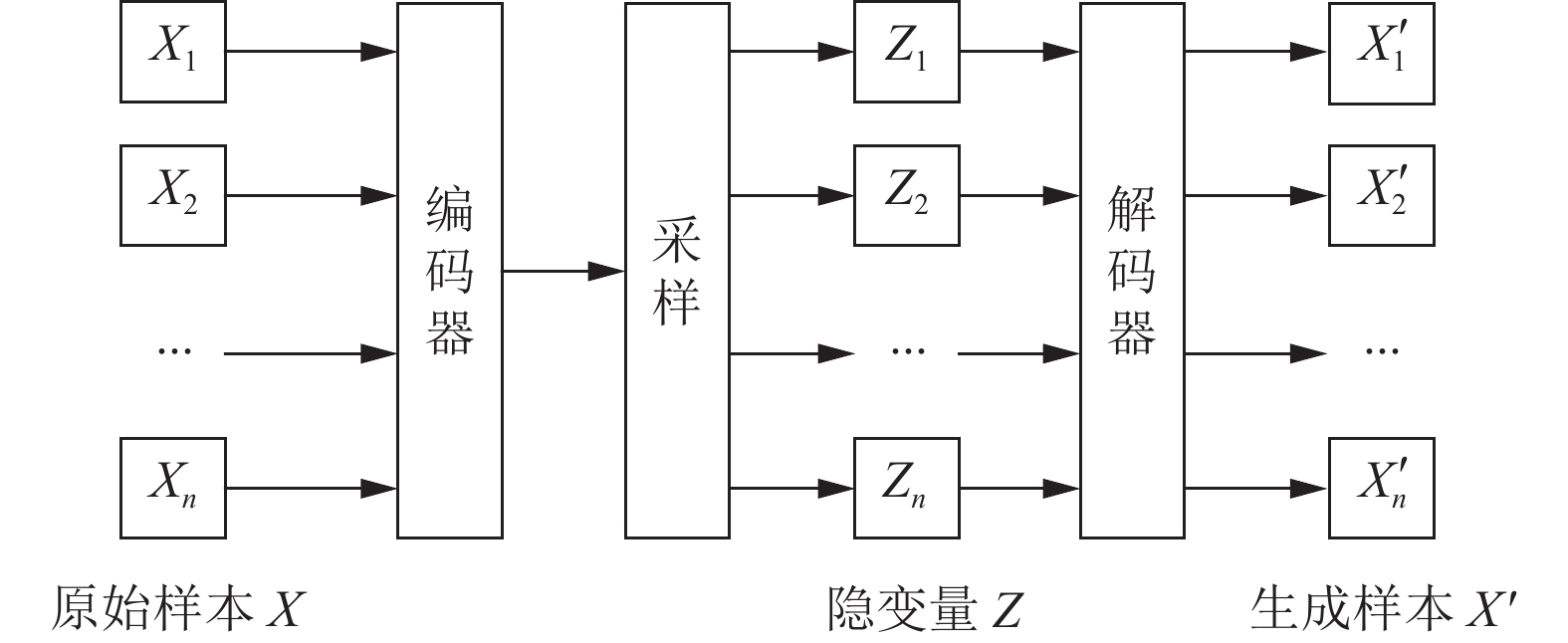
|
图 1 VAE数据扩充基本架构 |
其中编码器将观测空间中独立同分布数据X转换为隐空间表示Z , 而解码器将隐空间表示解码回原始数据空间, 得到X' , 即:
| Z−Enc(X)=q(Z|X) | (1) |
| Z′∼Enc(X)=q(Z|X) | (2) |
隐藏变量Z的均值和标准差为μ和σ, 一般使得Z服从高斯分布, VAE网络的损失函数如式(3):
| LVAE=EZ−Q(Z|X)[log(P(X|Z))]+DKL(Q(Z|X)‖P(Z)) | (3) |
其中, EZ–Q(Z|X)是P(X|Z)的似然期望, Q(Z|X)为近似后验分布, P(X|Z)为解码过程需要学习的条件分布, P(Z)为先验分布, 为了简化将正态分布N(0, 1)作为先验分布, DKL为KL散度. 第1项根据实际需要可选择二值交叉熵或者平方误差, 第2项 KL 散度为:
| DKL(Q(Z|X)||P(Z)=−12⋅∑(1+logσ2−μ2−σ2) | (4) |
为了解决模型因为随机采样无法使用反向传播算法的问题, VAE 引入了“重参数技巧”, 先引入一个参数, 对其采样, 然后 Z 通过式(5)计算变换得到:
| Z=μ+ε+σ | (5) |
具体的数据扩充流程步骤如下.
1)以少数故障样本作为VAE的输入, 利用VAE训练输入数据特征, 学习其分布.
2)依据正态分布N(0, 1)采样隐变量并输入生成器生成的指定数量的样本.
3)重复步骤1)和2), 将生成的样本与原始样本进行融合, 完成对原始样本的扩充, 用于后续的网络训练的输入.
2 基于GRU网络的直流充电桩故障预测 2.1 GRU网络模型RNN是一种常用的神经网络, 具有短期记忆的能力. 在对数据进行建模时, RNN对信息具有一定的记忆能力, 但随着递归次数的增加, 容易出现权重级数爆炸或者消失的问题, 从而导致RNN训练时的收敛困难. 而长短期记忆网络(long short-term memory, LSTM)网络则通过引入门的机制, 使得网络具有更强的记忆, 弥补了RNN网络的缺点[18], 但是在训练过程中需要引入更多的参数, 使得训练难度大大增加, 因此, 文中为了简化训练难度, 采用GRU网络, GRU通过将遗忘门和输入门组合在一起的方式减少了门的数量, 能够在保证记忆能力的同时, 提升网络的训练效果[19], GRU的单个单元网络基本结构如图2所示. 文章基于GRU网络框架对直流充电设施进行故障预测. 将采集点A、B的电压U、电流I、功率P以及充电模块C的温度T, 作为输入时间序列x, 输出故障类型为y向量.
在该网络中, 每个网络单元的输入和输出关系如下:
| rt=σ(Wirxt+bir+Whrht−1+bhr) | (6) |
| zt=σ(Wizxt+biz+Whrht−1+bhz) | (7) |
| nt=tanh(Winxt+bin+rt×(Whnht−1+bhn)) | (8) |
| ht=(1−zt)×nt+zt×ht−1 | (9) |
| yt=σ(Wyt⋅ht) | (10) |
其中, Wir、Wiz、Win、Whn、Wyt表示权重矩阵; bir、bhr、biz、bhz、bin、bhn表示偏置向量; xt为t时刻的输入; ht–1为t–1时刻的隐藏状态, 初始时刻隐藏状态为0; ht为t时刻的隐藏状态; rt, zt, nt, 分别为重置门、更新们以及计算候选隐藏门; σ表示Sigmoid激活函数. 在每个单元传递过程中, rt用来控制需要保留之前的记忆. 如果rt为0, 则

|
图 2 GRU基本结构 |
2.2 粒子群优化GRU网络模型
若采取随机初始化GRU网络参数, 很难准确地得到理想的结果. 为了更好地初始化GRU网络参数, 利用粒子群优化(particle swarm optimization, PSO)算法对学习率、迭代次数、隐含层神经元个数进行训练[20], 来优化GRU网络模型, 具体优化步骤如下.
步骤1. 首先, 初始化粒子群的参数, 设置PSO的参数: 粒子群数量Num=100, 迭代次数tmax=50, 搜索维度D=5.
步骤2. 对粒子群的位置和速度进行初始化, 设置取值范围, 利用随机初始化方法进行设置; 随机生成第i个粒子位置Xi=(l, m, h1, h2, h3), 其中l为GRU网络的学习率取值范围为[0.001, 0.01]; m为GRU算法迭代次数, 取值范围为[10, 500]; 隐藏层数量设置为3层, h1、h2和h3分别为第1层神经元个数、第2层神经元个数和第3次神经元个数, 共同取值范围为[1, 100]; 粒子的速度Vi=(Vi1, Vi2, Vi3, Vi4, Vi5).
步骤3. 确定GRU网络搜索时间步长T, 步长与GRU网路每个输入数据的采集频率有关, 文中对充电模块输入、输出的电压和电流每秒进行采样, 因此时间步长设为1.
步骤4. 确定PSO的适应度函数, 利用初始化的粒子群构建GRU神经网络框架进, 将训练集的实际结果与预测值的结果比较, 每次训练批数(batch)为B, 其中适应度函数如下:
| f(y)=1BB∑i = 1(y−y′)2 | (11) |
其中, y为实际结果,
步骤5. 迭代计算, 计算每一次迭代后粒子的位置, 通过不断调整粒子的速度和位置, 使得最终逼近最优位置, 从而或者最优解. 速度和位置更新公式如式(12)和式(13):
| Vt+1i=wVti+c1r1(Pti−Xti)+c2r2(Ptg−Xti) | (12) |
| Xt+1i=Xti+Vt+1iT | (13) |
其中,
| T=1n√t | (14) |
| n=1+lntmax | (15) |
通过不断迭代得到最优解后, 将粒子群中最优的位置参数对应到GRU的学习率、迭代次数以及隐藏层1、2和3层的神经元个数.
步骤6. 进行充电桩故障预测. 利用PSO算法确定的最优初始参数对GRU神经网络进行训练, 达到最大迭代次数后, 将数据输入训练好的模型进行判断分类, 输出最终充电桩故障预 测结果.
2.3 支持向量机改进PSO-GRU模型GRU算法输出层激活函数通常采用Softmax函数, 其作为一种回归型函数, 在最终的分类结果中只能进行单分类, 而采用SVM则可扩展进行多分类问题的处理[21], 对充电桩故障进行多分类预测. 因此, 为了进一步提高故障预测的分类效果, 采用SVM优化GRU的输出, 通过利用SVM替换GRU中的Softmax激活函数作为最后输出的故障分类器[22]. 进行网络训练时, 将GRU和Softmax激活函数组合进行误差反向传播, 最小化损失函数, 训练相关参数. 在模型验证阶段, 运用训练好的GRU-SVM网络模型进行故障预测, 由SVM输出预测故障类型. SVM数学模型如下:
| \mathop {{\text{min}}}\limits_{w, b, \xi } \frac{1}{2}||w|{|^2} + C\sum\limits_{i = 1}^n {{\xi _i}} | (16) |
| \begin{gathered} {\rm{s.t.}}\;\;{y_i}(w \cdot {x_i} - b) \geqslant 1 - {\xi _i}, \; {\xi _i} \geqslant 0, \;\;\;\;i = 1, 2, \cdots , N \\ \end{gathered} | (17) |
其中, C为惩罚项,
| k({x_i}, {x_j}) = \exp ( - g||{x_i} - {x_j}|{|^2}) | (18) |
其中, g=1/(2σ)2基于此函数的 SVM 的分类决策函数为:
| f(x) = {sgn} \left(\sum\limits_{i = 1}^N {{\alpha _i}{y_i}k({x_i}, {x_j}) + b} \right) | (19) |
其中, 拉格朗日乘子α≥0.
结合VAE数据扩充处理, 最终PSO-GRU-SVM优化模型流程图如图3.

|
图 3 PSO-GRU-SVM故障分析流程 |
3 算例分析
以南京市区域直流充电桩为例, 通过检测充电桩的输入电压、电流, 输出电压、电流, 充电模块温度的历史数据, 处理提取出所需正常数据与故障数据, 利用VAE对故障数据进行扩充, 得到合适数量的训练集和测试集, 其中1500个训练集, 300个测试集. 利用文中提出的PSO-GRU-SVM模型进行分析, 对6种故障类型进行预测分类, 分别为输出过压故障、欠压故障、充电模块过温、输出过流、直流输出短路故障以及绝缘异常. 故障类型如表1所示.
| 表 1 故障类型 |
直流充电桩故障预测模型如图4所示, 利用采集的数据进行训练, 本实验利用训练集得到粒子群优化的GRU参数为分别为学习率l=0.004, GRU训练次数m=128, h1、h2、h3分别为24, 36, 12. 图5(a)和图5(b)为利用PSO-GRU-SVM网络训练过程和测试过程得到的准确率及损失误差情况. 由图5可以看出, 测试集中迭代达到100次以后开始出现过拟合现象, 为了改善这种情况, 训练集引入Dropout方法. 加入Dropout后的测试集和训练集准确率及损失误差情况如图6(a)和图6(b)所示, 可以看出利用Dropout方法能够有效改善过拟合现象.
3.1 故障预测结果分析进一步对比改进后模型的效果, 分别利用GRU-Softmax模型、PSO-GRU-Softmax模型以及文中提出的PSO-GRU-SVM模型进行充电桩故障分析, 3种算法模型测试与训练时间如表2所示, 测试集预测结果如表3所示.
从表2可以得到, 在模型运行时间方面, 改进的 PSO-GRU-SVM的训练用时为 59.82 s, 比传统 GRU-Softmax高出6.18 s (PSO+SVM 训练时间), 比PSO-GRU-Softmax算法多出3.04 s (SVM与Softmax的时间差); 3种算法的测试时间相差微小, PSO-GRU-SVM略有优势, 为 0.843 s, 时间最长为GRU-Softmax算法, 为0.887 s. 从表3中可以得出, 改进的预测模型的准确率均值高达99.6%, 而使用了PSO-GRU-Softmax作为分类器的模型以及传统的模型的预测准确率分别为 99%和98.3%. 由此可见, 文中提出的算法获得了有效的预测准确率提升.
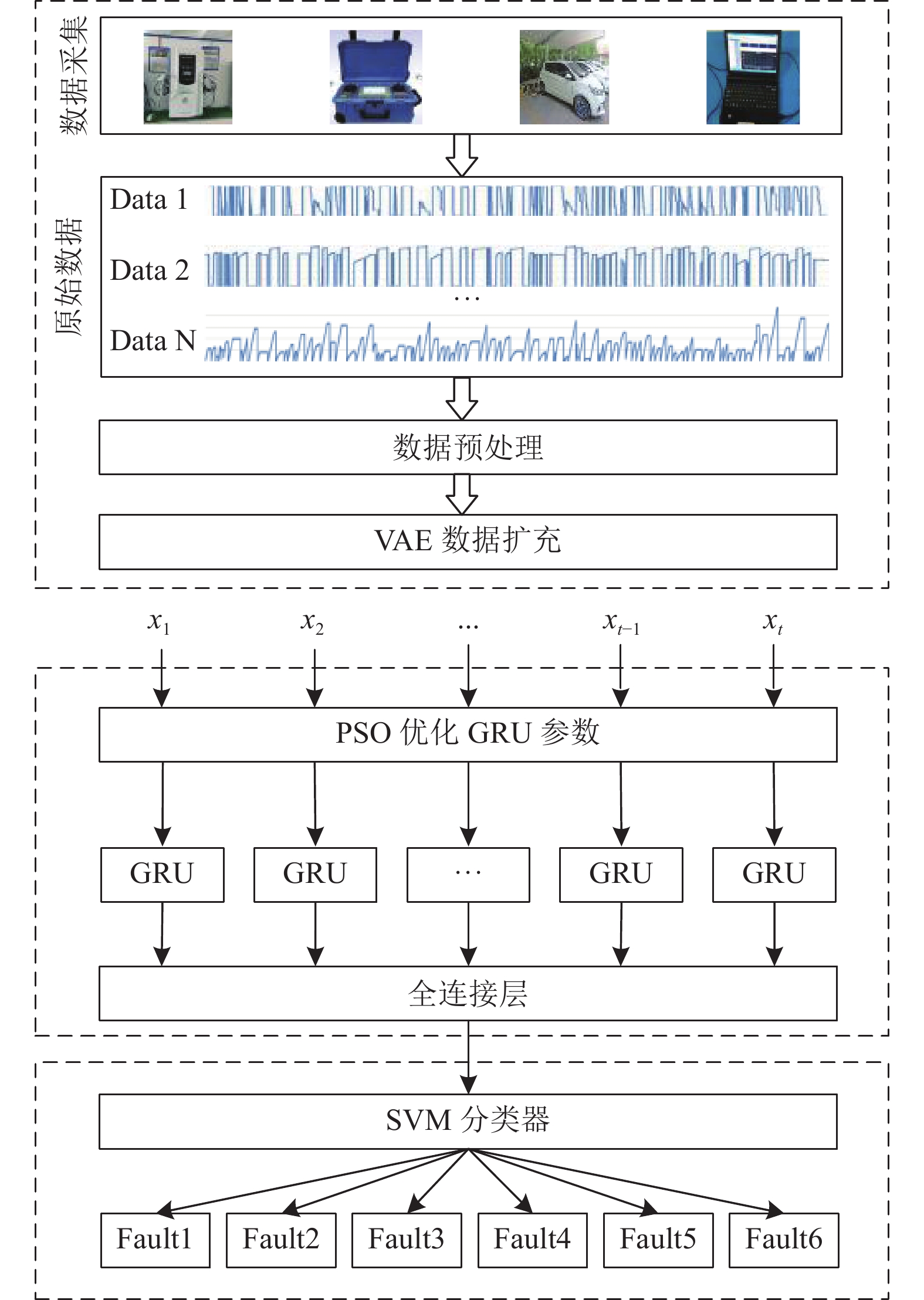
|
图 4 改进GRU直流充电桩故障预测模型 |
根据图7可以看出, 在测试样本中文中提出的算法仅有1个故障分类预测错误, 为直流输出短路被预测为输出过流故障, 其他均正确; 而采用PSO-GRU-Softmax错误判断3个样本, 其中2个直流输出短路故障被判断为输出过流故障, 其中1个过温故障被误判断为过流故障; 传统的GRU-Softmax模型故障判断错误最多, 为5个样本数据, 其中2个直流输出短路故障被判断为输出过流故障, 其中2个过温故障被误判断为过流故障, 一个输出过流故障被误判断为输出电流短路故障. 可以得知, 在充电模块过温、输出过流、输出短路3个故障容易误判, 其中改进的PSO-GRU-SVM算法在故障特征学习过程中效果最好, PSO-GRU-Softmax算法次之, 传统的GRU-Softmax最差. 算例表明, 改进的 PSO-GRU-Softmax 算法的故障预测准确性明显优于其他两种算法.
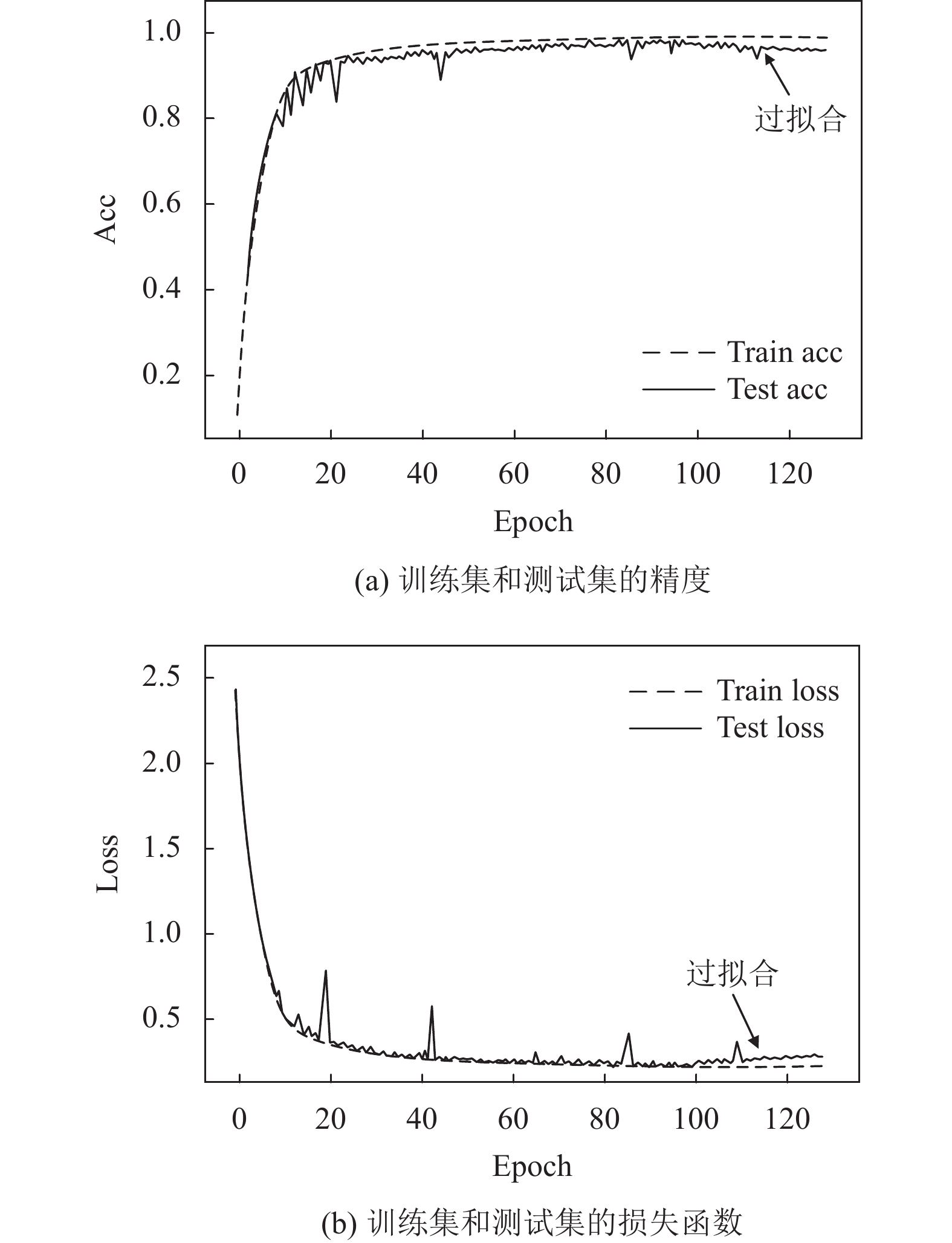
|
图 5 未加入Dropout训练集和测试集精度和损失函数 |

|
图 6 加入Dropout训练集和测试集精度和损失函数 |
| 表 2 测试与训练时间对比 (s) |
| 表 3 充电桩不同模型故障预测结果数据 |
3.2 与其他算法对比分析
为了进一步验证文中提出的故障预测方法的可靠性, 利用前馈神经网络(back propagation, BP)和卷积神经网络两种算法对进行故障预警诊断对比. 对相同的样本数据进行训练处理, 训练过程文中不再详细描述, 具体诊断精确度如图8所示.
从图8可以看出, 无论是训练集还是测试集, 文中提出的PSO-GRU-SVM算法的精度最高. 因此, 从对GRU网络改进的角度, 以及横向对比其他网络算法的角度, 算例结果都验证了文中提出算法在直流充电桩故障预测中的可行性与有效性. 不仅如此, 该方法也同时给其他领域的故障预测与诊断提供了有一定的方法与参考.
4 结论本文针对直流充电桩具体故障数据少的特点, 利用VAE进行数据扩充得到训练集与测试集, 然后通过粒子群算法对GRU网络初始参数进行优化, 同时利用SVM替换原始的Softmax函数对故障输出分类进行改进, 提出了PSO-GRU-SVM直流充电桩故障预测算法, 在算例分析过程中通过加入Dropout方法解决了测试集过拟合现象, 并利用算例分析了PSO-GRU-Softmax和传统的GRU-Softmax算法, 对比分析3种网络的混淆矩阵热力图, 结果表明文中提出的算法有效地提高了故障预测的精度; 进一步对比BP神经网络与CNN网络的预测效果, 结果同样显示了文中提出的算法具有更高的准确性. 同时, 也为其他领域的故障预测提供借鉴.

|
图 7 充电桩故障预测在不同算法模型的测试集上的混淆矩阵热力图 |

|
图 8 3种不同网络模型的训练集与测试集故障预测精度 |
| [1] |
蔡黎, 张权文, 代妮娜, 等. 规模化电动汽车接入主动配电网研究进展综述. 智慧电力, 2021, 49(6): 75-82. DOI:10.3969/j.issn.1673-7598.2021.06.012 |
| [2] |
周衍涛, 戴军, 苑惠丽, 等. 城市电动汽车充电设施需求预测与规划布局研究. 电力系统保护与控制, 2021, 49(24): 177-187. DOI:10.19783/j.cnki.pspc.CDZ001 |
| [3] |
苏宇锋. 农村新能源汽车配套设施建设的技术——评《新能源汽车充电设施安装与维护》. 热带作物学报, 2021, 42(1): 359. |
| [4] |
Wang JJ, Wei QQ, Li C, et al. Quality analysis and research of charging facilities for electric vehicles. Journal of Physics: Conference Series, 2020, 1626: 012038. DOI:10.1088/1742-6596/1626/1/012038 |
| [5] |
唐葆君, 王翔宇, 王彬, 等. 中国新能源汽车行业发展水平分析及展望. 北京理工大学学报(社会科学版), 2019, 21(2): 6-11. DOI:10.15918/j.jbitss1009-3370.2019.7261 |
| [6] |
南斌, 徐成司, 董树锋, 等. 考虑多充电模式的充电桩优化控制策略. 电力工程技术, 2021, 40(5): 1-9. DOI:10.12158/j.2096-3203.2021.05.001 |
| [7] |
Jiang LR, Diao XH, Zhang YX, et al. Review of the charging safety and charging safety protection of electric vehicles. World Electric Vehicle Journal, 2021, 12(4): 184. DOI:10.3390/wevj12040184 |
| [8] |
徐广腾, 杜科, 张涛, 等. 电动汽车充电设施检测技术及故障分析. 供用电, 2018, 35(10): 19-24, 43. DOI:10.19421/j.cnki.1006-6357.2018.10.004 |
| [9] |
谢信喜, 王士同. 适用于区间数据的基于相互距离的相似性传播聚类. 计算机应用, 2008, 28(6): 1441-1443, 1493. |
| [10] |
朱熀秋, 樊帅. 基于改进连续隐马尔可夫模型的六极径向主动磁轴承转子位移软测量. 中国电机工程学报, 2021, 41(11): 3933-3942. DOI:10.13334/J.0258-8013.PCSEE.201007 |
| [11] |
Deng Q, Söffker D. A review of HMM-based approaches of driving behaviors recognition and prediction. IEEE Transactions on Intelligent Vehicles, 2022, 7(1): 21-31. DOI:10.1109/TIV.2021.3065933 |
| [12] |
姚欣, 邢砾云, 辛平. 基于小波特征提取与深度学习的微电网故障诊断与分类方法. 智慧电力, 2021, 49(12): 17-24. DOI:10.3969/j.issn.1673-7598.2021.12.004 |
| [13] |
李彦枝, 陈昌红, 谢晓芳. 基于改进卷积神经网络的极光图像分类算法研究. 南京邮电大学学报(自然科学版), 2019, 39(6): 86-93. DOI:10.14132/j.cnki.1673-5439.2019.06.013 |
| [14] |
陈海峰, 冯源. 基于CNN的雷达目标分类识别技术研究. 现代雷达, 2022, 44(4): 38-43. DOI:10.16592/j.cnki.1004-7859.2022.04.006 |
| [15] |
孟海宁, 童新宇, 石月开, 等. 基于ARIMA-RNN组合模型的云服务器老化预测方法. 通信学报, 2021, 42(1): 163-171. |
| [16] |
杨英, 唐平. VAE_LSTM算法在时间序列预测模型中的研究. 湖南科技大学学报(自然科学版), 2020, 35(3): 93-101. DOI:10.13582/j.cnki.1672-9102.2020.03.014 |
| [17] |
张永宏, 张中洋, 赵晓平, 等. 基于VAE-GAN和FLCNN的不均衡样本轴承故障诊断方法. 振动与冲击, 2022, 41(9): 199-209. DOI:10.13465/j.cnki.jvs.2022.09.026 |
| [18] |
王宏伟, 孙文磊, 张小栋, 等. 基于优化VMD复合多尺度散布熵及LSTM的风力发电机齿轮箱故障诊断方法研究. 太阳能学报, 2022, 43(4): 288-295. DOI:10.19912/j.0254-0096.tynxb.2020-0457 |
| [19] |
李浩君, 方璇, 戴海容. 基于自注意力机制和双向GRU神经网络的深度知识追踪优化模型. 计算机应用研究, 2022, 39(3): 732-738. DOI:10.19734/j.issn.1001-3695.2021.08.0345 |
| [20] |
李建伟, 刘成波, 郭宏, 等. 基于PSO-RBF神经网络的刀具寿命预测. 计算机系统应用, 2022, 31(1): 309-314. DOI:10.15888/j.cnki.csa.008265 |
| [21] |
安国庆, 史哲文, 马世峰, 等. 基于RF特征优选的WOA-SVM变压器故障诊断. 高压电器, 2022, 58(2): 171-178. DOI:10.13296/j.1001-1609.hva.2022.02.023 |
| [22] |
姜媛媛, 牛牧原, 陈万利. 基于IWOA-SVM的电路软故障诊断. 电子测量技术, 2022, 45(2): 159-165. DOI:10.19651/j.cnki.emt.2108111 |
 2023, Vol. 32
2023, Vol. 32



