随着遥感卫星技术的发展, 通过视频卫星实现对目标的检测和跟踪在智能交通、自然灾害监测和军事侦察等方面具有重要的作用. 近年来, 基于相关滤波的跟踪方法凭借较快的计算速度和较高的精度成为目标跟踪领域的主流算法之一. Bolme等[1]首先将相关滤波方法用在跟踪领域, 提出了最小平方误差输出和(minimum output sum of squared error, MOSSE)滤波算法. Henriques等[2]利用循环移位进行样本采样在MOSSE的基础上提出了核循环结构(circulant structure of tracking-by-detection with kernels, CSK)算法. Danelljan等[3]在CSK的基础上利用颜色空间(color name, CN)特征, 提高了算法有效性. Henriques等[4]将CSK算法的灰度特征换成方向梯度直方图(histogram of oriented gradient, HOG)特征, 提出了核相关滤波(kernel correlation filter, KCF)跟踪算法. 上述算法忽略了目标空间关系, Zhang 等[5]通过贝叶斯框架对目标和其周围区域建立时空关系提出了时空上下文 (spatio-temporal context, STC) 算法.
近年来, 目标跟踪算法主要是针对传统视频中运动目标进行研究, 而针对卫星视频中运动目标的研究较少. Shao等[6]在核相关滤波算法中使用光流和梯度直方图作为特征进行目标跟踪; Xuan等[7]先利用卡尔曼预测目标区域, 再进行核相关滤波操作减少边界效应问题; Wang等[8]在CSK算法的基础上加入Gabor滤波器增加目标的特征实现更稳健的跟踪; 韩鸣飞等[9]以KCF算法为框架, 融合目标灰度特征和HOG特征提高目标跟踪的鲁棒性; Zhang等[10]在相关滤波算法的基础上加入卷积网络预测模型实现目标跟踪.
对于卫星视频运动目标存在相对于背景尺寸很小、目标缺少清晰的特征信息的问题. 本文结合目标的运动信息、时空背景和外观模型进行跟踪, 以KCF算法为基本框架增加了基于颜色特征的时空上下文模型分别训练两个跟踪器, 并且加入了改进的基于运动目标像素的检测分割算法, 同时得到3个目标候选区域对目标进行最终相关计算得到目标最优位置.
1 目标分割和跟踪方法本文分别利用HOG特征、CN特征和像素值信息训练得到独立的两个跟踪器和一个检测分割器. 首先提取目标的HOG特征利用岭回归方法和核函数训练得到第1个目标跟踪器; 接着利用CN特征对目标及其局部背景区域的上下文信息建立空间模型得到第2个目标跟踪器; 然后利用首帧图像初始化样本模型, 对候选区域进行像素计算得到检测分割器; 最后根据两个目标跟踪器和检测分割器分别得到两个目标跟踪区域和一个检测分割区域. 实验发现, 利用3个候选区域进行特征融合得到的结果没有分别计算响应值进行最大值比较得到目标位置的效果好, 于是本算法利用目标的互补信息对3个候选区域分别求取最大响应值, 将得到的3个最大响应值进行比较得到最优目标位置. 如图1.
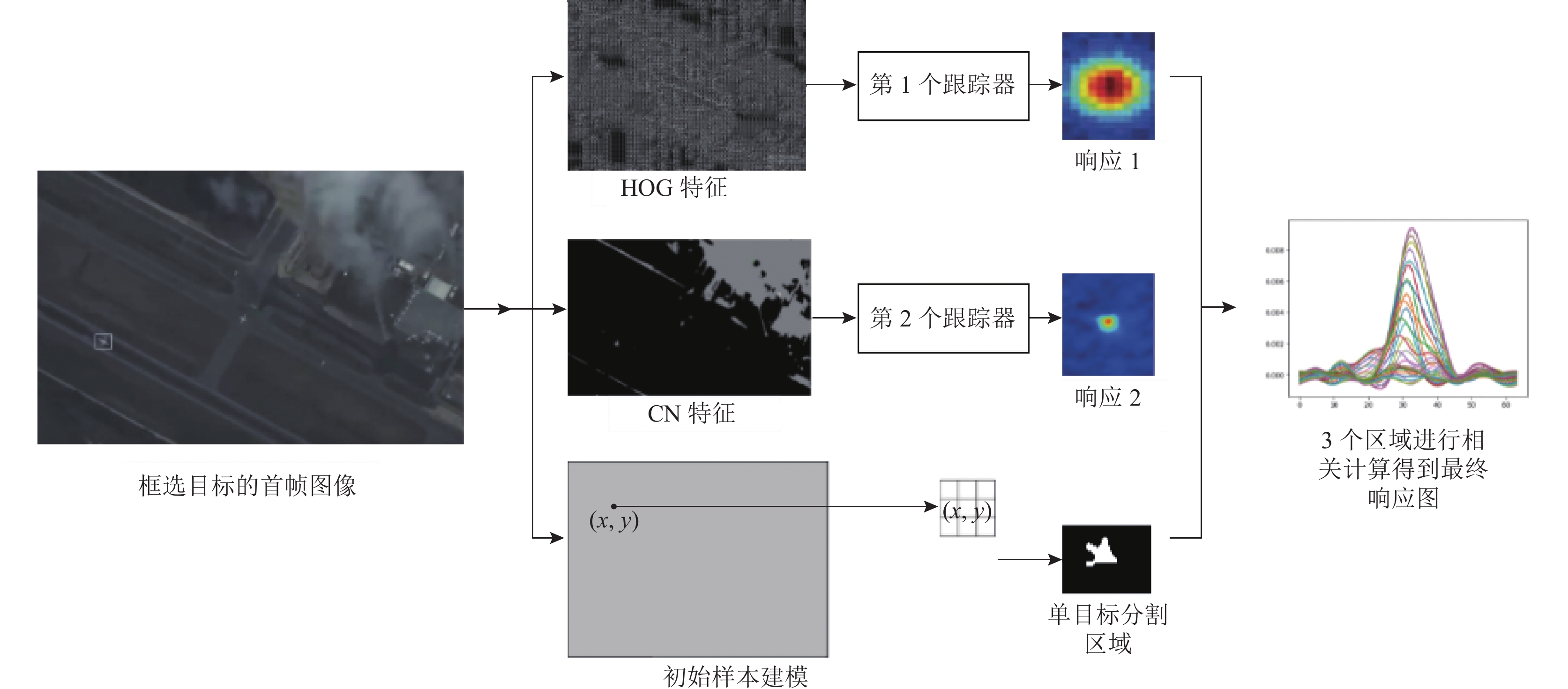
|
图 1 目标预测流程图 |
1.1 第1个目标跟踪器
根据首帧框选的目标区域提取HOG特征, 进行循环移位得到大量正负样本训练非线性回归器, 然后通过相关计算得到响应矩阵的最大值位置, 此位置就是目标中心位置. 将样本使用岭回归方法对函数
| minw∑i(f(xi)−yi)2+λ‖w‖2 | (1) |
其中,
对式(1)求导, 并扩展到复数域得:
| ˆw=ˆx⊙ˆyˆx⊙ˆx∗+λ | (2) |
其中,
通过引入高斯核函数, 将原始非线性问题转换成线性问题, 并在傅里叶域转换得到核函数回归解:
| ˆα=ˆyˆkxx+λ | (3) |
根据训练好的滤波器对目标窗口区域进行滤波计算, 得到输出置信图.
| ˆf(z)=ˆkxz⊙ˆα | (4) |
其中,
| kxx′=exp(−1σ2(‖x2‖+‖x′‖2−2F−1(ˆx∗⊙ˆx′))) | (5) |
完成视频一帧的目标跟踪后, 需要更新跟踪器的模板参数α和样本参数x, 即:
| α=(1−ε)α+εnew_α | (6) |
| x=(1−ε)x+εnew_x | (7) |
由于卫星视频中目标只占少量像素, 很少的目标信息无法实现良好的跟踪. 于是我们利用目标及局部区域背景的CN颜色特征建立空间关系增强跟踪器的性能. 将首帧目标区域与其局部区域背景建立一个空间上下文模型, 对图像进行卷积操作, 获得置信图, 置信图最大的位置作为最佳目标位置.
假定当前帧目标位置为x*, 则图像特征集合为
| c(x)=P(x|o)=∑c(z)∈XcP(x,c(z)|o)=∑c(z)∈XcP(x|c(z),o)P(c(z)|o) | (8) |
其中,
| P(x|c(z),o)=hsc(x−z) | (9) |
| P(c(z)|o)=Ici(z)wσ(z−x∗) | (10) |
其中,
目标置信图描述了区域各点为目标的概率大小, 公式定义为:
| c(x)=P(x|o)=be−|x−x∗α|β | (11) |
其中, b为归一化常数; β为形状控制参数; α为尺度参数.
结合上下文先验模型和置信图公式得到时空上下文模型表达形式为:
| hsct,ci(x)=F−1(F(be−|x−x∗α|β)F(Ici(x)wσ(x−x∗))) | (12) |
然后更新得到t+1帧的时空上下文模型为:
| Hstct+1,ci=(1−ρ)Hstct,ci(x)+ρhsct,ci(x) | (13) |
其中,
利用得到的模型与图像进行卷积得到目标置信图, 目标在t+1帧的位置由置信图中最大值决定, 即式(14):
| x∗t+1=argmaxx∈Ωc(x∗t)ct+1(x)=argmaxx∈Ωc(x∗t)F−1(11∑i=0F(Hstct+1,ci(x))⊙F(˜It+1,ci(x)wσ(x−x∗t))) | (14) |
其中,
考虑到卫星视频中背景相对静止, 于是利用改进的ViBe算法对运动目标检测分割. ViBe算法[11]是一种像素级前景检测算法, 不关注运动目标的特征信息, 所以此算法对于卫星视频中的运动目标检测有较好的效果. 由于ViBe算法是通过初始化背景模型, 对每一帧图像的所有像素值进行差值计算得到动态区域, 导致检测速度较低、容易产生鬼影现象, 针对原ViBe算法存在的问题, 本文利用视频帧的时间关系, 对每一帧的目标区域与背景模型相应位置进行像素值计算, 实现单目标的检测分割, 从原理上降低了ViBe算法产生的鬼影、动态背景干扰问题, 提高了运动目标检测分割的效果和速度.
改进的ViBe算法利用视频首帧图像进行背景建模, 对首帧图像的每个像素点及其8个相关邻域随机选取20个像素组成该像素的背景模型, 通过循环执行此步骤, 将首帧图像的所有像素值完成建模操作. x像素点处的背景样本集可以表示为:
| M(x)={p1,p2,⋅⋅⋅,pN} | (15) |
其中,
然后将每帧的目标区域代替原始整张图像与背景模型对应的位置进行像素值计算, 设定半径阈值R和匹配阈值A, 将像素差值与半径阈值R进行对比, 如式(16)所示, 将大于阈值R的进行计数, 数值超过匹配阈值A, 则表示像素变化较大, 定义该点为前景像素; 数值小于匹配阈值A, 则表示像素变化较小, 定义该点为背景像素, 如式(17)所示.
| abs(p−pi)⩾ | (16) |
| \left\{ {{S_R}\left( {p\left( x \right)} \right) \cap \left\{ {{p_1}, {p_2}, \cdot \cdot \cdot, {p_N}} \right\}} \right\} \geqslant A | (17) |
将检测区域判断为背景的每个像素点有1/φ的概率更新自己及其邻域的模型样本值. 其中像素点连续B次被检测为前景, 则将其更新为背景点.
1.4 最终目标位置本文利用两个跟踪器和检测分割器得到独立的3个候选区域, 对候选区域进行相关计算分别得到对应候选区域的最大响应值r1, r2, r3, 选取其中的最大值rmax, 得到最终目标位置. 如式(18)所示.
| {r_{\max }} = \max \left( {{r_1}, {r_2}, {r_3}} \right) | (18) |
本文算法的实验是在i5-6500 CPU, 主频3.2 GHz, 内存4 GB的台式电脑上进行的, 实现本文算法的平台为PyCharm. 实验中所用参数参考ViBe算法设置: 半径阈值R为20, 匹配阈值
为了验证算法的跟踪性能, 在3组卫星视频数据集上测试了KCF算法和本文算法. 本文算法在plane_03序列中的准确率和成功率分别为1和0.776, KCF算法在plane_03序列中的准确率和成功率分别为0.183和0.157; 本文算法在plane_06序列中的准确率和成功率分别为1和0.739, KCF算法在plane_06序列中的准确率和成功率分别为0.097和0.073; 本文算法在ship_01序列中的准确率和成功率分别为1和0.443, KCF算法在ship_01序列中的准确率和成功率分别为0.505和0.152. 如图2、图3和图4所示.
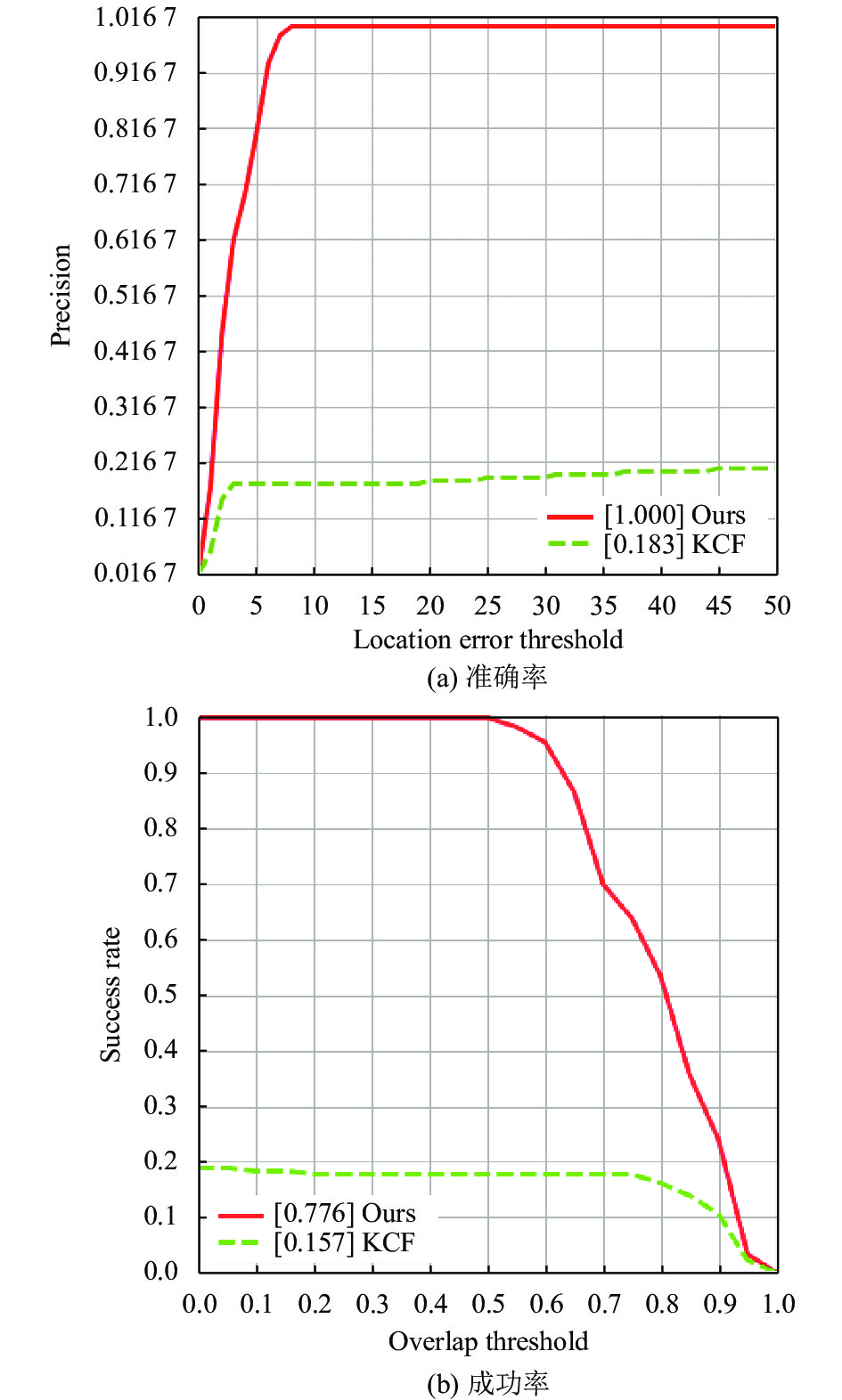
|
图 2 plane_03序列中的准确率和成功率对比图 |
2.2.2 定性分析
为了更直观评估算法的目标分割效果, 将本文算法与ViBe算法在plane_03和plane_06视频序列上进行了对比实验, 原ViBe算法只能对整幅图像进行检测分割, 存在严重的鬼影和动态背景干扰问题, 改进算法大大缓解了鬼影和动态背景干扰问题, 而且实现了对单个目标的检测分割. 如图5和图6所示.
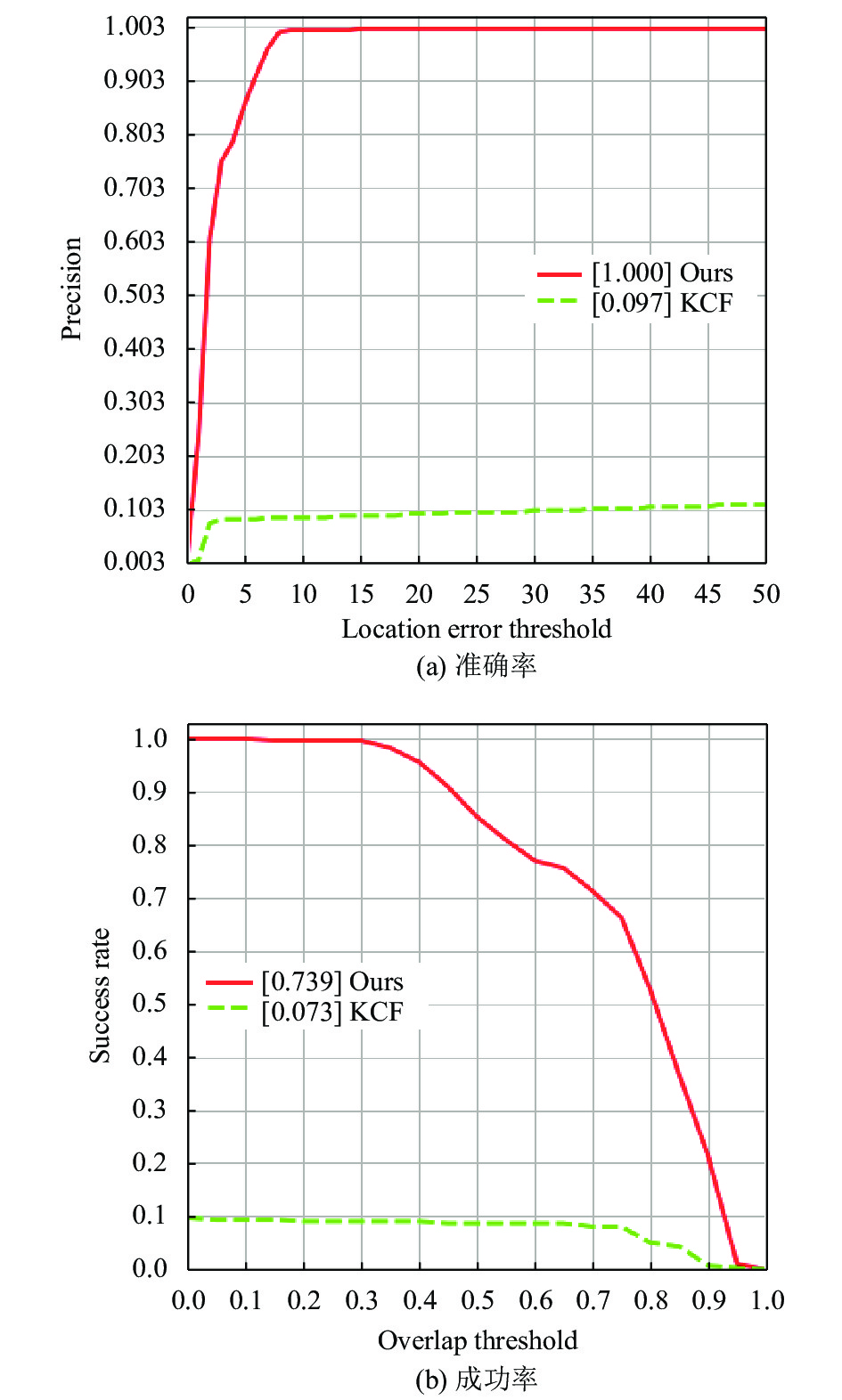
|
图 3 plane_06序列中的准确率和成功率对比图 |
为了更直观评估算法的跟踪性能, 将本文算法与KCF算法分别在plane_03、plane_06和ship_01视频序列上进行了对比实验, 其中红色框代表本文算法跟踪结果, 蓝色框代表KCF算法跟踪结果. 本文算法相较于KCF算法在卫星视频中可以实现更加稳定准确的跟踪. 如图7、图8和图9所示.
3 结论针对卫星视频中的小目标, 本文提出一种简单的方法可以同时实现对单目标的检测分割和跟踪两个任务. 分别结合特征信息、运动信息和背景信息训练得到两个跟踪器和一个检测分割器, 并将跟踪结果和检测结果分别进行相关计算得到最优目标位置. 实验结果表明, 算法可以成功实现单目标的分割和跟踪, 提高了卫星视频中目标的跟踪性能.
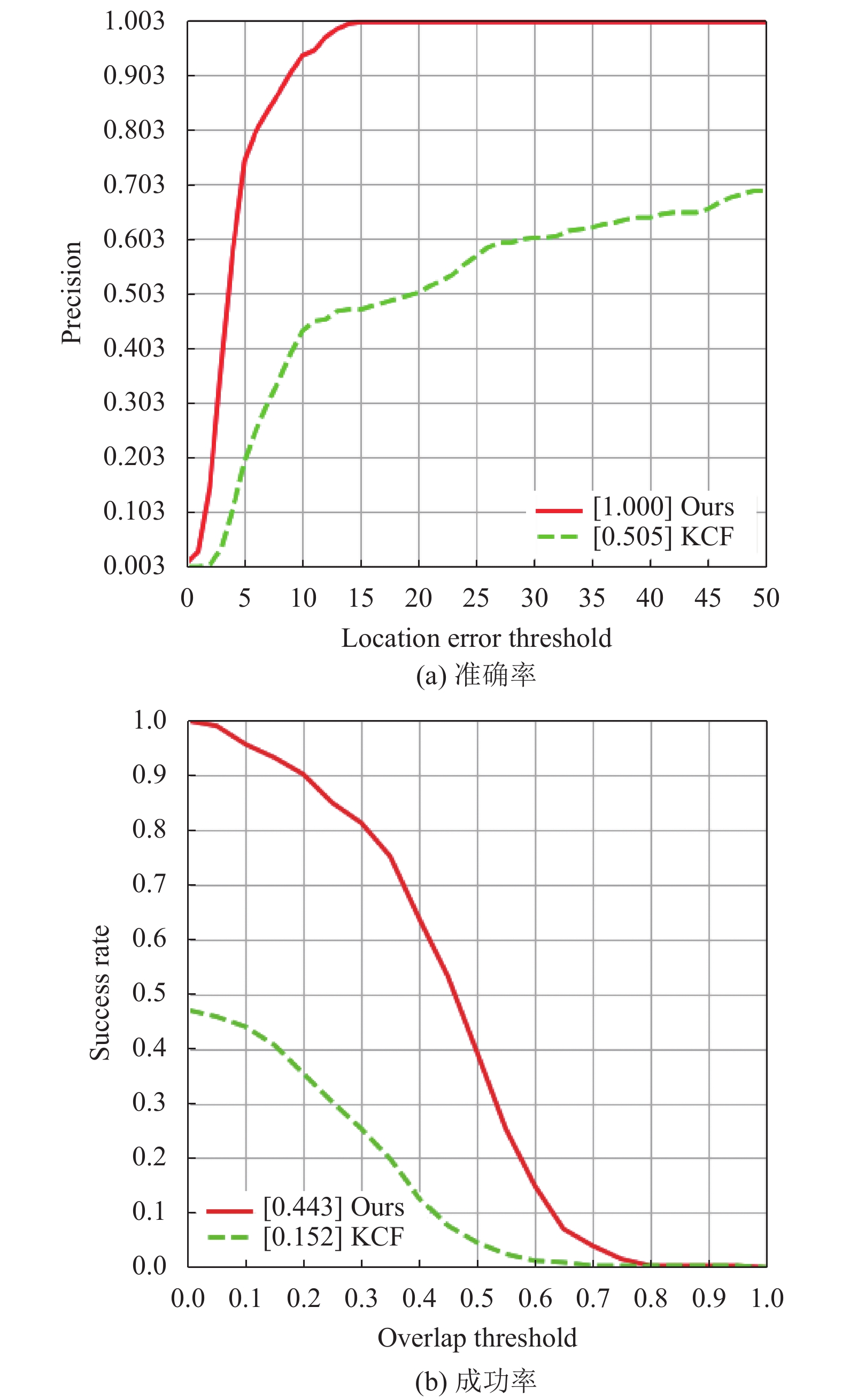
|
图 4 ship_01序列中的准确率和成功率对比图 |

|
图 5 ViBe算法与改进算法在plane_03序列分割结果对比 |

|
图 6 ViBe算法与改进算法在plane_06序列分割结果对比 |

|
图 7 两种算法在plane_03序列跟踪结果 |

|
图 8 两种算法在plane_06序列跟踪结果 |

|
图 9 两种算法在ship_01序列跟踪结果 |
| [1] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [2] |
Henriques JF, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels. Proceedings of the 12th European Conference on Computer Vision. Florence: Springer, 2012. 702–715.
|
| [3] |
Danelljan M, Khan FS, Felsberg M, et al. Adaptive color attributes for real-time visual tracking. Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 1090–1097.
|
| [4] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [5] |
Zhang KH, Zhang L, Liu QS, et al. Fast visual tracking via dense spatio-temporal context learning. Proceedings of the 13th European Conference on Computer Vision. Zurich: Springer, 2014. 127–141.
|
| [6] |
Shao J, Du B, Wu C, et al. Can we track targets from space? A hybrid kernel correlation filter tracker for satellite video. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8719-8731. DOI:10.1109/TGRS.2019.2922648 |
| [7] |
Xuan SY, Li SY, Han MF, et al. Object tracking in satellite videos by improved correlation filters with motion estimations. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(2): 1074-1086. DOI:10.1109/TGRS.2019.2943366 |
| [8] |
Wang YM, Wang TY, Zhang G, et al. Small target tracking in satellite videos using background compensation. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(10): 7010-7021. DOI:10.1109/TGRS.2020.2978512 |
| [9] |
韩鸣飞, 李盛阳, 万雪, 等. 融合特征的卫星视频车辆单目标跟踪. 中国图象图形学报, 2021, 26(11): 2741-2750. |
| [10] |
Zhang WH, Jiao LC, Liu F, et al. MBLT: Learning motion and background for vehicle tracking in satellite videos. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 4703315. DOI:10.1109/TGRS.2021.3109028 |
| [11] |
Barnich O, Van Droogenbroeck M. ViBe: A universal background subtraction algorithm for video sequences. IEEE Transactions on Image Processing, 2011, 20(6): 1709-1724. DOI:10.1109/TIP.2010.2101613 |
| [12] |
Zhao MQ, Li SY, Xuan SY, et al. SatSOT: A benchmark dataset for satellite video single object tracking. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5617611. DOI:10.1109/TGRS.2022.3140809 |
 2023, Vol. 32
2023, Vol. 32



