随着有限化石燃料日益枯竭和碳减排需求转趋刚性, 光伏发电等可再生能源发电技术发展迅猛^[1]. 然而, 受太阳辐照度和气象影响的光伏输出功率的变化也给电网的运行带来了严峻的挑战. 随着光伏渗透率逐年递增, 准确预测光伏发电功率可以有效提高电网实时控制性能和经济效益^[2].

为提高光伏发电功率预测精度, 学者们展开了大量研究. 统计模型通过时间序列法^[3]、回归分析法^[4]、神经网络法^[5]等建立历史数据与输出功率的映射关系估算发电量, 因建模简单, 广泛应用于光伏发电功率短期预测中. 其中深度神经网络因泛化能力强、能深入挖掘时间序列间的关联性, 为光伏发电功率预测提供了强大支撑. 文献[6]通过量化天气类型与主成分分析(PCA), 使用长短期神经网络(long short-term memory, LSTM)网络提高光伏预测精度. 文献[7]采用PCA对相似样本提取主成分作为神经网络的输入, 简化网络结构. 然而上述预测方法只考虑了历史信息对时序预测的单向影响, 忽视了未来数据信息流与当前时刻的双向联系. 双向长短时记忆(bidirectional long short-term memory, BiLSTM)网络通过双向LSTM提取时序数据的正反向特征来挖掘时序数据的前后联系, 能有效提高光伏功率的预测精度^[8].

日前光伏序列属于非平稳序列, 针对其随机性强、表现出复杂的日周期性等特性, 文献[9,10]分别使用经验小波变换与变分模态分解(variational mode decomposition, VMD)将原始非平稳光伏序列分解成相对平稳的子序列, 并对各子序列分别预测后再组合, 有效提高预测精度.

此外, 日前光伏预测作为多步预测问题, 使用深度神经网络训练与预测不仅需要占用大量建模时间和计算资源, 还容易陷入局部最优, 因此需对神经网络的权重和阈值进行优化. 文献[11]将相似日理论和蝙蝠算法优化最小二乘支持向量机LSSVM相结合, 避免LSSVM陷入局部最优从而提高预测精度. 文献[12]用遗传算法对BP神经网络的连接权值进行优化, 以达成对网络的改进. 但上述优化算法需要参数较多且耗时长, 布谷鸟搜索(cuckoo search, CS)算法参数更少且具有较好的参数智能寻优性能^[13]. 因此, 本文提出CS算法优化的基于变分模态分解和添加注意力机制(attention mechanism, AM)的BiLSTM日前光伏发电功率预测模型(VMD-BiLSTM-AM-CS). 首先, 针对光伏序列波动性较大, 使用VMD将日前光伏序列分解为相对平稳的子模态, 结合皮尔逊相关系数分析法选取影响各模态的关键气象因子共同作为预测模型的输入. 其次, 使用BiLSTM充分学习时序数据的正反向特征, 添加注意力机制, 赋予网络隐藏层单元不同的权重, 使得预测模型从长时间序列输入中关注重点信息. 最后, 采用CS算法对网络层的权系数与偏置进行优化, 解决神经网络易陷入局部最优的问题. 实验结果表明, 本文所提模型有效提高日前光伏预测精度.

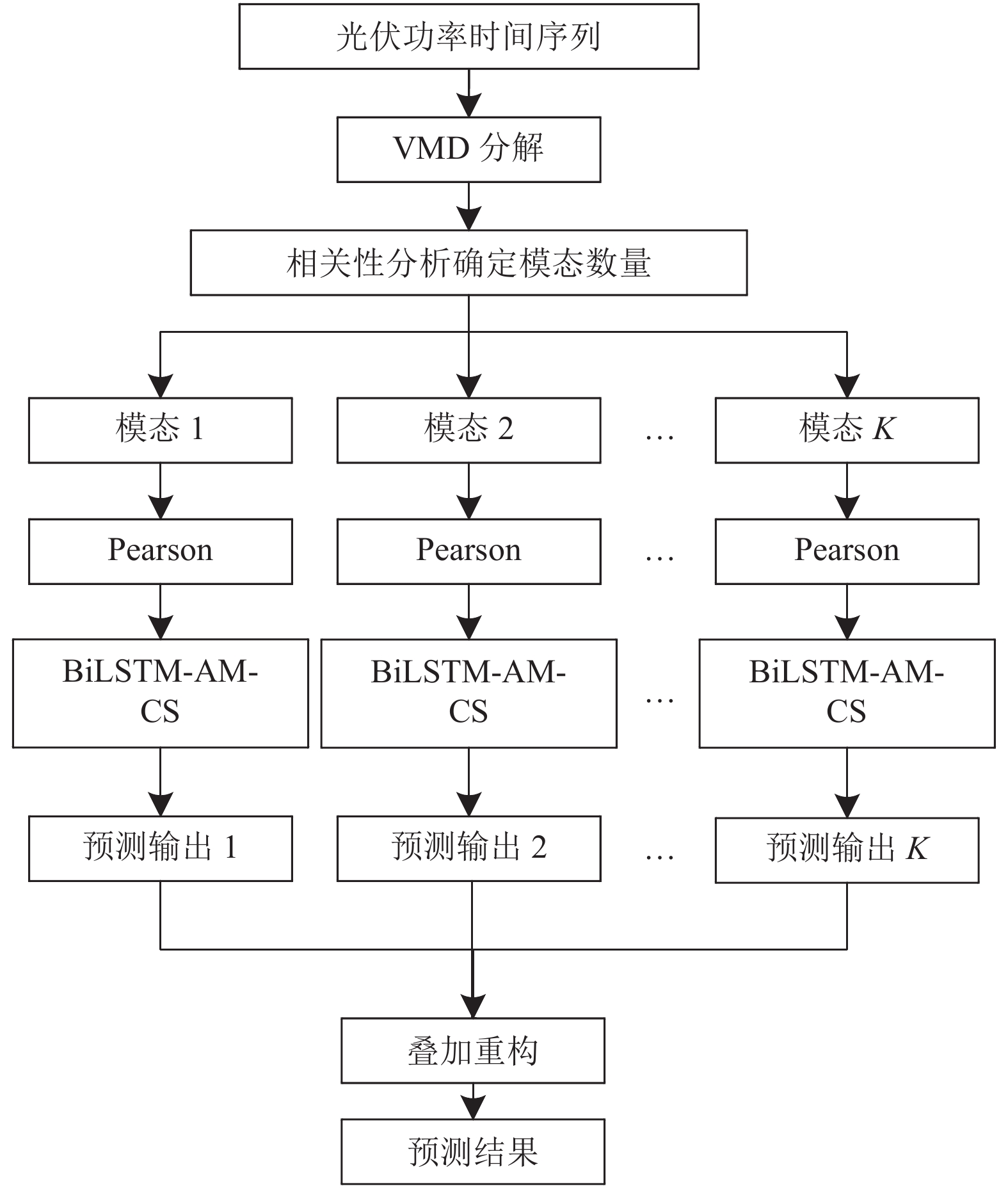
1 日前光伏功率预测模型构建

VMD-BiLSTM-AM-CS日前光伏功率预测模型如图1所示, 步骤如下.

(1) 对原始光伏功率序列进行数据清洗, 去除离群值和缺失值后利用VMD方法进行分解, 结合相关性分析确定模态数量, 得到K个模态.

(2) 将各模态光伏序列进行归一化处理, 结合皮尔逊相关系数筛选出影响不同模态的关键气象因子.

(3) 针对分解后的K个模态与关键气象因子分别构建BiLSTM-AM预测模型, 使用CS算法优化网络参数.

(4) 将各分量的预测结果叠加, 重构得到待预测日光伏功率的预测值.

1.1 VMD分析

光伏发电序列具有明显的日周期性和强烈的波动性, 属于非平稳序列. VMD算法作为一种新的非递归、自适应、准正交的信号分解方法^[14], 将光伏出力数据从时域转化到频域内进行分解, 可以有效捕捉光伏发电功率的非线性特征. 其步骤如下.

(1) 建立变分约束问题

$ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_{\left\{ {{u_k}} \right\}, \left\{ {{\omega _k}} \right\}} \left\{ {\displaystyle\sum\limits_{{\text{k}} = 1}^K {\left\| {{\partial _t}\left[ {\left( {\delta (t) + \frac{j}{{\pi t}}} \right)* {u_k}(t)} \right]{{\rm{e}}^{ - j{\omega _k}t}}} \right\|} _2^2} \right\}} \\ {{\rm{s.t.}}\displaystyle\sum\limits_{k = 1}^K {{u_k}(t) = f(t)} } \end{array}} \right. $

(1)

其中, *为卷积运算符, $ f(t) $ 为光伏出力序列, ${u_k}{\text{ = }}\{ {u_{\text{1}}}, {u_{\text{2}}}, \cdots , {u_k} \}$ 、 $ {\omega _k}{\text{ = }}\left\{ {{\omega _{\text{1}}}, {\omega _{\text{2}}}, \cdots , {\omega _k}} \right\} $ 为分解后K个频带分量和对应的中心频率, $ \delta (t) $ 为脉冲函数.

(2) 无约束变分求解

引入拉格朗日乘子λ和二次罚因子α, 用于求解上述变分问题, 增广的拉格朗日算子如下所示:

$ \begin{split} & L(\{ {u_k}\} , \{ {\omega _k}\} , \lambda ) = \alpha \mathop \sum \limits_{k = 1}^K ||{\partial _t}[(\delta (t) + \frac{j}{{\pi t}}){*}{u_k}(t)]{{\rm{e}}^{ - j{\omega _k}t}}||_2^2 \\ &\qquad\qquad { + ||f(t) - \mathop \sum \limits_{k = 1}^K {u_k}(t)||_2^2 + \left\langle {\lambda (t), f(t) - \mathop \sum \limits_{k = 1}^K {u_k}(t)} \right\rangle } \end{split} $

(2)

采用交替方向乘子法得到式(1)的最优解, 其中模态分量 ${u_k}$ 和中心频率为 ${\omega_k}$ 迭代过程为:

$ \hat u_k^{n + 1}(\omega ) = \frac{{\hat f(\omega ) - {{\displaystyle\sum\nolimits_{i \ne k} {\hat u} }_i}(\omega ) + \dfrac{{\hat \lambda (\omega )}}{2}}}{{{\text{1 + 2}}\alpha {{(\omega - {\omega _k})}^{\text{2}}}}} $

(3)

$ \omega _{{k}}^{n + 1} = \frac{{\int_0^\infty {\omega {{\left| {{{\hat u}_k}(\omega )} \right|}^2}} d\omega }}{{\int_0^\infty {{{\left| {{{\hat u}_k}(\omega )} \right|}^2}} d\omega }} $

(4)

拉格朗日算法的算子λ迭代过程如式(5):

$ {\hat \lambda ^{{{n + 1}}}}(\omega ) \leftarrow {\hat \lambda ^{{n}}}(\omega ) + \tau \left(\hat f(\omega ) - \sum\limits_{k = 1}^K {\hat u_k^{n + 1}(\omega )} \right) $

(5)

其中, $\tau $ 为噪声容限.

当满足迭代精度时停止, 即:

$ \sum\limits_{k = 1}^K {\left\| {\hat u_k^{n + 1}{{ - }}\hat u_k^n} \right\|_{\text{2}}^{\text{2}}} {\text{/}}\left\| {\hat u_k^n} \right\|_{\text{2}}^{\text{2}} \lt \varepsilon $

(6)

1.2 气象因子选取

在光伏电站的内部技术参数基本保持不变的情况下, 从外部气象因素(如辐照度、温度、湿度等)中筛选出影响光伏输出功率的主要因素至关重要. 需要对这些影响变量与光伏序列各模态进行相关性分析, 利用皮尔逊相关系数 $R(X, Y)$ 计算两个变量X与Y之间的线性相关程度:

$ R(X, Y) = \frac{{\displaystyle\sum\limits_{i = 1}^n {({X_i} - \bar X)({Y_i} - \bar Y)} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({X_i} - \bar X)}^2}} \displaystyle\sum\limits_{i = 1}^n {{{({Y_i} - \bar Y)}^2}} } }} $

(7)

由式(7)可知, 相关系数的绝对值越大, 相关性越强.

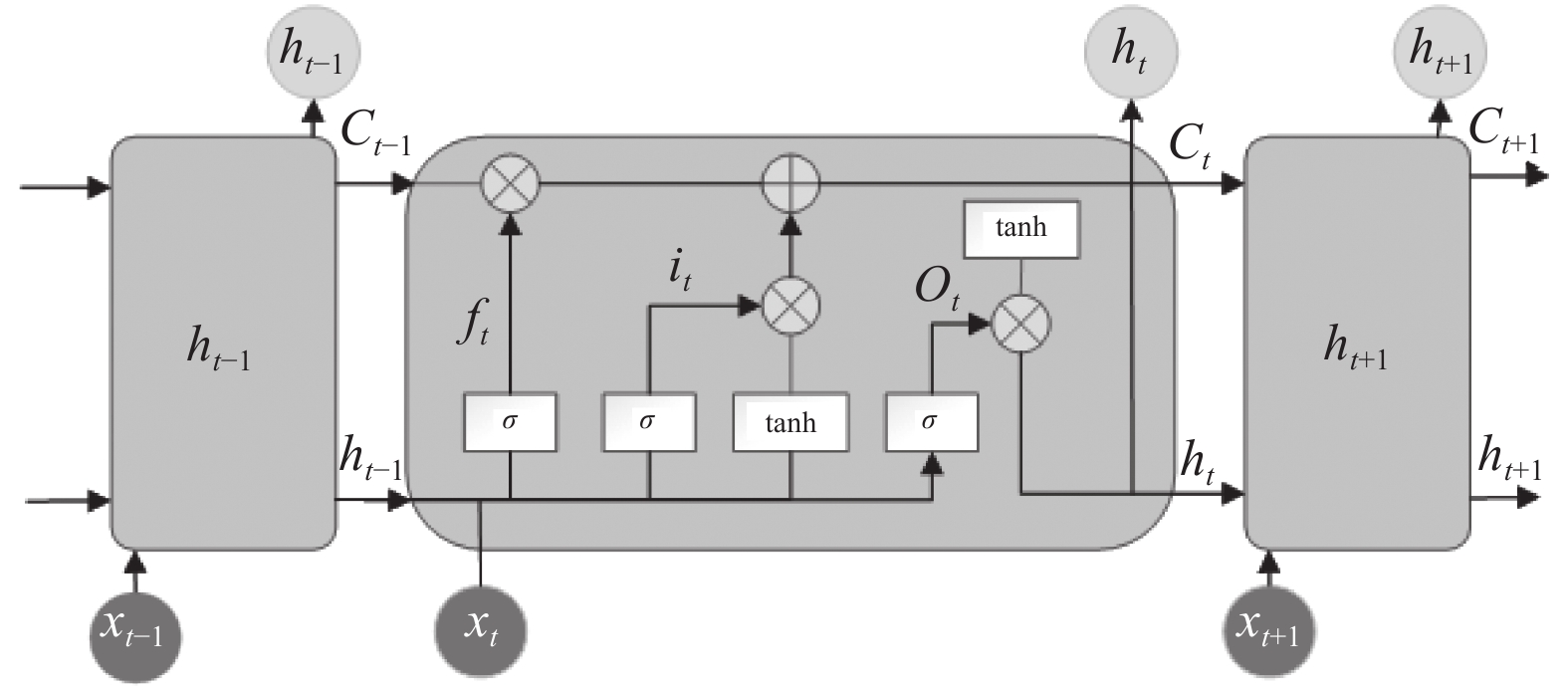
1.3 BiLSTM模块

LSTM网络是循环神经网络的变形^[15], 由3个存储门组成, 即输入门( ${i_t}$ )、输出门( ${o_t}$ )和遗忘门( $ {f_t} $ ). 其结构如图2所示.

LSTM不仅可以挖掘光伏功率的时序特征, 还可以学习长期依赖关系, 降低在模型训练时梯度失控的风险. $ {x_t} $ 、 ${h_t}$ 分别表示t时刻的输入与输出, ${C_t}$ 表示t时刻LSTM隐藏节点状态, 其更新过程如下所示:

$\left\{ { \begin{split} & {f_t} = \sigma ({W_f} \cdot [{h_{t - 1}}, {x_t}] + {b_f}) \\ & {i_t} = \sigma ({W_i} \cdot [{h_{t - 1}}, {x_t}] + {b_i}) \\ & {o_t} = \sigma ({W_o} \cdot [{h_{t - 1}}, {x_t}] + {b_o}) \\ & {\widetilde C_t} = \tanh ({W_c} \cdot [{h_{t - 1}}, {x_t}] + {b_c}) \\ & {C_t} = {f_t} * {C_{t - 1}} + {i_t} * {\widetilde C_t} \\ & {h_t} = {o_t} * \tanh ({C_t}) \end{split} } \right.$

(8)

其中, $ {W_f} $ 、 $ {W_i} $ 、 $ {W_o} $ 、 $ {W_c} $ 为权重矩阵, $ {b_f} $ 、 $ {b_i} $ 、 $ {b_o} $ 、 $ {b_c} $ 为对应偏置, $ \sigma $ 为ReLU激活函数, $\tanh $ 为双曲正切函数.

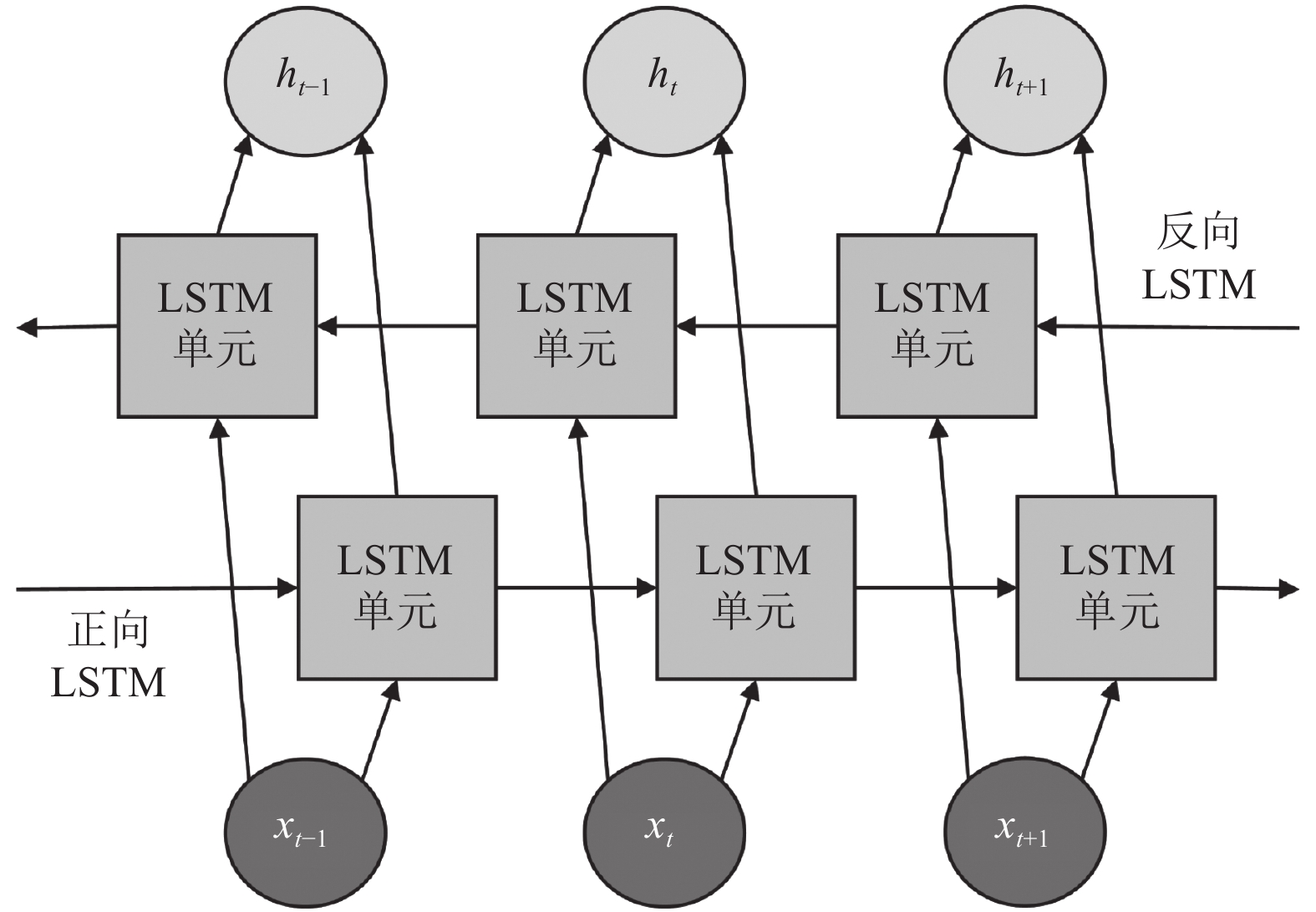
LSTM通过挖掘历史光伏序列信息来预测下一时刻的输出, 然而某一时刻的输出往往同时依赖历史与未来时刻的状态信息. BiLSTM结构图如图3所示, 其由正反向两个LSTM网络组成, 可以分别利用时间序列的前后变化规律进行双向预测^[16], 预测更具全局性与整体性, 有效提高光伏预测精度, 具体计算公式如下:

$ {{{H}}_t} = {h_{tf}} \oplus {h_{tb}} $

(9)

其中, ${{{H}}_t}$ 表示BiLSTM的隐藏状态向量; $ \oplus $ 为向量拼接操作; $ {h}_{tf}、{h}_{tb} $ 分别表示前向和后向LSTM的隐藏状态向量.

1.4 注意力机制

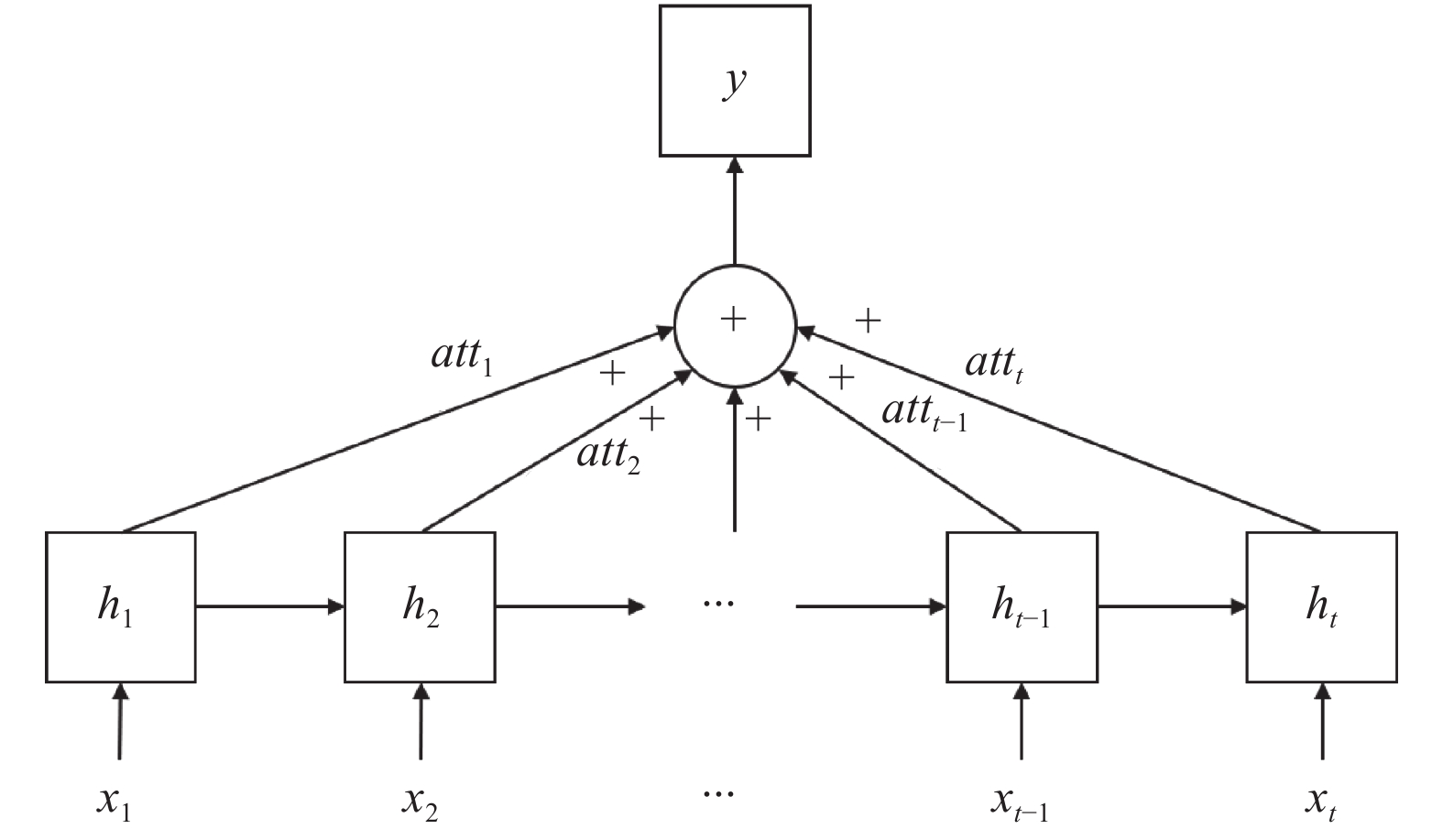
BiLSTM虽能捕获双向序列信息, 但无法从长时间序列中突出关键信息的影响. 通过引入注意力机制, 可以动态调整神经网络隐藏层的权重, 在不增加模型计算与存储的基础上专注学习重要信息以提升预测精度, 其结构图如图4所示.

注意力机制重要计算公式如下:

$ {e_t} = \tanh (w{h_t} + b) $

(10)

$ at{t_t} = \frac{{\exp ({e_t})}}{{\displaystyle\sum\limits_{j = 1}^T {\exp \left( {{e_j}} \right)} }} $

(11)

$ {O_t} = \sum\limits_{t = 1}^T {at{t_t}{h_t}} $

(12)

其中, ${e_t}$ 为BiLSTM网络t时刻输出向量 ${h_t}$ 对应的注意力权重得分, w为权重矩阵, b为偏置向量, $at{t_t}$ 为注意力权重向量, ${O_t}$ 为注意力机制在t时刻的输出, T为输入序列维度.

1.5 CS算法

布谷鸟搜索算法是一种模拟布谷鸟寻找产卵的鸟窝而随机游走的群体优化算法, 用以解决复杂、非线性问题^[17]. 与遗传算法、粒子群算法等其他优化算法相比, CS算法所需参数少、操作简单、随机搜索路径更优, 并且能够收敛到全局最优解.

CS的主要思想基于两种策略: 布谷鸟的巢寄生和Levy的飞行机制. 通过Levy的飞行机制为寻找孵化卵子的最佳宿主巢, 设可利用的鸟窝数量为m, 可建立如下高效优化模型:

$ \left\{ {\begin{split} & {x_i}(t + 1) = {x_i}(t) + \alpha \oplus Levy(\lambda ) \\ & i = 1, 2, \cdots , m;\;t = 1, 2, \cdots \end{split} } \right.$

(13)

其中, ${x_i}(t)$ 是第t代的第i个鸟窝的位置, $\alpha $ 是步长, $Levy(\lambda )$ 为随机搜索路径, 其飞行公式为:

$ Levy(\lambda ) \sim \frac{{\Phi \times {{u}}}}{{{{\left| v \right|}^{\frac{1}{\beta }}}}}, \beta \in (1, 3] $

(14)

其中, u, v都服从标准正态分布. $\Phi $ 满足:

$ \Phi {\text{ = }}{\left\{ {\frac{{\Gamma (1 + \beta )\sin \left(\pi \dfrac{\beta }{2}\right)}}{{\Gamma \left\{ {\left[ {\dfrac{{1 + \beta }}{2}} \right]\beta {2^{\frac{{\beta - 1}}{2}}}} \right\}}}} \right\}^{\frac{{\text{1}}}{\beta }}} $

(15)

2 算例分析

本算例所有仿真实验在Python 3.6版本、Tensor- Flow1.12.0和Keras 2.2.0 运行环境下进行. 采用的实验数据选用美国国家能源部可再生能源实验室(NREL)亚利桑那州地区2006年1月到2006年12月的实测光伏功率数据与气象数据, 样本的采样周期为30 min, 光伏电站额定装机容量为104 MW.

使用平均绝对误差(MAE)、均方根误差(RMSE)和拟合度(R²)作为模型的评价指标, 其表达式如下:

$ MAE = \frac{1}{N}\sum\limits_{t = 1}^N {\left| {{y_t} - {{y_t'}}} \right|} $

(16)

$ {\textit{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{t = 1}^N {{{\left( {{y_t} - {{y_t'}}} \right)}^2}} } $

(17)

$ {R^2} = 1 - \frac{{\displaystyle\sum\limits_{t = 1}^N {{{\left( {{y_t} - {{y_t'}}} \right)}^2}} }}{{\displaystyle\sum\limits_{t = 1}^N {{{\left( {{y_t} - \bar y} \right)}^2}} }} $

(18)

其中, $ {y_t} $ 为实际值, $ {y'_t} $ 为预测值, $ \bar y $ 为实际值的平均值, N为样本数量.

2.1 数据预处理

(1) 异常值处理

原始的光伏功率与气象数据因为包含缺失值和离群值, 并不能直接用于预测, 因此需对其进行数据清洗, 去除离群值和缺失值.

(2) 数据标准化

为了消除物理维度的差异, 加快模型的收敛速度, 需要对数据进行标准化.

$ \widetilde x(i) = \frac{{x(i) - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $

(19)

其中, $ x(i) $ 为原始光伏序列或气象序列样本; $ \widetilde x(i) $ 为标准化处理后的序列; $ {x_{\min }} $ 和 $ {x_{\max }} $ 为样本数据的最小值和最大值. 归一化处理后, 数据的值都在[0, 1]内.

(3) 数据集划分

训练集、验证集、测试集按照70%、10%、20%的比例进行划分.

2.2 基于变分模态的光伏功率分解结果

为确定模态数K的取值, 对不同模态数下分解出的相邻的模态分量的相关性进行分析, 求解其皮尔逊相关系数, 结果如表1所示. 当K=5时, 模态4和模态5的相关性显著增强, 此时存在模态重复或产生额外的噪声, 因此K=4时分解效果最好.

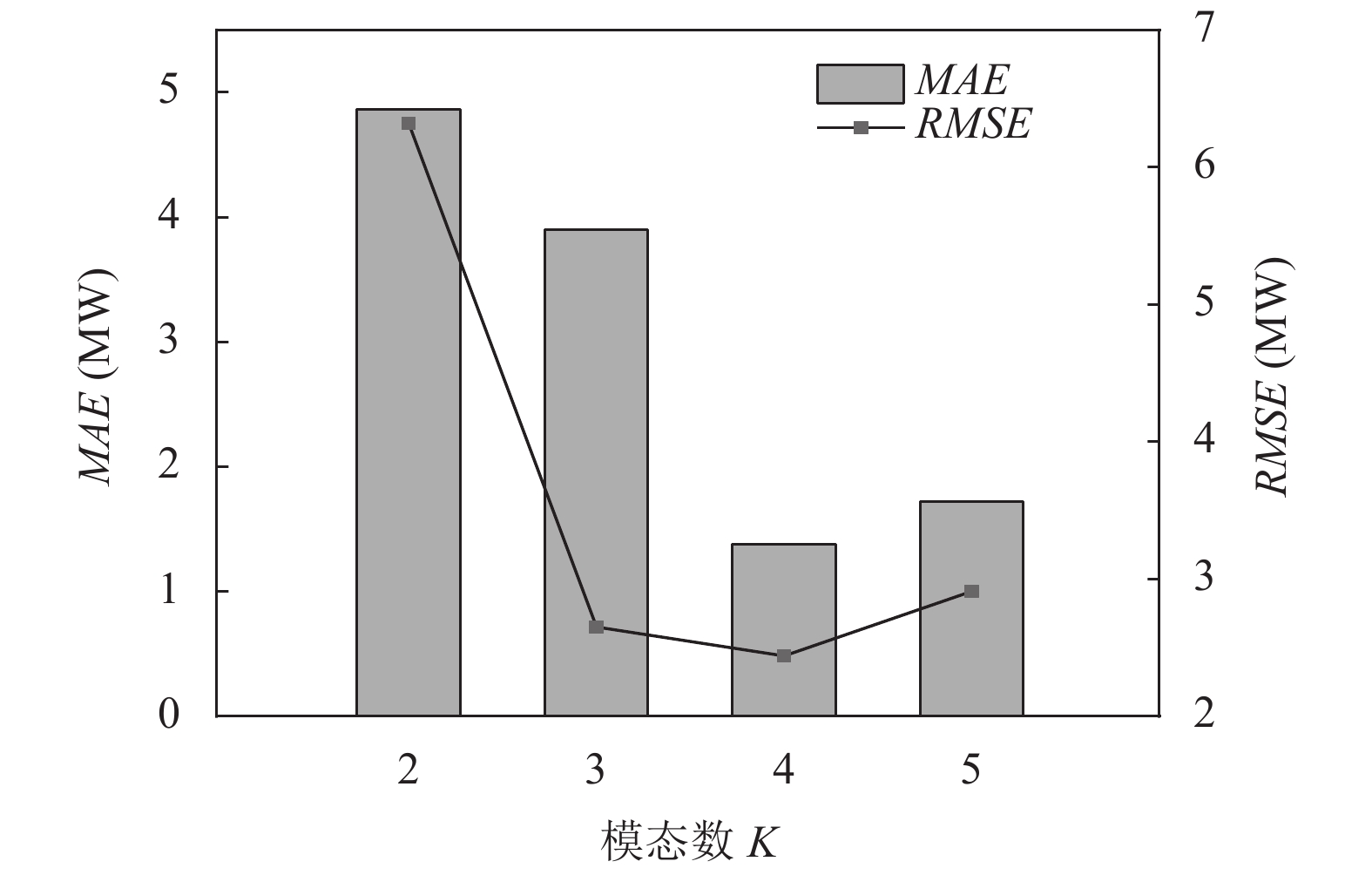
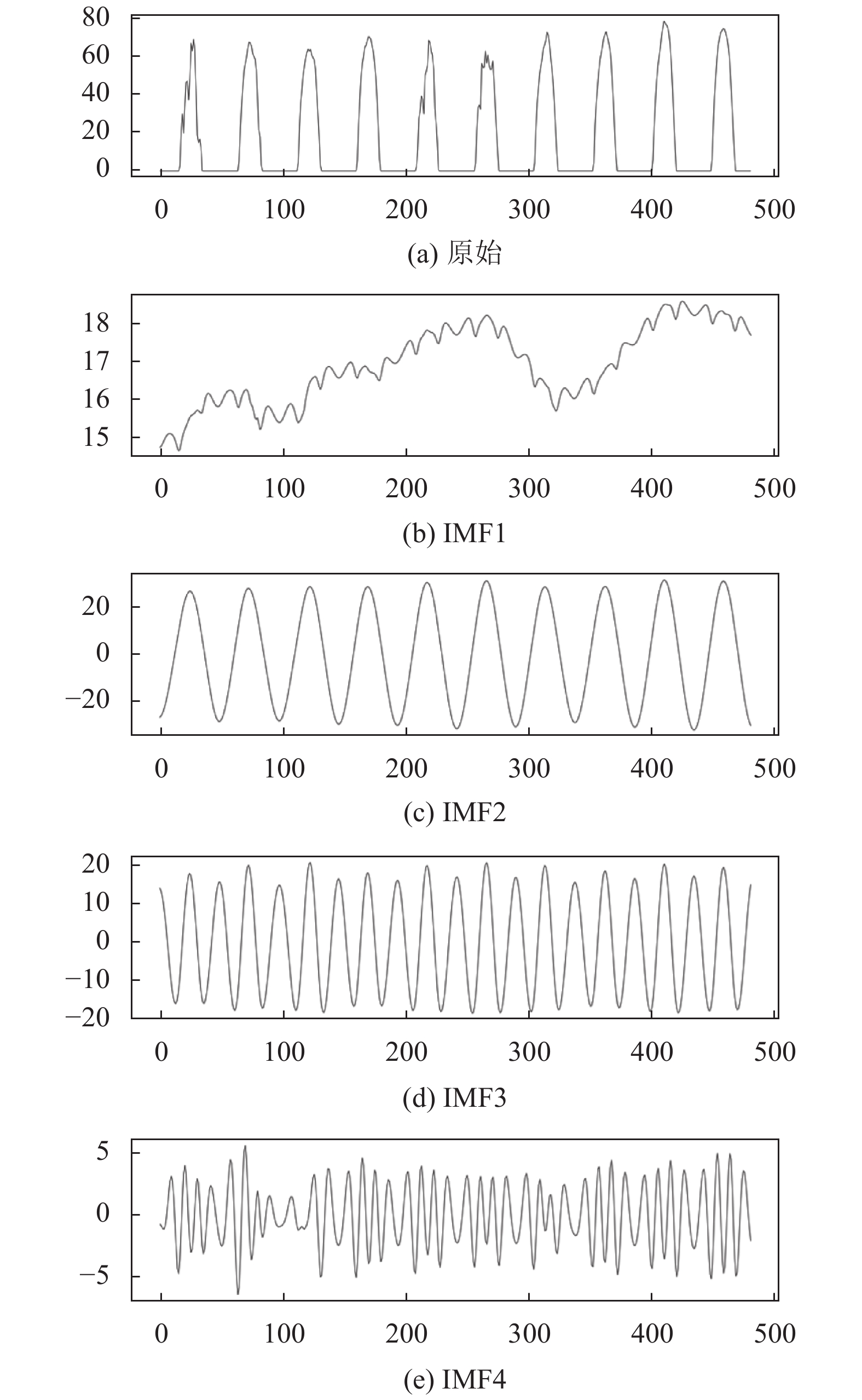
图5展示了真实光伏功率与不同VMD分解模态下的重构值间的差异, 由MAE及RMSE结果可得, 当模态数K为4时, 重构误差最小, 验证了结合相关性分析确定模态数量的有效性. K=4时分解结果如图6所示, 其中第一个序列为光伏功率的原始信号, IMF1–IMF4表示光伏功率分解后得到子模态, 显然VMD分解后的不同模态不仅平稳性更强, 且很好地保持了原光伏数据的趋势特征.

2.3 各模态气象因子选取结果

经VMD分解的光伏序列各模态与气象因素之间的皮尔逊相关系数如表2所示.

由表2可知, 影响不同模态的关键气象因子大不相同, 因此对各模态分别选取气象特征是有必要的, 此处选择相关系数绝对值大于0.3的气象因素作为输入特征来训练模型, 如在模态2中选取直接辐射、法向辐射、水平散射辐射、太阳天顶角、风速、相对湿度、温度、紫外线辐照度作为关键气象因子. 考虑到模态4没有相关性强的变量, 输入特征仅为该模态历史序列.

2.4 模型参数

预测过程中, 模型的输入数据为待预测日前一天的光伏出力与关键气象因子, 输出为待预测日的光伏发电功率.

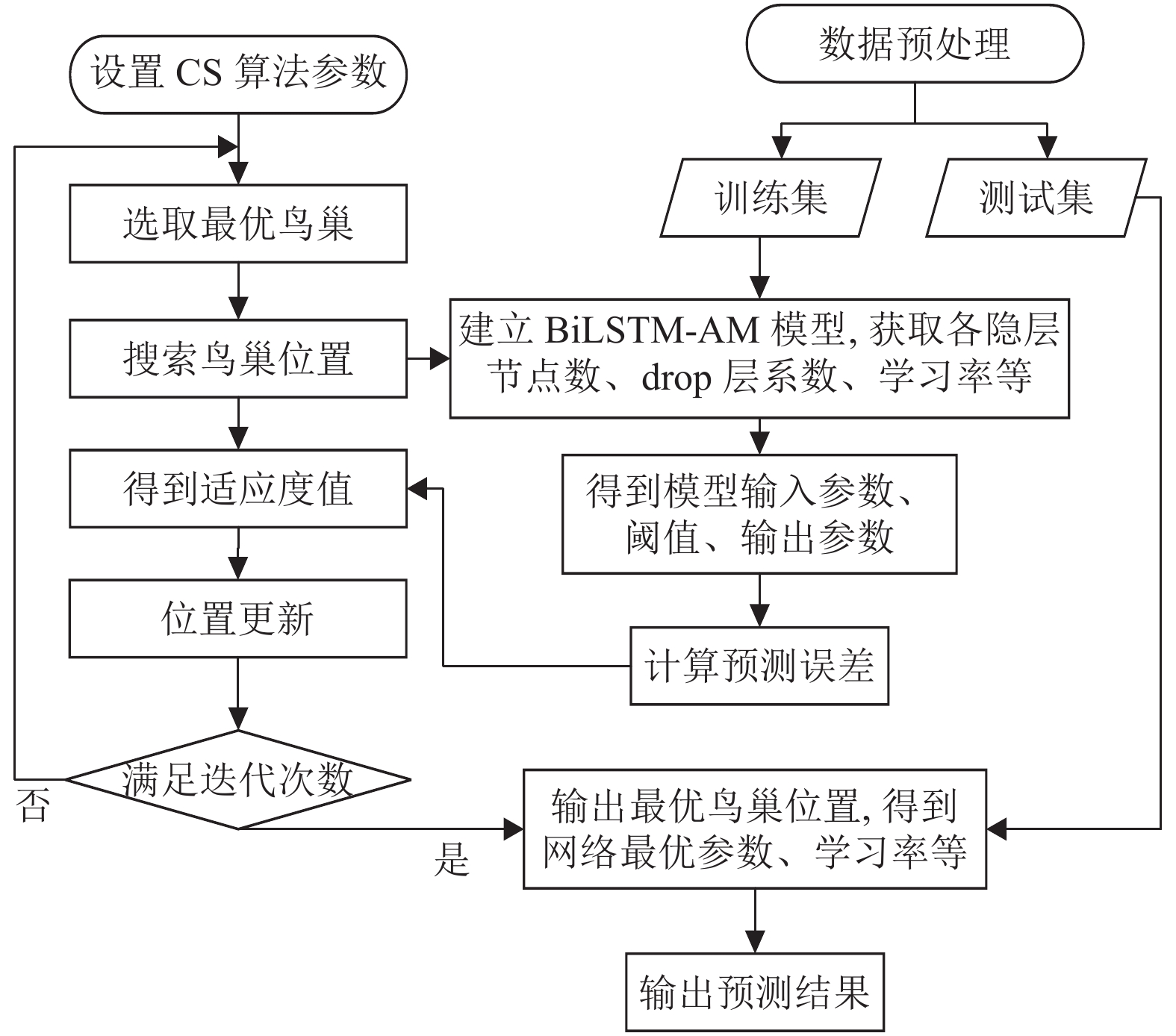
BiLSTM-AM网络的权系数在训练过程中使用的损失函数为MAE, 优化器为Adam^[18], 容易陷入局部最优值. 对此, 本文引入CS算法调整BiLSTM-AM内部隐含层神经元数量、学习率和dropout层系数, 设置CS算法中各参数: 种群数量P=150, Levy飞行参数β=1.5, 更换鸟巢位置概率pa为0.25, 最大迭代次数为300. 其训练过程如图7所示.

最终BiLSTM-AM模型参数优化选择结果如表3.

2.5 算法复杂度分析

(1) VMD算法

为评估VMD算法的性能, 分别采用经验模态分解(empirical mode decomposition, EMD)、奇异谱分析(singular spectral analysis, SSA)与VMD算法对光伏功率数据进行分解, 每组实验重复10次, 比较各算法平均运行时间如表4所示. 可以看出, VMD分解平均运行时间最短, 算法复杂度最小. 由于需要多重迭代更新, EMD分解的平均运行时间显著高于其他算法.

(2) CS算法

CS算法每一代总的时间复杂度为^[19]:

$ T(n) = 3{\rm{O}}(n + f(n)) + {\rm{O}}(n) = {\rm{O}}(n + f(n)) $

(20)

其中, f(n)为优化n维问题的目标函数.

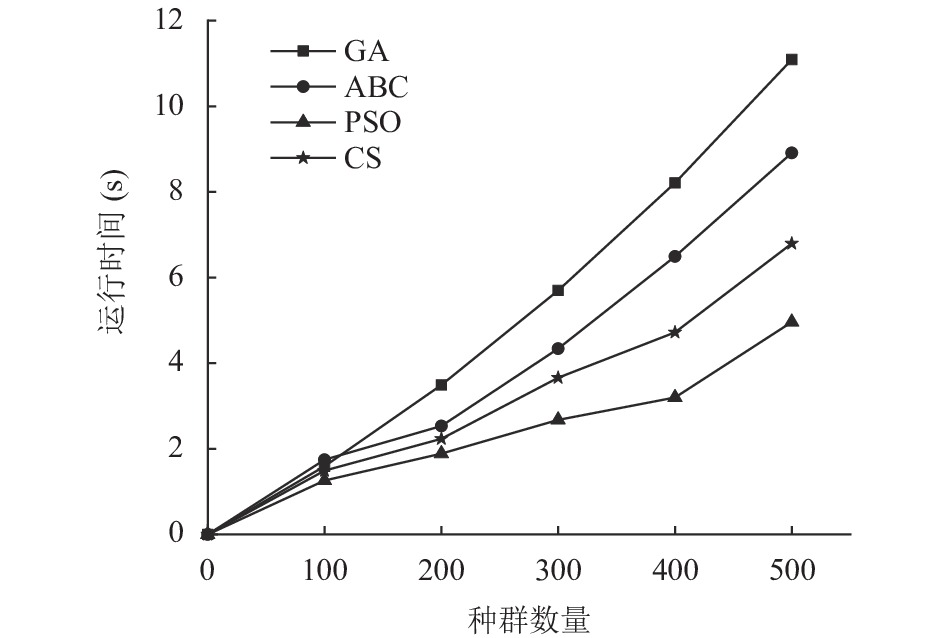
优化算法的运行时间与种群数量P、迭代次数iter、维度n密切相关. 在迭代次数iter=500、维度n=3不变的前提下, 改变种群的数量以对比不同数据规模下的算法时间性能. 图8展示了粒子群优化算法(particle swarm optimization, PSO)、遗传算法 (genetic algorithm, GA)、人工蜂群算法(artificial bee colony algorithm, ABC)与CS算法的运行时间对比图. 可以看出, CS算法运行时间虽略高于简单、运行速度快的PSO算法, 但相比其他优化算法较低, 具有一定优越性.

2.6 光伏功率预测对比实验

为验证上文分析建立的光伏功率预测模型的有效性, 分别与日前模型VMD-BiLSTM、BiLSTM-AM、VMD-LSTM-AM、VMD-BiLSTM-AM进行比较, 预测误差指标对比见表5, 表中最佳预测结果以加粗表示. 可以看出, VMD-BiLSTM-AM-CS模型具有最佳的性能, 各指标结果均最优. 通过对比模型VMD-LSTM-AM与VMD-BiLSTM-AM, 后者预测误差更低, 表明BiLSTM通过将前向和后向特征信息结合, 相比单向LSTM可以挖掘更多有效信息; 通过对比本模型与VMD-BiLSTM、BiLSTM-AM模型的预测误差, 验证了注意力机制与VMD分解的有效性; 此外, VMD-BiLSTM-AM-CS显然较未使用CS优化的模型预测效果更佳, 验证了CS参数优化有效改善了网络性能, 进一步提高了预测精度.

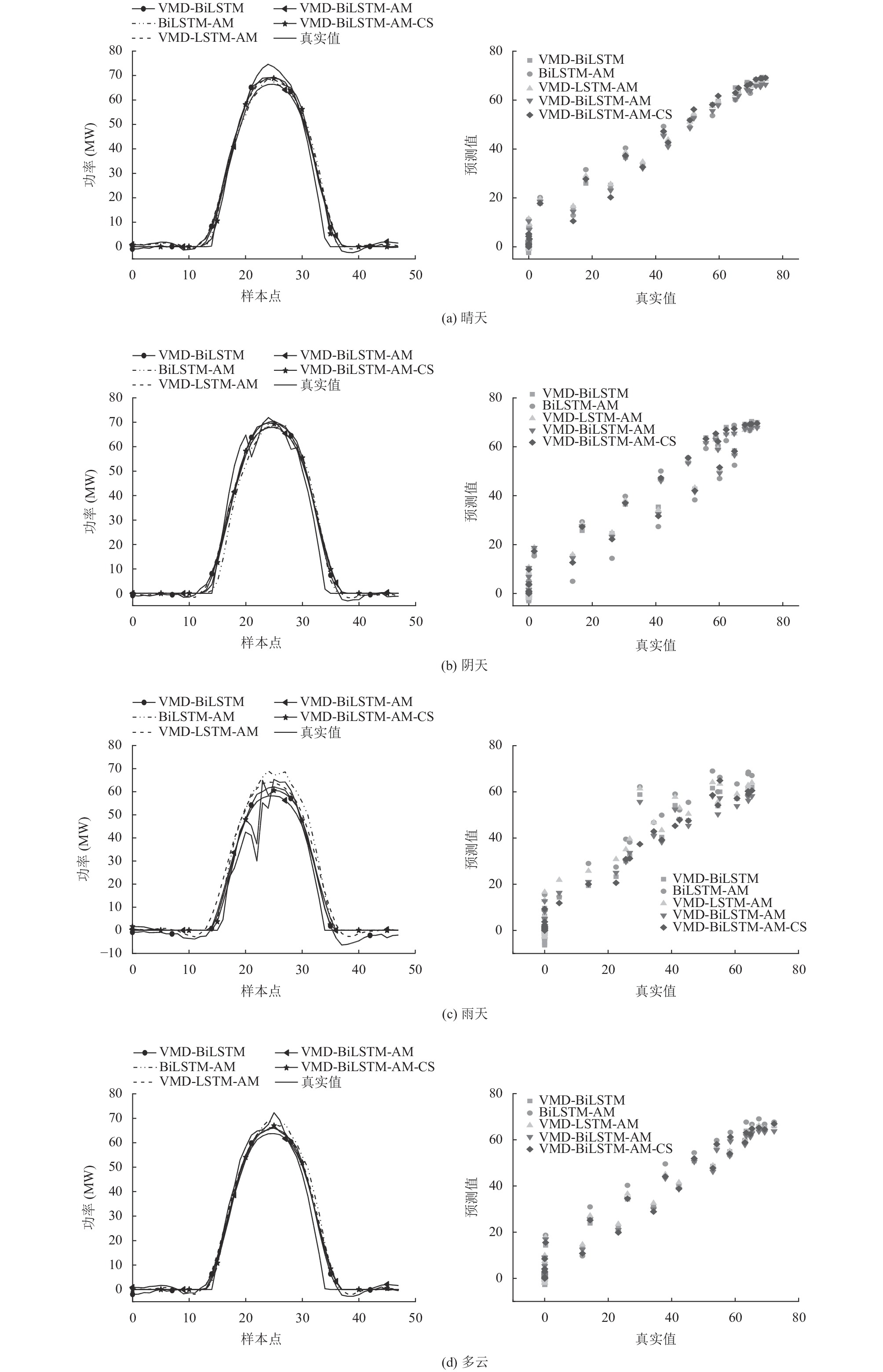
为进一步验本文模型在不同天气类型下的预测有效性, 本文选取10月22日(晴天), 10月28日(阴天), 11月14日(雨天), 11月3日(多云)作为预测日. 分别与日前模型VMD-BiLSTM、BiLSTM-AM、VMD-LSTM-AM、VMD-BiLSTM-AM进行比较, 预测结果如图9所示, 预测误差见表6, 表中每种气象类型下的最佳预测结果以加粗表示.

由各模型不同气象类型下的仿真结果对比分析可得: 本文所提模型的预测曲线更加贴近实际光伏发电功率曲线, 在不同的天气条件下, VMD-BiLSTM-AM-CS模型的MAE均低于其他模型, R²均高于其他模型, 其中晴天的预测误差最低, 阴天预测误差最高. 不同气象类型下, VMD-BiLSTM、BiLSTM-AM模型的预测误差均高于本模型, 尤其是雨天, 本模型的MAE分别降低了45.6%与51.4%; 与模型VMD-LSTM-AM相比, VMD-BiLSTM-AM的MAE、RMSE均更低, 验证了不同气象类型下BiLSTM特征提取效果更优秀; 此外, VMD-BiLSTM-AM-CS较未使用CS优化的模型精度更高, 在雨天和多云天气下MAE分别降低了27.8%、17.7%, 提高了模型的泛化能力. 综上所述, 该模型在不同天气下运行具有较强鲁棒性, 提高了日前光伏预测精度.

3 结论

本文提出了CS算法优化的VMD-BiLSTM-AM日前光伏发电功率预测方法, 该方法通过VMD将原始序列分解为不同模态较为平稳的序列, 降低了不同光伏序列间的相互影响; 再为各序列分别选取关键气象因子, 使用BiLSTM网络充分挖掘光伏序列与气象因子的双向时序特征, 结合注意力机制突出关键信息对预测结果的影响; 最后利用CS算法进行网络参数智能寻优, 防止陷入局部最优. 实例分析表明, 该方法有效提高了日前光伏预测精度, 在不同气象条件下均具有更优异的性能.