2. 西安工程大学 计算机科学学院, 西安 710048
2. School of Computer Science, Xi’an Polytechnic University, Xi’an 710048, China
交通是经济发展的基础和纽带, 对城市群的建立和发展有巨大的支撑和带动作用[1]. 早期城市道路以水泥砼路面为主, 成年累月、经轮载反复作用和受环境因素影响, 已出现不同程度的破损, 道面承载力降低, 直接影响车辆平稳行驶, 维修问题已引起各级行业主管部门的高度重视[2].
关于道面的病害检测, 很多学者都对其进行了研究. 目前普遍采用的是检测车检测手段[3], 现有检测车受道路限制, 检测的宽度一般小于3.75 m, 单张图像对应的路面区域非常有限[4], 既不能满足较长纵向裂缝和大规模网状裂缝的研究、测量, 也无法对某个面积较大的道路破损作出全面的展示, 且在需要对路面破损目标进行统计分析时, 对单张图像进行检测也极易发生漏检、错检等现象. 因此实现路面图像的拼接是必要的, 即可以提高检测效率, 也可以给道路管理部门定位病害提供帮助[5].
水泥路面图像是一种弱纹理图像. 弱纹理表面的图像配准一直以来是计算机视觉领域具有挑战性的问题[6]. 由于弱纹理表面本身缺少丰富的纹理信息, 其像素邻域的灰度分布具有相似性, 因而像素点可分性较差, 常见的基于灰度梯度的特征提取算子如Harris、SIFT、ORB等在弱纹理表面不再适用[7, 8]. De-Maeztu等人[9]和Chen[10]提出了一种基于能量函数优化的方法, 通过平滑约束项实现了对弱纹理区域匹配准确率的提升, 然而在对于大面积的弱纹理区域而言, 其配准错误率仍然较高. Jiang等人[11]尝试通过颜色分割的方式实现小面积的弱纹理区域配准, 但是该方法依赖于颜色分割的精度, 同时当弱纹理区域面积较大时其准确率不高, 在路面场景下, 水泥弱纹理表面色彩单调导致其不能适用. DeTone等人[12]提出一种估计配准单应性矩阵的神经网络用于图像配准过程, 利用神经网络学习待配准图像之间进行图像变换的映射关系, 在给定两幅待配准图像之后, 直接端到端计算出单应性矩阵, 可以避免了中间参数的转换, 在对弱纹理图像配准中达到了很好的效果. 这也给本文使用神经网络进行路面图像的配准[13]提供了良好的思路.
为了将小面积的弱纹理路面图像进行完整、精确的拼接[14], 本研究以智能手机作为路面图像的采集工具, 结合神经网络, 提出了一种基于LoFTR算法[15]的图像拼接方法. 为了缩短神经网络处理的时间, 本文提出先局部拼接再扩展的思想, 在确保拼接准确度的同时提高了拼接速度[16].
1 LoFTR特征匹配算法原理LoFTR是一种局部图像特征匹配方法, 其目的是找到输入的两幅图像中同时存在的相同物体实例, 并输出其位置信息、匹配关系. 区别于传统基于特征点的匹配算法, 如SIFT、ORB算法等, 该算法没有检测特征点的步骤, 由模型直接输出匹配对. 具体的算法流程区别如图1.

|
图 1 基于特征点和基于深度学习的匹配算法流程对比 |
由图1可知基于深度学习的特征提取替代了传统算法的特征点检测部分, 且配准网络是基于特征向量的, 后续步骤则是各方法的具体流程, 结果都是产生可靠匹配对. 因此, 基于深度学习的特征匹配替代传统的特征匹配是可行的.
1.1 算法基础1)特征提取网络
图像配准网络是对图像的特征图进行匹配, 因此原始图像需经过特征提取网络转化成特征图, 才能进行特征匹配.
特征提取采用特征图金字塔网络(feature pyramid networks, FPN), 金字塔的结构同时融合了高层和低层的语义特征信息, 使得每一层的语义信息都得到了加强. 其网络结构如图2, 左侧自底向上, 每经过一次卷积, 特征图尺寸减半, 共生成3级特征图. 中间1×1卷积是对左侧特征进行组合, 同时对主干网络起到梯度缓冲作用. 低分辨率的特征图经上采样后与下一层按元素相加, 迭代直到生成最终的分辨率图. 最右侧3×3卷积生成最终的特征映射, 同时减少了上采样的混叠效应. 最终, 本文需要的是原图的1/2级和1/8级特征图, 即P2和P4.
2)注意力机制
注意力机制是对输入模型的每一项进行分配权重的机制, 权重取决于输入项之间的相互作用. 因此, 注意力机制有信息聚合的作用, 图像配准阶段使用注意力机制可以使得两幅图像中相似的特征点凸显出来, 利于后续精确匹配. 注意力值的计算公式为:
| $ A{{ttention(Q, K, V) = {\textit{Softmax}}(Q}}{{{K}}^{\rm{T}}}{\text{)V}}{\text{}} $ | (1) |

|
图 2 特征提取网络结构 |
对于图像对{A, B}, 待查询图像A的特征点表示为Qi, Kj和Vj表示召回图像B的特征点.Softmax函数用来计算查询向量Qi和键向量Kj的相似度, 越大表示这两个特征越相似, 利用该相似度与真值Vj加权求和, 可得到注意力值. 此过程实现了特征的聚合, 聚合了两幅图像上所有相似的特征点.
LoFTR算法中主要采用的是基于空间方法的图注意力网络, 样本空间是所提取特征点的编码信息, 包括特征点的位置、由传统方法或深度卷积方法获得的该像素及其邻域的特征及特征置信度[17].
假设输入特征向量x, 经过3个参数矩阵
| $ A{{ttention(Q, K, V}}{{\text{)}}_{{i}}}{\text{ = }}\frac{{\displaystyle\sum\nolimits_{j = 1}^N {sim({Q_i}, {K_{{j}}}){V_j}} }}{{\displaystyle\sum\nolimits_{j = 1}^N {sim({Q_i}, {K_{{j}}})} }} $ | (2) |
| $ {{sim(}}{{{Q}}_i}{\text{, }}{{{K}}_{{j}}}{\text{) = }}\phi {{\text{(}}{{{Q}}_i}{\text{)}}^{\rm{T}}}\varphi {\text{(}}{{{K}}_{{j}}}{\text{)}} $ | (3) |
其中,
| $ \phi {{(x) = }}\varphi {{(x)}} = {{elu(x) + 1}} $ | (4) |
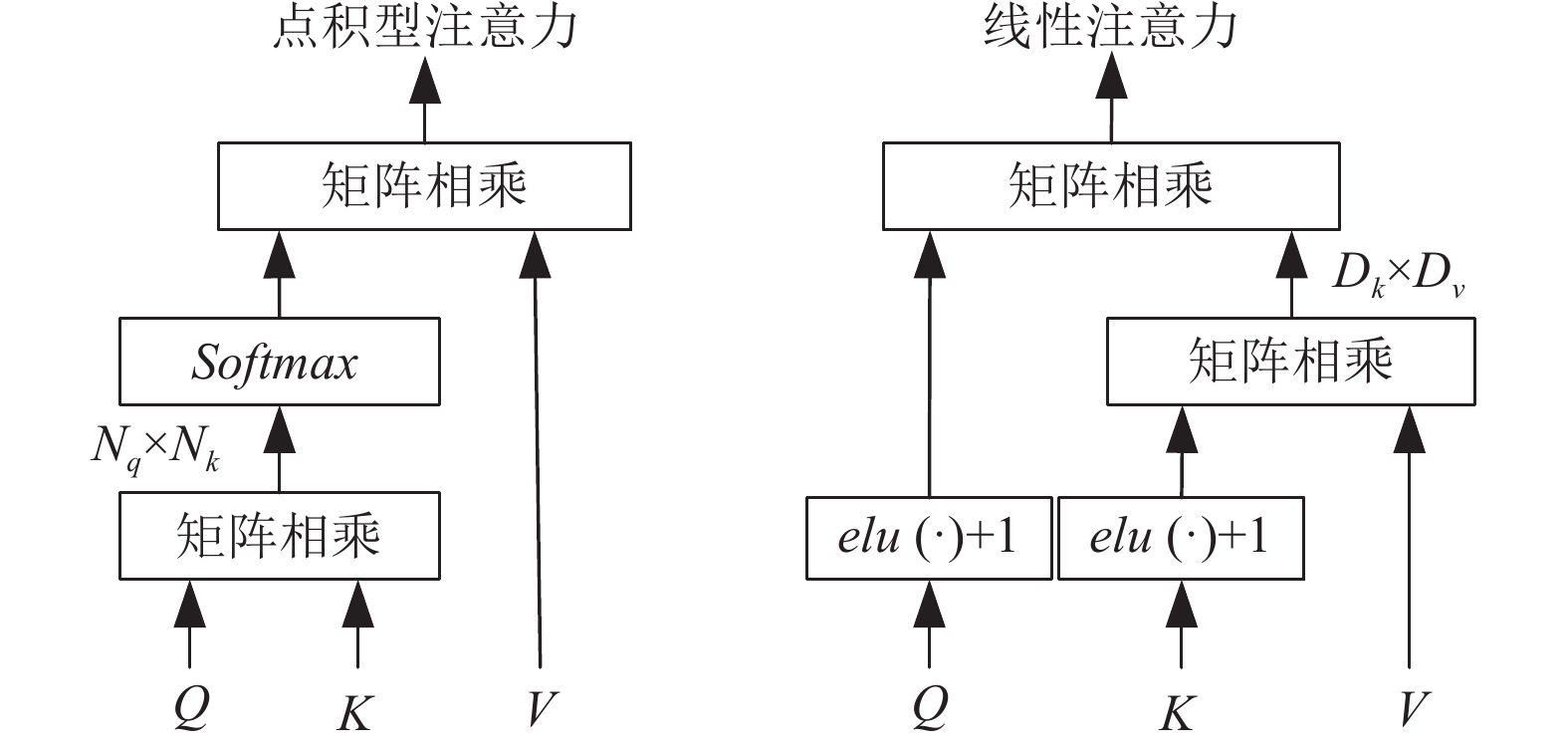
图3对比了不同注意力机制的注意力层. Q, K, V都是N×D矩阵, 经典的点积型注意力机制中长度为N的向量Q、K之间的点乘操作其复杂度时O(N2), 对于特征匹配任务, N与图像的像素总数成正相关. 本研究使用的LoFTR算法为了减轻Q、K点积的计算成本, 使用了线性注意力, 即替换原注意力层的核函数为
3) 局部特征变换器(LoFTR)模块
该模块的作用是将输入的局部特征转换为与上下文和位置有关的量. 此过程的核心是Transformer, 为了使用功能强大的Transformer, 需要下采样得到特征图, 在匹配任务中, 会使得匹配变差. 为优化此问题, LoFTR模块通过不停地迭代使用自注意力和交叉注意力获得高精度的匹配关系.
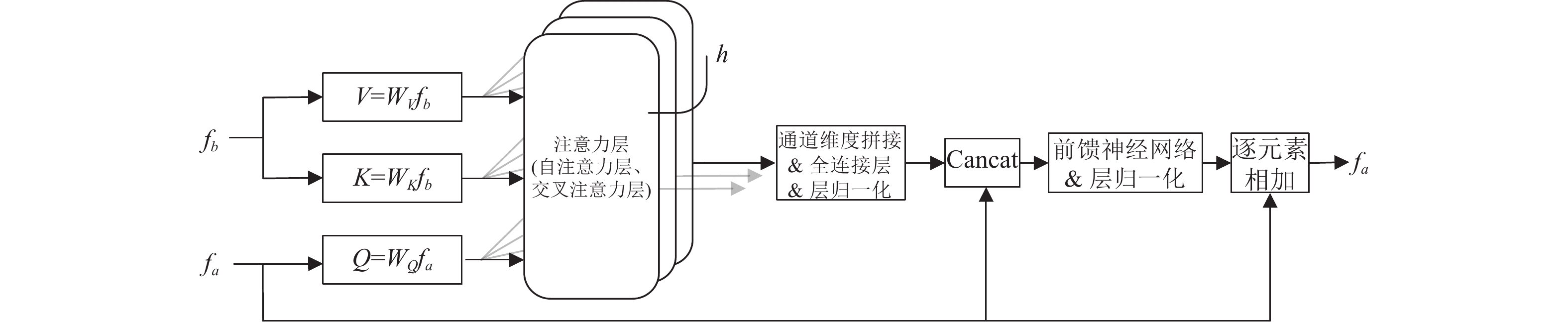
Transformer的编码器由多个顺序连接的编码器层叠加. 编码器层的具体操作步骤如图4, 输入两幅图像A、B的特征图
|
图 3 点积型、线性注意力机制的注意力层对比 |
|
图 4 LoFTR编码器层结构 |
编码器层的核心是多头注意力机制, 由多个交替的自注意力层和交叉注意力层构成, 以使匹配达到紧密收敛[18]. 自注意力层和交叉注意力层使用的是多层图神经网络, 核心思想是对特征进行变换. 自注意力层使得每个点关注其周围所有点的关联, 融合本张图片的邻域信息. 交叉注意力层使得点关注与另一幅图上的所有点的关联, 融入待匹配图像的信息.
1.2 算法流程LoFTR算法包含4个步骤: 全局特征提取、将粗略的局部特征转换为易于匹配的特征表示、粗略匹配模块、精细匹配模块.
1) 全局特征提取. 输入两幅待匹配图像, 使用带有特征图金字塔网络的标准卷积结构提取多层次的特征[19]. 分别是原始图像维度的1/8的粗级特征, 以及1/2的细级特征.
2) 粗略的局部特征转换为易于匹配的特征表示. 把低分辨率的特征图展平为一维向量, 添加位置编码后传递到 LoFTR 模块, 提取位置和上下文相关的特征信息, 既融合本张图像的邻域信息和融入待匹配图像的信息. 直观地说, LoFTR 模块将这些特征转化为易于匹配的特征表示.
3) 粗略匹配模块. 使用乘积的方式先计算所有位置的匹配得分矩阵, 然后使用dual-Softmax方法计算最优匹配, 再通过互近邻算法过滤掉一些离群匹配对, 得到粗略的匹配预测.
4) 精细匹配模块. 若匹配点对(i1,j1), (i2, j2)在粗匹配中, 则将其映射到相应的精细特征图中, 并把映射区域裁剪出来, 输入LoFTR模块, 提取精细的匹配特征, 记作FA和FB, 然后计算FA中心特征与FB中所有特征的匹配概率, 再计算该概率分布, 即可计算出FB中的亚像素精度的匹配点位置.
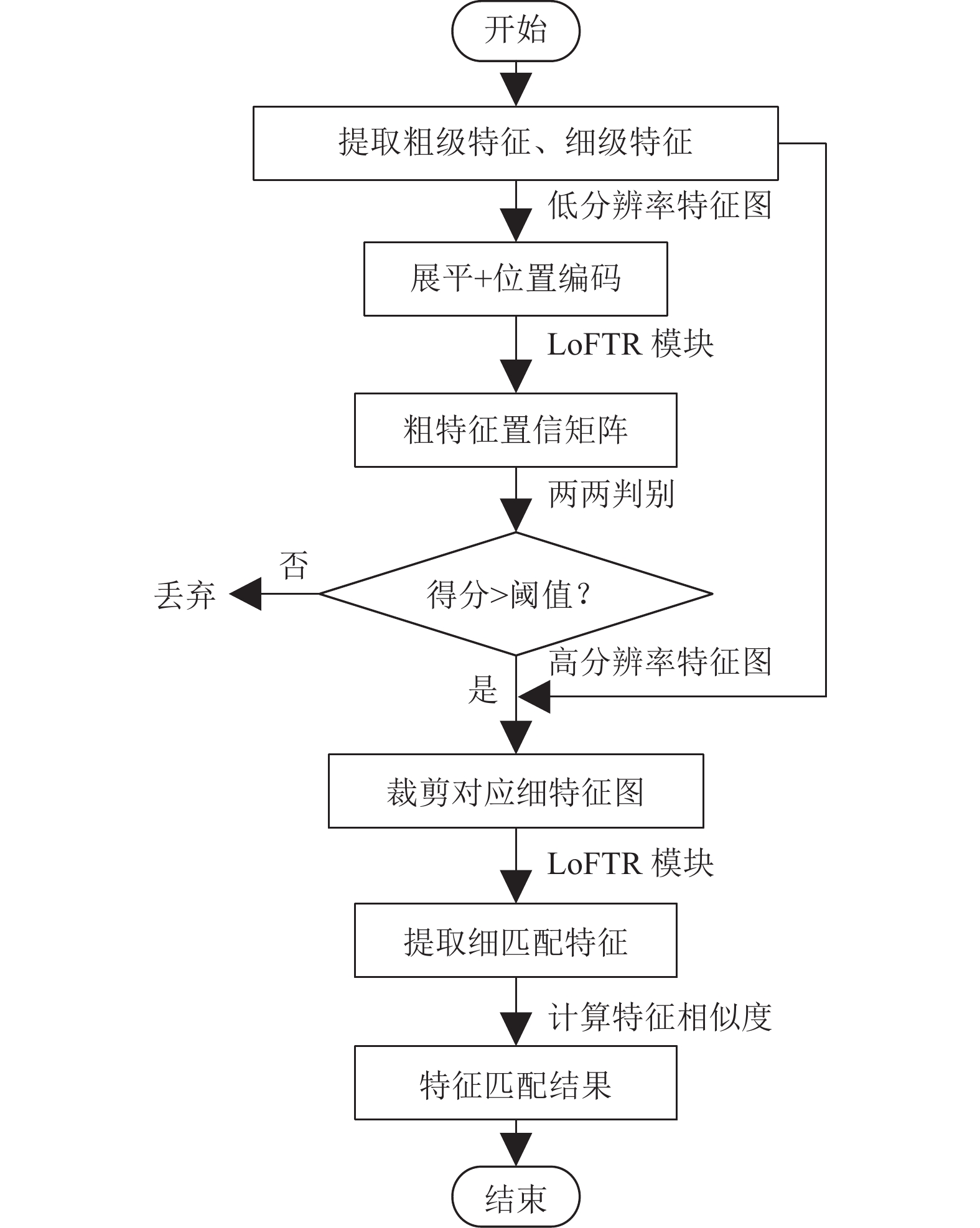
LoFTR算法的总流程如图5所示.
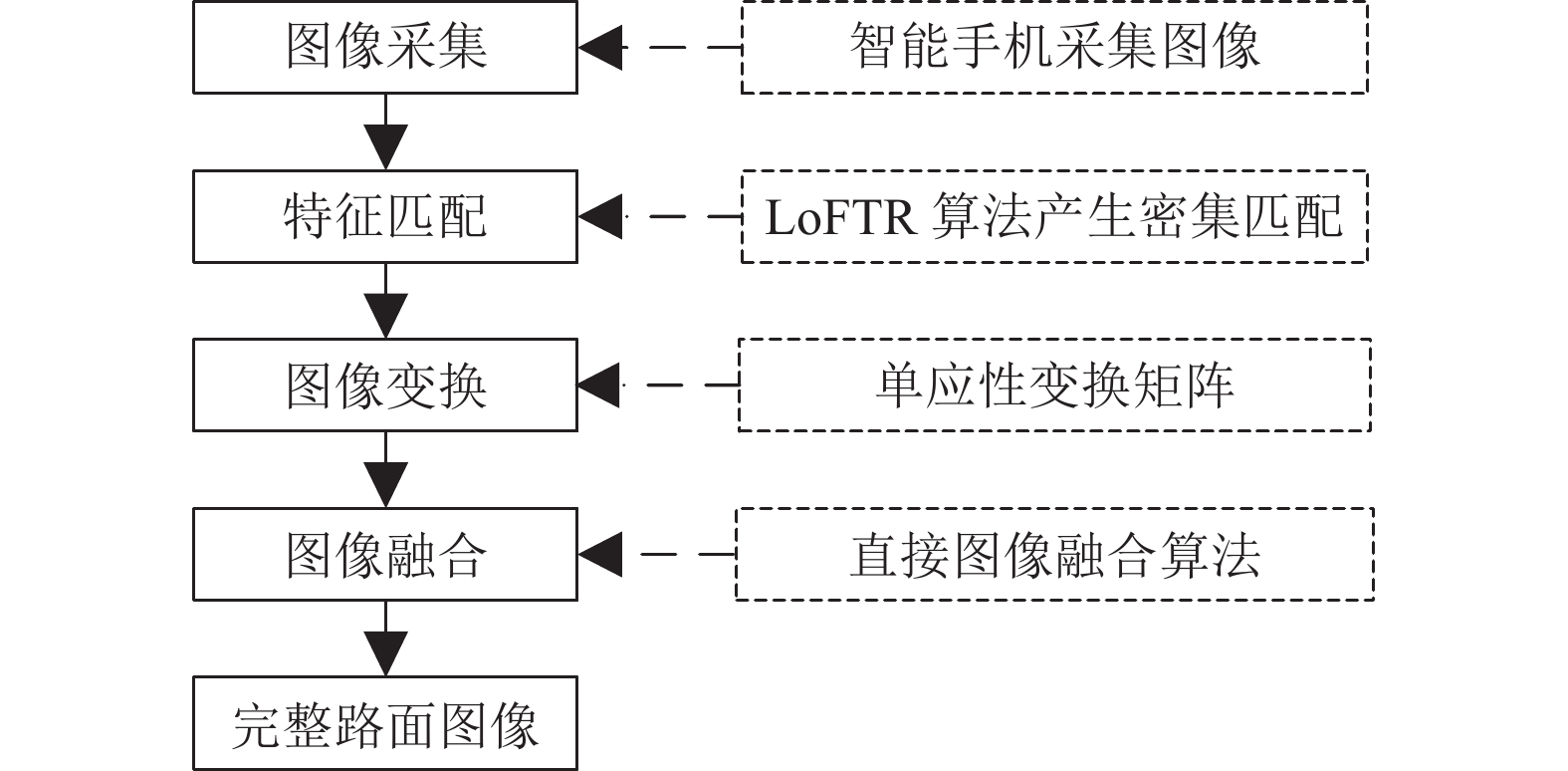
2 拼接模型与实现 2.1 拼接流程路面图像拼接的实现步骤如图6所示, 共分为4个部分.
1)图像采集, 采用智能手机配合可移动落地支架作为图像采集工具, 以获取数据集.
2)特征匹配, 输入图像经过深度学习LoFTR算法, 产生密集匹配.
3)图像变换, 根据匹配结果, 将两幅图像变换到同一坐标系下. 根据式(5)可以计算出单应性矩阵H, 待拼接图像利用矩阵H代表的空间投影关系, 变换到与参考图像一致的坐标系下[20]. 式(5)中(x', y')和(x, y)是待配准图像和基准图像的匹配点对. 式(6)表示H矩阵是由尺度因子、相机内参数矩阵和外参矩阵组成的.
| $ \left[ {\begin{array}{*{20}{c}} {{{x}}'}\\ {y'}\\ 1 \end{array}} \right]{\rm{ = }}H{\rm{\cdot}}\left[ {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{h_{11}}}&{{h_{12}}}&{{h_{13}}}\\ {{h_{21}}}&{{h_{22}}}&{{h_{23}}}\\ {{h_{31}}}&{{h_{32}}}&{{h_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x\\ y\\ 1 \end{array}} \right]$ | (5) |
| $ H = {{s}}\left[ {\begin{array}{*{20}{c}} {{{{f}}_{{x}}}}&\gamma &{{{{u}}_0}} \\ 0&{{{{f}}_{{y}}}}&{{{{v}}_0}} \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{r}}_1}}&{{{{r}}_2}}&{{t}} \end{array}} \right] $ | (6) |
|
图 5 LoFTR算法流程图 |
|
图 6 路面图像拼接流程 |
4)图像融合, 对重叠区域进行处理, 完成拼接过程. 进行图像变换之后, 因拍摄过程的亮度、角度不同, 拼接后的图像可能会存在接缝, 因此需使用图像融合方法处理重叠区域, 以减弱接缝. 由于本研究的结果图像需要尽可能多的保留裂缝等细节信息, 因此采用基于Harr小波变换的图像融合算法[21], 将待融合图像进行小波分解, 得到一系列不同频段的、反映图像局部特征的子图像, 用不同的融合规则对子图像进行处理, 最后利用小波逆变换得到融合图像.
设图像大小为M×N, 其二维离散小波变为:
| $ {W_\varphi }({j_0}, m, n) = \frac{1}{{\sqrt {MN} }}\sum\limits_{x = 0}^{M - 1} {\sum\limits_{y = 0}^{N - 1} {f(x, y){\varphi _{{j_0}, m, n}}(x, y)} } $ | (7) |
| $ W_\psi ^i(j, m, n) = \frac{1}{{\sqrt {MN} }}\sum\limits_{x = 0}^{M - 1} {\sum\limits_{x = 0}^{N - 1} f } (x, y)\psi _{j, m, n}^i(x, y), i = \{ H, V, D\} $ | (8) |
逆变换为:
| $ \begin{gathered} {{f}}(x, y) = \frac{1}{{\sqrt {MN} }}\sum\limits_m {\sum\limits_n {{W_\varphi }({j_0}, m, n)} } {\varphi _{{j_{0, m, n}}}}(x, y) \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}+\frac{1}{{\sqrt {MN} }}\sum\limits_{i = H, V, D} {\sum\limits_{{{j}} = {{{j}}_0}}^\infty {\sum\limits_{{m}} {\sum\limits_n {W_\psi ^i} } } } (j, m, n)\psi _{j, m, n}^i(x, y) \\ \end{gathered} $ | (9) |
设待拼接两幅路面图像的低频系数分别为
| $ \begin{split} &{{f}}_l^F(x, y) =\\ &\left\{ {\begin{array}{*{20}{l}} {{{f}}_l^A(x, y)}, \\ {{{w}} \cdot {{f}}_l^A(x, y) + (1 - w){{f}}_l^B(x, y)}, \\ {{{f}}_l^B(x, y)}, \end{array}\begin{array}{*{20}{l}} {(x, y) \in A且(x, y) \notin (A \cap B)} \\ {(x, y) \in (A \cap B)} \\ {(x, y) \in B且(x, y) \notin (A \cap B)} \end{array}} \right. \end{split} $ | (10) |
设高频系数分别为
| $ {{f}}_h^F(x, y) = \left\{ {\begin{array}{*{20}{c}} {{{f}}_h^A(x, y)}, \\ {{{f}}_h^B(x, y)}, \end{array}} \right.\begin{array}{*{20}{c}} {\left| {{{f}}_h^A(x, y)} \right| > \left| {{{f}}_h^B(x, y)} \right|} \\ {\left| {{{f}}_h^A(x, y)} \right| < \left| {{{f}}_h^B(x, y)} \right|} \end{array} $ | (11) |
为了减轻配准阶段网络的压力, 不仅要对输入图像进行下采样处理, 每次拼接时, 也尽可能只在相邻图像的重叠区域找寻特征点和产生匹配对. 本文提出了一种局部拼接方法, 先对图像进行下采样至912×684像素, 确定重叠区域, 如图7所示.
假设Img1、Img2、Img3对应实际路面从左到右, 则只需在Img1右侧456×684像素区域找寻与Img2相关的匹配点即可. 若将Img1和Img2拼接完的结果记为ResImg1, 则当ResImg1与Img3继续拼接时, 特征匹配阶段也仅需输入ResImg1最右侧的456×684像素区域和Img3即可.

|
图 7 局部拼接方法流程图 |
因此特征匹配网络运行时间不会随着待拼接图像数量的增多而大幅增加. 网络每次只需对456×684像素区域和912×684区域进行配准. 产生的匹配对经过筛选后, 可以求得两幅图像的单应矩阵. 将后者区域坐标变换到前者的像素坐标下, 再采用基于小波变换的图像融合技术处理图像接缝, 可完成两块小区域的拼接. 再把原来未输入网络的图像区域加入到拼接结果中, 如Img1的前半部分、ResImg1的左侧部分, 产生完整的拼接结果.
3 实验过程与结果分析 3.1 数据集设置以随机获取的水泥路面图像为例进行分析. 为了更安全、高效地获取路面图像, 以智能手机搭配移动支架作为图像采集工具, 通过控制支架的移动拍摄不同区域路面的图像, 移动支架及其参数如图8所示. 本次研究选用的智能手机型号为华为nova6 4G版, 采集的图像像素为3648×2736. 在图像采集过程中, 需尽量确保手机摄像头主光轴与地面正交, 而且与地面保持相同的高度(约70 cm), 对采集到的图像, 需尽量保证至少20%的重叠率.
实验共拍摄路面图像716幅, 选出90%即644幅样本进行配准网络的训练, 其余10%即72幅样本测试. 考虑到不同时段拍摄的路面图像的亮度、对比度不同, 划分时训练集和测试集时, 图像按需均匀分配以保证实验的有效性. 实验平台的操作系统为Windows 10, CPU为Intel(R) Xeon(R) Gold 5118, GPU为NVIDIA Quadro P5000, RAM为64 GB. 模型训练的参数设置如表1所示.

|
图 8 移动支架实物、参数图 |
| 表 1 LoFTR模型训练参数 |
本研究将列举两个算例研究路面拼接方法的可行性, 如图9所示. 图9(a)是一处不连续裂缝的分段图像, 图9(b)是一处连续裂缝的分段图像, 图像编号代表采集的先后顺序. 由于采集到的图像为高分辨率图像, 为了在保证清晰度的基础上缩短拼接时间, 需要将分辨率下采样至684×912像素.

|
图 9 各算例的分段图像 |
3.2 实验结果
1)训练集配准结果
本文采用特征筛选率对图像配准算法进行评估, 筛选方法均为RANSAC, 其计算公式如下:
| $ 特征点筛选率 = \frac{配准产生的特征对 - 筛选之后的特征对}{配准产生的特征对} $ | (12) |
由式(12)看出, 配准产生的特征对质量越高, 经过筛选之后的特征对越多, 筛选率越低.
由于SIFT算法在传统基于特征点的配准算法中最具代表性, 因此选取SIFT算法与LoFTR算法的特征筛选率进行对比. 在整个训练集上的特征筛选率如图10, 可看出LoFTR的特征筛选率均低于SIFT, 因此LoFTR配准精度高于SIFT.

|
图 10 特征筛选率 |
2)算例1拼接结果
本文使用4种图像拼接方案分别对两组算例进行拼接, 对比拼接效果. 拼接方案分别基于SIFT、SURF、ORB和LoFTR特征匹配算法.
局部的拼接质量影响全局的路面病害显示效果, 故先研究4种拼接方案对于相邻两幅图像的拼接. 选取分段图像1-3和分段图像1-4, 如图11. 图12分别展示各方案对图8数据的特征匹配结果.

|
图 11 算例1的分段图像1-3和分段图像1-4原图 |
由于匹配结果自带欧氏距离, 欧式距离越小, 代表两个点相似程度越高, 因此本研究通过设置阈值为0.75对匹配结果进行筛选. 表2可以看出各算法的匹配结果经过筛选后, 剩余的高质量匹配数量. 结合图9可以发现, SIFT、ORB产生的匹配对几乎没有相似度高的; SIFT算法虽然可以产生相似度高的匹配, 但数量很少, 并且正确的匹配全部出现在裂缝周围, 既纹理较强的区域; LoFTR算法相比前3种算法特征匹配最佳, 虽然也存在误匹配, 但在这些算法中, 误匹配率是最低的, 而且在弱纹理区域仍然可以寻找到大量正确的匹配对. 本文基于LoFTR算法加入局部拼接方案, 在保持LoFTR算法良好结果的基础上, 进一步降低了误匹配率, 在所有匹配结果中效果最好.
由于SIFT、SURF算法在特征匹配阶段产生大量的错误匹配, 满足要求的匹配对已不足4个, 因此不能计算出变换矩阵, 就不能完成后续的拼接工作. 故图13仅展示SURF、LoFTR、LoFTR+局部拼接方法关于分段图像1-3与分段图像1-4的拼接结果.
由图13(a)看出SURF算法的拼接效果很差, 只对裂缝所在区域有良好的拼接, 图像下面的弱纹理区域存在明显的错位、形变现象, 且接缝明显; 从图13(b)和图13(c)看出, LoFTR算法和本文算法结果一致, 这是由于两者产生的密集匹配几乎是一致的, 拼接效果良好, 图像过度平缓, 无拼接错位及鬼影现象, 正确地展示了两幅图像中裂缝的走向及相对定位. 这说明对于大面积、弱纹理的路面图像, 传统的SIFT、ORB、SURF算法的特征提取能力大大减弱, 已经不再适用. 而针对弱纹理图像还能产生大量密集匹配的深度学习算法, 在图像拼接中展现出巨大的优势.
对拼接两幅图像的拼接时长进行测试, 表3是基于LoFTR算法的拼接方案和局部拼接方案的时长对比. 发现局部拼接方法相较于基于LoFTR算法的拼接方法, 特征匹配阶段所消耗的时间缩短了4.2 s, 拼接两幅图像的总时间缩短了4.9 s. 结合图12分析出本文拼接方案不仅提高了特征匹配质量, 还缩短了拼接时间.

|
图 12 图像匹配结果 |
| 表 2 各匹配算法产生的匹配经筛选前后的数量对比 |

|
图 13 图像拼接结果 |
| 表 3 LoFTR算法加入局部拼接方法前后运行时间对比(s) |
因为后续的实验结果均应用采用LoFTR+局部拼接方法, 故下文为简化起见, LoFTR算法表示LoFTR+局部拼接方法.
图14是各算法关于算例1整体的拼接效果. 从图14(a)看出SIFT算法最多只能实现3副图像的拼接, 图14(b)看出SURF算法只能实现2副图像的拼接, ORB算法不能实现拼接, 而本文算法能实现整体的拼接. 如图14(c), 可以清晰地看到裂缝的脉络, 且整幅图像的像素过渡自然, 两边的水泥板刻槽也接近平行, 验证了本文算法在道路图像拼接的可行性.
表4表示各算法每次拼接过程中的匹配数量变化情况, 这些匹配是经过筛选误匹配后的. 第1次拼接是指算例1中的分段图像1-0和分段图像1-1拼接, 第2次拼接是指第1次拼接结果与分段图像1-2拼接, 以此类推. 由表4可知SIFT、SURF、ORB算法找寻的特征对普遍比较少, 且随着拼接次数的增加, 特征对数量整体呈下降趋势, 直到匹配数量过小, 已不能完成后续拼接. 但LoFTR算法产生的匹配对经过筛选之后仍然有大量的存在, 验证了LoFTR算法特征匹配结果的正确性.
3)算例2拼接结果
由于ORB算法对于算例2第1次拼接的特征匹配阶段, 产生的匹配几乎全是误匹配, 因此无法进行后续的拼接. 故图15展示SIFT、SURF、LoFTR算法对算例2的拼接结果, 同时对结果图像进行了标注.

|
图 14 算例1拼接结果 |
| 表 4 各算法每次拼接的匹配数量对比 |

|
图 15 算例2的拼接结果 |
从图15看出, 3种算法均能产生拼接结果, 但拼接效果好坏不一致. 结果图的左下方黑色区域高度代表整体图像的倾斜程度, 由图15可知SURF算法对应的高度最高, 为132.05像素, 因此拼接结果倾斜度最高, 其次是SIFT算法, LoFTR算法最优; 分段图像2-2在3个结果图中较为突出, 对其距离结果图边缘的长度进行测量, 能分析结果图上侧边缘的过度平缓程度, 也可以评价中间结果图质量的好坏, 图15(b)中图像2-2距离结果图边缘长度最短, 为17.604像素, 故SURF算法对分段图像2-2拼接的效果较差, 对图像的拉伸形变最严重, 其次是SIFT算法, LoFTR算法表现最好, 上侧边缘最平缓; 最后对结果图像最右侧黑色区域的倾斜角度进行测量, 发现SURF算法整体倾斜最严重, 倾斜角度为9.798°, 其次是SIFT算法为8.501°, 本文算法表现最优, 为8.259°. 验证了本算法对于路面拼接相较于传统算法更加精确.
结合算例1的结果, 证明了本文拼接方案对于不同的路面图像适应力更强、更加通用.
4)算例2定量分析
由于ORB算法无法对路面图像进行拼接, 因此下面只展示SIFT、SURF、LoFTR算法关于算例2拼接结果的图像质量定量分析结果, 从3个方面来进行评估, 分别是均方误差、拼接时间、匹配点筛选率.
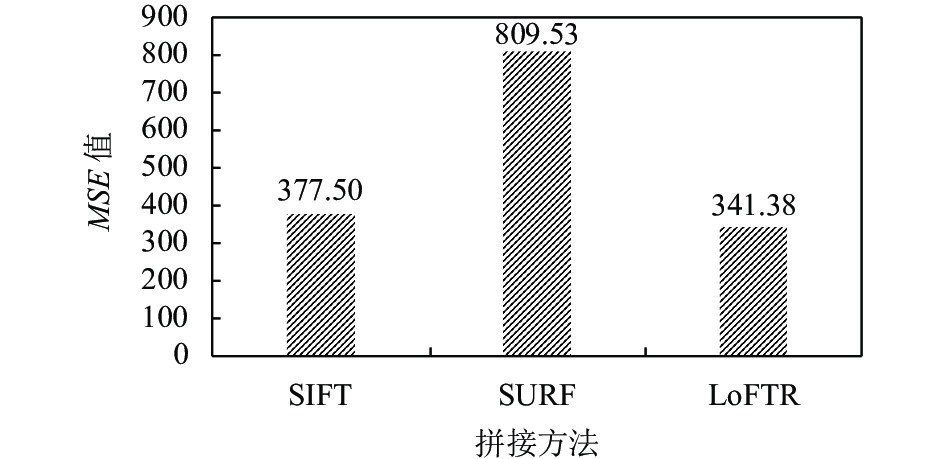
均方误差(mean squared error, MSE)用来度量原始图像与拼接图像之前的像素距离, 评价拼接质量.MSE的值越小, 说明两者像素距离越小, 拼接效果越好, 结果图质量越高, 反之, 拼接效果越差. MSE计算公式如下:
| $ {\textit{MSE}} = \frac{1}{{{{mn}}}}\sum\limits_{i = 0}^{m - 1} {\sum\limits_{j = 0}^{n - 1} {{{[I\left( {i, j} \right) - K\left( {i, j} \right)]}^2}} } $ | (13) |
从图16看出LoFTR算法的MSE值最低, 即拼接效果越好. 其次是SIFT算法, SURF算法的拼接效果最差.
拼接时间用来评价算法的运算效率. 算例2完整的拼接过程中, SIFT算法用时最少, 只用63.6 s就能完成拼接; 其次是SURF算法, 用时65.4 s; LoFTR算法用时最长, 需耗费104.8 s. 这是因为深度学习网络的处理阶段, 需要耗费时间才能完成高质量的匹配任务.
表5展示图像在每一次拼接过程中特征点的筛选情况, 筛选的是不可靠的匹配对. 平均筛选率越低, 代表算法产生可靠的匹配对越多. 由表6看出LoFTR算法的平均筛选率最低, 是28.3%, 因此LoFTR算法不仅能产生大规模的特征匹配对, 而且这些匹配对大多都是可靠的.
|
图 16 各拼接方法的MSE值对比 |
| 表 5 各模型每次拼接的特征对数量 |
| 表 6 各模型每次拼接的筛选率(%) |
4 结论
本文基于随机获取的水泥路面图像数据, 采用基于LoFTR算法的图像拼接技术, 生成宽幅路面图像, 把所有分段图像的纹理聚集在一起显示, 为道路病害检测部门提供更大范围的路面信息. 除此之外, 研究提出的局部拼接方法很大程度缩短了拼接时间. 虽然与传统拼接方法相比, 拼接时间仍然较长, 但拼接结果的MSE值最低, 拼接效果也最佳, 因此仍具备显著优势. 后续将研究如何进一步缩短图像拼接的时间, 使路面图像拼接方法更高效.
| [1] |
Zhang YQ. Development model of urban ecological transportation an analysis based on Beijing. E3S Web of Conferences, 2021, 253: 01004. |
| [2] |
柳青. 市政道路水泥混凝土路面病害分析及处理. 住宅与房地产, 2020(5): 227. |
| [3] |
Hu ZL, Qi YJ, Bai L. Development survey of highway pavement and tunnel inspection vehicles in foreign countries. Forestry Machinery & Woodworking Equipment, 2016, 44(5): 4-7. |
| [4] |
唐金学, 黄永华, 胡世峰. 道路检测车及道路检测方法、装置: 中国, 201911079608.7. 2020-03-24.
|
| [5] |
Lü Y, Qu SR. An algorithm of pavement crack image registration and mosaic based on SIFT algorithm. Journal of Highway and Transportation Research and Development, 2012, 29(2): 23-28. |
| [6] |
Yang XY, Jiang G. A practical 3D reconstruction method for weak texture scenes. Remote Sensing, 2021, 13(16): 3103. DOI:10.3390/rs13163103 |
| [7] |
李彦飞. 关于弱纹理人脸图像匹配方法的改进研究. 计算机仿真, 2016, 33(7): 331-334. DOI:10.3969/j.issn.1006-9348.2016.07.072 |
| [8] |
程鹏飞, 周修庄, 唐玲, 等. 一种面向弱纹理图像的特征点描述子. 北京邮电大学学报, 2021, 44(6): 13-19. DOI:10.13190/j.jbupt.2021-072 |
| [9] |
De-Maeztu L, Villanueva A, Cabeza R. Near real-time stereo matching using geodesic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(2): 410-416. DOI:10.1109/TPAMI.2011.192 |
| [10] |
Chen SY, Wang ZJ. Acceleration strategies in generalized belief propagation. IEEE Transactions on Industrial Informatics, 2012, 8(1): 41-48. DOI:10.1109/TII.2011.2172449 |
| [11] |
Jiang W, Trulls E, Hosang J, et al. COTR: Correspondence Transformer for matching across images. Proceedings of 2021 IEEE/CVF International Conference on Computer Vision. Montreal: IEEE, 2021. 6187–6197.
|
| [12] |
DeTone D, Malisiewicz T, Rabinovich A. SuperPoint: Self-supervised interest point detection and description. Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops. Salt Lake City: IEEE, 2018. 224–236.
|
| [13] |
吕卫, 赵薇, 褚晶辉. 一种基于卷积神经网络的图像配准方法: 中国, 201811193622.5. 2019-03-29.
|
| [14] |
黄静. 低重叠率和弱纹理图像的快速拼接算法. 湖南科技大学学报(自然科学版), 2016, 31(2): 88-92. DOI:10.13582/j.cnki.1672-9102.2016.02.015 |
| [15] |
Sun JM, Shen ZH, Wang Y, et al. LoFTR: Detector-free local feature matching with Transformers. Proceedings of 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 8918–8927.
|
| [16] |
杨娜. 用于公路破损路面的图像拼接技术研究[硕士学位论文]. 天津: 河北工业大学, 2011.
|
| [17] |
朱张莉, 饶元, 吴渊, 等. 注意力机制在深度学习中的研究进展. 中文信息学报, 2019, 33(6): 1-11. DOI:10.3969/j.issn.1003-0077.2019.06.001 |
| [18] |
Niu ZY, Zhong GQ, Yu H. A review on the attention mechanism of deep learning. Neurocomputing, 2021, 452: 48-62. DOI:10.1016/j.neucom.2021.03.091 |
| [19] |
李艳荻, 徐熙平, 王佳琪. 基于自适应分块金字塔匹配核的特征提取算法. 光子学报, 2017, 46(12): 1210001. |
| [20] |
许佳佳, 张叶, 张赫. 基于改进Harris-SIFT算子的快速图像配准算法. 电子测量与仪器学报, 2015, 29(1): 48-54. DOI:10.13382/j.jemi.2015.01.006 |
| [21] |
雒福佐. 基于小波分析与RANSAC匹配的雷达图像拼接研究. 自动化与仪器仪表, 2022(2): 199-203, 208. DOI:10.14016/j.cnki.1001-9227.2022.02.199 |
 2023, Vol. 32
2023, Vol. 32


