1 引言

计算机系统的安全性广泛受到人们的关注. 根据数据显示, 2020年上半年, 我国境内感染计算机恶意程序的主机数量约304万台, 同比增长25.7%, 位于境外的约2.5万个计算机恶意程序控制了我国境内约303万台主机. 因此, 从终端层面对计算机的安全性进行检测变得越发重要. 入侵检测系统作为防火墙、强认证和用户特权等预防性技术的补充, 可以监控网络或其他系统的异常行为, 其对于网络和终端的检测能力, 已经成为互联网技术安全管理的重要组成部分^[1]. 然而, 由于网络流量和终端类型日益复杂化、多样化, 传统的基于签名技术的入侵检测系统越来越难以胜任入侵检测的任务. 因此, 基于异常技术的入侵检测系统是目前的重点研究方向.

目前入侵检测的相关研究主要集中在网络层面. 如Ahmim等人^[2]提出的基于决策树和规则概念的入侵检测方法, Lin等人^[3]提出的一种称为聚类中心和最近邻的检测方法, Cui等人^[4]提出的一种用于系统日志异常检测的卷积自动编码器方法, 还有基于卷积神经网络的字符级入侵检测方法^[5], 均用于网络流量检测. 然而, 仅依靠网络级的安全检测无法保证终端的安全性, 因为授权用户的密码可能会被入侵者破解^[6], 此时网络级的检测将不起作用.

某些早期的终端级入侵检测方法的检测对象是系统调用系列. 如Cabrera等人^[7]提出通过长度固定的系统调用序列来检测终端是否存在异常行为. Lee等人^[8]把该问题当作分类问题, 采用机器学习分类器把系统调用序列区分为正常和异常2种类别. 此外, 宋海涛等人^[9]提出基于模式挖掘的异常识别算法. 然而, 系统调用级别的颗粒度太细, 不仅导致过大的系统开销, 检测准确性也难以保证. 此外, 一些入侵检测方法把终端的操作日志作为检测对象. 在这方面作出重要贡献的是Ryan等人^[10], 他们首先提出用人工神经网络在终端提取用户特征的方法. 此外, DuMouchel^[11]创建了连续的基于命令序列的概率转移矩阵作为用户模型. 最后, Schonlau等人^[12]测试了建立用户模型的各种统计方法. 与本文密切相关的方法是由Lane和Brodley^{[13, 14]}提出的, 他们使用基于实例学习和隐马尔可夫模型技术, 把用户的行为划分为若干个聚簇. 由于基于实例学习技术在归类用户的行为类别时只参考部分相近的实例, 从而限制了问题的复杂性. 然而, 该方法的前提条件是异常实例占比很小, 并且该方法存在需要为实例设置标签、运行时开销较大的缺陷. 在文献[13,14]的基础上, Sequeira等人^[15]以命令相似度为指标, 使用动态聚类算法对数据集进行分类来建立用户模型. 他们的方法放宽了数据预处理的限制, 然而, 他们没有考虑命令表达的多样性问题. 据作者所知, 现有的终端级入侵检测方法大多需要为训练数据预先设置标签, 并且需要大量的训练数据集和较长的训练时间. 此外, 这些方法均没有解释聚簇的含义.

本文研究的是基于异常技术的终端级入侵检测问题, 提出了一种终端级入侵检测算法TL-IDA, 并提出了对应的滑动窗口判别法. TL-IDA算法依靠终端的操作日志对用户进行建模, 模型接收终端输入并采用滑动窗口判别法判断是否为异常操作. 为了实现该算法, 在数据预处理阶段构建特征向量时引入了统计学的常用指标, 并设计了符合本问题的动态聚类算法. 最后, 本文总结了操作日志存在的4种行为类别. 在实验部分, 采用K折交叉验证法和控制变量法对数据集进行了测试, 实验结果表明TL-IDA算法比类似的算法更好. 本文的主要贡献有:

(1) 提出了终端级入侵检测算法TL-IDA.

(2) 提出了滑动窗口判别法用于识别异常行为.

(3) 总结了操作日志的行为类别.

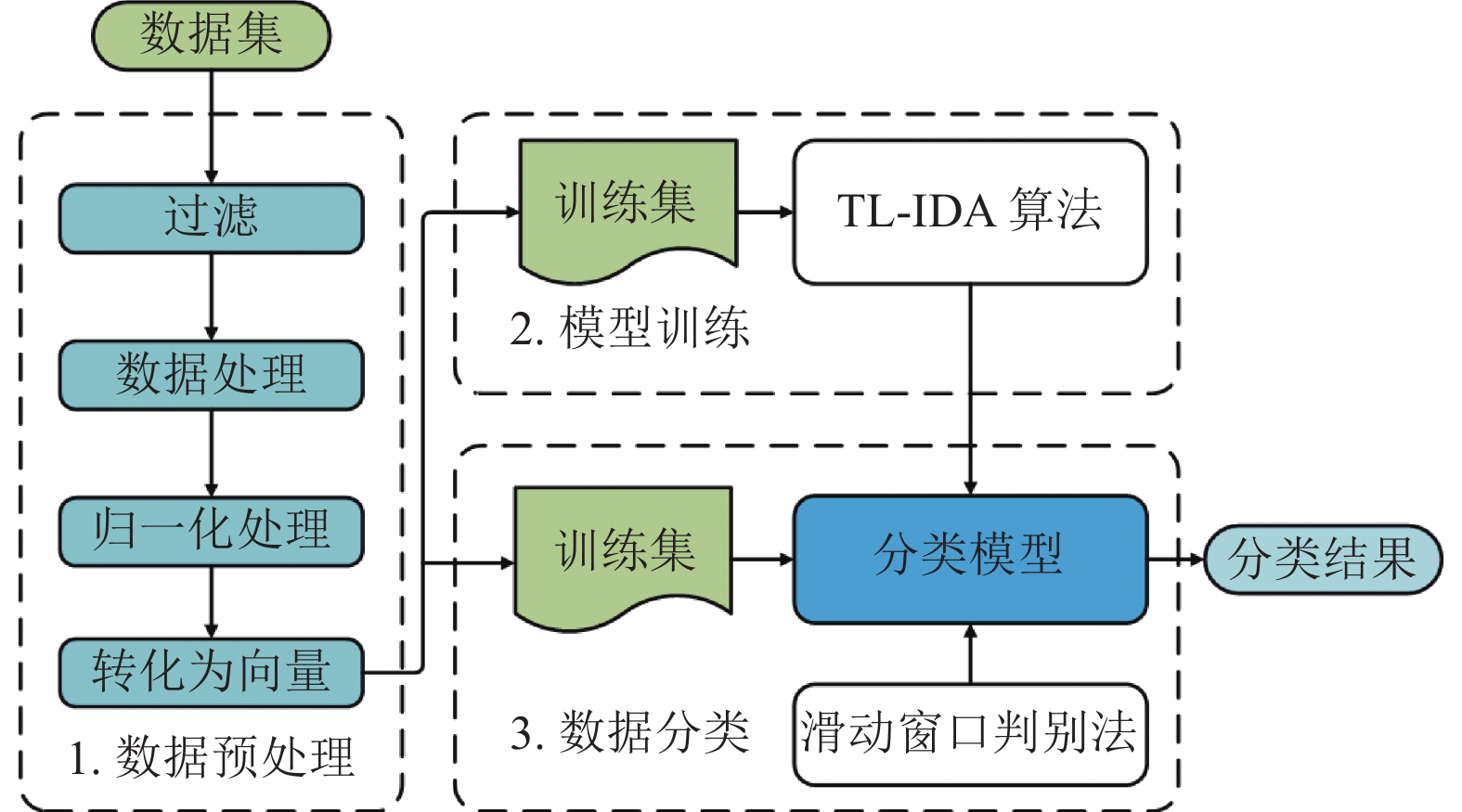
2 TL-IDA算法

本文提出的TL-IDA算法包括数据预处理和模型训练2个部分. 第3部分使用训练好的模型结合滑动窗口判别法对输入进行数据分类. 图1是入侵检测方法的处理流程.

2.1 数据预处理

操作日志由大量历史命令组成, 需要对日志进行预处理后才能用于建模. Sequeira等人^[15]认为, 日志中的单个命令不能保留用户的使用习惯, 但连续的小块命令序列可以, 并且, 把日志转化成连续的小块命令序列集还可以生成大量样本用于模型的训练和测试, 因此, 本文借鉴了该思想. 此外, 为了尽可能去除噪音干扰, 在分割日志的命令序列前, 还需要进行数据清理, 把不存在的命令删除. 表1展示了长度为4的命令序列, 设定子命令序列长度为2、步长为1时的切割结果.

得到子命令序列集后, 需要进行数值化处理, 把子命令序列逐个转化为特征向量, 为此, 本文引入了统计学的常用指标来保留用户特征. 首先, 定义两个子命令序列的相似度为这两个序列的最长公共子序列(longest common subsequence, LCS). 假设命令序列S₀={t₀=ls–l, t₁=vi,t₂=ps–ef,t₃=vi}, S₁={t₀=vi, t₁=ps–ef, t₂=vi, t₃=touch}. 根据定义, S₀和S₁的LCS为{vi, ps–ef,vi}, 相似度为3. 然后, 对操作日志统计以下数据:

(1) 所有命令的出现次数.

(2) 单个命令的出现次数.

(3) 单个命令的所有可选参数的出现次数.

(4) 单个命令的单个可选参数的出现次数.

(5) 用户的特征序列.

对于(5), 先统计每个子命令序列与其他的子命令序列的累计相似度, 再以累计相似度最高的前20%子命令序列作为用户的特征序列. 最后, 定义特征:

(1)x₁: 命令的平均出现频率.

(2) x₂: 可选参数的平均出现频率.

(3) x₃: 与特征序列的最大相似度除以序列长度.

则每个子命令序列的特征向量为(x₁, x₂, x₃), 在这个特征向量中, x₁和x₂保留了命令的频率特征, x₃保留了命令的顺序特征.

2.2 TL-IDA算法设计

完成数据预处理后, 需要设计算法对特征向量进行聚类. 显然, 传统的K-means算法不适合本问题, 原因在于无法预测K的值(即合理聚簇个数). Ahamed等人^[16]提出的动态聚类算法解除了必须提前设置K值的限制, 但对于本问题表现不够理想. 为此, 本文设计了TL-IDA算法, 它主要由3个函数组成. 在分析这3个函数之前, 先介绍3个工具函数如下.

(1) $ dist(X, Y)=\sqrt{{\displaystyle {\sum }_{i=1}^{m}{({x}_{i}-{y}_{i})}^{2}}}, {x}_{i}\in X, {y}_{i}\in Y $ , 用于计算特征向量X, Y的距离. 假设特征向量维度为 $ m $ , 则函数的时间复杂度为O(m).

(2) $inter(SC)={\rm{min}}(dist(c_i, c_j)), c_i, c_j\in S_C, i\ne j$ , 用于计算聚簇间的分离度. 其中,S_C是聚簇的中心集, c_i, c_j分别是第i个聚簇和第j个聚簇的中心. 假设K为聚簇个数, 则函数的时间复杂度为O(K²m).

(3) $ intra({S_c}, {S_p}) = \dfrac{{\displaystyle\sum\nolimits_{i = 1}^K {\dfrac{{\displaystyle\sum\nolimits_{j = 1}^{{n_i}} {dist({s_j}, {c_i})} }}{{{n_i}}}} }}{K}, {S_{{p_i}}} \in {S_p} $ , 用于计算所有聚簇的整体紧凑度, 时间复杂度为O(mn).其中, S_p是聚类后的样本集, S_pi是第i个聚簇的样本集, n_i是第i个聚簇的样本个数.

2.2.1 BaseClustering

首先介绍BaseClustering函数, 它实现了基础的聚类功能. 该函数流程分为2个步骤: (1) 选择K个样本作为聚簇的中心, 将样本逐个分配到与其最近的中心的聚簇中, 得到一个聚类结果; (2) 更新每个聚簇的样本均值作为聚簇的新中心. 重复以上步骤, 直到所有聚簇的中心不再变化为止. 算法伪代码如算法1.

算法1. BaseClustering(S, K)

输入: (S, K), S是待聚类的样本集

输出: (S_c, S_p), S_c是聚簇中心集, S_p是聚簇样本集

1: S_c←Randomly select K samples

2: do

3:　　 for i←1; i≤K; i++do

4:　　　　 S_pi← $\scriptstyle \varnothing $

5:　　 end for

6:　　 for s inS do

7:　　　　 for c_i in S_c do

8:　　　　　　 if dist(s, c_i) is min then

9:　　　　　　　　 S_pi←S_pi∪s

10:　　　　　　 end if

11: 　　　　 end for

12:　　 end for

13:　　 recalculateS_c

14: while S_c change

15: return S_c, S_p

接下来通过例子模拟该函数的执行过程. 假设S={s₀=(0.972, 0.716), s₁=(0.776, 0.501), s₂=(0.515, 0.314), s₃=(0.305, 0.675),s₄=(0.755, 0.923),s₅=(0.605, 0.704), s₆=(0.634, 0.088), s₇=(0.445, 0.932), s₈=(0.427, 0.571), s₉=(0.298, 0.238)}, K=2. 首先, 随机选取中心集S_c={c₀=s₁, c₀=s₃}. 然后, 把样本分配到距离最近的中心的聚簇(第8、9行), 则第1次迭代得到:

S_p={S_p0={s₀, s₁, s₂, s₄, s₅, s₆}, S_p1={s₃, s₇, s₈,s₉}},

S_c={c₀=(0.368, 0.604), c₁=(0.709, 0.541)}.

由于S_c发生变化, 继续第2次迭代(第14行), 得到:

S_p={S_p0={s₀, s₁, s₂,s₄, s₅, s₆}, S_p1={s₃, s₇, s₈, s₉}},

S_c={c₀=(0.368, 0.604), c₁=(0.709, 0.541)}.

由于S_c没有变化, 因此跳出循环, 聚类计算完成. 分析可知, 每次迭代必然导致样本到达所属聚簇中心的距离之和减少, 因此函数具备收敛性.

显然, BaseClustering函数的基本操作为dist(第8行), 它的时间复杂度为O(m). 当样本个数为n、指定聚簇个数为K时, 该函数执行一次 ${\rm{while}}$ 迭代的时间复杂度为O(Kmn), 假设完成聚类计算需要执行 $ \delta $ 次迭代, 则函数的复杂度为O( $ \delta $ Kmn).

2.2.2 DynamicClustering

为了解除BaseClustering函数需要设置K值的限制, 本文设计了DynamicClustering函数. 该函数通过聚簇间的分离度(inter_val)和聚簇的紧凑度(intra_val)来判断聚类是否停止. 算法伪代码如算法2.

算法2. DynamicClustering(S)

输入:(S), S是待聚类的样本集

输出:(S_c,S_p), S_c是聚簇中心集, S_p是聚簇样本集

1: K←1

2: new_inter←min float number

3: new_intra←max float number

4: do

5:　　 K←K+1

6:　　 S_c, S_p←BaseClustering(S, K)

7:　　 old_inter←new_inter

8:　　 old_intra←new_intra

9:　　 new_inter←inter(S_c)

10:　 new_intra←intra(S_c, S_p)

11: 　 ConditionA←old_inter<new_inter

12: 　 ConditionB←old_intra>new_intra

13: while ConditionA and ConditionB

14: return S_c,S_p

使用第2.2.1节BaseClustering函数的输出结果来模拟DynamicClustering函数的执行过程. 首先, 根据S_p和S_c, 可以通过工具函数inter和intra得到inter_val=0.346, intra_val=0.563. 然后, 把K自增为3, 再次调用BaseClustering函数, 得到:

S_p={S_p0={s₀, s₁, s₄, s₅}, S_p1={s₃, s₇, s₈}, S_p2={s₂, s₆, s₉}},

S_c={c₀=(0.777, 0.711), c₁=(0.392, 0.726), c₂=(0.482, 0.213)}.

计算得到inter_val=0.384, intra_val=0.497. 由于ConditionA和ConditionB同时成立(第11、12行), 表明K=3时的聚类效果更好, 因此保留本次修改并执行K=4时的迭代(第13行). 同理可得:

S_p={S_p0={s₁, s₂,s₆}, S_p1={s₃,s₅, s₇, s₈}, S_p2={s₀, s₄}, S_p3={s₉}},

S_c={c₀=(0.641, 0.301), c₁=(0.446, 0.721), c₂=(0.864, 0.820), c₃=(0.298, 0.238)}.

计算得到inter_val=0.349, intra_val=0.389. 由于ConditionA不成立, 表明K=4时的聚类效果并不优于K=3时的聚类效果, 因此放弃本次修改, 聚类计算完成. 该函数的极端情况为每个聚簇只保留一个样本, 因此该函数具有收敛性.

观察可知, DynamicClustering函数迭代时计算量最大的操作为调用BaseClustering函数(第6行). 在最极端的情况下, 每个聚簇只保留一个样本, 此时时间复杂度达到最坏. 由于单次聚类计算的时间复杂度为O( $ \delta $ Kmn), 因此最坏时间复杂度为O( $ \delta $ Kmn²).

2.2.3 AdjustCluster

在聚类完成后, 为了提高聚簇的紧凑度和聚簇间的分离度, 设计了AdjustCluster函数. 该函数流程分为2个步骤: (1) 对于每个聚簇, 该函数把到中心距离大于阈值T_dist的样本移除; (2) 更新每个聚簇的中心. 重复以上步骤直到中心不再变化. 算法伪代码如算法3.

算法3. AdjustCluster(S_c, S_p, T_dist)

输入:(S_c, S_p, T_dist), S_c是聚簇中心集, S_p是聚簇样本集, T_dist是聚簇的半径

输出: (S_c, S_p),S_c是聚簇中心集,S_p是聚簇样本集

1: do

2:　　 for c_i in S_c do

3:　　　　 for S_pi in S_p do

4:　　　　　　 for s in S_pi do

5:　　　　　　　　 if dist(s, c_i)>T_dist then

6:　　　　　　　　　　 S_pi←S_pi–s

7:　　　　　　　　 end if

8:　　　　　　 end for

9:　　　　 end for

10:　　 end for

11:　　 recalculate S_c

12: while S_c change

13: return S_c, S_p

接续DynamicClustering函数的输出结果来模拟AdjustCluster函数的执行过程. 假设T_dist为0.2, 根据伪代码第5至7行, 对S_p和S_c的迭代计算得到:

dist(s₀, c₀)=0.195<T_dist, S_p0保留s₀

dist(s₁, c₀)=0.210>T_dist, S_p0移除s₁

dist(s₄, c₀)=0.213>T_dist, S_p0移除s₄

dist(s₅, c₀)=0.172<T_dist, S_p0保留s₅

dist(s₃, c₁)=0.101<T_dist, S_p1保留s₃

dist(s₇, c₁)=0.213>T_dist, S_p1移除s₇

dist(s₈, c₁)=0.159<T_dist, S_p1保留s₈

dist(s₂, c₂)=0.106<T_dist, S_p2保留s₂

dist(s₆, c₂)=0.197<T_dist, S_p2保留s₆

dist(s₉, c₂)=0.186<T_dist, S_p2保留s₉

因此:

S_p={S_p0={s₀, s₅},S_p1={s₃, s₈}, S_p2={s₂, s₆, s₉}},

S_c={c₀=(0.789, 0.710), c₁=(0.366, 0.623), c₂=(0.482, 0.213)}.

由于S_c发生变化, 继续执行迭代(第12行) , 同理可得:

dist(s₀, c₀)=0.1835<T_dist, S_p0保留s₀

dist(s₅, c₀)=0.1835<T_dist, S_p0保留s₅

dist(s₃, c₁)=0.0801<T_dist, S_p1保留s₃

dist(s₈, c₁)=0.0801<T_dist, S_p1保留s₈

dist(s₂, c₂)=0.1058<T_dist, S_p2保留s₂

dist(s₆, c₂)=0.1967<T_dist, S_p2保留s₆

dist(s₉, c₂)=0.1859<T_dist, S_p2保留s₉

dist(s₉, c₂)=0.1859<T_dist, S_p2保留s₉

观察发现, 本次迭代没有移除样本点, 因此S_c保持不变, 调整操作完成. 由于每个聚簇的样本有限, 因此该函数具备收敛性.

AdjustCluster函数的基本操作为dist(第5行). 假设样本个数为n, 聚簇个数为K, 迭代次数为 $ \gamma $ , 则函数的时间复杂度为O( $ \gamma $ Kmn).

本文主要设计了3个函数来实现TL-IDA算法. 首先, BaseClustering函数实现最基本的聚类功能, 其次, DynamicClustering函数通过聚簇间的分离度和聚簇的紧凑度是否更好来判断聚类计算是否停止, 取消了需要提前输入K值的限制. 最后, AdjustCluster函数用于清除边缘的样本, 使得聚类的结果更好. 对比3个函数的时间复杂度可知, TL-IDA算法最差的时间复杂度为O( $ \delta $ Kmn²), 通常情况下, 样本数n远大于聚簇个数 $ K $ 和向量维度m, 因此TL-IDA算法的时间复杂度为O(n²)级别.

2.3 方法对比

本文方法的检测对象是终端级操作日志, 对比Cabrera等人^[7]、Lee等人^[8]和宋海涛等人^[9]对系统调用级数据进行分析的方法, 本文方法的系统开销更小. 同时, 与Ryan等人^[10]基于人工神经网络的入侵检测方法对比, 本文方法在很大程度上缩短了训练时间. 与本文密切相关的Sequeira等人^[15]对比, TL-IDA算法的时间复杂度为O(n²)级别, 而他们的算法时间复杂度为O(n³)级别, TL-IDA算法有更好的时间复杂度. 表2更为详细地对比了本文与其他5种终端级入侵检测方法的差别.

由于文献[7,8,10]并未给出算法时间复杂度的推导, 并且该算法时间复杂度取决于模型的学习率、批次大小等超参数, 因此无法准确计算文献[7,8,10]的算法时间复杂度. 但通常而言, 在训练集数据量相同的情况下, 文献[7,8,10]的方法的训练时间更长.

3 滑动窗口判别法

由于数据集可能包含噪音, 直接通过单个子命令序列是否属于某个聚簇来判断是否产生异常是不可取的, 因为这将导致过高的误报率. 本文提出了一种滑动窗口判别法, 用于判断是否真正产生异常. 该方法定义了一个大小为n(n>1)的窗口, 每次以步长为1的幅度向前滑动, 当窗口内出现 $ m $ 个或以上异常序列(m<n), 则判定产生了异常. 图2展示了n为5, m为3的滑动窗口判别法的工作方式.

3.1 有效性证明

首先证明滑动窗口判别法可以有效提高算法的识别率. 假设TL-IDA算法对单个子命令序列的识别率为P_rcg, 通过单个子命令序列判断是否产生异常的识别率R_sin=P_rcg, 而使用滑动窗口判别法的识别率R_win= $\displaystyle\sum\nolimits_{i = m}^n {C_n^i} $ P_rcgⁱ(1–P_rcg)^n–i当终端输入全为异常序列, 且P_rcg=0.7, n=7, m=4时, 代入上述式子可得, R_sin=0.7, R_win=0.8741, R_sin<R_win, 因此使用滑动窗口判别法的识别率更高, 算法性能更好.

然后证明滑动窗口判别法可以有效降低算法的误报率. 假设TL-IDA算法对单个子命令序列的误报率为P_fa, 通过单个子命令序列判断是否产生异常的误报率R_sin=P_fa, 而使用滑动窗口判别法的误报率R_win= $\displaystyle\sum\nolimits_{i = m}^n {C_n^i} $ P_faⁱ(1–P_fa)^n–i. 当终端输入全为正常序列, 且P_fa=0.4,n=7, m=4时, 代入上述式子可得, R_sin=0.4, R_win=0.2897, R_sin>R_win, 因此使用滑动窗口判别法的误报率更低, 算法性能更好.

3.2 滑动窗口判别法设计

下面将通过3个公式介绍滑动窗口判别法. 首先是判断单个子命令序列s是否属于某个聚簇的公式, 其表达式如下:

$ {{F_{1}(s, c) = }}\left\{ {\begin{array}{*{20}{c}} {1, }&{dist(s, c) \leqslant T_{{\rm{dist}}}} \\ {0, }&{dist(s, c) > T_{{\rm{dist}}}} \end{array}} \right. $

(1)

其中, c为聚簇的中心. 该公式规定, 如果子命令序列s与聚簇的中心c的距离小于或等于T_dist, 则该序列属于c代表的聚簇, 此时F₁的值为1, 否则为0.

有了式(1)之后, 可以进一步判断单个子命令序列在模型中是否异常, 判断公式如下:

$ F_{2}(s) = \left\{ {\begin{array}{*{20}{c}} {1, }&{\displaystyle\sum\nolimits_{i = 1}^K {F1(s, ci)} < 1} \\ {0, }&{\displaystyle\sum\nolimits_{i = 1}^K {F1(s, ci)} \geqslant 1} \end{array}} \right. $

(2)

其中, K为模型的聚簇个数. 该函数使用式(1)依次判断s是否属于某个聚簇并累加式(1)的值, 如果s属于某个聚簇, 该累加值大于或等于1,F₂(s)=0, 则s为正常序列. 反之, 当F₂(s)=1时, 表明s不属于任何聚簇, 则s为异常序列.

最后, 通过式(2) , 可以得到滑动窗口判别法的公式, 该公式表达如下:

$ F_{3}(S_{n}) = \left\{ {\begin{array}{*{20}{c}} {1, }&{\displaystyle\sum\nolimits_{i = 1}^n {F_{2}(si)} \geqslant m} \\ {0, }&{\displaystyle\sum\nolimits_{i = 1}^n {F_{2}(si)} < m} \end{array}} \right. $

(3)

其中, S_n表示过去 $ n $ 个子命令序列集. 该公式规定, 对于过去 $ n $ 个子命令序列, 依次使用式(2)检测单个子命令序列是否异常, 再统计S_n中被标记为1的序列个数. 如果在过去n个子命令序列中, 有m个或以上序列被标记为异常, 则判定产生了异常.

本小节介绍了滑动窗口判别法的工作原理, 并介绍了该方法主要的3个函数. 首先, F₁判断单个子命令序列是否属于某个聚簇, 它的衡量标准是该序列与聚簇中心的距离是否小于T_dist. 然后, F₂在F₁的基础上判断单个子命令序列是否为异常序列, 它通过判断子命令序列是否属于模型中的任意一个聚簇完成. 最后, F₃查看了过去n个子命令序列的整体异常情况来判断是否产生异常. 本文通过推导证明了滑动窗口判别法比单个子命令序列为标准的方法性能更好.

4 实验结果及分析

本文使用普渡大学提供的数据集进行实验. 该数据集包含9组经过清理的用户数据, 这些数据来自普渡大学的8位UNIX计算机用户在长达2年的时间里的历史命令. 其中, USER0和USER1是由同一个用户在不同的平台和不同的项目上工作生成的. 除非特别声明, 默认选择USER0的日志文件作为训练集, 其余的文件作为测试集. 同时, 为了便于理解, 采用聚簇的样本包含率而不是长度来描述T_dist. 在本次实验中, 设置子命令序列长度为5, 设置T_dist为包括约85%样本的距离, 设置滑动窗口n大小为7,m为4.

4.1 识别率和误报率的实验结果

为了便于与现有的终端级入侵检测相关文献作对比, 本文采用和文献[14, 15]相同的识别率和误报率来衡量TL-IDA算法的有效性. 该评价指标如下:

(1) 识别率 = $ \dfrac{用户\text{A}样本在模型\text{B}的被检出数}{用户\text{A}样本数} $ , 其中, 模型B通过用户B的样本训练得到.

(2) 误报率 = $ \dfrac{用户\text{A}样本在模型\text{A}的被检出数}{用户\text{A}样本数} $ , 其中, 模型A通过用户A的样本训练得到.

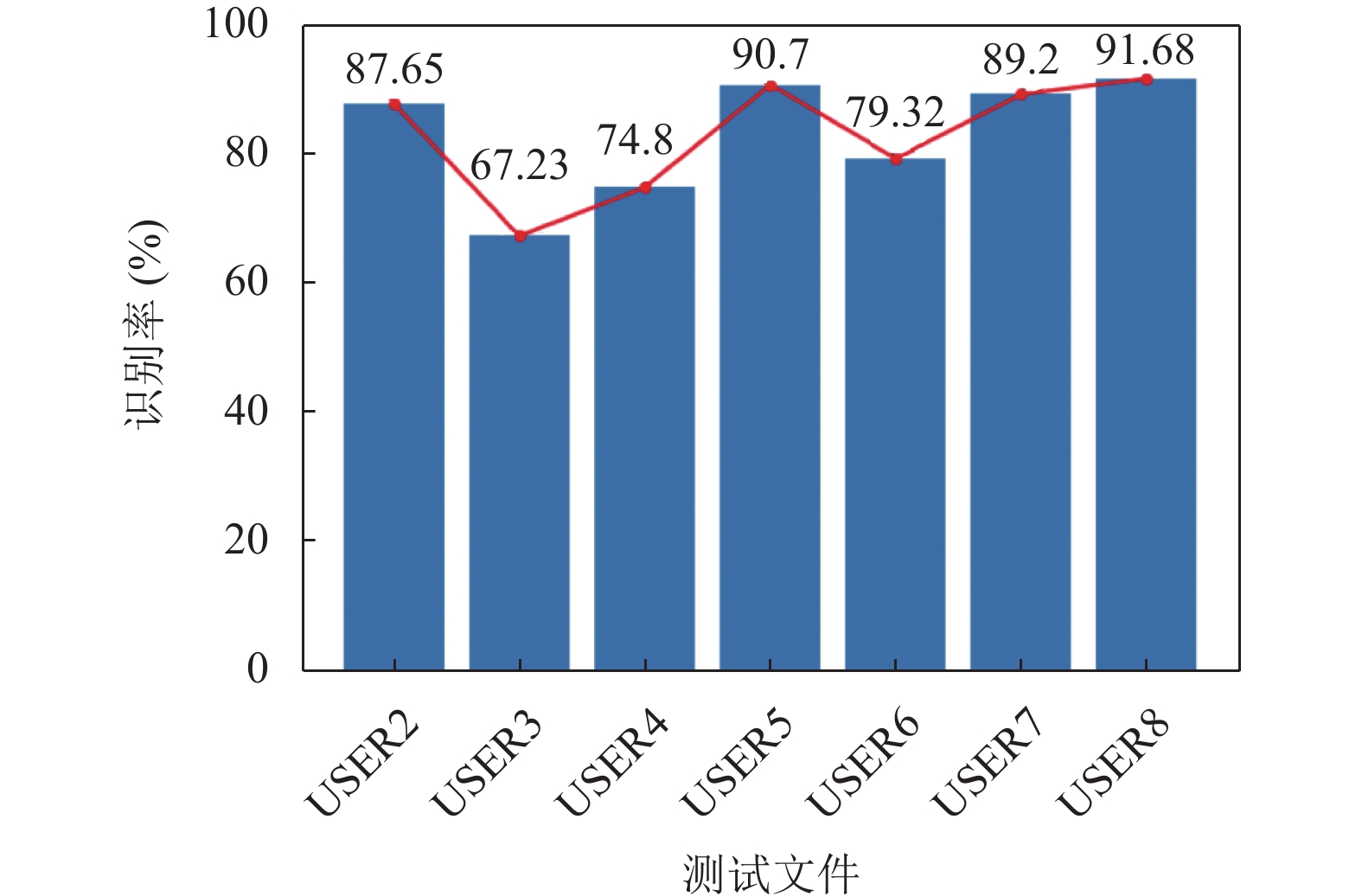
为了测试算法的识别率, 选择除USER1外的其余文件作为测试集, 用它们在以USER0为训练集的模型上的被检出率来衡量算法的识别率. 排除USER1的原因是它和USER0来自同一个用户. 在实验中, 测试集被平均分成5个片段, 依次对这些片段进行单独测试, 实验结果是所有单独测试的平均值. 得到的实验数据如图3所示.

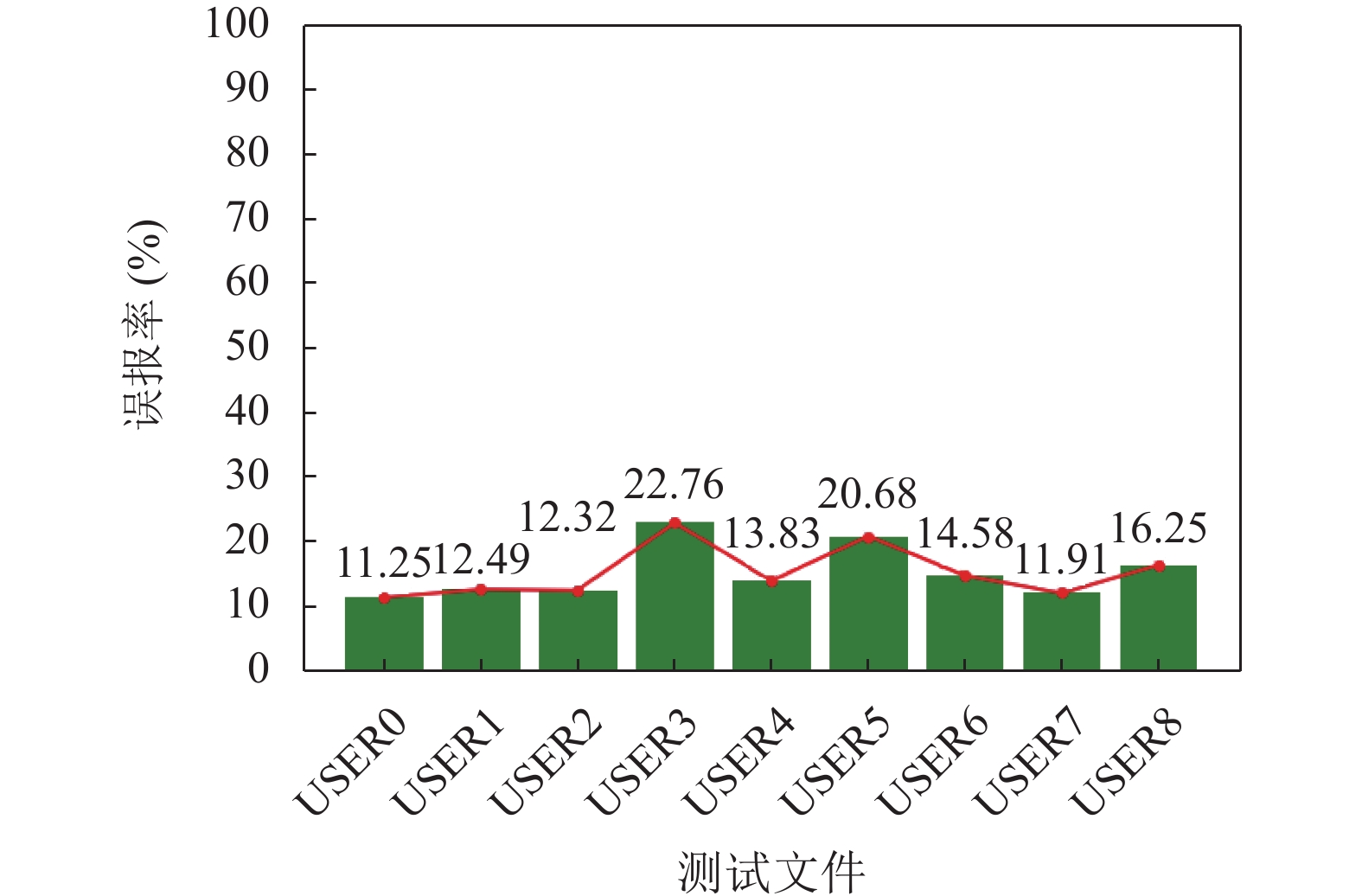
本文采用5折交叉验证法测试算法的误报率. 单个用户文件被分割成5个片段, 每次选择1个片段用于测试, 其余4个片段用于训练. 测试单个文件时, 依次更换不同的片段作为测试集, 得到该文件的单次完整实验数据. 本次实验对每个用户文件进行10次完整测试, 实验结果是每个完整测试的平均值. 图4展示了实验数据.

4.2 子命令序列长度的影响

本文采用控制变量法测试不同子命令序列长度对应的识别率和误报率. 对于识别率, 选取USER0为训练集, USER8为测试集. 对于误报率, 选取USER0作为5折交叉验证的数据集. 实验数据如表3所示.

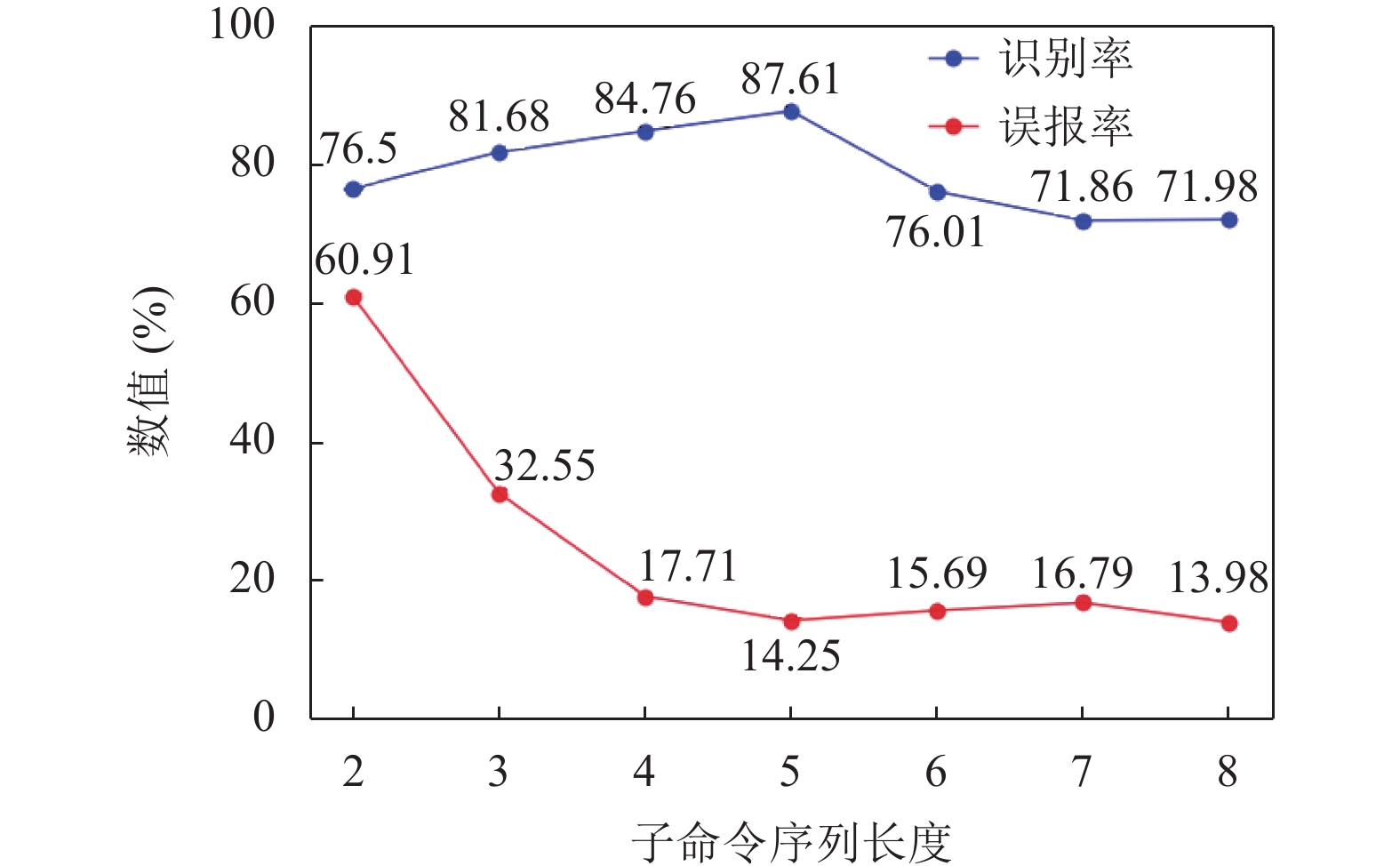
分析数据可以发现, 随着子命令序列长度不断增加, 算法的识别率不断上升, 当子命令序列长度为5时达到峰值, 随后不断下降. 而误报率在子命令序列长度为2时非常高, 随着子命令序列长度增加, 它先迅速下降, 然后趋于稳定. 这是因为当长度过短时, 子命令序列的颗粒度太细, 几乎不包含用户操作的有效信息, 因此识别率和误报率的随机性很大. 当长度过长时, 识别率下降的原因是因为失去了用户操作的“时间局部性”信息, 而误报率保持在一个相对稳定的数值是因为特征向量中的x₃相对稳定, 使得特征向量被正确聚类. 图5更为直观地显示了实验结果.

4.3 实验结果对比

在同样的数据集下, TL-IDA算法的异常检测率平均为83%而误报率低至平均15%, 该成果对比Lane等人^[14]的成果(分别为74%和28%)有较大的提升. 对比Sequeira等人^[15]的方法 (分别为80%和15%), TL-IDA算法除了进一步提升了识别率和降低了误报率之外, 同时考虑了命令表达多样性的情况. 图6直观地展示了实验结果对比.

4.4 聚簇类别分析

对终端的操作日志进行聚类, 应该至少得到用户常规行为类别(I类)和用户偶然行为类别(II类) 2种聚簇, 而代表用户新行为类别(III类)和入侵者行为类别(IV类)的聚簇可能不存在, 下面讨论4种聚簇类别的特点和分布.

用户常规行为类别(I类). 这类聚簇代表的是用户最常用的命令. 根据统计显示, 用户的常规行为占比是最高的, 因此这类聚簇应该是样本最多的聚簇, 并且大多数样本的特征向量x₁、x₂和x₃均不为0.

用户偶然行为类别(II类). 这类聚簇代表的是由用户误操作和用户罕见操作组成的命令. 前者是因为用户输入了正确的命令同时输入了错误的可选参数导致(错误的命令输入已经在数据预处理时删除了). 这导致特征向量的x₂和x₃接近0而x₁不为0. 后者的样本数量占比较少, 由于命令出现次数较少, 因此特征向量表现为x₁和x₃接近0而x₂不为0.

用户新行为类别(III类). 这类聚簇代表的是用户在终端上很少执行的一些命令, 可能由用户在新的项目或在不同的环境工作导致. 区分III类聚簇和IV类聚簇是提高识别率、降低误报率的关键. 在初始时, 用户新行为会被归类为II类聚簇, 随着命令使用次数增加, 它会逐渐往I类聚簇迁移, 当使用次数足够多时, 它将不再是“新行为”, 而是“常规行为”, 因此这类聚簇通常会分布在第I类和第II类聚簇之间.

入侵者行为类别(IV类). 这类聚簇代表的是入侵者使用的命令, 是需要识别的主要类别. 由于入侵者的操作习惯和合法用户的操作习惯很可能不一致, 因此它们的命令序列也会有差别, 所以这类聚簇的特点是样本数量较少并且与I类聚簇的距离较远.

5 结束语

本文研究的是终端级异常检测算法, 为了提升异常检测技术的识别率, 本文提出了一种终端级入侵检测算法TL-IDA. 对比现有的终端级入侵检测算法, TL-IDA算法的时间复杂度为O(n²)级别, 为同类算法最好. 此外, 该算法的异常检测率平均为83%而误报率低至平均15%, 在相同的数据集下优于文献[14, 15]报告的结果, 并且在训练时不需要为训练集设置标签. 此外, TL-IDA算法的另一个优势是需要设置的超参数更少, 这些超参数通常需要大量的测试才能确定, 更少的超参数意味着更短的训练时间. 最后, 本文归类了聚簇的类别并且总结了它们的特点, 这些归类将更有利于安全分析人员分析系统的行为. 下一步将考虑使用生成对抗网络把攻击行为伪造成正常行为, 通过改进算法识别这些伪装攻击, 提升入侵检测算法对伪装攻击行为的识别能力, 进一步完善入侵检测算法.