2. 哈尔滨工业大学(威海) 网络与信息中心, 威海 264200;
3. 威海天之卫网络空间安全科技有限公司, 威海 264200
2. Network and Information Center, Harbin Institute of Technology at Weihai, Weihai 264200, China;
3. Weihai Cyberguard technologies Co. Ltd., Weihai 264200, China
渗透测试是一种通过模拟攻击者攻击, 来评估目标系统安全性的测试方法. 安全测试工程师模拟攻击者执行渗透动作, 从当前状态到达目标状态过程使用的渗透动作序列称为渗透路径, 渗透测试的核心是发现目标系统中存在的渗透路径. 但是系统中的网络拓扑和服务十分复杂, 并不是所有的渗透路径都能成功, 为此安全测试工程师需要选择成功率最高的渗透路径, 这被称为当前系统中的最优渗透路径.
渗透测试过程高度依赖专家知识发现渗透路径, 这使得人工成本过高, 渗透测试的周期过长. 文献[1,2]介绍了攻击图模型, 通过收集系统信息, 分析系统中特定网络资产的风险, 预测攻击成功后可能产生的后果, 辅助进行渗透测试, 降低渗透测试成本. 但是对于复杂场景来说, 生成的攻击图过于复杂, Yousefi等人[3]提出一种新的攻击图分析方法, 生成简化攻击图, 王晓凡等人[4]提出使用并行算法, 来加快大规模网络下发现最优渗透路径的过程.
目前, 强化学习[5]是一种有效的方式来解决顺序决策问题, 因此可以使用强化学习来发现最优渗透路径. 文献[6,7]应用Q-learning算法, 将渗透测试中的漏洞选择过程转换为强化学习的动作选择过程, 直接与真实环境进行交互学习, 建立状态漏洞Q值表, 从而达到发现最优渗透路径的效果. 周仕承等人[8]提出了一种改进的深度强化学习算法, 该算法融合了优先经验重放、双重Q网络、竞争网络和噪声网络等机制, 实现了在较大规模网络场景下发现最优渗透路径. 高文龙等人[9]提出在DDQN (double deep Q-network)算法的基础上增加了路径启发信息和深度优先渗透的动作选择策略, 加速智能体的学习过程, 使得算法可以更快收敛.
文献[10–12]将攻击图模型与强化学习模型结合, 同时借助MulVAL工具生成攻击图. 文献[10]通过建立得分矩阵, 使用深度强化学习算法搜索最优渗透路径, 文献[11]借助强化学习来识别系统中的关键主机和关键路径. 但是, 强化学习的训练是基于环境交互的, 真实环境的训练成本过高, 为此文献[12]使用DQN (deep Q-network)算法在Nasim模拟器[13]上进行训练, 寻找最优路径.
由于攻击图模型随状态变化节点增长过快, 以及深度强化学习在渗透测试过程中存在实用性不强和收敛困难的问题, 本文提出了面向MDP图使用强化学习中的价值迭代算法来发现最优渗透路径, 价值迭代算法已被证明收敛. 本文研究将攻击图中的推论节点和规则节点映射到MDP的状态和动作, 并且根据渗透动作的难度赋予动作执行代价和转移概率. 在此基础之上, 利用价值迭代算法估计各个渗透路径对于单目标的价值, 可以得到初步估计的最优渗透路径. 然而在复杂的渗透测试场景中, 可能存在渗透动作失效的问题, 为此可以使用重规划算法, 通过重新估计渗透动作的价值, 获取最优渗透路径. 最后, 针对单目标方法的局限性, 提出了多目标状态表示方法, 进一步讨论面向多目标的应用场景.
1 相关工作 1.1 马尔可夫决策过程马尔可夫决策过程是完全可观测环境下顺序决策问题的数学描述, 是强化学习问题的理论基础. MDP由五元组(S, A, R, T, γ)构成, S表示状态集合, A表示可执行动作的集合,
强化学习通过与环境进行交互来学习, 在给定状态下, 智能体采取行动, 环境返回奖励或者惩罚, 通过找到最优策略使得累积奖励达到最大值.
1.2 攻击图建模MDP图攻击图是采用图的表示方式来展示和评估计算机网络中攻击路径的技术. 其中逻辑编程攻击图, 采用逻辑推理引擎, 通过设置漏洞利用、访问链推导等推理规则, 对网络的配置信息和漏洞信息进行分析, 推导出从起始点出发, 到达目标的所有攻击路径. 由3种节点组成, 其中矩形节点是谓词, 代表推理的初始依据, 包括网络连接性, 漏洞的存在性等. 椭圆形节点代表推理规则, 如漏洞利用规则, 多跳访问规则等. 菱形节点是派生谓词, 代表推理结论, 如通过漏洞利用规则得出的以用户权限执行任意代码等.
将攻击图映射为MDP图, 攻击者的起始位置作为初始状态, 所有的谓词节点作为状态, 规则节点作为动作, 使用可重边有向图表示MDP图, 为每个MDP图节点绑定攻击图节点编号作为属性, 将最优路径选择建模为智能体在MDP图中的每个分支节点的最优动作选择, 节点冒号左侧的数字为重新编号后得到的, 右侧数字是攻击图中对应的节点编号.
2 基于价值迭代算法的最优渗透路径发现强化学习中引入价值的概念, 将策略的价值称为
| V∗(st)=max | (1) |
价值迭代算法是经典的强化学习算法, 通过采用贝尔曼最优方程来计算状态动作价值. 如式(2)所示:
| \begin{split} {Q^*}({s_{{t}}}, {a_t}) =& \sum\limits_{{s_{t + 1}}} {T({s_t}, a, {s_{t + 1}})\times [R({s_t}, a, {s_{t + 1}})} \\ & + \gamma \max {Q^*}({s_{t + 1}}, {a_{t + 1}})] \end{split} | (2) |
最优状态动作价值
首先, 在渗透测试过程中, 可以使用Nmap等扫描工具对系统中的各个主机进行扫描, 获取主机的漏洞信息和路由信息. 然后根据定义的领域规则文件, 得到主机漏洞间的关联关系, 建立攻击图. 然后将攻击图转换为MDP图, 寻找最优渗透路径.
其次, 由于扫描工具的限制, 漏洞扫描的结果可能并不准确, 存在漏洞误报的情况. 同时系统用户可能修改系统配置信息, 使得渗透动作失效, 初始得到的渗透路径并不能保证渗透成功, 需要根据实际情况进行调整. 但是对整个系统的状态进行实时跟踪并更新MDP图的代价较大, 在初始得到的最优渗透路径的基础上, 根据渗透过程中遇到的实际问题调整, 重新寻找最优渗透路径.
最后, 当渗透测试过程中存在多个攻击目标时, 安全测试工程师需要获得到达多个目标的全局最优渗透路径. 如果分别计算到达多个目标的最优路径, 路径之间可能存在重合, 因此为多个目标单独计算最优路径并不能得到全局最优的渗透路径.
本节的内容主要如图1所示, 通过针对当前渗透测试中存在的3个主要问题, 提出了相应的解决方案.
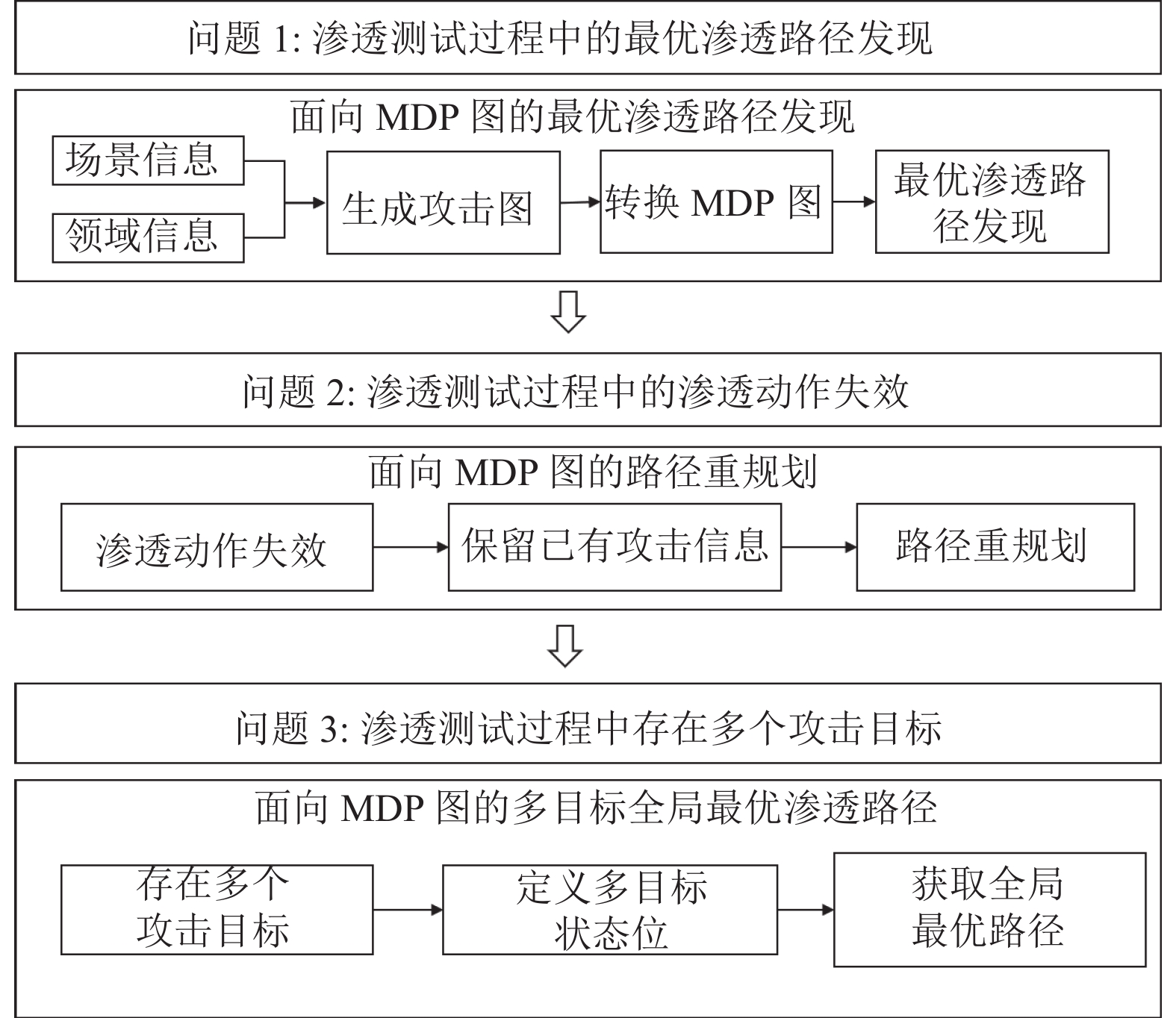
|
图 1 基于价值迭代算法的最优渗透路径发现 |
2.1 面向MDP图的最优渗透路径发现
根据得到的MDP图, 本文引入价值迭代算法, 由于MDP图是已知的, 使用价值迭代算法可以直接进行渗透动作的价值计算, 由于每个状态实际只有少量可以执行的动作, 所以实际不存在的状态动作对的Q值可以设置为负无穷大, 在迭代中只需要考虑可能的状态转移过程, 无需考虑MDP图中没有的边. Q值反映了当前状态下各动作的价值大小, 选择当前状态下Q值最大的动作.
计算马尔可夫决策过程的奖励和状态转移概率, 首先考察单步渗透动作的执行代价和转移概率. 不同的渗透动作有不同的执行代价cost和转移概率prob. 渗透动作的漏洞复杂度指标access可以参考公共漏洞评分系统CVSS评分中的access complexity评分, 分为高, 中, 低这3类, 分别对应不同的转移概率, 如0.3, 0.6, 0.9. 漏洞利用脚本质量script根据脚本库中每个漏洞脚本的质量评分, 如Metasploit Framework脚本库中按照excellent, good, normal, none等分级, 质量越好, 漏洞利用成功的可能性越高. 渗透测试过程中状态的转移概率由prob, access和script三者的乘积表示, 渗透动作代价和转移概率共同决定了智能体成功进入下一状态需要付出的代价, 如式(3)所示.
| T({{{s}}_t}, a, {s_{t + 1}}) = prob(a)\times access(a)\times script(a) | (3) |
当渗透动作失效时, 需要保留已有的攻击信息, 重新计算最优渗透路径, 使得到达目标状态的累积奖励值最大. 首先, 删除MDP图中失效渗透动作对应的边. 此时, 所有访问过的节点都是安全测试工程师已经掌控的状态, 重规划不需要重新从MDP图的起始点出发. 将当前已经成功掌握的节点合并为一个虚拟节点, 作为重规划的起点. 路径重规划过程的流程如下.
步骤1. 根据第2.1节得到的最优渗透路径进行渗透测试, 同时检测渗透动作是否失效.
步骤2. 如果渗透动作失效, 修改状态转移矩阵, 同时删除MDP图中到达失效渗透动作对应的边.
步骤3. 将已经成功掌握的节点合并为虚拟节点, 忽略合并节点内部之间的连接关系.
步骤4. 重新执行价值迭代算法, 获取新的最优渗透路径, 从虚拟节点选择最优渗透动作.
步骤5. 如果渗透动作成功, 继续按照最优渗透路径执行渗透测试, 失败则返回步骤2.
2.3 面向MDP图的多目标全局最优路径为了表示安全测试工程师对已经掌握状态的持续控制, 以MDP图节点个数作为一维向量S的长度表示当前环境的状态,S的第i位是0代表状态i尚未被掌握, 是1代表状态i被掌握.
通过向量表示, 攻击者可以从已掌握的任意状态出发, 但是状态数量随MDP图中节点个数呈指数增长, 在具有n个节点的情况下, 可能的状态数多达2n. 本文通过列表存储出现过的状态来缓解状态空间爆炸的问题. 算法的结束状态是状态向量中目标的状态位都为1, 在判断到达结束状态时, 获得较大的正奖励. 智能体到达任意子目标并不设置奖励, 使得能够发现全局最优路径. 流程如算法1所示.
算法1. 面向MDP图的多目标全局最优路径
1) 初始化节点数目N, 起始状态S0为N维向量
2) 初始化状态转移矩阵TM, 状态值函数矩阵VM为空
3) 初始化列表states记录起始状态S0, 误差delta
4) states, TM, VM= ExploreState(states, state, TM,VM)
5) For i=1, …, Iteration_num do
6) For j=1, …, len(states) do
7) state = states[j]
8) If is_reached_end_state(state) then
9) continue
11) End If
12) delta = ValueIteration(state, TM, VM)
13) If delta < delta then
14) break
15) End If
17) End For
18) End For
3 实验分析为了验证方案在实际应用问题中的有效性, 本文基于Cyborg模拟器[14]中的动作设计了相应的规则, 以便可以在模拟器中验证最优渗透路径, 同时模拟失效渗透动作, 利用价值迭代算法解决渗透测试过程中的最优路径发现问题. 攻击规则与模拟器动作匹配如表1所示.
| 表 1 攻击规则与模拟器动作 |
3.1 实验环境
本文定义了随机拓扑生成类, 保持子网的结构不变, 通过修改子网中的主机和服务信息, 可以生成不同拓扑规模的环境. 固定实验子网结构如图2所示, 攻击者与子网s1直接相连, 最终的目标在子网s7. 每个子网包含相同数目的主机, 但是主机系统类型不同, 网络连接规则定义如下: 相邻子网间的任意主机之间可以相互访问, 且只能被前一个子网中的主机访问. 例如子网s3的上一个子网为s1, 子网s6的上一个子网为子网s4和子网s5.
为了展示实验过程, 本文设计演示系统, 系统功能包括: MDP图生成, 单目标发现最优渗透路径, 重规划指导渗透, 多目标发现全局最优渗透路径. 系统架构如图3所示.

|
图 2 实验子网结构 |
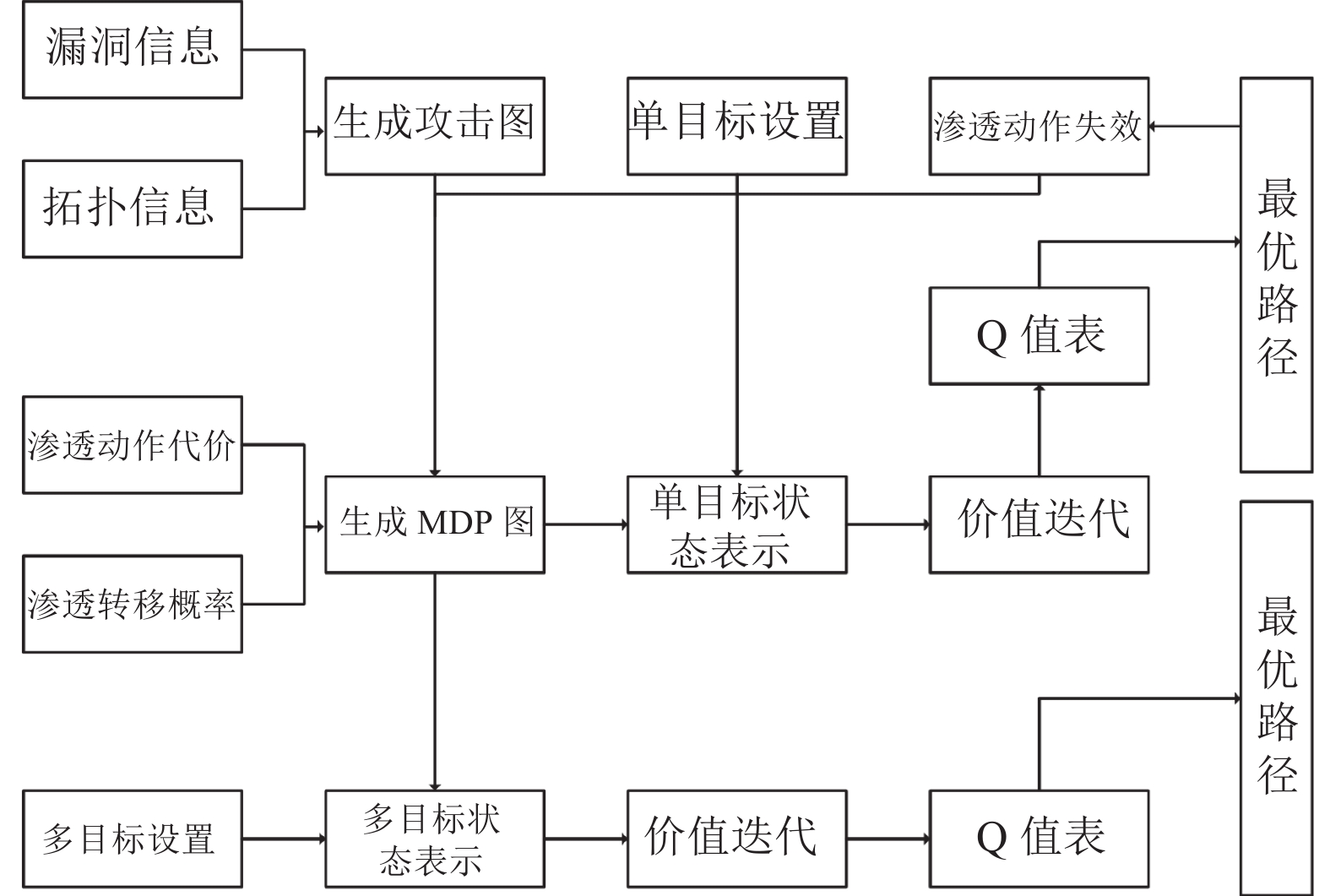
|
图 3 系统架构 |
为了不失一般性, 本文分别在不同节点规模下进行实验, 表2为5个不同拓扑的攻击图规模, 分别统计了子网中的主机数、攻击图节点数、攻击图边数.
| 表 2 单目标攻击图规模 |
由于使用价值迭代算法需要定义相关参数, 参数取值如表3所示. 实验使用4核, 主频为2.53 GHz的CPU, 内存为8 GB, 操作系统为Kali (2022-04-01) x86_64 GNU/Linux, Python版本为3.8.16.
| 表 3 算法参数设置 |
3.2 实验结果分析
在文献[10], 作者通过将简化攻击图作为深度强化学习模型的输入, 算法可以较快收敛, 发现最优渗透路径. 本文提出基于价值迭代算法, 计算状态价值函数来得到最优策略, 获得最优渗透路径. 为了不失一般性, 在不同拓扑规模下重复50次实验, 实验统计了AutoDRL与本文方案的平均运行时间.
图4主要展示不同节点规模下, AutoDRL与本文方案在发现最优渗透路径方面的性能. 在节点规模较小时, AutoDRL发现最优渗透路径的耗时低于价值迭代算法, 但是随着节点规模的增加, 本文方案保持了较低的计算时间增长, 能够更快发现最优渗透路径.

|
图 4 不同节点规模下的最优渗透路径发现时间 |
由于存在渗透动作失效的情况, 需要进行路径重规划. 传统的重规划算法一般是将距离目标最近的路径点作为起点, 重新规划出到达目标的路径. 高文龙等人[15]提出根据已经掌握节点的出度, 选择出度最大的节点作为重规划的起始节点, 可以有效减少重规划次数. 本文提出了一种新的重规划算法, 可以在已经掌握节点信息的基础上, 重新计算最优渗透路径. 实验定义失效渗透动作的比例占所有渗透动作的30%, 每次随机选取30%的动作为失效渗透动作, 重复进行50次实验, 将本文提出的重规划算法与最大出度优先算法进行比较, 对发现最优路径的成功率, 平均运行时间和平均重规划次数等方面进行比较分析.
图5(a)主要展示不同节点规模下, 本文提出的方案与最大出度优先算法发现最优路径的成功率有相同的性能表现. 从图中可以看到, 在节点数为134时的成功率最低, 由于此时到达目标的路径较少, 本文方案和最大出度优先算法均难以到达目标. 随着节点数的增加, 可以使得发现最优路径的成功率达到100%.
图5(b)主要展示不同节点规模下, 本文提出的方案平均运行时间更快. 从图中可以看出, 在节点数小于1000的场景中, 两种算法的单次运行时间均小于10 s, 但是随着节点数剧增, 运行时间快速增加, 本文提出的方案消耗时间始终低于最大出度优先算法, 消耗时间减少了约5.48%–23.61%.

|
图 5 重规划算法性能比 |
图5(c)主要展示了不同节点规模下, 本文提出的方案平均重规划次数更少, 可以减少重规划失败带来的多次重规划, 减少到达目标所需时间. 随着节点数的增加, 本文提出的方案保持相对更加稳定的变化, 平均重规划次数减少了约1.5%–24.69%.
在渗透测试过程中会存在多个攻击目标, 如果分别对多个目标发现最优渗透路径, 没有利用到已经掌握的节点信息, 无法发现全局最优路径, 为此本文提出了一种多目标最优渗透路径发现算法. 为了验证算法的有效性, 同时便于展示, 提供了一个简单的示例网络拓扑, 如图6所示.
每个子网下有一台主机, 在子网s3和s6中还分别包括攻击目标1和目标2. 采用单目标方法时, 到达每个目标都给予奖励, 多目标时在到达全部目标时一次性给予奖励. 生成的MDP图中节点的描述如表4所示.

|
图 6 示例网络拓扑 |
| 表 4 MDP图节点描述 |
图7(a)展示了采用本文提出的多目标算法获得的全局最优渗透路径, 图7(b)展示了采用单目标方法获得到达目标1的最优渗透路径, 图7(c) 展示了采用单目标方法获得到达目标2的最优渗透路径. 其中状态17为起始状态, 代表攻击者的起始位置, 状态1代表攻击者成功对目标1进行破坏, 状态39代表攻击者成功对目标2进行破坏. 可以看到本文提出的多目标算法成功识别了跳转的关键节点, 使得到达状态22后, 分别到达状态1和状态39. 但是如果分别计算到达目标1和目标2的最优渗透路径, 可以看到攻击者在状态8会选择不同的两条路径. 通过比较, 证明了本文提出的多目标算法的有效性, 可以避免不必要的渗透动作被执行.
为了不失一般性, 本文基于5个不同拓扑规模的攻击图进行实验, 实验子网结构如图6所示, 改变子网中的主机和漏洞信息, 同时保持攻击目标不变. 表5分别统计了不同拓扑规模下子网中的主机数、攻击图节点数、攻击图边数.

|
图 7 多目标全局最优渗透路径 |
| 表 5 多目标攻击图规模 |
图8展示了不同节点规模下的平均运行时间, 在节点数为42时, 平均运行时间为0.48 s, 当节点数增加到150时, 平均运行达到2360.94 s. 图8还展示了不同节点规模下的内存消耗, 随着节点数的增加, 算法的运行内存消耗缓慢递增, 在节点数为150时的内存消耗为258.16 Mb, 与节点数为42相比, 内存消耗增长了约18.76%.
4 结论与展望本文主要研究了基于攻击图的渗透测试过程, 将攻击图映射成MDP图, 然后使用了两种状态表示方法来发现最优渗透路径. 在单目标渗透测试场景下, 直接将MDP状态节点作为状态, 基于不同拓扑规模下, 使用价值迭代算法快速计算各步动作的价值, 从而获取最优的渗透路径. 进一步探讨渗透动作失效的情况下, 提出重规划算法, 可以重新发现最优渗透路径. 在面向多目标的情景下, 提出了多节点状态表示方法, 考虑了共同路径的代价复用, 从而最小化总路径的代价. 接下来的工作是考虑优化价值迭代算法的状态转移函数和多目标算法的搜索过程, 本文对于状态转移概率直接采取了相乘的形式, 没有全面考虑各个概率对于最终能够成功进行状态转移的权重. 此外, 多目标算法的运行时间随着节点数的增加呈现快速增长的趋势, 考虑使用启发式算法来优化状态发现过程.
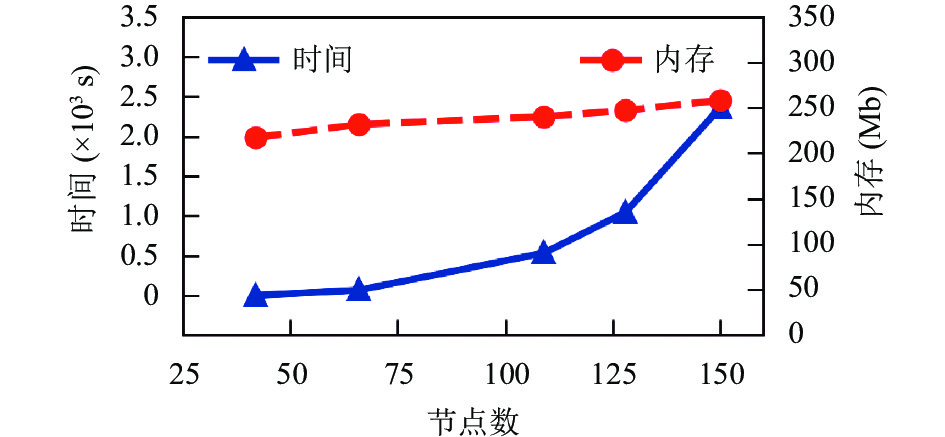
|
图 8 多目标算法性能 |
| [1] |
Zenitani K. Attack graph analysis: An explanatory guide. Computers & Security, 2023, 126: 103081. |
| [2] |
王硕, 王建华, 汤光明, 等. 一种智能高效的最优渗透路径生成方法. 计算机研究与发展, 2019, 56(5): 929-941. DOI:10.7544/issn1000-1239.2019.20190012 |
| [3] |
Yousefi M, Mtetwa N, Zhang Y, et al. A novel approach for analysis of attack graph. Proceedings of the 2017 IEEE International Conference on Intelligence and Security Informatics (ISI). Beijing: IEEE, 2017. 7–12.
|
| [4] |
王晓凡, 周天阳, 臧艺超, 等. 大规模网络渗透测试路径规划方法研究. 计算机应用与软件, 2023, 40(5): 324-330. DOI:10.3969/j.issn.1000-386x.2023.05.048 |
| [5] |
Sutton RS, Barto AG. Reinforcement Learning: An Introduction. 2nd ed., Cambridge: MIT Press, 2018.
|
| [6] |
赵海妮, 焦健. 基于强化学习的渗透路径推荐模型. 计算机应用, 2022, 42(6): 1689-1694. |
| [7] |
李腾, 曹世杰, 尹思薇, 等. 应用Q学习决策的最优攻击路径生成方法
. 西安电子科技大学学报, 2021, 48(1): 160-167. DOI:10.19665/j.issn1001-2400.2021.01.018 |
| [8] |
周仕承, 刘京菊, 钟晓峰, 等. 基于深度强化学习的智能化渗透测试路径发现. 计算机科学, 2021, 48(7): 40-46. DOI:10.11896/jsjkx.210400057 |
| [9] |
高文龙, 周天阳, 赵子恒, 等. 基于深度强化学习的网络攻击路径规划方法. 信息安全学报, 2022, 7(5): 65-78. |
| [10] |
Hu ZG, Beuran R, Tan YS. Automated penetration testing using deep reinforcement learning. Proceedings of the 2020 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW). Genoa: IEEE, 2020. 2–10.
|
| [11] |
Gangupantulu R, Cody T, Rahma A, et al. Crown jewels analysis using reinforcement learning with attack graphs. Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI). Orlando: IEEE, 2021. 1–6.
|
| [12] |
Chowdhary A, Huang DJ, Mahendran JS, et al. Autonomous security analysis and penetration testing. Proceedings of the 16th International Conference on Mobility, Sensing and Networking (MSN). Tokyo: IEEE, 2020. 508–515.
|
| [13] |
Gangupantulu R, Cody T, Park P, et al. Using cyber terrain in reinforcement learning for penetration testing. Proceedings of the 2022 IEEE International Conference on Omni-layer Intelligent Systems (COINS). Barcelona: IEEE, 2022. 1–8.
|
| [14] |
Foley M, Hicks C, Highnam K, et al. Autonomous network defence using reinforcement learning. Proceedings of the 2022 ACM on Asia Conference on Computer and Communications Security. Nagasaki: ACM, 2022. 1252–1254.
|
| [15] |
高文龙, 周天阳, 朱俊虎, 等. 基于双向蚁群算法的网络攻击路径发现方法. 计算机科学, 2022, 49(S1): 516-522. |
 2023, Vol. 32
2023, Vol. 32



