计算机系统应用  2023, Vol. 32 Issue (12): 276-283   PDF    
引用本文
白鹭, 鲁思琪, 信昆仑, 任鹏, 朱赫, 穆旭东. 神经网络与解释模型在非结冰期含沙量预测中的应用. 计算机系统应用, 2023, 32(12): 276-283.http://www.c-s-a.org.cn/1003-3254/9338.html   
Bai L, Lu SQ, Xin KL, Ren P, Zhu H, Mu XD. Application of Neural Networks and Interpretation Models in Sediment Concentration Prediction During Non-ice Period. Computer Systems and Applications, 2023, 32(12): 276-283(in Chinese).http://www.c-s-a.org.cn/1003-3254/9338.html   
神经网络与解释模型在非结冰期含沙量预测中的应用
白鹭1, 鲁思琪2, 信昆仑2, 任鹏1, 朱赫1, 穆旭东1     
1. 银川中铁水务集团有限公司, 银川 750004;
2. 同济大学 环境科学与工程学院, 上海 200092
收稿日期：2023-06-09; 修改日期：2023-07-12; 采用时间：2023-07-27; csa 在线出版时间：2023-10-27
通讯作者：信昆仑, E-mail: xkl@tongji.edu.cn.
摘要：基于大量历史数据的预测在环境治理、城市交通等领域已经成为必不可少的一个环节, 预测的准确性对实际生产、调度等工作有着重要影响. 受自然因素或人为因素的影响, 一些数据表现出高波动性以及不确定性, 导致无法充分发挥预测模型的最大优势. 本研究以非结冰期含沙量预测为案例, 探究了针对高波动性数据预测的优化方法, 发现通过基于SHAP方法的特征选择优化、数据平稳化以及前期聚类可以有效降低对高波动数据的预测误差, MAE从初始模型的1.502降低到0.194, 其中数据平稳化的优化效果最显著, MAE降低了76.51%, 但随着平稳化的阶数增大, 预测结果反而变差, 这是由于随着平稳化的阶数越高, 后续指数化的阶数也对应提升, 从而导致误差的指数倍增长. 此外, 将聚类结果作为特征输入可以有效“引导”多层感知机的参数学习过程.
关键词: 高波动数据    预测优化    人工神经网络    模型可解释性    特征选择    
Application of Neural Networks and Interpretation Models in Sediment Concentration Prediction During Non-ice Period
BAI Lu1, LU Si-Qi2, XIN Kun-Lun2, REN Peng1, ZHU He1, MU Xu-Dong1     
1. Yinchuan China Railway Water Group Co. Ltd., Yinchuan 750004, China;
2. College of Environmental Science and Engineering, Tongji University, Shanghai 200092, China
Abstract: Prediction based on historical data has become essential in many fields, such as environmental management and urban transportation. Prediction accuracy plays a key role in practical production, scheduling, and other tasks. However, due to natural or human factors, some data exhibits high volatility and uncertainty, unable to fully achieve the potential of prediction models. Taking the sediment concentration prediction during the non-ice period as a case study, this study explores optimization methods for predicting high-volatility data. The results show that the feature selection optimization based on the Shapley additive explanations (SHAP), the data smoothing, and early-stage clustering can reduce prediction error of high-volatility data. The mean absolute error (MAE) decreases from 1.502 in the initial model to 0.194, and data smoothing shows the most significant optimization effect with a reduction of 76.51% in MAE. However, the increasing smoothing order results in poorer prediction results, which is because the subsequent rising exponentiation order correspondingly leads to an exponential increase in error. Additionally, employing clustering results as feature inputs can “guide” the parameter learning of multi-layer perceptron.
Key words: high-volatility data     prediction optimization     artificial neural network     model interpretability     feature selection    

随着城市化进程的加速和智能化技术的不断发展, 大量数据被广泛应用于环境治理、城市交通等领域, 为了使这些数据更充分高效地利用并指导生产、调度等, 预测已经成为必不可少的一个环节. 林昱道等 [1]采用一维卷积神经网络对短期需水量进行预测, 并利用预测结果指导供水管网优化调度方案的制定和实施; 也有研究利用自回归移动平均模型(autoregressive integrated moving average, ARIMA)对交通流量进行预测[2], 用来缓解交通拥堵, 减少碳排放, 提高交通运营效率, 后续特提出很多改进模型[3–5].

然而一些数据受自然因素以及人为因素等影响, 表现出高波动性以及不确定性, 进而导致无法发挥预测模型的最大优势, 因此, 解决高波动性数据预测与优化问题, 提高预测准确性和可解释性成为一个重要的研究内容.

SHAP (Shapley additive explanations)方法是一种用于解释模型预测结果的算法[6,7], 能够帮助评估特征与预测结果之间的关系, 提高模型的可解释性. 许多研究利用该方法解释预测模型, 探究不同特征对输出结果的贡献度[8–11], 但是很少有研究利用其对模型输入特征选择优化. 此外, 对于提高预测准确性, 目前很少有研究对其进行系统探究.

因此, 本研究旨在: 1)基于SHAP方法对输入特征进行筛选, 以期提高初始预测模型性能; 2)探究针对高波动数据预测的优化策略; 3)探究不同优化策略对预测准确度的影响. 为达到以上目的, 本文将河流非结冰期含沙量预测作为研究案例, 利用时间长度为20年的真实历史数据进行训练及测试, 以期探究出具有普适性的预测优化策略.

1 数据与方法 1.1 数据描述

本研究案例预测目标是QTX水文站非结冰期(4月–11月)监测点次日悬浮泥沙浓度, 使用黄河取水断面上下游两个水文测量站的历史日均平均流量和日均平均悬浮泥沙浓度数据(分别为上游的XHY水文站和下游的QTX水文站), 以及ZN气象站的气温和降雨数据. 各个站点的位置示意图见图1. 数据集时间长度为20年(2002.01.01–2021.12.31). 基于该数据集初步构建了23个特征, 包括4个QTX水文站含沙量数据(qtx_s1, qtx_s2, qtx_s3, qtx_s4)、4个QTX水文站河流流量数据(qtx_r1, qtx_r2, qtx_r3, qtx_r4)、4个XHY水文站含沙量数据(xhy_s1, xhy_s2, xhy_s3, xhy_s4)、4个XHY水文站河流流量数据(xhy_r1, xhy_r2, xhy_r3, xhy_r4)、ZN气象站数据(t_1, t_2, p_1, p_2)以及3个自生产数据(mon, sin_d, sin_m), 具体特征及含义见表1.

图 1 水文站、气象站及取水泵站的站点位置分布图 Fig. 1 The location of hydrological station, meteorological station and water pumping station

1.2 数据预处理

由于原始数据集中包含了河流径流量, 悬浮泥沙浓度, 降雨量等不同物理含义的变量, 且其数值范围差异很大. 为了消除特征之间的量纲影响, 在模型预处理中使用式(1)将输入变量规范化至[0, 1].

$ {x_{{{in}}}} = \frac{{{x_i} - {x_{i, \min }} + \varepsilon }}{{{x_{i, \max }} - {x_{i, \min }} + \varepsilon }} $ (1)

其中, ${x_{in}}$ 是变量 $ i $ 规范化后的值, $ {x_i} $ 是原始值, ${x_{i, \max }}$ 和 ${x_{i, \min }}$ 分别是变量 $i$ 的最大值和最小值. $\varepsilon $ 是一个非常小的正值, 用来避免除零错误, 在我们的研究中将其设定为0.0001 $({x_{i, \max }} + {x_{i, \min }})$ .

表 1 特征构建及具体含义 Table 1 The construction and specific meaning of features

1.3 模型介绍与构建

多层感知机(multilayer perceptron, MLP)是一种前向结构的人工神经网络, 映射一组输入向量到一组输出向量[12]. MLP可以看作是一个有向图, 由多个的节点层所组成, 每一层都全连接到下一层. 除了输入节点, 每个节点都是一个带有非线性激活函数的神经元[13,14]. 每一层神经元都拥有权重矩阵、偏置向量, 使用算法来调整权重并减少训练过程中的偏差, 即实际值和预测值之间的误差[15]. 其主要优势在于其快速解决复杂问题的能力[16].

本研究构建的模型包括一个输入层, 一个隐藏层, 一个输出层, 其中输出层神经元数量为1, 隐藏层神经元数量根据特征数量通过试错法选择出的最佳参数. 使用Leaky ReLU (leaky rectified linear unit)作为隐藏层的激活函数[17]计算每个神经元的输出. 激活函数公式如式(2)所示.

$ y = \max (0, x) + \beta \min (0, x) $ (2)

其中, $\;\beta $ 为小的负常数, 通常为−0.01.

对于每个节点的权重与偏置项学习, 采用反向传播算法, 参数更新公式如式(3)、式(4)所示:

$ w_{i, j}^m(k + 1) = w_{i, j}^m(k) - \eta \frac{{\partial L}}{{\partial w_{i, j}^m}} $ (3)
$ b_{i, j}^m(k + 1) = b_{i, j}^m(k) - \eta \frac{{\partial L}}{{\partial b_{i, j}^m}} $ (4)

其中, $\eta $ 为学习率; $w_{i, j}^m$ 指第 $m - 1$ 层第 $i$ 个神经元与第 $m$ 层第 $j$ 个神经元相连的权重; $b_j^m$ 指第 $m$ 层第 $j$ 个神经元的偏置; $k$ 是指训练过程的迭代次数; $L$ 为损失函数.

1.4 Shapley值计算

SHAP方法的核心是计算每个特征变量的Shapley值, Shapley值可以度量每个特征对于预测结果的贡献值, 其核心思想是通过计算每个特征相对于其他特征的信息增益, 确定每个特征的重要性排名[18]. 计算公式为式(5)和式(6).

$ {\Phi _i} = \sum\limits_{S \subseteq N} {\frac{{|S|!(M - |S| - 1)!}}{{M!}}} [{f_x}(S \cup \{ {x_j}\} ) - {f_x}(S)] $ (5)
$ N = \{ {x_1}, {x_2}, \cdots , {x_M}\} /\{ {x_i}\} $ (6)

其中, ${x_i}$ 为单个样本中第 $i$ 个特征变量; $N$ 为不包括 $\{ {x_i}\} $ 的所有输入特征的可能集合; $S$ 为 $N$ 的子集; $|S|$ 为 $S$ 中的元素的个数; ${f_x}$ 为预测模型; ${f_x}(S \cup \{ {x_j}\} )$ 代表当样本中只有 $S \cup \{ {x_j}\} $ 中的特征变量时模型的预测值, ${f_x}(S)$ 代表样本中只有 $S$ 中的特征变量时, 模型的预测值. 二者相减即为第 $i$ 个特征变量在子集 $S$ 下的边际贡献.

1.5 优化路线

本文研究路线如图2所示.

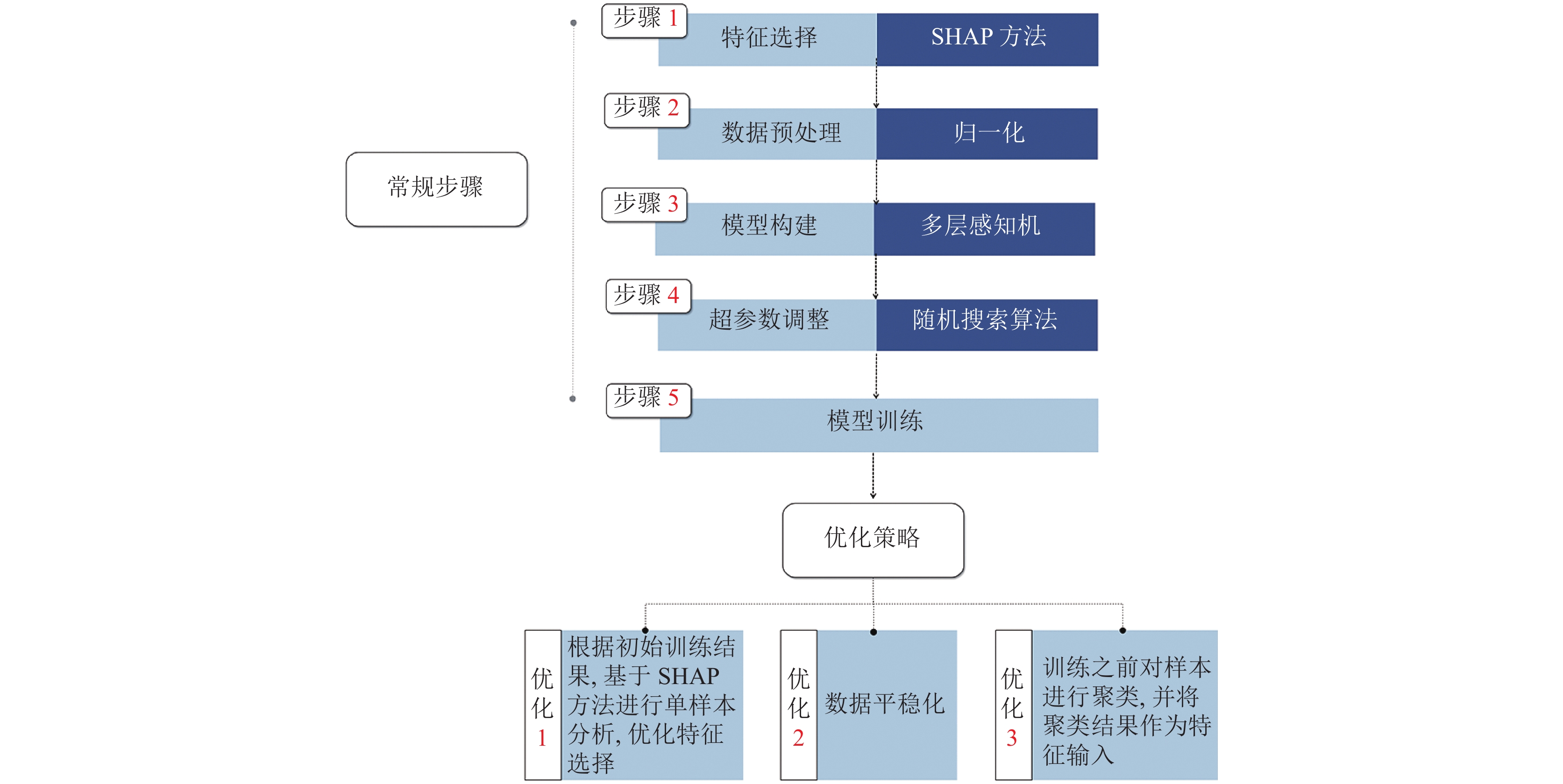
图 2 预测优化路线 Fig. 2 Route of prediction optimization

2 结果与讨论 2.1 初始训练结果与优化结果

基于SHAP方法对初步构建的23个特征(详见第1.1节)进行分析, 结果如图3所示. 图3中颜色代表特征值的大小, 而横坐标为SHAP值的大小, 例如, 从图3中可以发现qtx_s1的值越大越容易对模型输出结果产生正向推动, 因而样本点分布越广泛, 该特征对模型输出结果影响越大. sin_d以及sin_m这两个特征对应的样本点分布很广泛, 说明时间的周期性对预测较为重要. 此外, 持续的降雨会对河流泥沙含量较大影响, 尤其在汛期, 暴雨径流使土壤受到侵蚀, 使岸上的泥沙随径流进入河道, 但SHAP分析无法考虑p_1与p_2的交互效应, 因此综合考虑SHAP分析结果以及实际因素, 选取12个特征(sin_d, sin_m, qtx_s1, qtx_s2, qtx_r1, xhy_s1, xhy_s2, xhy_r1, mon, p_1, p_2).

初始训练结果以及优化过程结果如图4以及表2所示. 可以发现MSE从最初的2.896降低到0.158, 其中优化2 (即数据平稳化)的效果最为显著.

图 3 基于SHAP方法的特征重要性分析 Fig. 3 Feature importance analysis based on SHAP method

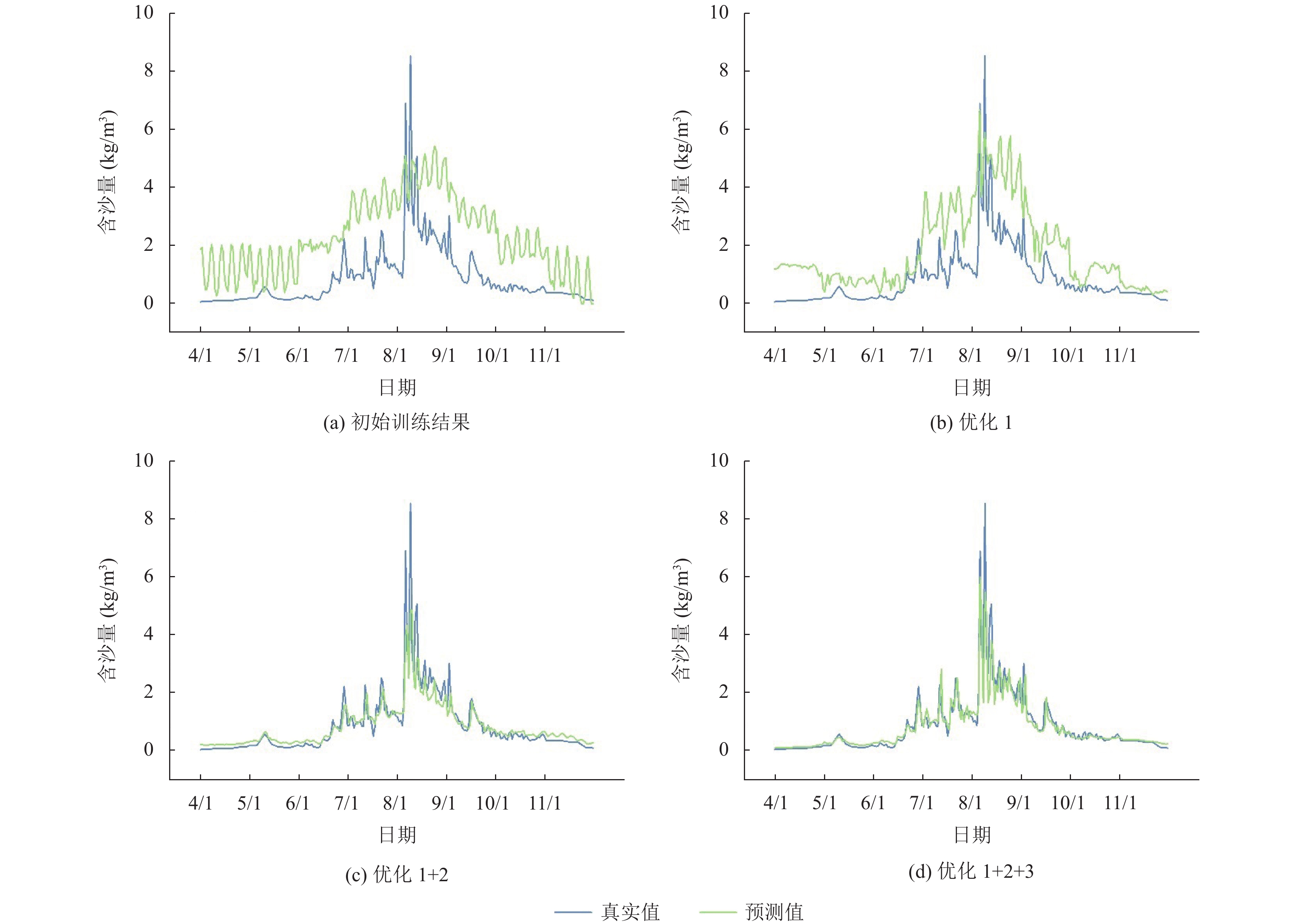
图 4 模型优化过程效预测结果展示 Fig. 4 The fitting effect in the process of model optimization

表 2 模型优化过程性能对比 Table 2 Performance comparison during model optimization process

2.2 初始训练结果与优化结果基于SHAP方法的特征优化

如图4(a)所示, 相比较真实值, 初始模型预测结果波动性较大, 因此选取波动性较大的几个点(图5)基于SHAP方法对其进行单样本分析, 图6(a)–(d)分别展示了A、B、C、D这4个点对应的分析结果, 颜色代表对预测结果的作用方向, 红色为正向推动, 蓝色为反向推动, 色块大小代表作用程度, 可以发现对于波动大的这4个点, sin_d对预测结果均有很显著的正向作用, 增大了预测误差, 这是因为sin_d的变化的周期较短, 不符合含沙量的变化特征. 因此在原来的特征体系中去掉sin_d, 并进行训练及测试, 测试结果如图4(b)所示, 可以看到波动性明显降低, 各类性能指标提高24.93%–43.71%.

图 5 样本点选取 Fig. 5 Sample point selection

图 6 基于SHAP方法的单样本分析 Fig. 6 Single sample analysis based on SHAP method

2.3 数据平稳化

如图7展示了原始数据以及经过多次数据平稳化之后结果, 可以看出原始数据波动较大, 含沙量最高为167 kg/m3, 最低为0.022 kg/m3, 经过一阶至三阶平稳化后数据波动幅度明显减小. 将平稳化之后的数据输入至经过优化1的模型, 图8及表3展示了不同平稳化阶数对应的预测效果. 发现经过一阶平稳化后, 预测结果显著提高, 但随着平稳化的阶数增大, 预测结果反而变差, MSE从0.210 (一阶)升至0.970 (三阶), 这是由于在得到预测结果后需要对其进行指数化来得到最终的预测结果, 那么平稳化的阶数越高, 后续指数化的阶数也对应提升, 从而导致误差的指数倍增长.

2.4 将聚类结果作为特征输入

在优化1 与优化2的基础上, 发现当含沙量较低或较高时, 预测误差较大, 因此为了更好地“引导”多层感知机网络的参数学习过程, 在预测之前对根据qtx_s1与qtx_s2的值进行聚类, 并将聚类结果作为输入特征. 聚类的详细信息见表4, 其中通过试错法最终确定准确率最高的聚类原则. 表2的预测结果显示, 优化3可以将预测误差降低到0.194, 在原来优化1与优化2共同作用的基础上MAE降低18.14%, MSE降低24.76%, 证明将聚类结果作为特征输入可以有效“引导”多层感知机的参数学习过程.

2.5 验证

为了保证经过优化后模型的普适性, 利用2021年数据进行验证, 结果如图9所示. MAE从初始模型的1.607到0.163, 因此可以证明这3种优化方法的有效性与普适性.

图 7 数据的平稳化结果 Fig. 7 The stationary results of data

图 8 不同平稳化阶数对应的预测效果 Fig. 8 The prediction effect corresponding to different stationary fold

表 3 不同平稳化阶数下模型预测误差对比 Table 3 Comparison of model prediction errors under different fold

表 4 聚类依据与结果 Table 4 Clustering basis and results

3 结论

通过基于SHAP方法的特征选择优化、数据平稳化以及前期聚类可以有效降低对高波动数据的预测误差, MAE从初始模型的1.502降低到0.194, 其中数据平稳化的优化效果最显著, MAE降低了76.51%, 但随着平稳化的阶数增大, 预测结果反而变差, 这是由于随着平稳化的阶数越高, 后续指数化的阶数也对应提升, 从而导致误差的指数倍增长. 此外, 将聚类结果作为特征输入可以有效“引导”多层感知机的参数学习过程.

图 9 优化方法普适性测试 Fig. 9 Test for optimization method universality

参考文献
[1]
林昱道, 赵平伟, 陈磊, 等. 基于一维卷积神经网络的短期用水量预测. 净水技术, 2022, 41(S1): 34-39. DOI:10.15890/j.cnki.jsjs.2022.s1.006
[2]
Ahmed MS, Cook AR. Analysis of freeway traffic time-series data by using Box-Jenkins techniques. Transportation Research Record 722. Washington: Transportation Research Board, 1979. 1–9.
[3]
Hamed MM, Al-Masaeid HR, Said ZMB. Short-term prediction of traffic volume in urban arterials. Journal of Transportation Engineering, 1995, 121(3): 249-254. DOI:10.1061/(ASCE)0733-947X(1995)121:3(249)
[4]
Lee S, Fambro DB. Application of subset autoregressive integrated moving average model for short-term freeway traffic volume forecasting. Transportation Research Record: Journal of the Transportation Research Board, 1999, 1678(1): 179-188. DOI:10.3141/1678-22
[5]
Ghosh B, Basu B, O’mahony M. Multivariate short-term traffic flow forecasting using time-series analysis. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(2): 246-254. DOI:10.1109/TITS.2009.2021448
[6]
Parsa AB, Movahedi A, Taghipour H, et al. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accident Analysis & Prevention, 2020, 136: 105405.
[7]
Shapley LS. A value for n-person games. In: Kuhn HW, Tucker AW, eds. Contributions to the Theory of Games (AM-28), Volume II. Princeton University Press, 1953. 307–317.
[8]
El Mokhtari K, Higdon BP, Başar A. Interpreting financial time series with SHAP values. Proceedings of the 29th Annual International Conference on Computer Science and Software Engineering. Toronto: IBM Corp., 2019. 166–172.
[9]
Bi Y, Xiang DX, Ge ZY, et al. An interpretable prediction model for identifying N7-methylguanosine sites based on XGBoost and SHAP . Molecular Therapy-nucleic Acids, 2020, 22: 362-372. DOI:10.1016/j.omtn.2020.08.022
[10]
陈曦泽, 贾俊峰, 白玉磊, 等. 基于XGBoost-SHAP的钢管混凝土柱轴向承载力预测模型. 浙江大学学报(工学版), 2023, 57(6): 1061-1070.
[11]
Mangalathu S, Hwang SH, Jeon JS. Failure mode and effects analysis of RC members based on machine-learning-based Shapley additive explanations (SHAP) approach. Engineering Structures, 2020, 219: 110927. DOI:10.1016/j.engstruct.2020.110927
[12]
Gardner MW, Dorling SR. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmo-spheric sciences. Atmospheric Environment, 1998, 32(14–15): 2627-2636. DOI:10.1016/S1352-2310(97)00447-0
[13]
Taud H, Mas JF. Multilayer perceptron (MLP). In: Camacho Olmedo MT, Paegelow M, Mas JF, et al., eds. Geomatic Approaches for Modeling Land Change Scenarios. Cham: Springer, 2018. 451–455.
[14]
Popescu MC, Balas VE, Perescu-Popescu L, et al. Multilayer perceptron and neural networks. WSEAS Transactions on Circuits and Systems, 2009, 8(7): 579-588.
[15]
Ramchoun H, Janati Idrissi MA, Ghanou Y, et al. Multilayer perceptron: Architecture optimization and training. Proceedings of the 2nd international Conference on Big Data, Cloud and Applications. Tetouan: ACM, 2017. 71.
[16]
Park YS, Lek S. Artificial neural networks: Multilayer perceptron for ecological modeling. Developments in Environmental Modelling, 2016, 28: 123-140.
[17]
Maas AL, Hannun AY, Ng AY. Rectifier nonlinearities improve neural network acoustic models. Proceedings of the 30th International Conference on Machine Learning. Atlanta, 2013.
[18]
Baptista ML, Goebel K, Henriques EMP. Relation between prognostics predictor evaluation metrics and local interpretability SHAP values. Artificial Intelligence, 2022, 306: 103667. DOI:10.1016/j.artint.2022.103667