随着基于位置服务(LBS)技术的发展, 越来越多的车辆位置移动数据产生并被存储下来, 这些海量数据中隐藏着大量的信息, 挖掘这些隐藏的信息即轨迹数据挖掘有助于城市交通管理决策, 有利于智慧交通城市的实现^[1]. 受到位置采样环境、采样设备精度及采样频率等因素的影响, 原始车辆轨迹数据中会普遍存在异常数据, 如轨迹数据定位信息出现较大偏差或车辆速度明显异常, 这对基于车辆轨迹数据的后续研究工作将产生重要的消极影响. 因此, 为了保证车辆轨迹数据质量, 检测、识别和过滤这些轨迹异常数据则成为轨迹数据挖掘预处理阶段的一个重要步骤.

车辆轨迹数据是指按固定周期从车辆的位置传感器中读取到的一系列轨迹点时间序列数据, 其中每个轨迹点数据包括采样时刻、当前经纬度坐标等内容. 在采集车辆轨迹数据的过程中, 由于环境和设备等因素的影响, 原始车辆轨迹数据中总是存在异常轨迹点数据. 其中, 常见的异常轨迹点是移动特征异常轨迹点, 表现为在车辆移动过程中, 连续多个采样点中所包含的速度、加速度、方向角等车辆移动特征数据不符合常理即超出合理数值阈值范围. 对于此类异常轨迹点, 常用的检测方法是直接对相邻轨迹点之间提取的速度、加速度或方向角等移动特征数据进行取值合理性检测. 例如, 康军等人^[2]计算相邻轨迹点之间速度, 通过最大速度限制, 将速度异常的轨迹点从数据中删除; 周洋等人^[3]根据轨迹点经纬度计算速度、加速度变量, 并依据变量值剔除异常轨迹点; Hsueh等人^[4,5]在对轨迹数据的预处理中, 速度超过阈值的轨迹点被视为异常值被剔除; Ebel等人^[6]将相邻轨迹点间的平均速度与预设速度阈值进行比较, 若轨迹点的速度超出阈值范围则被视为异常轨迹点; Mohamed等人^[7]使用轨迹点的速度和方向角等移动特征, 通过应用3个过滤器, 对异常轨迹点的检测和剔除; Patil等人^[8]使用更全面的轨迹点移动特征(距离、速度和加速度)的组合进行异常轨迹点的检测; Ma等人^[9]使用移动特征阈值对轨迹数据进行预处理, 将超出阈值的轨迹点视为异常轨迹点. 上述异常轨迹点的检测方法能够高效的将移动特征异常的轨迹点检测出来, 在大量的轨迹计算文献中都有成功运用.

但是, 在研究过程中我们发现了一种特殊的异常轨迹点, 如图1所示, 在距离周围路段相对较远的较小的空间范围内, 连续异常轨迹点g₇–g₁₄嵌入在正常的轨迹点序列中, 其移动特征数据并无异常, 但是在实际路网中却不存在和该轨迹点匹配的真实路段. 这些异常轨迹点主要是由于车辆在某些特定区域(如科技园区)的内部道路上行驶, 而这些内部道路在电子地图的路网数据中并不存在. 我们将上述异常轨迹点称作隐性位置异常轨迹点, 这些异常轨迹点用传统的基于移动特征的异常轨迹点检测方法难以检测, 若直接将其看作正常的轨迹点, 并进行后续的地图匹配处理则必定会产生匹配错误, 从而对后续一系列基于位置服务(如车辆行为分析, 序列模式挖掘等)的准确性造成不利影响.

隐性位置异常轨迹点呈现出一定的时空局部聚集性, 传统的异常点检测方法是根据轨迹点间的时空关系进行判断, 忽略了轨迹点和路段的空间关系, 导致难以检测出这种异常轨迹点. 综上, 本文提出一种针对隐性位置异常轨迹点的检测方法, 旨在通过利用轨迹数据的时空特性, 有效识别车辆轨迹中容易被忽略的隐性位置异常数据. 该方法通过Geohash编码^[10]和浮动网格^[2]筛选出初始核心异常轨迹点; 针对每个核心异常轨迹点进行简单聚类, 探索时空范围内的其他隐性位置异常轨迹点; 最终, 检测出隐性位置异常轨迹点集. 通过实验结果表明, 本文所提方法可以有效检测出隐性的位置异常轨迹点, 在提高车辆行为分析和交通管理等领域的准确性和效率方面具有重要意义.

1 位置异常轨迹点问题描述

本文所涉及的相关定义如下.

定义1. 车辆轨迹 $(T)$ : 由同一车辆的一系列时间连续的轨迹点所组成的时间序列称为车辆轨迹T, 其中 $T = ({g_1}, {g_2}, \cdots, {g_n})$ , $ \forall {g_i} \in T, {g_i} = (id, time, lon, lat) $ , 且 $ id $ 表示产生轨迹的车辆的车牌号, $ time $ 表示采样时刻, $ lon $ 和 $ lat $ 分别该时刻轨迹点的经度和纬度坐标.

定义2. 道路网络: 使用有向图 $G(V, E)$ 表示道路网络, 其中 $V$ 表示道路网络中路段交点集合, $E$ 表示道路网络中路段集合. 其中, $\forall e \in E,\; e = (id, ps)$ , $e.id$ 表示路段的唯一标识, $e.ps$ 是电子地图中表示路段的一组二维经纬度点的序列, $\forall p \in e.ps, p = (lon, lat)$ , 其中 $p.lon$ 、 $p.lat$ 分别表示路段 $e$ 的经纬度点的经度值和纬度值.

定义3. Geohash网格^[10]: 本文采用定长Geohash编码方式将路网 $G(V, E)$ 划分成固定大小的矩形网格, 对于每个Geohash网格均存在一个全局唯一且定长的Geohash编码 $I{D_{{\text{Geo}}}}$ , 则对于 $ \forall p \in e.ps \wedge \forall e \in E $ 总是包含在一个唯一的Geohash网格中. 设Geohash网格的长和宽分别表示为 $ {L}_{g}和{W}_{g} $ , 且本文中都定为常数.

定义4. Geohash网格索引 $(M)$ : 是路网的各个Geohash网格编号 $I{D_{{\text{Geo}}}}$ 到该网格所包含的路段集合 $ {C_e} $ 的索引. 索引中每一项均表示为一个键值对, $\forall r \in M, r = \{ (I{D_{{\text{Geo}}}}:{C_e})\} $ , 其中, $I{D_{{\text{Geo}}}}$ 为Geohash网格编号, $ {C_e} $ 为编号为 $I{D_{{\text{Geo}}}}$ 的Geohash网格所包含的所有的路段集合, 可定义为 ${C_e} = \{ e|\forall e \in E \wedge \exists p \in e.ps \to geohash(p) = I{D_{{\text{Geo}}}}{\text{\} }}$ , 其中 $geohash()$ 表示根据经纬度点计算其所在的Geohash网格的网格编号的标准方法.

定义5. 浮动网格: 给定一个轨迹点 $ {g_i} $ , 其浮动网格 $ {c_{{g_i}}} $ 为以 $ {g_i} $ 的经纬度坐标为中心的一个边长为L的正方形区域. 对于一个车辆轨迹T中所包含的每个轨迹点均存在一个与其对应的浮动网格. 对于任一个浮动网格 $ {c_{{g_i}}} $ , 设其对应的4个顶点分别表示为 $ v_{{c_{{g_i}}}}^{lu}, v_{{c_{{g_i}}}}^{ru}, v_{{c_{{g_i}}}}^{rd}, v_{{c_{{g_i}}}}^{ld} $ .

定义6. 轨迹点候选路段集合 $ ({C_{{\text{condi}}}}) $ : 给定一个轨迹点 $ {g_i} $ , 设其对应的浮动网格为 $ {c_{{g_i}}} $ 且该浮动网格对应的4个顶点分别为 $ v_{{c_{{g_i}}}}^{lu}, v_{{c_{{g_i}}}}^{ru}, v_{{c_{{g_i}}}}^{rd}, v_{{c_{{g_i}}}}^{ld} $ , 则由Geohash()方法可确定 $ {c_{{g_i}}} $ 的4个顶点分别所对应的Geohash网格及其编号表示为 $ ID_{{c_{{g_i}}}}^{lu} $ , $ ID_{{c_{{g_i}}}}^{ru} $ , $ ID_{{c_{{g_i}}}}^{rd} $ , $ ID_{{c_{{g_i}}}}^{ld} $ . 根据Geohash网格索引M可获得上述Geohash网格所包含的路段集合, 表示为 $ C_e^{(i0)} $ , $ C_e^{(i1)} $ , $ C_e^{(i2)} $ , $ C_e^{(i3)} $ , 则轨迹点 $ {g_i} $ 的候选路段集合 $C_{{\text{condi}}}^{(i)}$ 可定义为 $C_{{\text{condi}}}^{(i)} = C_e^{(i0)} \cup C_e^{(i1)} \cup {C^{(i2)}_e} \cup C_e^{(i3)}$ , 其中 $C_e^{(ij)}$ 为浮动网格第 $j$ 个顶点所在Geohash网格对应的路段集合, $0 \leqslant j \leqslant 3$ .

定义7. 隐性位置异常轨迹点集合 $ ({C_o}) $ :在车辆轨迹序列中, 移动特征数据总是满足阈值约束, 但在实际路网中却不存在与之匹配的真实路段的轨迹点, 将其称之为隐性位置异常轨迹点. 根据隐性位置异常轨迹点的判断条件的不同, 可将其分为两类即核心位置异常轨迹点和位置异常轨迹点, 其中对于一个轨迹点O, 如果其候选路段集合 $C_{{\rm{condi}}}^O = \varnothing$ , 则称O为核心位置异常轨迹点, 而位置异常轨迹点需要通过本文所提的隐性位置异常轨迹点聚类算法进行判断. 隐性位置异常轨迹点集合 $ {C_o} $ 则定义为当前轨迹序列中所有的核心位置异常轨迹点和位置异常轨迹点的集合.

本文所提的隐性位置异常数据的检测方法是指: 给定车辆行驶轨迹 $T$ 和道路网络 $G(V, E)$ , 根据Geohash网格索引 $M$ 及浮动网格候选路段选择方法和隐性位置异常轨迹点聚类方法, 在轨迹 $T$ 中检测隐性位置异常轨迹点集合 $ {C_o} $ .

2 基于聚类的隐性位置异常数据检测方法 2.1 隐性位置异常点的特征与检测方法的关联分析

隐性位置异常轨迹点的特征为点远离路段并且具有一定时空聚集性, 因此, 在检测这些点时, 需要使用一种方法来定位这些点, 并将其周围可能存在的异常点识别出来. 而浮动网格与聚类算法结合的方法可以很好地满足这一需求.

浮动网格的特性是可以根据轨迹点来动态调整网格的大小和位置, 从而有效地检索出距离该轨迹点一定范围内的路段, 具体见第2.2节; 因此, 对于远离路段的隐性位置异常点, 可以通过浮动网格来检测它们. 聚类算法是一种无监督学习方法, 可以将具有相同特征的数据分为一组; 在这种情况下, 将浮动网格检测出的隐性位置异常点为中心, 使用聚类算法, 将该轨迹点周围具有相似时空属性的轨迹点分为同一异常轨迹点类簇, 作为核心位置异常轨迹点的补充. 因此, 浮动网格与聚类算法结合的检测方法可以有效地定位远离路段且具有一定时空聚集性的隐性位置异常点.

本文所提出的隐性位置异常数据检测方法主要包含两个步骤: 第1步是确定核心位置异常轨迹点数据, 即当轨迹序列中的一个轨迹点通过浮动网格确定的候选路段集合为空时, 即可以确定其为核心位置异常轨迹点; 第2步是面向核心位置异常轨迹点, 根据隐性位置异常数据的局部聚集性假设, 采用聚类算法检测聚集在核心位置异常轨迹点附近的在其他位置异常轨迹点. 最终检测出正常轨迹中的隐性位置异常轨迹点.

2.2 核心位置异常轨迹点的选取方法

(1) 路网网格划分

本文首先使用Geohash网格划分方法^[2,11], 将城市道路网络 $G(V, E)$ 按照相同大小的Geohash网格划分为多个网格区域. 其中, 每个网格均有一个全球唯一的字符串类型的网格编号 $I{D_{{\text{Geo}}}}$ ; 同时, 根据Geohash网格编号长度的不同, 相对应的每个网格的大小也会不同, 即网格编号长度越长, 网格的个数越多, 单个网格覆盖范围越小; 网格编号长度越短, 网格的个数越少, 单个网格覆盖范围越大.

如图2中给出了以7字符长度划分出的4个Geohash网格的示意图, 其中4个网格的 $I{D_{{\text{Geo}}}}$ 分别为wqj76q、wqj76w、wqj76m和wqj76t. 采用Geohash网格系统进行路网网格化划分的优势在于当判断路网中各位置点所在网格编号时, 仅通过标准化的计算即可获得其所在的网格编号, 用于划分路网的网格信息不需要提前生成和保存.

路网 $G(V, E)$ 经过Geohash网格划分后, 对于 $\forall p \in e.ps, \forall e \in E$ , 通过 $geohash(p)$ 即可获得的其对应的Geohash网格编号, 因此可容易计算每条路段所对应的1个或多个Geohash网格, 通常一个Geohash网格会覆盖多条路段. 为了快速找到Geohash网格中包含的路段, 本文进一步构建了Geohash网格索引 $M$ , 该索引以Geohash网格编号为Key以查询该网格所覆盖的所有路段. 所建立索引 $M$ 部分数据如表1所示, 通过该索引, 能够根据给定的Geohash网格编号 $I{D_{{\text{Geo}}}}$ 快速查询到其所覆盖的路段集合 ${C_e}$ .

(2) 浮动网格以及候选路段集合的设定

对于移动的车辆的轨迹T中的轨迹点 $ {g_i} $ , 本文采用定义5中所定义的浮动网格方法获得定义6所定义的候选路段集合 $ C_{{\text{condi}}}^{(i)} $ . 例如在图2中, 轨迹点 $ {g_0} \in T $ 的浮动网格对应的矩形的4个顶点分别为 $ {v_0}, {v_1}, {v_2}, {v_3} $ , 经过 $geohash$ 方法计算可知其对应的Geohash网格编号分别为wqj76q、wqj76w、wqj76m和wqj76t. 利用Geohash网格索引M, 即可获得上述4个网格所覆盖的路段集合即为轨迹点 $ {g_0} $ 的候选路段集合.

(3) 核心位置异常轨迹点的确定

对于 $ \forall {g_i} \in T $ , 如果其通过浮动网格获得的候选路段集合 $ C_{{\text{condi}}}^{(i)} = \varnothing $ , 即4个网格中都不存在路段, 则 $ {g_i} $ 被确认为核心位置异常轨迹点. 核心位置异常轨迹点的候选路段集合为空集, 在轨迹数据预处理环节的地图匹配过程中就无法找到其匹配路段, 这就对轨迹数据的后续分析产生的一定的影响, 因此有必要把这类轨迹点在轨迹数据预处理之前检测出来.

当确定核心位置异常轨迹点, 根据隐性位置异常数据的局部聚集性假设, 则必然在核心位置异常轨迹点周围存在其他隐性位置异常点, 此类轨迹点的候选路段集合并不为空且其移动特征参数往往也在正常的阈值范围内, 在传统的轨迹异常检测环节中是无法检测出来的, 而且通过地图匹配也能确定其各自的匹配路段, 但此类轨迹点实际上并不是在路网中的路段上移动, 因此地图匹配结果往往也是错误的, 因此此类位置异常轨迹点相对其他类型的异常轨迹点更为隐蔽且难以检测, 这也是本文将其和核心位置异常轨迹点统称为隐性位置异常点的原因. 为了检测核心位置异常轨迹点周围的其他隐性位置异常点, 本文提出了一种面向隐性位置异常点检测的聚类方法.

2.3 面向隐性位置异常点检测的聚类方法

在已知核心位置异常轨迹点的条件下, 对于其周围的其他隐性位置异常轨迹点的检测, 通过本文所提出的一种简化的聚类算法对其进行聚类检测. 由于本文仅关注隐性位置异常轨迹点所构成的类簇, 因此所检测的轨迹点数据可分为两类, 一类是属于隐性位置异常类簇的轨迹点, 一类则是不属于上述类簇的轨迹点. 面向隐性位置异常点检测的聚类方法通过迭代的方式仅不断更新隐性位置异常类簇集合.

假设在进行隐性位置异常点检测之前能够获得当前车辆在设定的时段内的完整轨迹点序列. 首先对轨迹序列逐点判断其是否为核心位置异常轨迹点, 设第j个轨迹点 $ {g_j} \in T $ 被确定为核心位置异常轨迹点, 则以 ${g_j}$ 为第j个隐性位置异常类簇的初始的类簇中心 $ {g_{{\text{center}}}} $ , 即作为聚类算法的输入. 隐性位置异常点的聚类方法的伪代码算法1所示.

算法1. 聚类算法伪代码

输入: 车辆轨迹 $\scriptstyle T$ , Geohash网格索引 $\scriptstyle M$ , 类簇中心 $\scriptstyle {g_{{\text{center}}}}$ .

输出: 核心点聚类结果 $\scriptstyle {C_o} $ .

1. 输入车辆行驶轨迹 $\scriptstyle T$ , $\scriptstyle {C_o} \leftarrow {g_{{\text{center}}}}$

2. $\scriptstyle step \leftarrow 1$ // 初始化步数

3. $\scriptstyle j \leftarrow {\textit{indexOf}}(T, {g_{ {\text{center} } } })$

4. While $\scriptstyle j - step > 0 $ do

5.　 If $\scriptstyle {g_{j - step} }{\text{ } }{\rm{is}}{\text{ } }{\rm{not}}{\text{ } }O$ then

6.　　 $\scriptstyle dis \leftarrow ||{g_{ {\text{center} } } } - {g_{j - step} }|{|_{{\rm{greatCircle}}} }$

7.　　 $\scriptstyle {C_{{\text{condi}}}} \leftarrow getCondidates({g_{j - step}}, M)$

8.　　 $\scriptstyle pdis \leftarrow d({g_{j - step}}, {C_{{\text{condi}}}}) $ //计算最小投影距离

9.　　 If $\scriptstyle pdis > dis$ then

10.　　　 $\scriptstyle {C_o}.add({g_{j - step}})$ //将 $\scriptstyle {g_{j - step}}$ 加入异常类簇

11.　　　 $\scriptstyle {g_{{\text{center}}}} \leftarrow updateCenter({g_{j - step}}, {g_{{\text{center}}}})$

12.　　 Else

13.　　　 $\scriptstyle {\bf{break} }$

14.　　 End If

15.　 End If

16.　 $\scriptstyle step \leftarrow step + 1 $ //向前进一步迭代

17. End While

18. return $\scriptstyle {C_o} $

开始以 $ {g_j} $ 为中心按照时间顺序开始向前和向后逐跳遍历其他非核心位置异常轨迹点, 其中伪代码只给出向前遍历, 而向后遍历与向前同理.

首先向前遍历 $ {g_{j - 1}} $ , 如果该轨迹点已经被判定为隐性位置异常轨迹点, 那么直接进入下一次循环, 否则得到 $ {g_{j - 1}} $ 候选路段集合为 $C_{{\text{condi}}}^{(j - 1)}$ , 设 $ d({g_{j - 1}}, C_{{\text{condi}}}^{(j - 1)}) $ 是轨迹点 $ {g_{j - 1}} $ 到其候选路段集合中路段的最小投影距离, $ d({g_{j - 1}}, {g_{{\text{center}}}}) $ 是轨迹点 $ {g_{j - 1}} $ 与 $ {g_{{\text{center}}}} $ 的距离. 如果 $ d({g_{j - 1}}, {g_{{\text{center}}}}) < d({g_{j - 1}}, C_{{\text{condi}}}^{(j - 1)}) $ , 则将 $ {g_{j - 1}} $ 加入隐性位置异常类簇并更新隐性位置异常类簇中心(更新算法如式(1)所示), 然后对 $step$ 加一; 否则视轨迹点 $ {g_{j - 1}} $ 为正常轨迹点, 并结束这一方向的判断.

然后, 用上述方法向后遍历并检测, 直到停止这一方向的检测. 至此聚类算法的向前和向后的迭代过程完成, 最后得到隐性位置异常类簇 $ {C_o} $ .

上述伪代码中, $getCondidates$ 表示第2.2节中基于浮动网格提取轨迹点候选路段方法, $ d({g_{j - step}}, {C_{{\text{condi}}}}) $ 表示根据轨迹点和候选路段集合得到轨迹点到路段的最小投影距离, $updateCenter$ 利用已有的隐性异常轨迹点类簇中心 $ {g_{{\text{center}}}} $ 和新增轨迹点 ${g_{j - step}}$ 来更新 $ {g_{{\text{center}}}} $ . 更新方法如式(1)中, $g_{{\rm{center}}}^{{\rm{old}}}$ 表示当前迭代时隐性位置异常类簇的中心位置, n表示当前迭代时隐性位置异常类簇中点个数. $ {g_{j - 1}} $ 表示当前需加入隐性位置异常类簇的点.

$ g_{{\rm{center}}}^{{\rm{new}}} = \frac{{g_{{\rm{center}}}^{{\rm{old}}} \times n + {g_{j - 1}}}}{{n + 1}} $

(1)

需要说明的是, 每次隐性位置异常点的聚类过程的触发条件是发现新的核心位置异常轨迹点. 在聚类过程中, 如出现时间连续的核心位置异常轨迹点, 则在同一次聚类过程中这些核心位置异常轨迹点不用判断, 自动进入隐性位置异常类簇; 如果隐性位置异常类簇持续不再更新, 则当前聚类过程结束. 然后, 继续从上次向后遍历检测的最后一个轨迹点继续开始搜索新的核心位置异常轨迹点, 一旦确定有新的核心位置异常轨迹点, 则触发新的隐性位置异常点的聚类过程.

2.4 并行化隐性位置异常轨迹点检测方法

面对持续增长的海量轨迹数据, 为了更高效地实现隐性位置异常轨迹点的检测, 本文提出了一种并行化隐性位置异常轨迹点检测方法.

要实现并行化隐性位置异常轨迹点检测, 首先需要对数据进行合理的分区, 车辆轨迹数据按照分区策略进行分布式存储. 本文以产生轨迹数据的车辆的车牌号的hash值为key对数据进行分区, 同一辆车的轨迹数据保存在同一数据分区. 由于分布式存储系统所能够支持的最大分区数是一个预设参数, 实际中车辆数量会超过系统的最大分区数, 在这种情况下, 采用式(2)计算轨迹数据分区的key:

$ key = Hashcode(id){\text{ }}{\rm{mod}}{\text{ }}m $

(2)

其中, $id$ 表示车辆的车牌号; Hashcode()表示计算hash值方法; m为系统最大分区数. 数据分区后, 一个分区中可能存在不同的车辆轨迹数据, 可通过使用分布式计算环境中的算子 $groupBykey$ 根据轨迹数据的id, 将同一个分区内的车辆的轨迹数据聚合成不同的组后再进行分析. 对聚合后的每组轨迹数据执行算法2中方法进行隐性位置异常轨迹点检测. 具体如下.

算法2. 隐性位置异常轨迹点检测伪代码

输入: 轨迹数据 $\scriptstyle T$ , Geohash网格索引 $\scriptstyle M$ .

输出: 检测的异常点集合 $\scriptstyle {C_o} $ .

1. 输入车辆行驶轨迹 $\scriptstyle T$ , $\scriptstyle {\textit{clusterps}} \leftarrow \varnothing$ , $\scriptstyle {C_o} \leftarrow \varnothing$

2. $\scriptstyle ts \leftarrow T.groupByKey(cid)$

3. For $\scriptstyle {\rm{each}}{\text{ } }t{\text{ } }{\rm{in}}{\text{ } }ts$ do

4.　 For $\scriptstyle i = 0{\text{ } }{\rm{to}}{\text{ } }t.len$ do

5.　　 $\scriptstyle {C_{ {\text{condi} } } } \leftarrow getCondidates({g_i}, M)$

6.　　 If $\scriptstyle {C_{ {\text{condi} } } } = \varnothing$ then

7.　　　 $\scriptstyle {C_o}.add({g_i})$ //将轨迹点加入异常类簇

8.　　　 $\scriptstyle clusterps.add({g_i})$ //将轨迹点加入核心位置异常轨迹点集合

9.　　 End If

10.　 End For

11. End For

12. For $\scriptstyle {g_{ {\text{center} } } }{\text{ } }{\rm{in}}{\text{ } }{\textit{clusterps}}$ do

13.　 $\scriptstyle {C_o} \leftarrow clustering(T, {g_{{\text{center}}}})$ //进行聚类检测

14. End For

15. return $\scriptstyle {C_o}$

(1) 针对轨迹数据 $T$ , 通过分组函数将每辆车的轨迹分到一个组, 针对每个车辆轨迹的轨迹点, 求取其候选路段集合, 如果候选路段集合为空, 那么将该轨迹点识别为隐性异常轨迹点, 并将其加入到核心位置异常点集合中;

(2) 遍历核心位置异常轨迹点集合, 针对每一个核心位置异常轨迹点, 进行算法1的隐性位置异常点的聚类方法并返回异常类簇, 最终返回所有的隐性位置异常轨迹点.

算法2中方法 $clustering()$ 是运用第2.3节中所提的聚类方法, 在获得一个新的核心位置异常轨迹点后, 检测该轨迹点附近是否存在其他隐性位置异常轨迹点并构建对应的隐性位置异常类簇.

3 测试及结果分析

本实验章节旨在评估所提出的隐性位置异常轨迹点检测方法的性能. 通过合适的评价指标来检测本文提出方法的准确性; 通过对比单机计算和并行计算下的计算延迟, 我们将探讨并行化对算法性能的影响. 通过这些实验, 我们能够验证本文方法在隐性位置异常轨迹点检测方面的准确性以及效率.

3.1 实验设置

(1) 测试数据

实验数据采用西安市市区路网数据以及西安市出租车真实GPS移动数据. 西安市市区路网包含24050条路段, 每条路段由路段编号, 路段经纬度坐标序列、路段长度以及路段类别组成. 轨迹数据包含了5辆车的连续轨迹序列, 总计大约12000个轨迹点, 轨迹数据的采样间隔为30 s, 每个轨迹点包含5个属性, 车辆车牌号、采样时刻、经度、纬度和速度. 对于上述轨迹数据, 采用人工标定的方法, 对真实的隐性位置异常轨迹点进行了标定, 其中将397个轨迹点标记为隐性位置异常轨迹点.

(2) 路网网格化和Geohash网格索引建立

实验使用Geohash网格法对西安市市区进行了网格划分, Geohash网格的编码长度设置为7字符长度, 从而将西安市区大约划分为97152个7字符Geohash网格, 每个的网格约为 $152\;{\rm{m}} \times 152\;{\rm{m}}$ 的矩形区域.

基于上述Geohash网格设定参数, 对于每条路段的经纬度坐标序列中的每个坐标点, 离线计算其对应的Geohash网格编码. 然后, 根据计算结果构建Geohash网格索引. 由于路网路段在不同区域分布密度不同, 有些网格中不存在路段. 对于所覆盖的路段集合为空的网格, 在索引中不进行记录, 最终得到Geohash网格索引共包括27956个有效Geohash网格.

(3) 测量指标

为了验证本文所提的隐性位置异常轨迹检测方法的效果, 本文采用了精确率(precision), 召回率(recall), F1-score^[12]来评价实验效果, 其中F1-score是对精确率和召回率的综合考量. 将正确识别的隐性位置异常轨迹点的情况定义为真正例(TP), 将检测是隐性位置异常轨迹点但实际却不是的情况定义为假正例(FP), 将检测为不是隐性位置异常轨迹点且实际也不是的情况定义为真反例(TN), 将检测出不是隐性位置异常轨迹点但实际是的情况定义为假反例(FN). 各指标的计算公式如下:

$ precision = \frac{{TP}}{{TP + FP}} $

(3)

$ recall = \frac{{TP}}{{TP + FN}} $

(4)

$ F1 {\textit{-}} score = \frac{{2 \times precision \times recall}}{{precision + recall}} $

(5)

3.2 实验结果

(1) 单机测试结果

1) 隐性位置异常轨迹点检测示例

如图3所示, 举例部分轨迹 ${g_{455}} - {g_{469}}$ 的检测结果, 其中方格为Geohash网格, 其中人工标定的异常轨迹点为 ${g_{457}} - {g_{465}}$ , 本文检测方法的检测结果为g₄₅₇−g₄₆₇. 从轨迹点 $ {g_{455}} $ 开始, 由于轨迹点 ${g_{455}} - {g_{457}}$ 离路段较近, 候选路段集合不为空, 所以被视为正常轨迹点, 而 ${g_{458}} - {g_{465}}$ 通过浮动网格筛选的候选路段集合为空, 被视为核心位置异常轨迹点, 但是在以 ${g_{458}}$ 为核心的聚类前向遍历的过程中, 因为 $ {g_{457}} $ 距离聚类中心 ${g_{458}}$ 更近, 所以也会将 $ {g_{457}} $ 识别为一个异常轨迹点. 以此类推, 轨迹点 $ {g_{466}} $ 、 $ {g_{467}} $ 虽然不是核心异常轨迹点, 但是其会被 ${g_{465}}$ 向后遍历识别为隐性异常轨迹点; 所以示例中的轨迹被识别为隐性异常轨迹点的为 ${g_{457}} - {g_{467}}$ . 虽然该实例对轨迹点 $ {g_{466}} $ 、 $ {g_{467}} $ 识别错误, 但从结果来看, 这对于后续的地图匹配等预处理影响不大, 但是如果使用移动特征异常轨迹点的判断方法来识别此轨迹段, 则难以检测其中的异常轨迹点, 因为这些轨迹点的速度, 加速度等车辆移动特征并没有超出正常范围.

2) 准确率分析

为测试不同边长浮动网格, 对检测效果的影响, 本文在测试时将浮动网格边长L分别设置为Geohash网格的相同边长、3/4边长和1/2边长, 即152 m, 114 m和76 m, 测试结果如图4.

在图4中, 纵轴表示评价指标得分, 横轴表示不同的评价指标, 不同图例对应于浮动网格边长L不同取值情况下的测试结果. 测试结果表明, 随着L的增加, 精确率逐渐增加, 召回率逐渐下降, F1-score在L=114 m时取得最好分数. 当浮动网格较小时, 在对轨迹点进行候选路段筛选时, 所确定的筛选区域即浮动网格4个顶点对应的Geohash网格范围相对较小, 有利于核心位置异常点的判断, 造成漏检的情况较少; 但同时易将一些偏离路段较远的正常轨迹点错误的标定位隐性位置异常轨迹点, 这样就存在纳伪现象, 造成精确率偏低. 当浮动网格较大时, 纳伪现象减少, 精确率呈现上升趋势, 但同时轨迹点候选路段筛选区域变大, 容易造成漏检, 因此召回率则呈现下降趋势. 在测试中, 当令浮动网格边长为L=114 m时, F1-score可达到最高值即0.91, 此时在准确率和召回率实现了折中均衡.

3.3 检测方法并行化性能测试

(1) 测试环境

为了能够处理大规模轨迹数据的隐性位置异常点检测, 本文在第2.4节提出了一种并行化隐性位置异常轨迹数据检测方法, 该方法在目前流行的大数据计算框架Spark环境中进行实现. 为了模拟大数据集群环境, 本文在Docker容器中部署了Spark+HDFS集群环境, 包括6个Spark Worker节点和3个HDFS DataNode节点, 其中Spark Worker节点负责所提方法的分布式并行计算, HDFS DataNode节点负责测试数据的分布式存储. 测试的硬件环境为4核CPU, 16 GB内存, 1 TB硬盘.

(2) 测试数据及数据分区数的确定

为了检测本文所提的并行化隐性位置异常轨迹数据检测方法的性能, 本文采集了西安市589辆出租车共计150万条轨迹点数据.

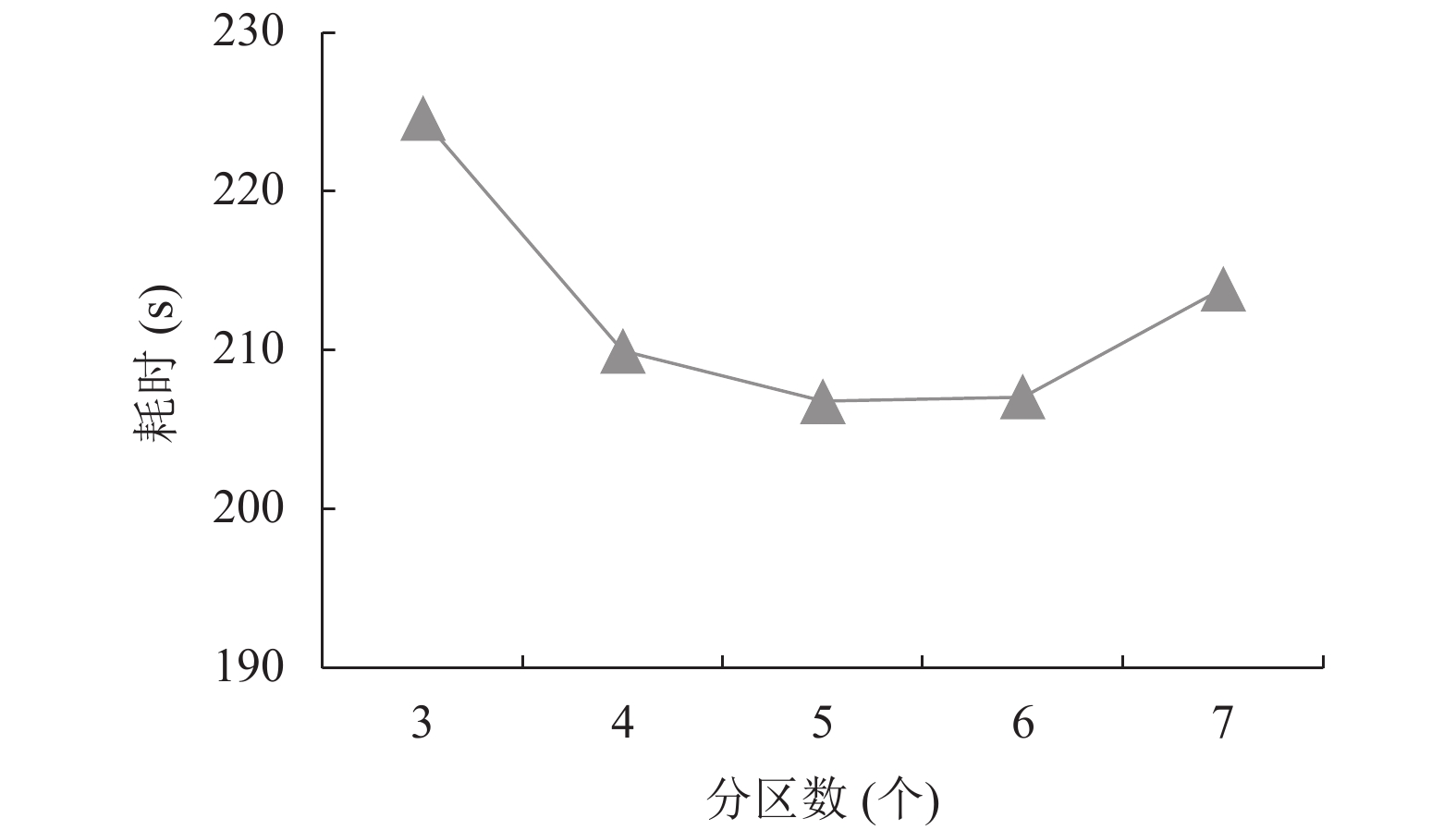
在分布式环境进行计算时, HDFS分区数对计算性能也会产生较大影响. 本文首先对150万条轨迹点数据, 在HDFS设置了3, 4, 5, 6, 7个分区数的情况下, 分别测试了本文所提方法的执行时间, 测试结果如图5所示.

由测试结果显示当CPU核数固定的情况下, 当分区数设置较大时, 则对于各个分区的计算就需要付出额外的调度时间损耗; 当分区数设置较小时, 则单个分区的数据量较大, 单节点的计算延迟就会增加, 从而导致总体计算延迟的增加. 在本次测试中, 当HDFS分区数为5时, 时间性能最好.

(3) 并行计算加速比测试及结果分析

本文将HDFS的分区数设置为5, 分别采用30万, 60万, 90万, 120万, 150万条轨迹点数据进行加速比指标测试. 加速比指标的计算采用如下公式:

$ sp = \frac{{{t_{{\text{single}}}}}}{{{t_{{\text{parallel}}}}}} $

(6)

其中, ${t_{\text{single}}}$ , ${t_{\text{parallel}}}$ 分别表示单机和并行化计算延迟.

不同数据规模条件下的单机和并行化计算延迟及加速比测试结果如表2所示, 并在图6中进行展示. 从中可以看出, 单机和并行方法的计算延迟都随数据量的增长而增长, 但并行方法增长幅度较单机慢; 并且在同等规模的隐性位置异常轨迹数据检测上, 并行化方法比单机方法要快接近一倍, 那是因为检测方法的并行化能够并行化数据, 同时利用多个计算资源进行任务处理, 提高了计算效率, 能够较好地适应大规模隐性位置异常轨迹数据的检测需要.

4 结论

在对大量实际轨迹数据进行分析研究的过程中, 我们发现了一种特殊的位置异常轨迹数据并将其称之为隐性位置异常轨迹数据, 其移动特征参数往往在正常的阈值范围内, 但实际这些轨迹数据并不是车辆在路网路段上行驶产生的, 而是在某些特定区域的内部道路上行驶产生的, 这些内部道路在电子地图的路网数据中实际并不存在. 隐性位置异常轨迹数据通过常规的异常轨迹检测方式难以发现, 同时路网中根本不存在和这些隐性位置异常轨迹数据对应的真实路段, 如果直接对其进行地图匹配则显然又会出错, 从而对后续的轨迹数据分析产生负面影响. 根据隐性位置异常轨迹数据的局部聚集性特征, 本文提出了面向隐性位置异常轨迹数据的检测方法并实现了并行化处理, 测试结果显示了所提方法的有效性. 异常轨迹数据检测是轨迹数据分析的一个基本环节, 本文所提方法是对常规的异常轨迹数据检测方法的一种有益补充. 同时, 本文所提方法仅利用了轨迹数据的时空特征进行异常检测, 结合更多的语义特征以实现更为高效的异常轨迹检测是下一步的研究方向.