2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
随着5G无线网络的快速发展, 越来越多要求低时延的计算密集型应用, 如智慧城市、无人驾驶汽车, VR, 云游戏等领域开始加速发展, 网络数据量急剧增加[1]. 这些领域的发展使用户对计算服务和质量有了新的要求. 但是对于移动设备而言, 其本身的计算能力是有限的, 如果提升移动设备的计算能力和电源储量[2,3], 必然会使移动设备的体积和价格大幅增长, 这不是用户希望的. 因此为了降低用户使用移动设备的成本, 同时让用户能够实时享受高性能高质量的计算服务, 移动边缘计算(MEC)被提了出来[4]. MEC不同于云计算, 云计算是将用户的计算任务放到云端服务器中去运行, 但是云端服务器一般都会距离用户所在位置很远, 这会造成一定的通信延迟, 而且当大量用户同时卸载时, 还会造成远程链路和核心网络的拥塞, 使用户体验变差. 移动边缘计算是将服务器放置在距离基站比较近的位置, 使得用户任务可以就近在网络边缘处被执行, 这会在很大程度上降低通信延迟和能耗并节省带宽. 移动边缘计算的这一特性非常契合5G高容量、低延时、低能耗的通信要求, 因此已被视作是5G发展的关键使能技术之一.
MEC是C-RAN (云无线接入网)的一种新范式, 它可以通过部署高性能服务器来提高网络边缘的计算能力. MEC服务器分布在靠近移动用户的地方, 移动用户可以通过无线信道将计算任务卸载到MEC服务器. 通过计算卸载, 移动用户可以显著减少应用的经历时延, 提高服务质量. 因此, 计算卸载和计算资源分配作为MEC系统的一个关键问题, 引起了人们极大的兴趣. 充分利用MEC服务器的计算资源, 合理决策用户任务是否应该卸载到边缘服务器, 以及卸载到哪一个边缘服务器, 提高边缘服务器的资源利用率和服务质量, 将为智慧城市、无人驾驶汽车等行业提供更有稳定, 更高效的基础计算服务, 有助于这些应用领域的快速发展.
MEC计算卸载的实验很难在现实网络中进行, 那需要花费巨大的成本, 所以MEC计算卸载的研究需要使用仿真环境来进行模拟, 但在MEC计算卸载目前的研究中, 大多数仿真实验都只考虑用户设备(UE)数量和边缘服务器数量, 他们并不考虑一个UE可能有多个计算任务, 而且大多数实验计算任务都是固定的, 但在实际环境中, UE数量是动态变化的, 每个UE的计算任务也是动态变化的, 所以只用静态数据测试卸载决策算法的性能是远远不够的, 因此如何设计一个更加精确的仿真实验环境也是需要考虑的问题. 另一方面随着人工智能领域的快速发展, 深度强化学习已经在自然语言处理、计算机视觉、机器人和游戏等领域进行了广泛应用并取得了较好的表现. 因此, 近几年国内外将深度强化学习应用于MEC计算卸载的研究也越来越多. 但是这些研究大多都只考虑降低UE用户的能源消耗和计算时延[5,6], 这样就会导致UE用户的计算资源有可能被大量浪费, 而随着MEC边缘服务器计算任务的饱和, 其他急需使用MEC边缘服务器的用户将无法正常进行计算卸载. 本研究主要贡献如下.
1)设计并实现了一个考虑UE用户数量可变, UE用户距离边缘服务器距离不定, UE用户任务数量及大小随机可变以及信号传输过程噪声问题的仿真实验环境.
2)在TD3的基础上提出了一种针对MEC计算卸载的改良版TD3模型, 用于解决离散动作空间的MEC计算卸载问题, 提高MEC计算卸载的效率和正确率, 以及边缘设备资源利用率.
3)在自主设计的仿真实验环境中测试对比了基线DDPG、TD3和结合本地优先策略的TD3的决策效果并进行了分析总结.
1 相关工作近年来, 国内外已经有许多关于MEC计算卸载的研究. 文献[7]提出了一种增强型多种群多目标鲸鱼优化算法, 并为了避免种群多样性的损失, 提出了一种新的领导者选择算法来引导种群搜索, 该算法可以很好地提高系统的响应速度和能源效率; 文献[8]对遗传算法, 差分进化算法, 粒子群优化算法和混合蛙跳算法4种算法进行了研究, 这些算法都具有全局搜索能力、鲁棒性强等优点, 可以有效地解决计算卸载问题; 文献[9]将计算卸载问题建模为了一个混合整数非线性规划问题, 并采用基于RLT的分支定界方法进行高效求解, 该算法所选择的卸载方案在延迟时间和能量消耗方面都具有较好的性能. 文献[10]在Kernighan Lin算法的基础上, 提出了一种基于谱图划分的图划分方法. 该方法通过将应用程序分解成多个子任务, 然后将这些子任务分配到不同的设备上进行计算, 提高系统的响应速度和能源效率. 文献[7–10]所使用的方法都没有考虑网络环境发生变化时决策方案应该如何进行改变, 而使用深度强化学习模型则可以根据网络环境的改变实时训练决策模型来动态适应环境变化, 从而增强模型的适应能力. 文献[11]提出了一种基于Q-Learning的机会式边缘计算中的计算卸载时间优化方法. 该方法通过不断学习, 自适应地调整计算卸载策略, 提高系统的响应速度和用户体验质量. Q-Learning是一种基于强化学习的优化算法, 可以通过学习和试错来寻找最优策略. 但是Q-Learning算法更新速度慢, 且预见能力不强. 文献[12] 提出了一种基于深度强化学习的计算卸载和资源分配算法AHP-DQN算法. 该算法通过学习决策动作和网络环境, 自动调整资源分配策略, 提高系统的响应速度和能源效率. 文献[13]提出了一种基于Dueling DQN的半在线的计算卸载模型, 通过强化学习来获取未知的环境信息. 该算法在不同的服务器场景下均能实现负载均衡. 文献[14]提出使用LSTM(长短期记忆)算法预测下一时隙资源利用状态, 然后使用一种分布式多智能体深度强化学习算法来解决计算卸载问题, 该算法有效地解决了计算卸载问题. 文献[15]提出了一种适用于连续动作空间的基于深度强化学习的自适应计算卸载算法, 并考虑了无线信道的多样性和相邻时隙之间的可用带宽, 该算法在随机环境中优于Dueling DQN和贪婪策略. 文献[12–15]使用了基于深度Q网络(DQN)的强化学习方法来进行计算卸载, 但是DQN对训练数据要求很高, 并且容易出现过估计问题.
以上这些研究都是只考虑降低延迟或者能耗, 并且UE用户数也是固定的, 每个UE也只有一个计算任务, 而本研究主要考虑在蜂窝网络中, 当UE数量和UE卸载任务不断变化的条件下, 考虑最大化资源利用率, 最小化卸载决策错误率的情况下, 设计实现一个本地资源优先使用的情况下的结合改进TD3的卸载决策算法. 实验表明该算法资源利用率比使用基线DDPG算法和TD3算法进行卸载决策有更高的资源利用率和更低的错误率.
在本研究中我们考虑采用本地优先的策略再结合深度强化学习进行计算卸载决策. 采用这种方法可以优先使用UE用户的计算资源, 在UE用户计算资源匮乏或者能源不足时, 在进一步考虑将计算任务进行卸载.
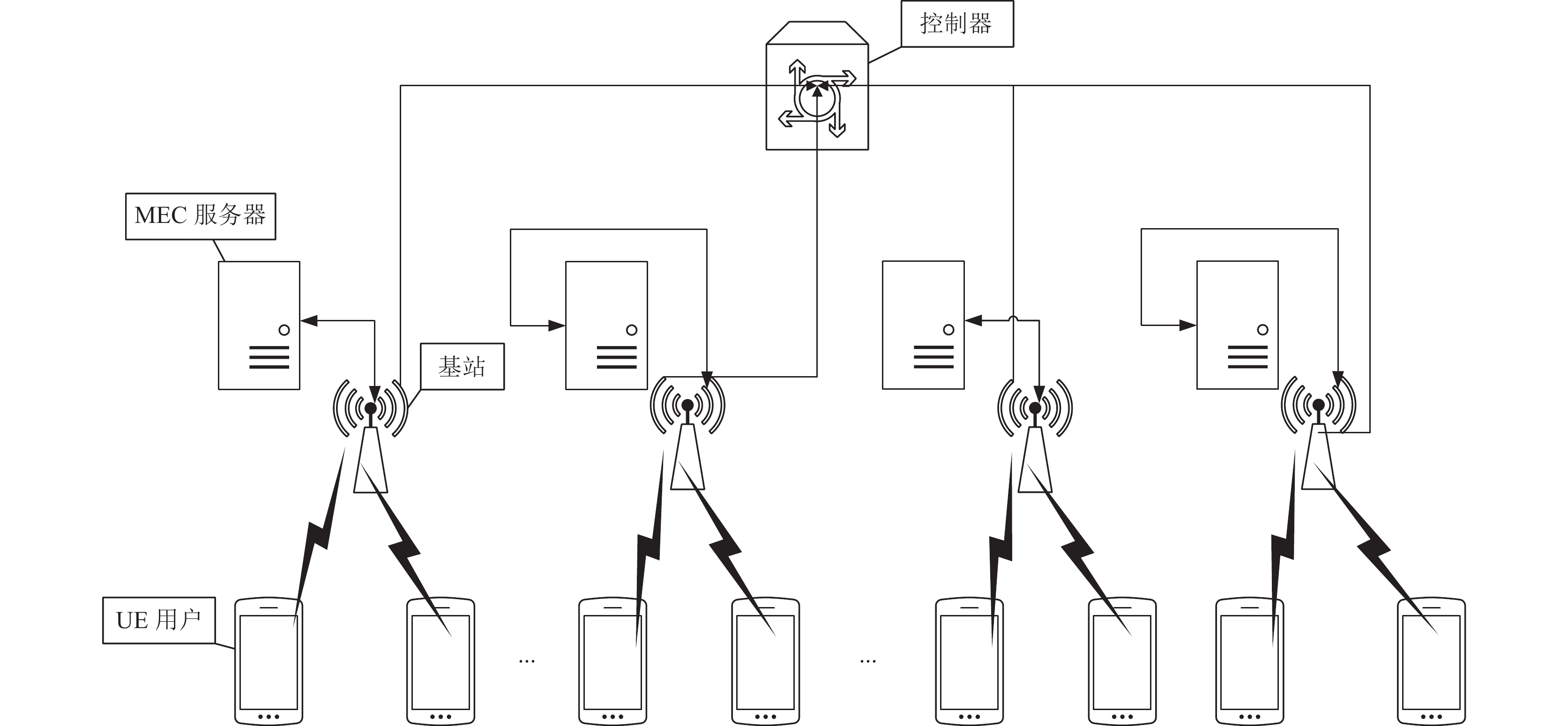
2 系统架构和问题建模 2.1 系统架构本研究将搭建一个MEC仿真环境, 该仿真环境中, 边缘服务器的性能各不相同, UE设备的性能也各不相同, 仿真环境还添加了UE到各个边缘服务器的距离, 除此之外还模拟了蜂窝网络的噪声来尽可能增加仿真环境的准确性. 仿真环境的网络模型如图1所示. 该仿真环境共有4部分组成, 分别是UE用户端、蜂窝网络基站、MEC服务器和总控制器. 其中UE用户用
|
图 1 网络架构图 |
控制器会维护一个MEC服务器列表用
本实验模拟移动通信中的使用的正交频分多址(OFDMA)来进行UE和基站之间的通信, 但是我们考虑每一个UE用户只和距离自己最近的基站进行直接通信, 因此不考虑使用相同子信道移动用户之间的影响且与同一个基站连接的用户均分基站带宽, 因此用户带宽可以表示为
| $ {L_{dB}} = 128.1 + 37.6 \times \lg \left( {dist} \right) $ | (1) |
| $ {h_{im}} = {10^{\frac{{{A_{dB}} - {L_{dB}} - {P_{dB}}}}{{10}}}} $ | (2) |
其中,
| $ {N_0} = {n_0} + 10\lg \left( {{B}} \right) $ | (3) |
其中,
| $ {\textit{SINR}}= \frac{P \times {h}_{im}}{{N}_{0}} $ | (4) |
| $ C= B \times \mathrm{ln}\left(1+{\textit{SINR}}\right) $ | (5) |
定义每一个UE的CPU计算频率为
| $ {T}_{n}^{{\rm{local}}} = {c}_{i} \times \frac{sum}{{F}_{n}^{{\rm{local}}}} $ | (6) |
其中,
| $ E_n^{{\rm{local}}} = \mu {(F_n^{{\rm{local}}})^2}{c_i} $ | (7) |
其中, μ为有效转化因子, 本研究中有效转化因子设为
| $ C_n^{{\rm{local}}} = it \times T_n^{{\rm{local}}} + ie \times E_n^{{\rm{local}}} $ | (8) |
其中,
| $ \left\{ {0 \leqslant it \leqslant 1, \; 0 \leqslant ie \leqslant 1, \; it + ie = 1} \right\} $ | (9) |
MEC服务器中的任务由UE用户卸载得到, 必须考虑任务卸载过程中的传输时延, 由式(5)我们可以算出数据的传输速率, 根据传输速率以及任务大小我们可以计算出传输时延
| $ T_n^{{\rm{up}}} = \frac{S}{C} $ | (10) |
其中,
| $ E_n^{{\rm{up}}} = {p_n}T_n^{{\rm{up}}} $ | (11) |
MEC服务器完成任务所要花费计算时间定义为
| $ {C}_{n}^{{\rm{edge}}}=it\left({T}_{n}^{{\rm{up}}}+\text{ }{T}_{n}^{{\rm{edge}}}\right)+ie\left({E}_{n}^{{\rm{up}}}+{E}_{n}^{{\rm{edge}}}\right) $ | (12) |
为降低所有UE用户的所有任务的总计算时延和能耗, 提高MEC服务器和UE用户移动设备的资源利用率, 以本地计算优先结合控制器集中控制的方式最大化资源利用率, 最小化任务平均计算成本. 系统总资源利用率定义为
| $ RU= \frac{{{\displaystyle \sum }}_{i\in m}C{R}_{i}^{{\rm{edge}}}+{{\displaystyle \sum }}_{i\in m}C{R}_{i}^{{\rm{local}}}}{{{\displaystyle \sum }}_{i\in m}{R}_{i}^{{\rm{edge}}}+{{\displaystyle \sum }}_{i\in m}{R}_{i}^{{\rm{local}}}} $ | (13) |
其中,
| $ AC= \frac{{{\displaystyle \sum }}_{i\in n}{a}_{i}{C}_{i}^{{\rm{local}}}+{{\displaystyle \sum }}_{i\in n}(1-{a}_{i}){C}_{i}^{{\rm{edge}}}}{n} $ | (14) |
其中,
| $ \left\{ {\begin{array}{*{20}{l}} {\max \left( {RU} \right)} \\ {\min \left( {AC} \right)} \end{array}} \right. $ | (15) |
为了防止UE设备以及该MEC服务器过载, 所以在任务卸载过程中应该满足一下约束:
| $ {\rm{s.t.}} \left\{\begin{array}{l}{C}_{1}:{a}_{ij}\in \left\{0, 1\right\}\\ {C}_{2}:0 < {P}_{i} < {P}_{i, {\rm{max}}}\\ {C}_{3}: {T}_{i} < {L}_{i}\\ {C}_{4}:{F}_{i}^{{\rm{local}}} < {F}_{i, {\rm{max}}}^{{\rm{local}}}, \; {F}_{j}^{{\rm{edge}}} < {F}_{j, {\rm{max}}}^{{\rm{edge}}}\\ {C}_{5}:{\displaystyle \sum }_{j=1}^{m}{a}_{ij}=1, \forall i\in n\end{array}\right. $ | (16) |
其中,
TD3算法又叫做双延迟深度确定性策略梯度, 他是在DDPG的基础上提出来的, TD3的目的是解决DDPG已经学习好的Q函数显著高估Q值导致策略被破坏的问题. TD3相对于DDPG主要引入了3个技巧来解决这个问题.
1) 采用截断的双Q学习, TD3会同时学习两个Q函数, 两个Q函数都使用一个目标, 两个Q函数中较小的值会被作为Q-target.
2) 采用延迟的策略更新, TD3没有采用同步训练动作网络和评价网络的方式, 而是以较低的频率更新动作网络, 以较高的频率更新评价网络.
3) 采用目标策略平滑, TD3在目标动作中加入噪声, 来使策略更难利用Q函数的误差.
本研究对TD3的改进主要涉及以下3个方面.
1) 由于TD3是用于连续动作空间的强化学习算法, 而本研究将计算卸载问题抽象为离散空间中的决策问题, 所以需要对TD3进行改进, 使其能够用于离散空间的决策问题, 因此本研究在TD3中加入了Softmax方法用来使TD3的连续动作转化为离散动作进行决策.
2) 本研究根据MEC计算卸载的目的, 定义了新的状态空间和奖励函数, 该状态空间主要考虑MEC服务器的剩余资源, 而奖励函数则分为奖励和惩罚两个部分, 这样可以使模型能够向着更高效的决策方向进行学习.
3) 将本地优先策略和TD3算法相结合, 以此来最大化总体资源利用率, 使更多的用户卸载可以得到满足.
本节将对卸载决策模型的设计和改进TD3与本地优先的决策算法进行详细介绍.
3.1 卸载决策模型TD3训练过程可以转化为MDP模型, 其中MDP模型中的状态主要设计3个: 1) 环境状态
1) 状态: 状态主要考虑当前MEC服务器的剩余资源, 单个MEC服务器的剩余资源计算如下:
| $ {\textit{SR}}_i^{{\rm{edge}}} = \left\{ {{\textit{SM}}_i^{{\rm{edge}}}, {\textit{SF}}_i^{{\rm{edge}}}} \right\} $ | (17) |
其中,
| $ s\left( t \right) = \left[ {{\textit{SR}}_1^{{\rm{edge}}}\left( t \right), \cdots , {\textit{SR}}_n^{{\rm{edge}}}\left( t \right)} \right] $ | (18) |
2) 动作: 动作主要是决策将任务卸载到哪一个MEC服务器中, 由于本研究采用本地优先的策略, 所以当任务请求卸载时表明本地资源或能量已经不能够支持计算任务, 因此只能选择卸载到某个MEC服务器中. 考虑卸载到所有MEC服务器的概率之和为一, 那么动作空间为:
| $ a\left(t\right)=\left[{a}_{1}^{{\rm{edge}}}\left(t\right), \cdots , {a}_{n}^{{\rm{edge}}}\left(t\right)\right]\text{, }{\displaystyle \sum }_{i=1}^{n}{a}_{i}^{{\rm{edge}}}=1 $ | (19) |
3) 奖励: 考虑当智能体卸载的任务超时, 或者所选择的MEC服务器剩余资源不足时为决策失误, 这时应该为惩罚, 而当任务卸载成功时, 我们应最大化资源利用率, 最小化平均计算成本, 所以奖励函数定义为:
| $ \begin{array}{*{20}{c}} {r\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {\mu \dfrac{{RU + 1}}{{AC + 1}}, \;\;\; {T_i} \leqslant {L_i}} \\ { - \mu \dfrac{{RU + 1}}{{AC + 1}}, \; {T_i} > {L_i}} \end{array}} \right.} \end{array} $ | (20) |
其中,
TD3适用于连续动作空间的决策问题, 但对于MEC计算卸载而言, 选择一个MEC服务器进行卸载并不是连续动作空间问题, 而是离散动作空间, 为了解决这个问题需要改进TD3的动作选择机制, 采用
| $ \begin{array}{*{20}{c}} {{\textit{Softmax}}\left( a \right) = \dfrac{{\exp \left( {{a_i}} \right)}}{{\displaystyle\mathop \sum \nolimits_{j = 1}^n \exp \left( {{a_j}} \right)}}} \end{array} $ | (21) |
加入
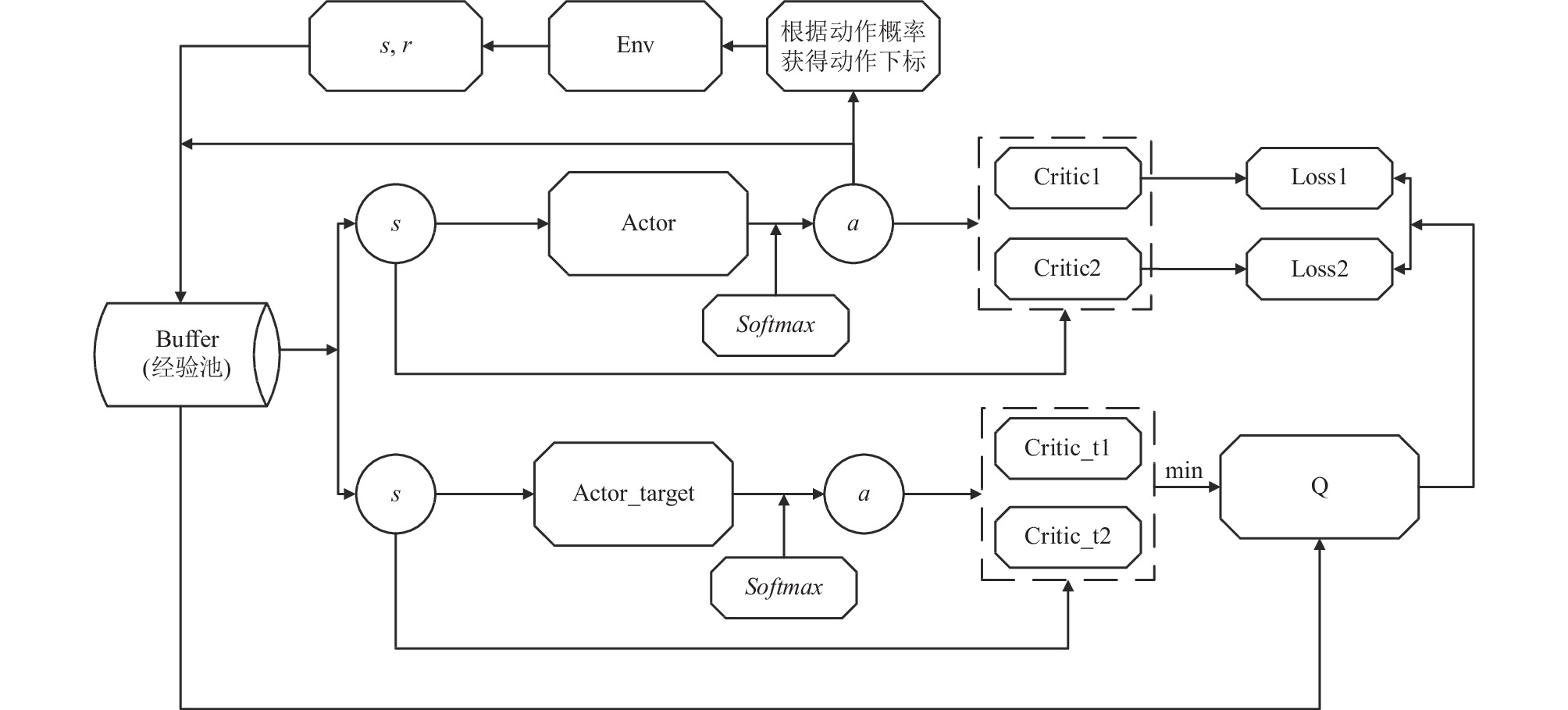
|
图 2 TD3算法架构图 |
首先进行初始化, 初始化网络结构和经验池后, 开始填充经验池, 经验池填满之前通过使用actor网络获得随机的动作进行决策并将环境状态、动作、奖励和下一个状态存入经验池, 经验池填充结束后, 每次执行动作就从经验池中进行随机采样, 然后利用样本进行学习, 更新actor和critic网络, 在使用软更新策略更新目标网络.
算法1. 改进TD3
1)初始化actor和critic网络
2)初始化actor_target和critic_target网络
3) 初始化经验池Buffer
4) for episode = 1, M do
5) 初始化环境Env
6) for t = 1, T do
7) 从actor网络中获取带有噪声的动作a(t), 在使用Softmax(a(t))获得概率分布
8) 根据动作概率进行采样将连续动作转化为离散动作_a(t)
9) 执行动作_a(t), 得到奖励r(t)和下一个状态s(t+1)
10) 将(s(t), a(t), r(t), s(t+1))存放进Buffer
11) if Buffer中样本数目大于batch size then
12) 从Buffer中随机采样batch size个样本进行训练
13) 更新critic网络和actor网络
14) 更新critic_target网络和actor_target网络
15) end if
16) end for
17) end for
4 实验结果 4.1 实验设置仿真实验使用的环境参数为Python 3.8, PyTorch 2.0.0+cu118, CUDA 12.1和Windows 10. 显卡为GTX1050Ti, 4 GB显存和24 GB内存. 仿真环境设有4个MEC服务器和可变个数的UE设备. 改进的TD3算法中的Actor网络和Critic网络均为4层全连接神经网络, Actor的两个隐藏层神经元个数分别为512和256, Critic的两个隐藏层神经元个数为256和128. Actor输出层使用Softmax进行激活, 其他激活函数均使用ReLU激活函数. 梯度下降优化算法为Adam优化器. Actor和Critic网络的学习率分别为0.0003和0.001. 目标网络采用软更新, 更新速率tau=0.005. 经验回放池大小设置为10000. 折扣因子γ=0.99. 仿真环境中UE设备和MEC设备等的仿真参数设置如表1所示.
| 表 1 仿真环境参数设置 |
本实验对比了一下3种卸载策略, 分别是3种由非本地优先的卸载策略DDPG算法、TD3算法和结合本地优先的TD3卸载算法.
4.2 实验结果对比分析仿真实验环境中UE设备随着时间动态生成计算任务, 通过这些任务来寻来你卸载决策模型, 本实验主要对比了随着任务数量不断增多, 模型决策的错误率和平均资源利用率的变化情况.
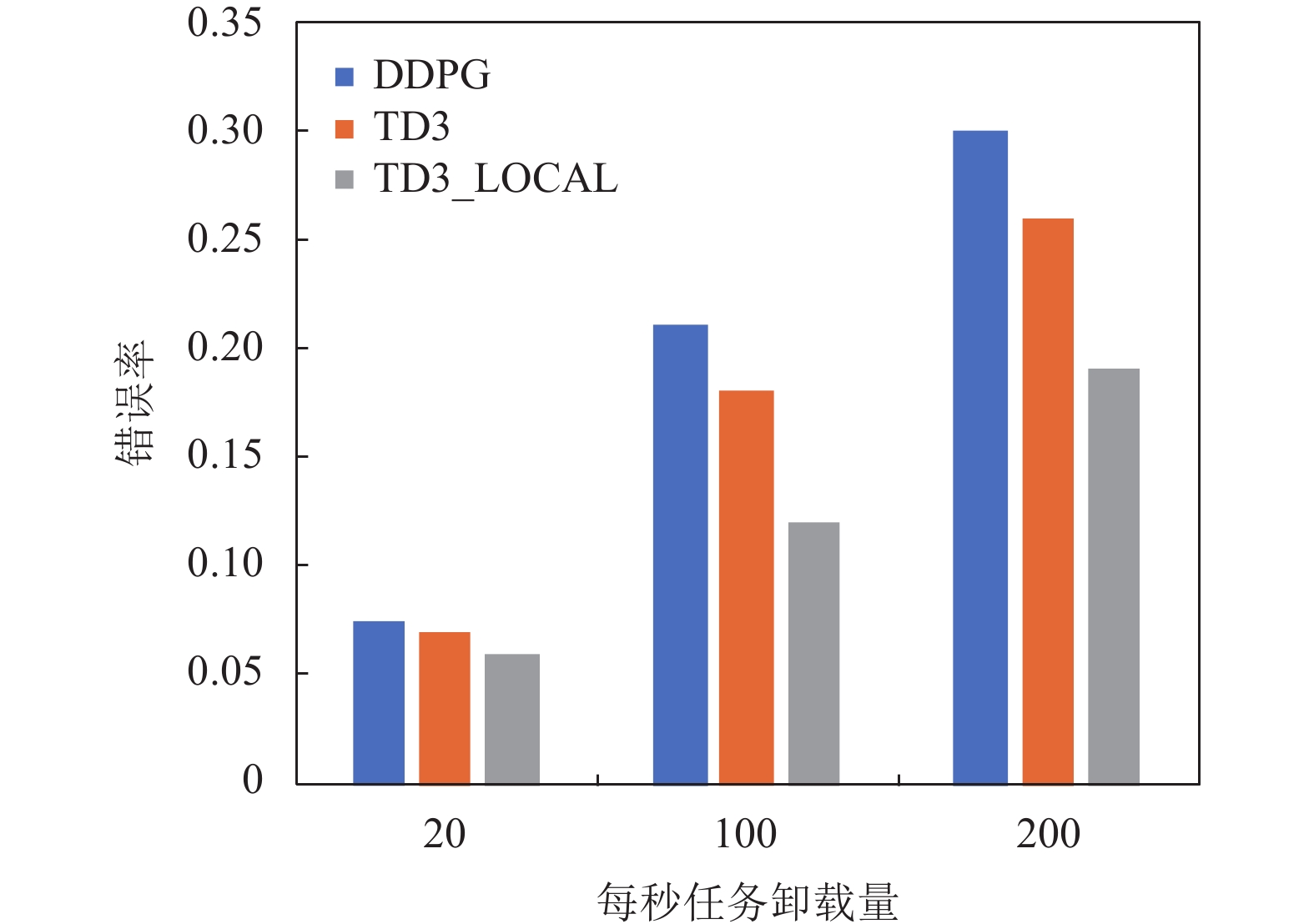
1) 本研究工作了记录了3组不同卸载频率下的错误率变化情况, 每组实验都执行了40万次计算卸载, 且每进行20次卸载决策记录一次决策错误率. 第1组实验控制任务卸载频率为20个/s, 在该频率下3个模型的训练结果如图3所示. 根据图3可以看出, 该频率下由于卸载任务比较缓慢, 3个模型决策错误率相差不大, 但是结合本地优先的TD3算法比DDPG算法决策错误率, 下降了1.5%. 第2组实验我们将卸载频率上升至100个/s, 实验结果如图4所示, 此时3个决策模型的错误率都开始增大, 其中DDPG算法增大了13.5%, TD3增大了11%, 而结合本地优先的TD3算法只增大了6%, 在该频率下结合本地优先的TD3算法决策错误率比DDPG降低了9%. 紧接着本实验又将卸载频率上升到200个/s, 实验结果如图5所示, 3个决策模型错误率又有了提升, 但在该频率下结合本地优先的TD3算法的决策错误率要比DDPG算法降低11%. 图6所示是对比了3个模型在3组实验中的最终决策错误率, 由图6可以看出, 随着任务卸载频率的上升, 3个模型的决策错误率都增加了, 但是结合本地优先的TD3算法能够表现出更好的决策效果.

|
图 3 卸载频率20个/s下的决策错误率 |

|
图 4 卸载频率100个/s下的决策错误率 |

|
图 5 卸载频率200个/s下的决策错误率 |
|
图 6 不同频率决策错误率 |
2) 图7展示在任务卸载频率为100个/s的情况下随着任务数目增多UE设备和MEC服务器的平均资源利用率的变化情况, 由图信息可以看出随着任务数量的不断增加, 平均资源利用率趋于稳定, 但考虑到不论是MEC服务器还是UE设备都存在资源阈值, 因为资源利用率过高会导致设备内存资源不够, 反而会降低运行效率, 因此设备资源利用率无法达到百分之百. 但是根据图7中统计结果可以看出, 随着任务数量增加最终结合本地优先的TD3卸载策略有一个更高的资源利用. 根据实验得出结合本地优先的TD3卸载策略平均资源利用率可以达到0.85左右, 而只使用TD3和DDPG进行卸载决策平均资源利用率只能达到0.78和0.73左右. 因此使用结合本地优先的TD3卸载策略能够达到一个更高的资源利用率和更低的决策错误率.

|
图 7 设备资源平均利用率 |
5 结论
本文主要研究了在多用户多MEC服务器且每个用户有多个任务的场景下计算任务卸载决策的问题. 实验考虑了蜂窝网络的延迟、噪声、能耗、UE用户位置、MEC服务器位置等问题来设计了一个仿真实验环境, 并使用该仿真环境以最大化资源利用率、最小化决策错误率为目标, 在TD3的基础上通过添加Softmax和本地优先策略来进行卸载决策仿真实验. 仿真实验表明, 结合了本地优先策略的TD3决策模型可以有效地降低决策错误率, 提高资源利用率. 但是本实验的不足之处是没有考虑用户任务的重要程度, 而是采用时间片轮转的方式执行任务, 这可能无法满足一些用户的对服务质量的要求, 在未来的实验中计划进一步考虑用户任务的执行顺序问题.
| [1] |
Wang D, Song B, Liu YJ, et al. Secure and reliable computation offloading in blockchain-assisted cyber-physical IoT systems. Digital Communications and Networks, 2022, 8(5): 625-635. DOI:10.1016/j.dcan.2022.05.025 |
| [2] |
Alshahrani A, Elgendy IA, Muthanna A, et al. Efficient multi-player computation offloading for VR edge-cloud computing systems. Applied Sciences, 2020, 10(16): 5515. DOI:10.3390/app10165515 |
| [3] |
Elgendy IA, Zhang WZ, Tian YC, et al. Resource allocation and computation offloading with data security for mobile edge computing. Future Generation Computer Systems, 2019, 100: 531-541. DOI:10.1016/j.future.2019.05.037 |
| [4] |
Li CL, Zhang Y, Luo YL. DQN-enabled content caching and quantum ant colony-based computation offloading in MEC. Applied Soft Computing, 2023, 133: 109900. DOI:10.1016/j.asoc.2022.109900 |
| [5] |
Jo S, Kim U, Kim J, et al. Deep reinforcement learning-based joint optimization of computation offloading and resource allocation in F-RAN. IET Communications, 2023, 17(5): 549-564. DOI:10.1049/cmu2.12562 |
| [6] |
Du TY, Li CL, Luo YL. Latency-aware computation offloading and DQN-based resource allocation approaches in SDN-enabled MEC. Ad Hoc Networks, 2022, 135: 102950. DOI:10.1016/j.adhoc.2022.102950 |
| [7] |
Yang B, Pang Z, Wang SL, et al. A coupling optimization method of production scheduling and computation offloading for intelligent workshops with cloud-edge-terminal architecture. Journal of Manufacturing Systems, 2022, 65: 421-438. DOI:10.1016/j.jmsy.2022.10.002 |
| [8] |
Mehta S, Kaur P. Efficient computation offloading in mobile cloud computing with nature-inspired algorithms. International Journal of Computational Intelligence and Applications, 2019, 18(4): 1950023. DOI:10.1142/S1469026819500238 |
| [9] |
Luo J, Deng XH, Zhang HG, et al. QoE-driven computation offloading for edge computing. Journal of Systems Architecture, 2019, 97: 34-39. DOI:10.1016/j.sysarc.2019.01.019 |
| [10] |
Mathur RP, Sharma M. Graph-based application partitioning approach for computational offloading in mobile cloud computing. Recent Advances in Computer Science and Communications, 2021, 14(1): 92-99. DOI:10.2174/2213275912666190716114033 |
| [11] |
Yang GS, Hou L, Cheng H, et al. Computation offloading time optimisation via Q-Learning in opportunistic edge computing. IET Communications, 2020, 14(21): 3898-3906. DOI:10.1049/iet-com.2020.0765 |
| [12] |
Chen GQ, Cai Q, Fu XB, et al. Research on algorithms of computing offloading and resource allocation based on DQN. Journal of Physics: Conference Series, 2021, 1748(3): 032047. DOI:10.1088/1742-6596/1748/3/032047 |
| [13] |
Song SN, Fang ZY, Zhang ZY, et al. Semi-online computational offloading by dueling deep-Q network for user behavior prediction. IEEE Access, 2020, 8: 118192-118204. DOI:10.1109/ACCESS.2020.3004861 |
| [14] |
Xu SL, Guo CL. Computation offloading in a cognitive vehicular networks with vehicular cloud computing and remote cloud computing. Sensors, 2020, 20(23): 6820. DOI:10.3390/s20236820 |
| [15] |
Ke HC, Wang J, Deng LY, et al. Deep reinforcement learning-based adaptive computation offloading for MEC in heterogeneous vehicular networks. IEEE Transactions on Vehicular Technology, 2020, 69(7): 7916-7929. DOI:10.1109/TVT.2020.2993849 |
| [16] |
Chen J, Gao Q, Wu Q, et al. A computation offloading scheme based on FFA and GA for time and energy consumption. Proceedings of the 10th International Conference on Computer Engineering and Networks. Singapore: Springer, 2021. 1500–1506.
|
| [17] |
Zhang XJ, Wu WG, Zhao ZH, et al. RMDDQN-learning: Computation offloading algorithm based on dynamic adaptive multi-objective reinforcement learning in Internet of vehicles. IEEE Transactions on Vehicular Technology, 2023.
|
| [18] |
Sellami B, Hakiri A, Yahia SB, et al. Energy-aware task scheduling and offloading using deep reinforcement learning in SDN-enabled IoT network. Computer Networks, 2022, 210: 108957. DOI:10.1016/j.comnet.2022.108957 |
| [19] |
Li J, Gao H, Lv TJ, et al. Deep reinforcement learning based computation offloading and resource allocation for MEC. Proceedings of the 2018 IEEE Wireless Communications and Networking Conference. Barcelona: IEEE, 2018. 1–6.
|
| [20] |
Li C, Xia JJ, Liu FG, et al. Dynamic offloading for multiuser muti-CAP MEC networks: A deep reinforcement learning approach. IEEE Transactions on Vehicular Technology, 2021, 70(3): 2922-2927. DOI:10.1109/TVT.2021.3058995 |
 2023, Vol. 32
2023, Vol. 32


