1 引言

根据观察到的行人轨迹, 行人轨迹预测旨在预测行人未来的位置坐标序列, 在自动驾驶、视频监控和视觉识别等各种应用中发挥着关键作用^[1]. 然而, 行人轨迹预测是一项极具挑战性的任务, 其难点主要在于: (1)人与人之间的交互是复杂的且难以捕捉的. 对于行人而言, 为了遵守一定的社会规范甚至规避危险, 在移动过程中也需要预测场景中其他行人的轨迹的能力, 从而动态的调整自己的路线, 但这种能力是难以建模的. (2)行人轨迹预测是一个多模态问题. 基于行人过于的轨迹, 应当产生多条可能的未来轨迹, 因此在进行轨迹输出时, 需要在考虑合理性的同时也需要考虑多样性. (3)轨迹输出的自洽性. 对于轨迹预测而言, 如果输出的轨迹会产生碰撞, 那么不但无法逻辑自洽, 而且在应用层面可能带来巨大的风险, 这通常是不能接受的.

目前, 国内外已经有多名学者对轨迹预测的行人交互问题而言, 进行了深入研究. 经典模型通过手工制作的能量函数来捕获人与人之间的交互^[2], 成功实现了真实社会中的交互问题, 但这种方法往往无法在拥挤的空间中建立人群交互. 而随着深度神经网络研究的进展, 已经有越来越多的循环神经网络模型应用到了轨迹预测任务之中并展现出了广阔的前景与强大的能力. 基于RNN的方法通过其潜在状态来捕获行人的运动, 并通过合并行人的潜在状态来模拟人与人之间的交互作用^[3,4]. 近年来, Transformer^[5]网络强大的能力使其变得流行, 它抛弃了语言序列的顺序性质, 只用强大的自我注意机制来建模时间依赖关系. 与RNN相比, Transformer架构的主要好处是使用自我注意显著改善了时间建模, 可以更好地捕捉行人之间潜在的互动^[6–8]. 然而, 无论是利用RNN模型或是自注意力机制进行人与人交互建模, 往往都会忽略空间结构信息. 而图神经网络^[9]的特殊形式, 让行人交互的空间结构的信息得到了直观且有效的利用, 在行人轨迹预测领域做出很多应用^[10–12], 效果得到了良好的提升.

行人轨迹预测结果的碰撞问题一直是此领域挥之不去的难题. 对于轨迹预测结果而言, 若产生碰撞, 则会带来模型自洽问题甚至安全问题. 有的避免碰撞方法是对预测结果强行加上一个手工的约束函数^[13], 这种物理约束的方法可能导致预测轨迹的生硬, 在合理性上稍显欠缺. 更多的深度学习模型通常通过让模型学习行人交互问题的建模^[14,15]来解决碰撞问题, 这种方法通常通过数据驱动数据集的学习, 可以产生合理轨迹, 但当产生碰撞情景时却无法修复——因为模型一直在学习正确的社会交互, 不知道何为“错误情况”. 因此减少碰撞的难度在于碰撞样本的缺失和训练方法的选择.

基于以上难点, 本文提出一种融合安全性的轨迹预测模型(safe spatio-temporal graph Transformer network for pedestrian trajectory prediction, S-STGTN), 如图1. S-STGTN是基于图注意力机制的神经网络模型, 通过图注意力机制来合理提取行人交互特征, 并提出一种无需手工标注的负样本生成方法, 通过对比表示学习来降低碰撞率以提高安全性.

2 融合对比学习的时空图网络

本文的主要结构使用了编解码结构. 首先是使用图注意力网络来提取行人特征, 通过此方法可以在进行轨迹预测时更好的考虑到他人带来的影响. 而针对轨迹预测中的安全问题, 即尽量地避免碰撞, 本文使用了对比表示学习的方法, 来在无需手动标注的情况下生成负样本, 解决了实际生活中碰撞样本少的问题, 来告知模型何种情况是不能接受的. 此外, 由于轨迹预测是一个多模态问题, 本文使用对抗生成网络来生成多种轨迹.

2.1 问题定义

行人轨迹预测, 即根据过去一段时间内的轨迹来推断出未来一段时间的可能轨迹. 假设场景中有N个行人, 且行人过去轨迹定义为已 $p_t^i$ , 行人未来预测轨迹定义为 $y_t^i$ , 行人未来真实轨迹定义为 $\hat y_t^i$ . 则本问题可以描述为已知行人i以及场景中其他行人j的历史时间段1到 ${T_{{\rm{obs}}}}$ 的轨迹 $p_t^i$ , $p_t^j$ 目标为预测他在未来时间段 ${T_{{\rm{obs}}}} + 1$ 到 ${T_{{\rm{pre}}}}$ 时间段内的轨迹 $y_t^i$ . 其中:

$ {p}_{t}^{i}=\{({x}_{t}^{i}, {y}_{t}^{i})\mid t=1, 2, \cdots, {T}_{{\rm{obs}}}\} $

(1)

$ {p}_{t}^{j}=\{({x}_{t}^{j}, {y}_{t}^{j})\mid t=1, 2, \cdots, {T}_{{\rm{obs}}}, j\in N\text{, }j\ne i\} $

(2)

$ y_t^i = \{ (x_t^i, y_t^i)\mid t = {T_{{\rm{obs}}}}, {T_{{\rm{obs}} + 1}}, \cdots, {T_{{\rm{pre}}}}\} $

(3)

$ \hat y_t^i = \{ (\hat x_t^i, \hat y_t^i)\mid t = {T_{{\rm{obs}}}}, {T_{{\rm{obs}} + 1}}, \cdots, {T_{{\rm{pre}}}}\} $

(4)

2.2 行人时空图网络

行人自身的轨迹是预测其轨迹最重要的输入之一, 而LSTM已经被证实了能从轨迹中提取带有描述甚至预测行人未来轨迹的隐藏特征, 因此本文采用LSTM对单人的历史轨迹进行编码.

图注意力网络(graph attention network, GAT)^[9]是一种基于注意力机制的图神经网络, 应用非常广泛, 它可以用于许多不同的任务, 包括图分类、图分割、图推理、图生成等, 在计算机视觉、自然语言处理、生物信息学、社交网络分析等解决了诸多实际问题^[16]. 本文利用图注意力网络的结构来建模场景中的行人网络, 并利用其注意力机制建模行人之间的交互, 有效模拟了真实社交场景下的未来轨迹输出. 与使用图卷积网络的SGCN^[12]等方法相比, 本文使用注意力机制对节点进行加权, 能够更准确地捕捉节点之间的依赖关系, 从而提供更精确的节点表示和预测能力.

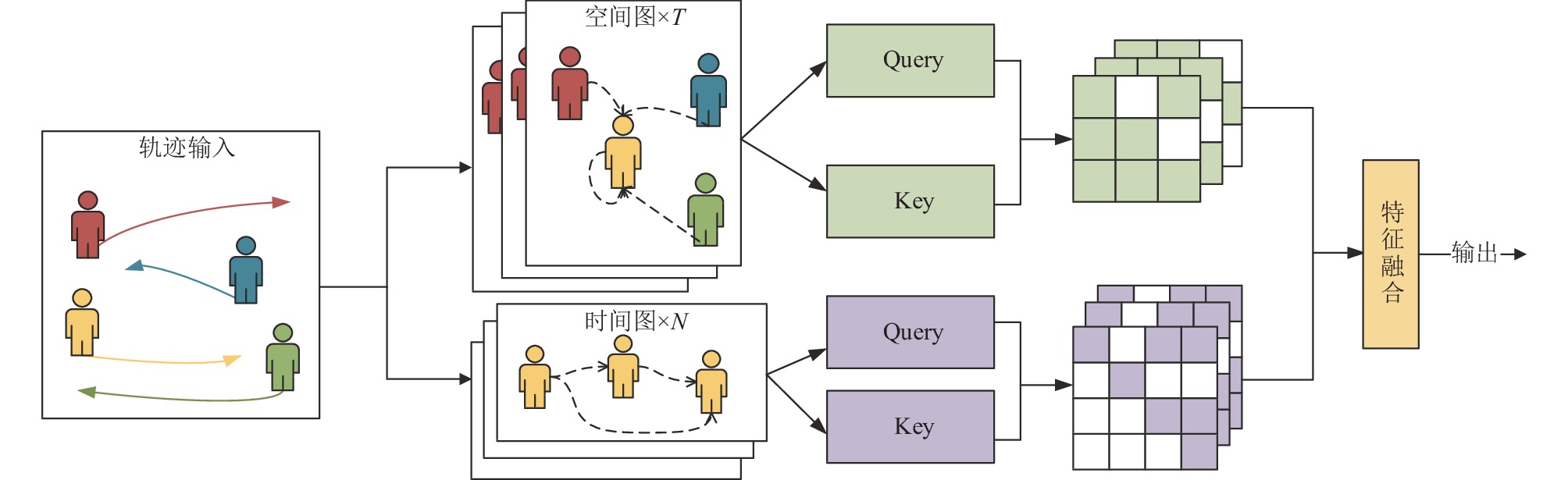
行人特征提取模块利用轨迹数据作为输入, 分为两个支部分提取图特征向量提取, 分别为时间特征提取和交互特征提取. 图结构可以完好地保存空间信息, 而自注意力机制则能提取人与人之间的交互问题. 然后将两个解耦的时空向量进行融合, 最后进行预测轨迹的输出. 图2展示了本文行人交互特征的提取过程, 行人交互特征的提取分为上下两个模块, 分别是时间模块与空间模块.

时间模块考虑到行人i自己本身的过去轨迹, 是一个典型的时间序列问题. 对于轨迹数据而言, 其中包含了在时间 ${T_{{\rm{obs}}}}$ 内场景中所有N个人的轨迹数据, 将这N个人的轨迹数据分别提取出来, 形成N个时间图 ${G}_{{\rm{tmp}}}\left(i\right)=\left({V}_{i}, {U}_{i}\right),\; i\in 1, 2, \cdots, N$ , 由 $ {V_i} $ 和 $ {U_i} $ 构成, 其中 ${V_i} = \{ v_i^t|i = 1, 2, \cdots, {T_{{\rm{obs}}}}\}$ 是 ${G_{{\rm{tmp}}}}$ 的顶点, 代表了行人i在观察时间 ${T_{{\rm{obs}}}}$ 内每秒的所有轨迹点的集合, ${U_i} = \{ u_i^{m, n}|m, n = 1, 2, \cdots, {T_{{\rm{obs}}}}\}$ 是 ${G_{{\rm{tmp}}}}$ 的边, 代表了行人i在时间m和时间n的轨迹点的关系. 有了此图之后, 就可以对行人i的轨迹点做出图注意力机制, 具体公式为:

$ ATT\left( {{Q^i}, {K^i}, {V^i}} \right) = \frac{{{\textit{Softmax}}\left( {{Q^i}{K^{i{\rm{T}}}}} \right)}}{{\sqrt {{d_k}} }}{V^{i{\rm{T}}}} $

(5)

其中,

$ {Q^i} = {f_Q}\left( {\left\{ {h_j^i} \right\}_{j = 1}^{{T_{{\rm{obs}}}}}} \right) $

(6)

$ {K^i} = {f_K}\left( {\left\{ {h_j^i} \right\}_{j = 1}^{{T_{{\rm{obs}}}}}} \right) $

(7)

$ {V^i} = {f_V}\left( {\left\{ {h_j^i} \right\}_{j = 1}^{{T_{{\rm{obs}}}}}} \right) $

(8)

而空间图则保存了在某一时刻t场景中人与人的交互信息. 对于轨迹数据而言, 在每个时间点t场景中都会有N个人, 这N个人之间的空间信息就形成了 ${T_{{\rm{obs}}}}$ 个空间图 ${G}_{{\rm{spa}}}\left(t\right)=\left({V}^{t}, {U}^{t}\right), t\in 1, 2, \cdots, {T}_{{\rm{obs}}}$ , 其中, ${V^t} = \{ v_n^t|n = 1, 2, \cdots, N\} $ , 为t时刻场景中的所有人, 代表了 ${G_{{\rm{spa}}}}\left( t \right)$ 的顶点, ${U^t} = \{ u_{i, j}^t|i, j = 1, 2, \cdots, N\} $ 为t时刻这些人之间的连接关系, 代表了 ${G_{{\rm{spa}}}}\left( t \right)$ 的边. 有了此图之后, 就可以对行人i和行人j在t时刻的轨迹点做出图注意力机制, 具体公式为:

$ ATT\left( {{q^t}, {k^t}, {v^t}} \right) = \frac{{{\textit{Softmax}}\left( {{{\left( {q_i^{t{\rm{T}}}k_j^t} \right)}_{i, j = 1:n}}} \right)}}{{\sqrt {{d_k}} }}\left[ {{v_i}} \right]_{i = 1}^n $

(9)

其中, $q_i^t = {f_q}\left( {h_i^t} \right), \;k_i^t = {f_k}\left( {h_i^t} \right),\; v_i^t = {f_v}\left( {h_i^t} \right)$ .

经过时间图与空间图的自注意力机制后, 就可以对两个图中的节点分别进行更新, 具体公式为:

$ h_i' = ATT\left( i \right) + {h_i} $

(10)

在得到更新后的时间图与空间图节点信息之后, 将他们连接起来通过全连接层, 得到融合了行人时空交互的新特征.

2.3 轨迹对比学习

长期以来的轨迹预测任务的指标大多聚焦在准确率即预测轨迹与真实轨迹的吻合率上, 但会忽视轨迹的碰撞率. 在基于数据驱动的轨迹训练任务中, 碰撞率总体来看保持在一个较低水准, 因为数据集中的轨迹点几乎不会产生碰撞, 模型自然也不会去“模仿”碰撞事件. 然而碰撞率是一个很重要的安全指标, 因此即使较小概率的碰撞率也是不可接受的, 因此有必要专门开拓一个模块来减少碰撞概率^[17]. 为此, 本系统加入了避免碰撞模块.

避免碰撞模块的主要思想利用了对比学习. 对于一个模型而言, 想让它知道什么是最佳答案, 则在告知其正确答案之外, 还需要告诉它错误答案, 这就是对比学习的主要思想. 对比学习可以在无需额外人工标注的基础之上获得更多的“正样本”与“负样本”. 其中, 如何对一个普通数据集进行采样而得到正负样本是对比学习的核心任务之一. 在轨迹预测的避免碰撞模块中, 正样本即普通的数据集中的轨迹(无碰撞样本), 而负样本则是碰撞样本, 设置负样本可以让模型在进行轨迹输出的时候, 尽量避免出现行人i与行人j在某一时间点处于相同的位置(即碰撞), 希望通过此举降低轨迹输出的碰撞率, 从而达到逻辑自洽的效果. 但由于负样本很少出现, 且人工标注开销过大, 所以本文采用了一种自动生成正负样本的方法, 如图3, 具体为以下公式:

$ 正样本抽取:\; {k}_{t+{t}_{0}}^{i, +}={p}_{t+{t}_{0}}^{i}+\epsilon $

(11)

$ 负样本抽取:\; {k}_{t+{t}_{0}}^{i, -}={p}_{t+{t}_{0}}^{j}+\Delta p+\epsilon $

(12)

其中, ${{k}}_{{{t}} + {{{t}}_0}}^{i, + }$ 为行人i在 ${{t}} + {{{t}}_0}$ 时刻的正样本, 只有一个. ${{p}}_{{{t}} + {{{t}}_0}}^{{i}}$ 为行人i在 ${{t}} + {{{t}}_0}$ 时刻的真实位置坐标, $\epsilon $ 为一个很小的常数, 作为随机噪声, 以防止过拟合. 而 ${{k}}_{{{t}} + {{{t}}_0}}^{{{i}}, - }$ 为行人i在 ${{t}} + {{{t}}_0}$ 时刻的负样本, 有多个. ${{p}}_{{{t}} + {{{t}}_0}}^{{j}}$ 为行人i的邻居j在 ${{t}} + {{{t}}_0}$ 时刻的真实位置坐标, 同样 $\epsilon $ 为随机噪声. 而 $\Delta {{p}}$ 则是负样本采样范围参数, 可以确定为一定的数值. 例如, 如果仅考虑两个行人不会发生碰撞, 则可以将 $\Delta {{p}}$ 设定为0.3 m , 即形成了以位置为圆心, 半径为0.3的圆, 即图3中的碰撞区.

同理, 如考虑到社交礼仪, 即正常情况下人并不会与其他路人贴着行走, 将 $\Delta {{p}}$ 设置为0.5 m, 则不但保证了不会发生碰撞, 也保证了社交距离. 因此形成了以行人位置为圆心, 半径为0.5的圆, 即图3中的不适区, 在此不适区内进行负样本采样, 可以让输出轨迹尽量远离此区域.

在得到了正负样本之后, 就可以引入对比学习的损失函数. 对比学习的损失函数通常包含一个度量函数与一个实际损失函数, 度量函数用于衡量数据样本与正负样本之间的距离, 实际损失函数用于对度量函数计算出的进行距离约束. 普通对比学习^[18]的的损失函数 ${{{L}}_{{\text{pair}}}}$ 为:

$ {L_{{\rm{pair}}}} = \left\{ {\begin{array}{*{20}{l}} {D{{\left( {q, k} \right)}^2}, k\sim {p^ + }(|q)} \\ {\max\left( {0, m - D{{\left( {q, k} \right)}^2}} \right), k\sim {p^ - }(|q)} \end{array}} \right. $

(13)

其中, ${{D}}\left( {{{q}}, {{k}}} \right) = {\left| {\left| {{{q}} - {{k}}} \right|} \right|_2}$ 为欧几里得距离. 这种最初版本的对比损失可以理解为, 让正样本之间的距离尽可能的近、且让负样本之间的距离尽量地大于指定边界m. 但这种损失收敛的速度较为缓慢, 样本之间的距离也较远. 因此在这里, 使用噪声对比估计损失函数 ${{{L}}_{{\text{NCE}}}}$ ^[19], 具体的公式为:

$ {L_{{\rm{NCE}}}} = - \log\frac{{{\rm{exp}}\left( {s\left( {q, {k^ + }} \right)} \right)}}{{{\rm{exp}}\left( {s\left( {q, {k^ + }} \right)} \right) + {\rm{exp}}\left( {s\left( {q, {k^ - }} \right)} \right)}} $

(14)

其中, q代表查询样本, ${{{k}}^ + }$ 代表正样本, ${{{k}}^ - }$ 代表负样本, 在轨迹预测任务中分别为预测行人i的过去的轨迹向量、预测行人i的未来的真实轨迹向量、行人i的邻居j的未来真实轨迹向量, 而s()为度量函数, 这里可以设为余弦相似度. ${{{L}}_{{\text{NCE}}}}$ 的核心思想是学习数据样本与噪声样本之间的数据分布的区别, 可以理解为一个二分类问题, 训练一个分类器以学习数据样本与噪声样本之间的区别.

2.4 轨迹生成

在轨迹预测任务中, 由于人的轨迹的不确定性, 因此需要生成多条备选轨迹. 本系统的轨迹生成模块主要采用InfoGAN结构^[20], 如图4.

不同于普通的对抗生成网络, InfoGAN加入了互信息损失来避免模式崩溃的问题. 本文中采取该结构可以有效地避免在生成不同的轨迹预测模块时, 生成轨迹过分相似的问题, 实现预测轨迹的多样化. 其中, 损失函数可以写为:

$ \begin{split} \mathop {\min }\limits_G \mathop {\max }\limits_D V\left( {D, G} \right) = & {E_{x\sim {p_{{\rm{data}}}}\left( x \right)}}\left[ {{\log}D\left( x \right)} \right] \\ &+ {E_{{\textit{z}}\sim {p_{\textit{z}}}\left( {\textit{z}} \right)}}\left[ {\log\left( {1 - D\left( {G\left( {\textit{z}} \right)} \right)} \right)} \right] \end{split}$

(15)

其中, D表示生成器, G表示判别器. x为来自真实样本的数据, 而z则是随机噪声. 通过这样的损失函数, 可以生成和真实样本很相近的数据, 即在轨迹预测任务中就是与真实未来轨迹相似的轨迹. 然而, GAN在生成多模态轨迹时, 很容易引起模式崩溃.

InfoGAN与GAN的区别主要在于输入与损失函数. 相比GAN的输入, InfoGAN首先将生成器输入噪声z分为了(z, c)两个部分, 其中z和GAN的z并无不同, 均为随机噪声, 而c则可以理解为可解释的隐变量. 而关于损失函数, 则分为了两部分. 对于噪声z的损失与GAN相同, 而对于c则引入了新的互信息损失 $I\left( {c;G\left( {{\textit{z}}, c} \right)} \right)$ , 因此, InfoGAN的损失函数可以写为:

$ \mathop {{\text{min}}}\limits_G \mathop {\max }\limits_D {V_I}\left( {D, G} \right) = V\left( {D, G} \right) + \lambda I\left( {c;G\left( {{\textit{z}}, c} \right)} \right) $

(16)

其中, ${{V}}\left( {{{D}}, {{G}}} \right)$ 为图4的生成器损失和对抗损失, ${{I}}( {{c}};{{G}}( {\textit{z}}, {{c}} ) )$ 为互信息损失. 互信息量用字母I表示, I(X;Y)就代表了X和Y之间的互信息量的大小.

根据图4可知, 生成器模块主要是由编码器-解码器结构构成, 解码器的输入为编码器的输出与随机噪声和可接受的隐变量, 输出为预测的轨迹. 而判别器模块分为两个部分, 分别是LSTM-Multi和LSTM-Discri. LSTM-Multi的输入为生成器中解码器的输出, 用于生成更多不同的样本, LSTM-Discri的输入为生成器中解码器的输出与真实轨迹向量, 用于鉴别收到样本的真假.

3 实验结果与分析 3.1 数据集

在本节中, 为了验证本文算法的有效性, 首先在行人轨迹预测的基准数据集 ETH^[21]和UCY^[22]上进行测试. 这两个数据集是包含了大量的社会交互, 这两个数据集中加起来共有1536名行人, 上千条真实轨迹, 包含行人绕开障碍物、单个行人与人群的相向而行、路口行人转弯等多种真实场景. 是行人轨迹预测常用的基准数据集. 其中, 又分别包含了5个人群数据集, ETH包含ETH和HOTEL数据集, UCY包含ZARA1, ZARA2和UNIV这3个数据集. 这在训练或评估阶段, 输入的是过去3.2 s的轨迹, 输出的是未来4.8 s的轨迹.

对于验证轨迹预测的准确性, 本文采用最终位移误差(final displacement error, FDE)和平均位移误差(average displacement error,ADE), 出于安全因素的考量还引入了碰撞率(collision rate, CR)行人之间的预测轨迹之间发生碰撞率. 公式分别如下:

$ ADE=\frac{{{\displaystyle \sum }}_{p=1}^{N}{{\displaystyle \sum }}_{t=1}^{{T}_{f}}{y}_{p}^{t}-{\hat{y}}_{p}^{t}}{N\times {T}_{f}} $

(17)

$ {\textit{FDE}}=\frac{{{\displaystyle \sum }}_{p=1}^{N}{y}_{p}^{t}-{\hat{y}}_{p}^{t}}{N} $

(18)

$ CR=\frac{{{\displaystyle \sum }}_{p=1}^{N}{{\displaystyle \sum }}_{t=1}^{{T}_{f}}{y}_{p}^{t}-{\hat y}_{p}^{t} }{N\times {T}_{f}}\Big|{ \left({y}_{p}^{t}-{\hat y}_{p}^{t}\right) \lt dis} $

(19)

3.2 实验结果

定量评估是通过运用数学模型对所要进行分析的对象在各项关键性能指标上的评估分析. 表1中列出了ETH和UCY数据集上以 ADE、FDE和CR为指标模型的评估结果, ADE与FDE用斜线隔开.

表1是本文的定量分析结果, 使用了多个经典模型或前沿模型进行对比. Social LSTM是最先提出“社交池”的模型, 利用池化层来通过邻居节点的特征捕捉社会交互, 轨迹更加合理合理, 也带来了更好的结果, 从而表现出了“社会交互”在行人轨迹预测领域的重要性. Social GAN^[23]是本文的轨迹生成器参考的模型, 考虑到行人轨迹的多模态性, 只输出一条轨迹无法满足真实场景的需求, 因此Social GAN输出了多条轨迹, 结果证明这更有利于得到准确轨迹. GAT是本文在提取时空特征时使用的模型, 通过图神经网络与自注意力机制结合, 有效地得到了社会交互特征, 得到良好结果. 而本文的S-STGTN模型的结果显然处于第1梯队, 值得注意的是, 虽然STGCNN^[7]最终的结果与本文模型相差不大, 但S-STGTN预测的结果的碰撞率得到大幅度的降低, 使轨迹更加的合理, 在将预测的轨迹应用到实际场景中也更加的安全.

在表2中, S-STGTN为本文的模型, S-STGTN-CL为消融对比表示学习模块之后的模型, 揭示了对比学习模块的重要作用. 可以看出, 对比表示学习模块在降低碰撞率的功能上十分有效, 在5个行人数据集上分别提升了58.1%, 20.9%, 31.3%, 54.2%, 50.4%, 大幅度提升了安全性. 同时, 对于ADE和FDE两个指标也有提升作用.

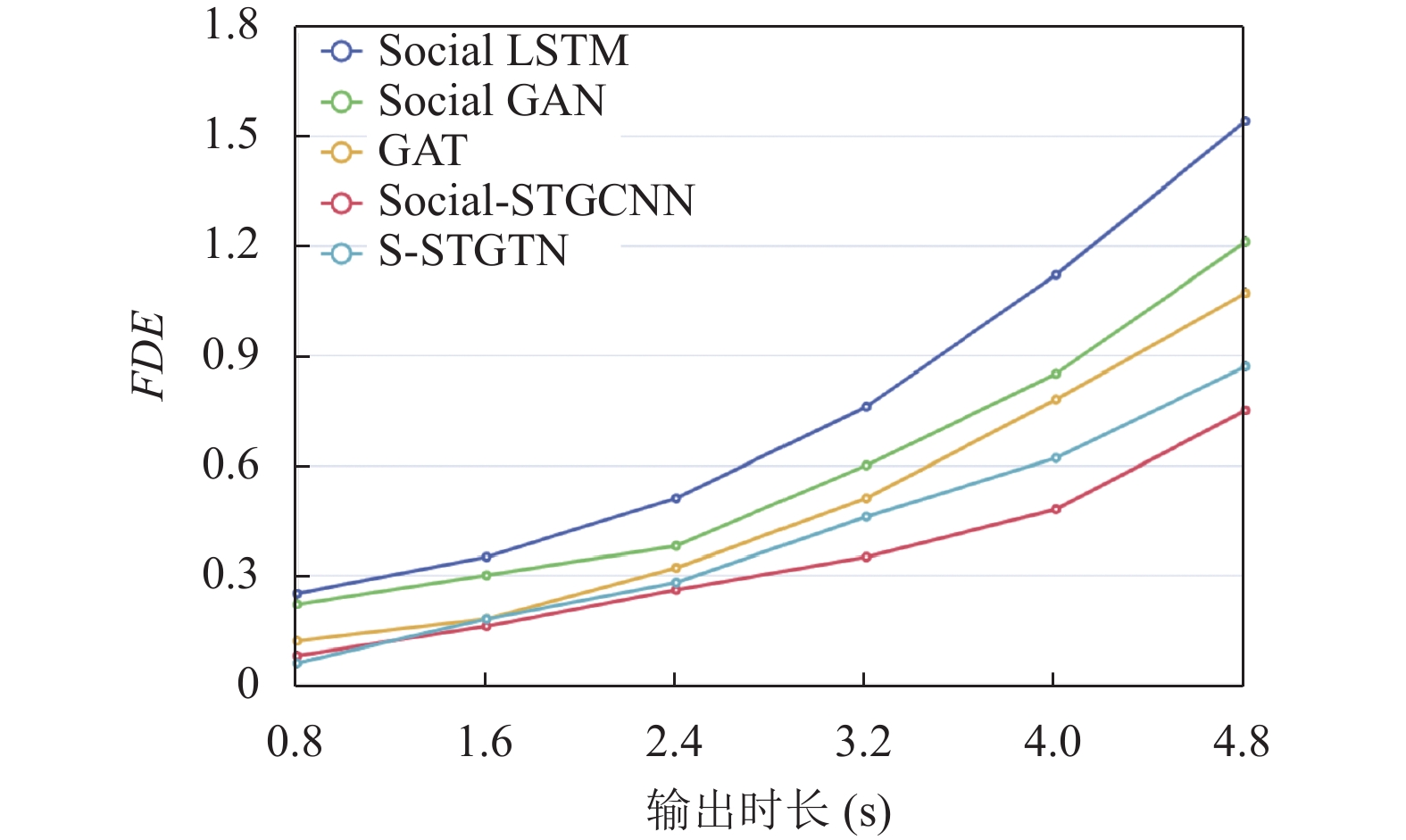
而考虑到算法的稳定性与可靠性, 当所需的输出时长增加时, 算法的ADE与FDE误差应该控制在一个合理的范围内.

图5和图6分别表现出了当预测时长从0.8 s到4.2 s时, 各个算法的误差趋势. 可以看出, 本文提出的S-STGTN算法在输出时间增加时, ADE与FDE的斜率相比其他流行的算法增加幅度较小, 说明了本算法的稳定性. 本文提出了一种融合安全性考虑的轨迹预测模型S-STGTN. 本模型基于图注意力网络, 并结合对比表示学习降低碰撞率, 使轨迹更加合理和安全. 经过在公开数据集ETH和UCY上的测试, S-STGTN模型取得了较好的预测效果, 并且与其他轨迹预测模型相比, 本模型有效降低了碰撞率, 且算法稳定性得到提升.