在数据挖掘过程中, 通常会存在一些偏离正常数据的对象, 这些对象被称为离群点. 根据偏离程度, 可将其分为强离群点和弱离群点. 强离群点[1]通常被视为异常点, 但不一定是错误的数据, 它们往往包含重要信息. 通过分析强离群点可以实现欺诈行为检测[2]、异常设备检测[3]以及网络安全检测[4]. 弱离群点[1]则被认为是噪声点, 噪声点会导致模型准确性降低、泛化能力不足等问题, 进而对数据分析的结果产生负面影响. 因此, 离群点的检测和处理是非常重要的.
离群点检测在机器学习和数据挖掘中具有广泛的应用, 它可以帮助发现异常行为、提高数据质量. 通常, 离群点检测根据参考集的大小可以分为全局离群点检测和局部离群点检测. 参考集是用来建模和计算离群点得分的一组基准样本集合. 在全局离群点检测方法中, 参考集通常包含数据集中的所有对象, 因此可以全面地考虑整个数据集的特征和分布. 全局离群点检测方法主要指基于统计模型[5]的方法. 而在局部离群点检测方法中, 参考集则是某个数据点邻近区域内的对象. 局部离群点检测方法包括基于密度的方法[6]、基于距离的方法[7]以及基于聚类的方法[8].
在众多离群点检测方法中, 基于聚类的方法因其较高的可扩展性和适用性而被广泛应用. 基于聚类的方法可以将数据点划分为相似的簇, 但对于离群点来说, 它们与其他数据点的差异较大, 往往无法被归类到任何一个簇中, 而是被单独作为一组. 在聚类任务中, 如果存在大量的离群点, 将会导致聚类效果显著下降, 从而影响后续的数据挖掘工作. 因此, 离群点的检测和剔除可以被视为聚类任务的预处理步骤. 然而, 将剔除离群点作为聚类分析的前提与使用聚类方法进行离群点检测的初衷背道而驰. 如何在不影响聚类任务和离群点检测效果的情况下正确处理离群点, 仍然是当前亟待解决的问题. 除此之外, 包括基于聚类方法在内的大多数传统离群点检测方法, 在选择阈值参数或确定离群点数量方面需要手动操作. 而这些参数需要根据先验知识或领域经验进行选择, 随意选择很容易导致结果不准确或不一致. 因此, 实现自动化选择阈值或确定离群点数量能够提高离群点检测的准确性和可靠性, 对于离群点检测具有重要意义.
针对上述问题, 本文提出了一种基于中心移动的轨迹离群点检测算法. 关键思想是使数据点向其K近邻(K-nearest neighbor, KNN)集合的中心移动, 促使每个数据点靠近更密集的区域. 这意味着每个数据点会更接近典型的数据点, 从而有效地抵消离群点对聚类的影响. 此外, 该方法计算所有数据点的异常值分数, 并将异常值分数的标准差作为全局阈值, 用于判定数据点是否为离群点, 从而避免了手动选择阈值参数. 本文算法在实现离群点检测的同时, 还可以完成对数据的聚类工作, 并进一步应用于后续的热点挖掘工作.
本文的主要贡献有以下3点.
(1)提出了一种基于中心移动的轨迹离群点检测算法, 将每个数据点移动到其KNN集合Ni的中心, 从而使其更加接近典型数据点, 以此来抵消离群点对聚类的影响.
(2)与传统离群点检测算法不同, 本文算法不需要手动选择阈值参数或确定离群点数量, 而是将所有数据点异常值分数的标准差作为全局阈值, 用于离群点的判定.
(3)不同于传统离群点检测算法的验证数据集, 本文采用渔船AIS轨迹数据集对所提算法进行验证. 相对于其他数据集, 轨迹数据集的离群点检测具有数据存在时序性、数据分布不均、数据维度高等难点. 尽管如此, 本文算法相较于其他算法的F1-score仍能平均提高0.18, 离群点检测时间也能平均减少5.3 s.
本文第1节介绍对轨迹数据进行异常检测的不同方法及各自研究现状. 第2节给出本文算法涉及的相关概念. 第3节详细介绍本文算法的流程. 第4节实验与结果分析. 第5节是结论与展望.
1 研究现状轨迹数据挖掘的目标是从大量移动对象中提取共同的特征, 为了实现这一目标, 需要对轨迹数据进行离群值的检测和处理. 由于轨迹数据具有时序性和连续性等特点, 使得单个真实轨迹数据点的分析价值有限, 这就导致了轨迹数据集中的离群点多为弱离群点, 即噪声数据. 在不同的研究领域中, 噪声数据所代表的含义和性质都有所不同. Zhu等人[9]认为轨迹领域中的噪声数据是指在某些相似性度量方面与大多数轨迹点存在显著差异的轨迹点. 由于轨迹数据的采集设备通常存在测量误差、信号干扰等问题, 导致噪声数据在实际应用中是难以避免的. 因此, 在对轨迹数据进行挖掘之前必须进行去噪处理, 避免噪声数据引起的偏差对后续数据分析产生负面影响.
由于轨迹数据具有数据量大、数据稀疏以及数据更新频率快等特点, 使得噪声数据的检测仍存在挑战性[10,11]. 现有的噪声数据检测方法主要分为3类: 基于历史轨迹数据的噪声检测、基于网格化的噪声检测、基于距离的噪声检测. Li等人[12]提出了一种基于历史轨迹相似性的度量方式, 称为时序噪声值检测框架(TOD). 该框架利用数据集的时序信息来检测噪声值. 它通过比较每个路段与其他路段在相同时间步长内的运动轨迹, 计算它们之间的相似性值, 并将历史相似性值记录在每个路段的时间邻域向量中. 当某个路段的相似性值与之前的历史值发生急剧变化时, 该路段被认为是噪声值. Chawla等人[13]将道路交通建模为一个基于时间依赖流的网络, 将城市划分为以主要道路为界的区域, 并通过识别各链路与历史流量配置文件的偏差来检测异常链路. Pang等人[14]对iForest算法与懒惰学习方法进行创新, 提出了一种异常检测方法. 该方法将每个轨迹划分到随机选定的不同单元格中, 并提出假设: 异常轨迹所涵盖的单元格数量应小于正常轨迹所涵盖的单元格数量, 从而实现异常数据的检测. Chen等人[15]提出了一种实时的异常轨迹检测方法iBOAT. 在该方法中, 使用固定窗口的方式来代替网格进行数据处理, 并通过计算阈值大小来检测异常轨迹. Knorr等人[16]以数据的速度和方向为切入点, 提出了一种基于距离的异常值检测方法. 计算轨迹对象之间的平均加权距离并作为判定指标, 来判断该轨迹是否异常. Lei等人[17]提出了一种基于聚类距离度量的轨迹异常检测方法, 用来检测AIS轨迹数据中的距离异常、航向异常和速度异常.
尽管以上方法在轨迹数据的噪声检测方面取得了一定效果, 但仍存在局限性. 在基于历史轨迹数据的噪声检测中, 由于轨迹数据在采集过程中可能存在定位误差、数据缺失等问题, 因此很难获取完全准确的历史轨迹, 这就导致了噪声数据的检测结果通常不够准确. 在基于网格化的噪声检测中, 需要手动设置一些参数, 如网格的划分单位、窗口的大小等. 因此, 噪声数据的检测结果与参数之间具有较强的关联性, 很容易受到参数的影响. 而基于距离的噪声检测方法对于噪声和异常值非常敏感, 即使是微小的距离变化, 都可能对检测结果产生较大的影响.
2 相关概念致力于抵消离群点对轨迹数据聚类的影响, 本文提出了一种基于中心移动的轨迹离群点检测算法. 该算法以最近邻思想和距离判定为基础, 以轨迹数据的特征空间为输入. 涉及的相关概念如下.
(1)最近邻: 是一种基于距离度量的概念, 通过计算数据点之间的距离来确定它们之间的相似性或接近程度. 常见的最近邻算法是KNN算法[18]. KNN算法的思想: 在数据集特征空间中, 计算某个数据点与数据集中所有数据点之间的距离, 选取距离最近的k个数据点作为其最近邻, 并根据最近邻的类别或属性值进行分类. 由于欧氏距离计算方法简单直观, 因此被视为一种常用的距离度量方法. 当特征空间的数据样本为N维时, 数据点x(
| d(x,y)=√n∑i=1(xi−yi)2 | (1) |
(2)距离判定: 是一种用来确定数据点是否为离群点的方法, 该方法基于设定的距离阈值来确定离群点. 如果一个数据点与其他数据点之间的距离超过了阈值, 就被认为是离群点.
(3)特征空间: 是指由多个特征组成的空间, 每个特征在空间中对应一个维度. 本文中的轨迹点特征空间可以表示为
本节讨论了基于中心移动的轨迹离群点检测算法CSOD的具体流程, 主要分为3个部分: 确定KNN集合、确定KNN集合的中心点以及判别离群点. 算法流程如图1所示.
3.1 基于特征距离确定KNN集合计算轨迹特征空间中不同数据点之间的距离, 为每个数据点找到k个最近邻居点. 由于轨迹数据包含经纬度特征, 因此使用欧氏距离公式计算球体表面上的轨迹距离的方法不再适用, 通常使用半正矢公式[19]来进行距离计算. 因此, 本文采用半正矢距离公式来计算两个轨迹点之间的地理位置距离. 当两个轨迹点的经纬度坐标为
| \begin{split} &{d}_{1}({p}_{j}, {p}_{k})\\ &=2r\cdot\mathrm{arcsin}\left(\sqrt{{\mathrm{sin}}^{2}A+\mathrm{cos}\left(la{t}_{j}\right)\cdot \mathrm{cos}\left(la{t}_{k}\right)\cdot {\mathrm{sin}}^{2}B}\right) \end{split} | (2) |
其中, A=
| {d_2}({p_j}, {p_k}) = \sqrt {\sum\limits_{i = 1}^n {{{\left( {{f_{ji}} - {f_{ki}}} \right)}^2}} } | (3) |
其中,
| dist({p_j}, {p_k}) = {d_1}({p_j}, {p_k}) + {d_2}({p_j}, {p_k}) | (4) |
其中,

|
图 1 算法流程图 |
3.2 基于边缘度得分确定KNN集合Ni的中心
为了消除离群点造成的负面影响, 我们让每个数据点向其KNN集合

|
图 2 轨迹点移动示意图 |
首先根据特征距离公式计算每个数据点的稀疏度得分: 将数据点
| spa{r_i} = \sum\limits_{j = 1}^k {dist\left( {{p_i}, {p_j}} \right)} ,\; {p_j} \in {N_i} | (5) |
其中,
| mar{g}_{m}={\displaystyle \sum _{n=1, n\ne m}^{k}spa{r}_{m}\cdot spa{r}_{n}} | (6) |
其中,
确定KNN集合
| scor{e_i} = mar{g_i} - marg | (7) |
其中,
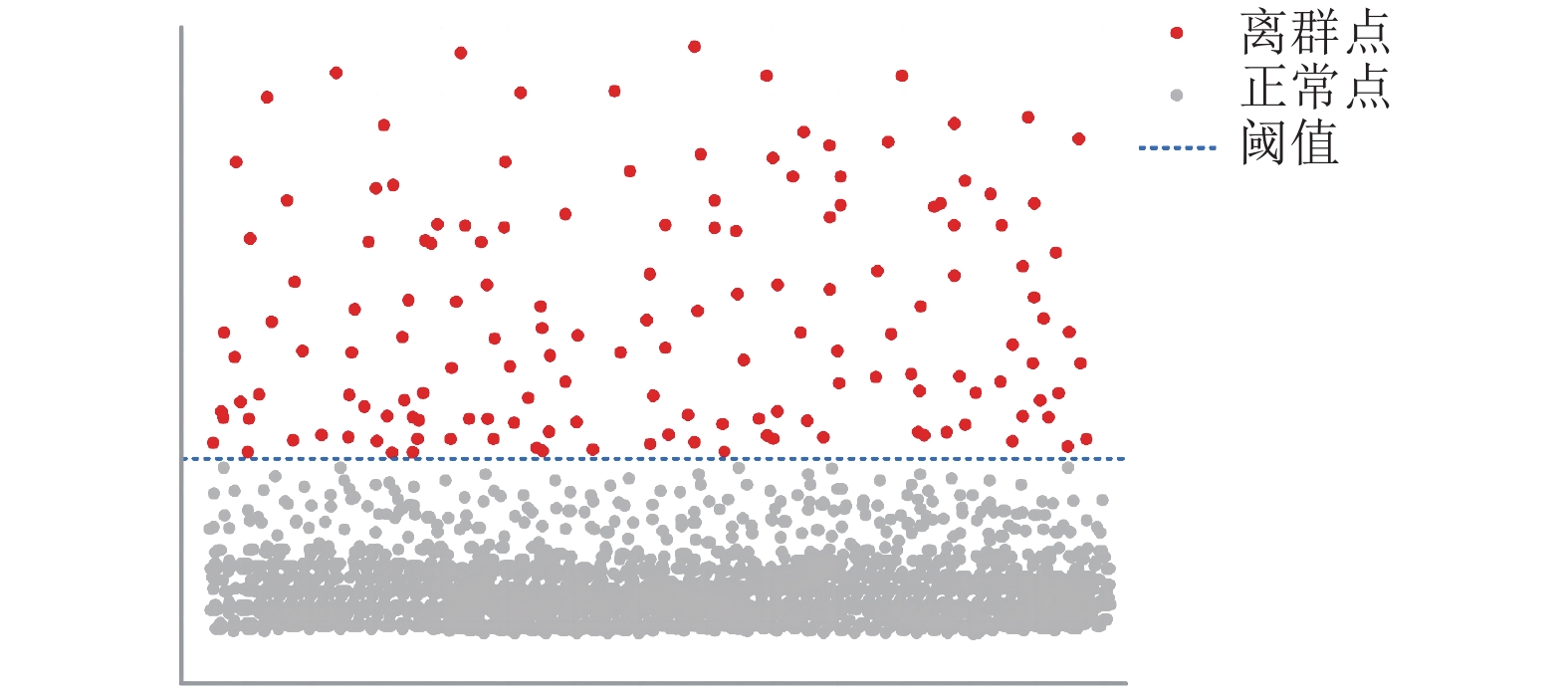
|
图 3 离群点判定示意图 |
基于以上描述, 本文设计的离群点检测算法流程如算法1所示.
算法1. CSOD算法
输入: 训练数据集
输出: 离群点集合.
1) 根据半正矢公式和欧氏距离公式分别计算数据点
2) 对步骤1)中得到的数据点
3) 计算数据点
4) 计算KNN集合中每个数据点的边缘度得分, 将边缘度得分最小的点记作KNN集合的中心点;
5)将数据点
6)迭代移动过程3次, 得到不同的簇和簇中心;
7)选择全体数据点异常值得分的标准差作为阈值, 超过阈值的点记作离群点并纳入到离群点集合.
上述算法使用全局阈值参数来标准化离群点检测. 与其他方法不同的是, 该方法不需要先验知识来设定噪声量, 从而使得该方法易于理解和实现. 我们将异常值得分超过阈值的点定义为离群点, 并进行剔除, 以便在后续的数据挖掘工作中继续使用该数据集. 此外, 聚类后的数据可以用来显示数据密集区域, 并结合网格区域等技术来挖掘轨迹数据的热点信息.
4 实验分析 4.1 实验数据本文实验中使用的轨迹数据来自浙江省海洋与渔业局, 该数据为东经[118°, 128°], 北纬[26°, 36°]海域2015年4月(10000数据量)、2015年5月(5000数据量)、2016年4月(5000数据量)的渔船轨迹数据. 由于AIS轨迹数据的采集容易受到设备故障、天气、海浪等因素的影响, 会导致采集到的定位数据出现缺失、漂移. 因此使用该数据之前需要进行预处理, 包括剔除缺失数据、保留有效字段等步骤. 具体的数据格式如表1所示.
| 表 1 渔船 AIS 数据格式表 |
图4以热力图的方式展示了2015年4月轨迹数据的分布情况, 可以直观地看到不同区域的轨迹点密集程度.

|
图 4 渔船轨迹数据热力图 |
此外, 在原数据集的
现有的离群点检测研究所采用的评估标准通常为二分类任务中的常用评价指标, 即精确率(Precision)和召回率(Recall). 精确率是指被算法标记为离群点的数据点中, 有多少是真正的离群点. 召回率是指在所有真正的离群点中, 有多少被算法正确地标记为离群点. 渔船AIS时空轨迹数据的分布具有随机性, 不同的分布情况会影响精确率和召回率的表现. 如果数据集中离群点的数量较多, 精确率可能会下降, 召回率可能会提高; 相反, 如果离群点数量较少, 精确率可能会提高, 召回率可能会下降. 因此, 为了避免这种影响, 我们采用F1-score作为实验评价指标. F1-score是基于精确率(Precision)与召回率(Recall)的调和平均数, 综合考虑了精确率和召回率两方面的因素, 对两者进行了调和, 从而能够保证离群点检测结果的准确性和完整性. 计算公式表示为:
| F1{\textit{-}}{score}=\frac{2\cdot Precision\cdot {Recall}}{Precision+Recall} | (8) |
| Precision = \frac{{TP}}{{TP + FP}} | (9) |
| Recall = \frac{{TP}}{{TP + FN}} | (10) |
其中, TP (true positive) 表示被正确标记为离群点的数量, 即真正的离群点数量; 而FP (false positive) 则表示被错误标记为离群点的正常点数量, 即误判为离群点的数量. 为了更好地评估本文算法性能, 除了将F1-score作为评价指标外, 我们还将离群点检测时间作为该实验的一个重要评价指标, 并与近年来的其他 4 种异常检测算法进行了对比实验.
4.3 实验结果与分析首先, 本文使用上述提到的AIS轨迹数据集对CSOD算法的聚类效果进行了验证, 实验效果如图5所示. 其中, 图5(a)表示原始轨迹数据的分布, 图5(b)表示经过CSOD算法聚类后的轨迹数据分布. 从图5(a)、(b)的对比可以看到, 原始轨迹数据点经过CSOD算法聚类后形成了不同的簇, 并剔除了分布在边缘的轨迹离群点.
为了评估CSOD算法的性能表现, 我们在数据集上运行了其他4种不同离群点检测算法, 分别是MO-GAAL[20]、NC[21]、iForest[22]、QUE[23], 并对它们的F1-score进行了分析. 5种离群点检测算法的F1-score结果如表2所示.
通过表2中5种算法的F1-score可以看出, 本文CSOD算法的F1-score指标在不同数据集上的表现均优于其他算法. 比如, 2015.04数据集中, 相较于表现最好的QUE算法高出0.06; 2015.05数据集中, 相较于表现最好的iForest算法高出0.07; 2016.04数据集中, 相较于表现最好的iForest算法高出0.06. 这表明CSOD算法能够更有效地消除离群点造成的负面影响, 并且能够更准确地识别数据集中的轨迹离群点.
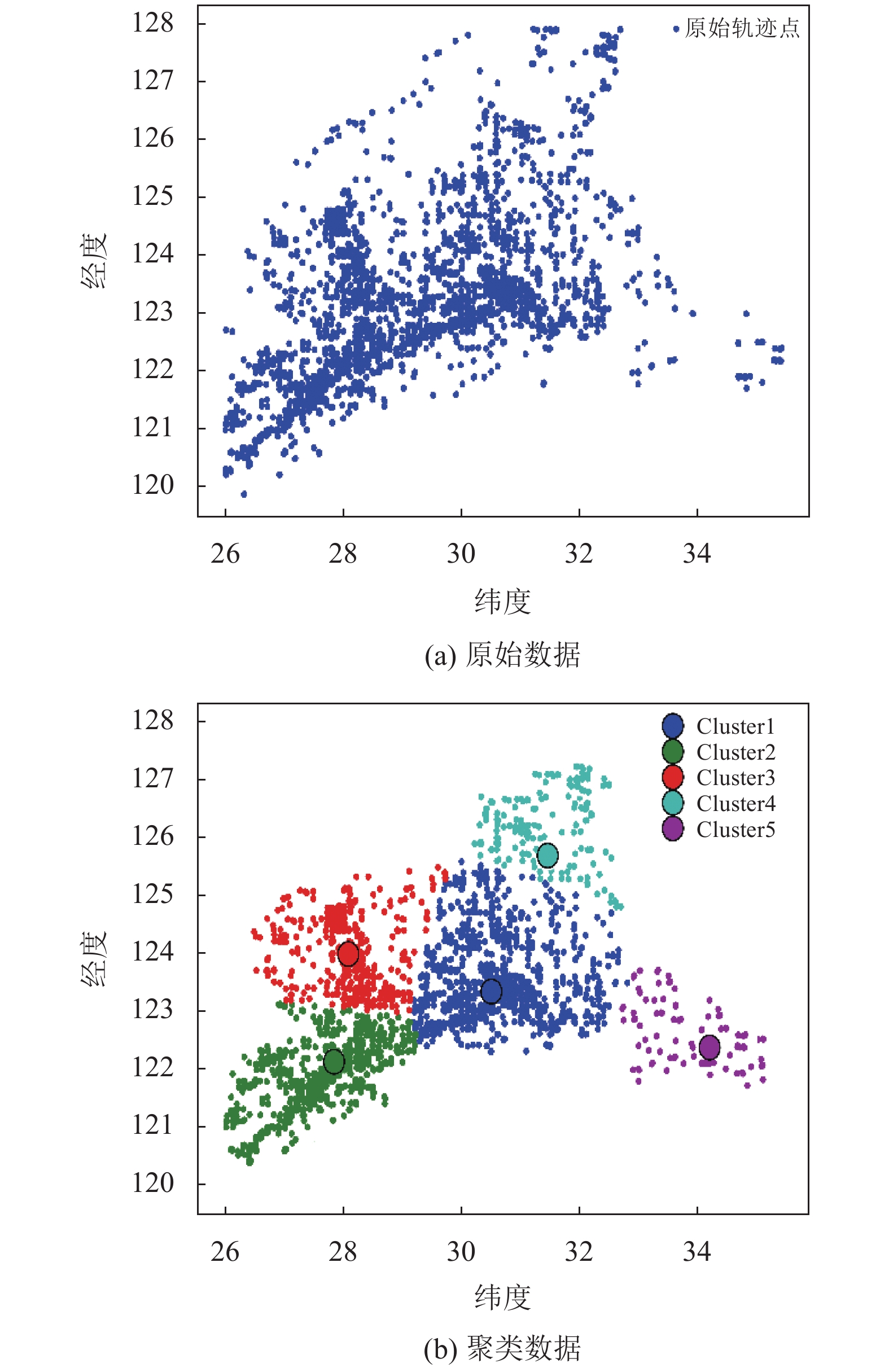
|
图 5 轨迹数据分布示意图 |
| 表 2 不同算法的最佳F1-score(k在2–27之间) |
另外, 比较了5种离群点检测算法在处理不同规模数据集时的时间消耗, 单位为s. 我们选择了2015年4月(10000数据量)与2015年5月(5000数据量)的AIS渔船轨迹数据进行实验. 具体运行时间如表3所示.
通过表3可以看出, CSOD算法在不同规模数据集上的时间消耗均优于其他算法. 比如, 在10000数据量的2015.04数据集中, 相较于耗时最短的NC算法减少了4.8 s; 而在5000数据量的2015.05数据集中, 相较于耗时最短的NC算法减少了3.1 s. 这表明CSOD算法具有更为精简的算法结构, 能够更高效地处理数据.
4.4 实验验证为了进一步验证本文算法的性能, 我们在2015年4月数据集的
通过图6的对比可以看出, 随着数据集中噪声量的增加, 5种离群点检测算法的F1-score在逐渐降低. 然而, 在噪声量相同的情况下, CSOD算法性能明显优于其他4种算法, 进而证明了本文算法具有更强的鲁棒性.
| 表 3 离群点检测时间(k=10) (s) |
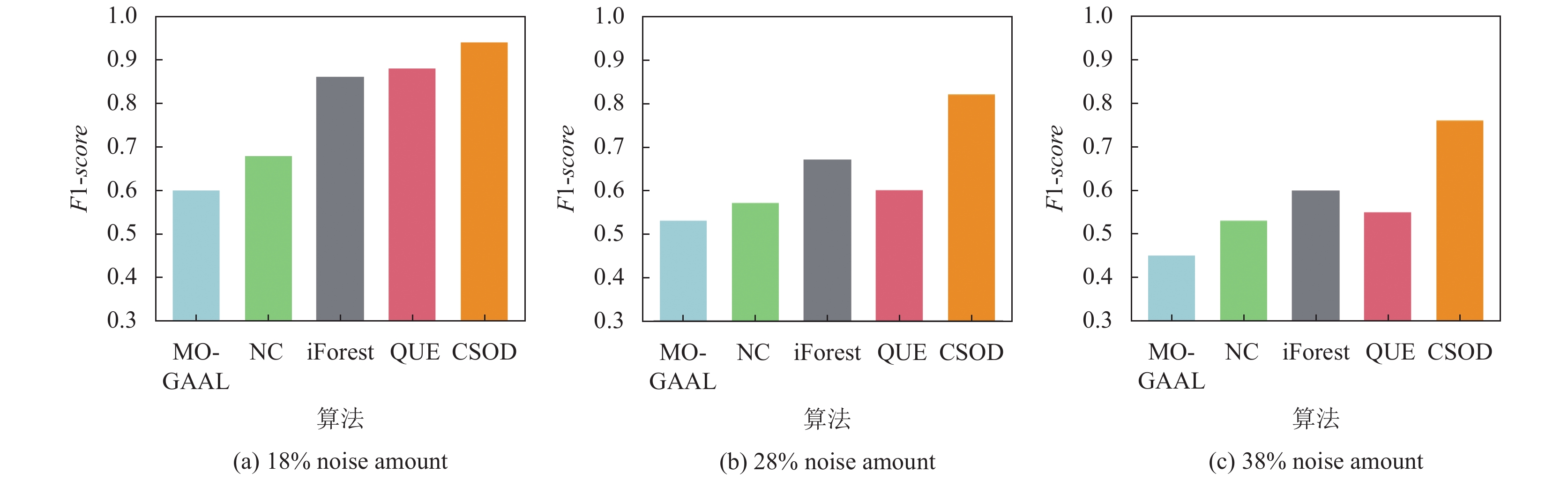
|
图 6 不同噪声量情况下的算法F1-score对比 |
5 结论与展望
本文提出了一种基于中心移动的轨迹离群点检测算法. 通过计算特征距离来确定每个数据点的KNN集合, 然后根据稀疏度计算边缘度得分来确定近邻集合的中心, 最后基于异常值得分的标准差来判定离群点. 我们在浙江海域AIS数据集上对该算法进行了评估, 并与4种经典的离群点检测算法进行了对比实验, 实验使用F1-score和算法运行时间作为评估标准. 结果表明, 本文算法的离群点检测效果明显优于其他算法, 并且在噪声量较高的数据集上也能表现出良好的性能. 未来, 本文算法可以在聚类基础上开展热点挖掘等工作, 以进一步提升算法的应用价值.
| [1] |
Knorr EM, Ng RT. Finding intensional knowledge of distance-based outliers. Proceedings of the 25th International Conference on Very Large Data Bases. New York: Morgan Kaufmann Publishers Inc., 1999. 211–222.
|
| [2] |
Domingues R, Filippone M, Michiardi P, et al. A comparative evaluation of outlier detection algorithms: Experiments and analyses. Pattern Recognition, 2018, 74: 406-421. DOI:10.1016/j.patcog.2017.09.037 |
| [3] |
Boukerche A, Zheng LN, Alfandi O. Outlier detection: Methods, models, and classification. ACM Computing Surveys, 2021, 53(3): 1-37. DOI:10.1145/3381028 |
| [4] |
Moustafa N, Hu JK, Slay J. A holistic review of network anomaly detection systems: A comprehensive survey. Journal of Network and Computer Applications, 2019, 128: 33-55. DOI:10.1016/j.jnca.2018.12.006 |
| [5] |
Andrysiak T, Saganowski L. Network anomaly detection based on statistical models with long-memory dependence. Proceedings of the 10th International Conference on Dependability and Complex Systems. Brunów: Springer. 2015. 1–10.
|
| [6] |
Breunig MM, Kriegel HP, Ng RT, et al. LOF: Identifying density-based local outliers. ACM SIGMOD Record, 2000, 29(2): 93-104. DOI:10.1145/335191.335388 |
| [7] |
Angiulli F, Basta S, Lodi S, et al. Reducing distance computations for distance-based outliers. Expert Systems with Applications, 2020, 147: 113215. DOI:10.1016/j.eswa.2020.113215 |
| [8] |
Pu G, Wang LJ, Shen J, et al. A hybrid unsupervised clustering-based anomaly detection method. Tsinghua Science and Technology, 2021, 26(2): 146-153. DOI:10.26599/TST.2019.9010051 |
| [9] |
Zhu XD, Zhang J, Li HZ, et al. FRIOD: A deeply integrated feature-rich interactive system for effective and efficient outlier detection. IEEE Access, 2017, 5: 25682-25695. DOI:10.1109/ACCESS.2017.2771237 |
| [10] |
Meng FR, Yuan G, Lv SQ, et al. An overview on trajectory outlier detection. Artificial Intelligence Review, 2019, 52(4): 2437-2456. DOI:10.1007/s10462-018-9619-1 |
| [11] |
Bhowmick K, Narvekar M. Trajectory outlier detection for traffic events: A survey. In: Bhalla S, Bhateja V, Chandavale A, et al., eds. Intelligent Computing and Information and Communication. Singapore: Springer, 2018. 37–46.
|
| [12] |
Li XL, Li ZH, Han JW, et al. Temporal outlier detection in vehicle traffic data. Proceedings of the 25th IEEE International Conference on Data Engineering. Shanghai: IEEE, 2009. 1319–1322.
|
| [13] |
Chawla S, Zheng Y, Hu JF. Inferring the root cause in road traffic anomalies. Proceedings of the 12th IEEE International Conference on Data Mining. Brussels: IEEE, 2012. 141–150.
|
| [14] |
Pang LX, Chawla S, Liu W, et al. On mining anomalous patterns in road traffic streams. In: Tang J, King I, Chen, L, et al., eds. Advanced Data Mining and Applications. Berlin: Springer, 2011. 237–251.
|
| [15] |
Chen C, Zhang D, Samuel Castro P, et al. Real-time detection of anomalous taxi trajectories from GPS traces. In: Puiatti A, Gu T, eds. Mobile and Ubiquitous Systems: Computing, Networking, and Services. Berlin: Springer, 2011. 63–74.
|
| [16] |
Knorr EM, Ng RT. Algorithms for mining distance-based outliers in large datasets. Proceedings of the 24th International Conference on Very Large Data Bases. New York: Morgan Kaufmann Publishers Inc., 1998. 392–403.
|
| [17] |
Lei B, Mingchao D. A distance-based trajectory outlier detection method on maritime traffic data. Proceedings of the 4th International Conference on Control, Automation and Robotics (ICCAR). Auckland: IEEE, 2018. 340–343.
|
| [18] |
Liu GY, Zhao HQ, Fan F, et al. An enhanced intrusion detection model based on improved KNN in WSNs. Sensors, 2022, 22(4): 1407. DOI:10.3390/s22041407 |
| [19] |
Alam CN, Manaf K, Atmadja AR, et al. Implementation of haversine formula for counting event visitor in the radius based on Android application. Proceedings of the 4th International Conference on Cyber and IT Service Management. Bandung: IEEE, 2016. 1–6.
|
| [20] |
Liu YZ, Li Z, Zhou C, et al. Generative adversarial active learning for unsupervised outlier detection. IEEE Transactions on Knowledge and Data Engineering, 2019, 32(8): 1517-1528. DOI:10.1109/TKDE.2019.2905606 |
| [21] |
Li XJ, Lv JC, Yi Z. An efficient representation-based method for boundary point and outlier detection. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1): 51-62. DOI:10.1109/TNNLS.2016.2614896 |
| [22] |
Liu FT, Ting KM, Zhou ZH. Isolation-based anomaly detection. ACM Transactions on Knowledge Discovery from Data, 2012, 6(1): 3. DOI:10.1145/2133360.2133363 |
| [23] |
Dong YH, Hopkins S, Li J. Quantum entropy scoring for fast robust mean estimation and improved outlier detection. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Red Hook: Curran Associates Inc., 2019. 545.
|
 2023, Vol. 32
2023, Vol. 32



