随着中国经济持续增长和用电需求的快速增加, 智能电网技术正在逐步成熟. 这项技术能够实现电力系统的自动化、信息化和互动化, 使电网达到现代化水平. 在智能电网中, 阀冷系统^[1]具有重要的地位, 它负责电力的整流和逆变, 其工作效率和可靠性至关重要. 阀冷系统分为内冷水系统和外冷水系统, 并涉及多个关键指标, 如进阀温度、出阀温度、进水压力和出水压力等. 进阀温度是其中最为关键的指标, 它可能直接影响智能电网系统的安全性. 通过预测进阀温度, 工程师们可以及时发现潜在问题, 降低系统故障的概率, 并确保系统的稳定运行. 为了提前了解换流阀设备的运行情况, 工程师们需要定期收集阀冷系统中的各项指标, 并将其构造成时间序列格式的数据, 通过时间序列预测模型来对进阀温度进行预测.

近年来, 时间序列预测模型在风力、电力、股票等工业和商业领域中都具有广泛的应用价值. 现有的时间序列预测模型可以分为基于统计模型的方法和基于深度学习的方法. 基于统计模型的时间序列预测方法主要依赖于历史事件序列数据来预测未来数据. 例如ARIMA模型^[2]或指数平滑^[3], 这些方法通过考虑数据的趋势走向和季节性因素等先验知识, 对未来的数据进行预测. 然而, 在预测复杂的时间序列数据时, 这些模型和方法的效果并不理想, 主要是因为它们难以捕捉到复杂的非线性关系.

为了解决大规模多元时间序列预测问题, 基于深度学习^[4–9]的方法被广泛应用于复杂时间序列数据的建模, 并取得了显著的效果. 其中, 基于循环神经网络(recurrent neural network, RNN)架构^[4,5]的模型可以捕捉时间序列中的复杂模式以及处理任意长度的序列, 但是这类模型存在着梯度爆炸和梯度消失问题, 可能会导致训练效果不佳. 此外, RNN的变体^[6–8]对数据长期依赖存在局限性. 为了克服这些问题, 基于Transformer注意力机制^[9–16]的方法也被用来对序列进行数据建模, Informer模型^[10]在长序列预测方面表现最为显著, 它能够从多维时间序列中捕捉复杂的非线性关系, 并准确捕捉远程依赖关系.

然而, 现有的时间序列预测模型在注重全局依赖关系的同时, 忽视了局部特征信息的重要性. 特别是在基于注意力机制的模型中, 每个时间节点的注意力权重是由该节点与所有其他节点的关系计算得到的, 却忽视了节点之间的局部结构和局部依赖关系的重要性. 在实际的进阀温度预测任务中, 这些局部信息往往对近期温度的变化有着更强的预示性. 现有的模型^[8,9]大多是利用绝对位置信息进行编码, 当序列的长度和位置发生变化时, 绝对位置编码无法准确捕捉元素之间的局部结构和依赖关系. 因此, 本文通过引入相对位置编码, 并使用局部信息提取器来提升模型的局部信息捕捉能力.

此外, 由于环境条件、传感器本身的特性以及数据采集过程中的干扰, 温度传感器可能存在误差, 这种误差可能会影响阀冷系统的稳定性以及时间序列模型对指标的预测结果的准确性. 因此, 本文通过引入一定比例的高斯噪声的同时, 加入对抗训练方法进行对抗扰动, 以提升模型的预测性能和鲁棒性.

本文针对上述问题, 提出了Robust-InTemp, 该模型引入相对位置编码方法, 并提出一种局部信息提取器, 既能够考虑全局依赖关系, 又能够充分利用局部特征信息, 以提高时间序列预测的准确性和可靠性. 此外, 本文提出了两种策略进行对抗扰动, 通过加入基于规则的高斯噪声和基于梯度的对抗训练, 以降低温度传感器的误差对模型预测结果的影响.

为了评估Robust-InTemp模型的有效性, 我们在陈霖等人^[17]在实际工业场景中采集的valve数据集上进行了实验, 实验结果表明, 相较于最先进的Informer深度学习模型, Robust-InTemp在MSE评估指标提升了24.08%, $ {Q_{50}} $ -loss评估指标提升了13.49%, $ {Q_{90}} $ -loss评估指标提升了23.95%.

本文的贡献主要在以下几个方面.

1)本文提出适用于阀冷系统场景的时间序列预测模型Robust-InTemp, 该模型融合了对抗扰动和局部信息增强方法.

2)针对传感器误差问题, 本文引入了两种策略进行对抗扰动, 以提升模型的预测性能和鲁棒性.

3)本文引入相对位置编码方法, 并提出使用局部信息提取器, 更好地捕获时间序列中的局部特征信息, 以提升模型的预测性能.

4)本文在真实数据集valve上的实验结果表明, Robust-InTemp的表现优于现有传统模型和深度学习模型, 并具有更强的鲁棒性.

1 相关工作

当前已经有部分研究专注于阀冷系统中的进阀温度预测, 例如陈霖等人^[17]提出的T2VNN模型等, 它们通过TCN和LSTM深度学习方法对温度进行预测, 并表明了通过时间序列模型对该任务进行预测的有效性. 现有的时间序列预测模型可以分为基于统计模型的方法和基于深度学习的方法.

1.1 基于统计模型的方法

在时间序列预测领域, 基于统计的模型因其理论解释性强和实践中的有效性, 历来都是研究者的重要工具. 自回归模型(autoregressive model, AR)和移动平均模型(moving average model, MA)是基石, Ho等人^[2]提出ARIMA 模型, 它通过结合自回归(AR)、差分整合和移动平均(MA)模型来更好的理解和预测数据. 它在处理非平稳和具有季节性的时间序列时展现出更强的适应性. Hyndman等人^[3]提出指数平滑方法将每个位置的时间序列分解为季节和趋势分量, 从而有效地预测每个位置的未来时间步长.

1.2 基于深度学习的方法

在深度学习应用于时间序列预测的研究中, 许多不同的神经网络模型被引入用以捕捉复杂的时间依赖关系并进行有效的预测. Borovykh等人^[18]提出使用卷积神经网络 (convolutional neural network, CNN)进行时间序列预测, 并发现一维卷积核能够发现时间序列中的局部模式. Salinas等人^[5]提出使用循环神经网络的变种长短期记忆网络(long short-term memory, LSTM)进行时间序列预测, 其能够在网络的隐藏层保持“记忆”, 可以捕捉到跨时间步的信息. Zhou等人^[10]提出使用Transformer模型进行时间序列预测, 并对Transformer进行计算效率的改进, 其自注意力机制能够更好地捕捉序列中的长距离依赖性.

1.3 对抗扰动

对抗扰动^[19]是一种有意义的数据扰动方法, 特别是在面对数据集不足和数据集准确性不高的情况下. 常见的方法是添加高斯噪声^[20,21]、对抗性攻击方法^[22–26]等. Shorten等人^[20]通过大规模实验证明, 将噪声添加到训练集中可以降低模型的敏感性, 从而提高模型的泛化性能. 这些方法可以在保持数据属性不变的情况下对数据进行扰动, 从而欺骗深度学习模型, 提高模型的鲁棒性. 对抗训练^[27]主要是通过添加鉴别器或基于梯度的方式构造扰动, 形成对抗样本并将其加入原始数据集, 从而提升模型对对抗样本的防御能力, 增强模型的泛化能力和鲁棒性. 如何确定添加扰动的规模是对抗训练中的关键问题. Goodfellow等人^[22]首次提出对抗训练的概念, 通过在原始数据集中引入一定程度的扰动来训练对抗样本, 从而提升性能. Miyato等人^[23]提出FGM (fast gradient method), 根据具体的梯度生成更好的对抗样本. Madry 等人^[24]提出了PGD (projected gradient descent)方法, 从优化的角度提出了min-max公式, 确保扰动不过大, 构造出更强大的对抗样本.

1.4 位置编码

位置编码是在自然语言处理和深度学习中用于处理序列数据的一种重要技术, 主要目标是为序列中的每一个位置提供一种表示其相对或绝对位置的向量表示. Vaswani等人^[28]首次提出位置编码概念并引入绝对位置编码, 为输入序列中的每个位置分配一个表示其位置的信息, 为模型提供了一个稳定可靠的位置表示, 但是其无法直接捕捉序列中位置之间的相对关系. Shaw等人^[29]提出相对位置编码, 是一种基于位置之间相对关系的编码方法, 可以更好地捕捉序列中不同位置之间的局部依赖关系. Marcos 等人^[30]提出旋转位置编码, 其通过对位置编码向量进行旋转操作来捕捉序列中的位置信息, 可以在编码向量中模拟出不同的位置关系, 但是旋转编码只适用于长序列且会增加额外的学习负担, 相对位置编码更适合本任务.

2 数据建模

本节首先针对阀冷系统中进阀温度的预测问题进行数据建模, 然后针对本文提出的Robust-InTemp模型架构(图1)进行介绍.

2.1 问题建模

我国智能电网中阀冷系统检测设备被广泛应用. 每个设备都配备了多个监测指标. 将这些监测指标按照时间顺序排列可以得到一个包含进阀温度等多种指标的时间序列数据集. 在具有固定大小窗口的滚动预测设置下得到输入序列 $ {\chi ^t} = \{ x_1^t, \cdots , x_{{L_x}}^t|x_i^t \in {R^{{d_x}}}\} $ , 表明在 ${{t}}$ 时刻共有L种特征维度的序列作为输入, 具体特征维度包括时间、进阀温度、出阀温度、水压等. 模型在捕获到输入序列后, 输出为在 ${{t + 1}}$ 时刻预测的相应进阀温度 $ y_{}^{t + 1} $ . 基于此, 我们可以得到整个时间段中的预测进阀温度 $ {Y^t} = \left\{ {y_{}^0, \cdots , y_{}^t} \right\} $ . 对于模型的输出使用MSE指标来评价 $ {Y^t} $ 和真实进阀温度序列的误差, 使用 $ {Q_{50}} $ -loss和 $ {Q_{90}} $ -loss来评价模型的鲁棒性. 在接下来的章节中将详细介绍Robust-InTemp模型中的各个构建模块.

2.2 Robust-InTemp模型

Robust-InTemp (图2) 以Informer^[10] 作为基座模型, 采用了Seq2Seq架构, 以处理序列输入和输出的任务. 其中, Informer针对长序列预测问题对注意力机制进行了改进, 因此非常适用于进阀温度预测问题. 在此基础上, Robust-InTemp旨在增强模型对局部信息的建模能力. 它通过改进位置编码和注意力机制的方式来实现, 文中引入了相对位置编码^[29], 以捕获序列中的局部依赖关系. 同时, 提出了一种局部信息提取器, 它将提取到的特征信息与模型的自注意力值进行加权求和得到最终的特征信息, 使模型在处理最近的时间序列数据时能够更加关注局部变化. Robust-InTemp模型由编码器、解码器和局部信息提取器组成. 其中编码器和解码器的每个层级都包含两个主要组件: 多头注意力子层和全连接前馈子层. 此外, 为了保持数据的稳定性和有效性, 在每个子层之后都添加了一个归一化层.

2.2.1 相对位置编码

数据在输入编码器之前需要对输入数据进行特征编码, 特征编码包括标量投影、时间戳和位置编码. Informer模型采用绝对位置对序列数据进行编码:

$ PE(pos, 2k) = \sin \left( {\frac{{\textit{pos}}}{{{{\left( {2{L_x}} \right)}^{\frac{{2k}}{{{d_{{\text{model}}}}}}}}}}} \right) $

(1)

$ PE(pos, 2k + 1) = \cos \left( {\frac{{\textit{pos}}}{{{{\left( {2{L_x}} \right)}^{\frac{{2k}}{{{d_{{\text{model}}}}}}}}}}} \right) $

(2)

其中, $k\in \left\{1, \cdots , \left\lfloor \dfrac{{{d}}_{\text{model}}}{2}\right\rfloor \right\}$ , $pos$ 表示当前序列的节点位置, ${d_{{\text{model}}}}$ 表示输入的维度, ${L_x}$ 表示序列长度.

绝对位置编码在处理序列长度和位置顺序变化时存在限制, 无法准确捕捉元素之间的局部结构和依赖关系, 考虑到模型就是依靠前一段的时间序列来预测后续的时间序列, 因此Robust-InTemp模型引入相对位置编码, 其公式如下:

$ PE(i, j, 2k) = \sin \left( {\frac{{i - j}}{{{{\left( {2{L_x}} \right)}^{\frac{{2k}}{{{d_{{\text{model}}}}}}}}}}} \right) $

(3)

$ PE(i, j, 2k + 1) = \cos \left( {\frac{{i - {{j}}}}{{{{\left( {2{L_x}} \right)}^{\frac{{{{2k}}}}{{{{{d}}_{{\text{model}}}}}}}}}}} \right) $

(4)

其中, $i$ 和 $j$ 表示序列中的位置索引. 相对位置编码不仅考虑节点的绝对位置, 还考虑了节点之间的相对位置关系, 以增强局部的位置信息.

2.2.2 Encoder层

编码器可以有效地捕捉长序列输入的长期依赖性. 当输入序列进入编码器后, ${\chi _{{t}}}$ 作为第 $ t $ 个序列被构造成一个矩阵 $X_{{\rm{en}}}^t \in {R^{{L_x} \times {d_{{\rm{model}}}}}}$ . 编码器利用多头自注意力层来捕获输入的重要部分, 并将多头自注意力层的输出反馈给前馈神经网络.

Informer在多头自注意力层上进行了改进, 相较于传统Transformer模型, 它降低了常规自注意力计算复杂度和空间复杂度. 具体而言, Informer设计了一种名为ProbSparse的自注意力机制. 在传统自注意力机制中, 查询向量(query)和键向量(key)的每个元素都会参与到注意力分数的计算中. 然而, ProbSparse则是只选取查询向量和键向量中分值较大的一部分来计算注意力分数, 从而大幅度提高了计算效率. 其选取方法的具体公式如下:

$ M({q_i}, K) = \ln \sum\limits_{j = 1}^{{L_K}} {{{\rm{e}}^{\frac{{{q_i}k_j^{\rm{T}}}}{{\sqrt d }}}}} - \frac{1}{{{L_K}}}\sum\limits_{j = 1}^{{L_K}} {\frac{{{q_i}k_j^{\rm{T}}}}{{\sqrt d }}} $

(5)

$ \overline M ({q_i}, K) = \mathop {\max }\limits_j \left\{ \frac{{{q_i}k_j^{\rm{T}}}}{{\sqrt d }}\right\} - \frac{1}{{{L_K}}}\sum\limits_{J = 1}^{{L_K}} {\frac{{{q_i}k_j^{\rm{T}}}}{{\sqrt d }}} $

(6)

其中, $ {q_i} $ 表示query中的第i个维度, $ {k_j} $ 表示query中的第j个维度.

对于给定长度为 $ L $ 的序列, 模型对query向量中的q按照 $ 5 \cdot \ln L $ 的长度随机采样k, 根据式(5)计算每个query的稀疏性得分并选择 $ 5 \cdot \ln L $ 个query, 只计算 $ 5 \cdot \ln L $ 个query和key的点积结果, 进而得到attention结果. 其余没有用到的q和k则使用query和key的均值替代. 式(6)是式(5)的近似结果, 可以降低自注意力层的时间复杂度变为 ${\rm{O}}(L \cdot \ln L)$ .

为了更快地处理, 计算可以以矩阵的形式完成, 公式如下:

$ Attention(Q, K, V) = {\textit{Softmax}}\left(\frac{{\overline Q {K^{\rm{T}}}}}{{\sqrt d }}\right)V $

(7)

其中, $\overline Q $ 是与query大小相同的稀疏矩阵, 在稀疏度量为 $ M(q, K) $ 的尺度下它仅包含Top-u个q (u= $ 5 \cdot \ln L $ ).

此外, Informer同样采用多头注意力机制, 在多头的视角下, 每头的注意力生成不同的稀疏的query-key键值对, 从而避免丢失重要的信息.

2.2.3 局部信息提取器

为了提升Robust-InTemp模型的局部信息增强的能力, 模型在Informer的基础上提出了一种局部信息提取器(图3), 与Informer模型本身的自注意力机制进行融合. 其中, 自注意力机制负责全局依赖性的捕获, 而局部信息提取器则专注于局部结构和依赖关系的学习. 具体来说, 局部信息提取器采用一维卷积层进行局部特征的捕捉, 然后通过门控线性单元(gated linear unit, GLU)^[31] 进行特征选择和信息融合. 最后, 这两种机制的输出经过矩阵加权求和, 生成最终的特征表示. 通过这种方式, Robust-InTemp能够充分捕捉和利用时间序列数据中的全局和局部信息, 从而进一步提升预测的准确性.

具体来说, 一维卷积层通过在输入序列上滑动一个固定大小的窗口进行局部特征提取. 窗口中的每个元素与卷积核相对应, 然后对窗口内的数据进行加权求和, 形成新的特征. 这个过程可以表示为以下公式:

$ {y_i} = f\left( {\sum\limits_{j = 0}^{k - 1} {{w_j} \cdot x_{i \times s + j}^t + b} } \right) $

(8)

其中, $f$ 是激活函数, $s$ 是卷积步长, ${w_j}$ 表示卷积核的第 $j$ 个权重, $b$ 是偏置项.

GLU对一维卷积的输出分成两部分, 其中一部分会经过Sigmoid函数处理, 生成一组在0和1之间的值, 这些值作为“门”控制信息的流动. “门控”操作的目的是为了选择性地强化或抑制一维卷积的输出中的某些特征. 然后, 这些经过门控处理的值会与另一部分的输出进行逐元素相乘, 从而生成最终的特征表示. 这一过程可以通过以下公式表示:

$ GLU\left( {{x}} \right) = \sigma \left( {x \cdot {W_1} + {b_1}} \right) \odot \left( {x \cdot {W_2} + {b_2}} \right) $

(9)

其中, $x$ 是输入向量, $\sigma $ 是Sigmoid函数, ${W_1}$ 和 ${W_2}$ 是权重矩阵, ${b_1}$ 和 ${b_2}$ 是偏置向量.

GLU在模型中发挥着重要作用, 通过门控操作可以有选择性地过滤输入, 只保留重要的特征. 这种操作使模型能够有效地学习时序数据之间的局部依赖和关联信息. 此外, GLU的输出经过残差连接与原始嵌入层的输入相结合, 这种操作有助于保留输入的原始信息, 进而解决了梯度消失问题, 增强了模型的表示能力和泛化能力. 然后, 这个组合的输出进入全连接层进行后续处理.

2.2.4 Decoder层

解码器使用标准解码器结构, 它由两个相同的多头注意力层组成, 分别是掩码自注意力层和编码器-解码器注意力层. 利用生成推理(generative inference)可缓解长序列预测中的速度骤降问题. 将下面的向量反馈给解码器:

$ X_{{\rm{de}}}^t = {\text{Concat(}}X_{{\rm{token}}}^t{\text{, X}}_0^t{\text{)}} \in {R^{({L_{{\rm{token}}}} + {L_y}) \times {d_{{\text{model}}}}}} $

(10)

其中, $X_{{\rm{token}}}^t \in {R^{{L_{{\rm{token}}}} \times {d_{{\text{model}}}}}}$ 是开始的token, $X_0^t \in {R^{{L_{{y}}} \times {d_{{\rm{model}}}}}}$ 是目标序列的占位符.

掩码多头自注意力层在进行ProbSparse自注意力计算时采用了一种特殊的方法: 为了避免自回归过程中对未来位置的依赖, 我们将那些对应于未来位置的点积掩码设置为负无穷大. 这种处理使得在后续的Softmax操作中, 对应未来信息位置的权重接近于零, 进而实现了信息的因果传播. 最终, 经过全连接层的转化, 模型能够输出最后的预测结果.

2.3 对抗扰动 2.3.1 基于规则的高斯噪声

考虑到阀冷系统中的传感器经常受到恶劣的环境的影响, 这可能会导致数据读数出现误差. 经过相关资料的查阅^[32], 该传感器中可能会存在 $ \pm 0.5 $ ℃的误差, 而且随着季节、气候等环境变化, 传感器收集的数据分布可能会随着时间发生变化, 产生概念漂移现象, 这可能导致训练好的模型在面对新的、略有差异的数据时预测性能下降. 为了这些问题并更真实地模拟实际应用场景, 文中提出向原始数据中添加一定比例的噪声, 提升模型的泛化性能.

针对阀冷系统的数据集, 本文对进阀温度、出阀温度等维度添加噪声. 如图4所示, 假设坐标系中(x, y)表示x时刻传感器示数为y. 所使用的公式如下:

$ G(x, y) = f(x, y) + n(x, \hat y ) $

(11)

其中, $ n(x, \hat y ) $ 表示添加的噪声.

为了确保添加的噪声符合一定的分布规律, 可以使用高斯噪声^[21]对原始数据集进行扰动.

如图4(b)所示, 高斯噪声是指随机产生噪声的概率密度函数服从高斯分布, 高斯一维分布及其概率密度如下:

$ P(X) = N(\mu , {\sigma ^2}) $

(12)

$ n(x) = \frac{1}{{\sqrt {2{\text π} } \sigma }}{{\rm{e}}^{ - \frac{1}{2}{{(\frac{{x - \mu }}{\sigma })}^2}}} $

(13)

其中, μ表示均值, $ {\sigma ^2} $ 表示方差. 特别当μ=0, $ {\sigma ^2} $ =1时, X的分布为标准正态分布.

2.3.2 基于梯度的对抗训练

阀冷系统中的传感器每半小时记录一次数据, 这意味着要收集大量的数据以提升模型的预测性能需要相当长的时间. 为了解决这一问题, 文中选择利用对抗训练来增加数据集的多样性. 对抗训练是一种基于梯度的方法, 它通过向输入数据添加微小扰动来生成对抗样本, 使模型能够更好地应对各种干扰和攻击. 在确定扰动大小这一关键步骤中, 采用PGD方法^[26], 该方法相比于其他对抗训练方法在初始化时有一个随机的扰动而不是从0开始, 使得其可以在搜索空间中更广泛地探索, 有更大的机会找到成功的对抗样本, 还可以跳出某些局部最优解并探索全局最优解, 提高攻击成功率.

PGD是一个一阶的优化算法, 它从对抗鲁棒性的角度出发, 把寻找最优扰动的问题转化为寻找鞍点的问题. PGD将添加扰动的约束都规约到min-max最优化框架里, 然后在该框架内生成对抗样本去训练. min-max公式如下:

$ \mathop {\min }\limits_\theta \{ {E_{(x, y)\sim D}}[\mathop {\max }\limits_{\delta \in S} L(\theta , x + \delta , y)]\} $

(14)

其中, D为输入样本的分布, L为损失函数, S为扰动的范围空间. max函数是为了找到最坏情况的扰动, min函数是为了计算出最鲁棒的模型参数.

PGD的优化是在一个扰动半径为 $ \varepsilon $ 的空间中进行, 在每一步优化过程中, 如果走出扰动半径则会通过一个映射算法将其重置回扰动半径范围内以确保扰动不会过大始终保持在一个合理的范围内, PGD产生对抗样本的公式如下:

$ {x^{t + 1}} = \prod\nolimits_{x + S} {({x^t} + \alpha {sgn} ({\nabla _x}L(\theta , x, y)))} $

(15)

其中, $ \alpha $ 为小步的步长, $ S = r \in {R^d} $ , $ {\left\| r \right\|_2} \leqslant \varepsilon $ .

基于梯度的对抗训练PGD的算法步骤如算法1所示.

算法1. PGD算法

(1)对于输入input, 计算input的前向损失(loss)并进行反向传播得到梯度并备份;

(2) 对于每一步的t:

　　1) 根据embed矩阵的梯度计算出球面半径r, 并添加到embed矩阵中得到x+r, 如果超出范围则投影回 $\scriptstyle \varepsilon$ 内;

　　2) 如果t不是最后一步:

　　　　根据步骤1)中的x+r进行前向和反向计算得到梯度, 再继续执行步骤1);

　　 如果t是最后一步:

　　　　恢复(1)的梯度, 根据步骤1)中x+r进行前向和反向计算得到梯度并将梯度累加到(1)的梯度上, 跳出循环;

(3) 将embed矩阵还原为(1)时的值;

(4) 根据步骤2)中的梯度, 更新模型参数.

在每次循环迭代中, PGD算法计算目标函数的梯度进行微小的更新. 循环迭代次数决定了算法的收敛程度, 扰动大小 $ \varepsilon $ 是一个限制输入扰动的阈值, 确保扰动后的输入与原始输入之间的差异不会超过给定的范围. 为了模拟真实的场景, 这根据相关资料^[32]查阅, 实验中的 $ \varepsilon $ 设定为0.5.

3 实验分析 3.1 对比方法

为了评估Robust-InTemp模型的性能, 本文选取了5个基准方法, 这些方法被广泛应用于时间序列预测任务上.

● Autoregressive自回归模型^[33]是采用多步观察值加权的传统时间序列预测方法.

● ARIMA^[2]是一个适用非平稳时间序列预测的统计模型.

● DeepAR^[5]是基于LSTM的概率预测模型.

● LSTNet^[34]是结合自回归和LSTM的时间序列预测模型

● Informer^[10]是基于Transformer的时间序列预测模型.

3.2 评估指标

本文使用两个评价指标, 一个是针对预测结果的准确度, 另一个是从全局的角度来评估数据的分布和模型性能, 定义如下.

● 均方误差(MSE):

$ {\textit{MSE}} = \frac{1}{n}\sum\nolimits_{i = 1}^n {(y - {\hat y} )}^2 $

(16)

● 归一化分位数损失( $\rho {\textit{-}} {\text{risk}}$ , $ \rho \in (0, 1) $ ):

$ {Q_\rho }(y, \hat y ) = 2\frac{{\displaystyle\sum\nolimits_{i, t} {{P_\rho }({y_{i, t}}, {{\hat y }_{i, t}})} }}{{\displaystyle\sum\nolimits_{i, t} {\left| {{y_{i, t}}} \right|} }} $

(17)

$ {P_\rho }({y_{i, t}}, {{\hat y}_{i, t}}) = (\rho - {{ I}_{(y \leqslant \hat y )}})(y - \hat y) $

(18)

其中, y表示真实值, $ \hat y $ 表示预测值. MSE值越小表示预测的准确度越高. ${{ I}_{(y \leqslant \hat y )}}$ 是指标函数. $ {Q_{50}} $ 和 $ {Q_{90}} $ 分别表示 $\; \rho = 0.5 $ 和 $\; \rho = 0.9 $ 的分位数损失, 作为本次实验的评价指标, 两者也是越小代表模型性能越好.

3.3 数据和环境描述

实验数据集源自陈霖等人^[17]采集的电网阀冷系统中的4个传感器, 这些传感器代表的各项指标的记录频率为每30 min一次, 时间从2017年12月3日16:00开始到2019年7月31日23:30结束, 共有29057个数据. 该数据集一共有5个维度的数据, 分别是测量时间、进阀温度、出阀温度、进阀压力和冷却水电导率. 其中, 进阀温度被视为最重要的指标, 并在本实验中被选为预测目标. 我们遵循Zhou等人^[10]的方法, 数据集以时间顺序按照Informer模型中7:1:2的比例划分为训练集、验证集和测试集.

研究中涉及的实验部分均基于 PyTorch 框架^[35]实现, 对于基准方法的实现, 我们根据论文中的描述重新实现了这些方法, 并且这些方法的执行结果与原始论文中的结果接近.

实验运行的计算机的配置信息是: Intel 4210 CPU、8 GB 显存的 GeForce RTX 2070 GPU、Windows 操作系统.

3.4 实验细节

Robust-InTemp模型的具体超参配置如表1所示. 其中epoch表示实验的迭代次数, learning_rate表示学习率, batch_size表示每次数据输入的大小, activation表示激活函数, n_heads表示多头数目, optimizer表示优化器, encoder_layer表示编码器自注意力层数, decoder_layer表示解码器自注意力层数. 对于编码器, 每次输入的序列长度为96个, 涵盖了5个维度的数据. 对于解码器, 输入是48个时间序列的进阀温度数据, 其中后24个时间步被设为0进行学习, 解码器输出24个时间序列, 作为预测结果, 从而提供未来12 h的出阀温度参考. 在损失函数的选择方面, 一般的时间序列预测更多的是使用均方误差(MSE)、平均绝对误差(MAE)等. 然而, 现实世界中的时间序列数据集通常具有一定的随机性倾向, 为了从全局的角度去考察模型的性能, 需要使用多个损失函数来进行评估, 实验中使用归一化分位数损失函数(normalized quantile loss)^[13], 该损失函数通过改变分位数的大小来调整损失函数的形状, 实验中有两个分位数为0.5和0.9, 记为 $ {Q_{50}} $ -loss和 $ {Q_{90}} $ -loss.

3.5 实验结果

为了评估模型的性能, 实验中将预测的步长统一设置为24步,MSE指标的损失函数是分位数为0.5的结果. 具体实验结果如表2所示, 由表2中可以得知, 基于对抗扰动和局部信息提取器的模型在预测性能方面表现出明显的提升.

与传统的机器学习算法ARIMA相比, Robust-InTemp模型在MSE指标上提升了24.98%, $ {Q_{50}} $ -loss和 $ {Q_{90}} $ -loss分别提升了18.50%和35.87%, 这种提升是显著的, 这是因为ARIMA可以较好地捕捉序列中的短期依赖关系, 但在全局依赖关系方面的表现较差且局部信息提取器表现更好.

相对于Informer模型, 3个指标依次提升了24.08%, 13.49%和23.95%. 由此可以证明尽管Informer模型可以有效捕捉全局的依赖关系, 但是对于局部信息的捕捉能力有限, 从MSE指标提升24.08%可以看出, 本文方法中的相对位置编码和局部信息提取器可以有效解决这个问题. 为了有效提升模型的鲁棒性, 模型采用对原始数据集添加不同比例的高斯噪声, 以及在模型训练过程中采用基于梯度的对抗训练方法PGD, 从 $ {Q_{50}} $ -loss和 $ {Q_{90}} $ -loss指标的提升可以看出方法的有效性. 因此, 将基于对抗扰动和局部信息提取器的方法进行结合, 不仅提升了模型的预测性能和鲁棒性, 还使模型具有更好的抗干扰能力, 能够更好地应对数据中的噪声、概念漂移以及局部信息不明显等问题.

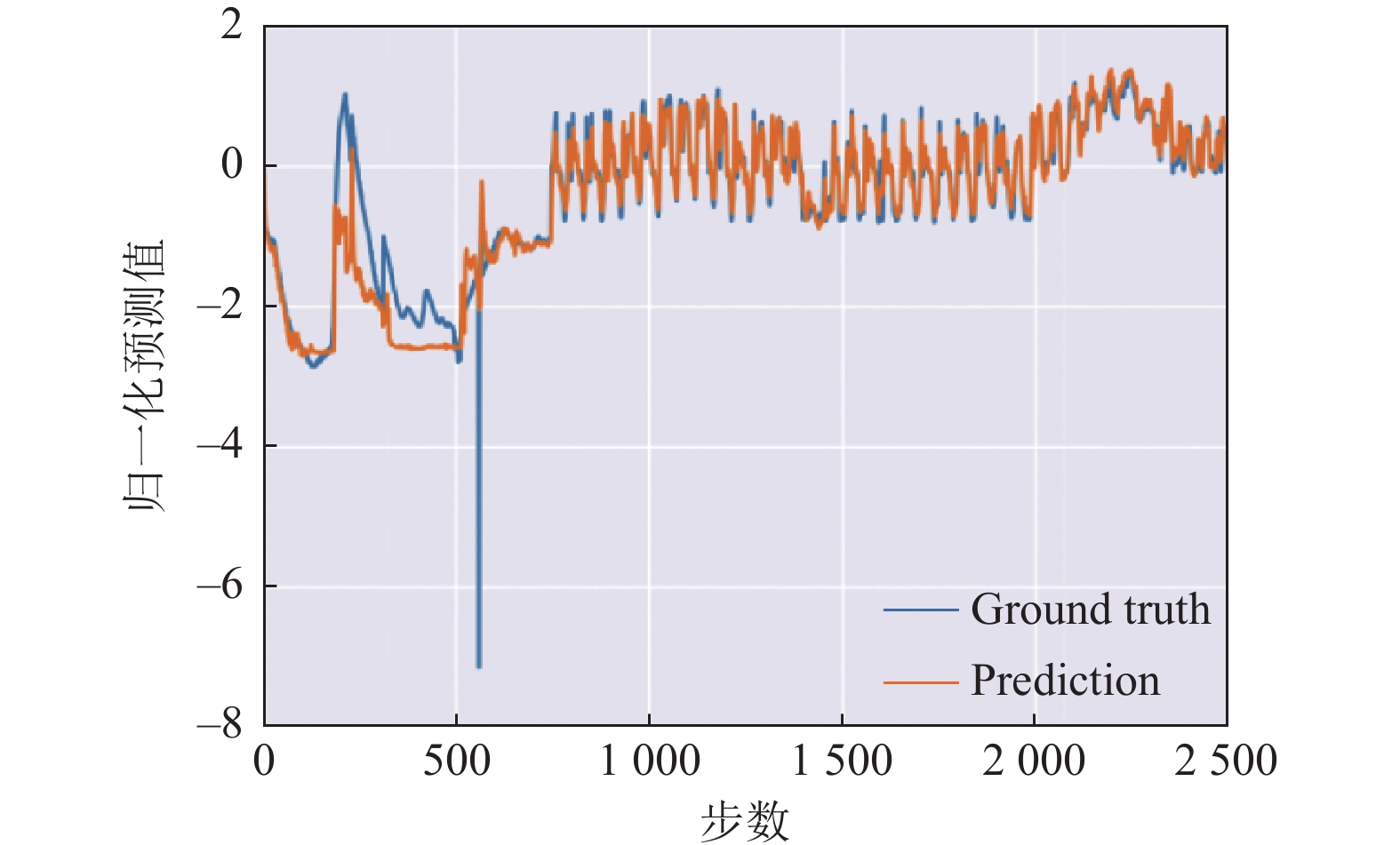
为了具体展示模型的预测结果, 分两种情况进行展示: 一是展示单次预测的24个步长, 如图5所示, 模型是通过前48个步长来预测未来的24个步长, 通过对前48个步长进行分析, 可以较好地预测出变化趋势. 二是对前2500个预测结果进行展示, 如图6所示. 图中黄色线表示预测结果, 可以明显看出Robust-InTemp模型可以高效地捕捉到全局的复杂模式, 并且能够很好地对局部信息进行捕捉. 另外, 蓝色真实值部分有一个明显的缺失值, 而模型也能很好的继续进行预测, 表现出较好的对抗能力.

3.6 消融实验

为了衡量Robust-InTemp中各个组成部分对于Robust-InTemp模型整体性能包括预测、鲁棒性等的效果提升, 设计相应的消融实验. 即对对抗扰动和局部增强机制进行单独的实验以验证其效果. 对于对抗扰动中两个方法: 添加基于规则的高斯噪声和基于梯度的对抗训练方法分别进行单独的实验. 对于局部信息增强的两个模块: 采用相对位置编码和局部信息提取器分别进行单独的实验. 另外, 为了验证模型的鲁棒性的提升, 向模型中添加不同比例的高斯噪声扰动, 共有4种比例分别是10%, 20%, 50%以及100%. 如表3所示, 可以得出以下结果.

(1) Robust-InTemp/G-10表示只用了添加基于规则的高斯噪声方法且噪声扰动比例为10并以此类推, Robust-InTemp/T表示只用了基于梯度的对抗训练方法. 不同比例的噪声对模型的预测性能均有不同程度的提升. 其中, 添加50%的噪声比例会使模型的预测性能达到最佳. 由此可以分别证明添加基于规则的高斯噪声方法和基于梯度的对抗训练方法均对模性的预测性能和鲁棒性有所提升;

(2) Robust-InTemp/R表示仅使用相对位置编码, Robust-InTemp/E表示仅使用局部信息提取器. 3个指标相较于原始Informer模型均有提升. 由此可以分别证明使用相对位置编码和局部信息提取器均对模型的预测性能和鲁棒性有所提升.

由此可以得出, 本文提出的4个不同的模块方法, 在评价指标中均优于原生的Informer模型, 除了个别指标模块单独进行实验的结果相较于Robust-InTemp模型没有达到最佳的预测性能. 综上所述, 本文所提出的几个模块方法对模型的整体性能均存在贡献.

4 总结

本文针对阀冷系统进阀温度预测问题, 提出了一个基于对抗扰动和局部信息增强的深度学习模型Robust-InTemp. 通过在原始数据集中添加基于规则的高斯噪声和使用基于梯度的对抗训练, 模型成功模拟了真实应用场景中传感器示数存在误差的情况, 从而提升了模型的预测性能和鲁棒性. 针对Informer模型对于局部信息捕捉不足的问题, 引入相对位置编码和局部信息提取器, 以提升模型对于局部信息的捕捉能力. 此外, 采用归一化分位数损失函数有助于更好地捕捉序列中的关系. 实验结果表明, 本文方法在模型预测和鲁棒性方面超越了多个传统模型以及深度学习模型. 通过消融实验证明本文提出的4个模块方法对模型提升均存在贡献.