基于自适应权重和莱维飞行的改进海鸥优化算法

引用本文

奚金明, 郑荣艳. 基于自适应权重和莱维飞行的改进海鸥优化算法. 计算机系统应用, 2023, 32(12): 171-179.http://www.c-s-a.org.cn/1003-3254/9326.html

Xi JM, Zheng RY. Improved Seagull Optimization Algorithm Based on Adaptive Weight and Levy Flight. Computer Systems and Applications, 2023, 32(12): 171-179(in Chinese).http://www.c-s-a.org.cn/1003-3254/9326.html

基于自适应权重和莱维飞行的改进海鸥优化算法

奚金明, 郑荣艳

贵州财经大学大数据统计学院, 贵阳 550025

收稿日期：2023-05-30; 修改日期：2023-07-03; 采用时间：2023-07-19; csa 在线出版时间：2023-09-21

通讯作者：奚金明, E-mail: 1510400395@qq.com.

摘要：在齿轮系设计问题中, 传统算法存在计算复杂与精度低等缺点, 海鸥优化算法(SOA)得益于其算法原理简单、通用性强、参数少等特性, 现多用于工程设计问题. 然而, 标准海鸥优化算法易出现寻优精度低、搜索速度慢等问题, 本文提出一种混合策略改进的海鸥优化算法(WLSOA). 首先, 利用非线性递减策略增强海鸥优化算法的探索开发能力, 提高寻优精度. 其次, 在海鸥攻击阶段引入自适应权重平衡全局与局部的搜索能力和加入莱维飞行步长对当前最优解进行扰动, 提高算法跳出局部最优值的能力. 然后分别使用WLSOA、黄金正弦算法、鲸鱼优化算法、粒子群优化算法、传统海鸥优化算法及最新提出的改进海鸥优化算法, 通过在9个经典的测试函数上进行仿真实验来探究WLSOA的性能. 结果表明, WLSOA比其他6种算法寻优精度更高, 收敛速度更快. 最后, 在齿轮系设计问题上, 通过与其他13种常见的群智能算法的比较表明, WLSOA的求解性能优于其他算法.

关键词: 全局搜索能力自适应权重莱维飞行步长测试函数

Improved Seagull Optimization Algorithm Based on Adaptive Weight and Levy Flight

XI Jin-Ming, ZHENG Rong-Yan

College of Big Data Statistics, Guizhou University of Finance and Economics, Guiyang 550025, China

Abstract: In gear train design, traditional algorithms exhibit drawbacks such as computational complexity and low accuracy. The seagull optimization algorithm (SOA) benefits from its simple algorithmic principle, strong universality, and few parameters, and is now commonly used in engineering design problems. However, the standard SOA is prone to problems such as low optimization accuracy and slow search speed. This study proposes a hybrid strategy improved seagull optimization algorithm (WLSOA). Firstly, it utilizes a nonlinear descent strategy to enhance the exploration and development capabilities of the SOA and improve optimization accuracy. Secondly, the adaptive weight balancing of global and local search capabilities and the addition of Levy flight steps to perturb the current optimal solution are introduced to improve the ability of the algorithm to jump out of the local optimal value. The performance of WLSOA is then explored through simulation experiments on 9 classic test functions, using WLSOA, golden sine algorithm, whale optimization algorithm, particle swarm optimization algorithm, traditional seagull optimization algorithm, and the newly proposed improved seagull optimization algorithm. The results show that WLSOA has higher optimization accuracy and faster convergence speed than the other six algorithms. Finally, in gear train design, a comparison with 13 other common swarm intelligence algorithms reveals that WLSOA has a better solving ability than other algorithms.

Key words: global search capability adaptive weight Levy flight step test function

近年来, 随着众多研究人员对优化算法的探索和发展, 新的群智能优化算法不断被提出, 广泛应用到经济调度问题、故障检测、数学领域、工程设计等问题中去寻找最优解^[1]. 典型的智能优化算法有粒子群优化算法^[2]、模拟退火算法^[3]、遗传算法^[4]等, 其中, Dhiman等人^[5]通过观察模拟海鸥迁徙和攻击行为, 于2019年提出了海鸥优化算法. 该算法通过模拟海鸥的迁徙和攻击行为构建理论模型实现对目标问题的求解. 与蚁群优化算法^[6]、烟花优化算法^[7]相比, SOA具有参数少、寻优能力强、易于理解的优点, 并且该算法成功应用在桁架设计、信号处理、系统控制、工程设计等问题上. 然而与其他智能优化算法类似, 标准SOA仍然存在收敛速度慢以及无法找到全局最优解的问题.

为解决海鸥优化算法存在的这些缺点, 众多学者提出了不同的改进策略: Liu等人提出了一种多机制海鸥优化算法, 算法结合了基于广义反对的自适应非线性权重和进化边界约束, 该算法在求解精度和收敛速度上有所提高^[8]. Xian等人借助Powell算法和随机曲线动作改进了海鸥优化算法, 使SOA具有更好的收敛能力, 提高模糊时间序列中预测模型的准确性^[9]. Wang等人提出了一种多目标量子启发海鸥优化算法, 采用了基于量子计算的叠加原理和反向学习策略对传统的海鸥优化算法进行改进^[10]. Long等人使用基于余弦函数的非线性逃逸能量因子以平衡全局勘探和局部开采, 并且引入了差分变异策略来逃避局部最优, 来估计光伏组件模型的未知参数^[11].

本文针对标准海鸥优化算法寻优过程中易出现寻优精度低、搜索速度慢等问题, 提出一种混合策略的改进海鸥优化算法. 首先利用非线性递减策略增强海鸥优化算法的探索开发能力, 提高寻优精度. 其次加入自适应权重, 使得算法在迭代初期的权值较大, 搜索范围广泛, 在后期的权值较小利于小范围精确搜索, 加快搜索速度. 最后加入莱维飞行步长以提高算法跳出局部最优能力, 并且对当前最优解进行扰动.

1 传统海鸥优化算法 1.1 海鸥迁徙

在海鸥迁徙过程中通常会从当前位置移动到下一个位置. 在移动过程中, 海鸥应满足避免碰撞这一条件. 算法通过添加变量 $ A $ 计算海鸥的新位置, 即:

$ {G_s}(t) = A \times {P_s}(t) $

(1)

其中, $ {G_s}(t) $ 表示不与其他海鸥发生碰撞的新位置, $ {P_s}(t) $ 为海鸥当前位置, t表示当前迭代次数, $ A $ 表示海鸥在给定搜索空间中的运动行为, 可表示为:

$ A = {f_c} - (t \times ({{{f_c}} \mathord{\left/ {\vphantom {{{f_c}} {Ma{x_{{\rm{iteration}}}}}}} \right. } {Ma{x_{{\rm{iteration}}}}}})) $

(2)

$ {f_c} $ 控制 $ A $ 的变化频率, 其值从2线性减小到0, t为当前迭代次数, $Ma{x_{{\rm{iteration}}}}$ 为最大迭代次数. 海鸥在迁徙过程中, 在不发生碰撞条件下, 会朝最佳位置的方向移动.

$ {M_s}(t) = B \times ({P_{bs}}(t) - {P_s}(t)) $

(3)

其中, $ {M_s}(t) $ 表示最佳位置的方向, $ {P_{bs}}(t) $ 表示当前海鸥最佳位置, $ {P_s}(t) $ 表示海鸥当前位置. $ B $ 是平衡全局搜索和局部搜索的随机数, 即:

$ B = 2 \times {A^2} \times {r_d} $

(4)

其中, $ {r_d} $ 为区间[0, 1]内的随机数, 海鸥在得到最佳位置后, 就会向最佳位置移动, 到达新的位置, 数学公式具体如下:

$ {D_s}(t) = \left| {{C_s}(t) + {M_s}(t)} \right| $

(5)

其中, $ {D_s}(t) $ 表示海鸥新位置, $ {C_s}(t) $ 表示不与其他海鸥存在位置冲突的位置, $ {M_s}(t) $ 表示最佳位置的方向.

1.2 海鸥攻击猎物

海鸥在空中攻击猎物时常常进行螺旋运动, 它们可以用翅膀和重量保持高度, 与此同时, 海鸥根据不同需要可以改变攻击角度和速度. 将海鸥在x,y, z平面中的运动行为描述为:

$ \left\{ {\begin{array}{*{20}{l}} {x = r \times \cos (\theta )} \\ {y = r \times \sin (\theta )} \\ {{\textit{z}} = r \times \theta } \\ {r = \mu \times {{\rm{e}}^{\theta \nu }}} \end{array}} \right. $

(6)

其中, r是螺旋运动的半径, 随机值 $ \theta $ 的取值范围为[0, 2 ${\text π}$ ], u和 v是和螺旋相关的常数, ${\rm{e}}$ 是以自然为对数的底数. 当u=1,v=0.1, $ \theta $ 从0递增到 $2{\text π}$ 时, 以x, y, z建立坐标系, 海鸥的运动轨迹如图1所示.

图 1 海鸥的运动轨迹

海鸥攻击猎物后的位置用式(7)表示:

$ {P_s}(t) = {D_s}(t) \times x \times y \times {\textit{z}} + {P_{bs}}(t) $

(7)

其中, $ {P_s}(t) $ 表示海鸥攻击猎物后的位置, $ {P_{bs}}(t) $ 表示当前海鸥的最佳位置.

海鸥优化算法步骤如下.

步骤 1. 初始化海鸥优化算法的相关参数.

步骤 2. 根据种群数量与边界来初始化种群位置.

步骤 3. 计算适应度值并保留全局最优位置.

步骤 4. 海鸥迁徙.

步骤 5. 海鸥攻击猎物.

步骤 6. 判断是否满足算法停止条件, 若满足, 则输出最优位置; 否则重复步骤 3–6.

2 改进海鸥优化算法 2.1 非线性递减策略

探索开发能力对于群智能优化算法来说非常重要^[12]. 而对于SOA, 海鸥迁徙过程的位置更新与 $ a $ 的取值相关. 因此, 选择一个合适的收敛因子 $ a $ 对SOA的探索开发能力至关重要. 然而在标准SOA算法中, $ a $ 的值随着迭代的进行呈线性递减, 这种方式虽然也能取得一定的效果, 但是收敛速度过于缓慢, 对算法求解最优解的灵敏度过于低下, 只有当迭代次数快要达到最大时, 收敛因子 $ a $ 才逼近零点, 但通常这样已经无法摆脱局部最优的困境, 因此传统SOA算法的收敛因子不能有效利用算法的优越性. 本文并提出一种基于平方形式的参数改进策略, 公式如下:

$ A = 1 - {\left(\frac{t}{{{T_{\max }}}}\right)^2} $

(8)

其中, t为迭代次数, $ {T_{\max }} $ 为最大迭代次数.

2.2 加入自适应权重策略

自适应权重是麻雀算法中需要调节的重要参数^[13], 它在早期迭代中拥有较大的自适应权重, 以扩大全局搜索范围, 让算法在早期迭代中尽可能剧烈的进行全局搜索, 以快速找到全局最优解, 同时, 在后期迭代中需要较小的惯性权重, 以提高算法的局部利用能力, 避免陷入局部最优解. 本文使用基于对数的自适应权重策略, 如下:

$ \omega = {\omega _{\min }} + ({\omega _{\max }} - {\omega _{\min }})\sin \left({\text π} + \frac{{t \times {\text π} }}{{2 \times {T_{\max }}}}\right) $

(9)

其中, ${\omega _{\max }}$ 为 $\omega $ 的最大值, ${\omega _{\min }}$ 为 $\omega $ 的最小值, t为当前迭代次数, $ {T_{\max }} $ 为最大迭代次数.

2.3 融合莱维飞行策略

莱维飞行具有遍历性和随机性^[14], 是一种非高斯的随机过程, 它的平稳增量服从莱维稳定分布, 其飞行轨迹是随机漫步的, 由小步长(短距离)的跳跃聚集在一块, 和偶尔大步长(长距离)的跳跃组成, 两者相互交替. 如果将该行为融入到SOA算法中, 对于前期的搜索, 大步长可以扩大搜索范围和探索发现, 有利于增强种群的多样性, 大大降低了麻雀陷入局部最优的风险. 而后期搜索, 全局最优解的范围基本已经确定, 小步长可以提高算法后期解的质量, 使算法得于收敛到全局最优.

将莱维飞行策略引入海鸥攻击猎物的公式, 对当前最优解进行扰动, 加强局部逃逸能力. 因为SOA会根据当前位置与海鸥最优位置的距离来进行位置更新, 改进后的SOA很大程度上降低了海鸥个体陷入局部最优的风险, 而且依旧可以充分发挥局部搜索的能力. 更新后的位置公式为:

$ {P_s}(t) = {D_s}(t) \times x \times y \times {\textit{z}} \times {L_{(\lambda )}} + {P_{bs}}(t) \times {L_{(\lambda )}} $

(10)

$ {L_{(\lambda )}} $ 为莱维飞行随机搜索路径:

$ L(s, \lambda ) = \mu \sim{s^{ - \lambda }}\begin{array}{*{20}{c}} , &{1 < \lambda \leqslant 3} \end{array} $

(11)

其中, s是莱维飞行随机步长.

这里, 一个布谷鸟的连续的随机跳跃/步长遵循幂乘规律步长分布, 可以用下式表示:

$ s = \frac{{{\sigma _\mu } \cdot \mu }}{{{{\left| \nu \right|}^{{1 \mathord{\left/ {\vphantom {1 \beta }} \right. } \beta }}}}} $

(12)

其中, u和 v服从随机正态分布, 可表示为:

$ \left\{\begin{split} &\mu \sim N(0, \sigma _\mu ^2),\; \nu \sim N(0, \sigma _\nu ^2), \;{\sigma _\nu } = 1\\ &{\sigma _\mu } = {\left( {\dfrac{{\Gamma (1 + \beta ) \cdot \sin \left({\text π} \cdot \dfrac{\beta }{2}\right)}}{{\Gamma ({{(1 + \beta )} / 2}) \cdot \beta \cdot {2^{{{(\beta - 1)} / 2}}}}}} \right)^{1/ \beta }} \end{split} \right.$

(13)

2.4 改进算法的复杂度分析

时间复杂度的大小取决于算法执行的次数, 标准SOA的时间复杂度取决于搜索空间维度 $dim$ 、最大迭代次数 $ {T_{\max }} $ 和种群规模 $ N $ , 复杂度为 ${\rm{O}}({T_{\max }} \times N \times dim )$ . WLSOA是由标准SOA改进而来, 根据WLSOA算法步骤可知, 引入的非线性收敛因子、惯性权重和莱维飞行增加了 ${\rm{O}}({T_{\max }} \times N \times dim )$ 的运算量, 所以WLSOA的时间复杂度可表示为 ${\rm{O}}(2{T_{\max }} \times N \times dim )$ , 时间复杂度相比于标准SOA更高. 如果优化问题的空间维度较高时, WLSOA的时间复杂度可近似表示为 ${\rm{O}}({T_{\max }} \times N \times dim )$ , 和标准SOA相同. 此外, 空间复杂度主要受空间维度dim和种群规模N的影响, 因此, 两种算法的空间复杂度均表示为 ${\rm{O}}(N \times dim )$ .

3 实验结果与分析

为测试本文所提算法的性能, 选取9个当前研究较为广泛的基准函数进行测试^[15,16], 以研究WLSOA. 表1概述了函数的公式和描述, 在表1中, 这些基准测试函数具有不同的特性, 即单峰、多峰、不可分离和组合特征. 函数的不同特性可以用来测试算法的不同能力. 例如, 由于单峰函数只有一个全局最优值, 对于测试算法的局部搜索能力非常有益. 多模态函数具有许多局部最优解, 非常适合评估算法跳出局部最优的能力即全局搜索能力.

表 1 基准测试的函数

函数类型	测试函数	搜索范围	最小值
单峰	$ {f_1}(x) = \displaystyle\sum {_{i = 1}^D} i \cdot x_i^2 $	${[ - 10, 10]^D}$	0
	${f_2}(x) = {10^6} \cdot x_1^2 + \displaystyle\sum {_{i = 2}^D} x_i^6$	${[ - 1, 1]^D}$	0
	${f_3}(x) = \max (\|{x_i}\|, 1 \leqslant i \leqslant D)$	${[ - 100, 100]^D}$	0
	${f_4}(x) = \displaystyle\sum {_{i = 1}^D} i \cdot x_i^4 + random(0, 1)$	${[ - 1.28,1.28]^D}$	0
	${f_5}(x) = {\displaystyle\sum {_{i = 1}^D\|{x_i}\|} ^{(i + 1)}}$	${[ - 1, 1]^D}$	0
多峰	${f_6}(x) = \displaystyle\sum {_{i = 1}^D} \|{x_i} \cdot \sin ({x_i}) + 0.1 \cdot {x_i}\|$	${[ - 10, 10]^D}$	0
	${f_7}(x) = 1 - \cos \left(2 \cdot {\text π} \cdot \sqrt {\displaystyle\sum {_{i = 1}^Dx_i^2} } \right) + 0.1 \cdot \sqrt {\displaystyle\sum {_{i = 1}^Dx_i^2} }$	${[ - 100, 100]^D}$	0
	${f_8}(x) = 0.1 \cdot D - \left(0.1 \cdot \displaystyle\sum {_{i = 1}^D\cos (5 \cdot {\text π} \cdot {x_i})} - \displaystyle\sum {_{i = 1}^Dx_i^2} \right)$	${[ - 1, 1]^D}$	0
	${f_9}(x) = \displaystyle\sum {_{i = 1}^D} (0.2 \cdot x_i^2 + 0.1 \cdot x_i^2 \cdot \sin (2 \cdot {x_i}))$	${[ - 10, 10]^D}$	0

表 1 基准测试的函数

本文对算法进行3个方面的性能测试: (1)在不同的维数和种群规模条件下进行独立测试, 根据测试结果评估改进算法的性能; (2)在相同迭代次数、函数维度和种群规模条件下, 比较WLSOA与WOA、PSO GSA、SOA及其变体在基准测试函数上的寻优精度和收敛速度, 验证得出WLSOA具有较强的竞争性; (3)在齿轮系设计优化问题上, 通过与其他13种算法比较, 验证了本文算法在解决实际问题有一定的优势, 具有实用性.

3.1 实验设置

为了使不同算法的比较具有公平性, 本文所有测试均在64位Windows 10系统, 处理器类型为Intel(R) Core(TM) i5-7200U CPU @ 2.50 GHz 2.70 GHz. 的相同实验环境下运行. 选用PyCharm编程实现各测试试验. 为了更好展现WLSOA的性能, 分别在10维、30维、50维、100维、300维、500维、1000维的情况下进行测试, 实验结果如表2和表3所示. 表4中所有算法维度为100, 种群规模为30, 迭代次数为100. 为防止结果出现偶然性, 每次实验独立运行20次, 统计20次实验的平均值与标准差作为最终评价指标, 实验结果如表2–表4所列.

表 2 不同维数和不同种群规模下的测试结果

D	函数	n=10		n=30		n=50
D	函数	V_ave	V_std	V_ave	V_std	V_ave	V_std
10	$ {f_1} $	1.0516E–235	0	2.4066E–230	0	4.0391E–227	0
	$ {f_2} $	2.1321E–244	0	3.3361E–240	0	3.4945E–239	0
	$ {f_3} $	1.5871E–116	6.4783E–116	7.6395E–117	1.8908E–117	4.0921E–116	8.6110E–122
	$ {f_4} $	8.9156E–04	7.6440E–04	1.0258E–03	8.7485E–04	8.3515E–03	7.8434E–04
	$ {f_5} $	1.411E–249	0	2.974E–246	0	3.287E–242	0
	$ {f_6} $	7.2950E–119	3.1517E–118	9.6841E–118	4.2212E–117	1.7081E–113	4.1305E–113
	$ {f_7} $	4.4766E–120	1.9509–119	8.9616E–117	2.8969E–116	2.9369E–114	1.2797E–113
	$ {f_8} $	0	0	0	0	0	0
	$ {f_9} $	2.7620E–237	0	1.4673E–235	0	3.7939E–230	0
30	$ {f_1} $	1.7655E–269	0	2.8894E–269	0	2.9698E–267	0
	$ {f_2} $	1.7525E–276	0	1.7355E–272	0	5.3640E–270	0
	$ {f_3} $	2.9380E–135	7.5725E–135	8.1724E–135	2.8718E–134	9.3986E–131	3.3518E–132
	$ {f_4} $	3.1384E–04	1.9644E–04	5.0427E–04	4.9910E–04	4.3220E–04	4.0769E–04
	$ {f_5} $	2.637E–279	0	5.087E–279	0	5.873E–279	0
	$ {f_6} $	6.4508E–135	2.4377E–134	4.4185E–135	1.4878E–134	2.4558E–134	1.0446E–133
	$ {f_7} $	3.2128E–134	7.3614E–134	6.9902E–134	2.8346E–133	1.5765E–132	5.6516E–135
	$ {f_8} $	0	0	0	0	0	0
	$ {f_9} $	3.8336E–263	0	3.5416E–272	0	8.6527E–258	0
50	$ {f_1} $	1.9572E–282	0	2.7380E–279	0	7.7461E–277	0
	$ {f_2} $	5.4713E–289	0	6.5941E–290	0	7.5378E–287	0
	$ {f_3} $	5.4108E–140	1.6202E–139	7.0908E–140	3.0391E–139	1.7198E–141	3.5498E–141
	$ {f_4} $	2.9541E–04	2.4175E–04	2.7277E–04	3.2254E–04	1.6360E–04	1.4186E–04
	$ {f_5} $	1.183E–294	0	1.863E–294	0	1.739E–292	0
	$ {f_6} $	2.2162E–141	9.1561E–141	1.2549E–141	3.0766E–141	8.7185E–139	3.7942E–138
	$ {f_7} $	2.9462E–139	1.2766E–138	1.0317E–137	4.4620E–137	1.6216E–136	6.8175E–149
	$ {f_8} $	0	0	0	0	0	0
	$ {f_9} $	4.7068E–280	0	5.8919E–280	0	2.7940E–280	0
100	$ {f_1} $	1.0814E–293	0	6.1696E–294	0	5.5527E–290	0
	$ {f_2} $	2.8962E–301	0	6.3591E–303	0	2.0002E–300	0
	$ {f_3} $	5.2740E–148	9.9778E–148	7.9474E–149	2.4713E–148	4.3195E–147	8.4675E–149
	$ {f_4} $	9.3140E–05	8.3432E–05	6.5969E–05	4.7904E–05	7.1113E–05	7.0889E–05
	$ {f_5} $	1.636E–308	0	1.794E–308	0	1.996E–308	0
	$ {f_6} $	3.1992E–150	1.0334E–149	2.0157E–148	6.1485E–148	3.3424E–148	9.3095E–148
	$ {f_7} $	4.2192E–147	1.7459E–146	9.0169E–148	2.3430E–147	3.9383E–148	1.1563E–147
	$ {f_8} $	0	0	0	0	0	0
	$ {f_9} $	3.4752E–295	0	6.1157E–294	0	3.2116E–295	0

表 2 不同维数和不同种群规模下的测试结果

表 3 高维度测试

函数	100维		300维		500维		1000维
函数	V_ave	V_std	V_ave	V_std	V_ave	V_std	V_ave	V_std
$ {f_1} $	2.28E–269	0	2.18E–264	0	1.14E–257	0	2.62E–243	0
$ {f_2} $	5.79E–270	0	2.00E–268	0	1.56E–268	0	1.32E–261	0
$ {f_3} $	2.52E–133	6.67E–133	1.85E–133	5.75E–133	6.68E–134	2.86E–133	6.68E–127	2.77E–127
$ {f_4} $	2.47E–04	1.98E–04	3.01E–04	2.47E–04	3.37E–04	2.92E–04	4.07E–04	3.50E–04
$ {f_5} $	3.035E–282	0	5.206E–281	0	3.596E–279	0	1.310E–276	0
$ {f_6} $	5.93E–135	2.04E–134	8.10E–134	2.11E–133	4.63E–134	1.48E–133	3.04E–134	1.09E–133
$ {f_7} $	1.86E–132	8.07E–132	1.17E–129	3.50E–129	1.64E–129	6.97E–129	2.46E–128	7.56E–128
$ {f_8} $	0	0	0	0	0	0	0	0
$ {f_9} $	3.15E–259	0	3.02E–259	0	2.93E–257	0	3.18E–255	0

表 3 高维度测试

表 4 对比算法的参数设置

3.2 实验结果 3.2.1 维数变化对本文算法影响

本文通过在不同的维数D与不同的种群规模n下去测试算法的性能, 选用表1中的9个函数对WLSOA进行测试, 结果如表2所示.

从表2和表3中可以看出, 本文算法不但对低维度的函数具有较好的全局搜索能力, 对于高维的函数也具有良好的性能. 由表2可知, WLSOA在函数 $ {f_8} $ 的测试结果中, 在不同维度和不同种群数量下都能收敛到全局最优值. 在函数 $ {f_4} $ 上, 随着函数的维度和种群规模的变化精确度改变并不明显. 另外, 在函数 $ {f_1} $ 、 $ {f_2} $ 、 $ {f_5} $ 、 $ {f_9} $ 上, 本文算法接近全局最优值. 当种群规模为30时, WLSOA对于100、300、500、1000维之间的函数优化结果如表3所示, WLSOA没有随着维度的增加而出现求解性能大幅下降. 而是呈现缓慢的下降趋势. 可以看出, 随着维度的变化, WLSOA在函数 $ {f_2} $ 、 $ {f_3} $ 、 $ {f_4} $ 、 $ {f_5} $ 、 $ {f_6} $ 、 $ {f_7} $ 、 $ {f_8} $ 、 $ {f_9} $ 上的求解精度几乎没有多大变化, 尤其是在1000维这种高维度上仍然能保持较好的性能, 说明该算法的适应性和稳定性更强. 反映出WLSOA在求解高维函数也具有一定的优势.

3.2.2 WLSOA与其他算法的比较

为了验证本文所提算法有效性, 本文选择WOA、PSO、GSA进行比较, 并且加入了传统SOA、与文献[17]所提出的改进海鸥优化算法(SOA1)和文献[18]所提出的改进海鸥优化算法(SOA2)的对比, 对比算法对应的参数选择和改进设计如表4.

仍然选择上述9个基准测试函数进行测试, 对比结果如表5所示. 可以看出, 相比于其他6种算法, WLSOA在函数 $ {f_1} $ 、 $ {f_2} $ 、 $ {f_3} $ 、 $ {f_5} $ 、 $ {f_6} $ 、 $ {f_7} $ 和 $ {f_9} $ 取得了较优的结果. 在函数 $ {f_1} $ 、 $ {f_2} $ 、 $ {f_5} $ 和 $ {f_9} $ 上, WLSOA 的求解精度更高, 更加贴近最优值. 在函数 $ {f_8} $ 上, 除WOA和PSO, 其他算法都能取得全局最优. 从运行结果的平均值和标准差大小能看出, WLSOA的寻优精度要明显优于其他6种智能算法且鲁棒性强.

表 5 在9个测试函数上的结果比较

函数	Index	WOA	PSO	GSA	SOA	SOA1	SOA2	WLSOA
$ {f_1} $	Mean	3.576E+01	7.538E+01	1.093E−54	2.455E−28	2.4187E−87	1.5050E−126	2.2782E−269
$ {f_1} $	St.dev	2.489E+01	1.179E+01	3.164E−54	8.586E−28	1.0542E−86	5.9644E−125	0
$ {f_2} $	Mean	1.602E−04	3.439E+00	8.289E−46	2.245E−55	2.5632E−125	2.1762E−140	5.7886E−276
$ {f_2} $	St.dev	2.380E−04	2.159E+00	2.872E−45	7.611E−55	1.0901E−124	6.7879E−139	0
$ {f_3} $	Mean	2.754E+01	2.841E−01	2.466E−19	7.218E−02	2.7468E−32	3.7610E−64	2.5224E−133
$ {f_3} $	St.dev	1.001E+00	2.452E−02	8.542E−19	2.431E−01	1.1915E−31	1.6394E−63	6.6715E−133
$ {f_4} $	Mean	8.721E−02	4.286E−02	7.138E−04	9.778E−04	7.508E−04	3.3026E−04	4.4659E−04
$ {f_4} $	St.dev	2.722E−02	1.631E−02	8.505E−04	8.656E−04	1.336E−04	5.2738E−04	1.9835E−04
$ {f_5} $	Mean	3.229E−06	3.616E−05	8.491E−57	7.704E−39	1.887E−112	1.736E−141	5.891E−280
$ {f_5} $	St.dev	1.336E−05	3.716E−05	3.701E−56	3.146E−38	8.227E−112	7.530E−141	0
$ {f_6} $	Mean	4.729E+00	6.346E+00	3.927E−29	1.346E−21	4.1504E−48	4.1504E−65	5.9264E−135
$ {f_6} $	St.dev	3.899E+00	7.405E−01	1.355E−28	3.149E−21	3.2877E−47	6.6774E−65	2.0369E−134
$ {f_7} $	Mean	2.869E−01	3.676E−01	2.365E−27	2.305E−02	5.3698E−43	2.4381E−65	1.8641E−132
$ {f_7} $	St.dev	9.945E−01	5.543E−02	5.781E−27	4.208E−02	1.3575E−42	8.3333E−65	8.0705E−132
$ {f_8} $	Mean	1.942E−01	4.954E+01	0	0	0	0	0
$ {f_8} $	St.dev	1.376E−01	5.173E−01	0	0	0	0	0
$ {f_9} $	Mean	4.736E−01	8.697E−01	6.775E−55	1.997E−26	4.3571E−90	5.5556E−132	3.1521E−262
$ {f_9} $	St.dev	4.168E−01	2.941E−02	1.904E−54	6.918E−26	8.3799E−89	1.8570E−131	0

表 5 在9个测试函数上的结果比较

为了更好地显示WLSOA跳出局部最优值的能力和收敛速度, 图2绘制了7个算法在各测试函数上的收敛曲线. 可以看出: WLSOA收敛速度明显优于其他6种算法, 大部分函数在少量迭代次数情况下就能找到最优值, 能有效节约寻优时间. 收敛至同样精度时, WLSOA的迭代次数明显更少. 证明了其搜索速度得到了有效增强.

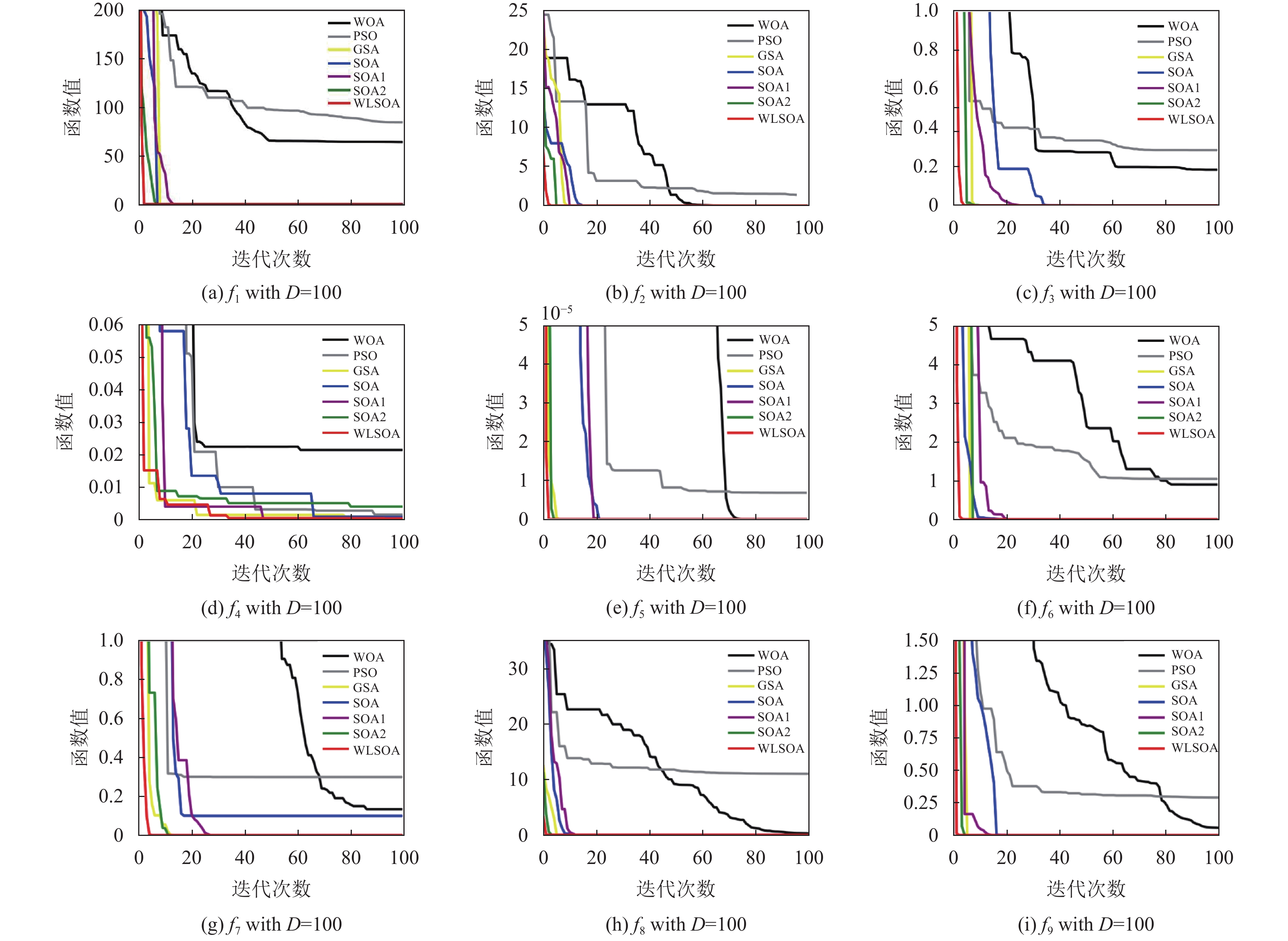
图 2 收敛曲线比较结果

综上所述, 本文所提出的多策略改进WLSOA不仅对比标准智能算法在寻优精度和收敛速度有显著的提升, 而且相较于当前较新的改进SOA, WLSOA 仍具有明显的优势.

3.2.3 改进策略对算法性能影响

由表5和图2可以看出, 采用自适应权重和种群策略(SOA1)和仅增加莱维飞行算子(SOA2)对SOA性能有较大改善, 但是其改进效果有限. 可以看出自适应权重对SOA 寻优性能具有一定的影响而莱维飞行算子对SOA性能影响较大, 但是采用自适应权重或者莱维飞行算子对算法性能的提升在大部分基准测试函数上仍与结合3种改进策略的WLSOA存在较大差距. 因此, 在结合自适应权重和莱维飞行有效性的基础上, 针对标准SOA算子固有的缺陷加入非线性递减策略, 当在测试函数上取得相同精确度时, WLSOA的迭代次数明显更少, 收敛速度更快, 且对大部分测试函数的寻优精度也明显高于SOA及其变体, 证明了SOA采用3种改进策略的有效性及合理性.

4 齿轮系设计问题

齿轮是一种重要的传动机构元件, 广泛应用于各种机械装置中. 例如混合器、手表、离合器、差速器、风扇、机床等, 它在这些产品中发挥着不可或缺的作用, 也是在机械领域最常见的机件之一. 在齿轮系统设计中, 一般要考虑到多个因素, 如传动比、载荷、材料强度等. 齿轮系设计是典型的优化问题之一.

4.1 齿轮系设计优化模型

齿轮系在我们日常生活中随处可见, 它的结构如图3所示. 齿轮系统设计问题通常是一种多目标优化问题, 需要考虑到多个目标函数, 它的变量是4个齿轮的齿数, 主要目标是使传动比最小化, 并根据这些目标函数来确定设计方案. 在实际工程应用中齿轮系设计问题通常被描述为一个带有不等式约束的优化问题. 其数学模型为:

图 3 齿轮系设计问题

$ \left\{ {\begin{array}{*{20}{l}} {\min{{\left(\dfrac{1}{{6.931}} - \dfrac{{{x_3} \cdot {x_2}}}{{{x_1} \cdot {x_4}}}\right)}^2}} \\ {12 \leqslant {x_1} \leqslant 60} \\ {12 \leqslant {x_2} \leqslant 60} \\ {12 \leqslant {x_3} \leqslant 60} \\ {12 \leqslant {x_4} \leqslant 60} \end{array}} \right. $

其中, $ {\left(\dfrac{1}{{6.931}} - \dfrac{{{x_3} \cdot {x_2}}}{{{x_1} \cdot {x_4}}}\right)^2} $ 为传动比的值, ${x_i}\;(i = 1, 2, 3, 4)$ 为齿轮的齿数.

4.2 测试结果分析

为验证WLSOA针对齿轮系优化的有效性, 采用GWO等14种算法对齿轮系的参数进行搜索和调整, 寻找最优解以达到设计要求. 本节的目标函数、变量范围以及表6中的其他13种算法数据全部来源于文献[22], 表6显示了14种群智能算法对齿轮系设计问题的最优解和各参数取值. 实验表明, 本文的改进算法是有意义的, 非线性递减策略和自适应权重增强了算法全局搜索能力, 莱维飞行步长对当前最优解进行扰动, 三者策略使算法获得更强的寻优能力. WLSOA相比于其他算法寻优效果更好, 获得了精确度更高的目标值. 是一种解决齿轮系设计问题的有效方法. 齿轮系的最小传动比为 $ 7.61 \times {10^{ - 16}} $ , 最优解为 $ {x_1} = 4.01 \times {10^1} $ , $ {x_2} = 1.22 \times {10^1} $ , $ {x_3} = 1.20 \times {10^1} $ , $ {x_4} = 2.53 \times {10^1} $ .

表 6 齿轮系设计问题的比较结果

算法	$ {x_1} $	$ {x_2} $	$ {x_3} $	$ {x_4} $	最优值
GWO	$ 4.03 \times {10^1} $	$ 2.46 \times {10^1} $	$ 1.20 \times {10^1} $	$ 5.08 \times {10^1} $	$ 1.18 \times {10^{13}} $
GJO	$ 5.00 \times {10^1} $	$ 1.71 \times {10^1} $	$ 1.26 \times {10^1} $	$ 2.98 \times {10^1} $	$ 1.52 \times {10^{13}} $
PSO	$ 5.13 \times {10^1} $	$ 2.10 \times {10^1} $	$ 1.48 \times {10^1} $	$ 4.78 \times {10^1} $	$ 3.08 \times {10^{ - 4}} $
BA	$ 5.75 \times {10^1} $	$ 1.95 \times {10^1} $	$ 1.86 \times {10^1} $	$ 4.37 \times {10^1} $	$ 1.53 \times {10^{ - 11}} $
ACO	$ 5.15 \times {10^1} $	$ 2.14 \times {10^1} $	$ 1.58 \times {10^1} $	$ 4.73 \times {10^1} $	$ 2.87 \times {10^{ - 5}} $
SA	$ 5.13 \times {10^1} $	$ 2.13 \times {10^1} $	$ 1.50 \times {10^1} $	$ 4.74 \times {10^1} $	$ 1.71 \times {10^{ - 4}} $
FPA	$ 5.12 \times {10^1} $	$ 2.25 \times {10^1} $	$ 1.80 \times {10^1} $	$ 5.59 \times {10^1} $	$ 4.83 \times {10^{ - 11}} $
DA	$ 5.24 \times {10^1} $	$ 1.70 \times {10^1} $	$ 2.30 \times {10^1} $	$ 5.17 \times {10^1} $	$ 3.02 \times {10^{ - 11}} $
MFO	$ 4.42 \times {10^1} $	$ 1.88 \times {10^1} $	$ 2.11 \times {10^1} $	$ 5.70 \times {10^1} $	$ 1.44 \times {10^{ - 14}} $
PBO	$ 5.01 \times {10^1} $	$ 2.33 \times {10^1} $	$ 1.48 \times {10^1} $	$ 4.79 \times {10^1} $	$ 1.37 \times {10^{ - 15}} $
FA	$ 5.01 \times {10^1} $	$ 2.44 \times {10^1} $	$ 1.40 \times {10^1} $	$ 4.64 \times {10^1} $	$ 6.52 \times {10^{ - 13}} $
SOGWO	$ 4.81 \times {10^1} $	$ 2.99 \times {10^1} $	$ 1.38 \times {10^1} $	$ 5.94 \times {10^1} $	$ 2.35 \times {10^{ - 11}} $
EO	$ 4.49 \times {10^1} $	$ 1.28 \times {10^1} $	$ 2.93 \times {10^1} $	$ 5.79 \times {10^1} $	$ 5.76 \times {10^{ - 14}} $
WLSOA	4.01×10¹	1.22×10¹	1.20×10¹	2.53×10¹	7.61×10⁻¹⁶

表 6 齿轮系设计问题的比较结果

5 结语

针对海鸥优化算法的缺点, 本文使用非线性递减策略代替线性递减策略, 增强了算法探索开发能力, 将自适应权重和莱维飞行步长引入SOA, 有效地提高了算法的全局搜索能力, 提出了WLSOA. 为了研究WLSOA的有效性和可行性, 在9个典型的基准测试函数进行测试, 测试结果表明: 本文提出的算法比基本的海鸥优化算法及其变体和其他基于群体的方法具有更好的性能, 在精确度和收敛速度方面得到了大幅提升. 值得注意的是, 本文算法在处理多峰高维的优化问题也具有一定的优势. 在齿轮系设计问题上, 相比于其他13种常用智能算法, WLSOA寻得最优解的能力也更强. 寻优精度更高且鲁棒性强, 在解决实际问题中也具有一定的竞争力.

下一步, 将考虑用改进的海鸥优化算法应用于无人机路径规划领域^[23], 为解决复杂的工程实际问题提供理论支持.

参考文献

[1]	Che YH, He DX. An enhanced seagull optimization algorithm for solving engineering optimization problems. Applied Intelligence, 2022, 52(11): 13043-13081. DOI:10.1007/s10489-021-03155-y
[2]	Meng XD, Li HC, Chen AS. Multi-strategy self-learning particle swarm optimization algorithm based on reinforcement learning. Mathematical Biosciences and Engineering, 2023, 20(5): 8498-8530. DOI:10.3934/mbe.2023373
[3]	Feng C, Zhang ZH, Xie LY, et al. Research on emergency supplies distribution based on improved simulated annealing algorithm. Academic Journal of Computing & Information Science, 2022, 5(10): 6-13.
[4]	Jiang LQ, Fu ZJ. Privacy-preserving genetic algorithm outsourcing in cloud computing. Journal of Cyber Security, 2020, 2(1): 49-61. DOI:10.32604/jcs.2020.09308
[5]	Dhiman G, Kumar V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowledge-based Systems. 2019(165): 169–196.
[6]	Fonooni B, Jevtic A, Hellström T, et al. Applying ant colony optimization algorithms for high-level behavior learning and reproduction from demonstrations. Robotics and Autonomous Systems, 2015, 65: 24-39. DOI:10.1016/j.robot.2014.12.001
[7]	Ehsaeyan E, Zolghadrasli A. FOA: Fireworks optimization algorithm. Multimedia Tools and Applications, 2022, 81(23): 33151-33170. DOI:10.1007/s11042-022-13093-7
[8]	Liu XY, Li GQ, Shao P. A multi-mechanism seagull optimization algorithm incorporating generalized opposition-based nonlinear boundary processing. Mathematics, 2022, 10(18): 3295. DOI:10.3390/math10183295
[9]	Xian SD, Chen KY, Cheng Y. Improved seagull optimization algorithm of partition and XGBoost of prediction for fuzzy time series forecasting of COVID-19 daily confirmed. Advances in Engineering Software, 2022, 173: 103212. DOI:10.1016/j.advengsoft.2022.103212
[10]	Wang YL, Wang WL, Ahmad I, et al. Multi-objective quantum-inspired seagull optimization algorithm. Electronics, 2022, 11(12): 1834. DOI:10.3390/electronics11121834
[11]	Long W, Jiao JJ, Liang XM, et al. Parameters estimation of photovoltaic models using a novel hybrid seagull optimization algorithm. Energy, 2022, 249: 123760. DOI:10.1016/j.energy.2022.123760
[12]	Gao P, Ding HQ, Xu R. Whale optimization algorithm based on skew tent chaotic map and nonlinear strategy. Academic Journal of Computing & Information Science, 2021, 4(5): 91-97.
[13]	Mo GL, Tan CZ, Zhang WG, et al. Dynamic spatiotemporal correlation coefficient based on adaptive weight. Financial Innovation, 2023, 9(1): 14. DOI:10.1186/s40854-022-00437-3
[14]	Wu L, Wu JW, Wang TB. Enhancing grasshopper optimization algorithm (GOA) with levy flight for engineering applications. Scientific Reports, 2023, 13(1): 124. DOI:10.1038/s41598-022-27144-4
[15]	Long W, Jiao JJ, Xu M, et al. Lens-imaging learning Harris hawks optimizer for global optimization and its application to feature selection. Expert Systems with Applications, 2022, 202: 117255. DOI:10.1016/j.eswa.2022.117255
[16]	Long W, Xu M, Jiao JJ, et al. A velocity-based butterfly optimization algorithm for high-dimensional optimization and feature selection. Expert Systems with Applications, 2022, 201: 117217. DOI:10.1016/j.eswa.2022.117217
[17]	Zhang SQ, Zhang NJ, Zhang ZQ, et al. Electric power load forecasting method based on a support vector machine optimized by the improved seagull optimization algorithm. Energies, 2022, 15(23): 9197. DOI:10.3390/en15239197
[18]	Chen J, Chen X, Fu ZF. Improvement of the seagull optimization algorithm and its application in path planning. Journal of Physics: Conference Series, 2022, 2216: 012076. DOI:10.1088/1742-6596/2216/1/012076
[19]	Yue YG, You HR, Wang SX, et al. Improved whale optimization algorithm and its application in heterogeneous wireless sensor networks. International Journal of Distributed Sensor Networks, 2021, 17(5): 155014772110181.
[20]	Chakraborty R, Sushil R, Garg ML. Hyper-spectral image segmentation using an improved PSO aided with multilevel fuzzy entropy. Multimedia Tools and Applications, 2019, 78(23): 34027-34063. DOI:10.1007/s11042-019-08114-x
[21]	Liu QX, Li N, Jia HM, et al. A hybrid arithmetic optimization and golden sine algorithm for solving industrial engineering design problems. Mathematics, 2022, 10(9): 1567. DOI:10.3390/math10091567
[22]	Yuan PL, Zhang TH, Yao LG, et al. A hybrid golden jackal optimization and golden sine algorithm with dynamic lens-imaging learning for global optimization problems. Applied Sciences, 2022, 12(19): 9709. DOI:10.3390/app12199709
[23]	Li J, Zhang WJ, Hu YT, et al. RJA-star algorithm for UAV path planning based on improved R5DOS model. Applied Sciences, 2023, 13(2): 1105. DOI:10.3390/app13021105