轨迹预测任务需要从带噪声的观测中估计目标真实的运动状态, 推理出目标未来的运动轨迹^[1]. 移动目标轨迹预测在智能交通^[2]、自动驾驶^[3]、飞行器拦截^[4]等领域具有巨大的研究前景和应用价值. 早期的轨迹预测研究大多先通过归一化、滑动平均^[5]、小波分解^[6]等数据预处理方法整合提取数据的特征, 帮助模型训练; 再使用一些概率统计方法进行预测. 如差分自回归移动平均模型^[7]、卡尔曼滤波器^[8]、隐马尔科夫模型^[9], 贝叶斯网络^[10]等. 然而, 这样的做法经常会导致预测效果取决于预处理效果的问题, 淡化了模型本身的作用, 使模型缺乏普适性^[11]. 此外, 在面对复杂、长期的非线性轨迹时, 传统的模型无法对点迹间的相互依赖进行有效建模.

对轨迹序列的预测任务可以看作是对多变量时间序列的处理. 基于神经网络的许多方法已运用于时间序列预测领域. 1986年, Elman等人提出循环神经网络(RNN), 通过递归推理处理序列, 学习序列的非线性特征^[12]. 1997年, Hochreiter等人提出长短期记忆力网络(LSTM), 在隐藏层中使用门机制, 记忆门记忆有效信息, 遗忘门遗忘不重要的信息, 缓解RNN梯度消失和爆炸的问题, 并能处理较长的依赖^[13]. 但在处理时间跨度更大的任务时, LSTM难以保持长期的依赖, 随着序列的增加, 梯度仍会消失.

Cho等人^[14]提出了Seq2Seq结构, 通过编码器(encoder)将输入序列的上下文特征编码为隐藏状态向量c, 解码器(Decoder)将隐藏状态向量c解码, 预测目标序列, 使模型可以应对输入序列和输出序列不等长的情况. DeepAR^[15]将Seq2Seq架构与LSTM结合, 使用两个LSTM模块分别作为网络的编码器和解码器, 进行时间序列预测; 但递归式模型的向量c只能由输入序列中最近一个字符的隐藏状态的非线性变换得到, 先前的信息将随着序列长度增加而减少, 难以包含全局的上下文信息. Transformer引入自注意力(self-attention)机制进行编码和解码. 评估点迹间的相关性, 并以此来对上下文分配注意力, 进行全局信息建模^[16], 但预测时编码器的递归推理会造成误差累积, 随着序列变长, 精度急剧下降. Informer^[17]开创性地使用生成式的推理过程进行序列预测, 一次生成所有的预测轨迹. 解决了误差累积问题, 加快了模型训练的速度, 更适合长序列的预测.

目前已经有许多工作将生成对抗网络(GAN)运用到序列预测任务中, ForGAN^[18]将历史轨迹数据作为标签, 通过输入噪声拟合真实未来轨迹的分布, 形成一个Conditional GAN^[19]. 但由基于RNN的网络构成的生成器和判别器难以学习非线性序列之间的复杂模式. Wu等人^[20]将Transformer与GAN相结合, 将Transformer作为生成器生成预测轨迹, 判别器进一步拟合真实轨迹的分布, 以期减小累积误差. 然而, 全连接网络构成的判别器提取特征能力有限, 难以向生成器提供有效的后验信息和稳定的梯度反馈.

目前移动目标轨迹预测领域的热点主要集中在行人和车辆等交通网络中的多变量轨迹预测. 除了目标的历史轨迹外, 研究很大程度上依靠可观察到的外部环境激励信息. Shafiee等人^[21]通过对道路的几何场景等静态物理信息以及其他行人和车辆的动态交互信息进行建模来辅助预测, Wu等人^[11]利用滑动平均方法强化时间序列的周期性以提升预测精度. 将外部因素作为协变量和轨迹信息一同输入模型, 期望从多维度原始数据端到端地学习目标的运动意图以提升轨迹预测的效果. 但对于船舶等二维移动目标和飞行器等三维移动目标来说, 天气、洋流、磁场等外部信息难以进行建模, 在时序信息中往往只能表现为状态噪声; 同时还受到雷达探测的观测噪声影响, 使观测轨迹失真, 难以捕捉运动意图. 现有的模型难以在这些任务上取得良好的效果, 而对此的研究又是十分必要的. 因此, 我们通过动力学建模和仿真, 建立了一个DT数据集. 作为上述单变量轨迹预测问题训练和验证的新基准, 并在此验证了本文模型的效果.

本文主要的贡献可以概括如下.

(1)提出时频域信息融合编码器, 在两个通道分别建模输入轨迹的时域信息和时频域信息, 将小波分解嵌入模型中, 配合频域自注意力提取低频趋势特性, 与时域上下文依赖融合, 增强模型建模长期趋势的能力.

(2)使用一种多尺度卷积判别器网络, 学习捕捉序列之间的多尺度局部动态特征, 通过对抗训练拟合真实轨迹, 提升序列级精度.

(3)在长期轨迹预测数据集DT上与相关的先进算法进行比较, 取得了最好的效果. 验证了模型的有效性.

1 相关工作 1.1 离散小波变换

小波变换是序列预测领域最常见的数据分解方法之一. 通过选取恰当的小波基函数, 小波变换可以使信号在时间域和频率域上都体现出良好的局部特性, 从而较好地从信号中获取到信息, 克服Fourier变换不能处理序列中突变和非平稳信息的缺点^[22].

小波变换有两个变量: 尺度因子 $ a $ 和平移因子 $ b $ . 尺度因子 $ a $ 控制小波函数的伸缩, 平移因子 $ b $ 控制小波函数的平移. 尺度是频率的倒数, 平移对应于时间. 一般来说, 对于采样轨迹这种离散信号可以采用离散小波变换, 将 $ a $ 、 $ b $ 离散化为式(1)的形式.

$ a = a_0^j, \; b = ka_0^j{b_0} $

(1)

其中, ${{{a}}_0} > 0, \; {b_0} \in R, \forall j, k \in Z,$ 小波基可以表示为式(2).

$ {\psi _{j, k}}(t) = {a^{ - \frac{1}{2}}}\psi (a_0^{ - j}t - k{b_0}) $

(2)

小波变换的完整公式如式(3)所示.

$ {W_f}(j, k) = {a^{ - \frac{1}{2}}}\int {f(t)*\overline {{\psi _{j, k}}(t)} dt} $

(3)

通过小波分解, 可以得到一个趋势序列和一个细节序列. 具体分解公式如式(4)和式(5)所示.

$ {a_{j + 1}} = G{a_j}, \; j = 1, 2, \cdots, N $

(4)

$ {d_{j + 1}} = H{a_j}, \; j = 1, 2, \cdots, N $

(5)

其中, $G, H$ 分别为低通、高通滤波器, ${a_j}, {d_j}$ 分别为趋势序列和细节序列. 在每次分解过程中, 得到的高频信息将被滤除, 低频信息则用于下一步的分解.

1.2 Transformer

Transformer将自注意机制与Seq2Seq架构相结合. 自注意机制可以根据关联程度向序列中的其他点分配注意力, 加强网络的特征提取能力. 具体地, 将输入乘以不同的权重矩阵, 得到可学习的查询 $ Q $ , 键 $ K $ 和值 $ V $ , 同时, 权重矩阵内分为多个头, 各自学习以全面学习高维信息. 通过 $ Q $ 和 $ K $ 的乘积得到序列各点的相似度, 再通过 ${\textit{Softmax}}$ 赋予各点注意力权重, 建模全局上下文信息, 最后的结果如式(6).

$ Attention(Q, K, V) = {\textit{Softmax}}\left(\frac{{Q{K^{\rm{T}}}}}{{\sqrt {{d_k}} }}\right)V $

(6)

1.3 生成对抗网络

生成对抗网络由一个生成器G和一个判别器D组成, 生成器接收一个随机噪声 ${\textit{z}}$ , 通过近似实际数据的分布得到生成数据 $G({\textit{z}})$ . 判别器接收真值 $x$ 和输出 $G({\textit{z}})$ , 通过最小化交叉熵损失函数, 判别器判定输入是真实分布的概率, 数据越真实, 概率越接近1, 反之概率越接近0. G和D交替训练构成一个动态的“博弈过程”^[23]. GAN的损失函数如式(7)所示.

$ \begin{split} & \arg {{\rm{min}} _G}{{\rm{max}} _D}{E_{x\sim{p_{data}}(x)}}[\log D(x)] + \\ &\qquad\qquad\quad {E_{{\textit{z}}\sim{p_{\textit{z}}}({\textit{z}})}}[\log (1 - D(G({\textit{z}})))] \end{split} $

(7)

其中, ${p_{data}}(x)$ 是真值序列, ${p_{\textit{z}}}({\textit{z}})$ 是噪声序列.

通过对抗训练, G的生成能力和D的判别能力都会越来越强, 最终G足以以假乱真, 达到“纳什均衡”状态, 使网络能够拟合真实数据的分布.

2 本文方法 2.1 整体架构

模型总体为Seq2Seq架构, 生成器由改进的Transformer构成, 观测序列输入encoder后首先进行升维, 将2维或3维的轨迹提高为512维, 提取高维隐藏状态; 再使用绝对位置编码方式对序列顺序进行编码, 如式(8)所示.

$ \left\{\begin{split} & P{E_{(pos, 2j)}} = \sin (pos/{(2L)^{\frac{{2j}}{d}}}), \\ & P{E_{(pos, 2j + 1)}} = \cos (pos/{(2L)^{2j/d}}),\\ & j = 1, 2, \cdots, d/2 \end{split}\right. $

(8)

其中, $pos$ 为位置指数. 将Transformer中的编码器改进为时频域信息融合模块, 增强趋势信息表征. 解码器只保留一层, 降低内存开销; 并采用生成式推理方法, 消除误差累积. 判别器是一个全卷积网络, 通过对抗训练提升模型对多尺度局部特征的学习能力. 编码器建模上下文长期趋势; 判别器拟合局部动态特征. 我们的方法是一种同时表示长、短期轨迹特征的有效方案. 网络模型的整体结构设计如图1所示.

2.2 时频域信息融合模块

编码器分为时域和时频域两个通道^[24]. 时频域通道做一次时域注意后堆叠3个时频域注意模块. 该模块通过小波分解和自注意力机制建模观测序列的低频趋势特性. 仅使用序列的频谱可能会导致时域信息的损失, 因此在另一个通道使用时域注意模块补偿全局时域序列信息. 最后将双通道信息进行融合, 馈入解码器.

在时域通道中, 自注意机制编码时域的全局上下文信息; 前馈神经网络将数据映射到高维, 获取更多的隐藏信息. 层归一化有助于网络层的稳定, 并起到正则化的作用. 通过残差连接, 可以降低模型复杂度, 减少过拟合.

一般信号在频域上相对时域更加稀疏, 且在高频部分的大量信息是所谓“噪声”. 在图像领域, 这些噪声可能是形状的边缘, 代表图片重要的细节. 但在轨迹预测问题上, 噪声往往由观测精度不够或外部环境干扰等原因造成, 无法进行预测^[25], 轨迹的长期趋势信息则大部分位于低频. 因此, 本文在频域通过小波变换分离轨迹的高低频分量, 将每次变换后的高频噪声分量丢弃, 对低频信息做进一步的处理.

与传统“预处理+模型”的模式不同, 本文使用Kymatio方法^[26], 可以将小波分解嵌入神经网络框架之中, 参与反向传播. 在得到小波分解下的低频信息后, 在频域运用自注意机制, 建模频域特征信息之间的长期依赖, 提取表征趋势的信息, 实现可学习的自适应滤波^[27], 进一步强化低频长期趋势依赖.

为了最大程度地刻画时间序列的不规则信息, 时频域选取具有正交性和紧支撑性的“sym8”小波^[28]进行离散小波分解, 这个过程可以将向量长度减半, 有效地提取出序列内在的趋势信息. 经过3层的小波分解-自注意力级联, 舍弃各阶段的高频噪声, 得到自适应滤波后的低频频域特征.

最后, ${X_{{\rm{input}}}} \in {R^{L \times d}}$ 在时域和频域分别得到输出 $X_{{\rm{output}}}^t \in {R^{L \times d}}$ , $X_{{\rm{output}}}^f \in {R^{L/8 \times d}}$ . 通过全连接层将频域输出映射至 $ {R^{L \times d}} $ . 这样, 就可以对张量进行拼接和卷积, 得到融合时频域特征的输出. 如式(9)所示.

$ {X_{{\rm{output}}}} = {\text{Conv1d}}(Concat(X_{{\rm{output}}}^t, MLP(X_{{\rm{output}}}^f))) $

(9)

2.3 多尺度全卷积判别器

为了进一步提升模型的预测精度, 弥补编码器在短期动态特征建模的欠缺, 模型采用生成对抗网络结构, 通过对抗训练进一步拟合真实的轨迹. 并且, 为了解决传统判别器中全连接网络提取特征能力有限的问题, 将其改进为由全卷积神经网络构成的多尺度判别器^[29], 可以有效地提取序列在各个尺度的局部特征信息.

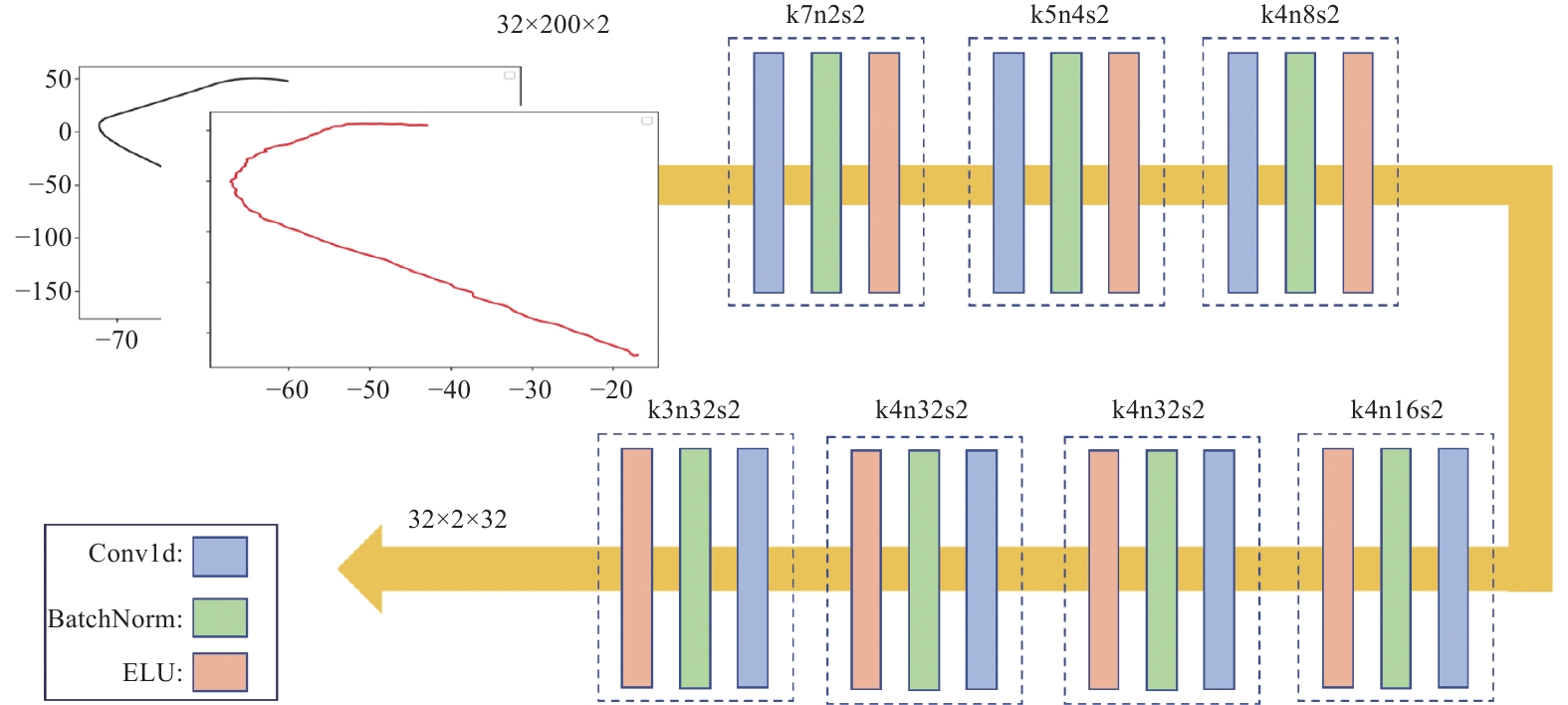
网络结构如图2所示, 由若干个卷积模块构成, 卷积的步长为2, 卷积核大小从 $ 7 \times 7 $ 开始, 随着网络深度增加而减小至 $ 3 \times 3 $ 获取轨迹在不同尺度下的特征表示. 随后进行归一化处理, 通过激活函数ELU(·)增强逼近能力. 最后将多层次的特征进行拼接, 得到判别器网络的最终输出.

在单一的生成网络之下, 模型会因过于拟合趋势特性而得到钝化、平缓的结果. 通过在判别器中与ground truth的“动态博弈”过程, 网络可以在不受突变、噪声影响的条件下学习到真实轨迹所具备的局部动态特征, 实现长期趋势与短期特征的均衡表征.

2.4 损失函数

为了能将基于Transformer的生成器与对抗训练有效结合, 我们使用了内容损失 ${l_G}$ 和对抗损失 ${l_D}$ 来提升模型的预测和估计性能. 其中, 内容损失函数使用轨迹预测问题最常用的均方误差; 对抗损失使用多尺度特征的平均绝对误差. 内容损失函数如式(10)所示.

$ {l_G}(\hat Y, Y) = \dfrac{{\displaystyle\sum\limits_{l = 1}^{\vartriangle L} {\displaystyle\sum\limits_{i = 1}^m {{{(\hat Y_l^i - Y_l^i)}^2}} } }}{{\vartriangle L \times m}} $

(10)

其中, $ Y $ 为真实轨迹, $ \hat Y \in {R^{\vartriangle L \times M}} $ 为预测轨迹, $\vartriangle L$ 为预测轨迹长度, $ m $ 为其空间维数.

多尺度判别器网络的对抗损失函数如式(11)所定义.

$ \begin{split} {{\rm{min}} _{{\theta _G}}}{{\rm{max}} _{{\theta _D}}}{l_D}({\theta _G}, {\theta _D}) = \frac{1}{N}\sum\limits_{n = 1}^N {{l_{{{mae}}}}({f_D}(G({x_n}), {f_D}({y_n}))} \\ \end{split} $

(11)

其中, $ mae $ 为平均绝对误差, $ {y_n} $ 是第 $ n $ 条真实轨迹, $G({x_n})$ 是生成器网络输出的预测轨迹, ${f_D}(x)$ 表示从轨迹 $ x $ 中提取的多尺度特征. 具体地, 函数 ${l_{mae}}$ 定义为式(12).

$ \begin{gathered} {l_{mae}}({f_D}(G({x_n}), {f_D}({y_n})) = \frac{1}{L}\sum\limits_{i = 1}^L {||f_D^i(G({x_n})) - f_D^i({y_n})|{|_1}} \\ \end{gathered} $

(12)

其中, $ L $ 为判别器网络中总的卷积层数, $f_D^i({y_n})$ 是轨迹 $ {y_n} $ 在判别器网络第 $ i $ 个卷积后提取的特征. 最后, 网络的损失函数 $ l $ 如式(13)所示.

$ l = {l_G} + \lambda {l_D} $

(13)

在训练过程中, 采用两个网络交替训练的策略. 首先训练生成器, 在固定判别网络梯度的情况下, 优化生成器网络, 使得生成器输出的序列能够在多尺度上拟合真实轨迹, 即最小化网络总的损失. 接着训练判别器, 在固定生成器对其的输入的情况下, 优化判别器网络, 增强网络对两种轨迹的特征提取和区分能力, 即最大化对抗损失. 不断重复上述过程, 随着训练的进行, 生成器和判别器网络都变得越来越强大. 多次训练后, 判别器能够识别真假轨迹的细微差异, 生成器能够很好地学习拟合轨迹的多尺度特征.

3 实验与分析

通过运动学建模和仿真, 我们建立并公开了DT数据集, 作为轨迹预测任务的新基准.

数据集包括二维和三维空间的模拟轨迹, 每个空间包含100000条轨迹的观测值和真实值, 长度均为500个点. 将数据集按照8:1:1的比例进行训练、验证和测试.

在训练阶段, 使用Adam作为优化器, 初始学习率设置为1E–4, 每2个epoch衰减一半, batchsize设置为32, 最终实验结果来自多次实验的平均值. 所有实验都在GTX TITAN 12 GB GPU上运行.

在轨迹预测任务中, 对我们的方法进行了验证. 基准模型包括以下序列预测问题的先进方法, RNN、LSTM、Transformer、LogTrans^[30]、Performer^[31]和Informer. 由于实验所需预测的轨迹较长, 递归式推理方法会导致内存爆炸, 无法进行实验, 本文的所有模型均采用Informer所使用的生成式推理方法.

3.1 轨迹预测任务

轨迹预测任务需要根据观测到的历史轨迹, 推理出目标后续的运动状态. 轨迹预测可分为中期预测和长期预测, 受到误差传播、非线性动力学的复杂模式和不确定性的影响, 长期预测更为困难. 在2D和3D的数据集上, 我们各进行中期和长期的预测实验. 具体地, 中期预测通过400个观测点推测未来100个点, 长期预测通过200个观测点推测未来300个点. 实验比较轨迹预测领域传统的评价指标平均位移误差ADE和终点位移误差FDE^[32]. ADE表示所有轨迹的预测点和实际点间的均方误差, FDE表示预测的轨迹目的地和真实目的地的距离, 两个指标越小, 说明预测的效果越好. 计算公式如式(14)和式(15)所示, 其中, $ N $ 为轨迹条数, $ {L_2} $ 范数为平均欧氏距离.

$ ADE = \frac{{\displaystyle\sum\limits_{n = 1}^N {\displaystyle\sum\limits_{l = 1}^{\vartriangle L} {||\hat Y_l^n - Y_l^n|{|_2}} } }}{{N \times \Delta L}} $

(14)

$ FDE = \frac{{\displaystyle\sum\limits_{n = 1}^N {||\hat Y_l^n - Y_l^n|{|_2}} }}{N}, \; l = \Delta L $

(15)

2D数据集上的实验结果如表1所示. 可以看出, 在长期和中期的预测任务中, 我们的方法均取得了最好的效果. 在长期预测中, ADE提升了4.1%–18.5%, FDE提升了17.5%–46%; 在中期预测中, ADE提升了8.1%–55%, FDE提升了16%–54.5%.

3D数据集上的预测结果在表2中列出, 我们的方法同样取得了良好的效果. 在长期预测中, ADE提升了2.4%–15.8%, FDE提升了11.7%–37%; 在中期预测中, ADE提升了9.2%–48.4%, FDE提升了15.9%–54.5%.

2D数据集长期预测的可视化结果如图3所示. 通过分析可知, 本文提出的方法在两种场景下的中长期轨迹预测任务中均取得了最好的效果.

3.2 消融实验

为了分析每个模块对网络模型产生的影响, 本文在2D数据集上进行长期轨迹预测消融实验. 变量分别为频域注意力模块(frequency domain attention, FDA), 时频域信息融合模块(time frequency fusion, TFF), 多尺度判别器模块(multi scale discriminator, MSD). 将Transformer作为基准模型, 所有模型同样均采用生成式推理方法. 消融实验的最终结果如表3所示.

结果表明, 通过时频域自适应滤波聚焦长期趋势是提升模型预测效果的有效方法, 多尺度判别器也能通过对抗训练优化网络参数. 并且, 通过将两个模块结合, 兼顾上下文长期趋势和多尺度细节特性, 可以取得更好的预测效果.

4 结论与展望

本文提出了一种基于时频域信息融合和多尺度对抗训练的目标轨迹预测方法. 首先建立时域和时频域两个通道. 通过小波分解和自注意机制在时频域进行自适应滤波, 提取轨迹低频趋势特性; 时域通过注意力机制建模长期上下文依赖. 然后将两个通道的信息融合. 最后通过一个全卷积判别器建模轨迹的多尺度短期微运动表示, 进一步拟合真实轨迹. 在轨迹预测任务上的实验结果表明, 本文提出的方法在性能上优于相对比的方法, 证明了本文方法的有效性.