20世纪80年代初引入医学影像诊断的核磁共振成像(MRI)技术是近年来一种新型的具有高度软组织分辨能力的高科技影像学检查方法, 磁共振图像的获取是通过进动的质子切割磁感线, 产生电信号, 信号频率的空间信息的存储位置存放在K空间的值上, 再通过反傅立叶变换, 就得到了我们看到的磁共振影像, 但是各因素间的相互制约导致核磁共振成像时间长、信噪比低、分辨率差等, 寻找一种采集时间短重构效果好的成像方式是临床核磁共振成像所考虑的最重要因素之一^[1]. 压缩感知技术是在满足测量矩阵与稀疏基的不相关性的前提下, 通过对K空间信号进行远低于奈奎斯特率值的高度欠采样, 边采样边压缩, 进而通过获得的测量矩阵与稀疏化后的信号所构成的非线性重构优化算法来恢复信号, 显著减少传感元数量、减少了采集时间、降低了存储空间等, 并获得很好的重建效果. 因此针对压缩感知的采样和重构学者们提出了众多算法.

完全填充的K空间获得最高质量图像的同时也会导致较长扫描时间, 在压缩感知里, 通过采集较少数据可以加快采集速度, 但同时会导致图像信噪比降低, 因此信号稀疏采集是关键, 可以忽略其余信号只捕获最重要的MR信号. Yuan等人^[2]提出了使用非下采样碎片变换对核磁共振图像实现了一个灵活的分解, 在每个级别上都有任意偶数的方向子带, 提供了足够的稀疏表示和任何方向的分解, 此算法的高方向灵敏度及最优近似特性提高了CS-MRI重建应用. Huang等人^[3]提出在多个小波帧上具有平均稀疏度的基础上提高平均信号稀疏性, 利用稀疏度平均先验的快速迭代收缩阈值算法进行CS-MRI重建. Kojima等人^[4]提出随机获取数据需要一个最优的随机欠采样模式, 在K空间中心区域估计了不同加速度因子和全采样范围的图像恢复精度, 指出可以通过增加高频区域的相位编码数来优化高斯分布参数从而提高空间分辨率. Kazama等人^[5]研究了非随机信号欠采样CS-MRI以稳定重建图像质量和避免采样点选择的任意性的可行性, 提出了一种利用在迭代重建过程中使用曲线变换作为稀疏变换函数的方法增加了傅里叶基和稀疏变换函数之间的非相干性. 即便采样技术相对成熟, 采样后数据集进行傅里变换时得到的图像仍然是有噪声的, 需要通过滤波等技术去除图像中的噪声以提高图像质量.

随着稀疏采集技术的逐步成熟, 采集后的重建算法也在不断创新. Yuan等人^[6]研究了两种不同的分析L1/2正则化的迭代半阈值算法求解非凸优化问题, 利用图像在紧帧下的稀疏K空间数据重建高分辨率的图像, 从而有效地缩短成像时间. 但是为获得最优图像非线性最优化算法需要一个迭代最优化过程, 这样就造成重建时间过长, 并且迭代可能陷入局部收敛. Mathew等人^[7]提出了采用“使用参数值处理稀疏正则化”与“估计后续迭代中使用的参数值”两个步骤交替最小化方法得到解. 此类基于最优化模型的重建方法一般需要设置各种优化参数, 而不恰当的参数设置会导致过约束, 从而造成重建图像看起来不自然, 如过平滑或残留欠采样伪影. He等人^[8]提出了一种能够在幅度和相位图像中捕获更多细节的基于双树复小波稀疏性的新方法, 该方法消除了由于相位跳跃而造成的幅度伪影. 但是目前广泛应用的基于整体变分(total variation)、小波等稀疏变换对于处理具有复杂结构的生物组织图像仍显得过于简单, 会引入阶梯状或块状伪影.

复杂的正则化与过程迭代会加大耗时和成本, 参数无法保证调到最优, 通过模糊的先验信息转化成的正则化不能确保符合通用需求. 近年来, 深度学习在图像修复领域的成功为MRI高速重建提升了可能性, 广泛的关注促使产生了多种将深度学习应用于CS-MRI的算法, 并且已经证明了深度学习能够在扫描时间差距不大的情况下同时提升图像重建质量. Hashimoto等人^[9]提出了利用卷积神经网络(CNN)作为先验信息, 实现了用原始K空间数据替换未填充区域的K空间修正, 使用迭代的方式实现了CS-MRI重建, 减少了混叠伪影. Ran等人^[10]提出了一种同时操作K空间和空间域数据的包含两个并行和交互式分支的MRI双域重建网络, 进一步提高了重构性能. Zhao等人^[11]提出了一种以高分辨率参考MR图像作为卷积神经网络的输入, 然后加入K空间数据校正步骤, 从欠采样的K空间数据中获得了更准确的重建结果. Njeh等人^[12]提出了基于自动编码器的体系结构的CS-MRI重建深度卷积编码器-解码器架构, 提供了更好地重建并保留了纹理图像的细节, 同时缩短了运行时间. Mardani等人^[13]提出了使用生成对抗网络(GAN)来建模高质量MR图像, 与传统的基于小波和基于字典学习的CS方案以及使用像素级训练的基于深度学习的方案相比, 此算法以更精细的纹理细节检索到更高质量的图像.

在本文中, 为了提高重建效果, 我们提出了一种新的深度学习结合BM3D优势的核磁共振成像算法. 与目前的方法不同, 盲降噪深度学习具有更好的去除自然噪声的能力, BM3D在图像细节保留有突出的优势, 所提出的算法将两者结合, 可以将深度网络的学习能力强但可解释性差和BM3D的去噪效果具有可解释性相结合以实现互相弥补.

1 基于稀疏基和先验信息的压缩感知核磁共振成像

图像在空间上的离散化称为采样, 也就是用空间上部分点的灰度值代表图像, 这些点称为采样点. 二维信号一般是采用采样矩阵对图像进行亚采样, 压缩采样在图像的稀疏域进行, 被称为采样即压缩. 许多真实信号本身并不是稀疏的, 而是在一些变换域中有一个稀疏的表示. 理论上MR压缩感知欠采样原理^[14]如下:

$ y = {F_u}x + g $

(1)

其中, $ x \in {C^N} $ 表示具有N个像素的MR原图(磁共振最终图像), M是测量值的长度, ${F_u} \in {C^{M \times N}} ( M \ll N )$ 表示部分欠采样算子如傅里叶编码矩阵, 依采样函数而定. 观测在K空间进行, $ y $ 表示测量数据, 使用高斯噪声向量 $g\sim N\left( {0, {\sigma ^2}} \right)$ 模拟真实场景的自然数据噪声.

磁共振信号采集是逐行填充的, 例如一幅256×256的磁共振图像, 则至少要扫描256次(相位编码), 每一次采集256个采样点(频率编码), 形成了K空间. 视野及成像的区域对固定大小的成像样品视野越大, 使样品在图像中越小, 大多数情况下使用正方形视野, 也就是数字化采样一般是按照正方形点阵取样的. 原始的MR图像存在但未被表示出来, 医疗检查过程中通过硬件设备获得了它的部分图像并对这部分图像进行了采样产生测量值. 本文主要研究实MR图像. $ x = \psi s $ 表示信号 $ x $ 在变换域 $ \psi $ 中可以被稀疏表示成s. 观测矩阵 $ \phi $ 与稀疏基 $ \psi $ 的乘积 $ \phi \psi $ 称为恢复矩阵. 核磁共振成像MRI信号重构的关键是在满足有限等距定理RIP的前提下“找到非稀疏信号 $ x $ 在中的稀疏表示 $ s $ ”. 通过观测矩阵求解稀疏系数s进而重构原始图像 $ x $ 是压缩感知进行图像恢复的关键, 重建算法的限定性结构通常构建成以下优化问题:

$ \mathop {\min }\limits_s {\left\| s \right\|_p}\begin{array}{*{20}{c}} {}&{{\rm{s.t.}}}&{y = \phi x, x = \psi s} \end{array} $

(2)

其中, p是范数, 当p=1时式(2)是一个凸优化问题, 可以用梯度下降法、变量分离法等许多算法来求解. 欠采样傅立叶编码矩阵算子有很多种, 填充K空间的数据直接来源于 MR 信号, 但它可以以任意的顺序进行采集填充. 在过去的几十年里, K空间的填充方式主要是逐条线性填充的笛卡尔方式, 现在随机和辐射状K空间填充方式越来越流行. 高斯随机采样更接近于真实噪声, 非常适合用于基于压缩传感(CS)的快速成像, 有利于实现细节重建、图像边缘留存及抑制成像伪影. 径向采样的K空间可以提供改善视场时间分辨率, 减少总扫描时间, 对于从径向采样的K空间重建图像, 插值起着重要的作用, 它可以在图像域或在频域(如重构方法)中实现.

基于全局稀疏性的方法能够快速进行图像重建, 但由于全局变换是固定的, 其重建质量有待提升. 近年来出现的有着出众重建效果的BM3D算法^[15]利用其去噪器隐含的先验知识进行非局部相似性图像重建, 基于寻找相似块进行协同滤波最后把同一个像素的不同滤波结果整合的思想^[16], 提出构建以下CSMRI优化框架, 对于第i次迭代, 重构图像的优化模型如下:

$ {\hat x^{\left( i \right)}} = \mathop {\arg \min }\limits_x \left\| {{F_u}x - y} \right\|_2^2 + \lambda \left\| {x - {x^{\left( {i - 1} \right)}}} \right\|_2^2 $

(3)

$ {x^{\left( i \right)}} = \mathop {\arg \min }\limits_x \left\| {x - {{\hat{x} }^{\left( i \right)}}} \right\|_2^2 + \kappa {\left\| {\Psi x} \right\|_2} $

(4)

其中, $ {x^{\left( {i - 1} \right)}} $ 表示当前的估计值, $ \lambda $ 、 $ \kappa $ 是正则化参数, $ \Psi $ 表示BM3D去噪中使用的解析稀疏算子, ${\hat{x} ^{\left( i \right)}}$ 表示中间图像. 式(3)可通过求导近似求其闭式解. 求解式(4)时, 直接利用BM3D去噪器近似求解. 但BM3D算法去噪先验有其自己的局限性, 如果待处理的图像具有非自相似性, 则使用BM3D去噪先验会带来过于光滑和不规则的结构等. 因此, 采用混合先验可能是一个更好的选择.

2 基于深度学习的稀疏表示模型 2.1 判别式学习先验去噪

与目前已有的多种手动设计的正则先验相比, 使用判别式学习方法自动学习出来的隐含在图像中的先验信息是一种更好的选择^[17]. 基于深度学习的卷积神经网络(CNN)采用数据驱动的策略, 通过对数据的学习探究图像中隐含的先验, 具有良好的特征提取能力, 其性能优于许多手动设计的去噪算子如BM3D. 另外, 由于CNN网络的运行往往结合GPU (graphics processing unit) 的并行运算能力使其具有高效的运行速度, 因此可加速其判别式学习能力. 由此, 从图像重构的性能和速度的角度考虑, 可以尝试采用基于判别式策略学习的深度CNN去噪器^[18]作为一种深度先验加入到MRI图像重构框架. 这种方法能够高效恢复图像依赖于迭代求解, 因此负面结果是极大的消耗时间.

2.2 网络结构模式

虽然仍处于早期阶段, 但深度神经网络的最新进展已经显示出了它们在计算机视觉和图像处理方面的潜力. Quan等人^[19]提出了一种新的基于深度学习的生成逆向模型用于快速和准确的CS-MRI重建. 该模型是全残余卷积自编码器和生成式对抗网络(GANs)的一种变体, 是单向部署在前馈网络, 重建过程非常迅速, 低至几十毫秒重建256×256图像, 即使采样率低至10%左右图像质量也是优越的.

基于深度学习的CS-MRI重建过程将CNN与CS相结合^[20]构造出如下优化模型:

$ \mathop {\min }\limits_x \frac{1}{2}\left\| {{F_u}x - y} \right\|_2^2 + \lambda R\left( x \right) + \zeta \left\| {x - {f_{{\rm{CNN}}}}\left( {{x_u}\left| {\hat \theta } \right.} \right)} \right\|_2^2 $

(5)

其中, ${f_{{\rm{CNN}}}}$ 是通过参数 $ \theta $ 的CNN正向传播, $ \mathrm{\zeta } $ 是另一个正则化参数, CNN网络被训练用以优化重建效果, $ \hat \theta $ 表示训练后的CNN优化参数. $ {x_u} = F_u^Hy $ 表明对y在K空间随机0填充欠采样重建后的图像, H表示Hermitian转置. MRI数据通常以复数形式编码了幅值和相位信息, 在深度学习中, 通常有两种表示方式, 一种是将虚部置零, 只保留实部信息, 另一种是将实部和虚部当作两个通道共同作为输入. 该论文提到为了减少计算量, 使用第1种方式.

深度神经网络的压缩感知MRI重建是一个由欠采样的K空间数据生成全重建图像的过程, 在这样的网络结构模式中, 这个能量最小化过程被神经网络的训练过程所取代. 具体来说, 压缩感知MRI的深度学习网络结构模式的基本思想通过网络训练使经验损失最小化^[21], 优化模型如下.

$ \mathop {\min }\limits_\theta \frac{1}{T}\sum\limits_{t = 1}^T {{{\left\| {{v^*} - {v_i}} \right\|}_2}} = \frac{1}{T}\sum\limits_{t = 1}^T {{{\left\| {v_i^* - B\left( {w, \Theta } \right)\left( {{{\textit{z}}_i}} \right)} \right\|}_2}} $

(6)

其中, z为网络的输入数据, T是训练数据个数, $ v $ 是输出数据即目标向量, $ B\left( {w, \Theta } \right) $ 是关于权值 $ w $ 和可训练网络参数 $ \Theta $ 的神经网络, $ {v^*} $ 为标签图像. 式(6)能够以损失最小化为约束通过使用非线性权值自适应求取网络的输出数据.

为得到质量较好的图像, 一般可采用“细量化粗采样图像缓变部分以避免假轮廓, 粗量化细采样图像细节部分以避免模糊”的准则进行重构. 将深度学习应用于图像重构需要考虑选择合适的网络架构实现网络复杂性和性能之间的权衡, 可以在K空间域和图像域中进行端到端训练实现这一平衡.

3 融合深度学习和传统方法的压缩感知核磁共振成像

深度技术通过学习对最终重建提供快速恢复, 然而由于数据驱动的重构行为不能保证根据领域知识的原则约束进行重建, 其重建过程的可靠性有待论证. 在本文中, 我们应用了一个组装CS-MRI原则模块的深度框架, 该框架将学习策略与传统重建能量的迭代求解器相结合. 该框架嵌入了一个最优的条件检查机制, 促进了高效和可靠的重建. 由多种先验知识构建的去噪器所表达的稀疏表示模型能够将多种去噪器蕴含的先验知识融合到图像重建中, 从而提升低采样率下MRI的重建质量.

MR过程中会产生有多个来源的高度复杂且不可预测的噪声, 因此消除现实世界的盲噪声即进行盲去噪是图像恢复中一个重要的问题. CBDNet深度学习算法^[22]可以从有噪声的样本学习图像中的噪声分布并实现盲去噪. CBDNet由A部分噪声估计子网络(CNNE)和B部分非盲去噪子网络(CNND)两部分组成, 非对称学习的噪声估计子网络可以有效抑制噪声, 利用这种非对称损失来提高对噪声的泛化能力. CNND结构包括5层全卷积(Conv+ReLU), 32个卷积核, 尺寸3×3. CNNE使用了一个没有pooling (池化)和BN (batch normalization)操作的5层全卷积网络; CNND则使用了一个16层的U-Net, 学习残差映射来预测结果. 经实验验证, 结合使用CNNE和CNND残差学习对高斯去噪操作不仅能保证网络训练快速稳定, 而且还能获得效果较好的去噪结果. CBDNet在训练过程中同时结合了合成噪声和真实噪声图像进行学习, 实现了交互式去噪, 提高了网络的去噪能力, 非常适合应用于医学核磁共振成像领域.

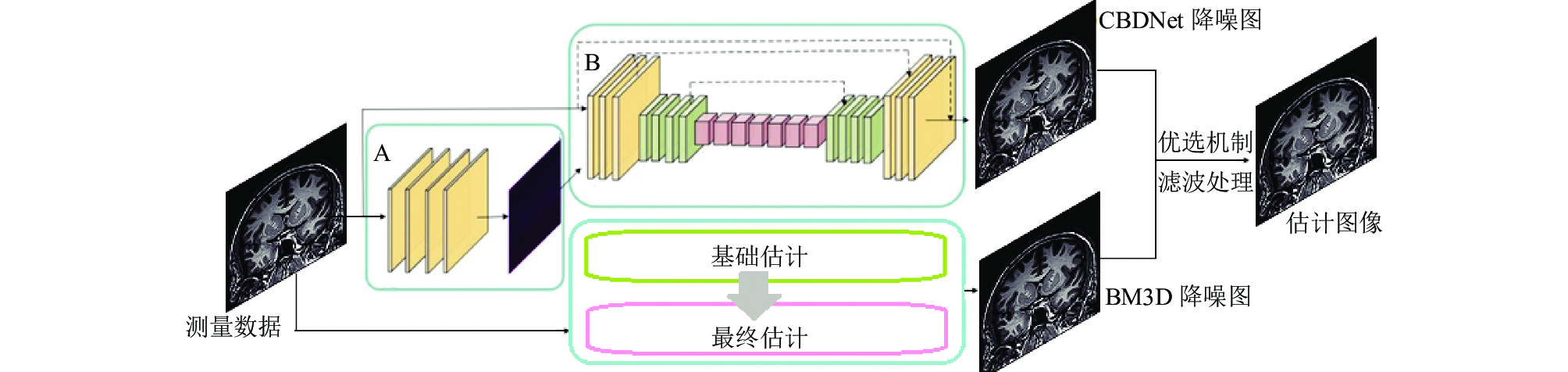
深度去噪器和传统去噪器各有优势, 因此本文试图利用基于两种去噪器联合解决现有CSMRI算法重建质量低的问题. 本文所研究的融合盲去噪CNN^[23]算法CBDNet和传统降噪器BM3D算法的总体构造如图1所示, AB两部分构成了CBDNet降噪器, BM3D降噪器由基础估计和最终估计两部分构成, 在联合降噪的过程中通过某种优选机制以及滤波处理等流程获得最终的估计图像.

本文所研究的联合降噪具体构建以下对应的优化模型:

$ \mathop {\min }\limits_{x, s} \left\| {{F_u}x - y} \right\|_{_2}^2 + \lambda {\left\| {Wx - s} \right\|_2} + \zeta {\left\| {s - \hat \alpha } \right\|_p} $

(7)

式(7)中第1项为保证重建图像 $ x $ 与测量数据 $ y $ 相匹配的数据保真项; 第2项、第3项为构建的基于深度去噪器和传统去噪器的稀疏表示模型. $ \lambda $ 为正则化参数用以平衡两项的比重, $ W $ 表示对应的解析稀疏算子( ${W^{\rm{T}}}W = E$ ), $ \zeta $ 是正则化参数, $ \hat \alpha $ 是经去噪后的图像 $I\left( x \right)$ 在 $ W $ 下的稀疏系数, $ s $ 与 $ \alpha $ 是相似的. 因此本文研究的混合降噪过程中稀疏表示模型如下:

$ \mathop {\min }\limits_s \left\| {WI - s} \right\|_2^2 + \zeta {\left\| {s - \hat \alpha } \right\|_p} $

(8)

$ G = \max \left\{ {{{\left| {{I_c}\left( {{x^{\left( {i - 1} \right)}}} \right) - {G^{\left( {i - 1} \right)}}} \right|}_2}, {{\left| {{I_b}\left( {{x^{\left( {i - 1} \right)}}} \right) - {G^{\left( {i - 1} \right)}}} \right|}_2}} \right\} $

(9)

$ \hat \alpha = T\left[ {WI\left( {{x^{\left( {i - 1} \right)}}} \right), \xi } \right] $

(10)

式(8)中 $ p $ 值本研究中取为0, 稀疏系数 $ \hat \alpha $ 的解需要依托迭代硬阈值法获取. $ I $ 依据式(9)求取, 其中 $ {I_c}\left( {{x^{\left( {i - 1} \right)}}} \right) $ 表示用深度降噪器, 用其获得降噪图像 $ {I_c} $ , $ {G^{\left( {i - 1} \right)}} $ 表示本轮图像恢复前的恢复图像, $ {G^{\left( 0 \right)}} $ 表示初始恢复图像. $ I $ 表示本轮降噪过程中由式(9)获得的恢复图像. 式(10)中根据实验效果 $T\left[ {WI\left( x \right), \xi } \right]$ 选用硬阈值算子进行求解. 稀疏表示系数 $ s $ 确定后, 采用式(11)求解估计图像:

$ \mathop {\min }\limits_x \left\| {{F_u}x - y} \right\|_2^2 + \lambda {\left\| {Wx - s} \right\|_2} $

(11)

对最小化代价函数式(11)进行求导推演出式(12), 表示对去噪器去噪后的图像进行某稀疏变换, 代表对图像进行某稀疏变换, 求出估计图像的系数变换, 在进行反变换求出最终的估计图像.

$ F{x^{\left( i \right)}} = f\left( {I\left( {{x^{\left( {i - 1} \right)}}} \right)} \right) + \frac{{f\left( {{G^0}} \right) - f\left( {I\left( {{x^{\left( {i - 1} \right)}}} \right)} \right)}}{{\left( {\lambda + 1} \right)I}} $

(12)

本文算法如算法1所示.

算法1. CBDNet-BM3D

输入: 测量数据 $ \scriptstyle y $ , 初始化估计图像 $\scriptstyle {G^{\left( 0 \right)}} = F_u^Hy $ , 参数 $\scriptstyle \lambda $ , $\scriptstyle \zeta $

输出: 由迭代产生的重构图像 $\scriptstyle {x^i} $

1) 对估计图像 $\scriptstyle {G^{\left( {i - 1} \right)}} $ 利用深度去噪器 $\scriptstyle {I_c}\left( {{x^{\left( {i - 1} \right)}}} \right) $ 进行滤波获得降噪图像 $ \scriptstyle {I_c} $ , 同时利用传统去噪器 $\scriptstyle {I_b}\left( {{x^{\left( {i - 1} \right)}}} \right) $ 进行滤波获得降噪图像 $\scriptstyle {I_b} $ ;

2) 由式(9)对降噪图像 $\scriptstyle {I_c} $ 与 $\scriptstyle I_{b} $ 依其求其与 $\scriptstyle {G^{\left( {i - 1} \right)}} $ 的相似性, 二者max择优获取综合降噪恢复图像 $\scriptstyle I $ ;

3) 由式(10)更新稀疏系数 $\scriptstyle \hat \alpha $ ;

4) 在其他变量视为已知量的情况下, 在K空间由式(12)通过 $\scriptstyle {G^{\left( {i - 1} \right)}} $ 和 $\scriptstyle {G^{\left( 0 \right)}} $ 求取估计图像的傅立叶变换得到: $\scriptstyle F{x^{\left( {i - 1} \right)}} $ ;

5) 对 $\scriptstyle F{x^{\left( {i - 1} \right)}} $ 进行IFFT变换计算新的估计图像 $\scriptstyle {x^i} $ , 也即 $ \scriptstyle {G^{\left( i \right)}} $ ;

6) 返回步骤(1), 直到迭代次数i符合设计要求.

4 实验结果

实验将对本文提出的算法(后续用CBDNet-BM3D算法指代)与5种不同MR图像重构算法的性能进行程序运行结果对比评价, 实验将对不同类型的MR图像在不同采样方式的不同欠采样率进行图像恢复, 以论证该方法的高效性、鲁棒性及泛化性等.

仿真实验软件环境: Windows 10系统, Matlab R2019b, Matconvnet深度学习框架. 仿真实验硬件环境: Intel(R) Core(TM) i9-9900 CPU, 主频3.10 GHz, 内存16.0 GB, 显卡为NVIDIA GeForce RTX 2060. 图像的重构质量通过采用信号重建质量测量指数峰值信噪比(peak signal to noise ratio, PSNR)和衡量幅图像相似度的指标结构相似性(structural similarity, SSIM)作为客观指标视觉效果作为主观指标来进行评价. 本文将所提算法CBDNet-BM3D与现有的4种算法进行对比. 这4种算法分别为经典的传统算法(BM3D-MRI^[24])和3种基于深度学习的算法(FFDNet^[18]、CSMRI-FFDNet^[25]、CBDNet^[23]).

本文实验所使用的图像块大小为, 算法中的所有测量值分别采用多种采样频率的高斯随机采样矩阵、径向采样矩阵、笛卡尔采样矩阵产生, 再使用ifftshift去中心化将低频和高频的位置还原(将白色的、亮的移动到图像四周, 将黑色的、暗的移动到图像中心), 实践证明变换后所产生的采样矩阵恢复效果比未变换前要好, 采样矩阵如图2所示, 图2(a)分别为3类采样矩阵, 图2(b)分别为3类采样矩阵的去中心化结果, 采样率均为20%. 图3是实验中所用到的6幅256×256的核磁共振图像.

表1是图像数据集中brain在不同采样率和采样算法下的PSNR和SSIM值, 实验结果表明高斯随机采样的图像恢复效果是最好的. 表1显示了在采样率分别为10%、20%和30%的高斯随机采样矩阵、径向采样矩阵、笛卡尔采样矩阵时使用5种不同重构算法得到的PSNR和SSIM值的均值和标准差. 表1数据显示, 当采样算子使用高斯随机矩阵时, CBDNet-BM3D算法的图像重构结果相对于其他4个算法呈现较优的状态. 在10%的采样率下, CBDNet-BM3D算法分别高于BM3D-MRI、FFDNet、CSMRI-FFDNet和CBDNet算法1.9383 dB、3.1657 dB、3.0823 dB和0.8092 dB; 在20%的采样率下, CBDNet-BM3D算法分别高于BM3D-MRI、FFDNet、CSMRI-FFDNet和CBDNet算法1.1389 dB、0.9457 dB、0.8401 dB和0.0888 dB; 在30%的采样率下, CBDNet-BM3D算法分别高于BM3D-MRI、FFDNet、CSMRI-FFDNet和CBDNet算法1.818 dB、1.3148 dB、1.1024 dB和0.1622 dB. 当计算混合降噪结果时, 先分别求基于深度去噪的滤波图像与基于BM3D去噪的滤波图像与上一轮循环中估计图像间的距离, 再使用max函数取两者中差异大的视为修复度更高. 实验中外循环取66次, 基于深度去噪修复度高的次数与基于BM3D去噪修复度高的次数比约为47:19, 数据表明深度去噪修复效果相对优于BM3D去噪修复效果, 并且二者结合应用修复效果更好.

为了评估本文提出算法对测量噪声的鲁棒性, 我们在具有加性高斯噪声的brain3d图上进行了实验, 如图4所示. CT讲的是密度, 细节清晰非常重要, brain3d图是T1加权像, 骨皮质是黑色暗的低信号, 皮下脂肪是白色亮的高信号, 脑室内的液体(脑脊液)是黑色的. 对本文所提出CBDNet-BM3D算法及其他4种算法的重构图像进行视觉对比, 其中8%的原始K空间样本被保留. 图4(b)–图4(f)显示了不同算法对同一副图像进行采样后恢复的结果图, 黄色框及蓝色框是对应的感兴趣区域的放大状态. 从图4中可看出, 基于传统的BM3D-MRI算法以及深度学习CBDNet算法重构效果具有一定的优势, 重构图像的边缘以及纹理保留了更多的细节信息, 且低伪影使得图像更为清晰, 实验结果进一步支持了我们提出的方法在存在较高测量噪声的情况下重建效果有很好的竞争能力.

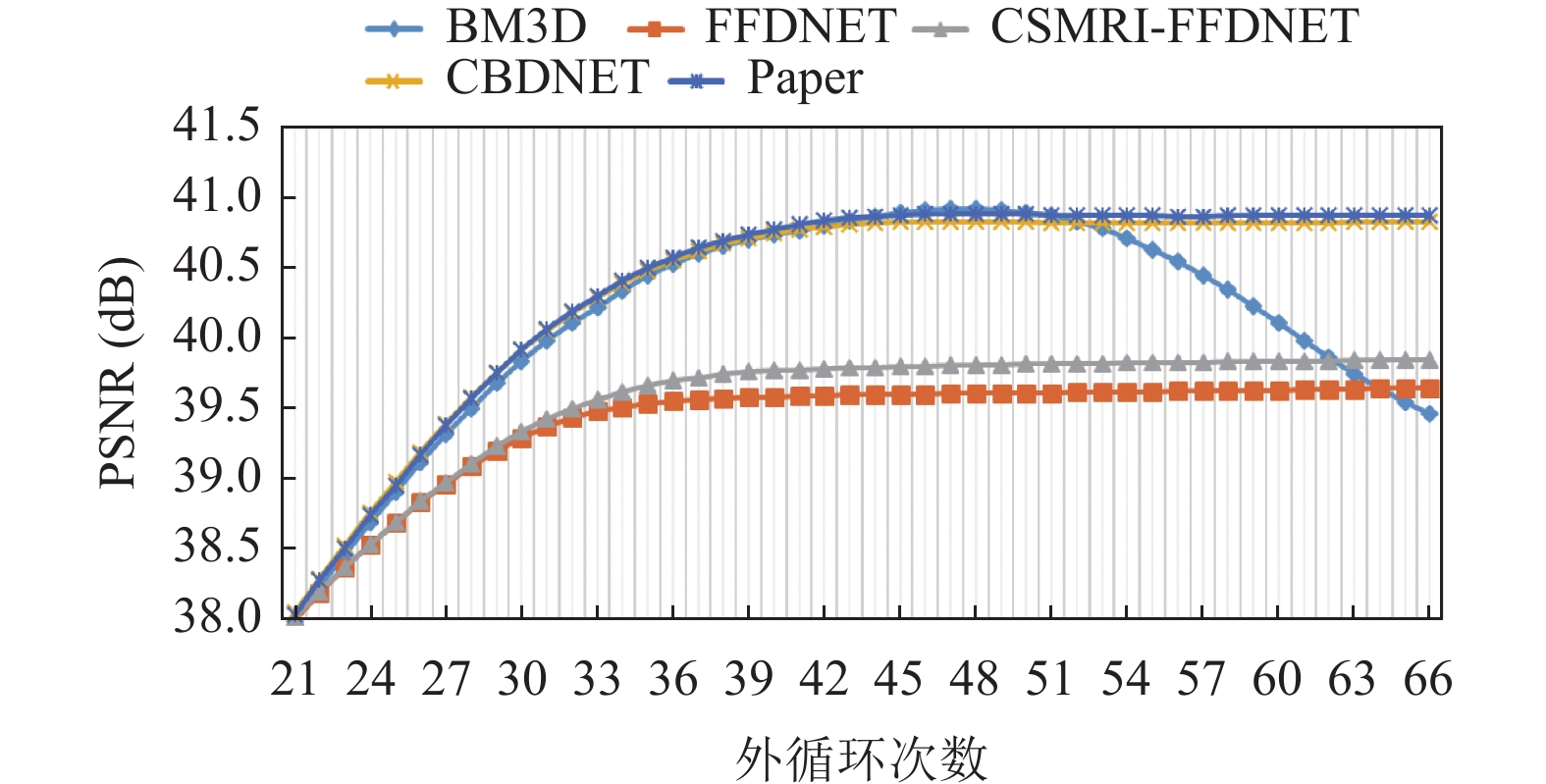
当采样率为30%高斯随机采样、迭代次数为660时运行时长如表2所示. 虽然数据显示各算法中运行时间BM3D算法最少, 但如图5所示, 取外循环为21–66次所对应的文中所提6种算法的PSNR值形成曲线图, BM3D算法峰值信噪比值程下抛物线状, 说明此算法图像恢复效果不稳定, FFDNet及CSMRI-FFDNet算法PSNR值上升后成稳定状态, 但其图像恢复效果不够理想. 数据统计可以看出CBDNet-BM3D算法优于其他4种算法且非常稳定.

重构算法获得的估计图像PSNR值差距大都在[–3, 3]范围内, 数值非常近似, 为更好地显示此类型的数据, 图6使用了堆积折线图展示随着采样率的提升各算法PSNR值的上升率. 在高斯随机采样率分别为1%、5%、10%、15%、20%、25%、30%、35%、50%的取值下, 从折线图可以看出, 最上面代表本文所提出算法的曲线斜率是最大的, 说明采样率越高本文所提出算法的图像恢复效果会更加显示其优势.

箱线图显示CBDNet-BM3D算法与其他4种对比算法的PSNR值, 方框内的线表示中值, 方框代表第25到第75个百分位数. 方框外线代表第10个和第90个百分位数, 上下水平线分别代表最小值和最大值. 实验数据表明, 深度学习算法与传统重构算法结合的算法效果均要优于单纯使用深度学习算法的重构结果. 表1和图7(b)显示BM3D算法的图像重构效果从数据上看非常有优势, 本文提出的方法是深度学习与传统重构算法的混合式重构算法, 图像恢复效果均优于其他算法, 这些结果证明了所提出的算法的有效性.

5 结论

本研究提出了利用CNN结合传统方式进行欠采图像的重构, 针对不足采样的K空间数据, 在经典的CNN算法CBDNet算法的基础上, 提出了基于深度神经网络去噪先验和BM3D算法的块压缩感知重构法, 得到以下结论.

(1) 该算法实现了抑制伪影、快速重建高质量MRI.

(2) 实验结果表明, 该理论有效降低了伪影并保留了细节信息, 加强了重构效果, 印证了我们提出的方法比单纯的深度学习方法或传统的块匹配方法更接近目标图像.

(3) 与此同时, 通过采用GPU的加速运算, 算法的计算复杂度较使用单一算法并未增加很多.

综上所述, 证明混合式CNN算法在MR图像领域非常具有现实应用价值.