2. 机器视觉与虚拟现实山西省重点实验室(中北大学), 太原 030051;
3. 山西省视觉信息处理及智能机器人工程研究中心, 太原 030051
2. Shanxi Key Laboratory of Machine Vision and Virtual Reality (North University of China), Taiyuan 030051, China;
3. Shanxi Province’s Vision Information Processing and Intelligent Robot Engineering Research Center, Taiyuan 030051, China
强化学习[1–3]在未知环境中的自适应性与自学习能力在导航问题[4–6]中表现出了较大的潜力, 但现有的算法大都应用于单智能体环境, 在多智能体环境中仍存在很多困难. 单智能体路径规划中智能体只用学习自己的策略, 所在的环境是稳定不变的, 奖励函数只需要考虑到目标点的距离以及与环境的碰撞问题. 而多智能体路径导航[7–11]中, 每个智能体的策略不断改变, 导致环境变得不稳定, 智能体间的交互也变得更加复杂, 智能体除了考虑与环境的碰撞问题, 还要考虑智能体之间的碰撞问题, 奖励函数设定也需要考虑各个智能体联合动作的影响, 大大增加了多智能体路径导航学习的难度, 出现效率低, 收敛速度慢的问题.
早期的工作尝试采用注意力机制[12]模拟智能体之间的关系, 学习可用的经验来加速多智能体强化学习过程. 文献[13]提出的ATOC算法[13]采用一个双向的 LSTM 网络作为通信群组之间的通信信道, 通过整合共享信息以进行合作决策, 依据注意力模块来决定是否进行通信. 文献[14]提出的MAAC算法[14]使用多头注意力机制减少对集中式Critic网络的输入, 适应了因智能体数量增加造成的输入空间的暴涨. 文献[15]提出的EPC算法[15]在Actor和Critic网络都使用注意力机制解决网络输入维度增大的问题, 以获得更好的性能表现. 文献[16]提出的Qatten算法[16]用多头注意力机制分解联合Q值, 度量每个智能体对全局系统的重要程度. 文献[17]提出的TarMAC算法[17]用基于签名的软注意力机制(soft attention)建立有针对性的通信, 适应动态的智能体数量. 这些算法的主要思想都是利用软注意机制, 通过Softmax函数学习智能体之间的关注程度. 然而, Softmax函数的输出值是一个相对值, 会将非零的小概率分配给不相关的智能体, 削弱了对相关智能体所给予的关注, 不能真正模拟智能体之间的关系.
针对软注意力机制分配权重不合理的问题, 本文用硬注意力机制(hard attention)弥补软注意力机制的缺陷, 提出了基于两级注意力机制的MADDPG-Attention算法. 在训练期间用硬注意力机制筛选需要关注的智能体, 对需要关注的智能体赋予概率值1, 对不需要关注的智能体赋予概率值0. 同时根据需要关注的程度利用软注意力机制分配权重, 建立智能体之间的学习关系, 加快多智能体强化学习的速度.
1 背景知识 1.1 马尔可夫博弈与纳什均衡在强化学习领域, 待解决的问题通常被描述为马尔可夫决策过程(MDP). 马尔可夫博弈[18]是马尔可夫决策过程在多智能体环境下的扩展. 纳什均衡是马尔科夫博弈问题的目标. 多智能体强化学习借助马尔科夫博弈将问题进行建模, 以纳什均衡为目标找到求解问题的方法.
马尔可夫博弈由多元组
纳什均衡是在多个智能体中达成的一个不动点, 对于其中任意一个智能体来说, 无法通过采取其他的策略来获得更高的累积回报. 纳什均衡不一定是全局最优, 但它是在概率上最容易产生的结果, 是在学习时较容易收敛到的状态.
1.2 MADDPG 算法MADDPG算法(multi-agent deep deterministic policy gradient)[19]是解决多智能体连续行为的确定性策略梯度算法. 它是DDPG算法[20–22]针对多智能体环境下的改进, 在Critic网络中加入了其他智能体的信息, 采用集中式训练分布式执行的架构, 在训练过程中由Critic网络集中式共享全局信息, 在执行过程中由Actor分布式获取局部信息, 即当前智能体的观测信息. 由于每个智能体都具有Critic网络, 因此MADDPG算法可以具有不同奖励函数的智能体, 在完全合作、完全竞争和混合关系的问题中都能取得较好效果.
MADDPG最初是由解决连续行为的策略梯度(PG)算法[23]演化而来, PG算法随着动作维度的增加, 计算性能消耗过大, 因此DeepMind提出了确定性策略梯度(DPG)算法[24]. 后来人们意识到了可以使用神经网络去拟合强化学习算法中的价值函数和策略函数, DeepMind又提出了深度Q网络算法(DQN)[25], 但不能解决连续空间的问题. DDPG算法是DPG算法与DQN算法的结合, 将DQN中用来拟合Q函数的神经网络用在了DPG框架中, 实现了基于深度神经网络的DPG算法, 可以很好地适应连续空间的问题. 由于多智能体环境的不稳定性, DDPG直接用于多智能体环境的表现不佳, 因此将DDPG算法扩展到多智能体深度确定性策略算法MADDPG.
2 MADDPG-Attention方法 2.1 两级注意力机制随着深度强化学习的发展, 注意力机制在多智能体强化学习领域的应用越来越广, 它对重要信息的合理利用, 在一定程度上促进了智能体的学习效果, 特别是硬注意力机制和软注意力机制的作用非常显著.
硬注意力机制是从输入的所有元素中选择一个子集, 迫使模型只能关注重要元素, 完全忽略其他元素. 虽然这恰好可以帮助智能体筛选与自己相关的信息, 但硬注意力机制对相关信息的学习是同等概率, 缺乏侧重性. 软注意力机制通过计算元素的重要性分布来分配学习权重, 这对学习其他智能体的经验提供了方案. 然而软注意力机制通常将非零的小概率赋给不相关的元素, 削弱了对真正重要元素的关注.
基于以上工作的启发, 本文提出基于两级注意力机制的多智能体强化学习方法MADDPG-Attention, 使用一层硬注意力机制将当前智能体与其他智能体按关联性区分, 再通过软注意力机制按重要性分布来分配学习权重, 达到对有用信息的合理利用, 从而提升MADDPG算法的性能.
硬注意力机制的结构如图1所示, 智能体的状态和动作进行拼接后经过一层全连接网络MLP和ReLU激活函数进行解码得到
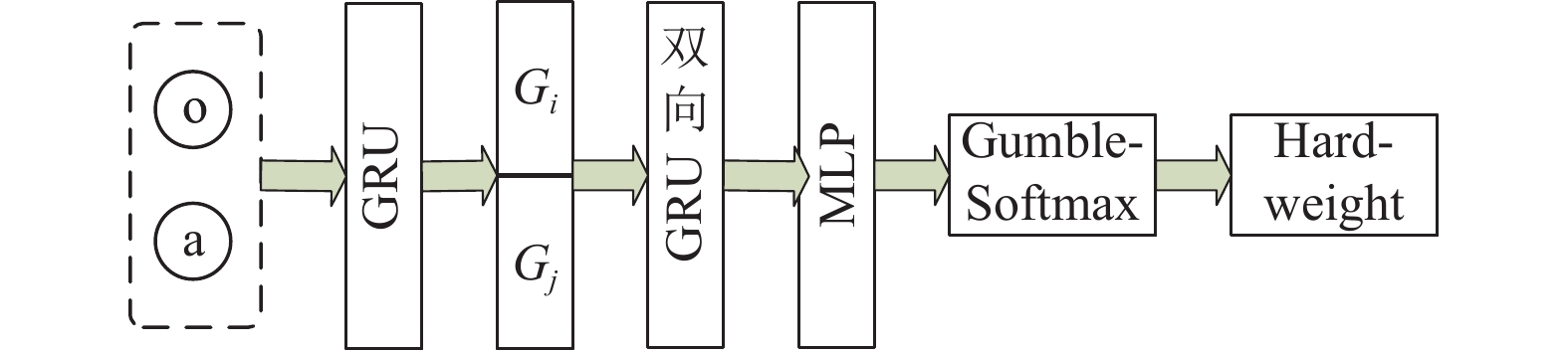
|
图 1 Hard-Attention结构框架图 |
软注意力机制的结构如图2所示, 将每个智能体的特征

|
图 2 Soft-Attention结构框架图 |
2.2 MADDPG-Attention网络结构
MADDPG算法中的Critic网络无差别的输入所有智能体的状态和动作, 学习没有重点, 针对该问题, 本文提出一种基于两级注意力机制的MADDPG方法. 该方法仍采用MADDPG算法集中训练分散执行的思想, 采用双重神经网络以及经验回放的结构, 具有训练稳定, 收敛速度快的特点.
Actor网络根据当前状态
Attention_Critic网络在训练阶段接收所有智能体的动作
Attention_Critic网络将动作和观测信息进行拼接得到
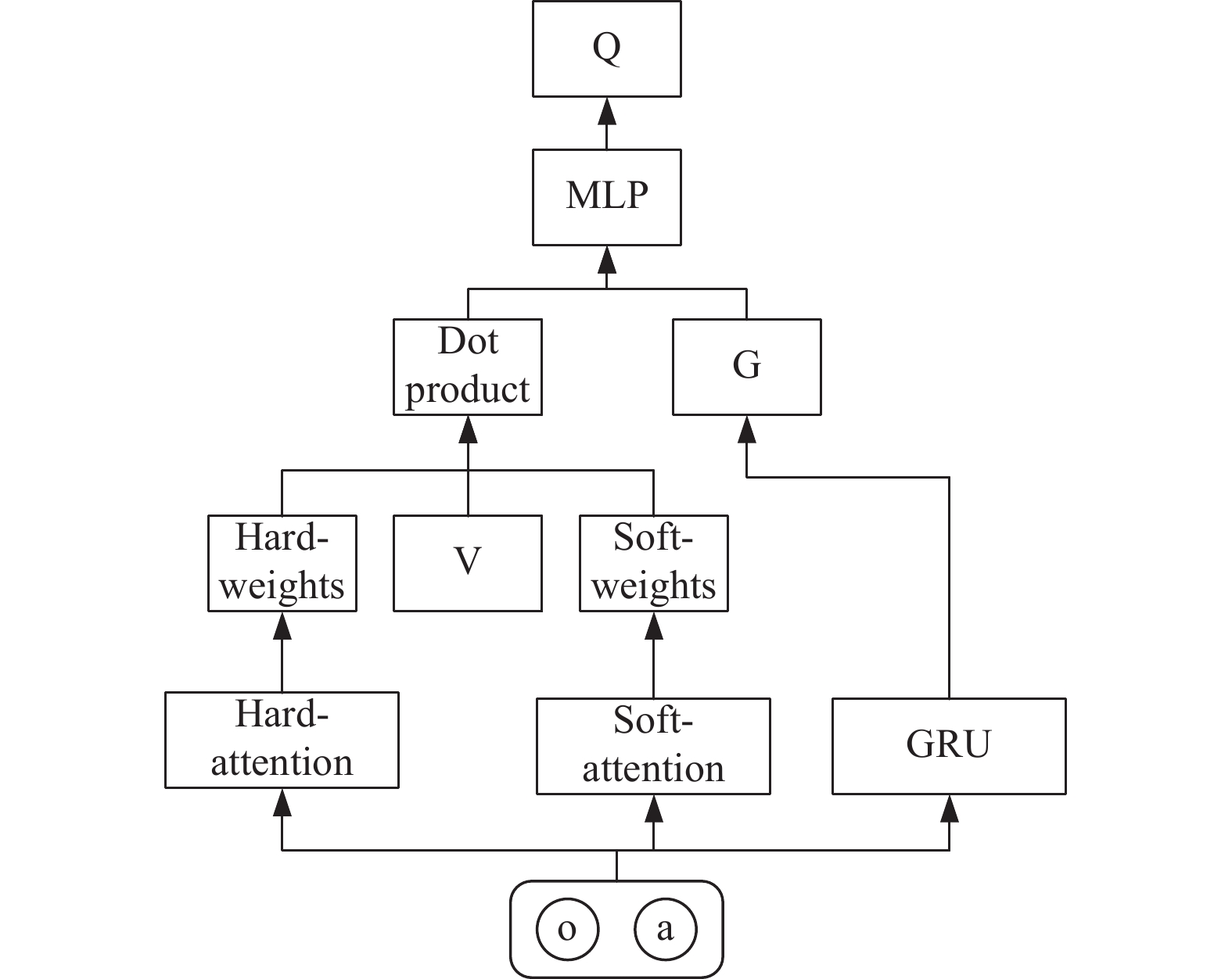
|
图 3 Attention_Critic网络结构 |
Target_Actor网络根据经验回放池中采样的下一状态
| ∇θiJ(μi)=Eo,a−D[∇θiμi(ai∣oi)∇aiQμi(o,a)|ai=μi(oi)] | (1) |
其中,
Target_Attention_Critic网络接收经验池中采样的下一状态
| L(θi)=Ex,a,r,x′[(Qμi(x,a1,⋯,an)−y)2], where y=ri+γˉQμ′i(x′,a′1,⋯,a′n)|a′j=μ′j(oj) | (2) |
其中,
多智能体强化学习中智能体通过与环境交互和试错来学习知识. 交互过程中智能体从环境中获得的信息称为观测空间, 依据观测空间智能体通过策略做出动作对环境进行回应. 合适的观测空间的设计对智能体的学习至关重要. 因此, 根据导航任务, 智能体的观测空间设计如表1所示. 实验环境是2维空间, 智能体和地标的个数都为k. 每个智能体的观测空间包括当前智能体的速度信息、位置信息、距离目标地标的距离、距离其他地标的距离和距离其他智能体的距离. 第i个智能体的速度信息由x轴的速度和y轴的速度
| 表 1 观测空间 |
2.4 奖励函数设计
奖励是智能体在采取了特定动作之后所得到的及时反馈, 智能体根据反馈去学习达到目标. 根据最终目标合理地设置奖励对智能体的学习非常重要. 依据奖励密度, 奖励分为稀疏奖励和稠密奖励. 稀疏奖励指的是只有在智能体达到目标状态或者完成任务才会获得奖励, 会导致智能体采取大量的随机动作, 忽略强化学习中非常重要的环境信息, 导致学习速度变慢. 而稠密奖励指的是智能体行动的每一个步骤都有奖励或惩罚, 促使智能体很快地学习到环境的信息, 起到良好的引导作用, 但过多的步骤奖励设置可能导致智能体专注于基本动作的实现, 达到局部最优解. 因此本文在稀疏奖励和稠密奖励之间寻找平衡, 设置成功奖励O、距离奖励D和碰撞惩罚C, 既保存了稀疏奖励的必要性, 又没有过分增加步骤奖励设置. 奖励函数
| R=−n∑i=1Di+C+O | (3) |
其中, 距离奖励
| Di=√(gix−pix)2+(giy−piy)2 | (4) |
碰撞惩罚
| C={−1,发生碰撞0, 无碰撞 | (5) |
成功奖励
| O={1, 覆盖地标0, 未覆盖地标 | (6) |
在多智能体强化学习领域中广泛使用的多智能体粒子环境上进行了仿真实验, 验证并对比了MADDPG-Attention算法、MADDPG算法、MAAC算法和DDMA算法的实验结果. 以测试阶段每100回合单个智能体的平均奖励、成功率和碰撞率为指标对算法性能进行评判. 其中MADDPG算法增加了高斯噪声探索, MAAC算法Critic网络使用了多头注意力增加算法的可扩展性, DDMA算法采用单智能体算法预学习多智能体策略, 并引入交互检测器提高学习效率.
3.1 多智能体粒子环境目前常采用多智能体粒子环境来对多智能体算法进行验证, 本文以其中的合作导航为实验环境, 通过控制二维空间中的粒子, 实现对于各类多智能体强化学习算法的验证及对比分析. 实验中, 智能体是运动的, 地标是静态的, 每回合结束后智能体位置和地标位置都会随机设置, 每个智能体要学会在避免碰撞的同时覆盖地标.
为了使实验环境更加贴近真实环境, 将合作导航环境转换为小车导航, 小车作为智能体, 需要在不碰撞的情况下合理规划路线以到达目标.
实验环境如图4所示, 采用3种不同的环境进行训练和测试. 3对3环境如图4(a)所示, 3个小车合作导航到3个地标(图标为房子), 训练开始之前为每个小车随机分配一个目标, 每个小车之间碰撞会受到惩罚, 到达目标则给予奖励. 4对2环境如图4(b)所示, 4个小车合作导航到两个地标, 每两个小车为一组, 随机为每组小车分配一个地标, 相同地标的小车碰撞不惩罚, 不同地标的小车碰撞会惩罚, 每个小车到达地标会给予奖励. 6对3环境如图4(c)所示, 6个小车合作导航到3个地标, 每两个小车为一组, 为每组小车分配一个地标, 相同地标的小车碰撞不惩罚, 不同地标的小车碰撞会惩罚, 每个小车到达地标会给予奖励.
3.2 实验参数设置MADDPG-Attention算法的实验参数如表2所示.
3.3 结果分析MADDPG-Attention、MADDPG、MAAC和DDMA这4种算法在3对3环境、4对2环境和6对3环境中训练100000回合, 每1000回合进行一次测试. 测试1000回合, 每100回合的进行一次统计, 取10次统计的平均值作为实验结果.
为了评估4种方法在测试环境中的性能, 选取成功率, 即100回合平均覆盖地标的次数进行测试. 3对3环境的测试结果如图5(a)所示, 4对2环境的测试结果如图5(b)所示, 6对3环境的测试结果如图5(c)所示.

|
图 4 合作导航 |
| 表 2 实验参数 |
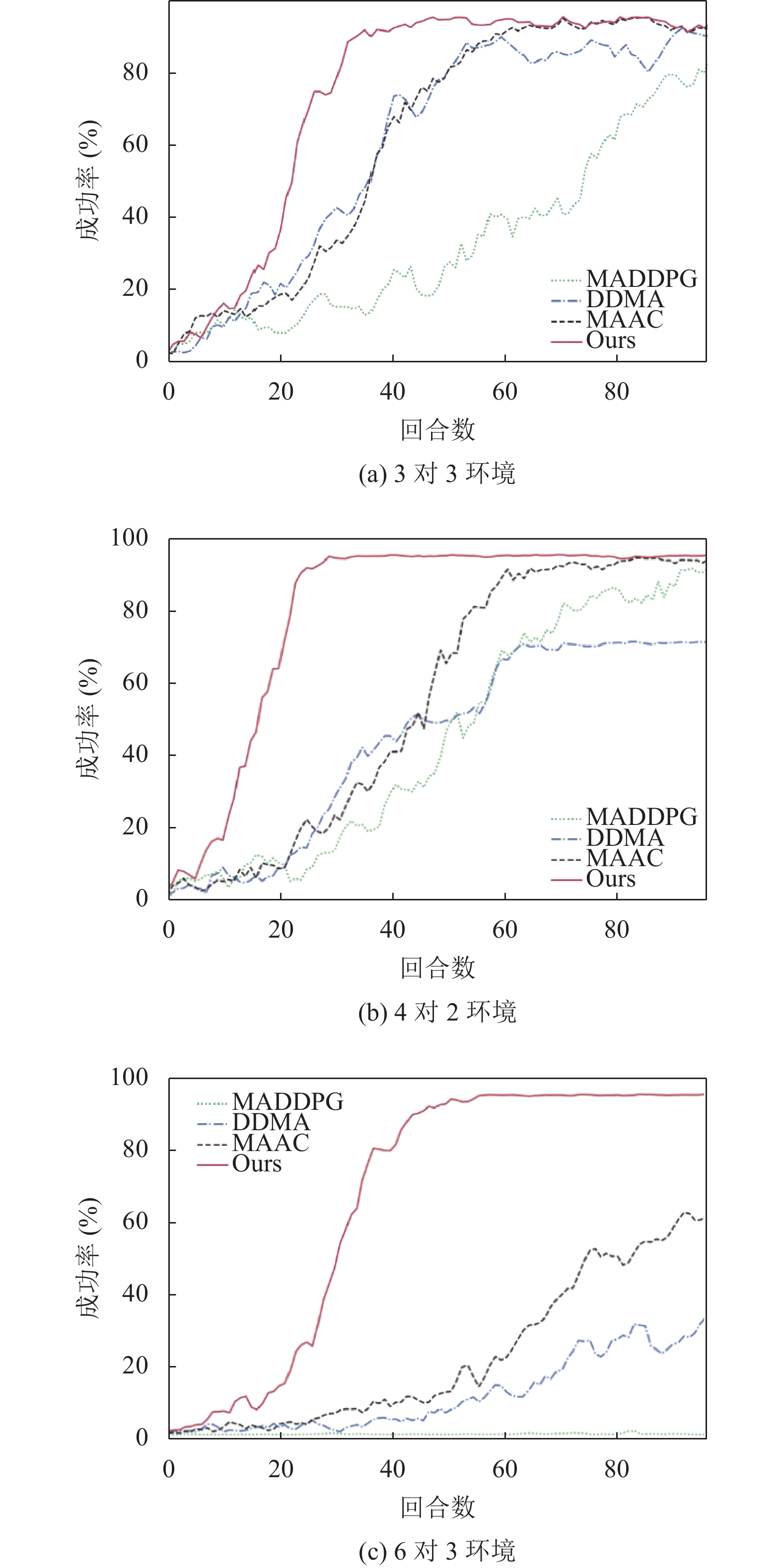
|
图 5 成功率 |
从图5(a)可以看出, MADDPG算法学习速度较慢, 最终成功率也只能达到80%左右, 效果略差. MAAC算法和DDMA算法60回合后成功率都可以到达90%以上, 可以较好地完成覆盖地标的任务. MADDPG-Attention算法25回合左右成功率就收敛到了90%以上, 学习速度最快. 从图5(b)可以看出MADDPG算法学习速度稳步上升, 在100回合后成功率收敛到93%左右, 学习效果较好. MAAC相对环境1来说, 学习速度有所下降, 60回合后也能收敛到95%左右. DDMA成功率出现明显下降, 60回合后收敛到72%左右. MADDPG-Attention算法收敛速度仍旧保持最快, 25回合左右就收敛到了96%左右. 从图5(c)可以看出MADDPG算法完全无法完成学习导航的任务, 成功率一直为0%左右. MAAC算法和DDMA算法60回合后成功率才有明显的上升, MAAC算法100000回合后成功率达到62%左右, 效果略好, DDMA算法100000回合后成功率达到30%左右, 效果较差. MADDPG-Attention算法收敛速度保持最快, 50回合左右收敛到了96%左右. 总体来说, MADDPG-Attention算法对于不同环境的迁移性很好, 随着智能体数目的增多仍能保持良好的表现.
使用平均碰撞次数评估4种算法的性能, 3对3环境的测试结果如图6(a)所示, 4对2环境的测试结果如图6(b)所示, 6对3环境的测试结果如图6(c)所示.
从图6(a)可以看出, MADDPG算法碰撞率初期处于较低的状态, 但80回合后出现了较高的起伏, 碰撞率略高, 结合成功率来看, MADDPG算法前期探索性不强, 80回合后才有明显的学习效果. MAAC算法处一开始碰撞率高, 且波动一直较大, 结合成功率来看, MAAC算法通过大量的碰撞去增加探索性来学习导航的目标, 学习的观念比较激进. DDMA算法碰撞率虽然一开始处于较低状态, 但60回合后碰撞率出现明显增加, 且持续时间较长, 结合成功率来看, DDMA算法在60–80回合之间成功率出现了下降, 说明DDMA算法的稳定性较差. MADDPG-Attention算法的碰撞率一直处于较低的水平, 没有明显波动, 结合成功率来看, 学习速度也一直保持稳定上升, 说明MADDPG-Attention算法的稳定性以及学习效率都较好. 从图6(b)可以看出, 4种算法因为智能体有同一目标的设定碰撞率有不同程度的增加, MADDPG算法碰撞率一直处于稳定的波动, 没有很好的学习到不碰撞的任务. MAAC算法、DDMA算法和MADDPG-Attention算法虽然前期碰撞率高, 但80回合后都保持在2%以下, 对不碰撞任务的学习效果较好. 图6(c)可以看出, MADDPG算法虽然碰撞率在1%左右, 但结合成功率来看, 没有学习到任何任务. MAAC算法仍旧保持激进的学习观念, 初期的碰撞率非常高, 且80回合后波动较大. DDMA算法一直保持较大的波动学习, 学习效果不稳定. MADDPG-Attention算法虽然前期碰撞率较低, 但45回合后出现了较大的波动, 结合成功率来看, 45回合后成功率逐渐趋于收敛, 说明MADDPG-Attention算法以牺牲一定的碰撞率来学习导航的任务.

|
图 6 碰撞率 |
3种实验环境中的实验结果显示, 随着环境复杂度的变化和智能体数目的增加, MADDPG算法逐渐失去了学习能力, 环境迁移性较差. MAAC算法以碰撞去学习探索, 学习观念较为激进, 学习效果较好. DDMA算法学习效果不稳定, 学习效果较差. MADDPG-Attention算法在3种环境中都保持了良好的学习效果, 环境的迁移性较好.
将3种环境的成功率和碰撞率结果汇总在表3中, 其中最优结果用粗体表示, 结果保留两位小数.
实验结果表示, 在3对3环境中, 本文算法碰撞率虽然较高, 但是成功率也最高, 相比MADDPG、MAAC和DDMA算法, 本文算法的成功率分别提高了10.38%、0.95%和2.11%. 在4对2环境中, 本文算法碰撞率较低, 成功率保持最高, 相比MADDPG、MAAC和DDMA算法, 本文算法的成功率分别提高了3.68%、1.37%和24.4%. 在6对3环境中, 本文算法碰撞率略高, 成功率仍然保持最高, 相比MADDPG、MAAC和DDMA算法, 本文算法的成功率分别提高了96.32%、34.33%和65.23%.
| 表 3 多个环境下的导航测试结果 |
总体来看, 在3对3环境中, 4种算法都有差不多的效果, 但在4对2环境和6对3环境中存在具有相同目标的智能体, MADDPG和DDMA算法对每个智能体给予同等的关注, 智能体数目增多后智能体之间的关系变得复杂, 无法学习到导航任务, 效果出现明显下降, 使用软注意力的MAAC算法虽然可以学习其他智能体的一些经验, 但随着智能体数目的增多, 不同目标的智能体会占据越来越多的不必要的注意力, 因此效果出现一定下降, 而MADDPG-Attention算法利用两级注意力机制只关注同一目标的智能体, 因而可以保持优越的性能. 综上所述, MADDPG-Attention算法的整体表现优于MADDPG、MAAC和DDMA算法.
3.4 实验探究为了进一步研究两级注意力机制对算法性能的影响, 对两级注意力的组合方式和单级注意力对MADDPG算法的表现进行实验分析.
3.4.1 注意力组合探究为了探索更优秀的注意力组合方式, 选取硬注意力与软注意力的乘积和硬注意力与软注意力的线性加权两种方式在6对3环境进行实验. 其中线性加权方式软注意力与硬注意力线性权值之和为1, 软注意力权值选取(0.1, 0.3, 0.5, 0.7, 0.9). 实验结果如图7所示.

|
图 7 组合探究成功率 |
实验结果显示, 本文硬注意力与软注意力乘积的方式优于所有线性加权的方式. 两种注意力的乘积可以把不相关智能体的权重赋为零, 而线性加权的方式仍会保留不相关智能体的权重, 只是会进一步缩小不相关智能体的权重, 虽然对软注意力有一定的帮助, 但选用两种注意力采取相乘的方式更为合适.
3.4.2 消融实验为了验证硬注意机制和软注意力机制对MADDPG算法性能的影响, 在6对3的环境中进行消融实验对比, 其中包括的算法有3种: 仅使用硬注意力机制的MADDPG+Hard算法、仅使用软注意力机制的MADDPG+Soft算法和本文基于两级注意力机制的MADDPG算法. 消融实验结果如图8所示.
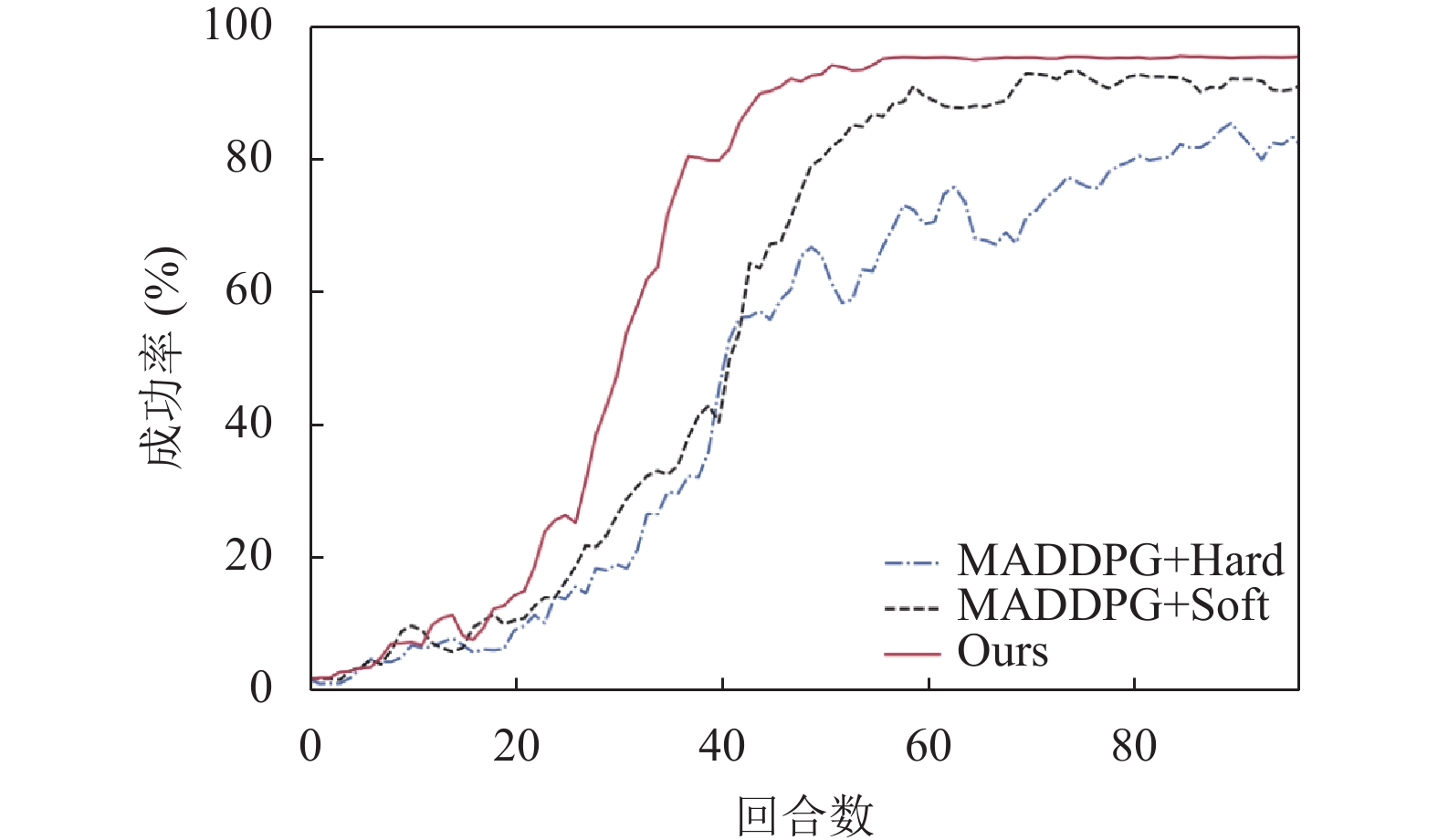
|
图 8 消融成功率 |
实验结果显示, MADDPG+Hard算法的成功率在80回合后收敛到80%左右, 学习速度最慢; MADDPG+Soft算法的成功率在60回合后收敛到90%左右, 学习速度有一定的提高; 本文基于两级注意力的MADDPG算法相较于单级注意力的算法无论是成功率还是学习速度均为最佳. 硬注意力弥补了软注意力权重分配不合理的缺陷, 两者相互耦合, 取得了更加优秀的性能.
4 结论与展望本文提出了一种基于两级注意力的MADDPG算法. 该算法通过在Critic网络增加硬注意力和软注意力机制实现了对其他智能体的有选择性的学习, 并在合作导航环境中在扩展性以及成功率等方面表现出了优秀的性能. 下一步研究将考虑在Actor网络中使用长短期记忆方法, 通过参考前序信息, 做到有预测的导航.
| [1] |
李茹杨, 彭慧民, 李仁刚, 等. 强化学习算法与应用综述. 计算机系统应用, 2020, 29(12): 13-25. DOI:10.15888/j.cnki.csa.007701 |
| [2] |
Lyu XG, Baisero A, Xiao YC, et al. A deeper understanding of state-based critics in multi-agent reinforcement learning. Proceedings of the 37th AAAI Conference on Artificial Intelligence. Washington: AAAI Press, 2022. 9396–9404.
|
| [3] |
Li PY, Tang HY, Yang TP, et al. PMIC: Improving multi-agent reinforcement learning with progressive mutual information collaboration. Proceedings of the 2022 International Conference on Machine Learning. Baltimore: PMLR, 2022. 12979–12997.
|
| [4] |
Papoudakis G, Christianos F, Schäfer L, et al. Benchmarking multi-agent deep reinforcement learning algorithms in cooperative tasks. arXiv:2006.07869, 2021.
|
| [5] |
Skrynnik A, Andreychuk A, Yakovlev K, et al. POGEMA: Partially observable grid environment for multiple agents. arXiv:2206.10944, 2022.
|
| [6] |
Christianos F, Schäfer L, Albrecht S V. Shared experience actor-critic for multi-agent reinforcement learning. Proceedings of the 34th International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 898.
|
| [7] |
项宇, 秦进, 袁琳琳. 结合向前状态预测和隐空间约束的强化学习表示算法. 计算机系统应用, 2022, 31(11): 148-156. DOI:10.15888/j.cnki.csa.008801 |
| [8] |
Arpino CPD, Liu C, Goebel P, et al. Robot navigation in constrained pedestrian environments using reinforcement learning. Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA). Xi’an: IEEE, 2021. 1140–1146.
|
| [9] |
Marchesini E, Farinelli A. Discrete deep reinforcement learning for mapless navigation. Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA). Paris: IEEE, 2020. 10688–10694.
|
| [10] |
Liu L, Dugas D, Cesari G, et al. Robot navigation in crowded environments using deep reinforcement learning. Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Las Vegas: IEEE, 2020. 5671–5677.
|
| [11] |
Koh S, Zhou B, Fang H, et al. Real-time deep reinforcement learning based vehicle navigation. Applied Soft Computing, 2020, 96: 106694. DOI:10.1016/j.asoc.2020.106694 |
| [12] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [13] |
Jiang JC, Lu ZQ. Learning attentional communication for multi-agent cooperation. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 7265–7275.
|
| [14] |
Iqbal S, Sha F. Actor-attention-critic for multi-agent reinforcement learning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 2961–2970.
|
| [15] |
Long Q, Zhou ZH, Gupta A, et al. Evolutionary population curriculum for scaling multi-agent reinforcement learning. Proceedings of the 8th International Conference on Learning Representations. Addis Ababa: OpenReview.net, 2020.
|
| [16] |
Yang YD, Hao JY, Liao B, et al. Qatten: A general framework for cooperative multiagent reinforcement learning. arXiv:2002.03939, 2020.
|
| [17] |
Das A, Gervet T, Romoff J, et al. TarMAC: Targeted multi-agent communication. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 1538–1546.
|
| [18] |
Littman ML. Markov games as a framework for multi-agent reinforcement learning. Proceedings of the 11th International Conference on International Conference on Machine Learning. New Brunswick: Morgan Kaufmann Publishers Inc., 1994. 157–163.
|
| [19] |
Lowe R, Wu Y, Tamar A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6382–6393.
|
| [20] |
殷雨竹, 陈建平, 傅启明, 等. 基于自监督网络的DDPG算法的建筑能耗控制. 计算机系统应用, 2022, 31(2): 161-167. DOI:10.15888/j.cnki.csa.008365 |
| [21] |
李卓远, 张德平. 基于BN-DDPG轻量级强化学习算法的智能兵棋推演. 计算机系统应用, 2023, 32(4): 293-299. DOI:10.15888/j.cnki.csa.009015 |
| [22] |
Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. Proceedings of the 4th International Conference on Learning Representations. San Juan: ICLR, 2016.
|
| [23] |
Sutton RS, McAllester D, Singh S, et al. Policy gradient methods for reinforcement learning with function approximation. Proceedings of the 12th International Conference on Neural Information Processing Systems. Denver: MIT Press, 1999. 1057–1063.
|
| [24] |
Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms. Proceedings of the 31st International Conference on International Conference on Machine Learning. Beijing: JMLR.org, 2014: I-387–I-392.
|
| [25] |
Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning. arXiv:1312.5602, 2013.
|
 2023, Vol. 32
2023, Vol. 32



