图数据作为一种非常重要的数据形式, 能够有效描述现实世界中各个事务的连接和关系. 现实世界中许多复杂的问题可以通过图建模和相关算法解决. 随着图数据规模的增大, 面临的挑战也会越来越多, 处理这些图数据的计算需求也会增加. 在处理大规模图时, 图分区具有广泛的应用. 例如在社交网络上, 图分区可以将社交网络划分为多个子图, 使得同一社区内的节点更可能连接在一起. 在物流与交通规划上, 将地理位置相近的节点划分到同一分区, 可以更好地管理和调度资源, 提高运输效率和减少交通拥堵. 在集成电路的设计和优化上, 可以减少电路布线的复杂性和信号传输的延迟, 提高电路性能.
为了高效的分析大规模图数据, 已经提出了一些分布式图处理系统, 例如Pregel[1], PowerGraph[2], GraphX[3], GraphLab[4], PowerLyra[5]. 这些系统通过图分区将计算任务划分成多个子任务, 并将他们分配给多个计算节点来实现. 由于数据放置通常会显著影响作业的执行效率[6], 它决定了每台机器的计算工作量以及它们之间的通信, 所以分布式系统性能很大程度上取决于图划分的质量[7]. 确保高质量的图分区是根据两个标准: 平衡机器之间的处理负载和最小化不同机器之间的通信成本[8]. 一个合理的图分区策略能够保证每个计算节点的负载均衡, 即分配数量近似相同的边给每个计算节点, 避免某些计算节点负载过重, 并能够减少计算节点之间的通信量. 在许多应用中, 图的规模非常大, 包含大量的顶点和边例如社交网络和生物网络等. 在处理这类大规模图时, 我们需要在合理的时间内对其进行分割, 以方便后续图算法的执行. 对于一些实时响应应用, 例如网络路由, 图分区算法需要在短时间内生成分区结果, 以便进行后续的处理. 然而现有的一些图分割方法在图分割质量上表现出色, 但它们往往伴随着较高的分区时间成本, 例如METIS需要超过8.5个小时来将一个有大约15亿条边的图划分为只有2个分区[9], 而Fennel也需要40 min[10], 这会影响到图分割算法对应用带来的计算效益. 尤其是随着图规模的增大, 这种影响也越来越大, 越发越不可忽视, 甚至使图分割算法给应用程序带来负收益. 所以我们需要在分割质量和算法的执行效率之间进行权衡[11], 在可接受的分割质量情况下, 快速执行图分割算法.
为此, 本文围绕着图分区算法为了更好的分割质量, 但是效率执行低的问题, 提出了基于广度优先遍历加权图生成的启发式图分区方法. 它能在可接受的分割质量情况下, 快速执行图分割算法. 实验结果表明, 我们的方法在小幅度牺牲图分割质量的情况下, 能显著提高图分割算法的执行效率. 这种权衡能够有效提升应用的整体性能.
1 图分割首先图分析的速度取决于最大子图的执行速度, 所以划分分区应该首先保证负载平衡[12]. 其次, 一些顶点可能在多个子图中存在需要保证顶点同步性, 所以图划分应该尽量地减少这些远程通信.
目前, 图分割有顶点分割和边分割两种类型. 其中, 顶点分割是通过切割边将顶点均匀的划分为不相交的分区, 边分割是通过切割顶点将边均匀的划分为不相交的分区. 然而构造平衡顶点划分的方法在幂律度分布图上表现不佳[8]. 在对真实世界幂律图进行分割时, 边分割算法的性能优于传统的顶点分割算法, 这是因为它可以将一个顶点分割成多个副本来分摊计算量[13]. 目前研究证明, 边分割比顶点分割在许多大型自然图上具有更好的效果[2,8].
1.1 准备工作图G=(V, E)表示为一个无向图, V表示顶点集, E表示边集, 将图G的边集E划分为不相交的p个边子集Ei.
1.2 分区评判标准为了证明图划分的有效性, 我们使用了两个度量标准即负载平衡因子[2,9]和复制因子[8].
负载平衡因子是评估子图负载平衡度量指标, 用来评估子图负载偏斜度. 负载平衡因子满足下式:
| maxi∈p{|Ei|}<α|E|p |
则评估负载平衡因子使用下式确定:
| α=maxi∈p{|Ei|}p|E| |
其中, α是用户可接受的负载偏斜度即负载平衡系数, p是分区的数量, |E|是边数量, |Ei|是分区i中边集的数量.
复制因子是评估通信成本的度量指标, 用来评估分区之间的远程通信量. 边分割即顶点切割方法采取了跨集群复制顶点的策略, 并将顶点分配给顶点相邻边所属的分区. 为了保证图分析结果的准确性, 就需要让复制顶点进行通信, 保证复制顶点分析结果的一致性.因此, 想要通信成本降低就必须要降低复制因子. 评估复制因子使用下式:
| RF=1|V|∑i∈p|Vi| |
其中, RF是复制因子, |V|是所有的顶点数量, |Vi|是分区i中顶点集数量.
2 算法实现我们的技术分为3个阶段: 基于广度优先遍历的加权图生成, 基于启发式的加权图分割, 加权图还原.
2.1 高质量图分区策略尽管现有的一些图分割算法拥有较好的分割质量但是有较高的分区时间开销, 尤其是对于大规模图来说, 它们面临的高分区时间开销问题是不可忽视的挑战. 例如METIS[14], NE[15].
其中, METIS通过一种启发式算法进行初始划分, 将图划分为多个较小的子图. 然后使用递归划分策略递归地分割子图为更小的子图, 直到达到划分要求.划分过程中, METIS利用图的结构和属性信息, 这就使得每个子图都需要存储相关的信息, 并且需要对整个图结构进行遍历和缩放这样就导致了较高的内存消耗和较低的分割效率.
NE算法需要总览全局, 每次分配边都需要提前计算每个顶点的邻居集合, 然后动态改变核心集和边界集合, 以及边集, 这对于大规模图来说时间开销较大.
虽然这些图分区拥有较高的分割质量, 但是同时也会拥有较高分割时间开销.
2.2 基于广度优先遍历的加权图生成为了减少算法执行时间, 我们将以多个顶点及其相关边组成的块为基本单位, 而不是以顶点为基本单位进行分区.
我们提出的方法是将一个大图转换成带权值的小图, 以块为基本单位进行分区. 在我们的方法中顶点都有唯一ID, 我们根据顶点ID将一定数量连续顶点及其相关数据作为一个块. 我们将块中所有顶点的出边和入边添加给块. 将块到块之间的边合成为一条边, 我们给这条边赋予一个权值, 权值为这个块中所有顶点连接到另外一个块中的顶点数量. 这样我们就以块为单位将大图转化成了一个带权值的小图.
然而仅按照顶点ID进行块划分, 由于图的不规则拓扑结构, 会导致块与块之间存在大量的边, 而且分割算法只会考虑块之间的边, 无法看见块内部的详细结构, 忽视块内部的边和连接关系, 使得分割结果在块内部不够优化, 无法充分利用块内部的局部性. 由于块的数量比顶点数量小得多, 这样以块为基本单位进行分区可以显著的加快分区速度, 但这样也会极大的影响分区策略的质量.
为了减轻这个影响, 我们将图选定一个顶点作为根节点进行广度遍历, 对图中顶点ID进行重新索引, 加强了数据局部性[16], 然后根据新的顶点ID对图进行分块, 这样使块内顶点更加紧凑, 减少了块与块之间的跨越边. 虽然图分割依旧会忽视块内部的结果使得最后的分割结果在块内部不够优化. 但是由于对图进行了广度遍历后再分块, 我们会将更多的边划分进块内部, 减少了块与块之间的边数量, 使得块内部结构更加紧凑, 加强了块内顶点之间的紧密连接, 使得块内局部性更好, 这样我们就减缓了以块为基本单位进行分区对分区质量的影响, 减轻了将大图转化成加权小图即以块为单位对图粗化, 再进行图分割对分割质量的影响.
例如图1(a)是初始图和粗化后的带权图. 其中我们将两个顶点为一块即顶点0、1为块0; 顶点2、3为块1; 顶点4、5为块2; 顶点6、7为块3; 顶点8、9为块4. 如图2(a)右图所示, 我们将大图转成了加权图, 这样加权图的边达到了16条.

|
图 1 加权图的生成 |
图1(b)左图是以顶点0为根节点对图进行了广度遍历, 对每个顶点分配了一个新的顶点ID, 根据新的顶点ID进行分块, 然后我们将图转化成加权图如右图所示, 加权图的边只有11条, 减少了32.25%.
当然我们不仅要考虑图分割算法的质量, 还要考虑图分割算法的效率. 块的大小是其中的关键, 块的大小过大, 那将导致加权图过小, 会导致丢失图的结构信息, 导致图算法分割质量下降. 若块的大小过小, 会占用大量的计算机资源并且导致图算法的分割效率较低. 我们需要在提高一定效率的同时还要尽力地去减少块的大小对算法质量的影响. 由于我们接下来使用的算法最坏情况下的时间复杂度为O(n2), 我们要使算法的时间复杂度为O(m), 其中n是图的顶点数, m是图的边数, 那样我们就需要使得:
| O(num_bulk2)=O(|E|) |
其中,
| BS=2√|E|DA |
其中,
| num_bulk=|V|BS=√E |
则分块后算法的时间复杂度为
在加权图分割阶段, 我们利用了NE (neighbor expansion)[15]对生成的加权图进行分割. NE算法的基本思路是需要遍历每个节点, 并计算它的邻居节点集合, 然后根据邻居节点的情况来划分子图. 在计算每个节点的邻居节点时, 需要遍历该节点的所有邻居节点, 并判断它们是否满足划分条件. 具体实施是有一个核心集C和边界集S, 边界集包含核心集, 当
| x:=argminv∈S∖C|N(v)∖S| |
即对于S\C的顶点, 从中选取一个其邻居在边界外最少的顶点, 这样能够保证分配邻居边的最大化, 保证了最小化顶点的重复率. 选取顶点加入核心集, 然后查找他的邻居, 将不在边界集的邻居加入边界集; 边界集中顶点之间所关联的边加入当前子图, 重复上述步骤, 直到满足负载均衡. 对于我们的加权图来说, 边界节点的邻居数量是在边界外每条边的权重之和.
如图2所示, 图2(a)是分块后的初始状态, 圆圈内部数字代表块中的内部边, 块与块之间边上的数字代表块与块之间边的数量即权值. 我们要将拥有210条边的图划分为两个分区, 初始两个分区为空, 我们设置分区0为当前分区, 我们选择Bulk 0分配给当前分区的核心集. 我们分别将邻居Bulk 1, Bulk 7, Bulk 8加入边界集. 从边界集中选择边界外边权重之和最小的块即Bulk 8, 它的边界外权重只有10, 此时分区0中的边数量80并没有达到规定阈值则将Bulk 8分配给当前分区的核心集, 同理我们将Bulk 7分配给当前核心集此时分区0的边数110超过的规定阈值. 我们设置分区1为当前分区, 随机选取Bulk 3作为核心集, 重复上述步骤, 直到所有的块被分配完成.
2.4 加权图还原在上述阶段已经对转换后的加权图进行了划分, 在这个阶段我们需要将加权图转回成原始的以顶点为基本单位的原始图. 我们之前保存了原始图中的顶点信息如权重、标识符、邻居信息等, 以及块中顶点信息和原始图中的边信息. 我们根据加权图顶点编号即块标识符ID来确定原始图中每个顶点的位置, 再使用原始图中边信息还原图的拓扑结构. 在还原图的过程中, 会存在一些边界问题, 例如跨分区的边, 我们将这些边划分给相关联的边数量最小的分区.

|
图 2 加权图分割 |
3 实验分析
我们在拥有两个E5-2650 v4@2.20 GHz (24核) CPU和256 GB RAM的机器上进行了实验. 在本节中, 我们将评估我们的算法. 顶点分割算法质量评估采用两个指标: 负载平衡和重复因子. 由于负载平衡影响过大, 我们首先保证每个分区都是1.1负载平衡的. 我们接下来比较了负载平衡和复制因子以及运行时间.
3.1 数据集我们实验使用了3个真实世界图进行评估(全部来自于SNAP[17]). 图数据集的详细信息如表1所示.
| 表 1 测试数据集信息 |
3.2 实验对比对象
我们将我们的图分区算法与其他现有的5个分区方法进行了比较, 包括RAND[2], Oblivious[2], HDRF[18], NE. 其中RAND是一种简单的随机分配方法, 通过一个给定的哈希函数将顶点随机映射到不同的分区. 由于哈希函数的随机性, 这种方法通常可以实现较好的负载平衡, 并且具有良好的可扩展性. Oblivious是一种贪婪启发式算法, 它以一种保持重复因子较低的方式贪婪地分配边. HDRF是一种由Oblivious改进的方法, HDRF是将边分配到其度最大的结点所在分区上. 具有比Oblivious更好的分区效果.
3.3 实验设计与结果分析我们在优先保证负载平衡的情况下评估了负载平衡、算法策略的运行时间、重复因子.
我们在3种不同的数据集使用不同的分区策略将图划分为25个不同的分区, 由于我们的分区策略是需要分块的, 根据算法的时间复杂度和我们可接受的算法执行效率, 我们将3个数据集依次设置为800、600、1000个顶点为一块.
表2显示了负载平衡的实验结果. 其中负载平衡使用负载平衡因子来衡量, 表2描述了各个数据集分区的最多边数量和最低边数量以及平均数量边, 根据负载平衡因子公式[2,9]计算出了负载平衡因子的结果.
| 表 2 负载平衡实验结果 |
从表2我们可以看出, 对于Road-net-CA数据集划分后, 负载平衡因子只有1.006, Livejournal数据集划分后的负载平衡因子1.015, Twitter数据集划分后负载平衡因子1.014. 这是由于在划分图时, 当分配一个块到一个分区中, 若分区的边数量超越了规定负载因子所到达的边数量, 我们会取消这个块的分配, 并开始下一个分区的分配.
图3显示了分割质量的实验结果, 其中分割质量由重复因子衡量. 从图3中可以看出NE图分割策略具有最低的复制因子, 其次是我们将其进行广度遍历(BFS)重新分配顶点ID将其进行分块后使用NE算法进行块分配. 我们可以看出在用我们方法分块之后, 在对生成的加权图进行分割, 虽然对分割质量有一定的影响, 但是这个影响是较小的, 是在可接受范围内的. 这是因为我们选定一个节点对图进行广度遍历后再分块, 加强了块内的局部性, 使得块内结构更紧凑, 块的内部边数量增多, 加强了块内顶点之间的紧密连接. 虽然图分割算法依旧会忽视块内部结构, 但是由于我们加强了块内部的局部性, 使得块内部结构对图分割结果并没有很大的影响.
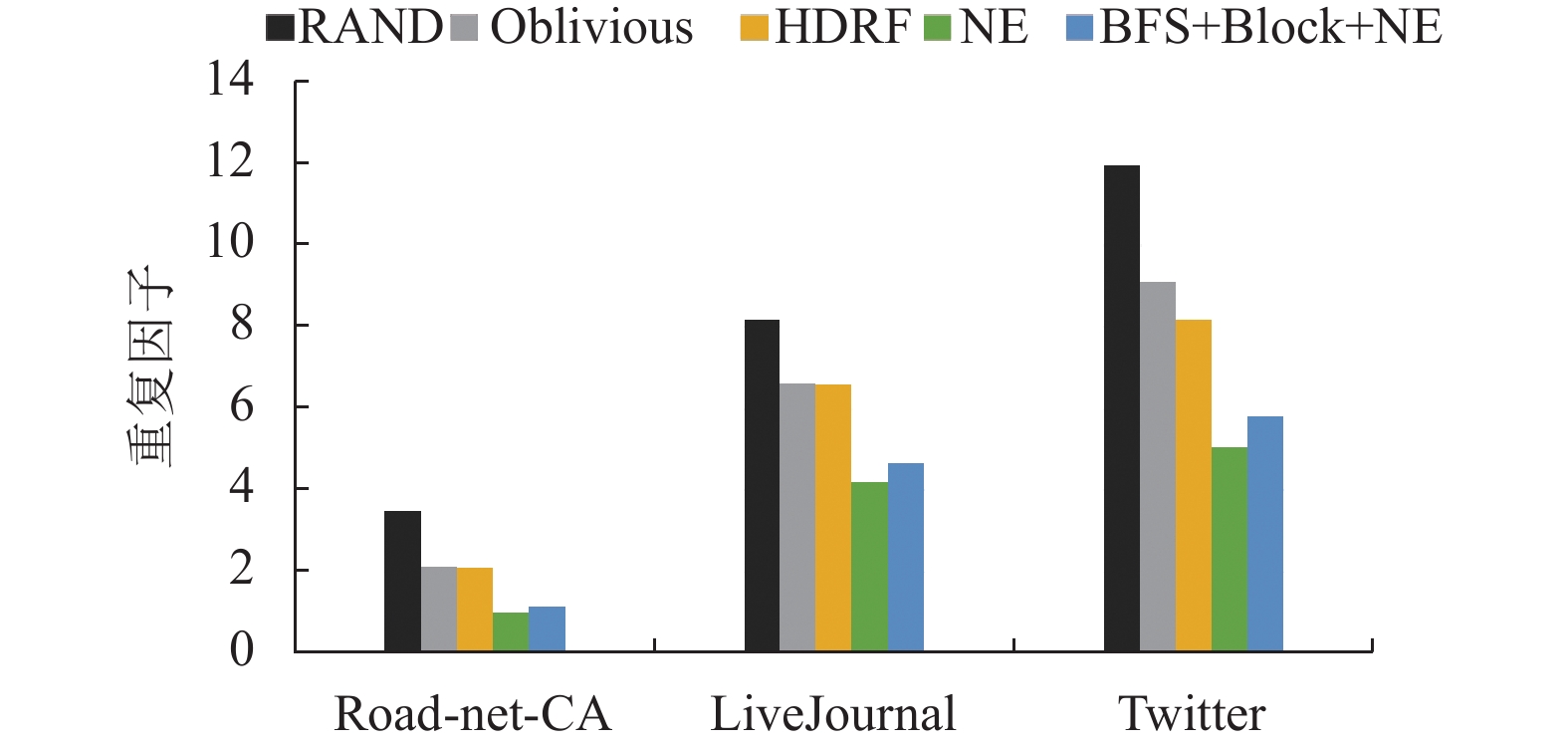
|
图 3 重复因子(负载平衡因子α=1.1, p=25) |
然而我们在考虑分区策略时, 我们不仅需要关注分区策略的分割质量, 也要考虑分割时间. NE图分割策略虽然有很高的分割质量, 但是它也有较高的分区时间, 算法的划分时间可能会影响分区策略带来的收益. 如果一个分区策略的划分时间过长, 可能会导致应用程序总的执行时间增加, 从而降低分区策略在计算阶段收益. 此时, 即使分区策略节省的计算时间很大, 但由于应用程序的执行时间增加, 导致分区策略的收益不明显, 甚至是负收益. 只有平衡好图分割质量和图分割速度, 才能确保整体应用程序执行时间得到最小化.
图4显示了算法执行效率的实验结果. 从图4中我们可以看出, 其中NE算法的执行时间最长, 并且高出对比算法的几倍, 这是因为基于启发式的方法很耗时, 因为每次对一条边进行划分决策时, 都需要锁定一个全局状态表[9]. 虽然NE具有最好的划分质量, 但是它的分区时间可能会图模型算法的总执行时间增加, 从而减少了分区策略质量在计算阶段收益.就划分速度而言, RAND是最快的. 它速度快, 分配均匀并且能够高度并行, 然而它会造成较高的复制因子, 所以我们一般不会考虑. 由于我们实现的分区策略是以块为基础的, 我们进行图分割算法是在我们粗化后的加权图上进行的, 其中加权图中的顶点就是我们划分的块, 且根据我们划分块的大小, 使得块的数量和块边的数量是远远少于原图中的顶点数和边数量的, 因此我们的分区策略提供了与RAND算法近似的划分速度.

|
图 4 分区策略的划分时间 |
4 结论和展望
当前的研究已经提出的许多图分区策略, 这些策略可以提高应用程序的性能. 然而由于大规模图数据的复杂性, 我们需要考虑多个因素, 才能做出最好的决策. 本文提出了一种基于广度优先遍历加权图生成的启发式图分割方法, 它在保证较好的分割质量情况下, 执行速度上优于当前流行的几种分区策略. 它在降低复制因子, 减少了通信开销的同时, 还拥有较快的分区速度, 能够实现高性能的图分析. 但是块仍然存在着块对图分区策略较高的影响, 在复制因子方面仍有改进空间.
| [1] |
Malewicz G, Austern MH, Bik AJC, et al. Pregel: A system for large-scale graph processing. Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data. Indianapolis: ACM, 2010. 135–146.
|
| [2] |
Gonzalez JE, Low Y, Gu HJ, et al. PowerGraph: Distributed graph-parallel computation on natural graphs. Proceedings of the 10th USENIX Symposium on Operating Systems Design and Implementation. Hollywood: USENIX Association, 2012. 17–30.
|
| [3] |
Gonzalez JE, Xin RS, Dave A, et al. GraphX: Graph processing in a distributed dataflow framework. Proceedings of the 11th USENIX Symposium on Operating Systems Design and Implementation. Broomfield: USENIX Association, 2014. 599–613.
|
| [4] |
Low Y, Gonzalez J, Kyrola A, et al. Distributed GraphLab: A framework for machine learning and data mining in the cloud. Proceedings of the VLDB Endowment, 2012, 5(8): 716-727. DOI:10.14778/2212351.2212354 |
| [5] |
Chen R, Shi JX, Chen YZ, et al. PowerLyra: Differentiated graph computation and partitioning on skewed graphs. ACM Transactions on Parallel Computing, 2019, 5(3): 13. DOI:10.1145/3298989 |
| [6] |
Ke QF, Prabhakaran V, Xie YL, et al. Optimizing data partitioning for data-parallel computing. Proceedings of the 13th USENIX Conference on Hot Topics in Operating Systems. Napa: USENIX Association, 2011. 13.
|
| [7] |
Ji SW, Bu CY, Li L, et al. Local graph edge partitioning with a two-stage heuristic method. Proceedings of the 39th IEEE International Conference on Distributed Computing Systems (ICDCS). Dallas: IEEE, 2019. 228–237.
|
| [8] |
Bourse F, Lelarge M, Vojnovic M. Balanced graph edge partition. Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014. 1456–1465.
|
| [9] |
Kong D, Xie XK, Zhang ZX. Clustering-based partitioning for large Web graphs. Proceedings of the 38th IEEE International Conference on Data Engineering (ICDE). Kuala Lumpur: IEEE, 2022. 593–606.
|
| [10] |
Tsourakakis C, Gkantsidis C, Radunovic B, et al. FENNEL: Streaming graph partitioning for massive scale graphs. Proceedings of the 7th ACM International Conference on Web Search and Data Mining. New York: ACM, 2014. 333–342.
|
| [11] |
Schlag S, Heuer T, Gottesbüren L, et al. High-quality hypergraph partitioning. ACM Journal of Experimental Algorithmics, 2022, 27: 1.9. DOI:10.1145/3529090 |
| [12] |
李贺, 刘延娜, 袁航, 等. 动态图划分算法研究综述. 软件学报, 2023, 34(2): 539-564. DOI:10.13328/j.cnki.jos.006705 |
| [13] |
Li H, Yuan H, Huang JB, et al. Group reassignment for dynamic edge partitioning. IEEE Transactions on Parallel and Distributed Systems, 2021, 32(10): 2477-2490. DOI:10.1109/tpds.2021.3069292 |
| [14] |
Karypis G, Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM Journal on scientific Computing, 1998, 20(1): 359-392. DOI:10.1137/s1064827595287997 |
| [15] |
Zhang CZ, Wei F, Liu Q, et al. Graph edge partitioning via neighborhood heuristic. Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax: ACM, 2017. 605–614.
|
| [16] |
Jo YY, Jang MH, Kim SW, et al. A data layout with good data locality for single-machine based graph engines. IEEE Transactions on Computers, 2022, 71(8): 1784-1793. DOI:10.1109/tc.2021.3107725 |
| [17] |
Leskovec J, Krevl A. SNAP datasets: Stanford large network dataset collection. https://snap.stanford.edu/data/
|
| [18] |
Petroni F, Querzoni L, Daudjee K, et al. HDRF: Stream-based partitioning for power-law graphs. Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. Melbourne: ACM, 2015. 243–252.
|
 2023, Vol. 32
2023, Vol. 32



