自动驾驶汽车将成为未来车辆领域的发展方向, 其核心是自动驾驶技术. 路径规划[1–7]作为自动驾驶技术的关键环节之一, 已成为自动驾驶领域的研究热点. Hou等[8]提出一种具有通信机制的增强蚁群算法进行路径规划, 通过个体之间的直接通信, 加速历史路径的整合, 同时对路径选择规则和启发式函数进行改进, 提高算法收敛速度和搜索效率; Liu等[9]提出一种基于改进灰狼算法的路径规划方法, 引入基于狮子优化算法的干扰因子和动态权值, 避免多样性的丧失, 但是跳出局部最优的能力有待加强; Kumar等[10]提出一种人工蜂群和进化规划算法结合的路径规划方法, 采用人工蜂群算法根据改进策略进行初步搜索, 之后采用进化算法对得到的可行路径进行细化, 降低搜索成本; 徐兴等[11]将灾变策略和内嵌A*算法的动态变异算子引入遗传算法中, 降低早熟现象并且提高算法后期的局部搜索能力, 同时具有多约束条件的适应度函数提高了所规划路径的平滑度, 但是每次灾变初始化种群, 降低了计算效率.
遗传算法 (genetic algorithm, GA) 虽然全局搜索能力强, 具有易于扩展其他算法的特性; 但是后期染色体相似度高, 存在早熟收敛问题[12–14]. 量子遗传算法 (quantum genetic algorithm, QGA)[15]是遗传算法结合量子计算产生的一种新兴智能优化算法. 根据量子态的叠加、纠缠等特性, 引入量子编码和量子旋转门更新操作, 相较于遗传算法, 量子遗传算法具有更好的种群多样性和收敛速度. 然而, 基本量子遗传算法主要依靠量子旋转门进行种群更新, 在组合优化问题[16–19]求解时, 仍存在稳定性低、收敛性差, 陷入局部最优不易跳出的问题.
本文提出一种基于梯度统计变异量子遗传算法的车辆路径规划方法, 采用动态调整量子旋转门策略, 在根据染色体适应度值动态调整旋转角步长的基础上, 引入梯度下降思想, 提高算法的收敛能力和全局搜索的稳定性; 根据染色体变化趋势的统计特性, 设计变异算子代替量子非门实现变异操作, 提出基于量子位概率密度的自适应变异策略, 以提高算法跳出局部最优的能力. 通过路径规划仿真实验分析, 验证算法有效性.
1 基本量子遗传算法量子位 (quantum bit, Qubit) 是量子计算机的最小信息单元, 在一个双态量子系统中, 一个量子位状态可描述为[20]:
| |φ⟩=α|0⟩+β|1⟩ | (1) |
其中, 量子态
| |α|2+|β|2=1 | (2) |
采用量子位编码初始化种群, 能够以小规模的种群包含复杂的种群信息. 一个初始化量子种群为
| qi(0)=|α1i1(0)α2i1(0)⋅⋅⋅αki1(0)⋅⋅⋅α1in(0)α2in(0)⋅⋅⋅αkin(0)β1i1(0)β2i1(0)⋅⋅⋅βki1(0)⋅⋅⋅β1in(0)β2in(0)⋅⋅⋅βkin(0)| | (3) |
其中,
量子遗传算法利用量子旋转门更新量子位的概率幅实现对问题的搜索寻优. 通常采用的量子旋转门如式(4)所示[21]:
| U(θ)=[cosθ−sinθsinθcosθ] | (4) |
其中,
更新后的量子态
| |φ′⟩=[α′β′]=U(θ)×|φ⟩=[cosθ−sinθsinθcosθ][αβ] | (5) |
其中,
在双态量子系统中, 量子位概率幅的更新如图1所示. 量子位概率幅的取值具有连续性, 因此量子遗传算法具备连续空间搜索能力.

|
图 1 量子位概率幅更新 |
2 梯度统计变异量子遗传算法 2.1 自适应量子旋转门
染色体更新过程中, 量子旋转门的旋转角度
量子门的旋转角度
| A=|α0α1β0β1| | (6) |
旋转角
考虑到同一代种群中不同染色体之间的差异, 以及不同代种群之间染色体基因位的变化趋势对群体进化的影响, 将旋转角度的大小和染色体适用度值联系起来, 同时引入梯度下降思想研究染色体基因位的变化趋势, 提出一种旋转角步长自适应调整的方法:
| θjir=−sgn(A)⋅θ0⋅exp(a⋅|fitbest−fiti|fitbest+(a−1)⋅|∇f(Xir)−∇frmin|∇frmax−∇frmin) | (7) |
| ∇frmax | (8) |
| \nabla {f_{r\min }} = \min \left\{ {\left| {\frac{{\partial f({X_i})}}{{\partial {X_{ir}}}}} \right|} \right\}{\text{ }}(i = 1, 2, \cdots , m) | (9) |
其中,
动态调整量子旋转门策略既考虑染色体适应度值又兼顾染色体基因位变化趋势, 当染色体适应度值距离最优染色体较远且量子位梯度变化较小时, 增大旋转角度, 加快收敛, 反之则需要减小旋转角度, 避免错过最优染色体, 以此提高算法的收敛速度和全局搜索的稳定性.
2.2 量子变异量子遗传算法虽然具有较强的全局搜索能力, 但仅通过量子旋转门进行种群更新, 易陷入局部最优. 因此, 需要对种群进行一定的扰动操作, 减少“早熟”现象的发生. 传统方法通常采用量子非门对种群中个体量子位的概率幅进行变异操作, 虽然一定程度上能够避免陷入局部最优, 但是当执行变异操作的染色体非常接近最优染色体时, 量子非门变异会造成量子位更新方向的反转, 可能造成种群动荡, 优秀染色体信息丢失. 另外, 该变异算子没有考虑种群中所包含的生物体信息及外部环境等干扰因素对染色体基因变异的影响, 缺乏群体观念.
从全局上, 根据过往染色体信息对当前染色体基因位的影响考虑量子位变异问题, 使量子变异操作能够在种群进化过程中施加合理的扰动, 避免种群过早收敛. 由于基因遗传信息随遗传代数的增加而递减, 当前染色体基因位受父代染色体的影响最大, 因此, 仅考虑父代染色体对当前染色体基因位的影响, 统计过往染色体基因位适应度值的梯度
| \nabla {Z_{ir}} = \nabla f({X_{ir}}) + o(\nabla f({X_{ir}})) | (10) |
其中,
根据染色体基因位的变化趋势设计概率密度函数:
| f(\nabla {Z}_{ir})={\displaystyle \sum _{l}^{5}{b}_{l1}\cdot\mathrm{exp}(-{((\nabla {Z}_{ir}-{b}_{l2})/{b}_{l3})}^{2})} | (11) |
其中,
将式(11)转化为概率分布函数:
| F(\nabla {Z}_{ir})={\displaystyle \sum _{l}^{5}{b}_{l1}\cdot{\displaystyle {\int }_{-\infty }^{{Z}_{ir}}\mathrm{exp}(-{((\nabla {Z}_{ir}-{b}_{l2})/{b}_{l3})}^{2})}} | (12) |
采用量子位梯度的概率分布作为变异算子对量子位概率幅进行变异操作, 如式(13)所示:
| \left\{ \begin{gathered} \alpha _{ir}^j(t) = \sqrt {1 - F(\nabla {Z_{ir}})} \\ \beta _{ir}^j(t) = \sqrt {1 - \alpha _{ir}^j{{(t)}^2}} \\ \end{gathered} \right. | (13) |
其中,
另外, 在种群进化过程中, 合理的变异概率有利于提高种群进化的多样性和稳定性. 根据种群中染色体的进化趋势, 提出基于量子位概率密度的自适应变异机制: 依据染色体基因位适应度值的梯度确定当前量子位的变异概率, 在染色体进化过程比较“平坦”时, 给予一个大的扰动概率, 使染色体跳出局部最优, 增加种群多样性; 在染色体进化过程比较“陡峭”时, 给予一个小的扰动概率, 避免破坏拥有优良基因的个体, 提高种群的稳定性. 依据自适应变异概率随机选择个体中的量子位, 施加变异操作, 自适应变异概率如式(14)所示:
| \begin{split} {p}_{m}&={P}(\nabla Z\geqslant \nabla {Z}_{ir})=1-F(\nabla {Z}_{ir})\\ &= 1-{\displaystyle \sum _{l}^{5}{b}_{l1}\cdot{\displaystyle {\int }_{-\infty }^{{Z}_{ir}}\mathrm{exp}\left(-{((\nabla {Z}_{lr}-{b}_{l2})/{b}_{l3})}^{2}\right)}}\end{split} | (14) |
梯度统计变异量子遗传算法的流程如图2所示.

|
图 2 梯度统计变异量子遗传算法流程图 |
3 基于梯度统计变异量子遗传算法的车辆路径规划
针对车辆路径规划问题, 本文的主要目标: 在规避静态障碍物的基础上, 得到一条长度最短的可行路径. 做出如下假设: 1) 车辆在有限平面空间中由起始点到目标点匀速移动, 2) 在车辆行驶过程中, 障碍物的形状大小、地理位置均不发生改变; 3) 车辆相对地图中的静态障碍物可看作一个质点.
3.1 构建环境地图以某工业园区建筑布局为例, 采用栅格地图[23]进行车辆路径规划研究, 如图3所示, 其中白色栅格表示可行驶区域, 黑色栅格表示障碍物. 车辆的起始点和目标点在图中用五角星符号标记.

|
图 3 20×20的栅格地图 |
3.2 车辆路径规划实现
利用梯度统计变异量子遗传算法规划车辆行驶路径, 首先需要进行路径编码, 通常采用空间位置点 (规划空间中的路径点作为染色体的基因位) 序列表示车辆行驶路径. 这种表示形式只需要考虑每个空间位置点的可行性问题, 有利于路径规划的计算. 假设规划空间为图3所示的栅格地图, 在规划空间内有

|
图 4 染色体编码 |
路径规划主要考虑安全性及路径代价, 本文以路径最短作为车辆路径规划的路径代价. 采用路径点评价函数
采用欧氏距离构造路径点评价函数, 如式(15)所示, 计算路径点到起始点和目标点的距离之和, 距离越小, 所需代价越小.
| \begin{split} \min point\_fit =& \sqrt {{{({x_{ir}} - {x_s})}^2} + {{({y_{ir}} - {y_s})}^2}} \\ & +\sqrt {{{({x_{ir}} - {x_g})}^2} + {{({y_{ir}} - {y_g})}^2}} \end{split} | (15) |
其中,
路径评价函数计算所有路径点依次连接的路径总长度, 如式(16)所示:
| \min way\_fit = \sum\limits_{r = 1}^{M - 1} {\sqrt {{{({x_{ir}} - {x_{ir + 1}})}^2} + {{({y_r} - {y_{ir + 1}})}^2}} } | (16) |
其中,
在车辆路径规划中, 根据式(6)–式(9)对染色体中路径点的每个量子位编码进行量子旋转门自适应更新. 由于路径点的适应度值是离散的, 染色体中路径点的梯度利用相邻两代的一阶差分表示:
| \nabla {f_{r\max }} = \max \left\{ {\left| {f\left[ {{X_{ir}}(t - 1)} \right] - f\left[ {{X_{ir}}(t)} \right]} \right|} \right\} | (17) |
| \nabla {f_{r\min }} = \min \left\{ {\left| {f\left[ {{X_{ir}}(t - 1)} \right] - f\left[ {{X_{ir}}(t)} \right]} \right|} \right\} | (18) |
其中,
通过统计过往染色体中路径点的梯度信息, 得到式(11)中参数的具体数值:
| {({{\boldsymbol{b}}_1}{\kern 1pt} {\kern 1pt} {{\boldsymbol{b}}_2}{\kern 1pt} {\kern 1pt} {{\boldsymbol{b}}_3})^{\rm{T}}} = \left[ \begin{gathered} 0.7521{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.1421{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.1519{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 0.6852{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.04352 \\ 0.5204{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2.072{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.1908 {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.4204{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 5.743 \\ 0.9951{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2.126{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.6099{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.01 {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2.565 \\ \end{gathered} \right] |
基于梯度统计变异量子遗传算法的车辆路径规划的总体流程如下.
1) 构建环境地图. 根据已知的规划空间构建栅格地图.
2) 初始参数设置及种群初始化. 设置种群规模popsize为
3) 初始量子位坍缩. 对初始种群
4) 初始路径适应度评价. 计算路径点的适应度值
5) 量子位坍缩. 对种群
6) 个体适应度评价. 计算路径适应度值
7) 量子旋转门自适应更新. 根据式 (6)–式(9) 得到每个量子位的旋转角度
8) 量子变异操作. 通过自适应变异机制确定量子位的变异概率
9) 判断是否满足最大迭代次数或收敛条件, 若满足, 则结束算法流程, 输出最短路径; 否则, 迭代次数
为了验证改进量子遗传算法在路径规划中的有效性, 采用栅格法构建车辆路径规划的环境地图, 将规模约为
对比4种算法的求解精度和收敛速度验证本文算法在路径规划中的性能.
在

|
图 5 popsize = 20的GA运行5次的规划路径 |
|
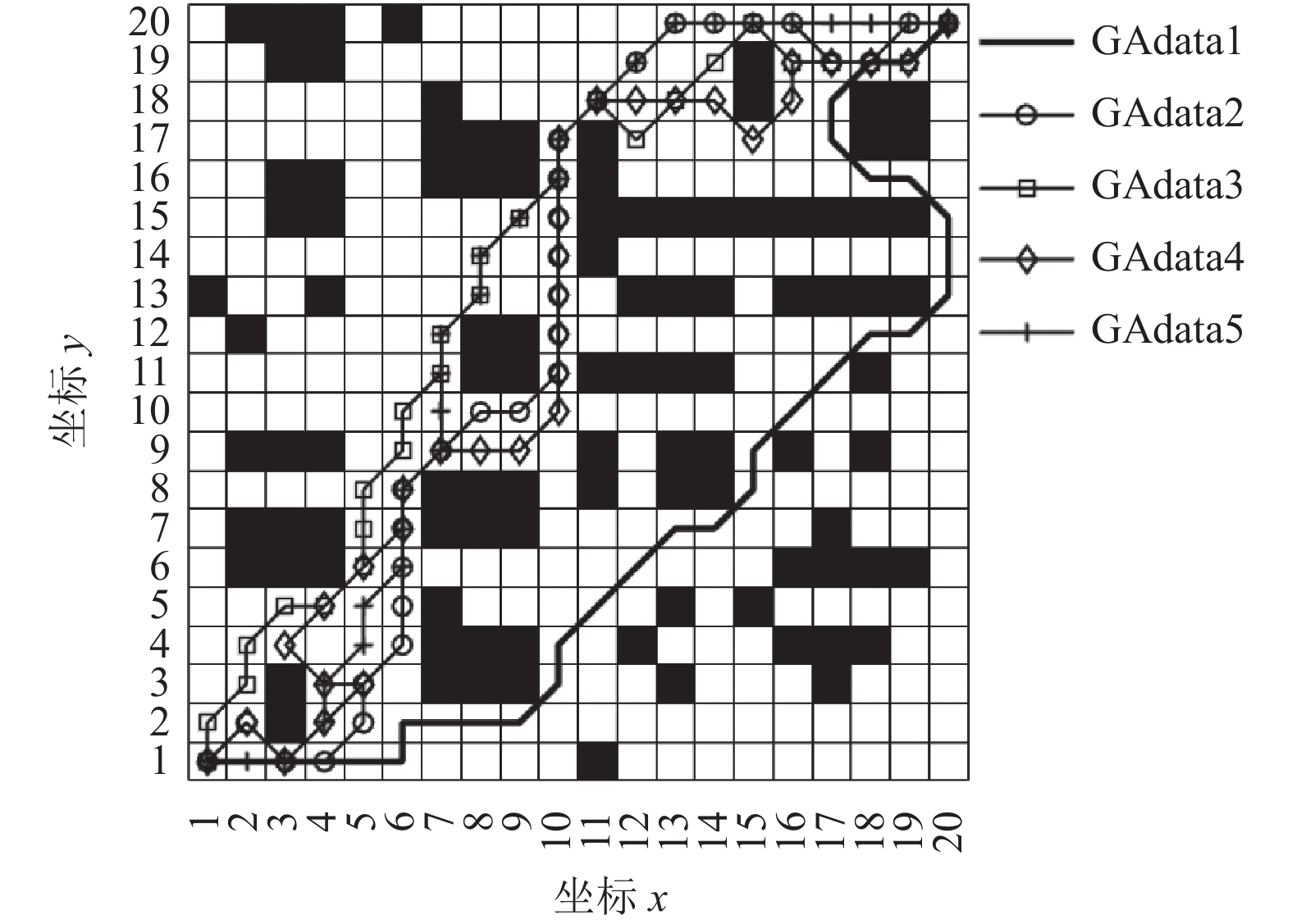
图 6 popsize = 100的GA运行5次的规划路径 |

|
图 7 QGA运行5次的规划路径 |
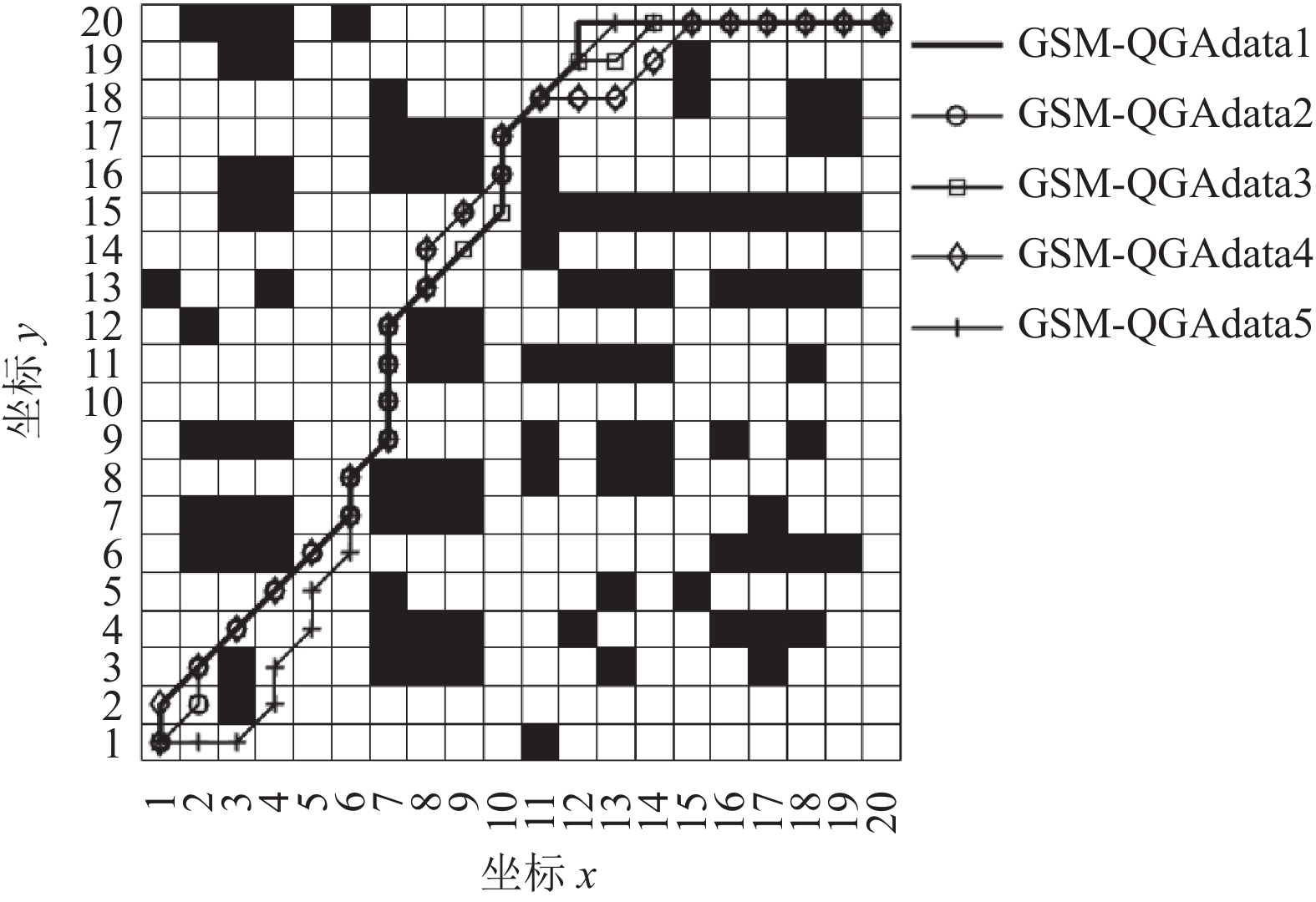
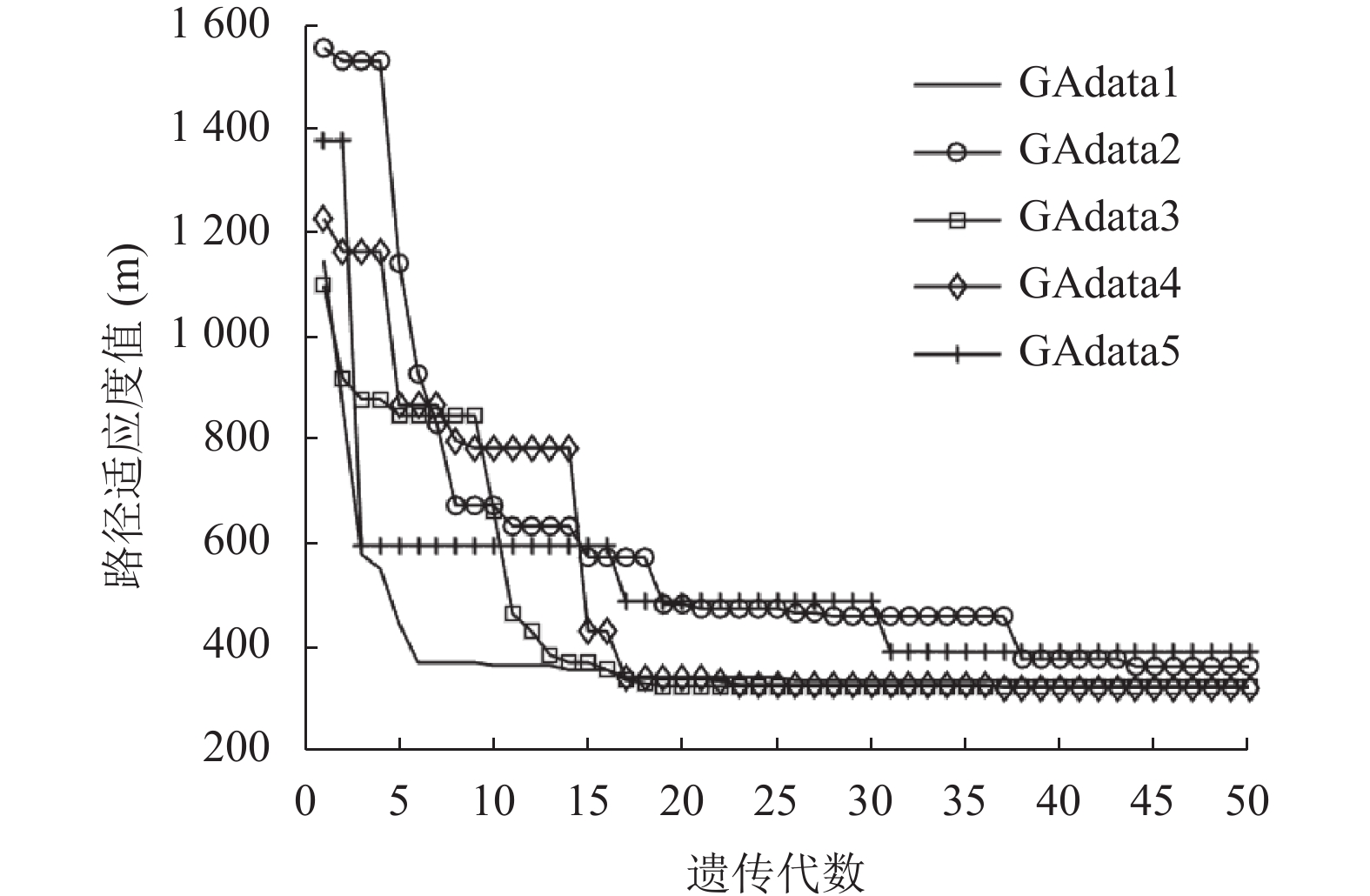
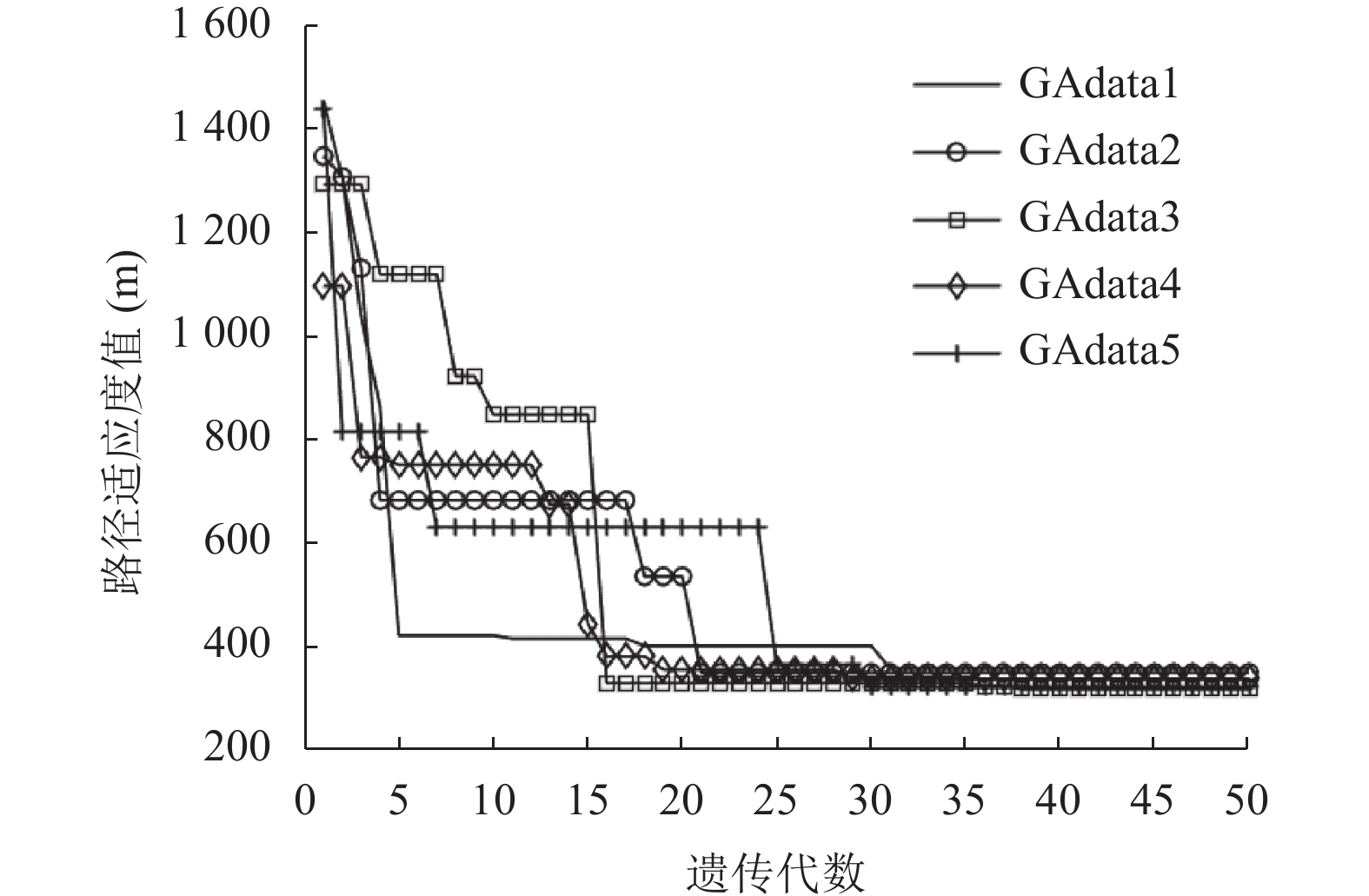
如图5–图14所示, 在相同种群规模的情况下, 当种群数量较少, GA所规划的路径明显过长且收敛速度较慢, 易陷入局部最优; 当扩大GA种群规模到100时, 其路径长度和收敛速度有所改善, 但路径距离仍然存在明显冗余; QGA和N-QGA虽然在路径距离上能够进一步优化, 但搜索到的路径变化较大, 算法稳定性不好, 收敛到最优解所需迭代次数较多, 总体收敛速度仍然有待提高; 本文提出的GSM-QGA能够有效地跳出局部最优值, 并且5次运行结果显示算法稳定性较好.

|
图 8 N-QGA运行5次的规划路径 |
|
图 9 GSM-QGA运行5次的规划路径 |
|
图 10 popsize = 20的GA运行5次的路径收敛曲线 |
|
图 11 popsize = 100的QA运行5次的路径收敛曲线 |

|
图 12 QGA运行5次的路径收敛曲线 |

|
图 13 N-QGA运行5次的路径收敛曲线 |
图15、图16能够更直观对比4种算法在路径规划中的求解精度和收敛速度. 由于算法有一定的搜索随机性, 本文将4种算法的5次运行结果进行统计, 如表1所示. 容易看出, GA在运行过程中收敛速度比较慢, 容易发生“早熟”现象, 且所规划的路径比较冗余. 相较于GA, QGA虽然所需迭代次数较少, 收敛很快, 但也难以跳出局部最优值, N-QGA由于量子非门变异算子的局部扰动, 使算法具有跳出局部最优的动力, 但其变异的幅度较大, 容易造成种群动荡, 收敛速度较慢; GSM-QGA通过自适应量子旋转门更新量子编码的路径点, 所需迭代次数少, 路径收敛速度更快, 另外, 根据过往路径信息设计的变异算子和变异策略, 更合理地对路径规划过程进行扰动, 有效控制算法陷入“早熟”, 得到的规划路径距离更短. 改进的量子遗传算法与其他3种算法相比, 平均路径长度分别缩短

|
图 14 GSM-QGA运行5次的路径收敛曲线 |

|
图 15 场景1中4种算法路径规划仿真图 |
为了进一步验证改进量子遗传算法在路径规划中的有效性, 在不同场景下进行对比实验. 选择两个不同的场景, 并将其划分为
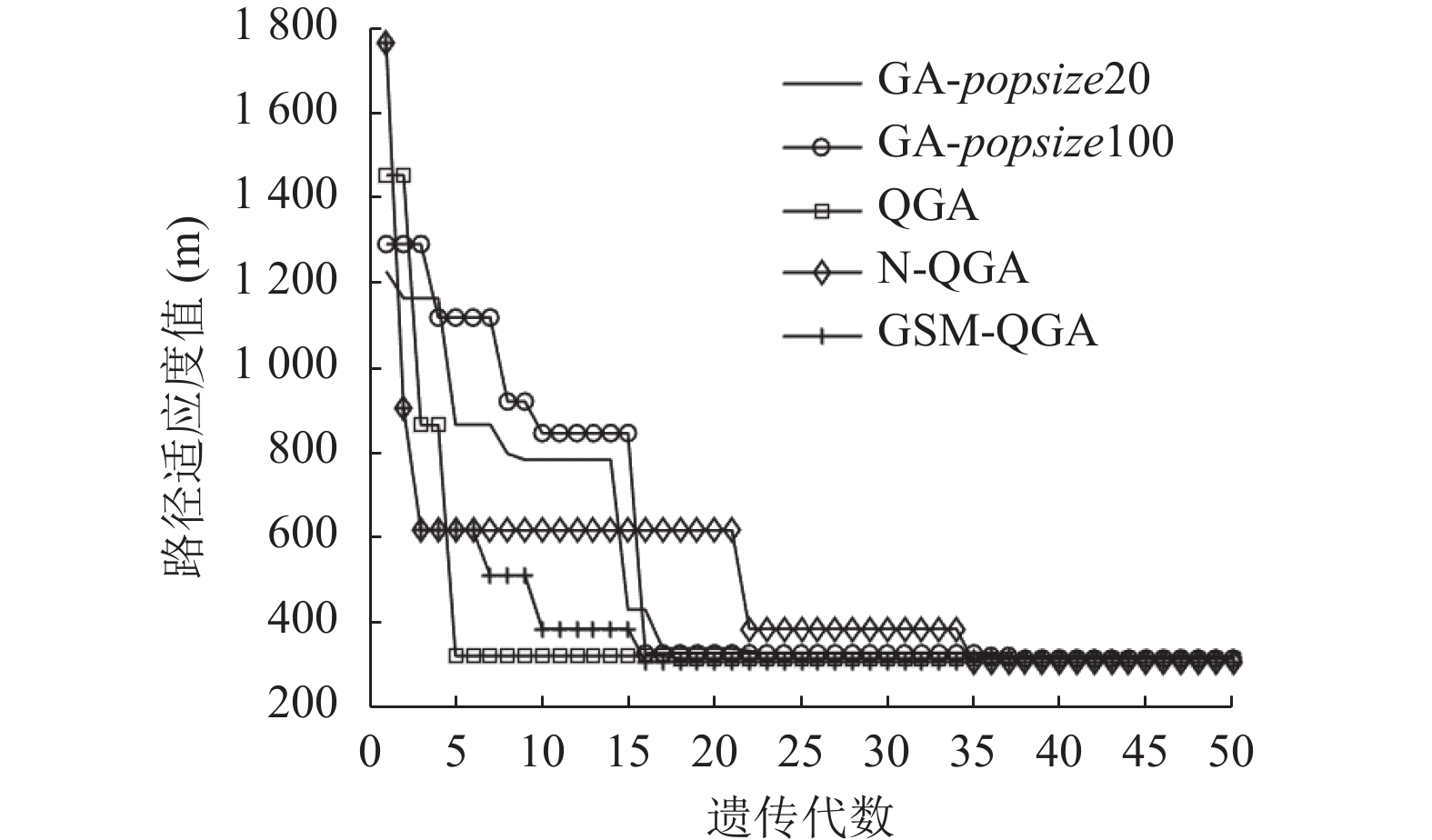
|
图 16 场景1中4种算法最优路径收敛曲线 |
| 表 1 4种算法5次运行结果统计表 |

|
图 17 场景2中4种算法路径规划仿真图 |

|
图 18 场景2中4种算法最优路径收敛曲线 |

|
图 19 场景3中4种算法路径规划仿真图 |

|
图 20 场景3中4种算法最优路径收敛曲线 |
5 结论与展望
针对遗传算法在进行车辆路径规划时存在的易早熟、收敛速度慢等问题, 本文提出了一种基于梯度统计变异量子遗传算法的路径规划方法, 算法在根据染色体适应度值动态调整旋转角步长的基础上, 引入梯度下降思想, 改善动态调整量子旋转门策略, 提高算法的收敛速度和搜索寻优的稳定性; 在量子变异部分, 依据染色体变化趋势的统计特性, 设计变异算子, 并提出基于量子位概率密度的自适应变异策略, 有效控制算法陷入局部最优. 结果表明, 改进的量子遗传算法不仅能够规划出一条规避障碍物的车辆可行路径, 并且在路径长度、收敛速度、算法稳定性等方面相比遗传算法、量子遗传算法、非门变异的量子遗传算法均具有优势. 在车辆行驶过程中, 往往存在动态障碍物, 接下来的工作将改进的量子遗传算法与其他算法结合, 进行车辆避撞研究.
| [1] |
Zhu DD, Sun JQ. A new algorithm based on Dijkstra for vehicle path planning considering intersection attribute. IEEE Access, 2021, 9: 19761-19775. DOI:10.1109/ACCESS.2021.3053169 |
| [2] |
Tang G, Tang CQ, Claramunt C, et al. Geometric A-star algorithm: An improved A-star algorithm for AGV path planning in a port environment. IEEE Access, 2021, 9: 59196-59210. DOI:10.1109/ACCESS.2021.3070054 |
| [3] |
Han S, Wang L, Wang YT, et al. A dynamically hybrid path planning for unmanned surface vehicles based on non-uniform Theta* and improved dynamic windows approach. Ocean Engineering, 2022, 257: 111655. DOI:10.1016/j.oceaneng.2022.111655 |
| [4] |
Luan PG, Thinh NT. Hybrid genetic algorithm based smooth global-path planning for a mobile robot. Mechanics Based Design of Structures and Machines, 2023, 51(3): 1758-1774. DOI:10.1080/15397734.2021.1876569 |
| [5] |
Luo Q, Wang HB, Zheng Y, et al. Research on path planning of mobile robot based on improved ant colony algorithm. Neural Computing and Applications, 2020, 32(6): 1555-1566. DOI:10.1007/s00521-019-04172-2 |
| [6] |
Tao QY, Sang HY, Guo HW, et al. Improved particle swarm optimization algorithm for AGV path planning. IEEE Access, 2021, 9: 33522-33531. DOI:10.1109/ACCESS.2021.3061288 |
| [7] |
陈晓冬, 王福威. 基于改进A*算法的AGV路径规划. 计算机系统应用, 2023, 32(3): 180-185. DOI:10.15888/j.cnki.csa.009020 |
| [8] |
Hou WB, Xiong ZH, Wang CS, et al. Enhanced ant colony algorithm with communication mechanism for mobile robot path planning. Robotics and Autonomous Systems, 2022, 148: 103949. DOI:10.1016/j.robot.2021.103949 |
| [9] |
Liu JY, Wei XX, Huang HJ. An improved grey wolf optimization algorithm and its application in path planning. IEEE Access, 2021, 9: 121944-121956. DOI:10.1109/ACCESS.2021.3108973 |
| [10] |
Kumar S, Sikander A. Optimum mobile robot path planning using improved artificial bee colony algorithm and evolutionary programming. Arabian Journal for Science and Engineering, 2022, 47(3): 3519-3539. DOI:10.1007/s13369-021-06326-8 |
| [11] |
徐兴, 俞旭阳, 赵芸, 等. 基于改进遗传算法的移动机器人全局路径规划. 计算机集成制造系统, 2022, 28(6): 1659-1672. |
| [12] |
Hao K, Zhao JL, Yu KC, et al. Path planning of mobile robots based on a multi-population migration genetic algorithm. Sensors, 2020, 20(20): 5873. DOI:10.3390/s20205873 |
| [13] |
Shao J. Robot path planning method based on genetic algorithm. Journal of Physics: Conference Series, 2021, 1881(2): 022046. DOI:10.1088/1742-6596/1881/2/022046 |
| [14] |
李敏, 黄敏, 程智锋, 等. 遗传算法在路径规划上的应用. 计算机系统应用, 2020, 29(8): 255-260. DOI:10.15888/j.cnki.csa.007417 |
| [15] |
Narayanan A, Moore M. Quantum-inspired genetic algorithms. Proceedings of the 1996 IEEE International Conference on Evolutionary Computation. Nagoya: IEEE, 1996. 61–66.
|
| [16] |
褚理想, 樊巧云. 基于量子遗传算法的多光电二极管布局优化. 红外与激光工程, 2019, 48(8): 0813002. |
| [17] |
Yang XM. Fuzzy control path planning of soccer robot relying on quantum genetic algorithm. Mobile Information Systems, 2022, 2022: 3498258. |
| [18] |
Nie Y, Yu XL. Optimization of deterministic pilot pattern placement based on quantum genetic algorithm for sparse channel estimation in OFDM systems. IEICE Transactions on Communications, 2020, E103.B(10): 1164-1171. DOI:10.1587/transcom.2019EBP3200 |
| [19] |
Chen ZC, Zhou WJ. Path planning for a space-based manipulator system based on quantum genetic algorithm. Journal of Robotics, 2017, 2017: 3207950. |
| [20] |
Amal RS, Ivan JS. A quantum genetic algorithm for optimization problems on the Bloch sphere. Quantum Information Processing, 2022, 21(2): 43. DOI:10.1007/s11128-021-03368-7 |
| [21] |
Li YB, Qin ST, Jing L. Research on flight trajectory optimization based on quantum genetic algorithm. Journal of Physics: Conference Series, 2020, 1549(2): 022074. DOI:10.1088/1742-6596/1549/2/022074 |
| [22] |
李士勇, 李盼池. 基于实数编码和目标函数梯度的量子遗传算法. 哈尔滨工业大学学报, 2006, 38(8): 1216-1218, 1223. |
| [23] |
李艳生, 万勇, 张毅, 等. 基于人工蜂群-自适应遗传算法的仓储机器人路径规划. 仪器仪表学报, 2022, 43(4): 282-290. |
 2023, Vol. 32
2023, Vol. 32



