图是一种重要的数据结构, 由于以往的关系型数据本身存在拓扑结构、查询效率等问题, 而图数据具有更强大的表达能力, 且可以将多种来源、多种类型的数据合并到一个图数据结构中进行分析, 并获得原本难以获得的分析结果, 因此, 图计算可以广泛地应用在社交网络^[1]、推荐系统^[2]、网络安全^[3]、文本检索和生物医疗等领域, 很多问题能在图论的支撑下使用图算法实现更高效的解决方式. 近年来, 随着大数据、数据挖掘、机器学习等领域技术的高速发展, 很多领域中的图规模变得异常庞大, 另外再加上自然图往往表现出非常倾斜的幂律分布power-law^[4]特性, 给图计算带来了巨大挑战. 为了应对海量图数据对计算性能的挑战, 分布式图计算系统已被广泛应用. 如何设计高效的图划分算法将大规模图划分为若干子图, 并将子图上的点和边数据及子图上的计算任务分配到多个节点上并行执行, 已成为分布式图计算系统研究中的热点问题.

异质图(heterogeneous graph)是指具有多种节点类型或边类型的图数据结构, 能够将现实世界中相互作用且类型各异的网络化数据建模为异质信息网络(heterogeneous information network, HIN)^[5]. 由于域名系统(domain name system, DNS)的正常运转需要大量的异构组件配合完成, 为了准确的描述域名系统中各组件之间的关联性和依赖性, 利用异质信息网络能够将其中相互作用的组件包括域名、IP地址以及逐级授权的域名服务器等, 完整的抽象为图结构^[6]. 通过对域名依赖网络的构建, 研究人员能够更好地理解域名系统的复杂性和演化规律, 实现对域名依赖关系的准确分析. 此外, 可基于域名系统中隐藏的丰富语义, 将域名解析场景抽象为的异质图^[7], 以挖掘域名解析间的全局关联性. 由于攻击者无法轻易伪造域名系统中域之间逐级授权的关系, 因此异质信息网络能够通过域名的特征分析域名之间的关联, 有利于恶意域名检测的研究^[8–10]. 利用DNS流量图来表示DNS查询序列, 可以检测受感染的客户端、恶意域名以及恶意DNS活动^{[11, 12]}.

现有的图划分算法都是基于同质图提出的, 对于异质图的处理没有考虑到以下问题: 1)异质图中不同类型的节点和边所存储的数据占用存储空间大小可能不同; 2)对于不同类型的节点和边可能会采用不同的处理算法, 其计算时间不同.

主流图计算引擎GraphX^[13]、PowerGraph^[14]等通常采用哈希算法、Grid算法^[15]或贪婪算法进行图划分, 这些图划分算法基于GAS模型^[16]、BSP模型^[17]和点划分模型. 其中, 哈希算法将各边随机均匀地分配到各分区上, 可以使图计算过程中分区内计算负载均衡, 但完全没有考虑图的拓扑结构, 可能使节点的复制系数过高, 导致分区间同步数据的开销过大. Grid算法通过限制节点复制系数的上限限制了分区间同步数据的开销上限, 但依然没有关注图的拓扑结构, 可能使大量相邻的边分配到不同的分区上, 导致分区间通信开销过大. PowerGraph中提出的贪婪算法包括Coordinated(协同)和Oblivious (遗忘)两种实现方式, 这个方法考虑到了图的拓扑结构, 在考虑计算负载均衡的同时, 尽量将相邻的节点和边分配到相同的分区上. 但该算法没有对度数高的节点与度数低的节点区分处理, 可能导致度数高的节点所在分区负载过大, 从而破坏负载均衡, 降低计算性能.

传统的图计算引擎多是离线计算系统, 这是因为以往的图计算多承担的是非实时的离线分析任务. 但是随着业务应用的发展, 图的规模越来越庞大, 一些在线任务也需要采用图计算模型进行计算^[18]. 近年来, 学者们又提出了在线图划分算法来应对在线图数据在划分后的负载倾斜问题. Petroni等人^[19]提出了HDRF(high-degree (are) replicated first)算法, 在节点分配决策中考虑节点度, 度数高的节点优先复制. Chen等人^[20]提出了混合划分算法Ginger, 对度数高的节点采用点划分, 对度数低的节点采用边划分, 从而获得负载均衡且复制系数低的效果. 但是, 上述图划分算法均未考虑异质图的计算特点, 忽略了异质图节点所运行任务在处理时间与所占存储空间上的差异, 从导致各节点负载的以及所占存储空间的不平衡, 以及计算过程中所占对异质图进行划分时效果不佳, 从而影响后续图计算的效率.

为了解决目前图划分算法在划分异质图时存在的问题, 本文提出了一种新的面向异质图的在线图划分算法, 该方法可以对异质图的节点和边的负载以及存储空间占用进行评估, 并根据评估结果划分异质图数据, 使图划分达到负载均衡、内存均衡、总吞吐量最大的效果, 进而提升了图计算过程的效率.

本文的贡献主要包括: (1)提出了一种面向异质图数据的在线图划分算法, 通过计算节点划分到不同分区上的负载均衡得分和边划分到不同分区上的数据均衡得分, 得到使异质图负载和内存占用均衡的划分结果; (2)对现有的GraphX图计算引擎进行改进, 使其适应在线图计算需求, 并将本文提出的在线图划分算法在改进后的图计算引擎中实现, 进而验证了方法的有效性.

1 基本概念与问题定义

定义1. 异质图. 异质图是指具有多种节点类型或边类型的图. 异质图 ${G}$ 可以表示为:

$ \begin{array}{c}G=\left(V, E\right)\end{array} $

(1)

其中, $ V=\{{v}_{1}, {v}_{2}, {v}_{3}, \cdots , {v}_{n}\} $ 表示异质图的节点集合, $ {n} $ 为节点的总数. 每个节点 $ v $ 均携带数据, 其节点函数记为 $ F\left(V_i\right) $ , 表示该节点对所携带数据进行的处理. 图中可有多种类型的节点, 每一类型节点所携带的数据量与节点函数均有所不同. $ {E=\{e}_{1}, {e}_{2}, {e}_{3}, \cdots , {e}_{m}\} $ , 表示图中的有向边集合, $ m $ 为边的总数. 每条边 ${e}_{i}=\{{v}_{{\rm{src}}}, {v}_{{\rm{dst}}}\}$ , 其中 ${v}_{{\rm{src}}}$ 、 ${v}_{{\rm{dst}}}\in V$ 每条边上携带边属性数据, 不同类型的边所携带的数据量不同.

图计算系统的计算负载分配和图划分算法密切相关. 现有的图计算系统大多基于GAS模型, 其计算负载也分为3个阶段产生, 即Gather阶段、Apply阶段和Scatter阶段. 其中Gather阶段和Scatter阶段与边的划分相关, Apply阶段与点的划分相关.

定义2. 分区负载. 分区 $ {P}_{i} $ 的负载为被分配到该分区的节点和边数据处理完所需要的计算资源, 表达式如下:

$ \begin{array}{c}{L}_{i}=\left({G}_{i}+{S}_{i}\right) \times \left|{e}_{i}\right|+\displaystyle\sum _{{v}_{j}\in {P}_{i}}{A}_{j}\end{array} $

(2)

其中, $ {L}_{i} $ 为分区 $ {P}_{i} $ 的负载, $ {G}_{i} $ 为Gather阶段在一条边上做汇集操作花费的资源, $ {S}_{i} $ 为Scatter阶段在一条边上做发送操作花费的资源, $ \left|{e}_{i}\right| $ 为分区 $ {P}_{i} $ 上分配到的边数量, $ {A}_{j} $ 为分配到分区 $ {P}_{i} $ 上的第 $ j $ 个节点的节点函数执行需要的计算资源.

为了提高图计算性能, 图划分的结果应该使所有分区上的计算负载尽量均衡, 这一方面需要不同分区上的汇集、分发、节点函数计算等操作的负载均衡, 另一方面由于现在的分布式内存计算系统内存占用会影响图计算的效率, 所以也需要不同的分区上边和节点的副本所占用的内存空间尽量均衡. 接下来我们对问题进行形式化定义, 表1为问题定义中用到参数列表.

定义图 $ G=(V, E), V=({v}_{1}, \cdots , {v}_{n}) $ 为点集合, $ E= ({e}_{1}, \cdots , {e}_{m}) $ 为边集合, $ P=({p}_{1}, \cdots , {p}_{k}) $ 为分区集合, 根据以上拓扑结构引出的问题模型如下.

点和边以批式数据形式到来, 根据节点的节点函数运行耗时 $ T $ 和数据量 $ {S}_{v} $ 、边的数据量 $ {S}_{e} $ , 将节点和边分配到不同的分区上去. 分区 $ {P}_{i} $ 的负载为 $ {L}_{i} $ . 所有分区的平均计算负载为:

$ \begin{array}{c}\overline{L}=\frac{\displaystyle\sum _{i=1}^{k}{L}_{i}}{k}\end{array} $

(3)

其中, $ k $ 为分区数.

所有分区中最大分区负载为:

$ \begin{array}{c}{L}_{{\rm{max}}}={\rm{max}}\{{L}_{1}, {L}_{2}, \cdots , {L}_{k}\}\end{array} $

(4)

分区 $ {P}_{i} $ 的内存空间占用由其节点与边所携带的数据量所占用内存空间组成, 为:

$ \begin{array}{c}\left|{P}_{i}\right|=\displaystyle\sum {S}_{v}+\sum {S}_{e}, \; \forall v\in {P}_{i}, \forall e\in {P}_{i}\end{array} $

(5)

所有分区的平均内存空间占用为:

$ \begin{array}{c} \overline {\left| P\right|}=\frac{\displaystyle\sum _{i=1}^{k}\left|{P}_{i}\right|}{k}\end{array} $

(6)

所有分区中最大分区内存空间占用为:

$ \begin{array}{c}{\left|P\right|}_{{\rm{max}}}={\rm{max}}\{\left|{P}_{1}\right|, \left|{P}_{2}\right|, \cdots , \left|{P}_{k}\right|\}\end{array} $

(7)

则分配节点的目标为: 找到使得 ${L}_{{\rm{max}}}-\overline{L}$ 最小的分发策略, 分配边的目标为: 找到使得 ${\left|P\right|}_{{\rm{max}}}$ 和 ${\left|P\right|}_{{\rm{max}}}-{\left| \overline P\right|}$ 最小的分发策略.

2 基于异质图计算平衡性的在线图划分算法 2.1 计算不平衡性度量

我们对异质图的计算不平衡性的定义分为两部分: 负载不平衡性和内存占用不平衡性. 这是因为在内存图计算引擎中, 不光计算节点上的运算负载会影响计算效率, 内存占用也会影响计算效率. 具体到异质图上的节点和边来说, 计算不平衡性可以以如下两部分来度量: 异质图中不同类型的节点上节点函数运行耗时不同、不同类型的节点和边上携带的属性数据所占的内存空间不同. 现在主流分布式图计算系统大多使用BSP模型, 在图计算的一次迭代中, 一旦某一个分区上的计算比较慢, 就会导致其他分区因为等待同步等待造成计算资源的浪费, 从而导致图计算引擎性能下降.

以往的图划分算法都没有关注过异质图的问题, 即把所有待划分的图都看做同质图, 对不同类型的节点和边采取同样的划分逻辑, 这会引起一系列问题: 1)如果对节点函数运行耗时不同的节点采取相同的划分逻辑, 会导致不同分区上计算负载不同; 2)对携带不同数据量节点和边采取相同的划分逻辑, 会导致不同分区上内存占用不同, 而内存占用会影响分布式内存处理系统的计算速度.

(1)负载不平衡因素

分区的计算负载主要取决于分区上边的数量和所有节点的节点函数复杂度. 本文不考虑计算集群的不平衡性, 即认为集群中每个计算节点的算力相同.

为了根据异质图的计算速度不平衡性进行图划分, 需要在图划分前获得节点的节点函数, 节点的类型是有限的, 每种类型节点有其对应的节点函数, 所以节点函数的运行耗时的取值也是有限的. 所有节点函数的运行耗时可以由用户在节点属性数据中直接给出, 也可以在进行图划分前评估. 计算节点函数的运行耗时需要提前获得不同类型节点的节点函数, 将其在系统中各运行100次取用时平均值作为运行耗时(T), 评估获得的T以(VertexType, T)键值对形式存储.

(2)存储不平衡因素

在图计算过程中, 一方面, 我们希望让计算需要的数据一直都在内存中, 不会因内存不足导致访问外存. 另一方面, 在图计算的迭代过程中, 一些计算中间量会被保存在内存中, 所以图计算有可能随着迭代过程内存溢出. 数据不平衡除了有可能导致内存溢出外, 也有可能导致性能的问题.

节点的类型是有限的, 每种类型节点有其对应的数据结构, 所以节点的携带的数据量取值也是有限的, 而本文中设定边的类型可以是无限多种, 所以边携带的数据量取值是无限的.

2.2 算法主要思想

本文中提出OGP-HG (online graph partitioning for heterogeneous graph)算法来针对异质图进行在线图划分, 根据现在常用的GAS图计算模型, OGP-HG算法从3个方向对异质图划分进行优化: 降低节点的复制系数; 使图计算在Gather、Apply、Scatter阶段的计算负载均衡; 使所有分区的数据量在各分区上平衡.

(1)降低节点的复制系数

基于图划分算法的研究我们发现, 在幂律图中, 聚类系数的分布随着节点度的增加而减小. 这意味着低度节点通常属于非常密集的子图, 而这些子图通过高度节点相互连接.

为了利用这一特性, OGP-HG算法在划分边数据时要尽量切割高度节点, 并在大量分区上复制这些高度节点的副本, 而对于低度节点则尽量不切割, 使其只存储到一个分区上. 由于幂律图中高度节点的数量非常低, 因此只对高度节点进行切割可以使复制系数减少. 具体实现上来说, OGP-HG算法可以在每个分区上维护一个带有节点部分度的表, 该表随着图划分的过程同时不断更新. 当一条新边被划分到某分区上后, 这个分区的节点部分度表中相应节点的度值将更新. 节点的部分度并不完全等于这个节点的实际度, 但它通常是一个节点实际度的良好指标, 可以一定程度上代表这个节点的实际度. 而如果维护全局的节点度表, 则图划分过程中需要频繁访问这个全局节点度表, 这会引起大量的内网通信, 导致图划分算法的效率过低.

(2)使图计算在Gather、Apply、Scatter阶段的计算负载均衡

Gather和Scatter阶段是图计算的汇集消息和发送消息阶段, 其计算负载主要与分区上的边数量有关. 为了使图计算在Gather和Scatter阶段的计算负载均衡, 要使各分区上边的数量大致相等.

Apply阶段是图计算的节点函数计算阶段, 以往的图划分算法都是基于同质图的, 所有节点的节点函数运行耗时相同, 所以并不关注节点的划分, 多数都是按照输入数据的顺序随机分区. OGP-HG算法关注异质图, 在每个分区上维护一个带有本分区上所有节点函数运行耗时之和的值. 每次将节点划分到节点函数总耗时最小的分区, 并更新这个分区的节点运行总耗时.

(3)使所有分区的数据量在各分区上平衡

内存空间占用是影响分布式图计算系统性能的重要因素, 所以要使各分区的数据量尽量均衡, 避免个别分区内存占用过高导致计算过慢, 使其余分区在同步时等待, 甚至造成内存溢出.

由于大多数图的边数量远大于点数据量, 所以我们主要关注边数据和边上两个节点的副本所占用的空间. 在每个分区上维护已经拥有的节点副本的表, 并维护一个带有本分区上所有节点和边数据量的值. 每次将边划分到总数据量最小的分区, 并更新这个分区的节点副本表和总数据量. 已经在分区上建立副本的节点不会重复在这个分区上建立副本, 也不会重复增加总数据量.

OGP-HG算法的目标可以表述为: 将异质图上的节点和边依次划分到给定的k个分区, 在划分过程中考虑节点的计算负载不同, 节点和边的属性数据量也不同, 在这种划分方式下使每个分区上的计算负载均衡, 内存占用平衡, 并最终使图计算的耗时减少, 达到在线图计算的要求.

根据算法主要思想的分析, 划分一条边时要考虑两方面因素, 一是降低复制系数, 二是考虑这条边和其两端节点的数据量, 划分这条边使各分区的内存占用和边数量尽量均衡.

对于降低复制系数因素, 我们参考HDRF算法, 提出划分边的目标函数的第1部分, 即复制分数:

$ {C}_{{\rm{REP}}}^{{\text{OGP-HG}}}\left({v}_{{\rm{src}}}, {v}_{{\rm{dst}}}, p\right)=g\left({v}_{{\rm{src}}}, p\right)+g\left({v}_{{\rm{dst}}}, p\right) $

(8)

其中,

$ g\left({v}_{{\rm{src}}}, p\right) =\left\{\begin{array}{l} 1+\dfrac{\delta \left({v}_{{\rm{dst}}}\right)}{\delta \left({v}_{{\rm{src}}}\right)+\delta \left({v}_{{\rm{dst}}}\right)}, 当p\in A({v}_{{\rm{src}}})\\ 0,\qquad\qquad\qquad\quad\; 当p\notin A({v}_{{\rm{src}}})\end{array}\right. $

(9)

$ g\left({v}_{{\rm{dst}}}, p\right) =\left\{\begin{array}{l} 1+\dfrac{\delta \left({v}_{{\rm{src}}}\right)}{\delta \left({v}_{{\rm{src}}}\right)+\delta \left({v}_{{\rm{dst}}}\right)}, 当p\in A({v}_{{\rm{dst}}})\\ 0,\qquad\qquad\qquad\quad\; 当p\notin A({v}_{{\rm{dst}}})\end{array}\right. $

(10)

这里 $ p $ 表示计算目标函数的分区, $ A\left(v\right) $ 表示已经有节点 $ v $ 副本的分区集合, $ \delta \left(v\right) $ 表示节点 $ v $ 在已划分子图上的部分度(即节点 $ v $ 在已划分的子图上有多少条邻边), $ g\left(v, p\right) $ 的意思是将节点的部分度归一化后再加一, 通过计算复制分数可以获得使图划分的复制系数最小的分区.

对于划分边的内存占用和边数量均衡因素, 我们改进了只考虑边数量的HDRF算法, 加入了对内存占用均衡的考虑, 提出划分边的目标函数的第2部分, 即平衡分数:

$ \begin{split} {C}_{{\rm{BAL}}}^{{\text{OGP-HG}}}\left({v}_{{\rm{src}}}, {v}_{{\rm{dst}}}, p\right) =&\lambda \frac{maxsi{\textit{z}}e-\left|p\right|}{\varepsilon +maxsi{\textit{z}}e-minsi{\textit{z}}e}\\ &+\mu \frac{maxmem-mem\left(p\right)}{\xi +maxmem-minmem} \end{split} $

(11)

平衡分数分为两部分, 其中第1部分用来平衡不同分区上边的数量, 参数 $ \mathrm{\lambda } $ 用来控制不同分区上边数量的不平衡程度, 当 $ \lambda =0 $ 时完全不考虑分区边数量的平衡性, $ \lambda $ 越大表示分区的边数量平衡性对于算法的影响程度越高. $ maxmem $ 和 $ minmem $ 是指当前所有分区中最大和最小的边数量, $ mem\left(p\right) $ 是 $ p $ 分区上已有边的数量. $ \varepsilon $ 为预设常数.

第2部分用来平衡不同分区上的内存空间占用, 参数 $\; \mu $ 用来控制不同分区上内存占用的不平衡程度, 当 $\; \mu =0 $ 时完全不考虑分区内存占用的平衡性, $\; \mu $ 越大表示分区内存占用的平衡性对于算法的影响程度越高. $ maxmem $ 和 $ minmem $ 是指当前所有分区中最大和最小占用存储空间, $ mem\left(p\right) $ 是 $ p $ 分区上已有数据占用的存储空间. $ \xi $ 为预设常数.

综合复制分数和平衡分数, 我们得出划分边数据的总目标函数为:

$ \begin{split} {C}^{{\text{OGP-HG}}}\left({v}_{{\rm{src}}}, {v}_{{\rm{dst}}}, p\right) =&{C}_{{\rm{REP}}}^{{\rm{OGP-HG}}}\left({v}_{{\rm{src}}}, {v}_{{\rm{dst}}}, p\right)\\ &+{C}_{{\rm{BAL}}}^{{\rm{OGP-HG}}}\left({v}_{{\rm{src}}}, {v}_{{\rm{dst}}}, p\right) \end{split} $

(12)

OGP-HG算法在计算一个节点应当分配到哪个分区上时, 需要得知这个节点的节点函数运行耗时. OGP-HG算法在计算一条边应当分配到哪个分区上时, 需要得知这条边和其两端点所携带的数据量. OGP-HG算法为划分节点和边分别设定了一个目标函数, 在划分每一个节点或边时, 计算这个节点或边在每个分区上的目标函数值, 然后将其划分到使其目标函数值最大的分区上. OGP-HG算法的核心就是设计这两个目标函数.

根据算法主要思想的分析, 划分一个节点时只用考虑其节点函数的耗时, 以保证各分区上的计算负载均衡, 因此我们提出了划分节点的目标函数:

$ {C}_{{\rm{BAL}}}^{{\text{OGP-HG}}}(v, p)=\frac{maxtime-{p}_{t}}{\varepsilon +maxtime-mintime} $

(13)

其中, $ maxtime $ 和 $ mintime $ 分别表示所有分区内已分配节点的最大、最小节点函数耗时, $ {p}_{t} $ 表示 $ p $ 分区内已分配节点的节点函数耗时, 遍历所有分区的 $ {p}_{t} $ , 找出使 ${C}_{{\rm{BAL}}}^{{\text{OGP-HG}}}\left(v, p\right)$ 取得最大值的 $ {p}_{t} $ , 即将节点 $ v $ 分配到当前计算负载最小的 $ p $ 分区. 这样依次分配到来的每一个节点, 可以使节点函数的计算负载在各分区均衡. 每分配一个节点后根据分配结果更新对应分区 $ p $ 的 $ {p}_{t} $ .

2.3 算法流程

使用OGP-HG算法对异质图进行在线图划分的具体步骤如下.

(1)异质图数据分别以点数据和边数据形式到来, 每当划分一条边数据时, 遍历所有分区, 找出使得分 ${C}^{{\text{OGP-HG}}}\left({v}_{{\rm{src}}}, {v}_{{\rm{dst}}}, p\right)$ 取得最大值的分区 $ p $ , 记为 ${p}_{{\rm{max}}}$ , 即将边分配到 ${p}_{{\rm{max}}}$ 分区上. 每分配一条边后根据分配结果更新 $\left|p\right|、A\left({v}_{{\rm{src}}}\right)、A\left({v}_{{\rm{dst}}}\right)、\delta \left({v}_{{\rm{src}}}\right)、\delta \left({v}_{{\rm{dst}}}\right)$

(2)每当划分一个点数据时, 根据节点函数时间复杂度 $ T $ 采用划分点的目标函数计算每个节点在各分区上的得分, 使分配节点后不同分区上的计算负载均衡.

(3)每分配完成一批数据后, 根据所有分区边数量的最大和最小值更新maxsize和minsize, 根据所有分区内存占用的最大和最小值更新 $ maxmem $ 和 $ minmem $ , 根据所有分区节点函数耗费时间的最大和最小值更新 $ maxtime $ 和 $ mintime $ .

(4)将划分好的节点和边组成图, 开始进行图计算迭代运算. 图计算中节点汇集所有邻居节点和邻边的信息并根据自己的节点函数进行计算, 获得计算结果. 当两次迭代的计算结果之差小于设定的收敛值后, 认为这个节点已经达到收敛, 下次迭代时就不会在这个节点进行计算.

(5)重复步骤(1)–步骤(4), 直到没有新的节点或边到来, 且所有节点都达到收敛, 此时, 图划分结束.

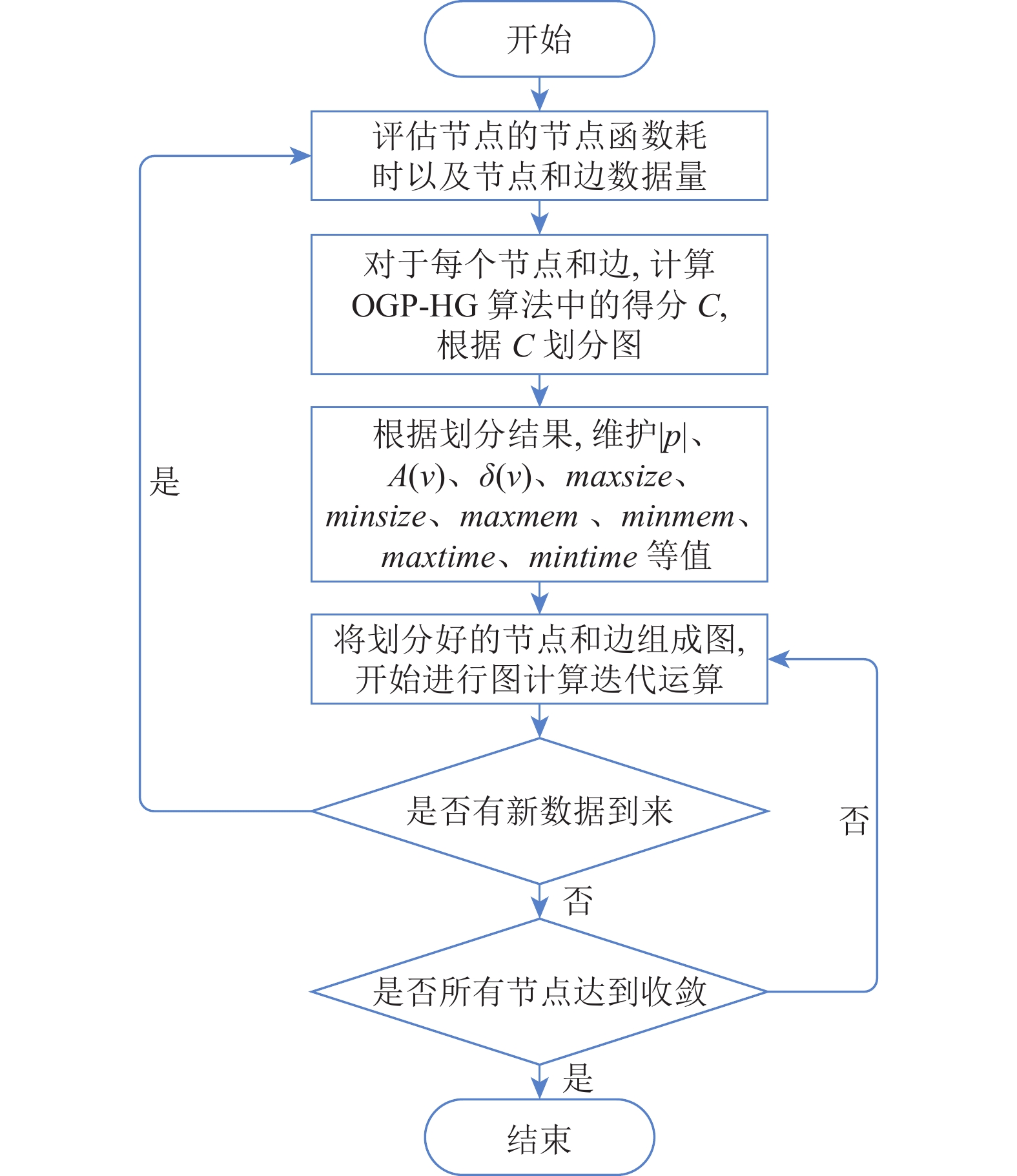
使用OGP-HG算法对异质图进行在线图划分的流程图如图1所示.

在本文所采用的图计算模型中, 所有计算节点都认为是相等的, 它们可以并行地读取图数据, 然后对图进行分割. 由于每个节点都有可能进行图分割任务, 所以当一个节点开始进行图分割任务时, 它就必须拥有所有需要的信息. OGP-HG算法使用的信息有: 节点的副本集合 $ A\left(v\right) $ 、节点的部分度 $ \mathrm{\delta }\left({v}\right) $ 以及各分区内存占用的最大值和最小值等. 为了方便讨论, 假设在 $ t $ 时刻, 整个图计算引擎有 $ n $ 个分区, 要划分的图有 $ m $ 个节点, $ k $ 条边.

因此, 对于OGP-HG 算法中各状态量的维护包括: (1)使用二维布尔数组维护 $ A\left(v\right) $ , 其中第1维代表所有节点, 第2维代表所有分区. 所以其空间复杂度在一个分区上为 ${\rm{O}}\left(n \times m\right)$ , 在所有分区上为 ${\rm{O}}\left({n}^{2} \times m\right)$ ; (2)在每个分区上使用整型数组维护 $ \delta \left(v\right) $ , 其空间复杂度在一个分区上为 ${\rm{O}}\left(m\right)$ , 在所有分区上为 ${\rm{O}}\left(n \times m\right)$ ; (3)在每个分区上使用浮点数变量维护边数量的最大值maxsize和最小值minsize、内存占用的最大值 $ maxmem $ 和最小值 $ minmem $ , 其空间复杂度在一个分区上为 ${\rm{O}}\left(1\right)$ , 在所有分区上为 ${\rm{O}}\left(n\right)$ ; 综合以上分析, OGP-HG 算法的空间复杂度为 ${\rm{O}}\left({n}^{2} \times m\right)$ .

对于OGP-HG 算法的计算耗时分为两部分: (1)计算启发式贪心算法的得分花费的时间, 由于 $ A\left(v\right) $ 和 $ \delta \left(v\right) $ 都采取数组存储, 不需要查找, 所以可以直接计算每条边和每个节点在所有分区上的得分, 故这部分的时间复杂度为 ${\rm{O}}\left(n \times \right(m+k\left)\right)$ ; (2)同步状态量花费的时间, 每次划分一条边后都要同步节点的 $ A\left(v\right) $ 和 $ \delta \left(v\right) $ , 由于每次同步只用同步状态量数组被修改的部分, 不需要全部更新, 故同步的时间复杂度为 ${\rm{O}}\left(n\right)$ ; 综合以上分析, OGP-HG 算法的时间复杂度为 ${\rm{O}}\left(n \times \right(m+k\left)\right)$ .

3 实验与评估 3.1 实验设置

本节使用了3个真实数据集对本文中的OGP-HG 图划分算法和在线图计算引擎进行了实验验证, 真实数据集分别来自Twitter社交网络数据^[21]、.uk域的快照生成图^[22]、美国路网图集^[23], 这3个数据集具有不同的数据规模和拓扑特性. 其中Twitter数据集是2010年爬取的Twitter网上的用户关注网络图, 其数据形式是一系列的边数据, 代表用户间的关注关系, 这一图数据集符合幂律分布; .uk域的快照生成图是英国2007年5月的网页快照关系图(UK2007-05), 图中的节点是当时的网页快照, 边是这些网页的关系, .uk域的快照生成图符合幂律分布; 美国路网图集(USA-Road)展示了美国的道路网络, 图中节点代表不同的地点, 边代表道路, 边上的属性表示物理距离, 这一图数据集不是网络数据集, 不符合幂律分布, 节点的度比较平均, 且普遍度很小.

但是, 本文要验证针对异质图的OGP-HG 图划分算法的效果, 但是异质图数据集资源很少, 为了验证OGP-HG 图划分算法对于图计算引擎内存占用均衡的影响, 我们要在这3个数据集上做一些修改. 我们自定义一种方法, 将这3个数据集上的边和节点都分为两类, 对这些边和节点标记类型, 并对不同类型的节点和边赋予不同数据量的属性数据, 这样就生成了具有多类型节点和边的异质图数据集.

本文一共进行了两组模拟实验. 第1组是不同图划分算法下数据均衡性对比实验和不同图划分算法下运行相同图算法耗时对比实验, 旨在检验不同图划分算法下对于实验指标的影响. 对比的图划分算法分别是GraphX自带的Grid算法、HDRF算法和本论文中提出的OGP-HG算法.

第2组实验只使用OGP-HG图划分算法, 在图划分结束后进行图计算, 对不同差异度的异质图下的运行效果, 这里的差异度主要指节点函数运行耗时的不同差值倍数. 这一组实验旨在检验本文中提出OGP-HG图划分算法对于不同异质程度的图数据会分别产生多大的效果.

为了对比不同节点函数运行耗时差值倍数下的运算耗时, 我们需要运行一个对异质图的不同节点采取不同处理逻辑的图算法. 这里我们将PageRank算法做了一个改变, 对于不同类型的节点, 额外加入不同级别的运算负载.

本文实验一共使用了6台服务器作为计算节点, 在这6台服务器上分布式部署Spark, 其中一台作为master节点, 其余作为worker节点. 同时Spark读取文件还需要使用Hadoop的HDFS, 也在这6台服务器上分布式部署Hadoop. 服务器参数如表2.

软件框架参数如表3.

3.2 评估分析

由图2(a)可以看出, 采用Grid算法的内存占用均值明显高于另外两个算法, 说明采用Grid图划分算法的划分结果复制系数过高, 导致内存占用较高, 而HDRF算法和OGP-HG算法的内存占用相近. 由图3(b)可以看出, 只有OGP-HG算法的划分结果内存占用的方差最小, 说明其划分结果的内存占用在各分区上最均衡. 综合两项指标我们得出结论, OGP-HG图划分算法可以使划分结果的内存占用较小的同时, 又使其内存占用最均衡. 内存占用较小是因为降低了复制系数, 减少了节点的副本. 而内存占用均衡是因为考虑了异质图不同类型和边的内存占用不同, 数据计算耗时将其分配到内存占用最小的分区.

图3是对OGP-HG与Grid和HDRF算法在图划分后进行图计算的计算耗时最大值对比, 这一节中采取的图算法为各节点计算负载相差10倍的PageRank算法. 我们在这里关注计算耗时的最大值, 是因为在线计算通常有时间要求, 只有每一批次的数据计算都能在下一批次数据到来前完成, 才能达到在线计算要求. 观察图3可知, OGP-HG算法相对HDRF最高可以节省约15%的时间, 且只有OGP-HG算法后的图计算可以每一组数据集都在2 s内完成, 如果批式数据到来的周期为2 s, 则只有采用OGP-HG算法的在线图计算引擎满足在线要求. OGP-HG算法耗时最少, 这是因为考虑到了异质图的计算平衡性, 每次分配节点和边时将其分配到负载最小的分区, 最终划分结果各分区计算负载均衡, 不会出现计算负载多的分区长时间等待的情况.

我们验证了OGP-HG算法对于异质图计算有较好的效果, 但是对于不同差异程度的异质图, 使用OGP-HG图划分算法的效果可能有很大不同. 为了验证这一猜想, 我们将修改后的PageRank算法在不同节点上的计算负载分别设定为1、10、20、30、40、50、60、70、80、90、100, 比较不同节点函数差值倍数的情况下OGP-HG算法划分结果对于异质图计算的效果, 以HDRF的运行耗时为基准, 实验结果如图4所示.

根据图4我们可以得知, 随着异质图不同类型节点的节点函数差异度增大, 使用OGP-HG算法后进行异质图计算对比HDRF算法节约时间从5%到40%不等, 而且节点差异程度越大, 使用OGP-HG算法后进行图计算的耗时越短, 即图计算的效率越高. 因此我们可以得出结论, OGP-HG算法对于差异程度越大的异质图的划分效果越好. 这是因为使用以往的图划分算法, 差异程度越大的异质图, 其划分结果负载不均衡的情况就会越突出, 图计算的效率就越差. 相较之下, OGP-HG算法的效果就会越好.

4 结论与展望

本文在研究异质图计算不平衡性的基础上, 提出了一种面向异质图数据的在线图划分算法, 并对此算法的时间和空间复杂度进行了分析. 为了验证该算法的效果, 本文还对面向异质图数据的在线图划分算法进行了多组实验, 实验结果表明该算法能提升异质图计算性能.

我们可以从以下几个方向展开后续工作: 1)减少OGP-HG算法进行图划分时候的状态量更新开销, 使图划分阶段耗时更小. 2)目前图神经网络领域有许多异质图方向的研究^[24–26], 后续可以以异质图神经网络的计算为案例, 更好地验证本文提出的异质图划分算法的效果.