2. 广东佛山联创工程研究生院, 佛山 528311
2. Guangdong Foshan Lianchuang Graduate of Engineering, Foshan 528311, China
近年来, 人体姿态估计作为计算机视觉领域中一项基础而具有挑战性的任务受到了广泛关注, 并在人体动作识别、行为分析和人机交互等任务中得到了广泛应用. 该技术的主要目标是定位人体骨骼关键点, 如肘部、腕部等, 以实现对人体姿势和动作的准确推测. 人体姿态估计技术在多个领域取得了出色的效果[1], 在基于视觉的人体姿态估计方面, 其具有低成本、便携等优势, 为智能健身提供了一种全新的交互方式[2,3], 并且通过将人体姿态估计技术与深度学习算法相结合, 并利用简单便携的设备, 如智能手机、智能手环等, 实现跳绳计数任务等应用. 这种结合使得人们可以更加方便地进行健身锻炼, 同时享受到姿势估计技术带来的精准监控和反馈.
早期基于卷积神经网络(CNN)的姿态估计直接从图像中预测关节点位置. 然而, 这种方法很难获得精确的坐标且鲁棒性较差, 为了解决这个问题, DeepPose[4]采用深度神经网络从图像中回归关键点的坐标, 虽然一定程度改善了精度问题, 但是网络的收敛速度非常缓慢, 预测的坐标还是不够准确. 为了改进精度和速度, Tompson等人[5]提出了使用热力图来表示关节点的信息, 热力图中的数值大小反映了该位置是关节点的概率大小, 通过寻找热力图中最大值的坐标从而确定关节点的位置, 这种使用热力图表示关节点位置的方法极大地推动了基于CNN的人体姿态估计方法的发展. 由于可以通过卷积操作直接生成热力图, 因此该方法在提高准确性的同时也提升了计算效率. Newell等人提出多次上采样和下采样堆叠而成的Hourglass模块[6], 使网络能够在不同的尺度上进行多次特征提取和融合, 从而获得更加准确和鲁棒的关键点估计结果. 2019年Sun等人提出的HRNet[7]更是在人体姿态估计任务中取得了SOTA级的表现, 他提出一种基于多分辨率子网络并行融合的人体姿态估计方法, 通过保持高分辨率特征来提高准确性. HigherHRNet[8]在基于HRNet的多分辨率网络上通过增加更高分辨率的特征金字塔结构, 引入了更丰富的多尺度特征信息, 以获得更准确、更精细的姿态估计结果. 同时它还利用强化的前项和后项空间转换器来提升特征的表达能力和姿态估计的鲁棒性, 在保持高效率的同时, 实现了更准确、更稳健的人体姿态估计.
但是由于算力和内存限制, 移动设备和嵌入式平台不适合部署大型网络[9], 因此, 目前的人体姿态估计网络难以得到广泛应用. Neff等人在HRNet基础上提出了EfficientHRNet[10], 通过采用轻量级网络设计和优化的特征融合策略实现了在计算效率和准确性上的平衡, 使得它在保持高分辨率特征的同时, 减少了模型的参数量和计算复杂度, 使得姿态估计更加高效而精确. Zhang等人[11]构建了一个轻量化的沙漏网络, 利用快速姿态蒸馏模型学习策略, 能够更有效地训练轻量化人体姿态估计网络.
而人体姿态估计关键点检测的方法大致分为两类: 一类是以HRNet为代表的自顶而下的网络框架, 另外一类是以OpenPose[12]为代表的自底而上的网络框架. 其中第1类一般都是先进行物体检测, 将图像中每个人的人体矩形框识别并进行裁剪, 最后在此区域内进行单人的人体关键点检测, 因为只在人体矩形框内进行单人检测, 所以去除了人体之外的干扰, 其准确率是目前姿态估计所有框架中最高的, 但是要先检测人体再进行关键点检测, 所以在多人人体关键点检测下, 其检测效率也会随之下降. 自底而上的算法则是直接先将图像中所有人体的关键点全部检测出来, 再通过关节点之间的关联进行拼接最后得到人体姿态, 该算法的优势在于它的检测效率和实时性比较高, 但是易受非人体因素干扰, 所以其精度相对较低.
但是大多数方法需要使用完整的骨架模型或较复杂的网络结构, 限制了它们在移动设备上的应用, 其低误差率、高实时性同算法的可实施性不可兼得. 而跳绳作为一种常见的运动方式且与人体姿态信息相关联, 传统的跳绳计数方法主要依靠人眼手动计数, 并且容易出现误差. 为了解决这个问题, 越来越多的研究者开始尝试采用基于模型的计数方法, 这些方法主要是通过使用运动捕捉设备, 如惯性测量单元(IMU)和深度相机或者额外的传感器和复杂的硬件[13–15], 来获取用户的行动信息, 并通过算法进行计数. 然而这些设备通常比较笨重, 难以携带, 且价格较高. 因此, 如何降低计数方法的设备依赖性, 提高其可行性和普及性, 成为一个研究难点.
针对以上这些问题本文提出了一种跳绳计数算法, 采用了一个端到端、自底而上方法的多人轻量级人体姿态估计网络来提取人体关键点坐标, 并且对网络的解码方法进行了优化, 采用了一种自适应感知解码方法, 降低了热图最大激活点映射回原图坐标时导致的量化误差, 然后用卡尔曼滤波将人体姿态估计网络预测的关键点坐标进行平滑滤波后, 最后再通过计算关节点的运动变化来进行跳绳计数. 实现在手机、嵌入式开发板等边缘计算设备上能够快速准确地完成跳绳计数任务, 同时为人体姿态估计算法进行应用落地提供一个参考方向.
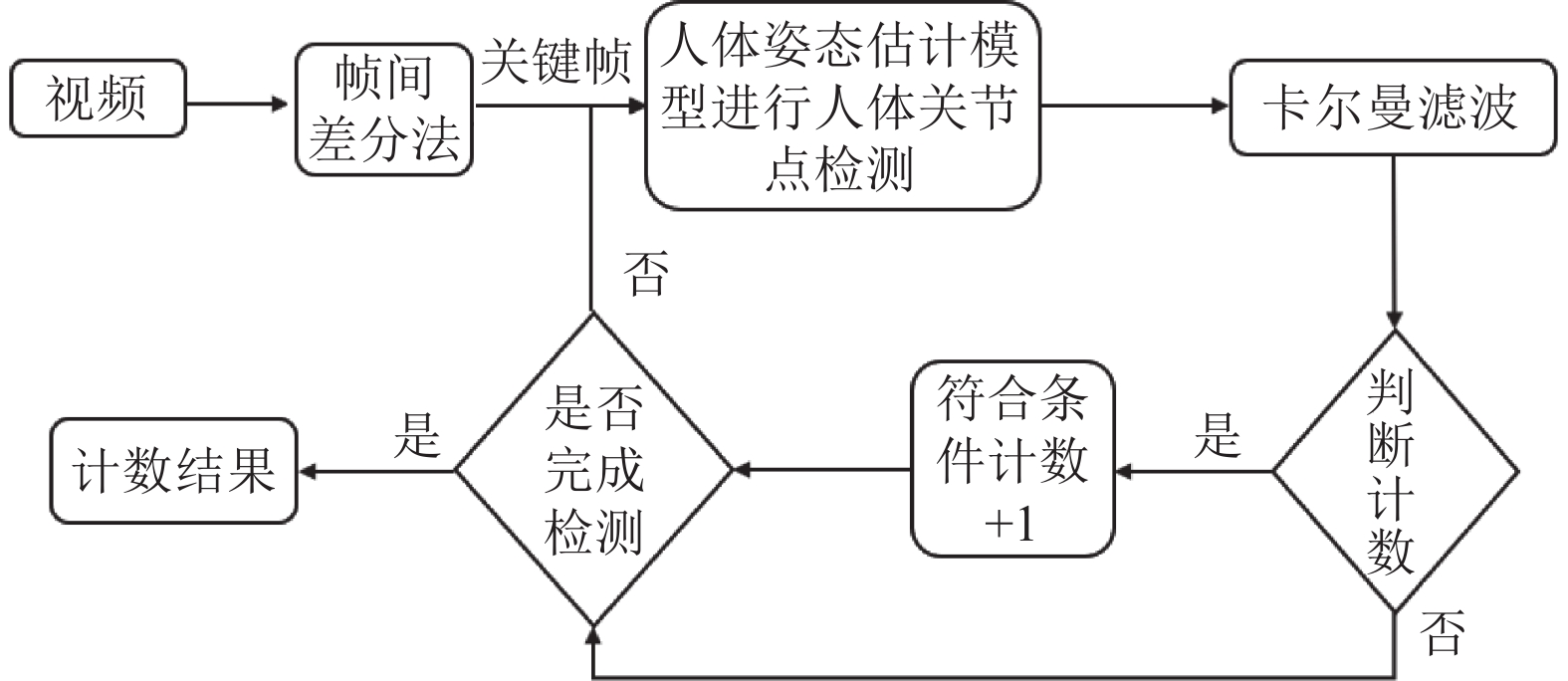
2 基于人体姿态估计的跳绳计数算法 2.1 算法流程本文提出的基于人体姿态估计的跳绳计数算法的实现流程如图1所示, 主要由提取关键帧、关键点检测、数据处理和判断计数4个部分构成. 首先, 输入跳绳视频并进行帧间差分法, 提取关键帧图像; 接下来, 利用优化的人体姿态估计模型进行关节点检测; 然后, 通过卡尔曼滤波将人体姿态估计模型得到的预测估计作为观测值进行修正, 以获得状态变量(关节点坐标)的最优估计; 最后, 通过关键点的坐标变化进行判断计数, 从而最终得到计数结果.
|
图 1 算法流程图 |
2.2 提取关键帧
帧间差分法[16,17]是一种通过在视频图像序列中相邻两帧进行差分运算来获取运动目标轮廓的方法. 该方法具有运行速度快、动态环境自适应性强以及对场景光线变化不敏感等特点. 本文利用该方法提取跳绳运动中人体关节点变化的关键帧图像. 但由于跳绳动作较快, 本文采用了三帧差分法. 具体实现为: 首先使用OpenCV库函数读取视频, 并将读取到的视频帧图像从BGR格式转换为LUV格式; 然后将连续3帧中每个像素点的灰度值进行差值运算, 并将得到的差值进行累加, 得到3帧图像的差分强度, 根据像素总数计算平均帧间差分强度; 接下来对序列进行卷积平滑运算, 平滑后的极值即对应着视频关键帧. 虽然本文采用的是三帧差分法, 但仍能较好地提取出跳绳动作的关键帧.
2.3 人体关键点检测 2.3.1 人体关键点检测模型自顶而下的算法虽然精度高但其实时性低且计算量都普遍偏大难以部署到边缘设备上, 所以本文选用的是基于自底而上的轻量级人体姿态估计网络LitePose[18]作为基础架构并在其解码部分进行优化.
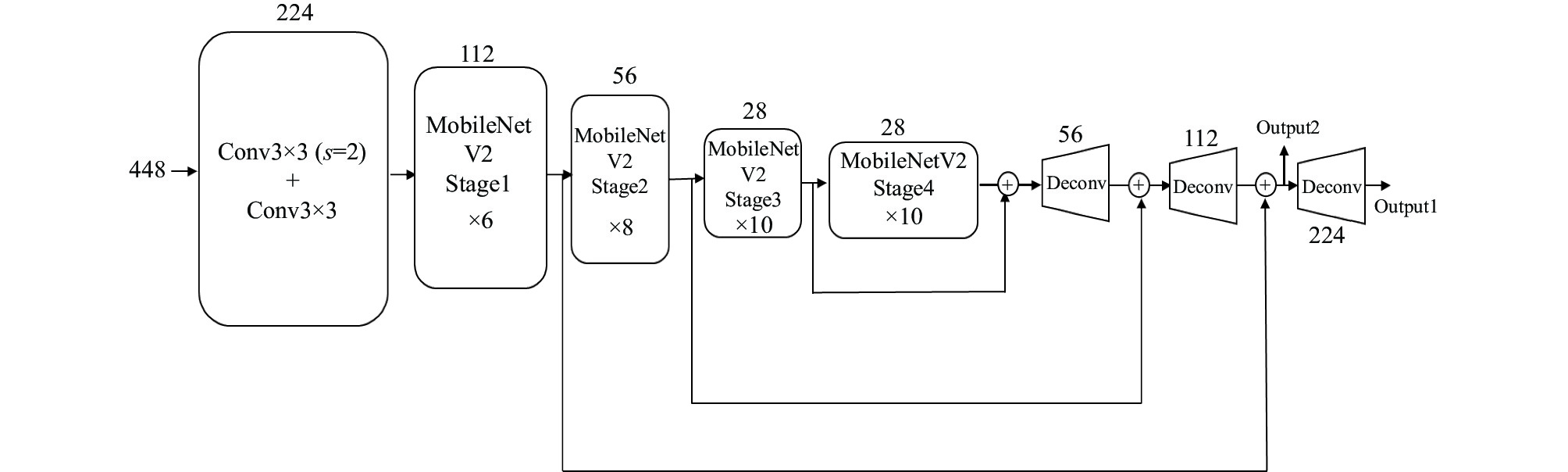
LitePose是现有即精确、网络结构简单、算力要求不高且能够在边缘端部署的多人实时姿态估计的高效架构设计. LitePose在HigherHRNet的基础上重新设计出了一个高效的单分支结构, 其结构如图2所示, 它采用了改进的MobileNetV2[19]作为主干网络提取特征, 使用了步长为7的大卷积核, 在只增加了很小的计算量的情况下, 增强了尺度变化的能力, 同时为了保持高分辨率特征, 将原有的上采样替换成了反卷积[20] , 不仅消除了高分辨率分支中的冗余细化, 还能以单分支的形式进行尺度感知的多分辨率融合. 检测出所有的关键点之后再使用关联嵌入的方法进行分组最后得到完整的人体姿态图.
|
图 2 LitePose-S网络结构图 |
2.3.2 解码过程
目前主流的人体姿态估计网络都是采用的基于热图的回归方法, 本文使用的LitePose也是基于热图回归的方式. 模型先将人体的每个关节坐标变成以其坐标为中心的二维高斯分布的关节热图, 再送入网络中进行监督, 这就是坐标编码, 但是为了降低计算量通常都是先进行下采样形成低分辨率热图; 在热图预测之后同样也需要将分辨率恢复并且将热图转换成原始坐标, 最终预测被认为是具有最大激活的位置, 称这一过程为坐标解码. 在预测生成的低分辨率热图上找到最大激活点再映射回原图得到关键点坐标这一解码过程中会存在量化误差, 对于这种误差, 现有的人体姿态估计都是采用Hourglass中的方法对最大激活点在解码之前进行后处理, 也就是将预测的坐标, 由最大激活位置向第2大激活位置的方向, 移动0.25个像素然后再上采样恢复成原图分辨率得到坐标.
这种手工设计偏移补偿解码方法预测出来的最大激活位置并不是原始图像中关节点的准确位置, 只是一个粗略大概的位置, 这种方法虽然能够手工的将误差进行补偿, 但是还是不能够使预测热图中的关键点解码成更加精确的原始坐标位置. 所以本文使用了一种自适应感知的解码方法去代替原先手工补偿的解码方法, 通过热图自己的分布结构来自适应预测出它最大激活点的位置, 从而使模型在解码过程中得到更准确的定位.
2.3.3 自适应感知解码因为热图的生成通常都是通过二维高斯核生成的, 但是发现模型预测的热图并不是严格遵守高斯分布的, 会出现多峰的情况, 会对解码方法造成负面影响, 因此在进行解码之前, 要先将热图进行平滑预处理.首先利用与训练数据具有相同变化的高斯核K来平滑多峰带来的影响, 具体操作如下:
| $ p' = K \circledast p $ | (1) |
其中,
同时为了保证和原始热图具有相同的分辨率, 还需通过式(2)对
| $ p' = \frac{{p' - \min\left( {p'} \right)}}{{\max\left( {p'} \right) - \min\left( {p'} \right)}}\times \max\left( p \right) $ | (2) |
平滑过后的热图就严格遵从与高斯分布, 因此预测的热图与真实热图相同, 其热图可以表示为:
| $ \mathcal{G} = \frac{1}{{\left( {2{\text π} } \right)|{{\Sigma }}{|^{\frac{1}{2}}}}}{\text{exp}}\left( { - \frac{1}{2}{{(x - \mu )}^{\rm{T}}}{{{\Sigma }}^{ - 1}}\left( {x - \mu } \right)} \right) $ | (3) |
其中,
| $ {{\Sigma }} = \left[ {\begin{array}{*{20}{c}} {{\sigma ^2}}&0 \\ 0&{{\sigma ^2}} \end{array}} \right] $ | (4) |
为了方便计算根据对数似然优化的原则, 将式(3)进行对数变化变成二次形式
| $ \begin{split} H\left( {x;\mu , {{\Sigma }}} \right) & = {\text{ln}}\left( \mathcal{G} \right) \\ &= - {\text{ln}}\left( {2{\text π} } \right) - \frac{1}{2}{\text{ln}}\left( {\left| {{\Sigma }} \right|} \right) - \frac{1}{2}{(x - \mu )^{\rm{T}}}{{{\Sigma }}^{ - 1}}\left( {x - \mu } \right) \end{split} $ | (5) |
解码的最终目的就是为了从热图中获得最大激活位置
| $ \begin{array}{c}{{\mathcal{D}}^{\prime }\left(x\right)|}_{x=\mu }={\dfrac{\partial {H}^{{\rm{T}}}}{\partial x}\Bigg|}_{x=\mu }=-{{\text{Σ}}^{-1}\left(x-\mu \right)|}_{x=\mu }=0\end{array} $ | (6) |
再利用泰勒定理去将预测热图中最大激活点
| $ \begin{split} H\left( \mu \right) =& H\left( h \right) + \mathcal{D}'\left( h \right)\left( {\mu - h} \right) \\ &+\frac{1}{2}{(\mu - h)^{\rm{T}}}\mathcal{D}''\left( h \right)\left( {\mu - h} \right) \end{split} $ | (7) |
其中,
| $ \mathcal{D}''\left( h \right) = {\left. {\mathcal{D}''\left( x \right)} \right|_{x = h}} = - {{{\Sigma }}^{ - 1}} $ | (8) |
最后通过式(5)–式(8)可以得到通过预测热图的最大激活点
| $ \mu = h - {\left( {\mathcal{D}''\left( h \right)} \right)^{ - 1}}\mathcal{D}'\left( h \right) $ | (9) |
得到极大值点的位置就可以通过式(10)进行还原得到预测的最终原始空间下的关节点坐标, 其表示如下:
| $ \hat p = \lambda p $ | (10) |
其中,
这种通过泰勒级数结合最大激活点的一阶偏导和二阶偏导来联合定位真正极值点位置的方法, 不仅能够自适应探索热图分布的统计信息, 从而去推断潜在的极值点位置, 比之前手工往第2大激活点位置偏移0.25个像素点要更具有理论上的说服力, 而且这种解码方式只需要计算每个预测热图最大激活位置的一阶偏导和二阶偏导, 并不会增加计算成本.
2.4 卡尔曼滤波卡尔曼滤波是通过观测信息和该数据的状态转移以及观测模型对状态进行滤波和预测, 它的优点在于其计算量小, 只需要建立数据和噪声对应的状态空间模型, 就可以通过上个时刻的状态来对当前时刻的状态进行最优估计. 模型在检测连续帧时由于人体关节点检测模型受外界噪声和其本身性能限制等一系列因素可能会出现检测人物未出现明显变化但是预测的关节点坐标却出现较大浮动的现象. 同时算法是根据模型预测的关节点坐标的周期性变化来进行计数, 所以为了使模型预测出来的关键点坐标更加精准, 本文采用了卡尔曼滤波[21]对模型检测出来的坐标进行一个平滑降噪, 减少噪声的干扰, 缩小坐标波动的阈值, 来降低坐标抖动误差并且过滤掉跳绳运动中人体关键点的一些极端异常值.
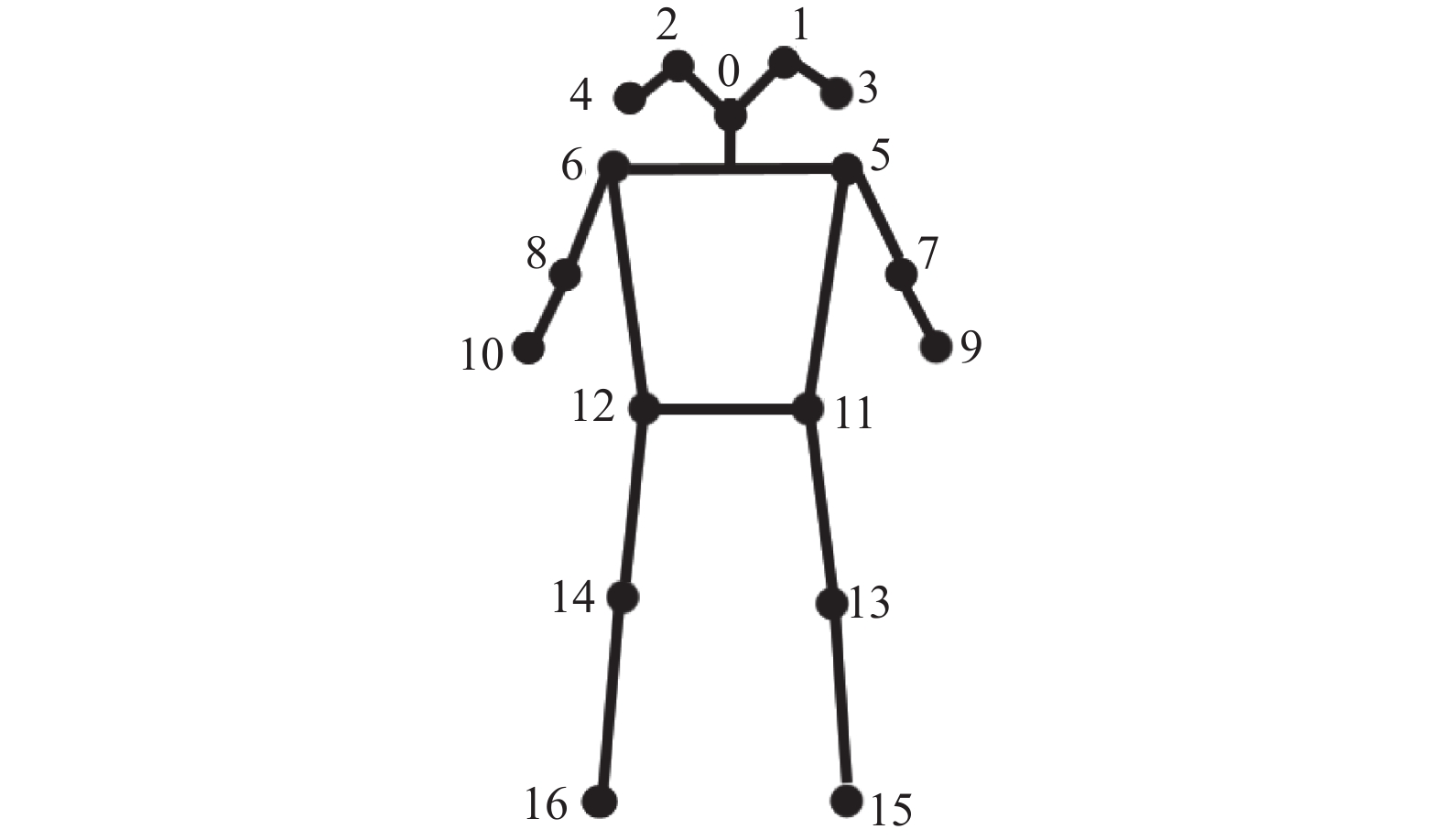
2.5 判断计数优化后的人体姿态估计模型可以更加准确地获取人体关节点的图像位置数据, 预测出17个关节点的骨骼拓扑(如图3所示). 结合关节点数据信息和人体跳绳运动中产生的关节点坐标随着人体起跳、落地不断呈现类似于正弦函数一样的周期性波动变化, 本文构建了跳绳计数算法. 具体来说, 在人体跳绳时, 其重心在竖直方向上一定会随着运动而发生明显变化, 因此本文选取了5、6、12、11这4个关节点纵坐标的中值作为跳绳计数的关键点; 每完成一次跳绳运动, 其关键点纵坐标一定会满足先上升后下降的周期性变化, 因此只需对当前关键帧的关键点纵坐标与上一关键帧的关键点纵坐标进行对比判断, 如果符合条件, 则进行计数. 具体判断流程如图4所示.
|
图 3 COCO数据集人体关键点拓扑 |

|
图 4 跳绳判断计数流程框图 |
3 实验结果与分析 3.1 实验环境与配置 3.1.1 实验数据
本文模型优化实验的数据集为COCO数据集, 跳绳计数实验则采用50个不同场景下以及跳绳速率不同的跳绳视频进行正确率测试, 6个室内外不同环境背景的跳绳视频进行误差率测试. 其中COCO数据集在计算机视觉领域中运用比较广泛, 本文采用的COCO2017进行在不受控制的条件下对多人的关节点进行定位, 其中训练集包括了118287张图片, 验证集中包含了5000张图片, 都是进行了17个人体关节点标注的人体实例. 所以本文将训练集(train2017)来对网络进行训练, 在验证集(val2017)上对模型进行评估, 并且与其他模型进行了比较.
3.1.2 评估标准其中在模型优化实验的验证中, 均采用人体关键点相似度 (object keypoint similarity, OKS)来计算模型预测的人体关节点的坐标与真实值(标签值)坐标之间的误差, 再通过设置不同的阈值来确定预测关节点的置信度. 其计算公式如下:
| $ O K S=\frac{\displaystyle\sum_i \exp \left(\dfrac{-d_{i}^{2}}{2 s^{2} k_{i}^{2}}\right) \delta\left(v_{i}>0\right)}{\displaystyle\sum_i \delta\left(v_{i}>0\right)} $ | (11) |
其中,
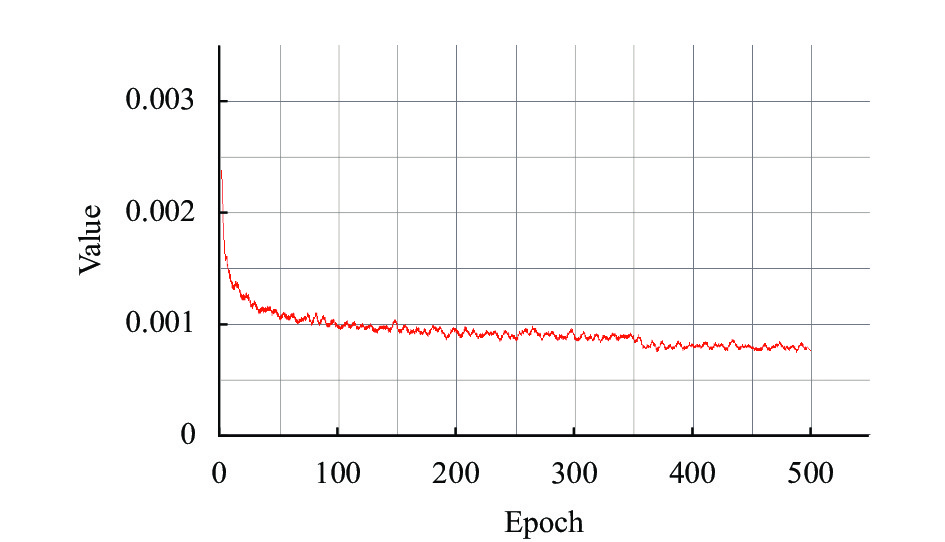
实验均在Ubuntu 20.04操作系统、i9-10940X 3.3 GHz的CPU、以及一个NVIDIA 3080 10 GB GPU组成的服务器上完成. 采用的是PyTorch 1.8.1 深度学习框架. 训练使用的是ADAM优化器, 对模型的训练总共500个周期, 批次大小为40, 初始学习率为0.001, 在第350和480个Epoch分别对其更新至0.0001和0.00001. 模型采用均方差来计算关节点预测损失和关节点关联嵌入损失去监督网络. 其总损失计算公式如下:
| $ L = {\lambda _{{\rm{pre}}}}{L_{{\rm{pre}}}} + {L_{{\rm{cls}}}} $ | (12) |
其中,
| $ {L_{{\rm{cls}}}} = {\lambda _{{\rm{push}}}}{L_{{\rm{push}}\_{\rm{loss}}}} + {\lambda _{{\rm{pull}}}}{L_{{\rm{pull}}\_{\rm{loss}}}} $ | (13) |
其中,
在跳绳计数实验中, 我们对
|
图 5 训练损失收敛曲线 |
3.2 关键帧提取实验
为了加快跳绳计数算法检测效率, 本文利用三帧差分法进行关键帧提取. 卷积平滑窗口大小设置为25, 如果窗口过大, 会导致差分图像中部分信息被掩盖, 容易造成局部运动感知不明显, 而窗口过小又无法抑分图像中的噪声达到抑制静态背景的效果. 经过实验发现, 卷积平滑窗口当为25的时候效果最佳, 而此时平滑之后的极值所对应的帧便是关键帧. 得到关键帧之后并且对帧图像进行一定剪裁和缩放使其大小为448×448的图像送入人体姿态估计模型中进行关节点检测. 这样不仅可以避免花费大量时间从头到尾的检测全部视频帧, 同时还可以减少连续帧之间由于人体姿态估计模型性能导致的抖动误差. 其跳绳运动中部分关键帧序列入图6所示.

|
图 6 部分关键帧序列 |
3.3 模型优化实验结果
本节在COCO验证集上将改良后的模型与其他模型进行对比实验来验证模型的准确性和可实施性, 其实验结果如表1所示. 由表可知, LitePose模型与其他先进的自底而上的人体姿态估计模型相比, 在包含更少的参数量和运算复杂度更低的基础上仍然取得了比较好的性能, 如对于PersonLab和Hourglass以及Higher-HRNet这类网络层数较深的复杂网络, LitePose-M仍然具有比较大的优势, 虽然在精度上有略微下降, 但是大幅度降低了计算量和参数量, 只牺牲一点精度就极大地增加了算法落地的可实施性, 相较于轻量级网络如OpenPose, LitePose-S在模型参数量和运算复杂度上分别降低了34.1%和44.4%, 同时平均检测精度mAP值也提升了32%. 对于更为先进的EfficientHRNet-H-2模型, 也同样在模型参数量和运算复杂度分别降低了67.5%和36.7%的基础上mAP值提高了7.4%. 所以由此可以表明LitePose高效的单分支结构能够更好地满足部署到计算力较低的边缘设备上的这一需求.
| 表 1 COCO val2017中模型对比结果 |
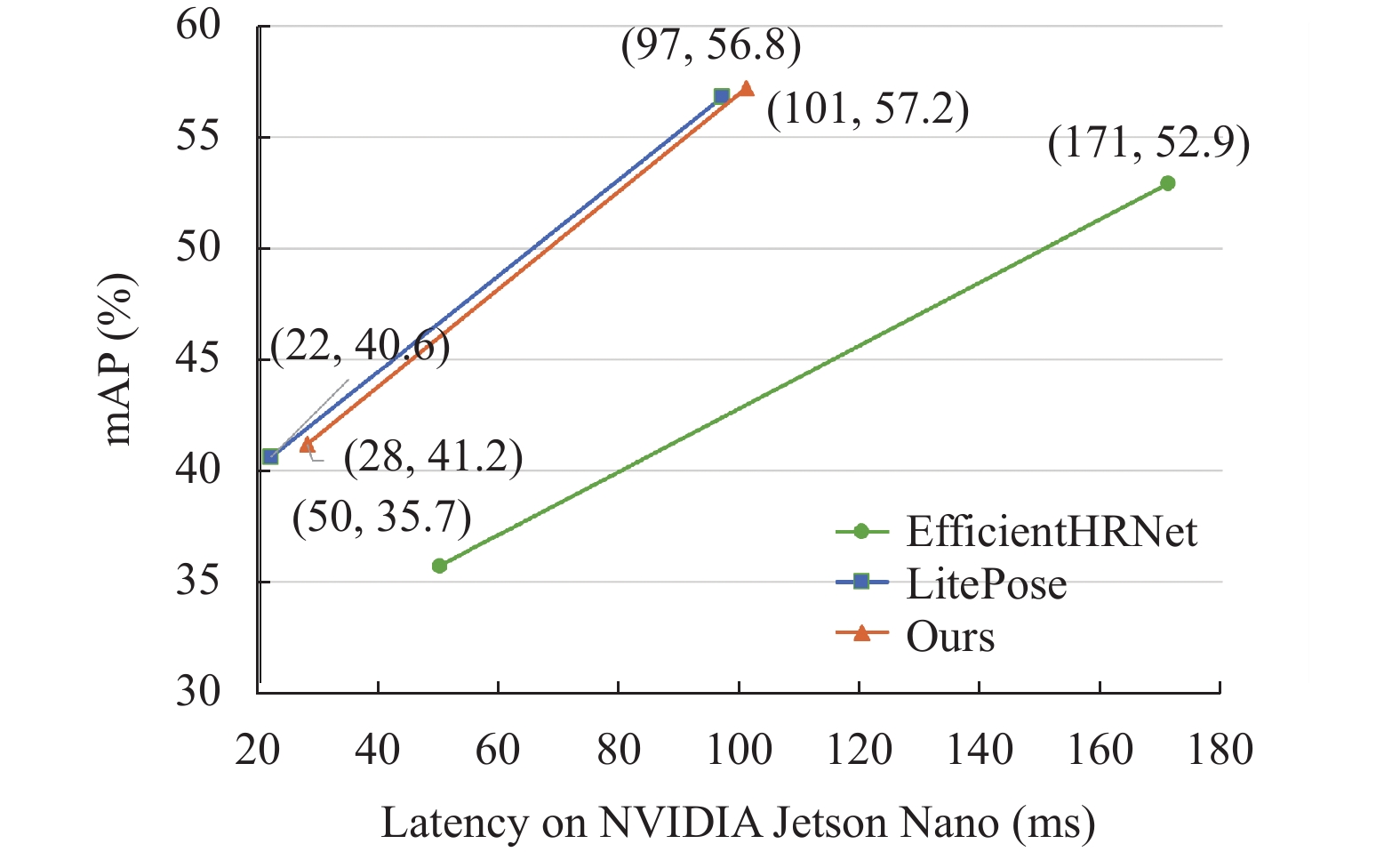
当同时在LitePose模型解码过程中使用自适应感知解码, 不仅使LitePose-S的精度提高了0.7%, 对于输入更低分辨率的XS模型平均精度也提高了1.5%, 而且其模型复杂度并未出现明显变化. 同时为了检测网络模型的可实施性本文在NVIDIA Jetson Nano上面测试了3类网络的延时, 结果如图7所示. 可以看出本文优化后的模型在提升了性能的同时其延时几乎没有太大变化. 这些结果足以表明, 自适应感知的解码方法确实能够在解码过程中保持计算量以及参数量不发生明显变化的前提下通过计算高斯分布热图的一、二阶偏导来自适应感知最大激活位置, 从而减少热图解码过程中坐标因为分辨率不同而导致的量化误差, 而优化的LitePose模型也同样在具有低参数量和低计算量的前提下, 拥有较于其它模型更优的检测精度, 能够更好地部署到计算力不强的边缘设备上, 因此本文算法采用改良的LitePose-S模型来进行人体关键点检测.
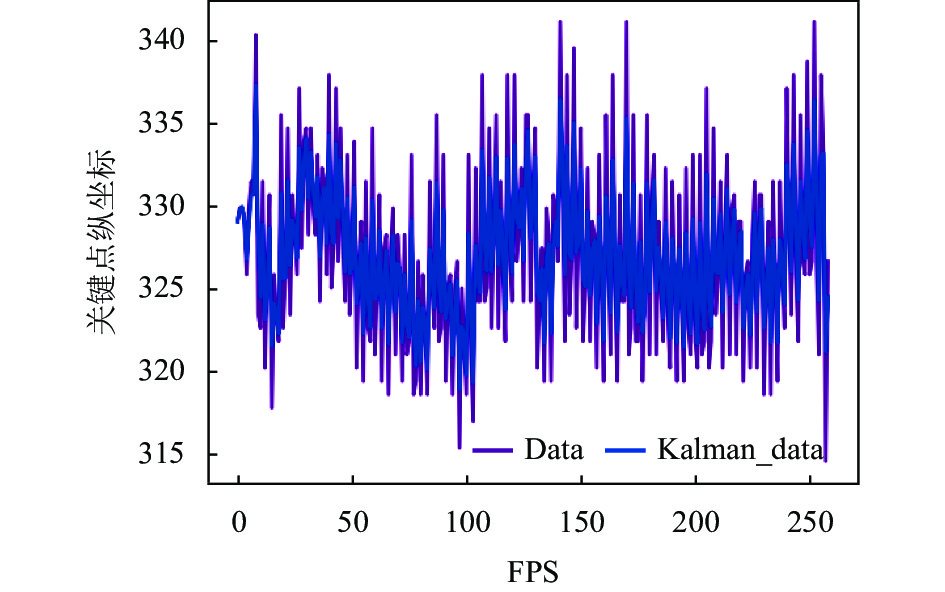
3.4 跳绳计数实验结果本文在互联网上收集了40个多种场景下的跳绳视频和10个一分钟速跳比赛的跳绳视频来对卡尔曼滤波的影响进行了消融实验以及对本文算法的性能进行一个评估, 实验结果如表2所示. 当不存在比赛级快速跳绳视频时, 且误差为0的时候增加卡尔曼滤波使算法的正确率提高了30个百分点, 并且随着误差范围的增大, 增加了卡尔曼滤波的算法正确率也同样比原始算法要高出很多, 特别是在误差为5的时候加了卡尔曼滤波的算法正确率高达95%比原始算法提高了27.5个百分点, 同时本节将其中一个视频关键点(5、6、11、12四点中值) Y值随时间的变化以及卡尔曼滤波之后的结果进行了可视化得到图8, 由图可以看出在经过卡尔曼滤波之后, 关键点坐标整体的浮动阈值变小了, 方差变小了, 其预测的坐标就更稳定, 由于模型性能导致的关键点坐标波动范围也会缩小, 并且通过滤波可以滤除一些模型预测错误的异常值坐标, 从而减小误差, 所以说明通过卡尔曼滤波进行平滑降噪、过滤极端异常值对跳绳计数是有效的.
|
图 7 模型可实时性对比图 |
| 表 2 卡尔曼滤波前后算法正确率对比结果 |
|
图 8 卡尔曼滤波前后的关键点坐标变化对比图 |
在计数实验中我们发现加入10个一分钟速跳比赛视频后, 无论采用原始算法还是本文算法, 正确率都有一定程度的下降. 这是因为一分钟速跳比赛的运动员在跳绳时, 为了达到更快的速度, 会尽可能让身体不发生大幅度跳跃, 导致人体关键点坐标变化非常小, 极大程度增大了关键点坐标的抖动. 同时, 受关键点检测模型性能影响, 预测的坐标精度并不高, 因此通过坐标变化计数这种快速跳绳比赛会产生较大误差.
同时为了检测算法的性能, 本文在不同环境下进行了实验, 包括室内和室外、亮度高和低以及背景复杂等情况. 实验结果如表3所示, 在较亮的室内环境下, 算法表现出完美的检测结果, 误差率为0, 但在亮度较低或背景比较复杂(多人场景)的情况下, 会出现一些误差. 然而在室内平均误差仍然较低, 仅为1.00%. 在室外环境下, 由于受背景噪声的干扰人体关键点检测的精度受到影响, 因此误差相对于室内有所增加. 特别是在有多人的复杂背景下, 误差率可达4%, 但室外平均误差仍仅为2.67%, 图9展示了6种场景下模型关节点检测的可视化结果, 发现在复杂情况下会存在漏检或者多检, 同时在亮度较低的场景下也会存在部分关节点检测不准确的情况. 但是实验结果显示, 本文算法无论在室内还是室外的环境下, 都表现出较好的性能, 误差率非常低. 特别是在室内环境下的检测中, 平均误差率仅为1%, 因此本文提出的基于改良轻量级人体姿态估计网络的跳绳计数算法是可行的.
| 表 3 不同场景下本文算法误差率的检测结果 |

|
图 9 不同场景下部分可视化结果 |
4 结论与展望
为了进一步推进轻量级人体姿态估计在边缘设备上的应用, 本文针对AI跳绳领域准确性不高的问题提出了一种基于轻量级人体姿态估计网络的跳绳计数算法. 通过对高效的轻量级人体姿态估计网络LitePose的解码方法进行改进, 使用了基于自适应感知解码方法的方案, 该方法利用了自身热图分布信息来推断最大激活点位置, 替代了传统手工补偿解码方法. 在不增加模型复杂度的情况下, 进一步提高了算法的检测精度, 并利用人体姿态数据构建跳绳计数算法, 能够在低计算量、低成本的边缘设备上实现了快速部署. 实验结果表明, 改进后的姿态估计模型无论是模型复杂度还是精度均优于其他自底而上的模型, 并且通过该模型构建的计数算法误差非常低, 能够通过在线视频快速准确地为人体跳绳进行计数, 其具有一定的落地应用价值, 比如健身和运动监测上通过计算和监测跳绳的次数, 可以实时评估运动质量、消耗的热量和达成的目标; 又或者运动教育和培训领域、通过该技术来监控学生或运动员的动作, 提供反馈和改进建议; 再或者可以与虚拟现实(VR)或增强现实(AR)结合, 创建与跳绳相关的互动游戏或应用程序, 人们可以在家中或健身中心使用这些应用程序进行有趣的跳绳训练, 并与其他用户进行竞争和交流.
经过可视化分析分析可以看出, 本文算法存在的一定问题: 一是在光线分布不均匀、背景偏暗或者包含多人场景的时候, 会出现关键点检测模型检测效果不理想的情况, 导致计数出现误差; 二是在一分钟快速跳绳比赛上面, 由于人体动作幅度太小, 导致无法进行精确计数. 但是本文算法仍有改进空间, 如何提高关键点检测精度, 以及进行多人实时检测将是下一阶段的主要研究方向.
| [1] |
刘圣杰, 何宁, 王程, 等. 2D人体姿态估计研究进展. 中国计算机用户协会网络应用分会2021年第25届网络新技术与应用年会论文集. 北京: 北京联合大学北京市信息服务工程重点实验室, 2021. 255–258.
|
| [2] |
李睿敏. 基于视觉数据的人体动作精细分类及评估方法研究[博士学位论文]. 西安: 中国科学院大学(中国科学院西安光学精密机械研究所), 2020.
|
| [3] |
Chen YC, Tian YL, He MY. Monocular human pose estimation: A survey of deep learning-based methods. Computer Vision and Image Understanding, 2020, 192: 102897. DOI:10.1016/j.cviu.2019.102897 |
| [4] |
Toshev A, Szegedy C. DeepPose: Human pose estimation via deep neural networks. Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 1653–1660.
|
| [5] |
Tompson J, Jain A, LeCun Y, et al. Joint training of a convolutional network and a graphical model for human pose estimation. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 1799–1807.
|
| [6] |
Newell A, Yang KY, Deng J. Stacked hourglass networks for human pose estimation. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 483–499.
|
| [7] |
Sun K, Xiao B, Liu D, et al. Deep high-resolution representation learning for human pose estimation. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 5686–5696.
|
| [8] |
Cheng BW, Xiao B, Wang JD, et al. HigherHRNet: Scale-aware representation learning for bottom-up human pose estimation. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 5385–5394.
|
| [9] |
葛道辉, 李洪升, 张亮, 等. 轻量级神经网络架构综述. 软件学报, 2020, 31(9): 2625-2653. DOI:10.13328/j.cnki.jos.005942 |
| [10] |
Neff C, Sheth A, Furgurson S, et al. EfficientHRNet: Efficient scaling for lightweight high-resolution multi-person pose estimation. arXiv:2007.08090, 2020.
|
| [11] |
Zhang F, Zhu XT, Ye M. Fast human pose estimation. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3512–3521.
|
| [12] |
Cao Z, Simon T, Wei SE, et al. Realtime multi-person 2D pose estimation using part affinity fields. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 1302–1310.
|
| [13] |
常丰田, 陈文超, 马勋举, 等. 双绳联动跳绳机的结构与功能设计. 机电技术, 2013, 36(4): 57-59. |
| [14] |
郭艺璇, 唐玉儒, 王慧, 等. 浅谈一种自发电跳绳. 科技创新与应用, 2014(33): 46. |
| [15] |
杨颂, 叶明超, 王若飞. 增量式旋转编码器零脉冲信号在电子计数装置中的应用. 数字技术与应用, 2012(8): 60-61. |
| [16] |
王振亚, 曾黄麟. 一种基于帧间差分和光流技术结合的运动车辆检测和跟踪新算法. 计算机应用与软件, 2012, 29(5): 117-120, 129. |
| [17] |
连仁明, 刘颖, 于萍, 等. 基于视频的人体姿态检测方法及其应用综述. 电脑编程技巧与维护, 2019(9): 127-129. |
| [18] |
Wang YH, Li MY, Cai H, et al. Lite pose: Efficient architecture design for 2D human pose estimation. Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New Orleans: IEEE, 2022. 13116–13126.
|
| [19] |
Sandler M, Howard A, Zhu ML, et al. MobileNetV2: Inverted residuals and linear bottlenecks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 4510–4520.
|
| [20] |
Xiao B, Wu HP, Wei YC. Simple baselines for human pose estimation and tracking. Proceedings of the 15th European Conference on Computer Vision. Munich: Springer, 2018. 472–487.
|
| [21] |
Kalman RE. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 1960, 82(1): 35-45. DOI:10.1115/1.3662552 |
 2023, Vol. 32
2023, Vol. 32


