群智能优化算法是一种新兴的演化技术, 该类算法基于模拟自然界生物的寻路行为从而总结出一定规律, 针对相应的生物寻路规律进行归纳总结建立数学模型. 目前群智能优化算法已经被许多学者研究关注, 如模拟了北美郊狼的社会组织结构的郊狼优化算法(coyote optimization algorithm, COA)^[1]、基于自然界鲸鱼群体行为的鲸鱼优化算法(whale optimization algorithm, WOA)^[2,3]、模拟了自然界中灰狼的种群等级和捕食机制的灰狼优化算法(grey wolf optimizer, GWO)^[4,5]、基于自然界授粉飞虫或蜜蜂采蜜行为的花授粉算法(flower pollination algorithm, FPA)^[6,7]、模拟乌鸦外出觅食的乌鸦搜索算法(crow search algorithm, CSA)^[8–10]、基于布谷鸟的寄生性育雏行为的布谷鸟搜索算法(cuckoo search, CS)^[11,12]和模拟麻雀种群躲避天敌并进行觅食的麻雀搜索算法(sparrow search algorithm, SSA)^[13]等. 麻雀搜索算法在2020年被Xue等人^[13]提出, 目前已经被广泛应用于许多领域. 例如张月栋等人^[14]将SSA算法应用于旅行商问题, 张姝等人^[15]将SSA算法用于路径规划问题的求解等. 旅行商是经典的优化问题之一, 即在所有的城市只有一位业务员, 每个城市只能到访一次且要走遍所有城市的情况下, 该业务员该如何规划城市到访的顺序. SSA算法的优点是易于实现, 并且可以在较短时间内找到较优解.

SSA算法因易于实现、速度快等特点吸引了不少研究学者, 但SSA算法仍存在难以找到最优解、搜索依赖精英种群、因自身特性易陷入局部最优等问题, 目前已有许多学者针对此类问题提出了解决方案, 如将SSA算法与其他算法缝合^[16]、加入扰动机制^[17]等, 本文在这些方法的基础上进行改进并应用于旅行商问题检验算法的性能.

本文针对以上问题提出改进型的麻雀搜索算法(improved sparrow search algorithm, ISSA), ISSA针对跟随者提出了正态偏移策略增强其勘探能力, 引入动态正弦扰动策略实现发现者对搜索步长和收敛速度的双向需求、加入反向学习机制帮助算法跳出局部最优. 为验证算法的有效性, 随机选取了6个标准测试函数进行测试.

1 麻雀搜索算法(SSA)

在SSA算法中, 麻雀种群分3个子群, 分别为发现者、跟随者和随机产生一定数量的警戒者. 其中带领种群移动的被称为发现者, 发现者的位置更新公式如下:

$x_{i, j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {x_{i, j}^t \cdot \exp \left( - \dfrac{i}{{\alpha \cdot iter}}\right){\text{ }},\;R2 < {\textit{ST}}} \\ {x_{i, j}^t + Q \cdot L{\text{ }},\qquad\quad \;\;\;R2 \geqslant {\textit{ST}}} \end{array}} \right.$

(1)

式(1)中, $i$ 为麻雀的序号, $i = 1, 2, \cdots, n$ ; $j$ 代表纬度, $j = 1, 2, \cdots, D$ ; $t$ 表示当前迭代到第 $t$ 次; $iter$ 为算法设定的最大迭代次数; $\alpha \in \left( {0, 1} \right]$ , 表示一个从范围中随机选取的随机数; $R2 \in \left[ {0, 1} \right]$ 代表预警值; ${\textit{ST}} \in \left[ {0.5, 1} \right]$ 代表安全值, 安全值和预警值共同组成发现者的移动条件; $Q$ 是正态分布随机数; L表示一个 $1 \times D$ 的矩阵; 当 $R2 < {\textit{ST}}$ 时, 此时较为安全, 发现者会积极扩大搜索范围搜索食物; 当 $R2 \geqslant {\textit{ST}}$ 时, 说明种群位置较差, 周围存在危险, 应当离开当前位置.

跟随者监视发现者移动并争抢位置, 当跟随者争抢位置失败时, 跟随者会飞行至其他位置, 其更新公式如下:

$x_{i, j}^{t + 1} = \left\{ {\begin{array}{*{20}{l}} {Q \cdot \exp \left(\dfrac{{{x_{{\rm{worst}}}} - x_{i, j}^t}}{{{i^2}}}\right){\text{ }},\quad\;\; i > \dfrac{n}{2}} \\ {x_p^{t + 1} + \left| {x_{i, j}^t - x_p^{t + 1}} \right| \cdot {A^ + } \cdot L{\text{ }},\;{\rm{other}}} \end{array}} \right.$

(2)

式(2)中, ${x_{{\rm{worst}}}}$ 为算法搜索范围中适应度值最差的位置; ${x_p}$ 是当前发现者已经探明的最优位置; $A$ 是 $1 \times D$ 的矩阵, 矩阵中元素的值将从1或 –1中随机选取; ${A^ + } = {A^{\rm{T}}}{(A{A^{\rm{T}}})^{ - 1}}$ ; $n$ 为设定的跟随着数量; 当 $i > n/2$ 时, 表示跟随者比较饥饿没有获得食物, 需要到其他位置获得食物提高适应度值; 当 $i \leqslant n/2$ 时, 表示跟随者获得食物. $n$ 为种群数量减去发现者和警戒者的数量, 当发现者和警戒者占种群数量分别为20%和10%时, 依据式(2), 跟随者中的65%会上前争抢食物, 剩下的35%则会继续向其他位置飞行觅食.

警戒者负责侦查预警, 提前告知危险, 所占比例为麻雀种群的10%或20%, 其位置更新公式如下:

$x_{i, j}^{t + 1} = \left\{ {\begin{array}{*{20}{c}} {x_{{\rm{best}}}^t + \beta \cdot \left| {x_{i, j}^t - x_{{\rm{best}}}^t} \right|{\text{ }},\;\;\;\;\;{f_i} > {f_g}} \\ {x_{i, j}^t + k \cdot \left( {\dfrac{{\left| {x_{i, j}^t - x_{{\rm{worst}}}^t} \right|}}{{{f_i} - {f_w} + \varepsilon }}} \right){\text{ }},\;{f_i} = {f_g}} \end{array}} \right.$

(3)

式(3)中 ${x_{{\rm{best}}}}$ 表示当前全局最优位置; $\; \beta$ 为标准正态分布随机数; $k$ 是 $\left[ { - 1, 1} \right]$ 内的一个随机数; ${f_i}$ 表示当前麻雀个体的适应度值; ${f_g}$ 为全局最优位置的适应度值; ${f_w}$ 为全局最差位置的适应度值; 最小参数 $\varepsilon$ 用于避免分母为0; 当 ${f_i} > {f_g}$ 时, 麻雀容易受天敌攻击, 当 ${f_i} = {f_g}$ , 麻雀意识到危险向其他麻雀靠近.

SSA算法对比其他优化算法虽然有不小优势, 但仍存在一些问题如最优解的搜索依赖于发现者、容易陷入局部最优等. SSA算法中跟随者和警戒者占群体的多数但寻优能力较弱, 因此SSA算法存在较大的改进空间.

2 改进型麻雀搜索算法(ISSA) 2.1 正态偏移策略

SSA算法搜索精度高度依赖于发现者的探索, 其余群体因初始位置较差在移动时难以得到较理想的效果. 本文借鉴重心偏移^[18]提出正态偏移策略优化种群, 非领导个体可以通过向重心位置偏移, 从而使群体在逐次迭代中逐渐偏向当前最优解. 使用公式如下:

$x{_{i, j}^{t{\prime}} } = x_{i, j}^t + \alpha \cdot \delta \cdot f\left( x \right)$

(4)

$\alpha = \frac{{\displaystyle\sum {_{i = 1}^n{x_{ij}}} }}{n} - {x_i},\;{\text{ }}j = 1, 2, \cdots, D$

(5)

$f\left( x \right) = \frac{1}{{\sigma \sqrt {2{\text π} } }}{{\rm{e}}^{ - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}}},\;{\text{ }}x \in \left( {0, iter} \right)$

(6)

其中, $x{_{i, j}^{t{\prime}} }$ 为重心偏移点, $\alpha$ 为同一麻雀不同维度均值与当前麻雀位置值的差, $\delta$ 为随机取值为 $\left( {0, 1} \right)$ 的 $1 \times D$ 矩阵, $f\left( x \right)$ 为标准的正态分布函数, 即 $\sigma = 1$ , $\mu = 0$ , 其中 $iter$ 为最大迭代次数, t表示当前迭代到第t次. 本策略为在每次迭代中以当前种群位置的重心进行正态偏移进而使种群逐渐向目标解移动, 同时正态偏移受缩放因子思想的启发, 其函数值从标准正态分布中按序取值, 在前期保证了拥有较强的开发能力, 在中期其函数值快速下降并后期趋近于0时保证了搜索不会跳过最优解, 本策略对于局部搜索类问题拥有较强的可行性和通用性.

2.2 动态正弦扰动策略

影响SSA算法性能的原因之一是发现者群体在面对全局搜索和局部搜索问题时难以双向平衡. 麻雀种群中发现者引领着种群, 发现者的勘探能力强弱将对算法的优化结果起到决定性的作用, 如果发现者移动范围较小将影响全局探索能力, 同时如果发现者的步长过大将容易错过全局最优解. 因此本文引入动态正弦扰动策略^[19]改进发现者的位置更新公式, 发现者可以遍历正弦函数上所有的点即整个单位圆, 将对空间的搜索问题转化为对圆的搜索. 同时在搜索过程中引入黄金分割系数, 实现发现者的搜索步长更加灵活, 使前期全局搜索和后期局部搜索的需求得到平衡, 使用公式如下:

$\begin{split} x_{i, j}^{t + 1} =& x_{i, j}^t \cdot \left| {\sin \left( {{r_1}} \right)} \right| + {r_2} \cdot \sin \left( {{r_1}} \right) \cdot \left| {\omega \cdot {x_1} \cdot {x_{{\rm{best}}}} - {x_2} \cdot x_{i, j}^t} \right| \end{split}$

(7)

${x_1} = \left( { - {\text π} } \right) + 2{\text π} \left(\frac{{3 - \sqrt 5 }}{2}\right)$

(8)

${x_2} = \left( { - {\text π} } \right) + {\text π} \left( {\sqrt 5 - 1} \right)$

(9)

$\omega = \frac{{\sin \left( {\dfrac{{i \cdot {\text π} }}{M}} \right)}}{2}$

(10)

其中, ${x_1}$ 、 ${x_2}$ 为参数, 随机数 $r{}_1$ 取值范围为 $\left[ {0, 2{\text π} } \right]$ , 随机数 $r{}_2$ 的取值范围为 $\left[ {0, {\text π} } \right]$ , $\omega$ 为缩放因子, ${P_{{\rm{best}}}}$ 为当前迭代中所得到的最好位置, $\left( {\sqrt 5 - 1} \right)/2$ 为黄金分割系数, $\sqrt 5 - 1$ 和 $\left(3 - \sqrt 5 \right)/2$ 分别为为适应不同阶段下麻雀种群中搜索者的任务而基于黄金分割系数引入的新系数.

2.3 反向学习机制

SSA算法中预警者因自身往往处于较差位置, 在躲避天敌时往往难以得到理想效果, 因此本算法针对此问题加入反向学习机制^[20], 预警者躲避天敌时将进行反向移动, 改进后预警者易于跳出局部最优解, 增强了搜索全局最优的能力. 其中判断条件以式(3)中 ${f_i}$ 和 ${f_g}$ 来确定. 式(3)中当 ${f_i} > {f_g}$ 时, 更新公式由于自身位置的局限性, 并不能较好完成预警的任务, 因此本文提出反向学习机制, 引入反向学习的思想替换式(3), 替换后更新公式如下:

$x{_{i, j}^{t{\prime \prime }}} = ub + lb - {r_3} \cdot x_{i, j}^t,\; {f_i} > {f_g}$

(11)

其中, $ub$ 和 $lb$ 分别为当前测试函数的上限和下限, ${r_3}$ 为区间为 $[0, 1]$ 的随机数, 在替换后依据式(10)预警者在躲避天敌攻击时拥有更广阔的移动范围并具有跳出局部最优的能力.

2.4 ISSA算法实现流程及描述

ISSA算法的具体实现流程如下.

1)初始化麻雀种群及相关参数.

2)计算各个麻雀的适应度值, 选出麻雀种群中的发现者, 其余为跟随者, 警戒者每次迭代中随机产生.

3)发现者根据式(7)移动, 跟随者根据式(2)跟随发现者移动.

4)预警者判断是否需要反向学习, 是则依据改进式(11)移动, 否则根据式(3)在附近移动.

5)麻雀种群依据式(4)进行正态偏移.

6)在当次迭代完成之后, 更新麻雀个体的适应度值和其他参数.

6)判断是否达到最大迭代次数, 是则跳出循环, 否则继续迭代返回步骤 3).

7)结束.

ISSA算法对比其他算法的不同在于ISSA提出正态偏移策略, 该策略有效调用了所有个体的位置进行偏移, 实现最优解的搜索. 移动能量按标准正态分布衰减有效保证前期算法的搜寻动力和后期快速收敛的需求. 并且ISSA算法引入了动态正弦扰动策略和反向学习机制, 有效提升了算法搜索最优解和跳出局部最优的能力.

3 实验仿真 3.1 测试函数

ISSA算法所采用的测试函数均从标准的23个benchmark测试函数中随机选取, 具体见表1.

表1中 ${f_1} - {f_5}$ 为单峰函数, ${f_6}$ 为多峰函数, 单峰函数一般用于测试算法的开发能力, 多峰函数一般用于测试算法的勘探能力.

3.2 仿真参数设置

本文选取WOA算法^[2]、GWO算法^[4]和SSA算法. 为公平起见, 所有算法种群数目设为30, 最大迭代次数设为500, 维度设为30, 其中麻雀种群中发现者在比例为20%, 警戒者为10%. 仿真实验在Matlab 2021B仿真平台下运行, 每种算独立运行50次, 其中为了减少随机性对实验的影响, 实验结果分别记录了平均值和方差, 如表2所示.

3.3 数据分析

通过实验可见在f₁–f₅单峰函数和 ${f_6}$ 多峰函数中ISSA算法的均值、最优解、最劣解和方差都明显优于GWO算法、SSA算法和WOA算法. 其中 ${f_1}$ 、 ${f_3}$ 函数的理论最优值为0, 而 ${f_6}$ 函数的理论最优值为–12 569.5. 由表2可知ISSA算法在 ${f_1}$ 和 ${f_3}$ 函数中均达到了理论最优值, 相对于SSA算法优化明显, 说明在增加了正态偏移和动态正弦扰动策略增强其局部搜索能力后, ISSA算法的搜索精度有了显著提升. ${f_6}$ 函数为多峰函数, 函数中有多个局部最优解, SSA算法中最优解未能逼近理论最优解, 陷入了局部最优中, 而ISSA算法均优化至理论最优解说明在增加了反向学习策略后, ISSA算法的逃逸局部最优能力有了显著提升. 而在 ${f_2}$ 和 ${f_4}$ 函数中, ISSA算法虽没有优化至理论最优解, 但最劣解仍然远优于其他算法的最优解. 而在 ${f_5}$ 函数中, ISSA算法优化效果虽没有其他测试函数显著, 但均值和最优解仍然优于其他算法.

实验证明ISSA算法的寻找全局最优值较强, 方差也趋于均值证明ISSA算法优化的稳定性. 由此可见ISSA算法的收敛精度优于其他算法.

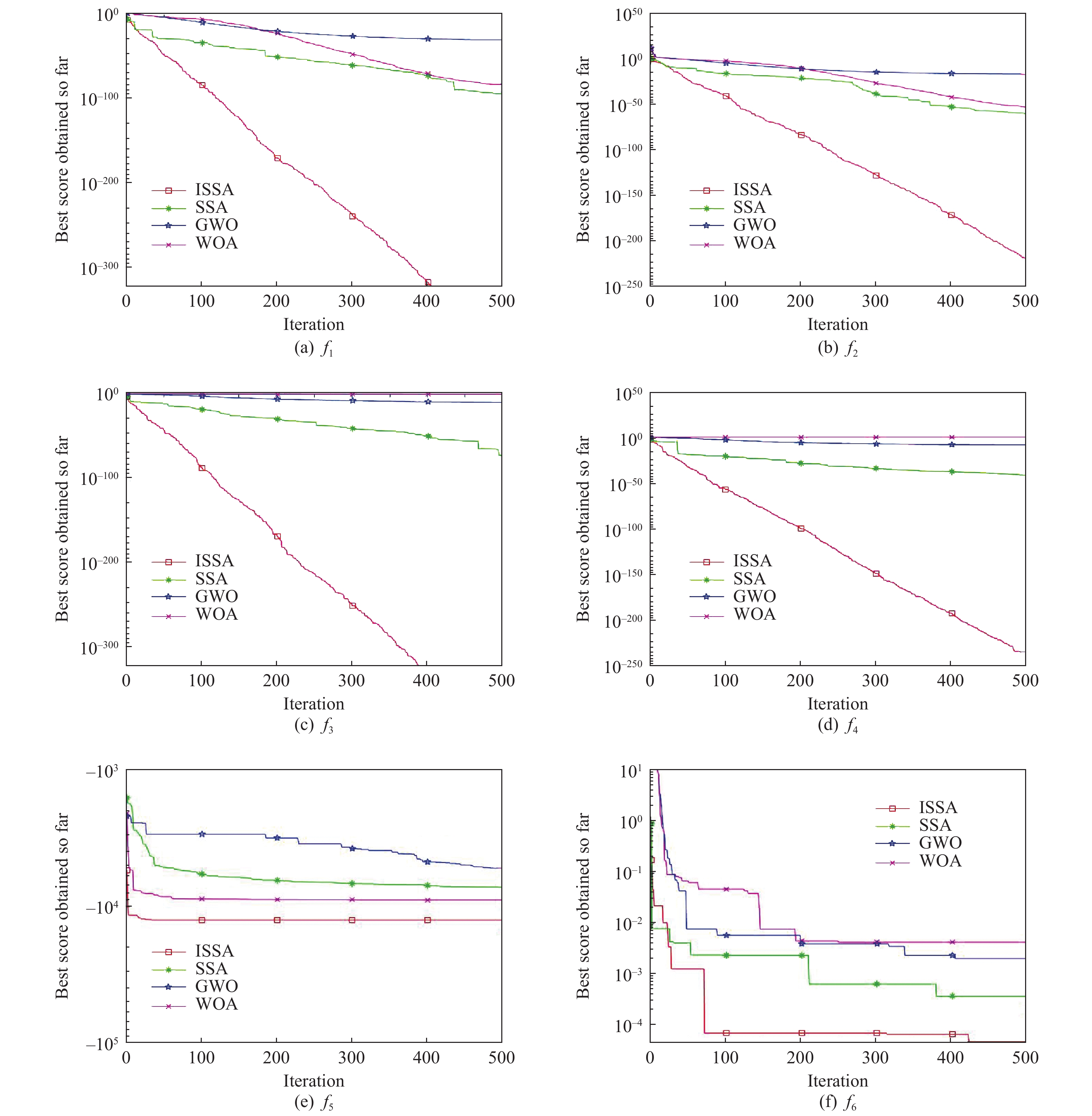
其次为直观显示ISSA算法的优越性, 本文绘制了测试函数的函数收敛曲线图, 将ISSA算法与SSA算法、WOA算法、GWO算法作对比实验, 结果如图1所示, 明显可以看出ISSA算法相对于其他算法收敛效果显著.

f₁–f₅均为单峰多维函数, 多用于评价算法的收敛能力. 其中 ${f_1}$ 、 ${f_2}$ 和 ${f_4}$ 由图1可以明显发现在收敛前期, 在从0迭代到100次的过程中ISSA算法收敛比SSA算法更快更稳定, 而到搜索后期, SSA算法搜索能力近乎停滞, 收敛曲线趋于平稳, 而ISSA算法的收敛曲线仍然陡峭, 由此证明ISSA算法在增加了正态偏移和动态正弦扰动策略后, 收敛效果提升较大, 局部开发能力比SSA算法更强. 在 ${f_3}$ 和 ${f_5}$ 中, 可以明显发现, ISSA算法在迭代到第50次的过程中收敛已明显优于其他算法并且在搜索后期保持明显优势, 说明ISSA算法的全局搜索能力在加入动态正弦扰动策略后已明显优于SSA算法. ${f_6}$ 为高维多峰函数, 有多个局部峰值用于测试算法对于复杂问题的能力, 结合收敛曲线和实验数据可知, 在 ${f_6}$ 函数中, 面对测试函数中多个局部最优解, ISSA算法在前50次迭代中已远超其他函数, 说明ISSA算法在增加了反向学习机制后, 对于高维复杂问题时寻优精度更高、收敛更快.

综上所述, ISSA算法相较于其他算法, 在单峰和多峰测试函数上表现出更好的收敛精度, 在收敛速度上比其他算法收敛更快, 具有明显的优势.

3.4 旅行商问题

建立城市数为51的模型, 并应用SSA算法和ISSA算法进行实验, 迭代次数为1000次, 麻雀数量为500, 实验次数为10次.

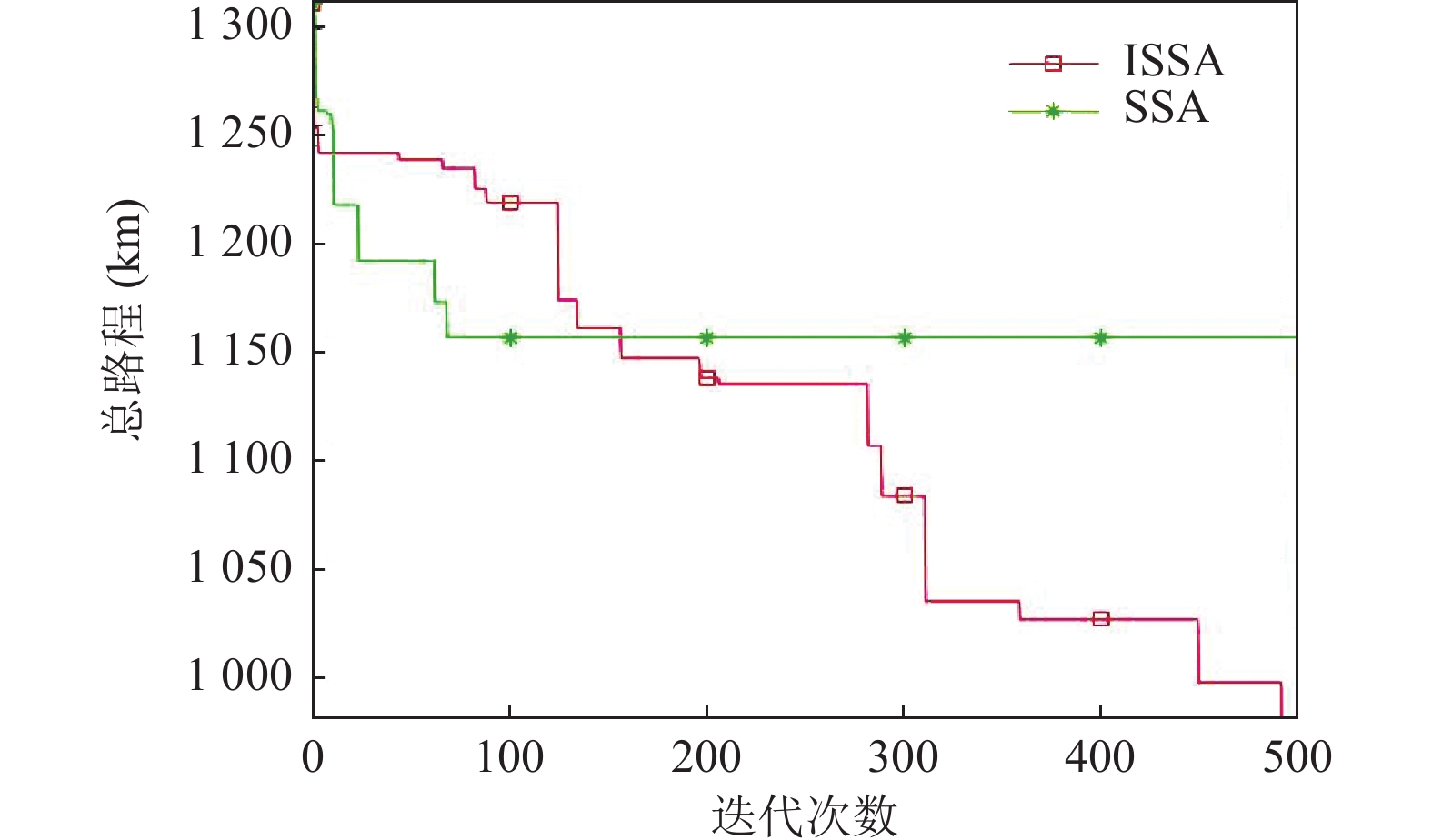
实验结果如图2所示, 可以发现ISSA算法虽然在初期寻得的总路程的质量不如SSA算法, 但是在收敛中期时, SSA算法已经结束了收敛, 但ISSA算法仍能有效寻得更优的路径. 实验有效证明了ISSA算法对比于SSA算法能有效提升性能, 对于实际应用问题有较强的解决能力.

4 结论与展望

SSA算法存在求解精度依赖于发现者, 容易陷入局部最优等缺点, 本文针对以上问题提出了ISSA算法, 通过正态偏移策略增强算法局部探索的能力; 引入动态正弦扰动改进发现者的位置更新公式, 提升发现者对种群的引领作用; 使用反向学习机制, 帮助算法跳出局部最优. 通过实验证明了ISSA算法能有效弥补SSA算法的不足, 具有更好的寻优性能. 接下来的研究工作是探索算法在求解无人机路径规划等工程问题中的应用, 以及建构多目标ISSA优化算法.